A Key Pre-Distribution Scheme Based on µ-PBIBD for Enhancing Resilience in Wireless Sensor Networks
Abstract
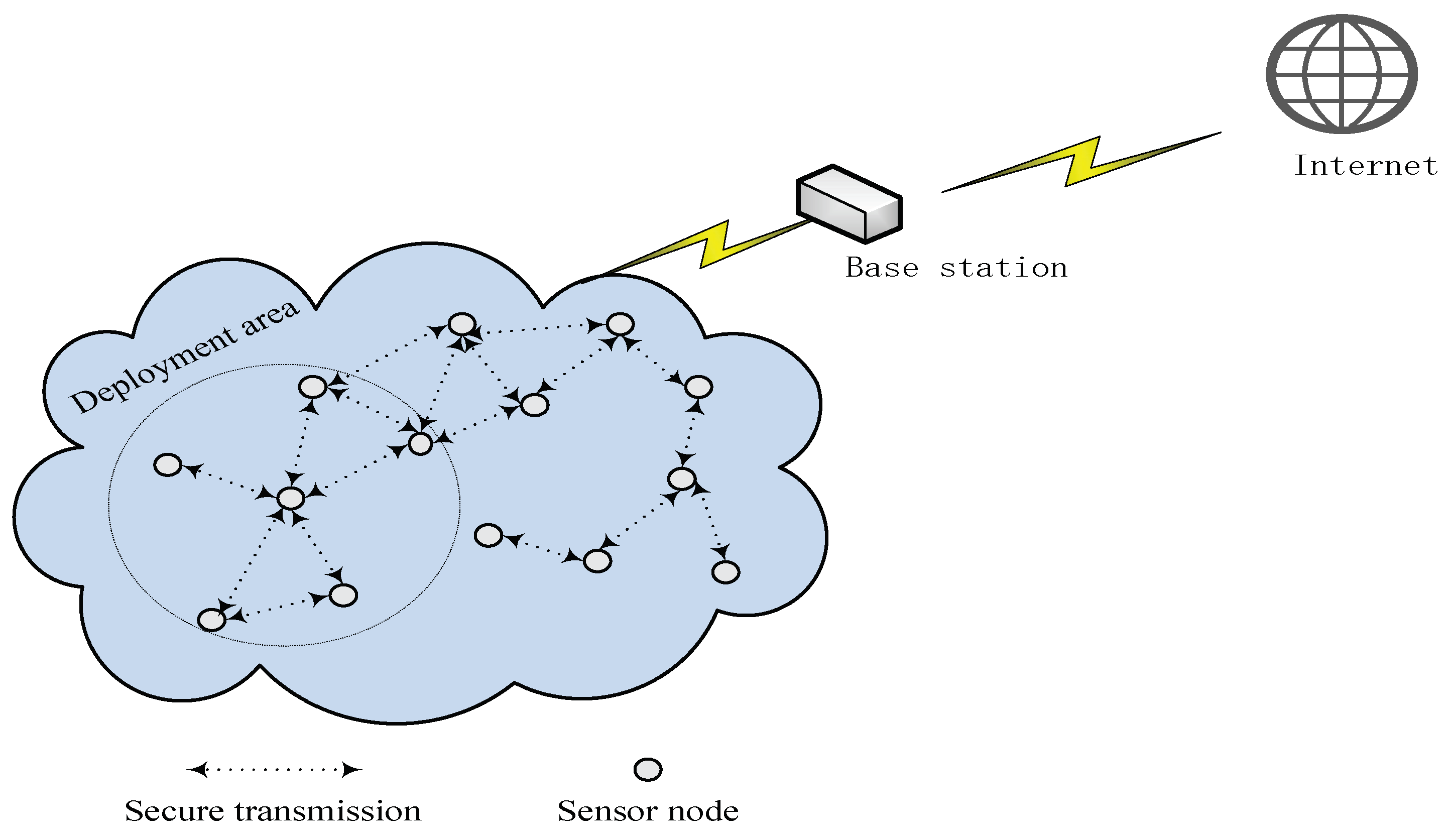
:1. Introduction
- A new combinatorial design (µ-PBIBD) is defined based on partially symmetric balanced incomplete block design.
- A µ-PBIBD is constructed in 2-D space, and a key pre-distribution scheme based on 2-D µ-PBIBD is proposed in which blocks are mapped to key rings. That is, shared-keys between nodes can be generated from common points between corresponding blocks. As a result, key connectivity of the proposed scheme depends on the construction of µ-PBIBD.
- To enhance network resilience of 2-D µ-PBIBD scheme, an Ex-µ-PBIBD is constructed by extending µ-PBIBD from 2-D space to 3-D space. Further, a key pre-distribution scheme based on 3-D Ex-µ-PBIBD is presented.
- Performance metrics of the proposed schemes are evaluated by theoretical analyses. Comparing with sBIBD scheme, RD and TD scheme, the results show that the proposed scheme has better scalability and higher resilience.
2. Related Works
3. Preliminaries
3.1. Combinatorial Design
- (1)
- Uniformity: Each block in B contains exactly k distinct points.
- (2)
- Regularity: Each point of V exists in exactly r different blocks of B.
- (3)
- Balance: Each pair of points of V exists in exactly blocks of B.
- (1)
- , for every and every .
- (2)
- Every two points from different groups occurs in exactly λ blocks of B.
{2, 4, 8, 12}, {2, 5, 9, 10}, {2, 6, 7, 11},
{3, 4, 9, 11}, {3, 5, 7, 12}, {3, 6, 8, 10}}.
3.2. µ-Partially Balanced Incomplete Block Design
- (1)
- Uniformity: Each block in B contains exactly k distinct points.
- (2)
- Regularity: Each point of V exists in exactly r different blocks of B.
- (3)
- Partial Balance: Each pair of points of V exists in different numbers of blocks of B.
- (1)
- (V, B) is regular, i.e., each point of V appears in exactly r different blocks of B.
- (2)
- (V, B) is uniform, i.e., the number of points in every block is k.
- (3)
- (V, B) is partial balance, i.e., every pair of points appears in blocks, for .
4. Key Pre-Distribution Based on µ-sPBIBD
4.1. A Construction of 2-D µ-sPBIBD
4.2. 2-D µ-sPBIBD Based KDP Scheme
4.2.1. Key Pre-Distribution Phase
4.2.2. Shared-Key Discovery Phase
4.3. 3-D Ex-µ-sPBIBD Based KPD Scheme
5. Theoretical Analysis
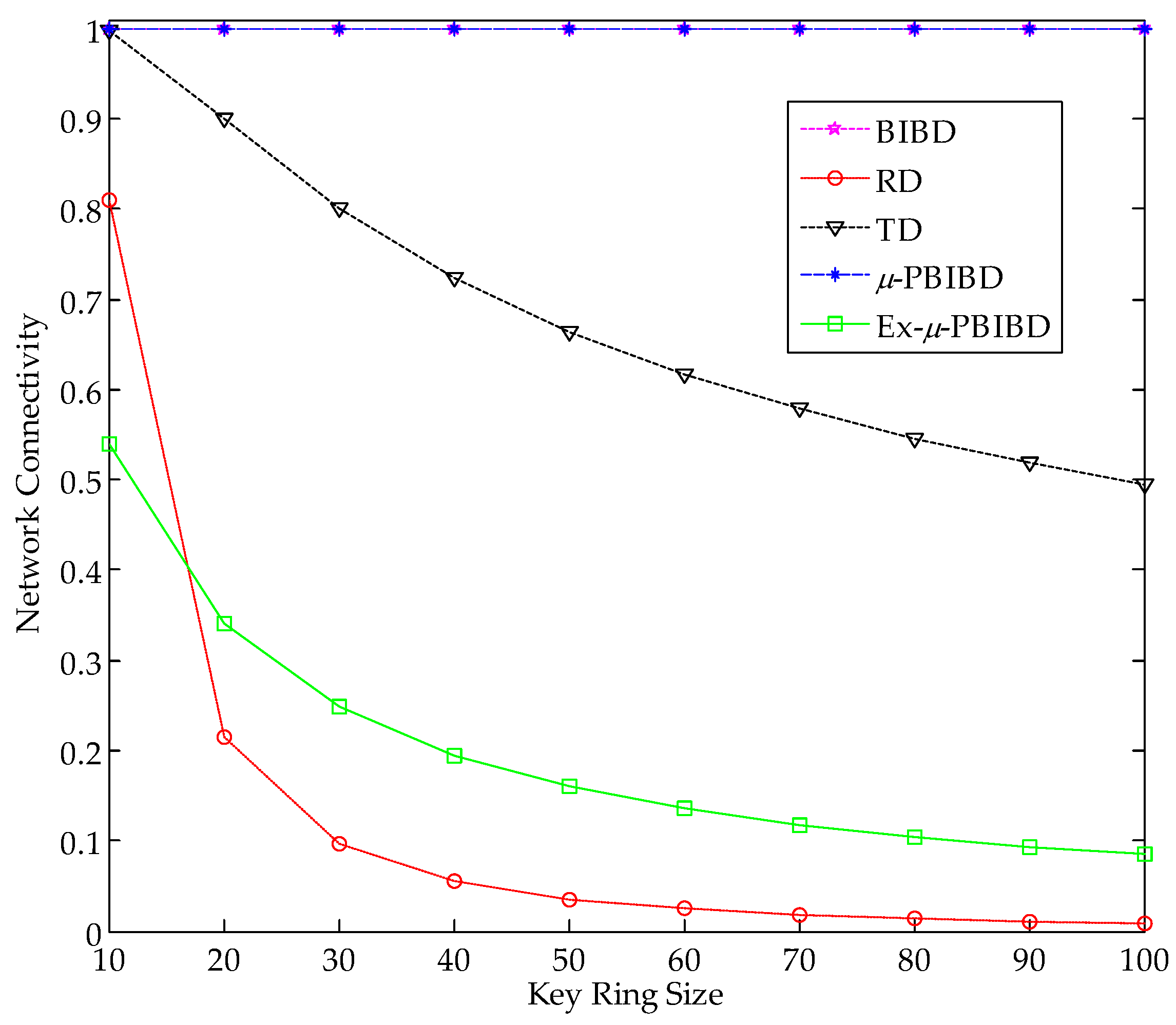
5.1. Key Connectivity
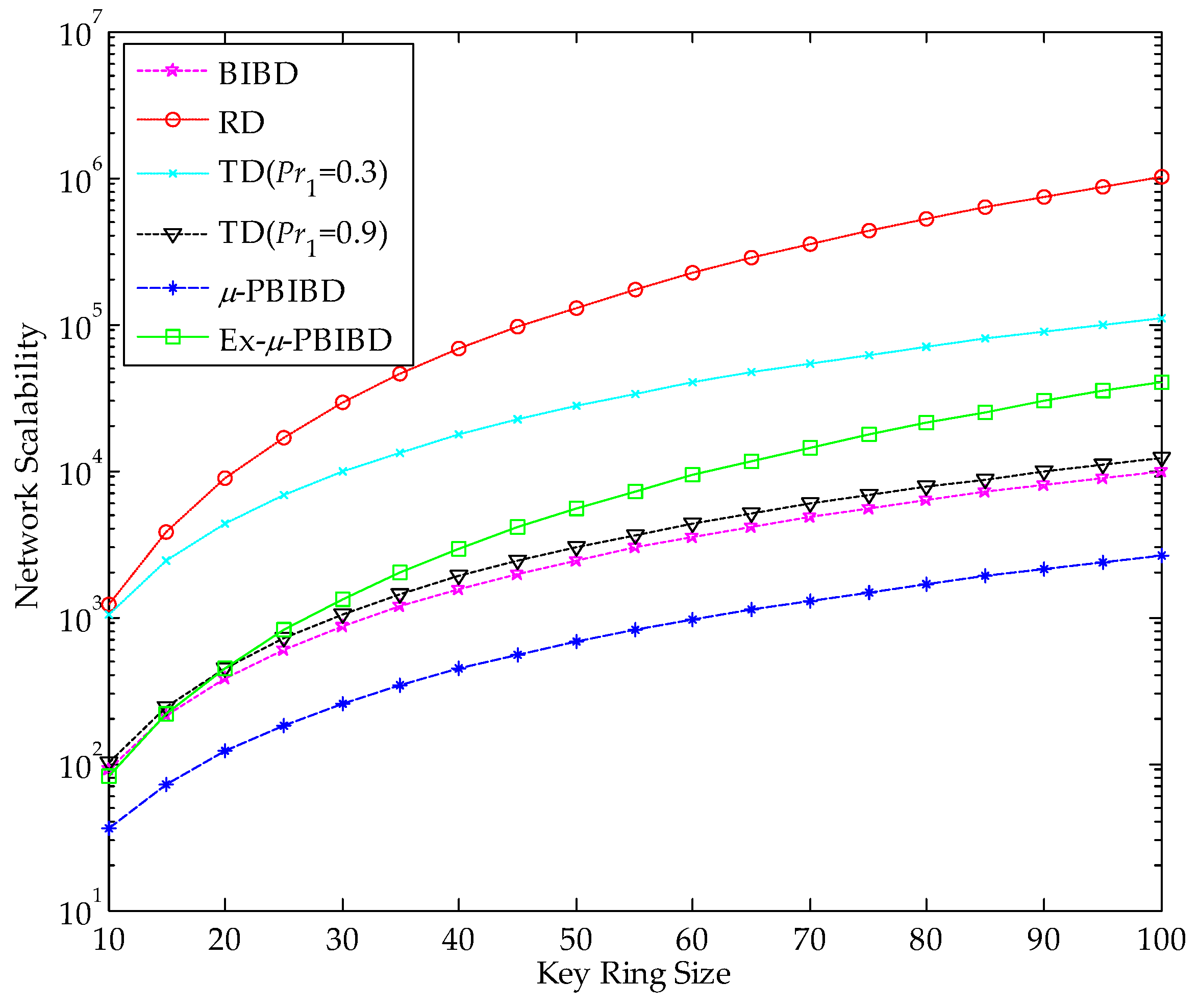
5.2. Network Scalability
5.3. Network Resilience
5.3.1. Resilience of 2-D µ-sPBIBD
- (1)
- In x captured nodes, there are at last two nodes, such as N3 and N4, that the corresponding blocks have the same row (or column) subscript as the blocks in N1 and N2.
- (2)
- In x captured nodes, there are one node, such as N3, that the corresponding block has the same row (or column) subscript as the blocks in N1 and N2, and then another node, such as N5, must be the node that corresponding block has the same column (or row) subscript as block in N3.
- (3)
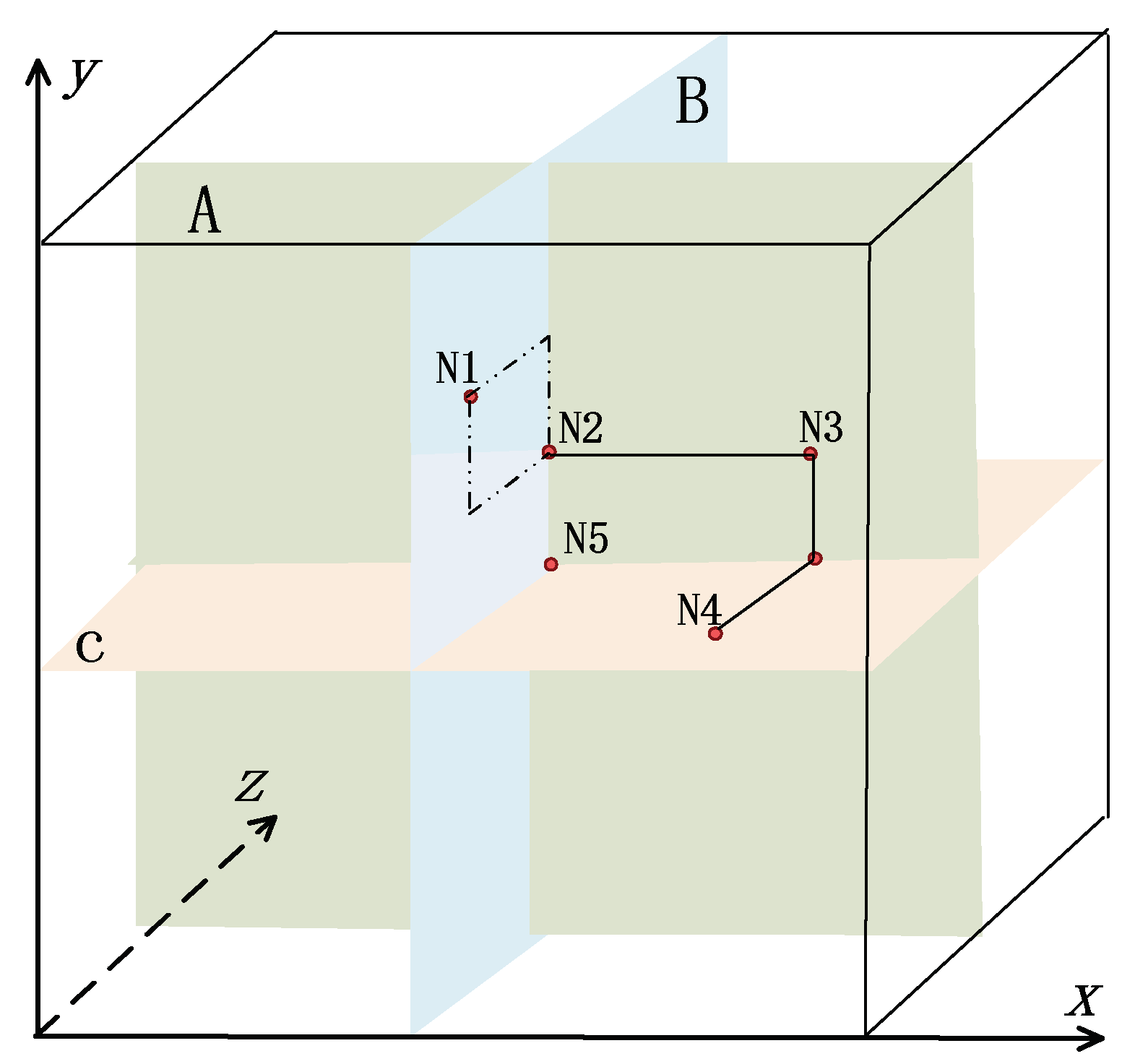
- In x captured nodes, if subscripts of blocks in x captured nodes are different with those of N1 and N2, x should be greater than or equal to q − 2 and there are at least q − 2 captured nodes that column (or row) subscripts of the corresponding blocks are different with those of N1 and N2. Meanwhile, column (or row) subscripts of corresponding q − 2 blocks are different from each other. For example, in Figure 3b, N5, N6, N7 and N8 are four nodes of x compromised nodes.
5.3.2. Resilience of 3-D Ex-µ-sPBIBD
6. Performance Comparison
6.1. Network Scalability
6.2. Key Connectivity
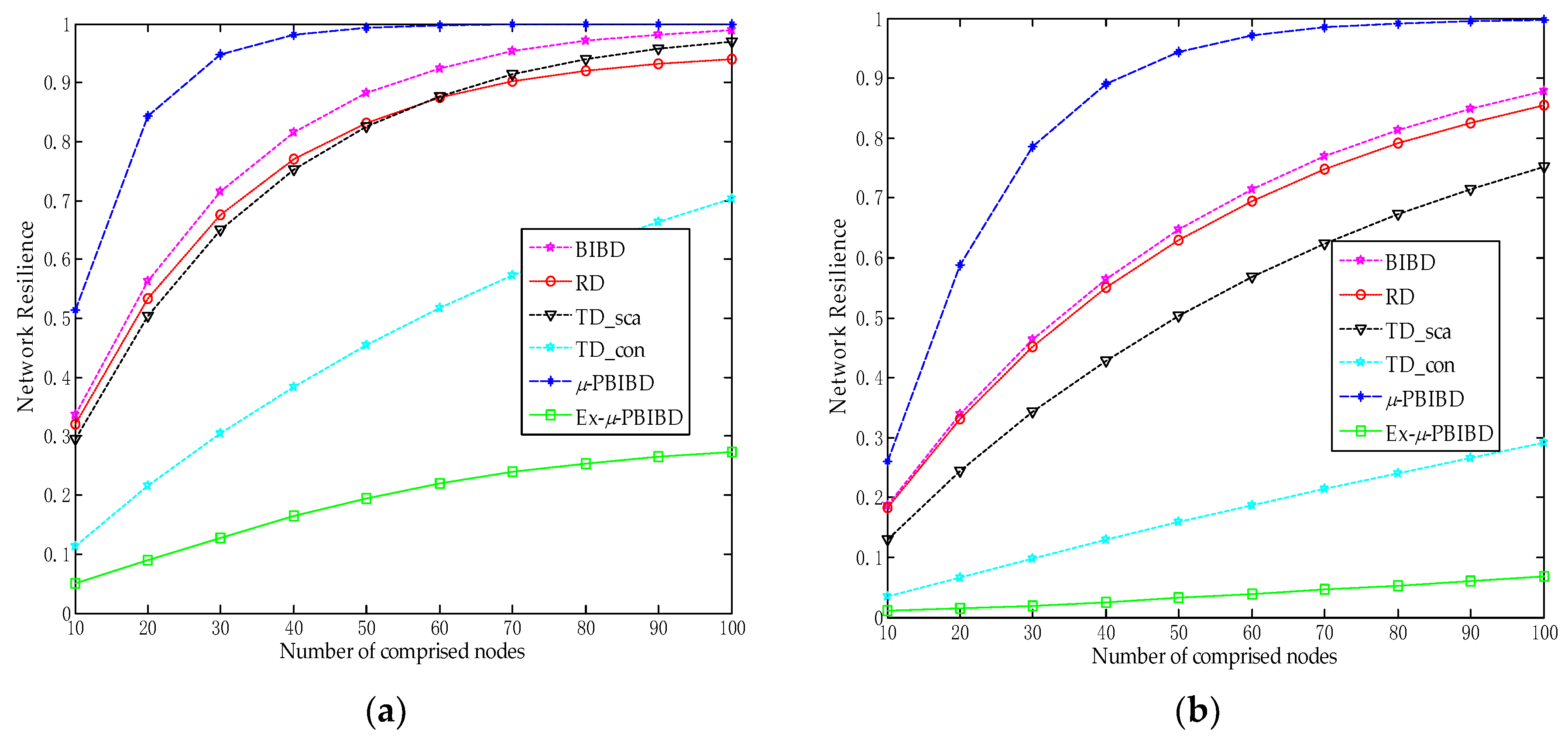
6.3. Network Resilience
6.4. Additional Analysis
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| V | The basic set |
| pi | The i point of V |
| v | The number of points in V |
| B | The block design of V |
| The i block in B | |
| d | The number of blocks in B |
| k | The number of points in a block (i.e., key ring size) |
| r | The number of blocks in which a point is contain |
| The number of blocks in which each pair of elements exist | |
| Balanced incomplete block design with parameter v, d, r, k, | |
| q | The order of finite projective plane corresponding to sB(q2 + q + 1, q + 1, 1) |
| G | A partition of V |
| The number of cases on the number of blocks in which each pair of points exist | |
| M | the number of senor nodes in WSNs |
| (a, b) | The point in V in 2-D µ-PBIBD |
| m, n | The number of row and column when V is viewed as 2-D space |
| The session key between nodes Ni and Nj | |
| Res(x) | The network resilience when an attacker captures x nodes |
| pro1 | The probability that two blocks share 2 keys |
| pro2 | The probability that two blocks share q − 2 keys |
| (a, b, c) | The point in V in 3-D µ-PBIBD |
| Con | The probability that two blocks have shared-key in Ex-µ-sPBIBD |
| Ni | The i node in WSNs |
References
- Mahmood, Z.; Ning, H.; Ghafoor, A. A Polynomial Subset-Based Efficient Multi-Party Key Management System for Lightweight Device Networks. Sensors 2017, 17, 670. [Google Scholar] [CrossRef] [PubMed]
- Ge, M.; Choo, K.K.R.; Wu, H.; Yu, Y. Survey on key revocation mechanisms in wireless sensor networks. J. Netw. Comput. Appl. 2016, 63, 24–38. [Google Scholar] [CrossRef]
- Lee, C.C.; Hwang, M.S.; Li, L.H. A new key authentication scheme based on discrete logarithms. Appl. Math. Comput. 2003, 139, 343–349. [Google Scholar] [CrossRef]
- Lee, C.C.; Lin, T.H.; Tsai, C.S. A new authenticated group key agreement in a mobile environment. Ann. Telecommun. Ann. Telecommun. 2009, 64, 735–744. [Google Scholar] [CrossRef]
- Tzeng, S.F.; Lee, C.C.; Lin, T.C. A Novel Key Management Scheme for Dynamic Access Control in a Hierarchy. Int. J. Netw. Secur. 2011, 12, 178–180. [Google Scholar]
- Bechkit, W.; Challal, Y.; Bouabdallah, A. A Highly Scalable Key Pre-Distribution Scheme for Wireless Sensor Networks. IEEE Trans. Wirel. Commun. 2013, 12, 948–959. [Google Scholar] [CrossRef]
- Bechkit, W.; Challal, Y.; Bouabdallah, A. A new class of Hash-Chain based key pre-distribution schemes for WSN. Comput. Commun. 2013, 36, 243–255. [Google Scholar] [CrossRef]
- Lee, C.C.; Li, C.T.; Chiu, S.T.; Lai, Y.M. A new three-party-authenticated key agreement scheme based on chaotic maps without password table. Nonlinear Dyn. 2014, 79, 2485–2495. [Google Scholar] [CrossRef]
- Zhan, F.; Yao, N.; Gao, Z.; Tan, G. A novel key generation method for wireless sensor networks based on system of equations. J. Netw. Comput. Appl. 2017, 82, 114–127. [Google Scholar] [CrossRef]
- Fakhrey, H.; Tiwari, R.; Johnston, M.; Al-Mathehaji, Y. The Optimum Design of Location-Dependent Key Management Protocol for a WSN with a Random Selected Cell Reporter. IEEE Sens. J. 2016, 16, 7217–7226. [Google Scholar] [CrossRef]
- Bala, S.; Sharma, G.; Verma, A.K. A survey and taxonomy of symmetric key management schemes for wireless sensor networks. In Proceedings of the Cube International Information Technology Conference, CUBE’12, Pune, India, 3–5 September 2012; pp. 585–592. [Google Scholar]
- He, X.; Niedermeier, M.; Meer, H.D. Review: Dynamic key management in wireless sensor networks: A survey. J. Netw. Comput. Appl. 2013, 36, 611–622. [Google Scholar] [CrossRef]
- Raghini, M.; Maheswari, N.U.; Venkatesh, R. Overview on key distribution primitives in wireless sensor network. J. Comput. Sci. 2013, 9, 543–550. [Google Scholar] [CrossRef]
- Pramod, T.C.; Sunitha, N.R. Key pre-distribution schemes to support various architectural deployment models in WSN. Int. J. Inf. Comput. Secur. 2016, 8, 139–157. [Google Scholar] [CrossRef]
- Gandino, F.; Montrucchio, B.; Rebaudengo, M. Key Management for Static Wireless Sensor Networks With Node Adding. IEEE Trans. Ind. Inform. 2014, 10, 1133–1143. [Google Scholar] [CrossRef]
- Gharib, M.; Yousefi’Zadeh, H.; Movaghar, A. Secure Overlay Routing Using Key Pre-Distribution: A Linear Distance Optimization Approach. IEEE Trans. Mob. Comput. 2016, 15, 2333–2344. [Google Scholar] [CrossRef]
- Zha, X.; Ni, W.; Zheng, K.; Niu, X.X. Collaborative Authentication in Decentralized Dense Mobile Networks with Key Predistribution. IEEE Trans. Inform. Foren. Secur. 2017, 12, 2261–2275. [Google Scholar] [CrossRef]
- Zhang, Y.; Liang, J.; Zheng, B.; Chen, W. A Hybrid Key Management Scheme for WSNs Based on PPBR and a Tree-Based Path Key Establishment Method. Sensors 2016, 16, 509. [Google Scholar] [CrossRef] [PubMed]
- Simplício, M.A., Jr.; Barreto, P.S.L.M.; Margi, C.B.; Carvalho, T.C.M.B. A survey on key management mechanisms for distributed Wireless Sensor Networks. Comput. Netw. 2010, 54, 2591–2612. [Google Scholar] [CrossRef]
- Lee, J.; Stinson, D.R. On the Construction of Practical Key Predistribution Schemes for Distributed Sensor Networks Using Combinatorial Designs. ACM Trans. Inf. Syst. Secur. 2008, 11, 5. [Google Scholar] [CrossRef]
- Xia, G.; Huang, Z.; Wang, Z. Key pre-distribution scheme for wireless sensor networks based on the symmetric balanced incomplete block design. J. Comput. Res. Dev. 2008, 45, 154–164. [Google Scholar]
- Paterson, M.B.; Stinson, D.R. A unified approach to combinatorial key predistribution schemes for sensor networks. Designs Codes Cryptogr. 2014, 71, 433–457. [Google Scholar] [CrossRef]
- Zhang, J.; Varadharajan, V. Wireless sensor network key management survey and taxonomy. J. Netw. Comput. Appl. 2010, 33, 63–75. [Google Scholar] [CrossRef]
- Lee, J.; Stinson, D.R. Deterministic key predistribution schemes for distributed sensor networks. In Proceedings of the 11th International Workshop on Selected Areas in Cryptography, SAC2004, Waterloo, ON, Canada, 9–10 August 2004; pp. 294–307. [Google Scholar]
- Lee, J.; Stinson, D.R. A combinatorial approach to key predistribution for distributed sensor networks. In Proceedings of the 2005 IEEE Wireless Communications and Networking Conference, WCNC 2005, New Orleans, LA, USA, 13–17 March 2005; pp. 1200–1205. [Google Scholar]
- Ma, C.; Zhang, B.Z.; Sun, Y.; Wang, H.Q. Based on pair-wise balanced design key pre-distribution scheme for heterogeneous wireless sensor networks. J. Commun. 2010, 31, 37–43. [Google Scholar]
- Xu, C.; Liu, W. Key Updating Methods for Combinatorial Design Based Key Management Schemes. J. Sens. 2014, 2014, 134357. [Google Scholar] [CrossRef]
- Dargahi, T.; Javadi, H.H.S.; Hosseinzadeh, M. Application-specific hybrid symmetric design of key pre-distribution for wireless sensor network. Secur. Commun. Netw. 2015, 8, 1561–1574. [Google Scholar] [CrossRef]
- Ding, J.; Bouabdallah, A.; Tarokh, V. Key Pre-Distributions From Graph-Based Block Designs. IEEE Sens. J. 2016, 16, 1842–1850. [Google Scholar] [CrossRef]
- Modiri, V.; Javadi, H.H.S.; Anzani, M. A Novel Scalable Key Pre-distribution Scheme for Wireless Sensor Networks Based on Residual Design. Wirel. Pers. Commun. 2017, 96, 2821–2841. [Google Scholar] [CrossRef]
- Gao, Q.; Ma, W.; Luo, W. A Combinatorial Key Predistribution Scheme for Two-Layer Hierarchical Wireless Sensor Networks. Wirel. Pers. Commun. 2017, 96, 2179–2204. [Google Scholar] [CrossRef]
- Çamtepe, S.A.; Yener, B. Combinatorial design of key distribution mechanisms for wireless sensor networks. IEEE/ACM Trans. Netw. 2007, 15, 346–358. [Google Scholar] [CrossRef]
- Henry, K.; Paterson, M.B.; Stinson, D.R. Practical Approaches to Varying Network Size in Combinatorial Key Predistribution Schemes. In Proceedings of the 20th International Conference on Selected Areas in Cryptography, SAC 2013, Burnaby, BC, Canada, 14–16 August 2013; pp. 89–117. [Google Scholar]
- Colbourn, C.J.; Colbourn, M.J. Algorithms in Combinatorial Design Theory, 1st ed.; Elsevier Science Publishing Company: New York, NY, USA, 1985; p. 69. ISBN 0444878025. [Google Scholar]
- Du, X.; Guizani, M.; Xiao, Y.; Chen, H.H. A routing-driven elliptic curve cryptography based key management scheme for heterogeneous sensor networks. IEEE Trans. Wirel. Commun. 2009, 8, 1223–1229. [Google Scholar] [CrossRef]

| µ-sPBIBD | KPD | Parameter | Value of Parameter |
|---|---|---|---|
| Basic set (point set) | Key pool | V | |
| Basic set size | key pool size | v | mn |
| Block | Key ring | ||
| Number of blocks | Number of key rings | d | mn |
| Block size | Key ring size | k | m + n − 2 |
| Number of common points between two blocks | Number of shared keys between two nodes | 2, m − 2, n − 2 |
| Ex-µ-sPBIBD | KPD | Parameter | Value of Parameter |
|---|---|---|---|
| Basic set | Key pool | V | |
| Basic set size | Key pool size | v | |
| Block | Key ring | Ba,b,c | |
| Number of blocks | Number of key rings | d | |
| Block size | Key ring size | k | |
| Number of common points between blocks | Number of shared-key between nodes |
| Combinatorial Design | Key Pool Size | Number of Key Rings | Key Ring Size |
|---|---|---|---|
| BIBD [3] | q2 + q + 1 | q2 + q + 1 | q + 1 |
| RD [30] | q2 + q + 1 | (q2 + q + 1)(q + 1) | q |
| Linear TD [20] | kq | q2 | k |
| 2-D PBIBD | q2 | q2 | 2q − 2 |
| 3-D EX-PBIBD | q3 | q3 | 3q − 3 |
| Parameter | Linear TD | Ex-PBIBD |
|---|---|---|
| k = 24 Con = 0.3 | M = 6241 Res(40) = 0.3915 Res(80) = 0.6297 Res(100) = 0.7112 | M = 729 Res(40) = 0.1642 Res(80) = 0.2533 Res(100) = 0.2728 |
| k = 36 Con = 0.213 | M = 28224 Res(40) = 0.2102 Res(80) = 0.3762 Res(100) = 0.4456 | M = 2179 Res(40) = 0.0587 Res(80) = 0.1131 Res(100) = 0.1390 |
| k = 48 Con = 0.166 | M = 82944 Res(40) = 0.1290 Res(80) = 0.2414 Res(100) = 0.2921 | M = 4913 Res(40) = 0.0251 Res(80) = 0.0533 Res(100) = 0.0677 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, Q.; Ma, C.; Yu, H.; Bian, X. A Key Pre-Distribution Scheme Based on µ-PBIBD for Enhancing Resilience in Wireless Sensor Networks. Sensors 2018, 18, 1539. https://doi.org/10.3390/s18051539
Yuan Q, Ma C, Yu H, Bian X. A Key Pre-Distribution Scheme Based on µ-PBIBD for Enhancing Resilience in Wireless Sensor Networks. Sensors. 2018; 18(5):1539. https://doi.org/10.3390/s18051539
Chicago/Turabian StyleYuan, Qi, Chunguang Ma, Haitao Yu, and Xuefen Bian. 2018. "A Key Pre-Distribution Scheme Based on µ-PBIBD for Enhancing Resilience in Wireless Sensor Networks" Sensors 18, no. 5: 1539. https://doi.org/10.3390/s18051539
APA StyleYuan, Q., Ma, C., Yu, H., & Bian, X. (2018). A Key Pre-Distribution Scheme Based on µ-PBIBD for Enhancing Resilience in Wireless Sensor Networks. Sensors, 18(5), 1539. https://doi.org/10.3390/s18051539




