Heart Rate Estimated from Body Movements at Six Degrees of Freedom by Convolutional Neural Networks
Abstract
:1. Introduction
2. Dataset
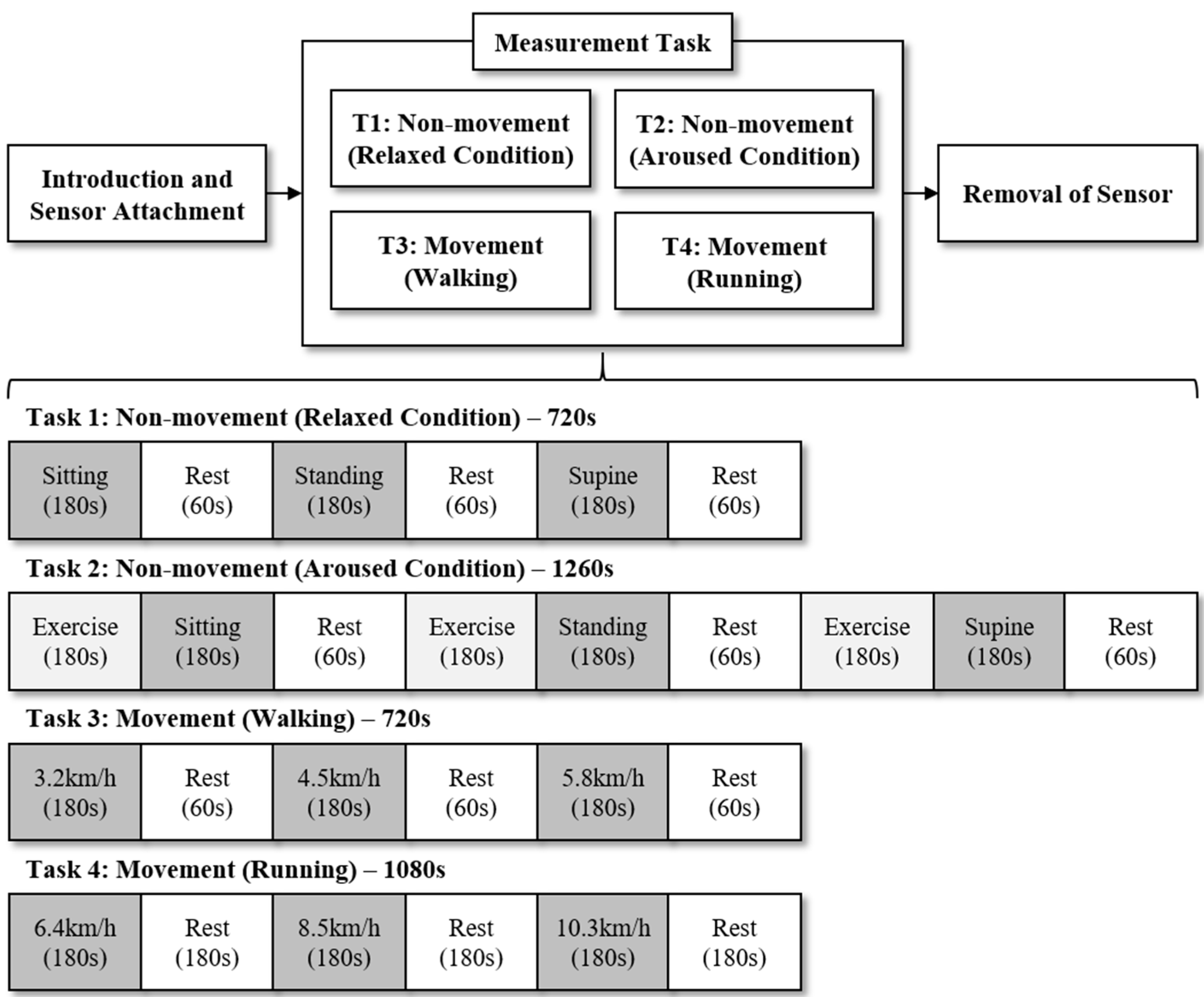
2.1. Experiment
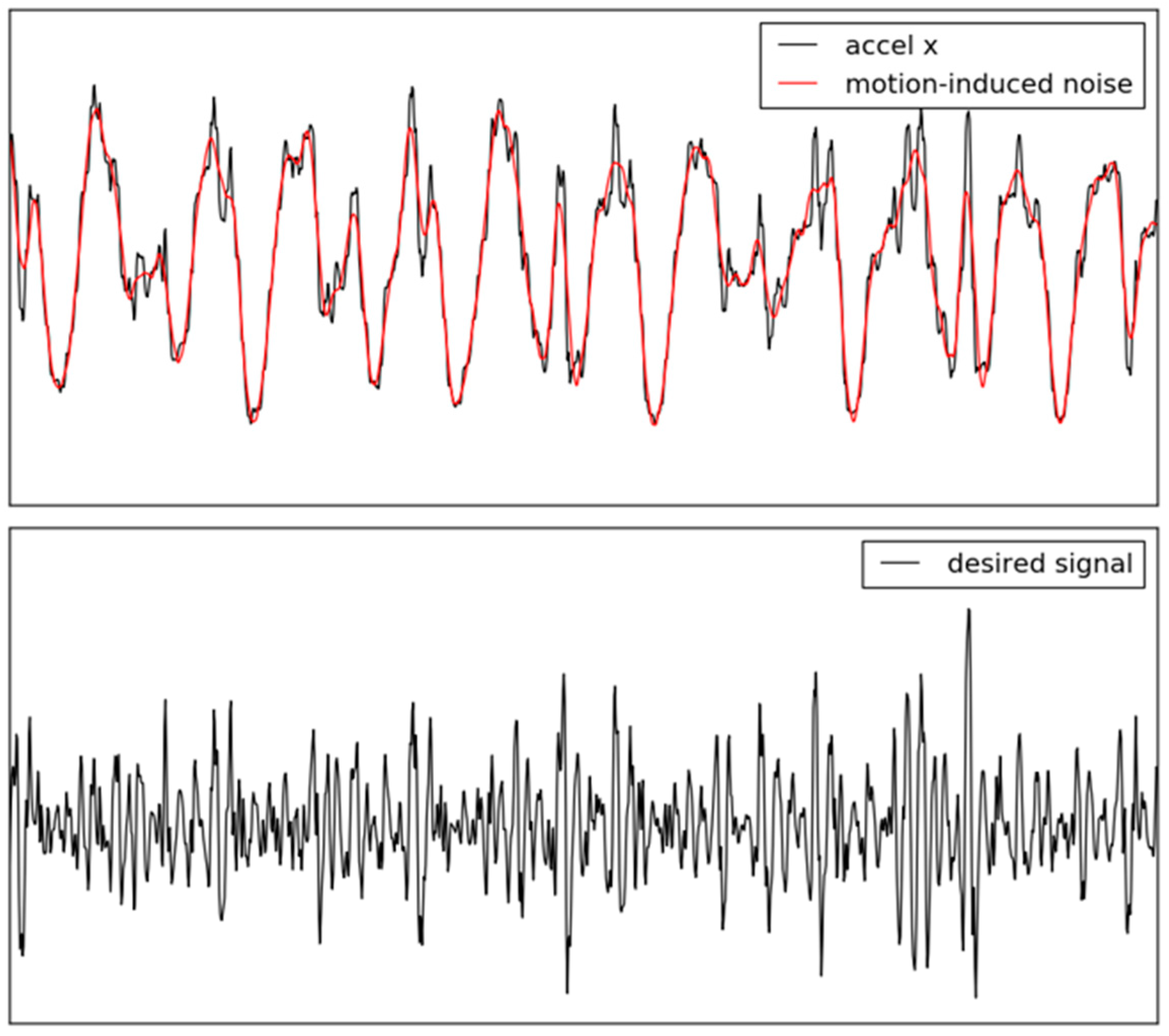
2.2. Formatting
3. Convolutional Neural Networks
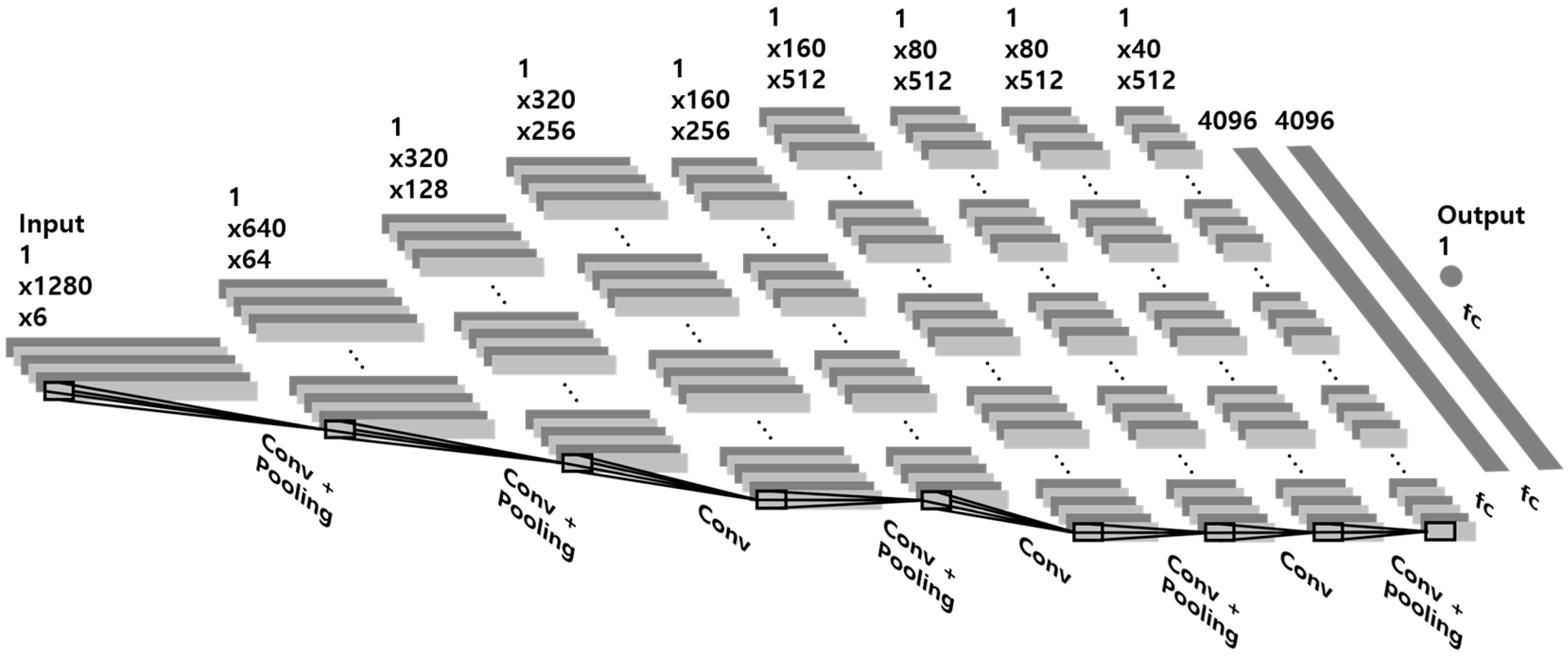
3.1. Baseline Architecture
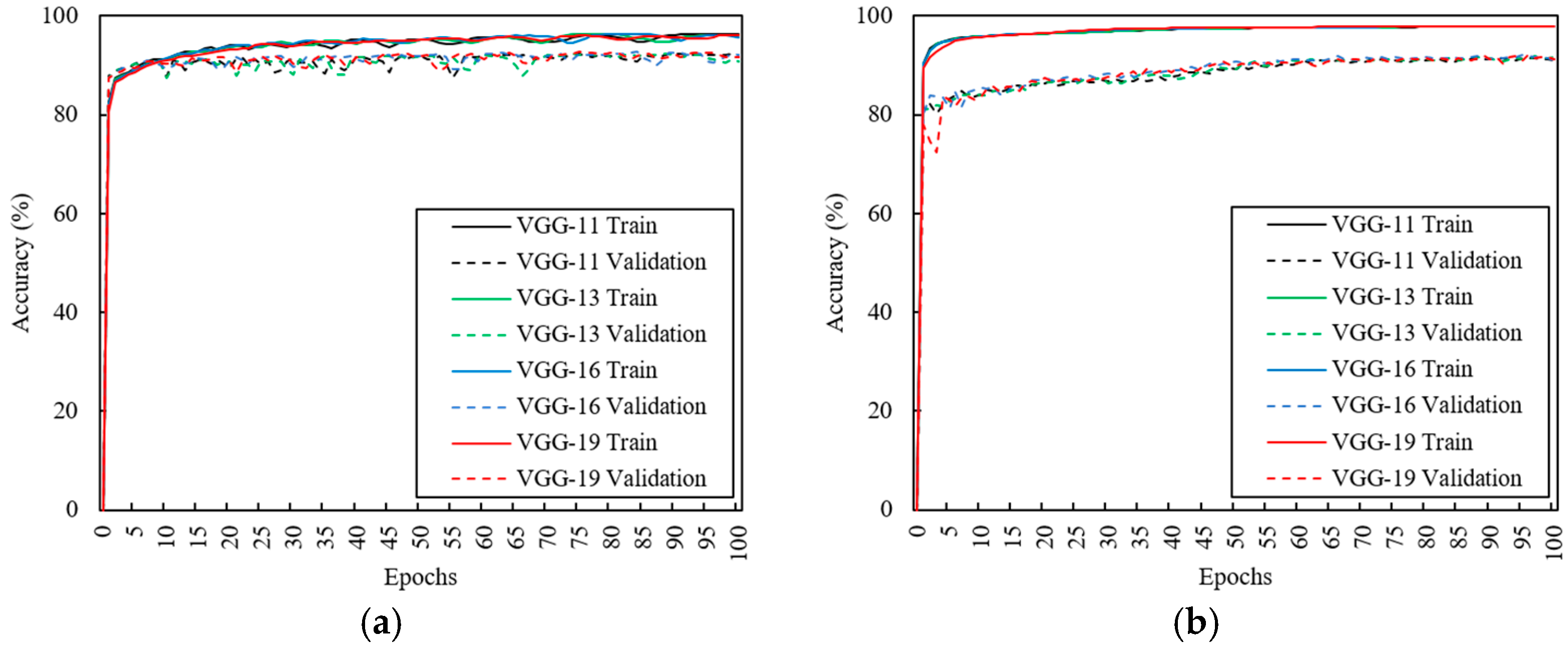
3.2. Effects of CNN Depth
3.3. Effects of Data Augmentation
3.4. Evaluation of Structural Risks
3.5. Optimal Architecture
4. Results
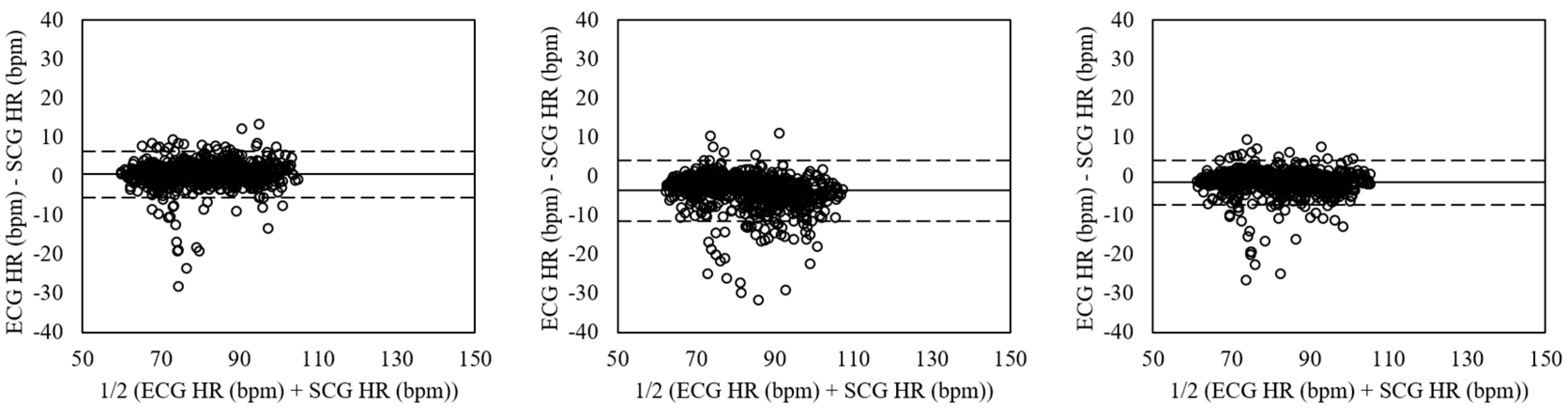
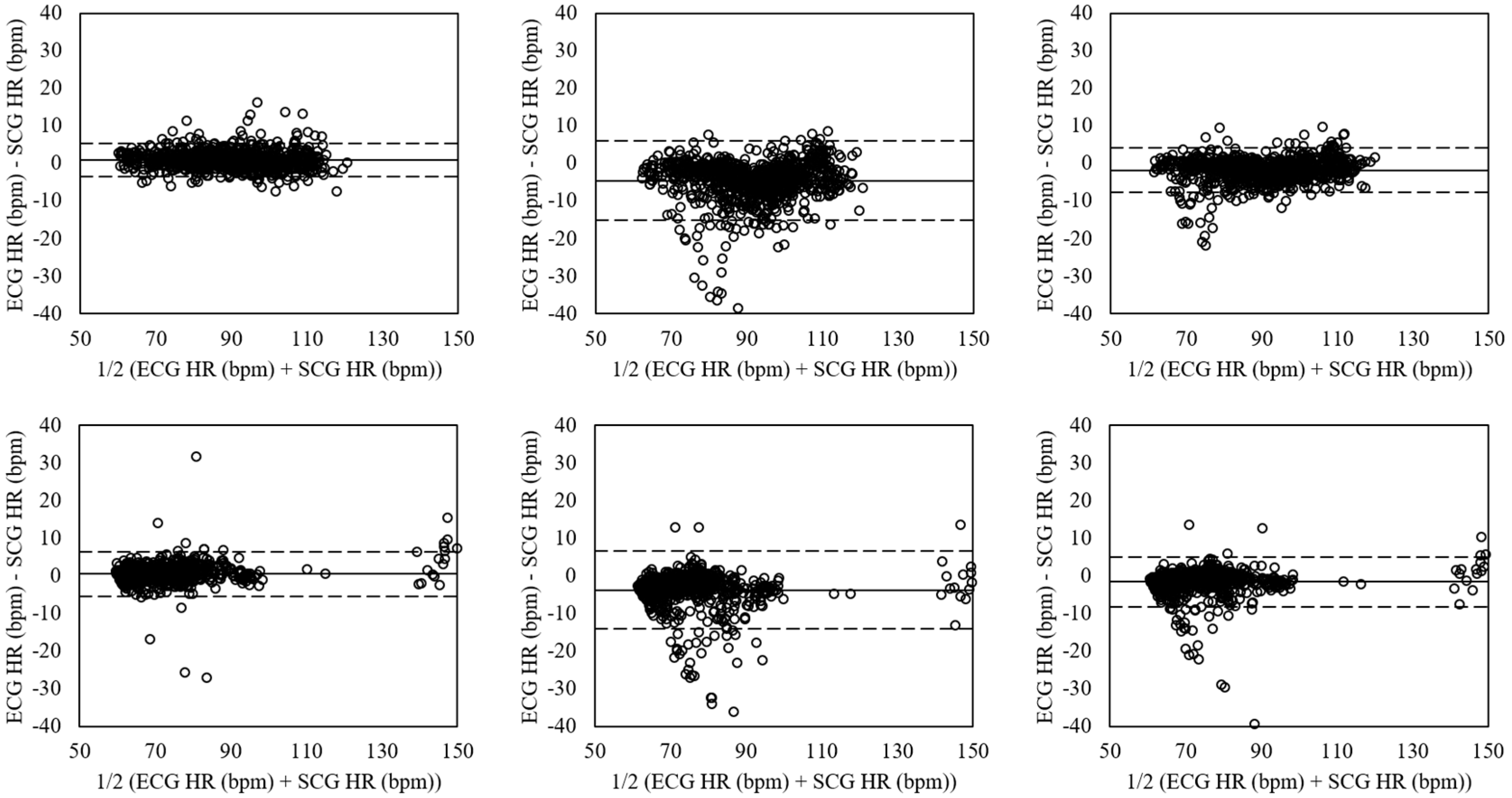
4.1. Estimation of Heart Rate in Relaxed Condition
4.2. Estimation of Heart Rate in Aroused Condition
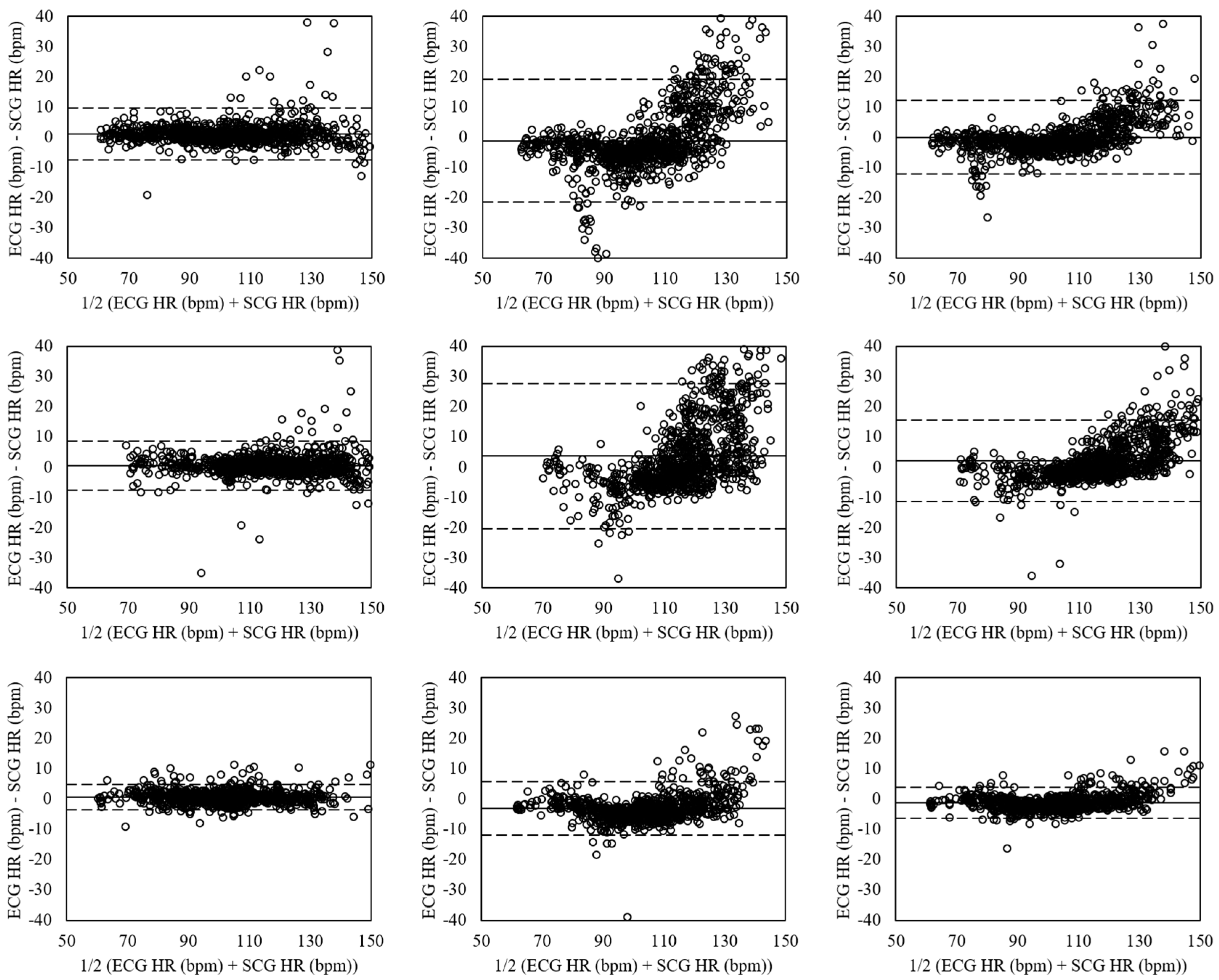
4.3. Estimation of Heart Rate for Walking
4.4. Estimation of Heart Rate for Running
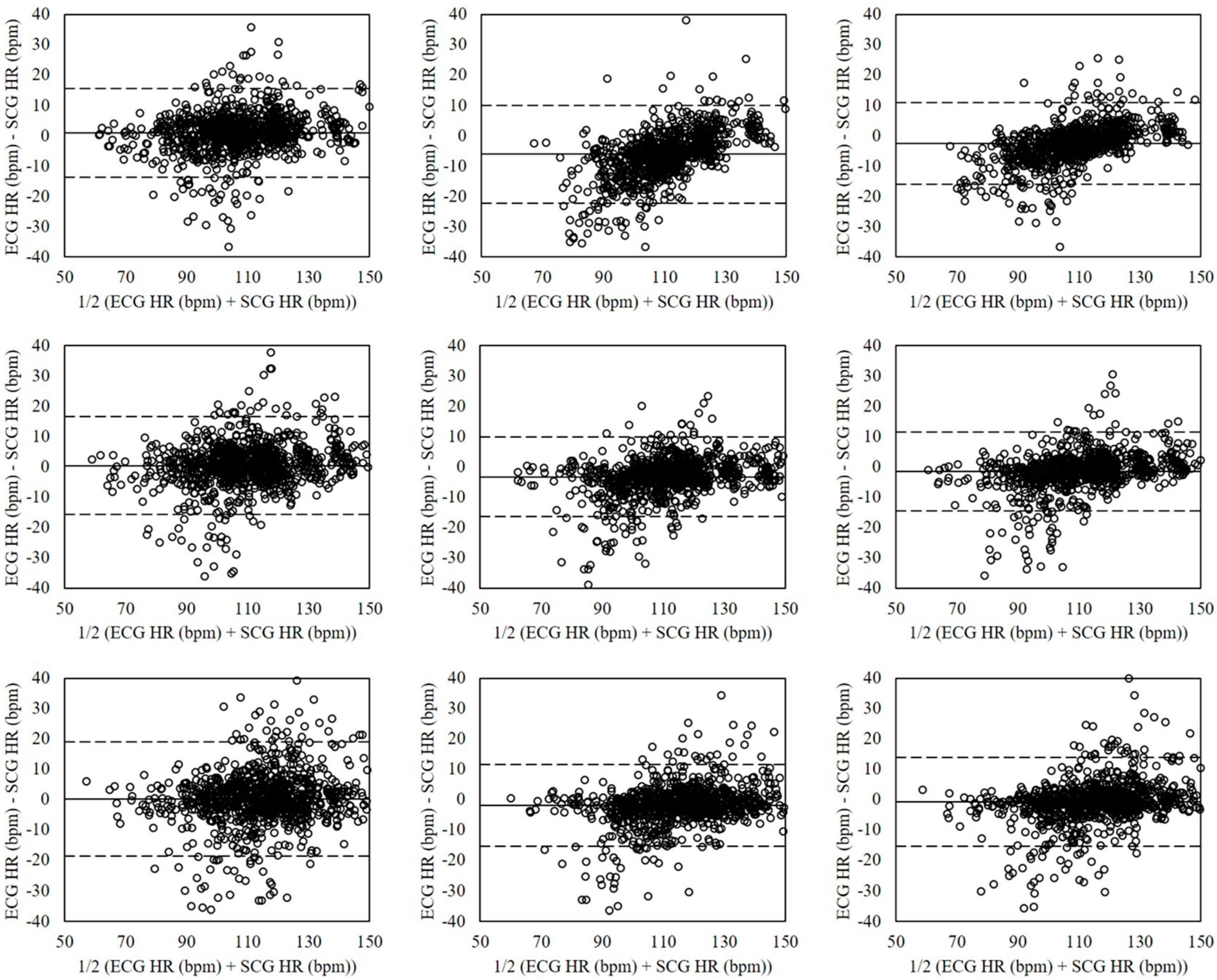
4.5. Comparison with Previous SCG Method Using Signal Processing
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bozhenko, B.S. Seismocardiography—A New Method in the Study of Functional Conditions of the Heart. Ter. Arkhiv 1961, 33, 55–64. [Google Scholar]
- Inan, O.T.; Migeotte, P.F.; Park, K.S.; Etemadi, M.; Tavakolian, K.; Casanella, R.; Zanetti, J.; Tank, J.; Funtova, I.; Prisk, G.K. Ballistocardiography and Seismocardiography: A Review of Recent Advances. IEEE J. Biomed. Health Inform. 2015, 19, 1414–1427. [Google Scholar] [CrossRef] [PubMed]
- Chuo, Y.; Kaminska, B. Sensor Layer of a Multiparameter Single-Point Integrated System. IEEE Trans. Biomed. Circuits Syst. 2009, 3, 229–240. [Google Scholar] [CrossRef] [PubMed]
- Di Rienzo, M.; Vaini, E.; Castiglioni, P.; Merati, G.; Meriggi, P.; Parati, G.; Faini, A.; Rizzo, F. Wearable Seismocardiography: Towards a Beat-by-Beat Assessment of Cardiac Mechanics in Ambulant Subjects. Auton. Neurosci. Basic Clin. 2013, 178, 50–59. [Google Scholar] [CrossRef] [PubMed]
- Di Rienzo, M.; Meriggi, P.; Rizzo, F.; Vaini, E.; Faini, A.; Merati, G.; Parati, G.; Castiglioni, P. A Wearable System for the Seismocardiogram Assessment in Daily Life Conditions. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Boston, MA, USA, 30 August–3 September 2011; pp. 4263–4266. [Google Scholar]
- Pandia, K.; Inan, O.T.; Kovacs, G.T.; Giovangrandi, L. Extracting Respiratory Information from Seismocardiogram Signals Acquired on the Chest using a Miniature Accelerometer. Physiol. Meas. 2012, 33, 1643. [Google Scholar] [CrossRef] [PubMed]
- Paukkunen, M.; Linnavuo, M.; Sepponen, R. A Portable Measurement System for the Superior-Inferior Axis of the Seismocardiogram. J. Bioeng. Biomed. Sci. 2013, 3, 1–4. [Google Scholar]
- Lee, H.; Lee, H.; Whang, M. An Enhanced Method to Estimate Heart Rate from Seismocardiography via Ensemble Averaging of Body Movements at Six Degrees of Freedom. Sensors 2018, 18, 238. [Google Scholar] [CrossRef] [PubMed]
- Migeotte, P.; De Ridder, S.; Tank, J.; Pattyn, N.; Funtova, I.; Baevsky, R.; Neyt, X.; Prisk, G. Three Dimensional Ballisto-and Seismo-Cardiography: HIJ wave Amplitudes are Poorly Correlated to Maximal Systolic Force Vector. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), San Diego, CA, USA, 28 August–1 September 2012; pp. 5046–5049. [Google Scholar]
- Pandia, K.; Ravindran, S.; Cole, R.; Kovacs, G.; Giovangrandi, L. Motion Artifact Cancellation to Obtain Heart Sounds from a Single Chest-Worn Accelerometer. In Proceedings of the International Conference of the IEEE Acoustic Speech and Signal Processing (ICASSP), Dallas, TX, USA, 14–19 March 2010; pp. 590–593. [Google Scholar]
- Paukkunen, M.; Parkkila, P.; Hurnanen, T.; Pänkäälä, M.; Koivisto, T.; Nieminen, T.; Kettunen, R.; Sepponen, R. Beat-by-Beat Quantification of Cardiac Cycle Events Detected from Three-Dimensional Precordial Acceleration Signals. IEEE J. Biomed. Health Inform. 2016, 20, 435–439. [Google Scholar] [CrossRef] [PubMed]
- Tadi, M.J.; Lehtonen, E.; Pankäälä, M.; Saraste, A.; Vasankari, T.; Terás, M.; Koivisto, T. Gyrocardiography: A New Non-Invasive Approach in the Study of Mechanical Motions of the Heart. Concept, Method and Initial Bbservations. In Proceedings of the International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 2034–2037. [Google Scholar]
- Migeotte, P.; Mucci, V.; Delière, Q.; Lejeune, L.; van de Borne, P. Multi-Dimensional Kineticardiography a New Approach for Wearable Cardiac Monitoring through Body Acceleration Recordings. In Proceedings of the XIV Mediterranean Conference on Medical and Biological Engineering and Computing (MEDICON), Paphos, Cyprus, 31 March–2 April 2016; pp. 1125–1130. [Google Scholar]
- Yang, C.; Tang, S.; Tavassolian, N. Utilizing Gyroscopes Towards the Automatic Annotation of Seismocardiograms. IEEE Sens. J. 2017, 17, 2129–2136. [Google Scholar] [CrossRef]
- Jia, W.; Li, Y.; Bai, Y.; Mao, Z.; Sun, M.; Zhao, Q. Estimation of Heart Rate from a Chest-Worn Inertial Measurement Unit. In Proceedings of the International Symposium on Bioelectronics and Bioinformatics (ISBB), Beijing, China, 14–17 October 2015; pp. 148–151. [Google Scholar]
- Yang, C.; Tavassolian, N. Motion Noise Cancellation in Seismocardiographic Monitoring of Moving Subjects. In Proceedings of the Biomedical Circuits and Systems Conference (BioCAS), Atlanta, GA, USA, 22–24 October 2015; pp. 1–4. [Google Scholar]
- Javaid, A.Q.; Ashouri, H.; Dorier, A.; Etemadi, M.; Heller, J.A.; Roy, S.; Inan, O.T. Quantifying and Reducing Motion Artifacts in Wearable Seismocardiogram Measurements during Walking to Assess Left Ventricular Health. IEEE Trans. Biomed. Eng. 2017, 64, 1277–1286. [Google Scholar] [CrossRef] [PubMed]
- LeCun, Y.; Boser, B.; Denker, J.S.; Henderson, D.; Howard, R.E.; Hubbard, W.; Jackel, L.D. Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1989, 1, 541–551. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet Classification with Deep Convolutional Neural Networks. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Tahoe City, CA, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Zeiler, M.D.; Fergus, R. Visualizing and Understanding Convolutional Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Zurich, Switzerland, 6–12 September 2014; pp. 818–833. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Kim, Y. Convolutional Neural Networks for Sentence Classification. arXiv, 2014; arXiv:1408.5882. [Google Scholar]
- Schlüter, J.; Grill, T. Exploring Data Augmentation for Improved Singing Voice Detection with Neural Networks. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Malaga, Spain, 26–30 October 2015; pp. 121–126. [Google Scholar]
- Um, T.T.; Babakeshizadeh, V.; Kulic, D. Exercise Motion Classification from Large-Scale Wearable Sensor Data Using Convolutional Neural Networks. arXiv, 2016; arXiv:1610.07031. [Google Scholar]
- Lutovac, M.D.; Tošić, D.V.; Evans, B.L. Filter Design for Signal Processing Using MATLAB and Mathematica; Lutovac, M.D., Ed.; Prentice Hall: Upper New Jersey River, NJ, USA, 2001. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv, 2014; arXiv:1409.1556. [Google Scholar]
- McKinley, S.; Levine, M. Cubic Spline Interpolation. Coll. Redw. 1998, 45, 1049–1060. [Google Scholar]
- Savitzky, A.; Golay, M.J. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Pan, J.; Tompkins, W.J. A Real-Time QRS Detection Algorithm. IEEE Trans. Biomed. Eng. 1985, 3, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the International Conference on Machine Learning (ICML), Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M. Tensorflow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv, 2016; arXiv:1603.04467. [Google Scholar]
- Um, T.T.; Pfister, F.M.; Pichler, D.; Endo, S.; Lang, M.; Hirche, S.; Fietzek, U.; Kulić, D. Data Augmentation of Wearable Sensor Data for Parkinson’s Disease Monitoring using Convolutional Neural Networks. In Proceedings of the ACM International Conference on Multimodal Interaction (ICMI), Glasgow, UK, 13–17 November 2017; pp. 216–220. [Google Scholar]
- Gharehbaghi, A.; Lindén, M. A Deep Machine Learning Method for Classifying Cyclic Time Series of Biological Signals using Time-Growing Neural Network. IEEE Trans. Neural Netw. Learn. Syst. 2017. [Google Scholar] [CrossRef] [PubMed]
- Altman, D.G.; Bland, J.M. Measurement in Medicine: The Analysis of Method Comparison Studies. Statistician 1983, 32, 307–317. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 8–10 June 2015; pp. 1–9. [Google Scholar]
- Huang, G.; Liu, Z.; Weinberger, K.Q.; van der Maaten, L. Densely Connected Convolutional Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Hinton, G.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. arXiv, 2015; arXiv:1503.02531. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv, 2013; arXiv:1312.6114. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Advances in Neural Information Processing System (NIPS), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]

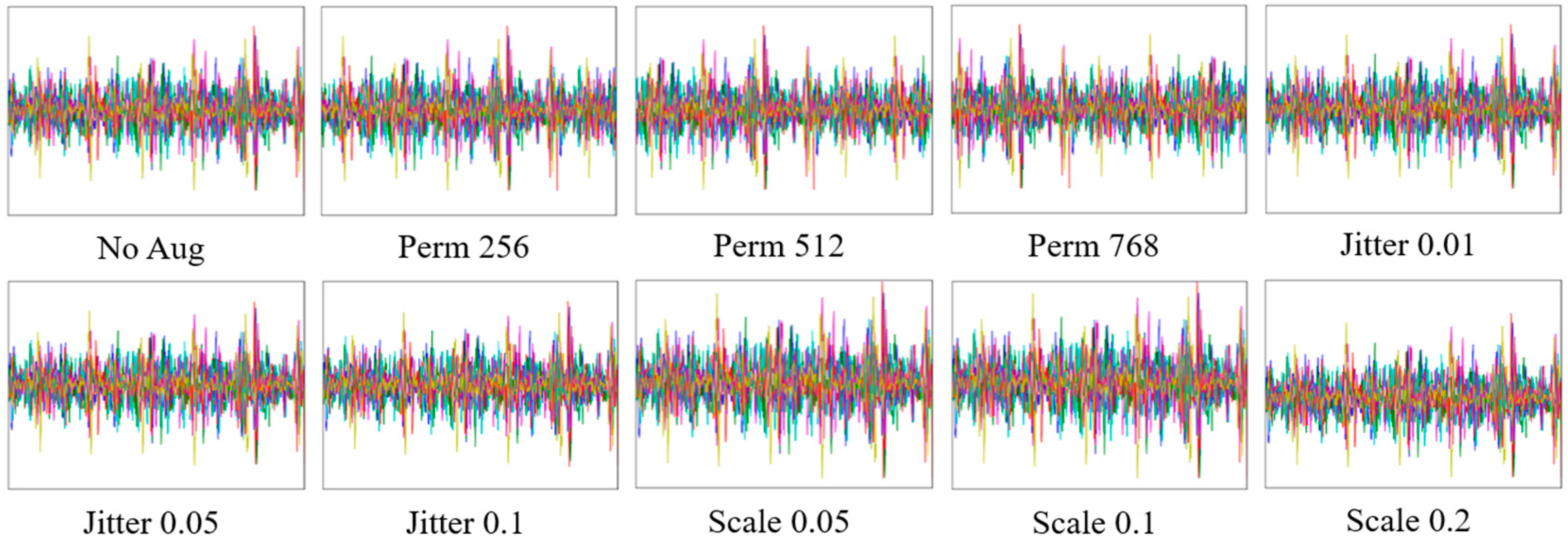

| No Aug | Aug | EN | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| VGG-11 | VGG-13 | VGG-16 | VGG-19 | VGG-11 | VGG-13 | VGG-16 | VGG-19 | |||
| Train | All | 97.46 | 97.33 | 97.46 | 97.19 | 95.32 | 95.08 | 95.27 | 95.33 | - |
| Test | Sit (R) | 97.20 | 97.14 | 97.57 | 97.41 | 93.65 | 94.22 | 93.45 | 95.16 | 96.37 |
| Stand (R) | 97.67 | 97.73 | 98.06 | 97.94 | 93.86 | 94.34 | 93.83 | 94.06 | 96.06 | |
| Sup (R) | 97.30 | 97.31 | 97.79 | 97.83 | 93.29 | 93.07 | 92.77 | 94.25 | 96.02 | |
| Sit (A) | 97.75 | 97.67 | 97.92 | 97.95 | 93.89 | 94.54 | 94.95 | 92.74 | 95.33 | |
| Stand (A) | 97.55 | 97.53 | 98.01 | 97.71 | 94.11 | 94.98 | 95.12 | 93.11 | 95.56 | |
| Sup (A) | 98.16 | 98.09 | 98.49 | 98.21 | 95.15 | 95.34 | 95.82 | 95.55 | 97.02 | |
| Walk (3.2) | 95.19 | 95.20 | 95.11 | 94.79 | 92.45 | 91.83 | 92.07 | 91.90 | 93.51 | |
| Walk (4.5) | 94.49 | 94.52 | 94.72 | 94.54 | 94.37 | 92.78 | 94.05 | 94.88 | 94.80 | |
| Walk (5.8) | 94.54 | 94.34 | 94.21 | 94.15 | 95.4 | 94.26 | 95.01 | 95.60 | 94.91 | |
| Run (6.4) | 93.54 | 93.31 | 93.29 | 93.36 | 94.69 | 93.61 | 94.47 | 95.03 | 94.16 | |
| Run (8.5) | 92.83 | 92.35 | 92.57 | 92.17 | 95.09 | 94.98 | 94.80 | 95.11 | 93.84 | |
| Run (10.3) | 92.48 | 92.20 | 92.05 | 91.70 | 94.62 | 95.18 | 94.85 | 94.93 | 93.49 | |
| All | 95.72 | 95.62 | 95.82 | 95.65 | 94.21 | 94.09 | 94.27 | 94.36 | 95.09 | |
| A-Test | 7.95 | 7.83 | 7.61 | 7.57 | 8.40 | 8.06 | 7.88 | 7.81 | 6.98 | |
| 3.11 | 2.97 | 2.43 | 2.44 | 5.21 | 5.10 | 4.67 | 4.82 | 2.85 | ||
| Posture | Signal | MAE | SDAE | RMSE | CC |
|---|---|---|---|---|---|
| Standing | VGG-16 (No Aug) | 1.92 | 2.40 | 3.08 | 0.954 ** |
| VGG-19 (Aug) | 3.90 | 3.72 | 5.39 | 0.934 ** | |
| Ensemble Network | 2.07 | 2.56 | 3.29 | 0.960 ** | |
| Sitting | VGG-16 (No Aug) | 1.72 | 1.69 | 2.40 | 0.984 ** |
| VGG-19 (Aug) | 5.05 | 4.91 | 7.04 | 0.905 ** | |
| Ensemble Network | 2.52 | 2.50 | 3.55 | 0.970 ** | |
| Supine | VGG-16 (No Aug) | 1.67 | 2.60 | 3.09 | 0.982 ** |
| VGG-19 (Aug) | 4.06 | 5.04 | 6.47 | 0.946 ** | |
| Ensemble Network | 2.17 | 3.12 | 3.80 | 0.977 ** |
| Posture | Signal | MAE | SDAE | RMSE | CC |
|---|---|---|---|---|---|
| Standing | VGG-16 (No Aug) | 2.23 | 3.92 | 4.51 | 0.976 ** |
| VGG-19 (Aug) | 7.54 | 7.22 | 10.44 | 0.866 ** | |
| Ensemble Network | 3.96 | 4.79 | 6.22 | 0.960 ** | |
| Sitting | VGG-16 (No Aug) | 2.34 | 3.47 | 4.19 | 0.975 ** |
| VGG-19 (Aug) | 8.58 | 9.43 | 12.75 | 0.763 ** | |
| Ensemble Network | 4.63 | 5.45 | 7.15 | 0.946 ** | |
| Supine | VGG-16 (No Aug) | 1.51 | 1.57 | 2.18 | 0.992 ** |
| VGG-19 (Aug) | 4.48 | 3.22 | 5.52 | 0.962 ** | |
| Ensemble Network | 2.28 | 1.81 | 2.91 | 0.988 ** |
| Speed | Signal | MAE | SDAE | RMSE | CC |
|---|---|---|---|---|---|
| 3.2 km/h | VGG-16 (No Aug) | 5.11 | 5.52 | 7.52 | 0.906 ** |
| VGG-19 (Aug) | 7.81 | 6.65 | 10.26 | 0.899 ** | |
| Ensemble Network | 5.03 | 5.29 | 7.30 | 0.930 ** | |
| 4.5 km/h | VGG-16 (No Aug) | 5.53 | 6.09 | 8.23 | 0.896 ** |
| VGG-19 (Aug) | 5.12 | 5.46 | 7.48 | 0.933 ** | |
| Ensemble Network | 4.26 | 5.35 | 6.84 | 0.935 ** | |
| 5.8 km/h | VGG-16 (No Aug) | 6.43 | 7.15 | 9.61 | 0.868 ** |
| VGG-19 (Aug) | 4.74 | 5.30 | 7.11 | 0.935 ** | |
| Ensemble Network | 4.76 | 5.83 | 7.52 | 0.922 ** |
| Speed | Signal | MAE | SDAE | RMSE | CC |
|---|---|---|---|---|---|
| 6.4 km/h | VGG-16 (No Aug) | 7.21 | 8.64 | 11.25 | 0.846 ** |
| VGG-19 (Aug) | 5.24 | 6.72 | 8.52 | 0.917 ** | |
| Ensemble Network | 5.43 | 7.40 | 9.17 | 0.899 ** | |
| 8.5 km/h | VGG-16 (No Aug) | 8.01 | 8.89 | 11.96 | 0.853 ** |
| VGG-19 (Aug) | 5.21 | 7.14 | 8.84 | 0.924 ** | |
| Ensemble Network | 5.94 | 7.64 | 9.67 | 0.908 ** | |
| 10.3 km/h | VGG-16 (No Aug) | 8.62 | 9.81 | 13.05 | 0.824 ** |
| VGG-19 (Aug) | 5.49 | 7.97 | 9.68 | 0.908 ** | |
| Ensemble Network | 6.38 | 8.61 | 10.72 | 0.886 ** |
| Condition | Method | MAE | SDAE | RMSE | CC |
|---|---|---|---|---|---|
| Sit (Relaxed) | Signal Processing | 4.83 | 6.97 | 8.39 | 0.737 ** |
| CNN | 2.07 | 2.56 | 3.29 | 0.960 ** | |
| Stand (Relaxed) | Signal Processing | 2.00 | 2.33 | 3.04 | 0.975 ** |
| CNN | 2.52 | 2.50 | 3.55 | 0.970 ** | |
| Supine (Relaxed) | Signal Processing | 18.05 | 17.27 | 24.78 | −0.084 |
| CNN | 2.17 | 3.12 | 3.80 | 0.977 ** | |
| Sit (Aroused) | Signal Processing | 1.93 | 3.81 | 4.22 | 0.973 ** |
| CNN | 3.96 | 4.79 | 6.22 | 0.960 ** | |
| Stand (Aroused) | Signal Processing | 2.46 | 2.59 | 3.54 | 0.981 ** |
| CNN | 4.63 | 5.45 | 7.15 | 0.946 ** | |
| Supine (Aroused) | Signal Processing | 1.64 | 2.53 | 2.98 | 0.986 ** |
| CNN | 2.28 | 1.81 | 2.91 | 0.988 ** | |
| Walk (3.2 km/h) | Signal Processing | 18.19 | 14.66 | 23.61 | 0.789 ** |
| CNN | 5.03 | 5.29 | 7.30 | 0.930 ** | |
| Walk (4.5 km/h) | Signal Processing | 14.05 | 12.66 | 19.43 | 0.867 ** |
| CNN | 4.26 | 5.35 | 6.84 | 0.935 ** | |
| Walk (5.8 km/h) | Signal Processing | 20.48 | 17.28 | 27.55 | 0.729 ** |
| CNN | 4.76 | 5.83 | 7.52 | 0.922 ** | |
| Run (6.4 km/h) | Signal Processing | 20.22 | 18.02 | 27.83 | 0.704 ** |
| CNN | 5.43 | 7.40 | 9.17 | 0.899 ** | |
| Run (8.5 km/h) | Signal Processing | 19.83 | 12.81 | 24.31 | 0.832 ** |
| CNN | 5.94 | 7.64 | 9.67 | 0.908 ** | |
| Run (10.3 km/h) | Signal Processing | 17.71 | 12.55 | 22.76 | 0.893 ** |
| CNN | 6.38 | 8.61 | 10.72 | 0.886 ** |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Whang, M. Heart Rate Estimated from Body Movements at Six Degrees of Freedom by Convolutional Neural Networks. Sensors 2018, 18, 1392. https://doi.org/10.3390/s18051392
Lee H, Whang M. Heart Rate Estimated from Body Movements at Six Degrees of Freedom by Convolutional Neural Networks. Sensors. 2018; 18(5):1392. https://doi.org/10.3390/s18051392
Chicago/Turabian StyleLee, Hyunwoo, and Mincheol Whang. 2018. "Heart Rate Estimated from Body Movements at Six Degrees of Freedom by Convolutional Neural Networks" Sensors 18, no. 5: 1392. https://doi.org/10.3390/s18051392
APA StyleLee, H., & Whang, M. (2018). Heart Rate Estimated from Body Movements at Six Degrees of Freedom by Convolutional Neural Networks. Sensors, 18(5), 1392. https://doi.org/10.3390/s18051392






