Multi-Aperture-Based Probabilistic Noise Reduction of Random Telegraph Signal Noise and Photon Shot Noise in Semi-Photon-Counting Complementary-Metal-Oxide-Semiconductor Image Sensor
Abstract
1. Introduction
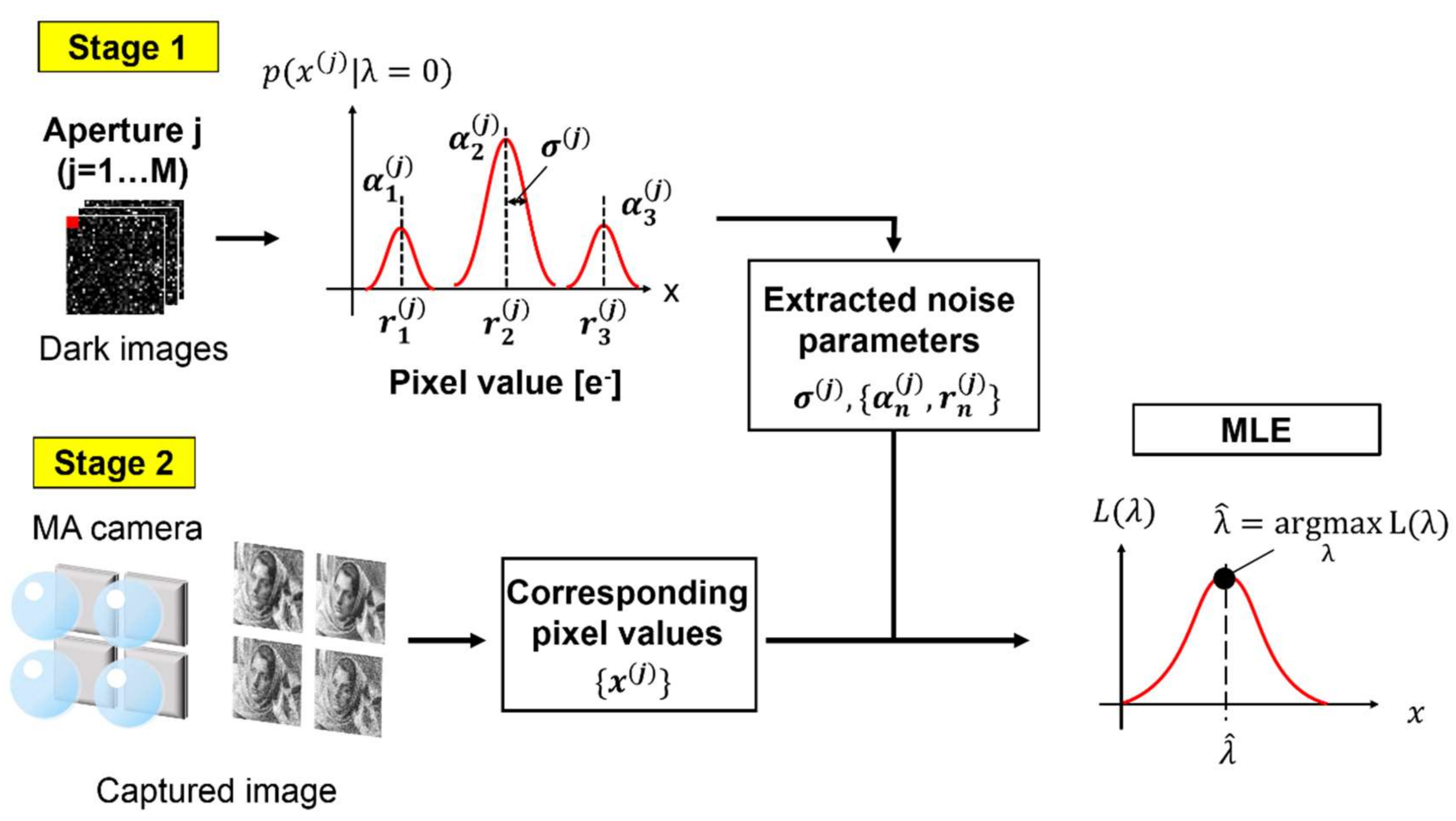
2. Probabilistic RTS Noise Reduction with Multi-Aperture Camera
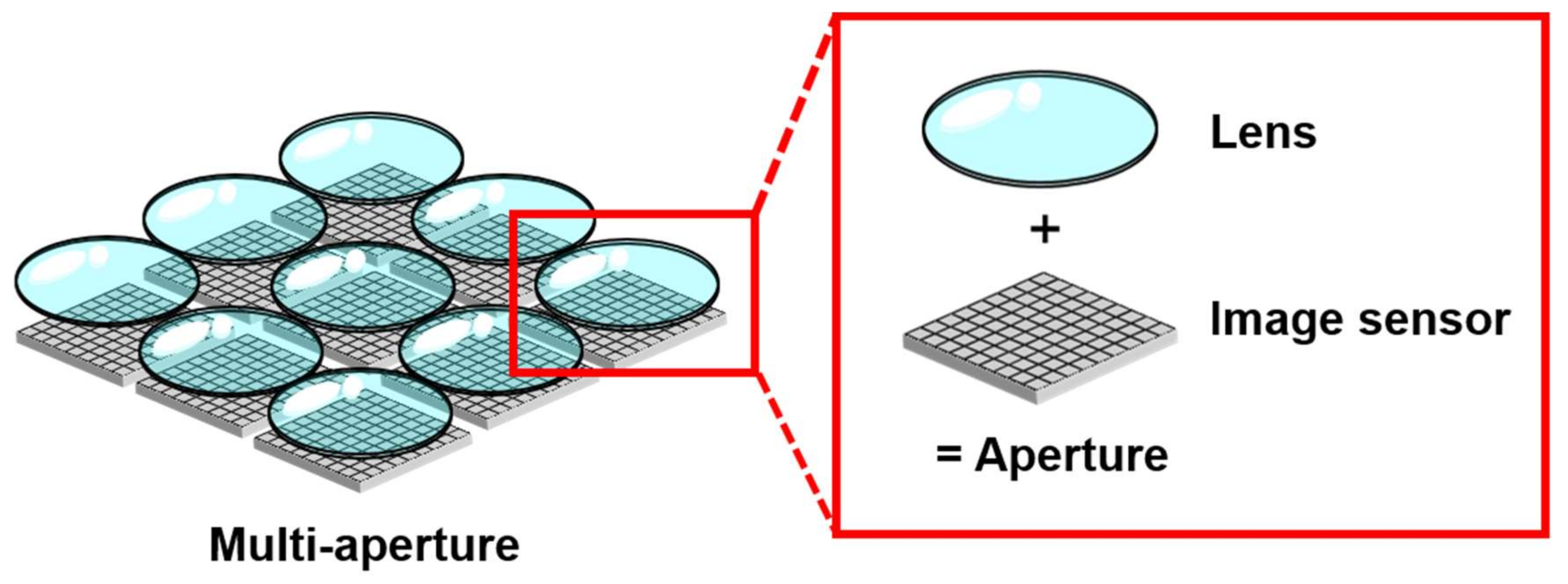
2.1. Multi-Aperture Camera
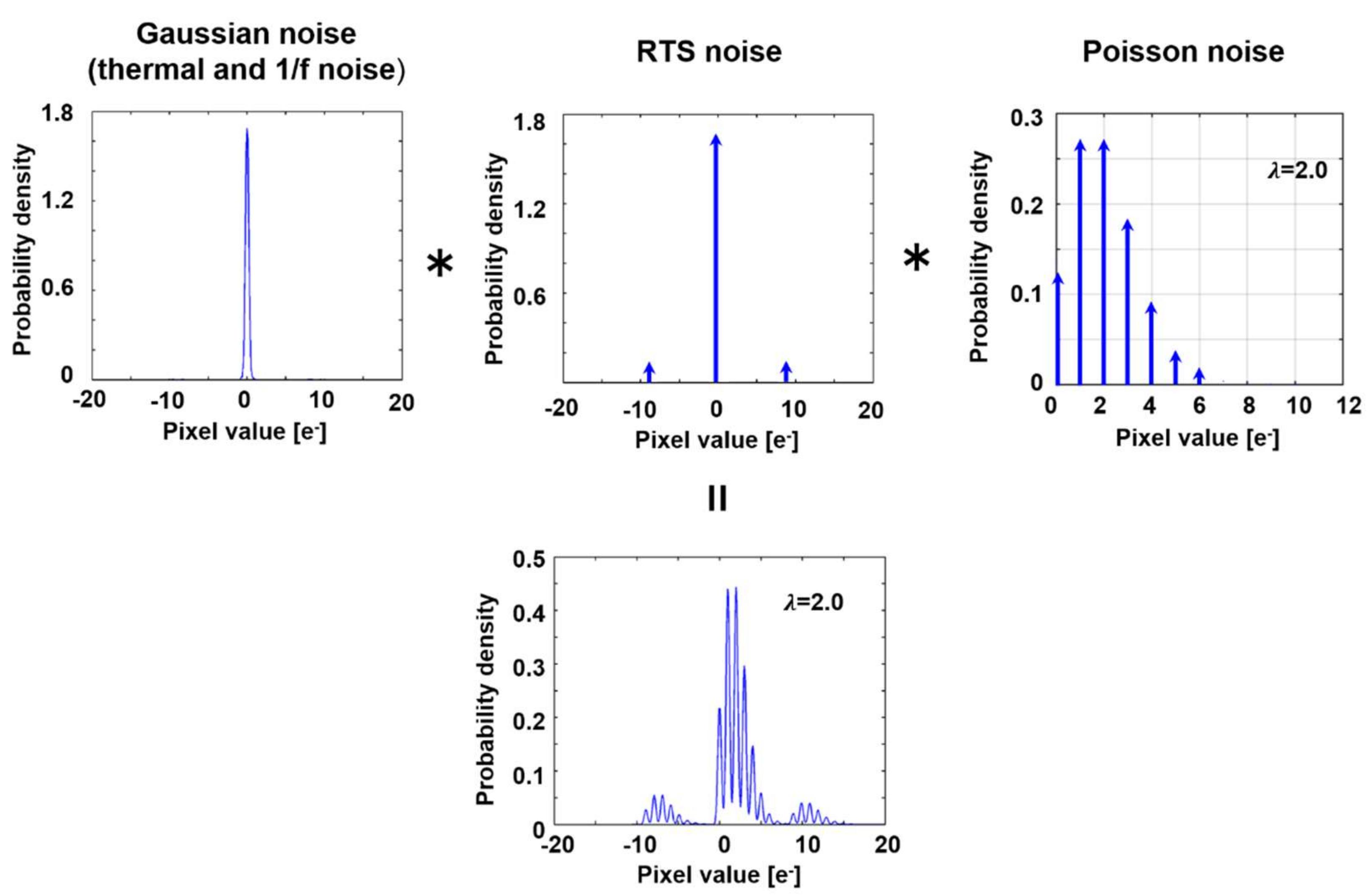
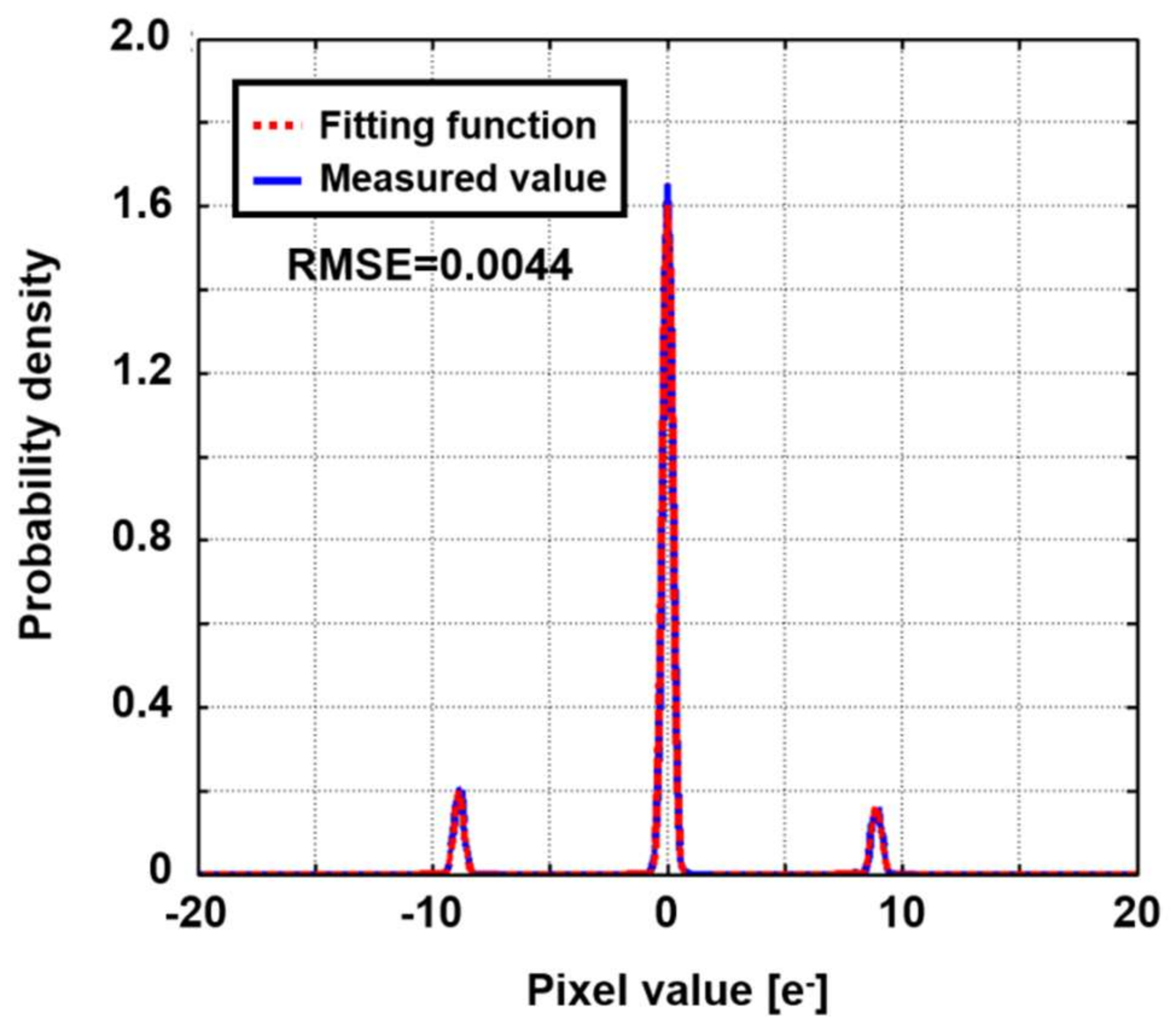
2.2. Noise Modeling of Semi-Photon-Counting-Level Low Noise CMOS Image Sensors
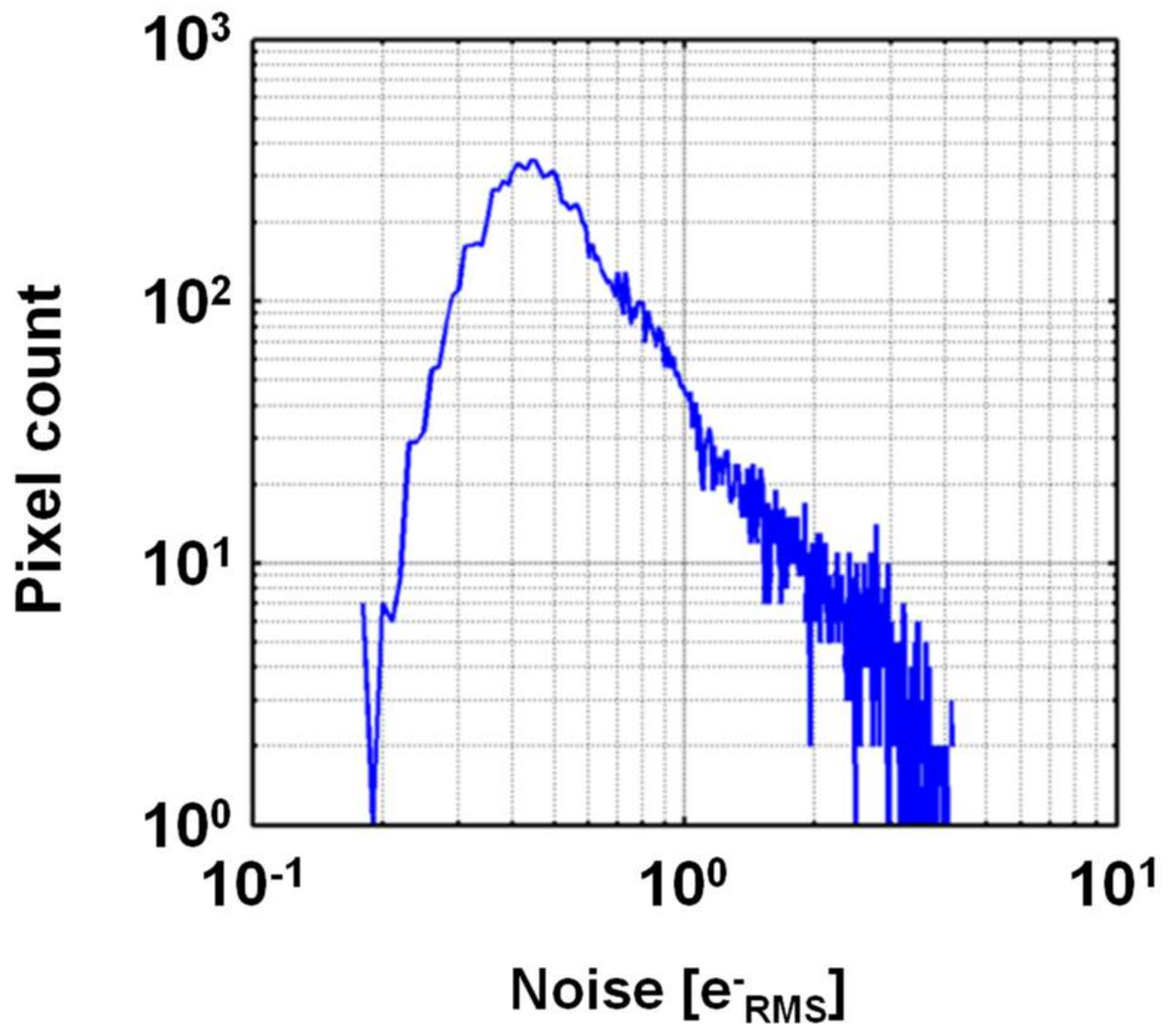
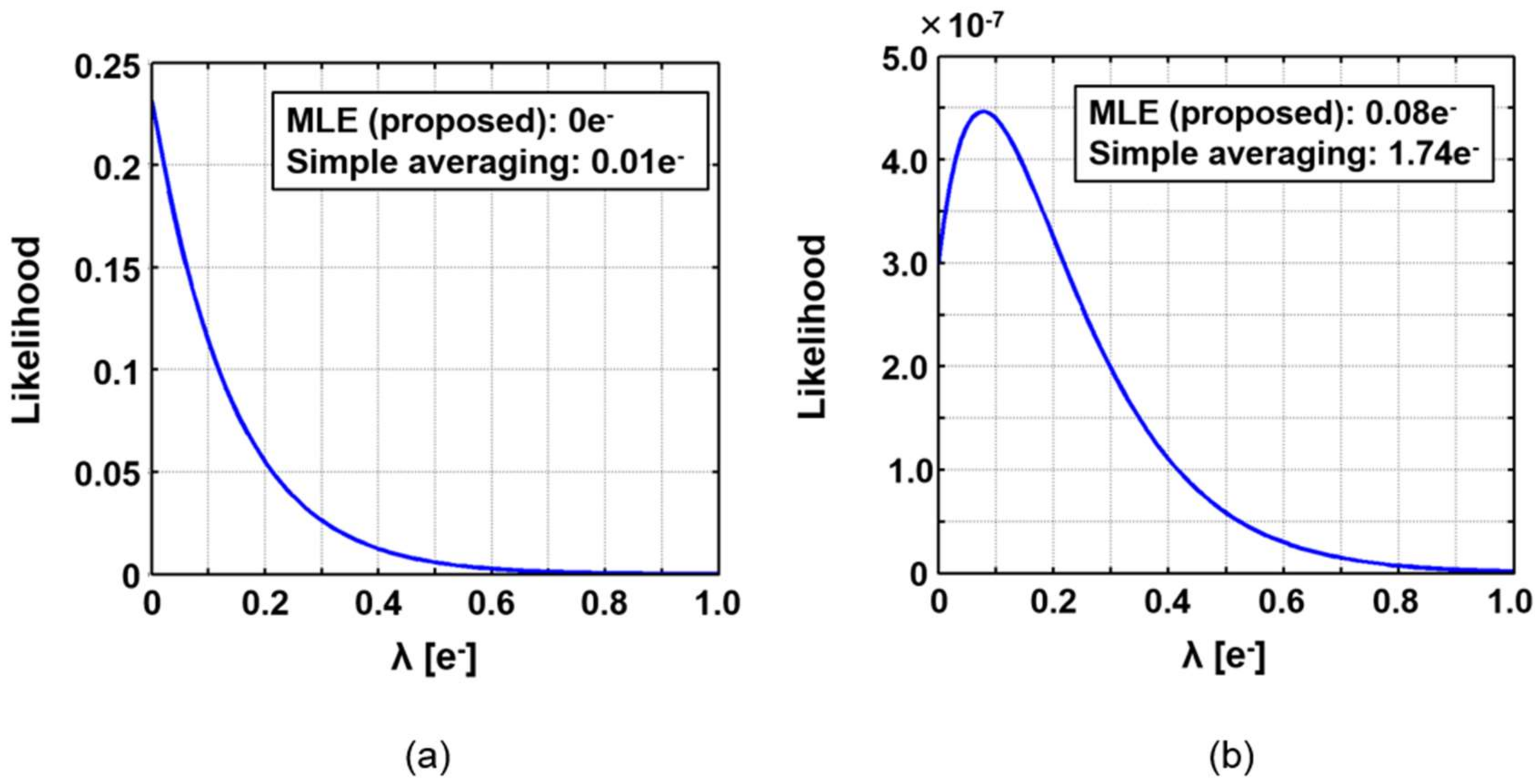
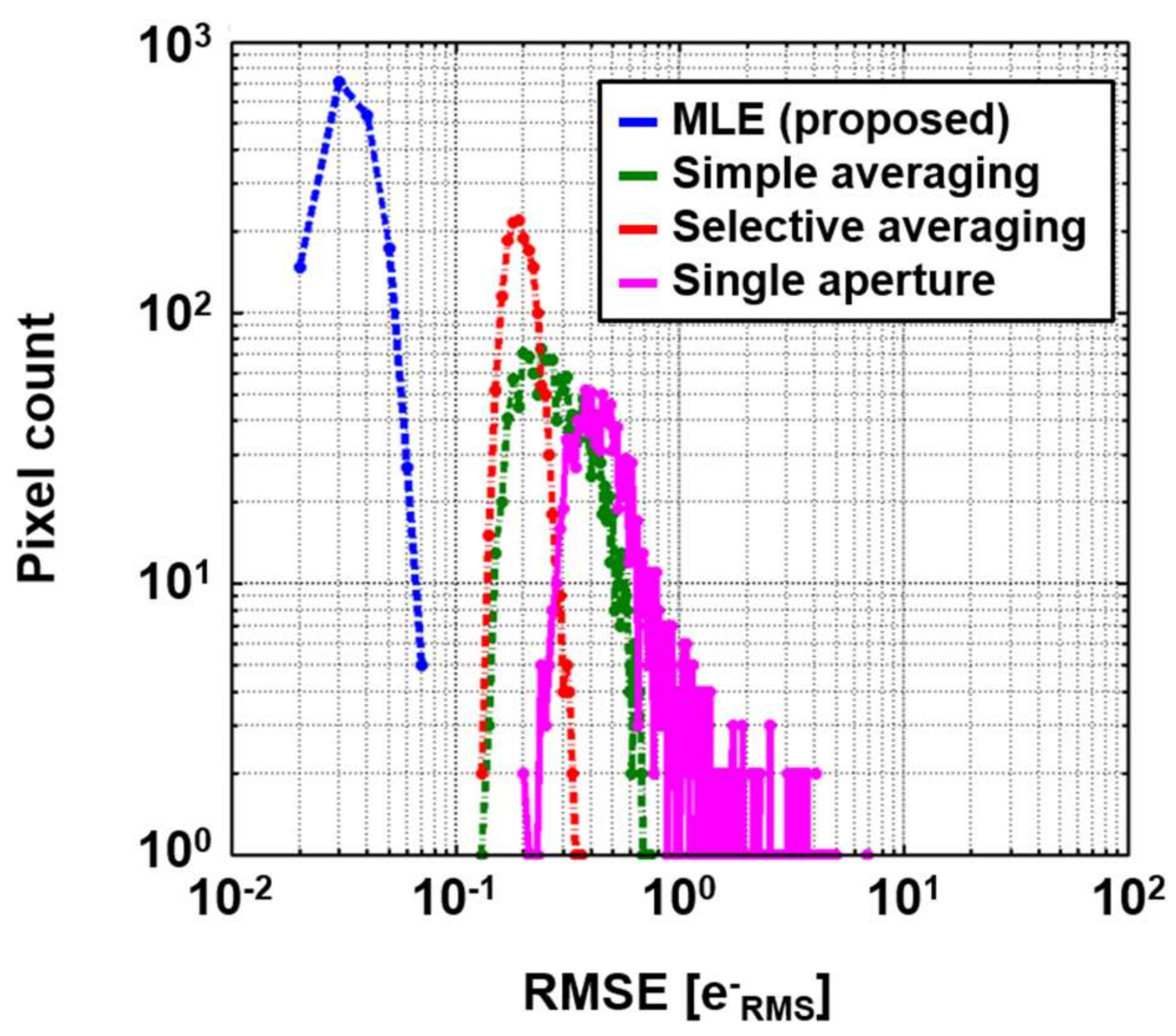
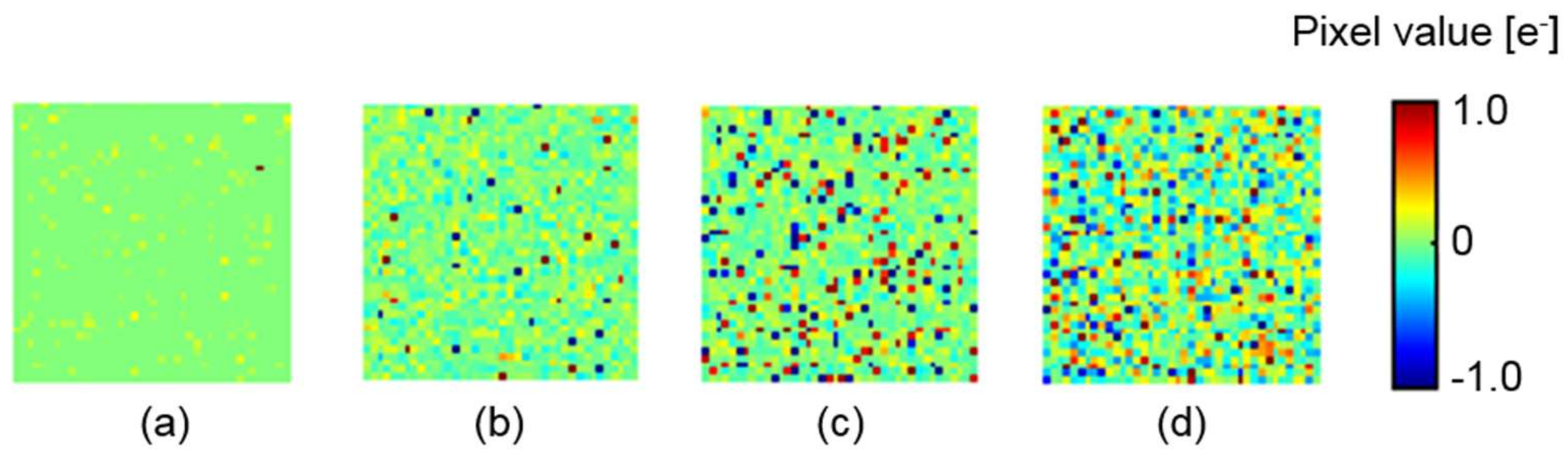
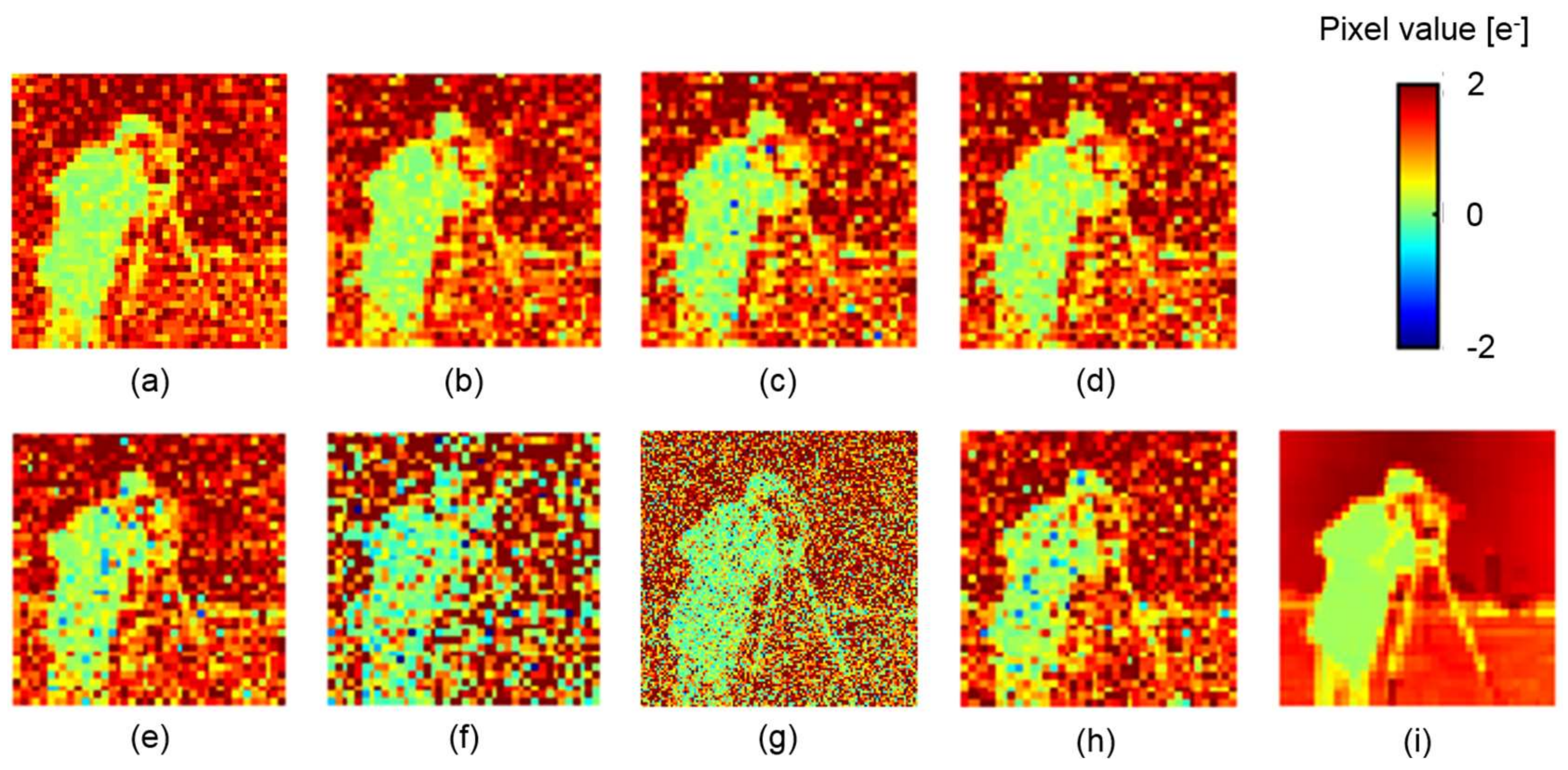
3. Verification by Simulation
4. Discussions
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tubbs, R.N.; Baldwin, J.E.; Mackay, C.D.; Cox, G.C. Diffraction limited CCD imaging with faint reference stars. Astron. Astrophys. 2002, 387, 21–24. [Google Scholar] [CrossRef]
- Niclass, C.; Sergio, M.; Charbon, E. A single photon avalanche diode array fabricated in deep-submicron CMOS technology. In Design, Automation, and Test in Europe; Springer: Dordrechtthe, The Netherlands, 2008; Volume 10, pp. 401–413. [Google Scholar]
- Aguilar, M.; Fay, D.A.; Ross, W.D.; Waxman, A.M.; Ireland, D.B.; Racamato, J.P. Real-time fusion of low-light CCD and uncooled IR imagery for color night vision. Proc. SPIE 1998, 3364, 124–135. [Google Scholar]
- Blum, R.S.; Liu, Z. Multi-Sensor Image Fusion and Its Applications; CRC Press: Boca Raton, FL, USA, 2005; ISBN 978-1-4200-2698-6. [Google Scholar]
- Jerram, P.A.; Pool, P.J.; Burt, D.J.; Bell, R.T.; Robbins, M.S. Electron Multiplying CCDs. In Proceedings of the SNIC Symposium, Stanford, CA, USA, 3–6 April 2006; pp. 3–6. [Google Scholar]
- Ives, D.; Bezawada, N.; Dhillon, V.; Marsh, T. ULTRASPEC: An electron multiplication CCD camera for very low light level high speed astronomical spectrometry. In Proceedings SPIE High Energy, Optical, and Infrared Detectors for Astronomy III; SPIE: Bellingham, WA, USA, 2008; Volume 7021, pp. 1–11. [Google Scholar]
- Tanioka, K.; Yamazaki, J.; Shidara, K.; Taketoshi, K.; Kawamura, T.; Ishioka, S.; Takasaki, Y. An avalanche-mode amorphous Selenium photoconductive layer for use as a camera tube target. IEEE Electron. Device Lett. 1987, 8, 392–394. [Google Scholar] [CrossRef]
- Dutton, N.; Parmesan, L.; Holmes, A.; Grant, L.; Henderson, R. 320×240 Oversampled Digital Single Photon Counting Image Sensor. In Proceedings of the 2014 Symposium on VLSI Circuits Digest of Technical Papers, Honolulu, HI, USA, 10–13 June 2014; pp. 1–2. [Google Scholar]
- Ma, J.; Fossum, E.R. Quanta Image Sensor Jot with Sub 0.3e− r.m.s. Read Noise and Photon Counting Capability. IEEE Electron. Device Lett. 2015, 36, 926–928. [Google Scholar] [CrossRef]
- Masoodian, S.; Ma, J.; Starkey, D.; Yamashita, Y.; Fossum, E.R. A 1Mjot 1040fps Stacked BSI Quanta Image Sensor with Cluster-Parallel Readout. In Proceedings of the International Image Sensor Workshop (IISW), Hiroshima, Japan, 30 May–2 June 2017; pp. 230–233. [Google Scholar]
- Wakashima, S.; Kusuhara, F.; Kuroda, R.; Sugawa, S. A linear response single exposure CMOS image sensor with 0.5e− readout noise and 76ke− full well capacity. In Proceedings of the 2015 Symposium on VLSI Circuits (VLSI Circuits), Kyoto, Japan, 17–19 June 2015; pp. 88–89. [Google Scholar]
- Seo, M.-W.; Kawahito, S.; Kagawa, K.; Yasutomi, K. A Read Noise 220-μV/e− Conversion Gain Reset-Gate-Less CMOS Image Sensor With 0.11-μm CIS Process. IEEE Electron. Device Lett. 2015, 36, 1344–1347. [Google Scholar]
- Seo, M.-W.; Wang, T.; Jun, S.-W.; Akahori, T.; Kawahito, S. A Read-Noise 32fps 0.5Mpixel High-Sensitivity RG-Less-Pixel CMOS Image Sensor Using Bootstrapping Reset. In Proceedings of the 2017 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 5–9 February 2017; pp. 80–81. [Google Scholar]
- Leyris, C.; Martinez, F.; Valenza, M.; Hoffmann, A.; Vildeuil, J.C.; Roy, F. Impact of Random Telegraph Signal in CMOS Image Sensors for Low-Light Levels. In Proceedings of the 32nd European IEEE Solid-State Circuits Conference, Montreux, Switzerland, 19–21 September 2006; pp. 376–379. [Google Scholar]
- Virmontois, C.; Goiffon, V.; Magnan, P.; Saint-Pe, O.; Girard, S.; Petit, S.; Rolland, G.; Bardoux, A. Total Ionizing Dose Versus Displacement Damage Dose Induced Dark Current Random Telegraph Signals in CMOS Image Sensors. IEEE Trans. Nucl. Sci. 2011, 58, 3085–3094. [Google Scholar] [CrossRef]
- Virmontois, C.; Goiffon, V.; Robbins, M.S.; Tauziède, L.; Geoffray, H.; Raine, M.; Girard, S.; Gilard, O.; Magnan, P.; Bardoux, A. Dark Current Random Telegraph Signals in Solid-State Image Sensors. IEEE Trans. Nucl. Sci. 2013, 60, 4323–4331. [Google Scholar] [CrossRef]
- Durnez, C.; Goiffon, V.; Rizzolo, S.; Magnan, P.; Virmontois, C.; Rubaldo, L. Localization of Dark Current Random Telegraph Signal sources in pinned photodiode CMOS Image Sensors. In Proceedings of the International Conference on Noise and Fluctuations (ICNF), Vilnius, Lithuania, 20–23 June 2017; pp. 1–4. [Google Scholar]
- Wang, X.; Rao, P.R.; Mierop, A.; Theuwissen, A.J.P. Random Telegraph Signal in CMOS Image Sensor Pixels. In Proceedings of the International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 11–13 December 2006; pp. 1–4. [Google Scholar]
- Tega, N.; Miki, H.; Osabe, T.; Kotabe, A.; Otsuga, K.; Kurata, H.; Kamohara, S.; Tokami, K.; Ikeda, Y.; Yamada, R. Anomalously Large Threshold Voltage Fluctuation by Complex Random Telegraph Signal in Floating Gate Flash Memory. In Proceedings of the International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 11–13 December 2006; pp. 491–494. [Google Scholar]
- Abe, K.; Sugawa, S.; Kuroda, R.; Watabe, S.; Miyamoto, N.; Teramoto, A.; Ohmi, T.; Kamada, Y.; Shibusawa, K. Analysis of Source Follower Random Telegraph Signal Using nMOS and pMOS Array TEG. In Proceedings of the 2007 International Image Sensor Workshop (IISW), Ogunquit, ME, USA, 7–10 June 2007; pp. 62–65. [Google Scholar]
- Gonthier, P.M.; Magnan, P. RTS noise impact in CMOS image sensors readout circuit. In Proceedings of the International Conference on Electronics Circuits and Systems (ICECS), Yasmine Hammamet, Tunisia, 13–16 December 2009; pp. 1323–1324. [Google Scholar]
- Gonthier, P.M.; Goiffon, V.; Magnan, P. In-Pixel Source Follower Transistor RTS Noise Behavior under Ionizing Radiation in CMOS Image Sensors. IEEE Trans. Electron. Devices 2012, 59, 1686–1692. [Google Scholar] [CrossRef][Green Version]
- Wang, X. Noise in Sub-Micron CMOS Image Sensors. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2008. [Google Scholar]
- Mendis, S.; Kemeny, S.; Gee, R.; Pain, B.; Kim, Q.; Fossum, E.R. CMOS active pixel image sensors for highly integrated imaging system. IEEE J. Solid-State Circuits 1997, 32, 187–197. [Google Scholar] [CrossRef]
- Zhang, B.; Kagawa, K.; Takasawa, T.; Seo, M.-W.; Yasutomi, K.; Kawahito, S. RTS Noise and Dark Current White Defects Reduction Using Selective Averaging Based on a Multi-Aperture System. Sensors 2014, 14, 1528–1543. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Kagawa, K.; Takasawa, T.; Seo, M.-W.; Yasutomi, K.; Kawahito, S. Low-light Color Reproduction by Selective Averaging in Multi-aperture Camera with Bayer Color-filter Low-noise CMOS Image Sensors. ITE Trans. Media Technol. Appl. 2015, 3, 234–239. [Google Scholar] [CrossRef][Green Version]
- Naemura, T.; Harashima, H. A Real-Time System for Image-Based Rendering from a Multi-View Video—Video-Based Rending. Trans. Virtual Real. Soc. Jpn. 1999, 4, 639–646. (In Japanese) [Google Scholar]
- Yang, J.C.; Everett, M.; Buehler, C.; McMillan, L. A Real-Time Distributed Light Field Camera. In Proceedings of the 13th Eurographics Workshop on Rending, Pisa, Italy, 26–28 June 2002; pp. 77–86. [Google Scholar]
- Wilburn, B.; Joshi, N.; Vaish, V.; Talvala, E.-V.; Antunez, E.; Barth, A.; Adams, A.; Horowitz, M.; Levoy, M. High Performance Imaging Using Large Camera Arrays. ACM Trans. Graph. (TOG) 2005, 24, 765–776. [Google Scholar] [CrossRef]
- Kugenuma, K.; Komuro, T.; Zhang, B.; Kagawa, K.; Kawahito, S. High-sensitivity Imaging Using a Multi-aperture Camera based on Imaging Synthesis with Disparity Compensation. In Proceedings of the International Workshop on Advanced Image Technology (IWAIT 2017), Penang, Malaysia, 6–8 January 2017; pp. 1–4. [Google Scholar]
- Fisher, R.A. On the mathematical foundations of theoretical statistics. Philos. Trans. R. Soc. 1922, 222, 309–368. [Google Scholar] [CrossRef]
- Lehmann, E.L.; Casella, G. Theory of Point Estimation, 2nd ed.; Springer: New York, NY, USA, 1998; ISBN 0-387-98502-6. [Google Scholar]
- Becker, J.; Wilhelmus, B.H. Optical Lens System Having a Relative Aperture Larger than f/1. U.S. Patent 2978957A, 11 April 1961. [Google Scholar]
- Green, P.; Sun, W.; Matusik, W.; Durand, F. Multi-aperture photography. ACM Trans. Graph. (TOG) 2007, 26, 68. [Google Scholar] [CrossRef]
- Ishida, H.; Kagawa, K.; Seo, M.-W.; Komuro, T.; Zhang, B.; Takasawa, T.; Yasutomi, K.; Kawahito, S. RTS and photon shot noise reduction based on maximum likelihood estimate with multi-aperture optics and semi-photon-counting-level CMOS image sensors. In Proceedings of the IS&T Electronic Imaging, Image Sensors and Imaging Systems 2017, San Francisco, CA, USA, 29 January–2 February 2017; pp. 80–83. [Google Scholar]
- Seo, M.-W.; Suh, S.-H.; Iida, T.; Takasawa, T.; Isobe, K.; Watanabe, T.; Itoh, S.; Yasutomi, K.; Kawahito, S. A Low-Noise High Intrascene Dynamic Range CMOS Image Sensor with a 13 to 19b Variable-Resolution Column-Parallel Folding-Integration/Cyclic ADC. IEEE J. Solid-State Circuits 2012, 47, 272–283. [Google Scholar] [CrossRef]
- Pavelka, J.; Šikula, J.; Tacano, M.; Toita, M. Activation Energy of RTS Noise. Radioengineering 2011, 20, 194–199. [Google Scholar]

| PSNR [dB] | RMSE [] | |
|---|---|---|
| Shot-noise limited | 14.52 | 0.36 |
| MLE (proposed) | 13.14 | 0.42 |
| Selective averaging | 11.61 | 0.51 |
| Selective averaging (non-negative values) | 11.76 | 0.49 |
| Simple averaging | 11.92 | 0.49 |
| Single aperture | 2.37 | 1.36 |
| Single aperture (120 × 120 pixels) | 2.20 | 1.54 |
| Single aperture (40 × 40 pixels binned from 120 × 120 pixels) | 11.76 | 0.49 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishida, H.; Kagawa, K.; Komuro, T.; Zhang, B.; Seo, M.-W.; Takasawa, T.; Yasutomi, K.; Kawahito, S. Multi-Aperture-Based Probabilistic Noise Reduction of Random Telegraph Signal Noise and Photon Shot Noise in Semi-Photon-Counting Complementary-Metal-Oxide-Semiconductor Image Sensor. Sensors 2018, 18, 977. https://doi.org/10.3390/s18040977
Ishida H, Kagawa K, Komuro T, Zhang B, Seo M-W, Takasawa T, Yasutomi K, Kawahito S. Multi-Aperture-Based Probabilistic Noise Reduction of Random Telegraph Signal Noise and Photon Shot Noise in Semi-Photon-Counting Complementary-Metal-Oxide-Semiconductor Image Sensor. Sensors. 2018; 18(4):977. https://doi.org/10.3390/s18040977
Chicago/Turabian StyleIshida, Haruki, Keiichiro Kagawa, Takashi Komuro, Bo Zhang, Min-Woong Seo, Taishi Takasawa, Keita Yasutomi, and Shoji Kawahito. 2018. "Multi-Aperture-Based Probabilistic Noise Reduction of Random Telegraph Signal Noise and Photon Shot Noise in Semi-Photon-Counting Complementary-Metal-Oxide-Semiconductor Image Sensor" Sensors 18, no. 4: 977. https://doi.org/10.3390/s18040977
APA StyleIshida, H., Kagawa, K., Komuro, T., Zhang, B., Seo, M.-W., Takasawa, T., Yasutomi, K., & Kawahito, S. (2018). Multi-Aperture-Based Probabilistic Noise Reduction of Random Telegraph Signal Noise and Photon Shot Noise in Semi-Photon-Counting Complementary-Metal-Oxide-Semiconductor Image Sensor. Sensors, 18(4), 977. https://doi.org/10.3390/s18040977




