3.1. The Mathematical Model and Verified Experiment of Inclination Angle Error
Based on the laser triangulation principle, a laser displacement sensor is mainly composed of laser driver, laser diode, collimating lens, imaging lens, photoelectric coupling surface CCD, and signal processing circuit. The basic principle is shown in
Figure 4, in which
X is the displacement of the measured object plane,
X’ is the displacement of the light spot image on the CCD,
α is the angle between the optical axis of imaging lens and the laser beam,
β is the angle between the optical axis of imaging lens and the CCD plane,
L is the object distance of imaging lens, and
L’ is the image distance of imaging lens. According to the theorem of similar triangles, it can be concluded that:
Equation (1) is the theoretical formula of laser triangulation, from which we can see the laser triangulation principle that the image displacement
X’ presented to CCD via imaging lens reflects the actual displacement
X of the measured object. In the actual measurement, to ensure the data acquisition accuracy of the sensor, the Scheimpflug condition must be met, i.e., the imaging lens and the CCD receiving plane intersect at the point C of the laser beam, and the Gauss’ law must be satisfied. From
Figure 4 and the principle formula, the displacement measured by a sensor takes the vertical incidence of laser beam to the measured object plane as a base; nevertheless, the actual surface topography of a workpiece is so complex that the incident beam is inevitably not coincident with the surface normal. The angle between the incident beam and the surface normal is called the inclination angle
θ (positive if clockwise), and this phenomenon is called the measuring point inclination angle. The reason for inclination error is that as the measuring point inclination angle changes the distribution of laser scattering field, the light received by the imaging lens is changed accordingly, with the result that the light spot centroid imaged in the CCD is not coincident with that at the time of vertical incidence. However, the sensor still calculates the displacement, providing there is no measuring point, and eventually the error is caused. Therefore, an inclination error model is to be built to effectively improve the data acquisition accuracy of the laser displacement sensor.
Under ideal conditions, the measured object plane is considered as a diffuse surface without absorption. According to the Beer-Lambert Law (as shown in
Figure 5), the spatial distribution of light scattering field is
in which
φ is the angle between the scattering beam and the normal of the object plane;
I is the power of the scattered light, which is in the angular direction with the normal of the object plane; and
I0 is the ideal power of the scattered light in the normal direction.
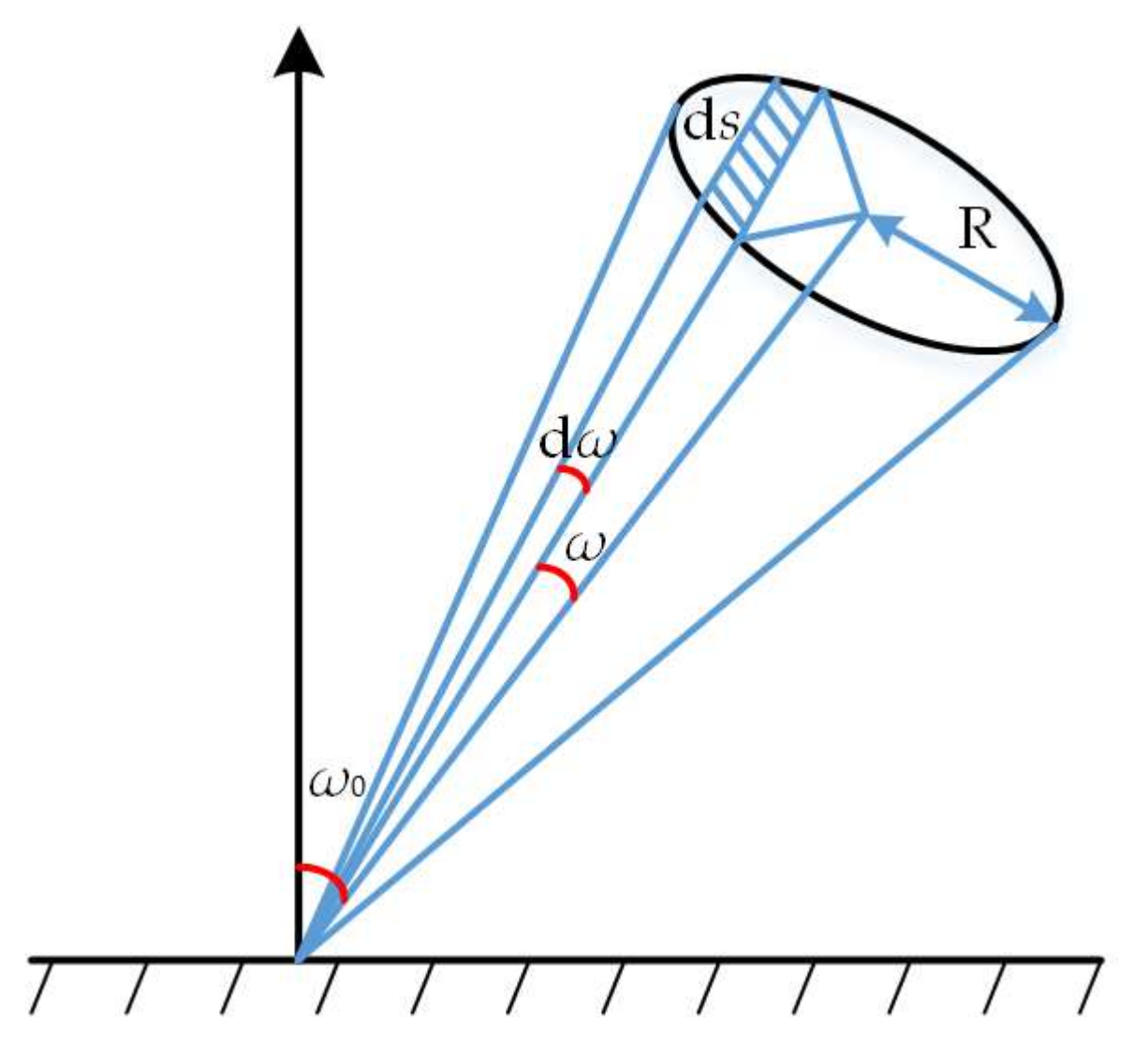
As shown in
Figure 6, we set d
s as the imaging lens surface vertical to the scattered light receiving surface, and then the light received in the unit time is
in which d
σ is the solid angle of the surface to the incidence point,
ω0 is the angle between the imaging lens axis and the normal of the measured object, and
ω is the angle between the imaging lens axis and the surface boundary. According to the geometrical relationship of the receiving surface in
Figure 6 and in combination with the Beer-Lambert Law, the light received by the imaging lens is
in which
R is the radius of imaging lens. Further, as
ω is very small, we approximately deem that sin
ω = tan
ω and
ω0 =
α −
θ, and hence it can be deduced that the angular position
ω1 of the light centroid line in imaging lens is
The projection point of the centroid line on the CCD is the centroid position of converged light spots, and the method for determining the position of the light centroid line on the CCD is given below.
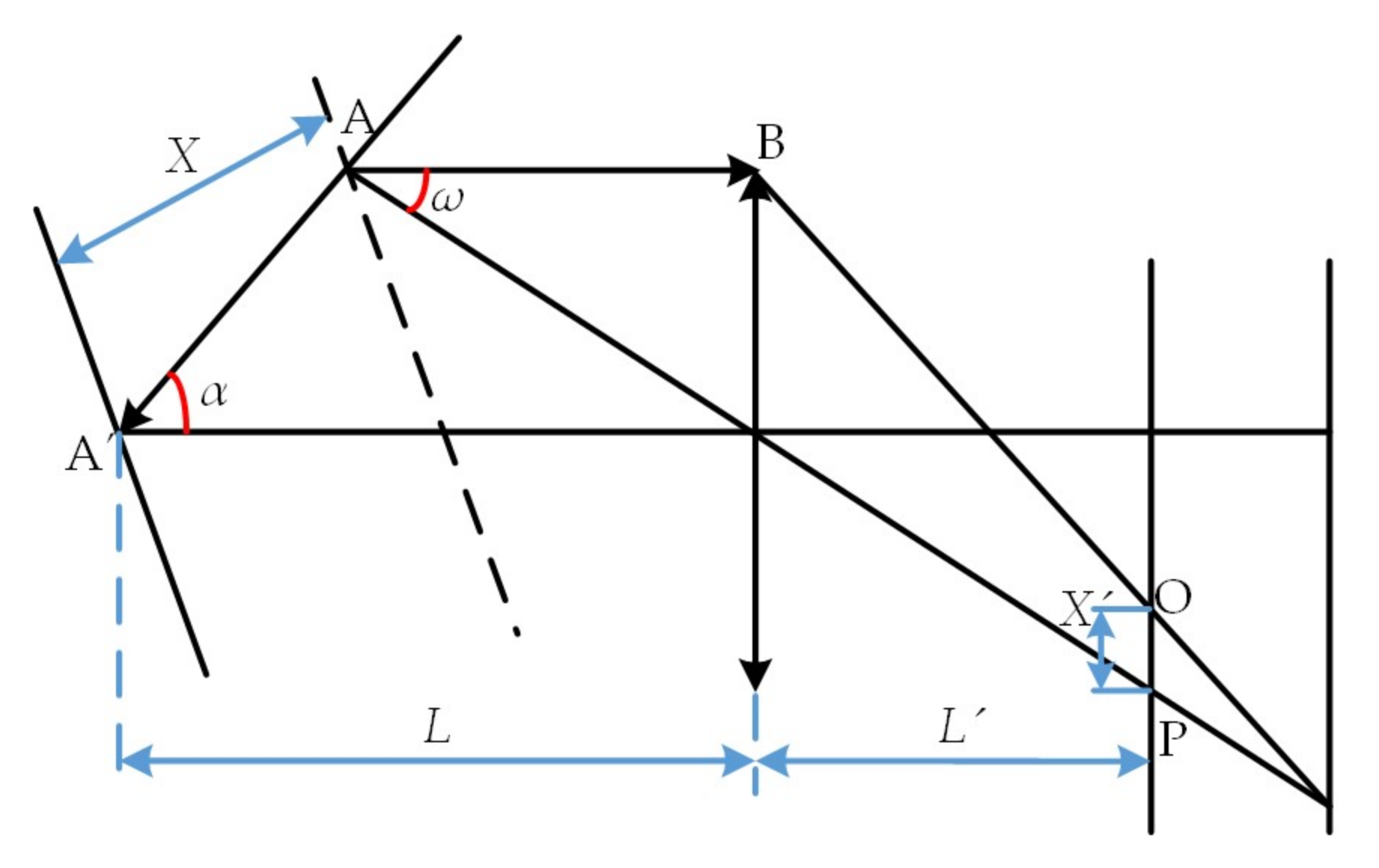
In the said paragraph, it is stated that in case of a measuring point inclination angle, the light centroid on the CCD relatively deviates from the geometric center of converged light spots, and the amount of deviation is the measuring point inclination error.
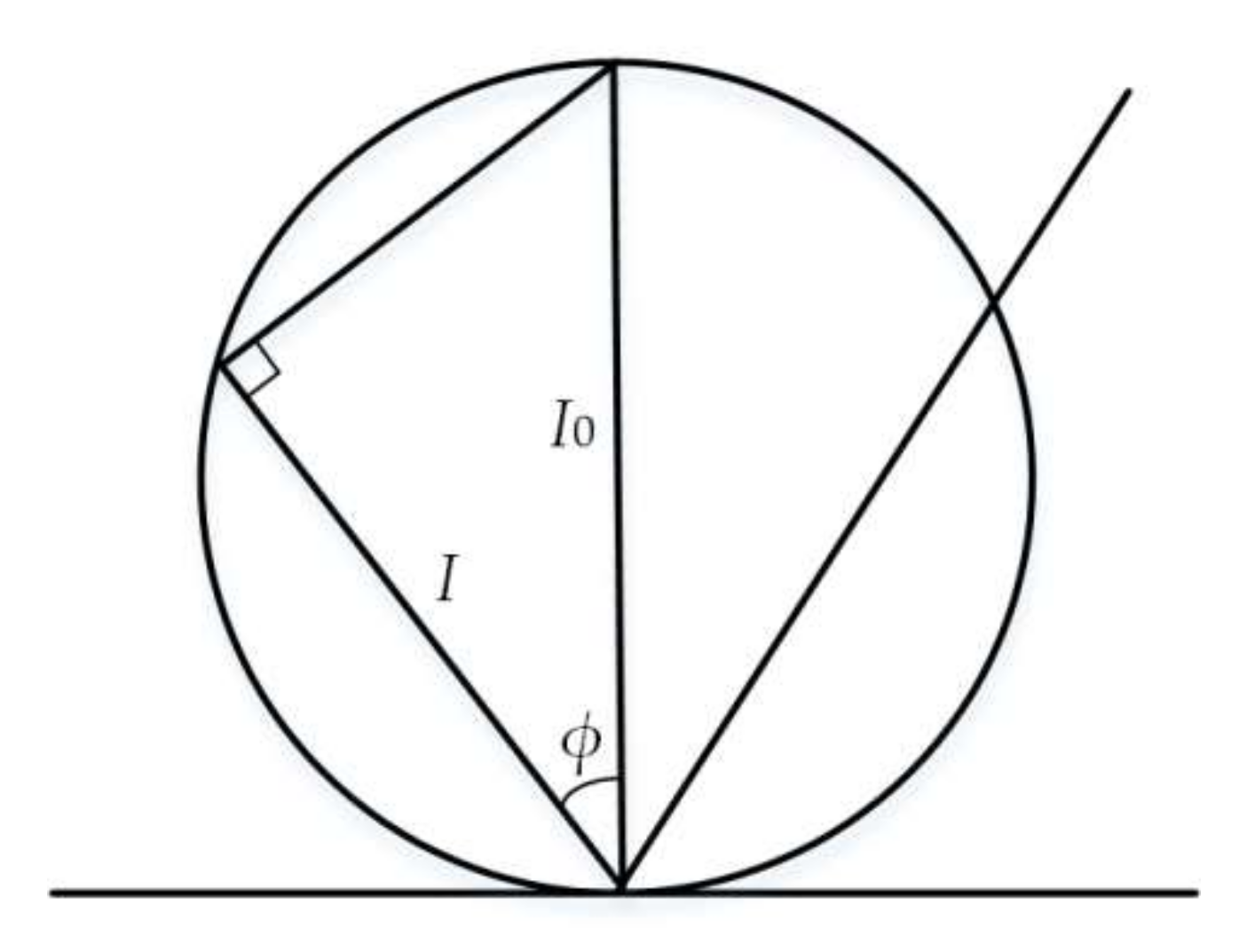
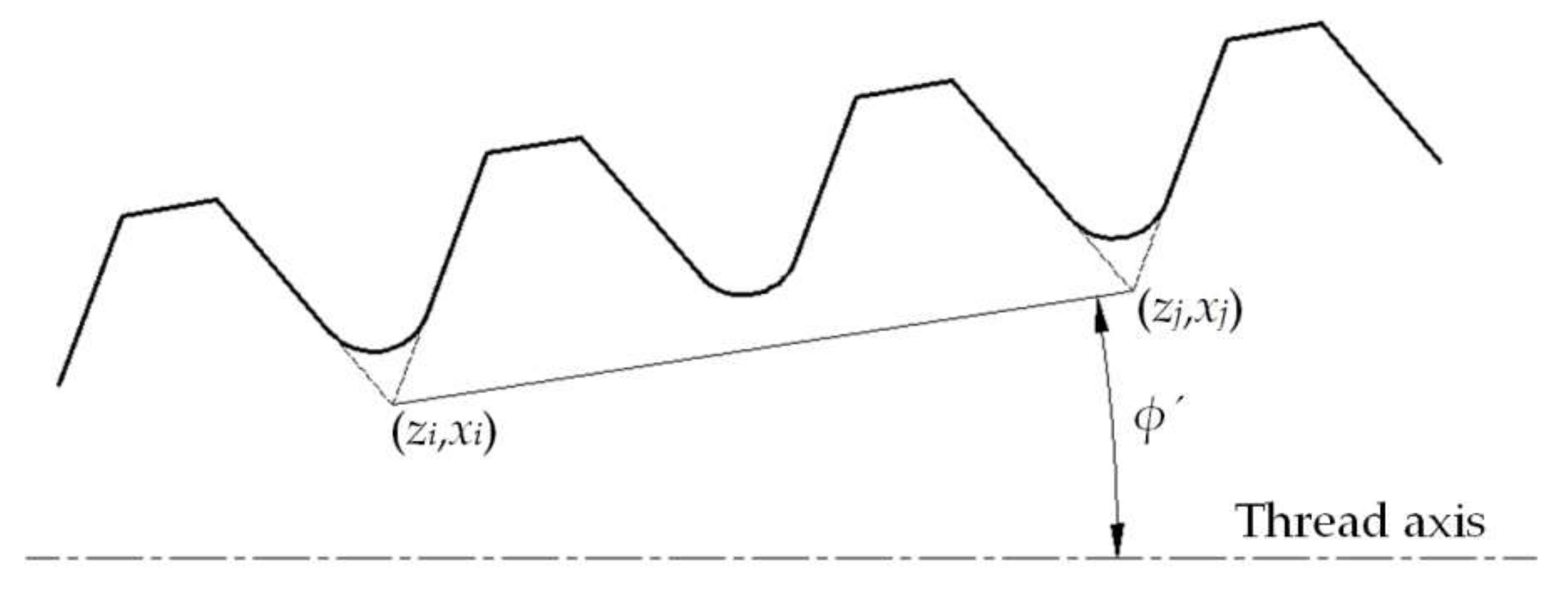
Figure 7 gives a schematic diagram of the light spot centroid, in which the point P on the CCD is the centroid position of the centroid line AB through the refraction of imaging lens. According to the geometrical relationship shown in
Figure 7, it can be reduced that the distance between the imaging point P of the light centroid line on the CCD and the imaging lens axis is
Combined with Equations (5) and (6), it can be concluded that when the incidence is vertical, i.e., the measuring point inclination angle is 0,
ω´ =
ω1, and
θ = 0, and when the inclination is accompanied by an inclination angle, i.e., the measuring point inclination angle is
θ,
ω´ =
ω1 and
θ ≠ 0, and the inclination error is
From Equation (7), it can be concluded that the measuring point inclination error is only related to the two variables of object plane displacement X and measuring point inclination angle θ, and the rest are the optical structural parameters of the laser displacement sensor. Through the analysis, it can be concluded that when the measuring point inclination angle is fixed, the measurement error increases with the increase of the measuring distance; when the measuring distance is fixed, the measurement error increases with the increase of the measuring point inclination angle; when θ > 0, the measurement error varies with the object plane displacement in the same direction; but when θ < 0, the measurement error varies with the object plane displacement in the opposite direction.
The said results are a quantitative model for the inclination error of the laser displacement sensor. Although some assumptions are made in the derivation process, and some parameters are approximated, the theoretical results are still somewhat deviated from the actual measurement values. However, in the engineering application, it is true that the quantitative model can effectively facilitate the data acquisition accuracy of the laser displacement sensor.
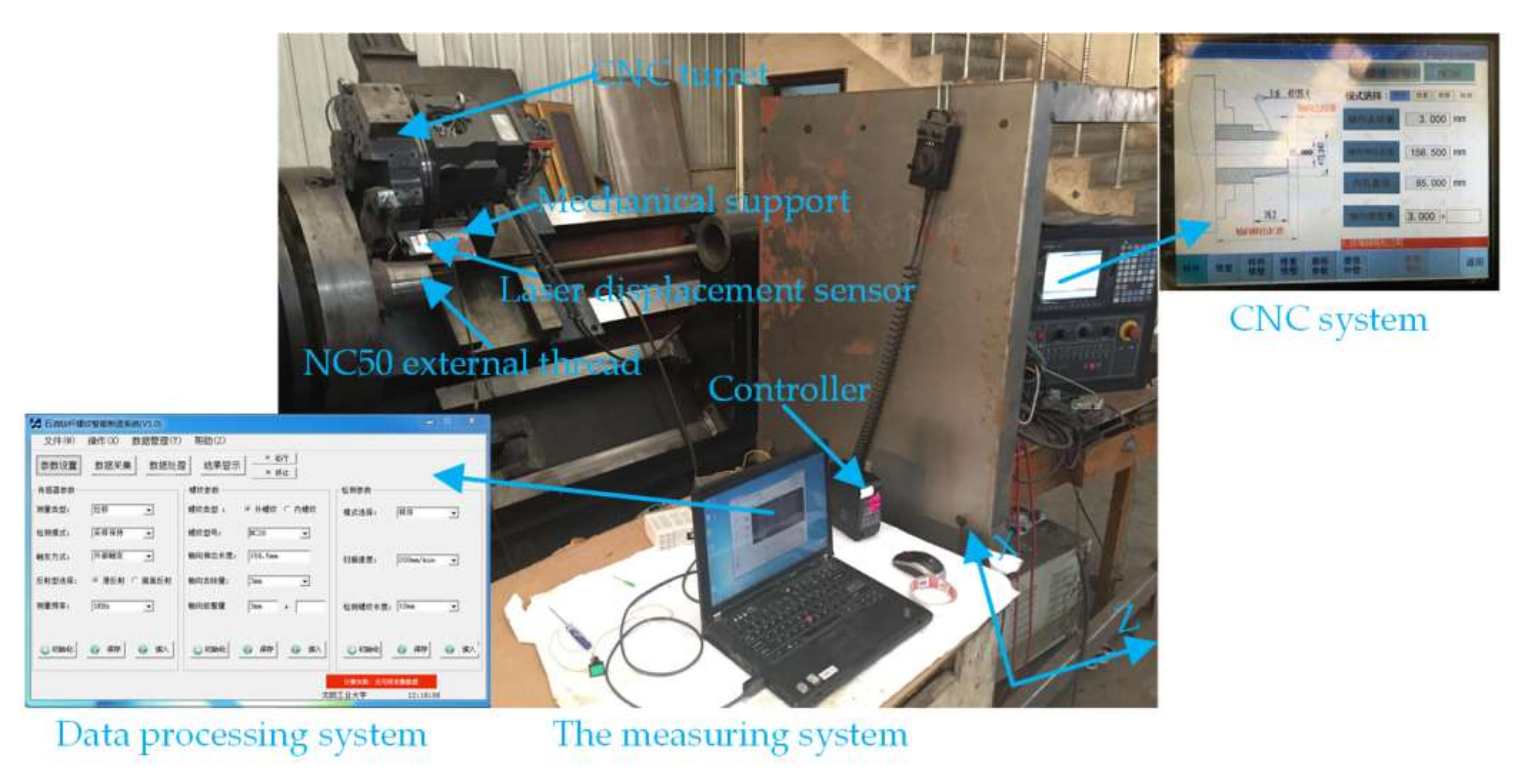
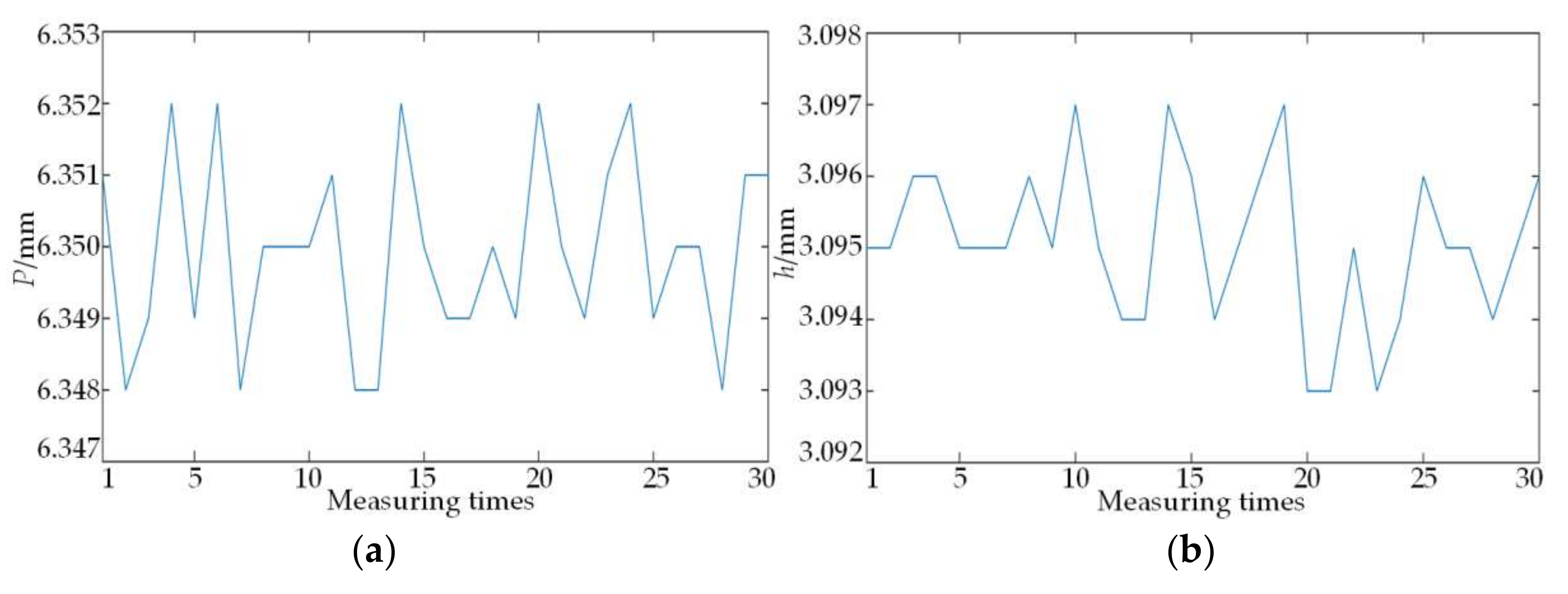
The inclination error experiment is composed of a four-axis vertical machining center, a laser interferometer, a laser displacement sensor, a sine bar, and a computer. The laser interferometer is manufactured by Renishaw, London England with the model of XL-30, with the specific measuring range of 30 m, the resolution of 0.01 μm, and the measurement error of ±0.1 ppm. The parameters of the laser displacement sensor and computer are both given in the said paragraphs.
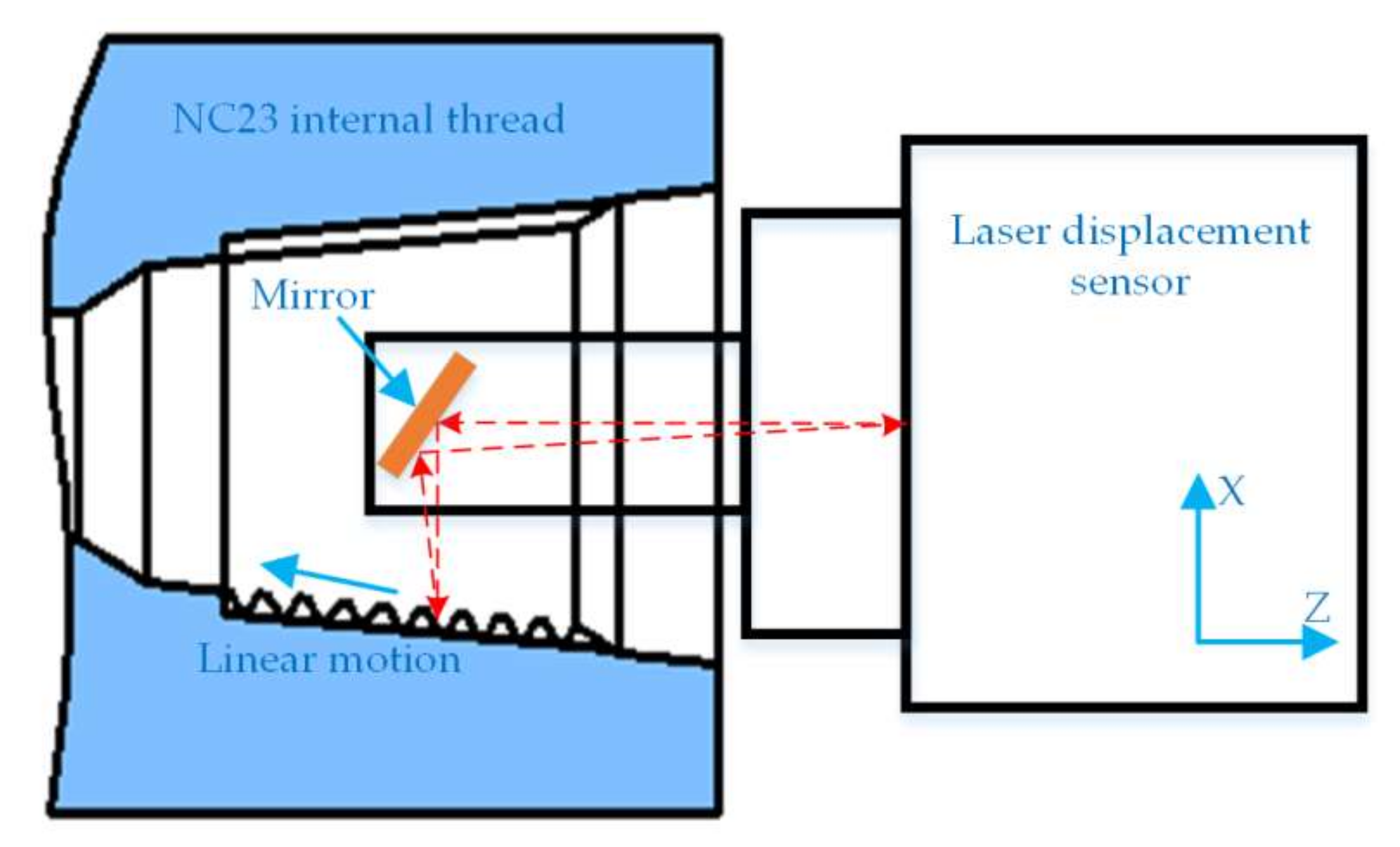
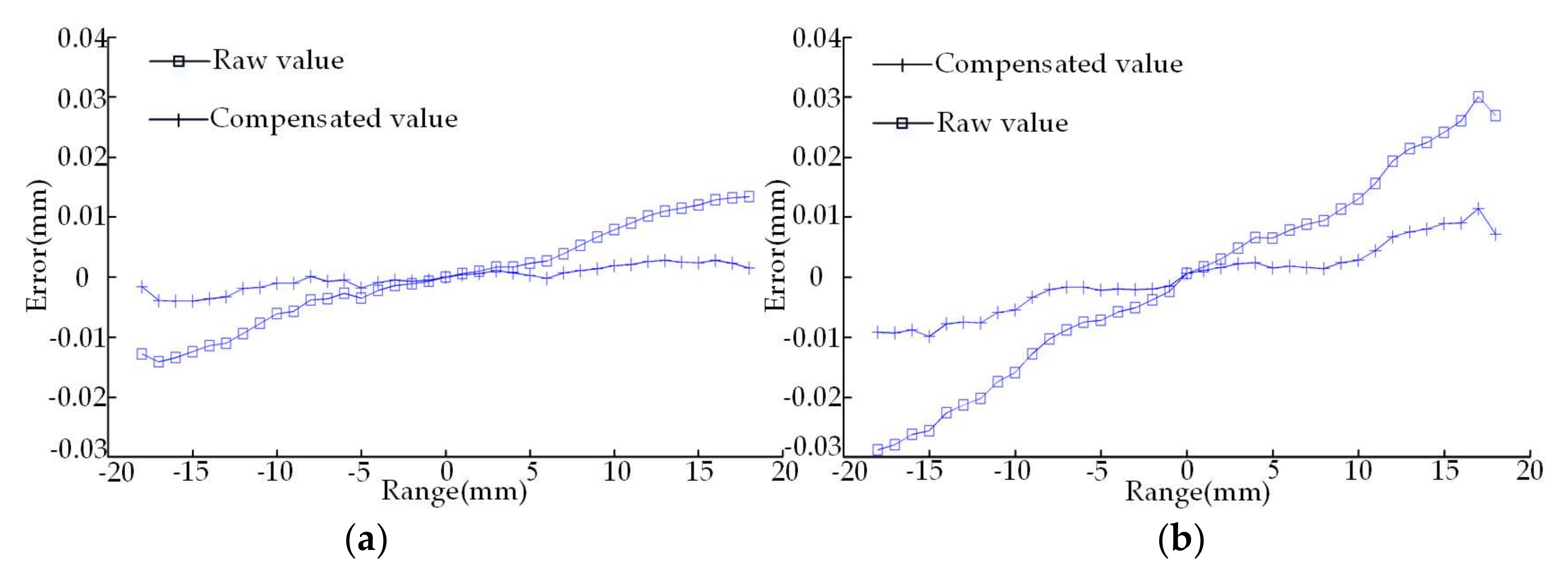
As the experimental process is shown in
Figure 8, the optical path components of the sensor and the interferometer are installed on the Z-axis and work platform of the machining center; the sine bar is placed on the work platform right below the sensor, and it can be jacked a certain angle by a gauge block; the sensor readings are shown on the controller; and the interferometer readings are displayed on the computer. After the start of the experiment, when the sensor and the interferometer move each 1 mm within the range of the laser displacement sensor, their values are recorded respectively. As the half of thread angle of the drill pipe is 30°, the measuring point inclination angle in the flank is 60°. For purpose of the preparation of the subsequent thread measurement experiment on the basis of verifying the inclination error model, the sine bars with the inclination angles 20° and 60° are built, along with the inclination error compensation shown in
Figure 9a,b.
Figure 9 demonstrates that when the inclination angle of the object plane is fixed, the measurement error of the laser displacement sensor increases with the increase of the measuring distance; and when the measuring distance is fixed, the measurement error of the laser displacement sensor increases with the increase of the inclination angle of the object plane. The inclination error experiment proves that the proposed mathematical model of inclination error is both accurate and effective. Through this model, we can not only quantitatively calculate the measurement error of the laser displacement sensor caused by the inclination angle but also significantly improve the data acquisition accuracy through error compensation.
3.2. An Improved Wavelet Threshold Denoising Algorithm and Simulation
The point cloud data acquired by the laser displacement sensor is affected by the surface properties and geometrical topography of thread and the structure of the measuring system, resulting in random noises in the measured data. Therefore, it is required to denoise the original data. In this section, we process the noises in the thread contour data by using the wavelet denoising method applied in the signal analysis. In the wavelet threshold denoising, the quantified threshold function is the key to denoising effects. At present, the threshold functions are mainly:
- (1)
The hard threshold function:
- (2)
The soft threshold function:
- (3)
The improved threshold function in Reference [
26]:
in which x is wavelet coefficient, is threshold, σ is the noise standard deviation in the point cloud data (i.e., noise intensity), and N is data amount. When it comes to the solution of actual problems, we need to estimate the unknown parameters.
The said three threshold functions all have some drawbacks, although they achieve certain denoising effects. In Equation (8), the hard threshold function is discontinuous in , which leads to the reconstruction oscillation of the wavelet coefficients with poor denoising degrees; in Equation (9), the real wavelet coefficients of the soft threshold function deviate from the estimated wavelet coefficients, which results in the poor approximation of the reconstructed data to the real data; and Equation (10) presents a multitude of improved threshold functions that improve the phenomenon of discontinuity but still fail to solve the deviation of wavelet coefficients in the wavelet decomposition. Therefore, there still remains data distortion to various degrees after denoising by these methods.
In view of the deficiencies of the said wavelet threshold denoising algorithm, a new wavelet threshold function is proposed, which cannot only control the constant deviation of wavelet coefficients but also fully ensure the function is continuous and high-order derivative within the threshold range. The new threshold function is
in which coefficients
a,
b (
a,
b > 0) are the adjusting parameters of the new threshold function, and when the random error of point cloud data is removed, the adjustment of the said two coefficients can change the variation mode of threshold function. The adjustment of coefficients
m (0 ≤
m ≤ 1),
n (0 ≤
n ≤ 1), which are approximated parameters of the reconstructed data in interval range, not only ensure the global continuity of the hard threshold function without oscillation but also effectively control the constant deviation of wavelet coefficients of the soft threshold function in the wavelet decomposition. Finally, the function still has all the advantages of traditional threshold functions. According to the said analysis, the new wavelet threshold function not only ensures the denoising effects but also avoids killing the real data. Moreover, the new wavelet threshold function is more flexible and performs better.
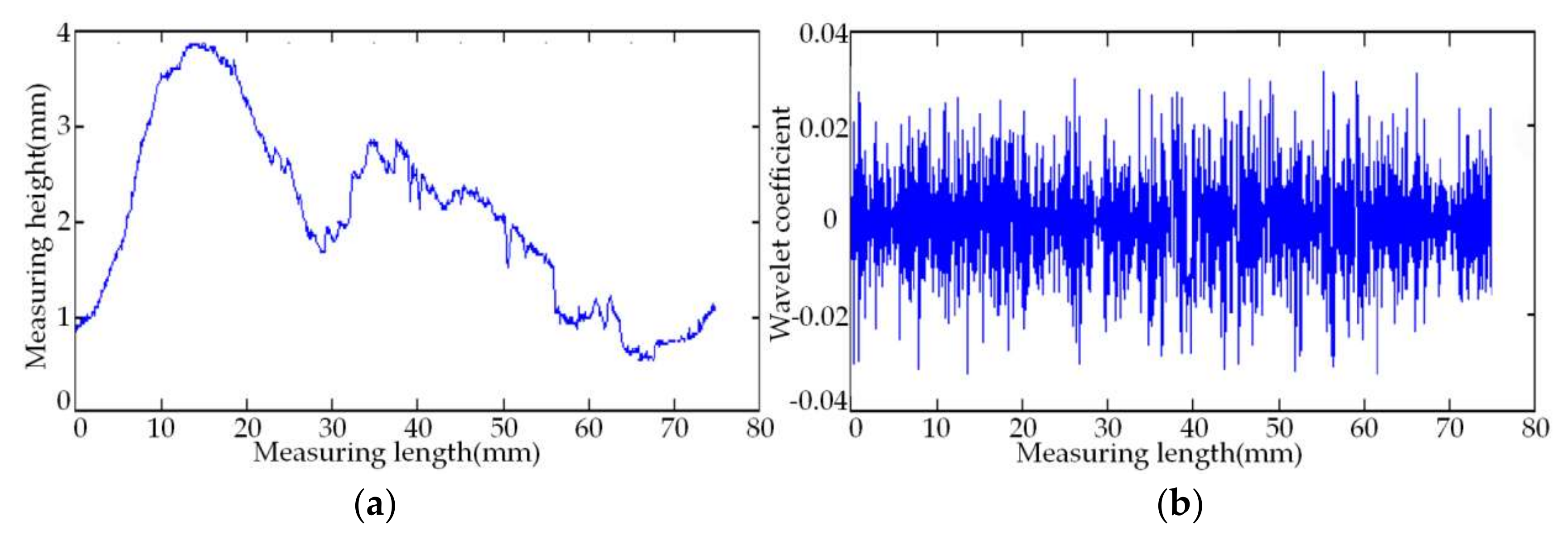
As shown in
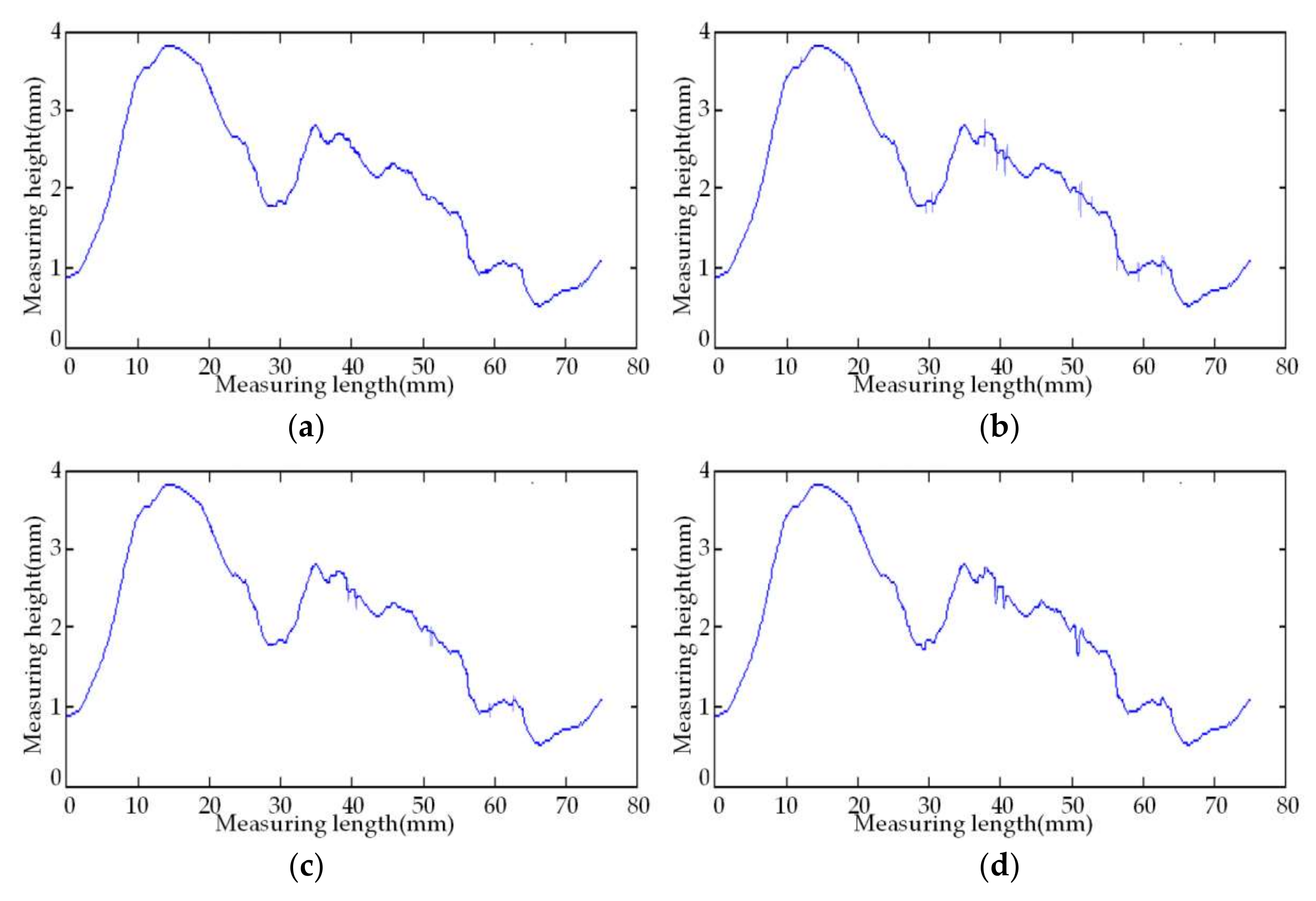
Figure 10, the simulation experiment employs a set of measuring point cloud data with random errors, as well as the original data and its wavelet-decomposed coefficients. Sym4, sym6, and sym8 in Symlets wavelets and db6, db8, and db10 in Daubechies wavelets are selected as the mother wavelet functions that are used to denoise the point cloud data. After comparison of the results, the sym8 wavelet is finally chosen to make the five-level wavelet decomposition of the set of data.
In order to prove the new threshold function’s ability to denoise the random errors in the noisy cloud data, we respectively employ the traditional soft and hard threshold functions, the improved threshold function in Reference [
26], and the proposed self-adaptive wavelet threshold function to denoise the data in
Figure 10. In this paper, the proposed wavelet threshold denoising algorithm uses the heuristic threshold rule (the Heursure rule) to carry out the self-adaptive threshold denoising. The parameters of the proposed improved threshold function are set to be
a = 5,
b = 2,
m = 0.6,
n = 0.9, and the experimental data after denoising are shown in
Figure 11.
Compared with the said four graphs, it can be clearly found that the soft threshold function performs better in denoising; nonetheless, it kills the real data details in a more severe way; the hard threshold function performs worse in denoising, and it cannot well filter random errors; and the improved threshold function in Reference [
26] solves the oscillation phenomenon caused by the discontinuity of the hard threshold function in
, improving the level of data denoising and various performance indicators. However, some real data details are filtered while enhancing the denoising capacity. The new self-adaptive wavelet threshold function proposed in this paper successfully solves the said problems. It not only avoids the oscillation phenomenon caused by the discontinuity but also controls the false deletion of the high-frequency signal in the real data information, improving the data reconstruction accuracy. Additionally, it achieves significant effects in the denoising and the maintenance of data reality and integrity.
In order to accurately compare the denoising effects of the traditional soft and hard threshold functions with the said two threshold functions, it is necessary to introduce a unified and objective assessment criterion. In this paper, quantitative analysis is conducted in accordance with three assessment indexes for the denoising performance, namely, signal-to-noise ratio, root-mean-square error, and smoothness:
- (1)
SNR (Signal-to-noise ratio) is defined as follows:
- (2)
RMSE (Root-mean-square error) of original data and denoised data is defined as follows:
- (3)
Smoothness is defined as follows:
in which is original data, is the data after the wavelet function denoising, and n is the number of data points. The definition is shown as follows: the greater the SNR (unit: dB) of the data after denoising is, the smaller the RMSE and the smoothness R value are. This indicates that the data after denoising is much closer to the original data, with better denoising effects.
The values of the said three assessment indexes after denoising by four threshold functions are shown in
Table 1. It can be seen from the table that the new self-adaptive wavelet threshold function proposed in this paper significantly outperforms other threshold functions in denoising the point cloud data.
3.3. Thread Contour Partitioning, Fitting, and Parameters Calculation
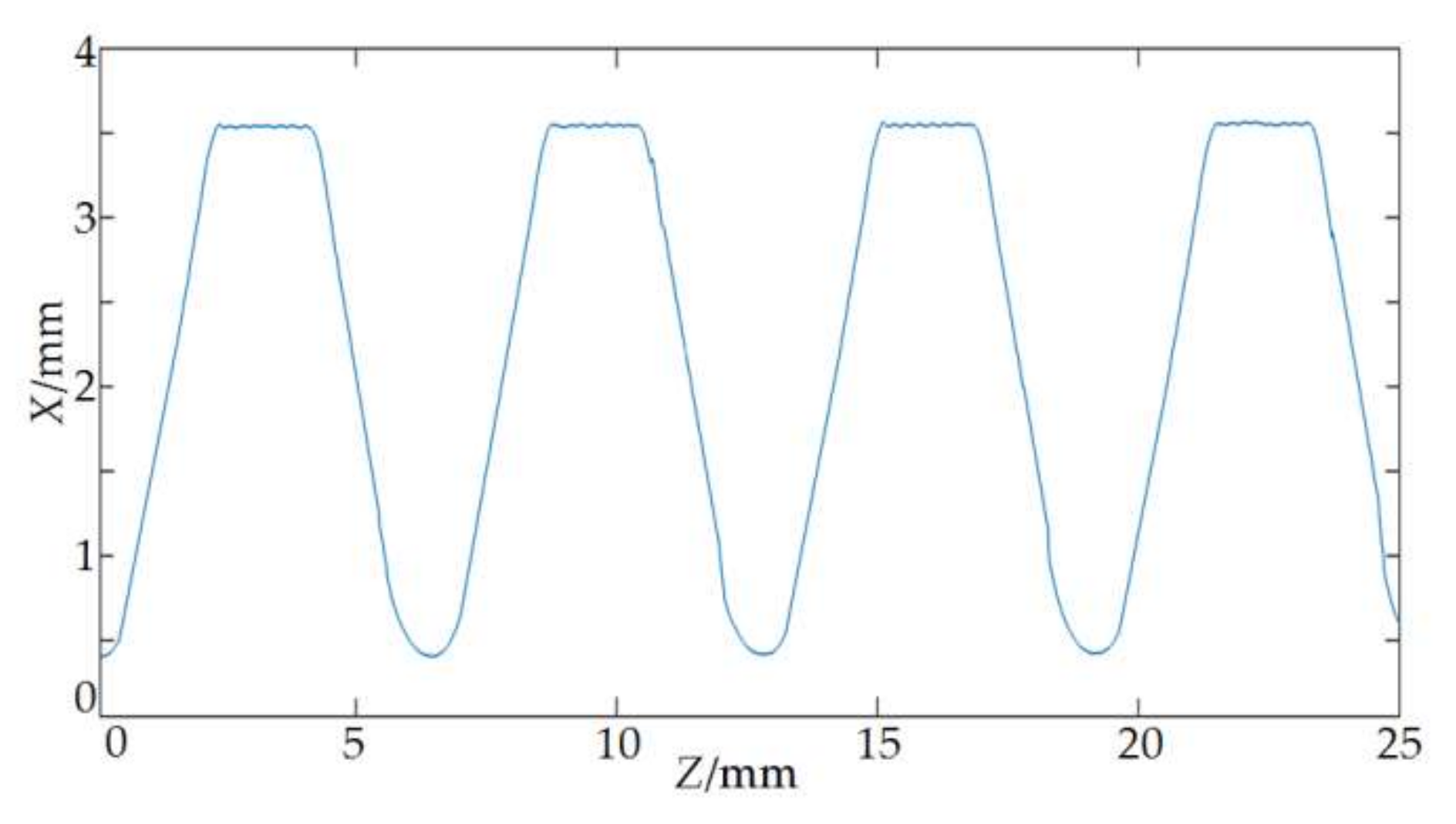
As shown in
Figure 12, the contour of the drill pipe thread is composed of threaded outside diameter and a rounded root and flank, and it has a periodic complex surface. Therefore, large deviations will be caused if the contour data after filtering is directly used to calculate the fitted curve. Accordingly, the discrete data points are reasonably segmented according to the geometrical characteristics of the contour, and then the regression models fitted in each section are combined to obtain the thread parameters.
After the comparison of all the measuring points after denoising, the maximum coordinate value
xmax along the vertical axis can be obtained, and the corresponding measuring point should be located on the outside diameter of the thread contour.
x1 =
xmax −
f (
f is the length of the tolerance band of thread outside diameter) is taken as the first horizontal dividing line, which divides the data points into two parts, and the point in the upper part of the dividing line
x =
x1 is taken as the point domain
P1 of the thread outside diameter. By virtue of the standard parameters of the drill pipe thread given in Reference [
27], the height
hin of the flank can be calculated.
in which
H is the original triangle height of thread profile,
fcn is the depth of truncation of crest,
rrn is the radius of rounded root, and
α/2 is the half of thread angle. After taking the second dividing line
x2 =
xmax −
hin and dividing the remaining data points, we can get
r flank domains
P2i (
i = 1, 2,…,
r) at the upper part of the dividing line
x =
x2 and s rounded root domains
P3j (
j = 1, 2,…,
s) at the lower part of the dividing line
x =
x2.
Actually, the weighted least squares (WLS) method is the most commonly-used data fitting method in engineering; this algorithm only considers the data vector and ignores the possible errors in the coefficient matrix. Therefore, how to deal with the error of the coefficient matrix in the fitting process is of great significance. Therefore, in this paper, the WTLS in Reference [
28] is employed to calculate the regression model of the contour data in each section.
First, the regression models of data segments of three different contours are given, and the regression coefficients of each fitting segment are calculated according to the WTLS in Reference [
28]. The crest, flank, and rounded root are shown in the following equation:
When the contour after segmentation is fitted, the regression model of each data segment is used to calculate the target parameters required by the system, namely, pitch
P, half of thread angle
α/2, thread height
h, as shown in
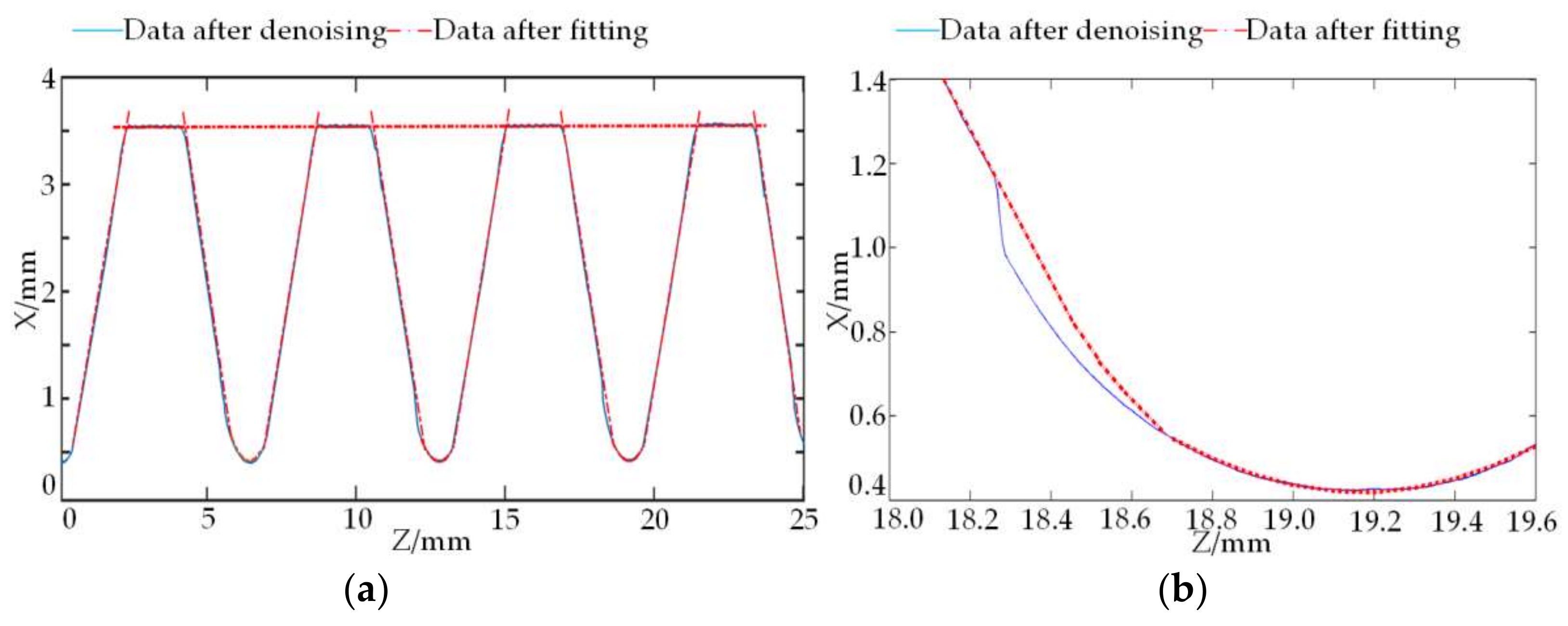
Figure 13.
The pitch can be obtained at the intersection point of the thread outside diameter and the flank fitted curve:
in which
φ is the half of standard cone angle.
The half of thread angle can be calculated by the slope of the flank curve:
The tooth height is defined as the distance between the thread outside diameter and the bottom of the rounded root (
h =
d1 −
d2), and its expression is
As shown in
Figure 13, taper can be obtained through the calculation of the half of cone angle
φ′:
in which
,
are the intersection coordinates of the flank curve.