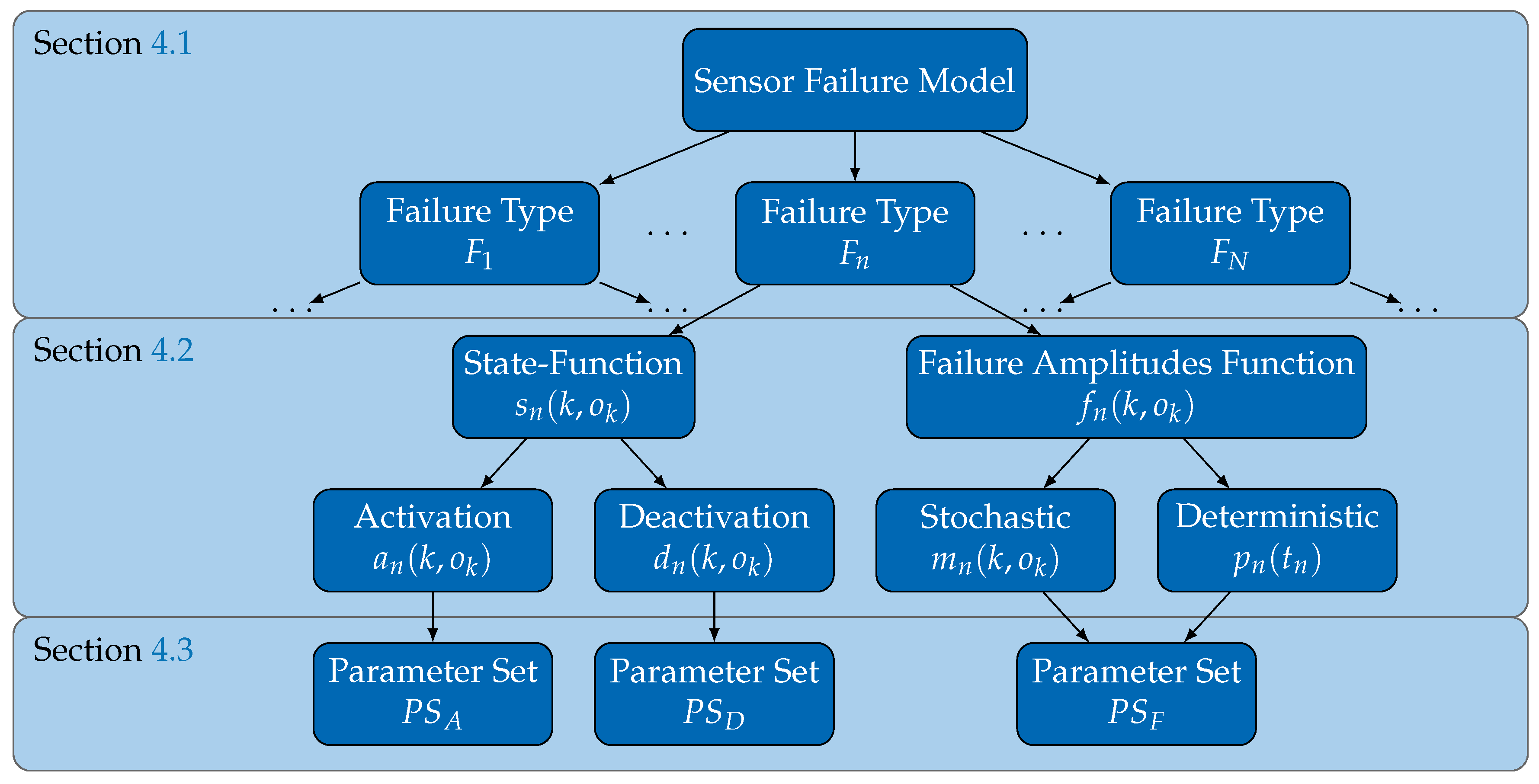
1. Introduction
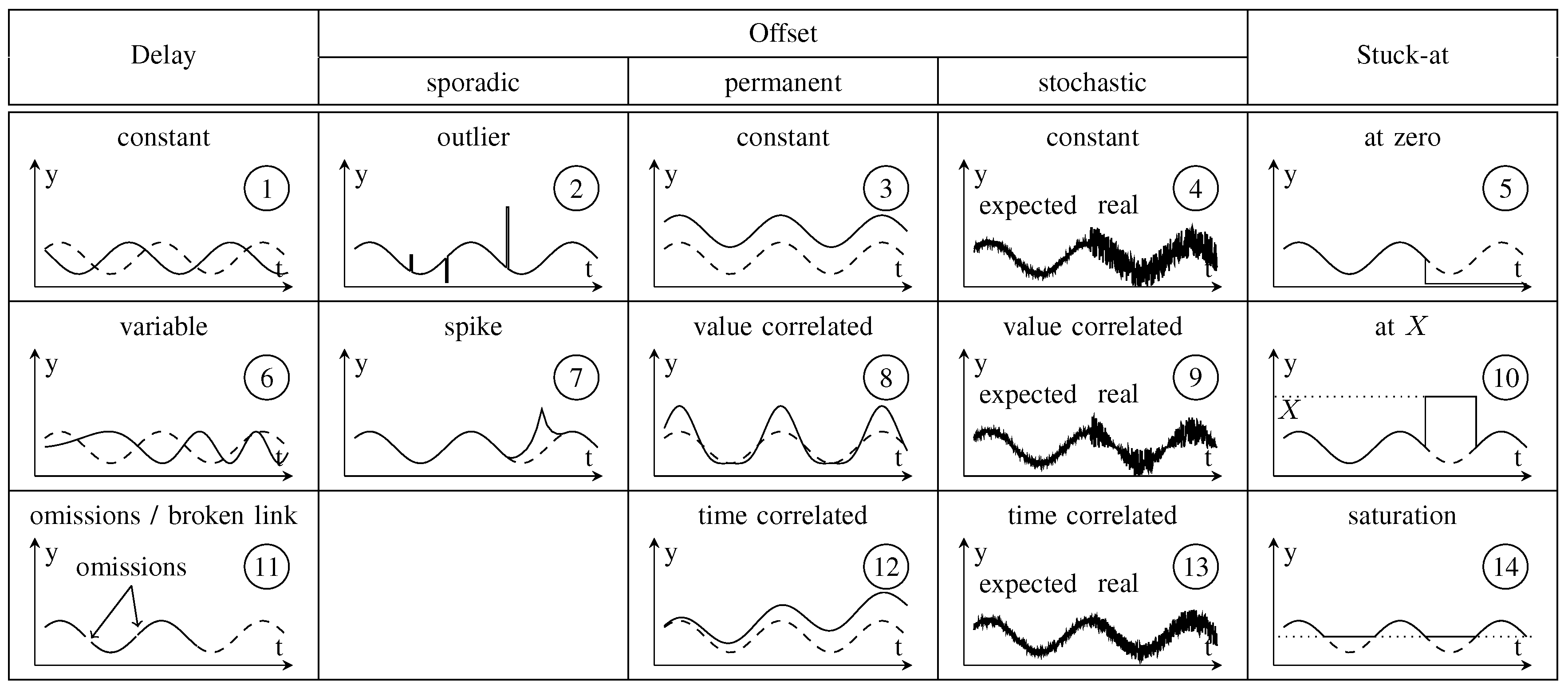
Reliable perception of environmental conditions based on (multimodal) sensors is a key feature for autonomously operating applications. However, the mapping process of relevant information from the real world on a digital representation is affected by external and internal disturbances. The different characteristics of possible failures (e.g., continuous or sporadic occurrence, value disturbance with constant, variable or correlated amplitude, absence of value) complicate the development of safety-oriented applications. In this case, engineers have to identify all disturbances that may possibly occur and evaluate their effect on the system’s properties. For this purpose, approaches such as
Failure Mode and Effect Analysis (FMEA) [
1],
Fault Tree Analysis (FTA) [
2], and
Event Tree Analysis (ETA) [
3] are commonly applied. Such methods leverage
failure models [
4] to represent a component’s failure characteristics and thereby support the selection process of appropriate fault tolerance mechanisms at a system’s design-time. At run-time, these tolerance mechanisms limit the effect of component failures and guarantee the system’s compliance with its required safety level. Key to this approach is the assumption that the system’s composition, i.e., its set of components, is determined at design-time and does not change at run-time.
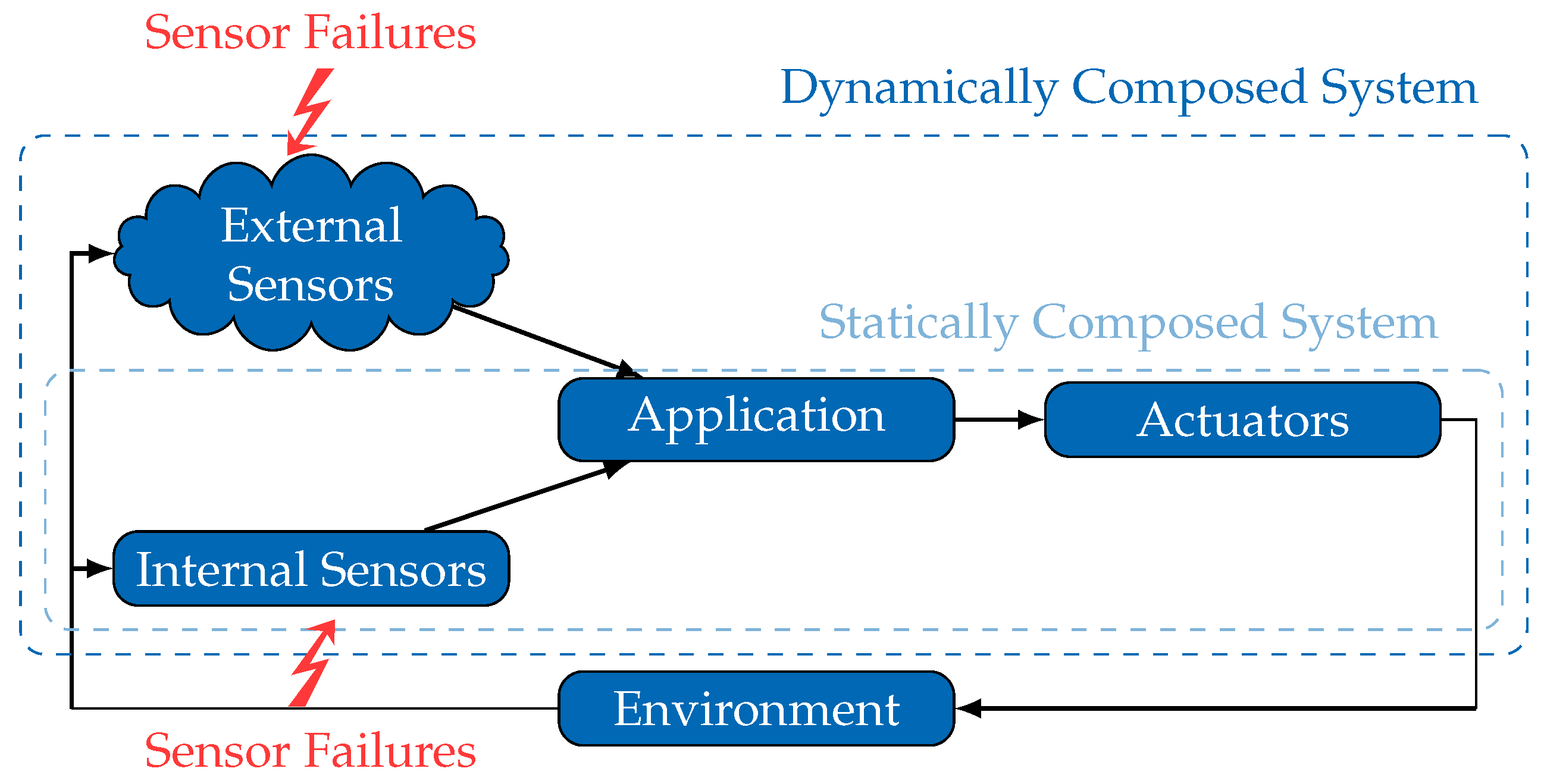
In contrast to such
statically composed systems, paradigms like Cyber-Physical-Systems [
5] and the Internet of Things [
6] propose increasing the autonomy of mobile systems by sharing their environmental information and achieving cooperative and/or collaborative behavior. The concept of spatially separated but temporarily integrated external sensors promises an extended coverage and reduces the requirements for local sensors. However, such
dynamically composed systems (see
Figure 1) represent a paradigm shift with respect to safety management and handling. Due to the fact that crucial information, such as failure characteristics of external sensors, are missing during the design phase, a number of engineering tasks (sensor selection, interface adjustment) need to be shifted from design-time to run-time. This specifically affects the safety analysis of external sensors, as the required information of the sensor’s failure characteristics may become available solely at run-time.
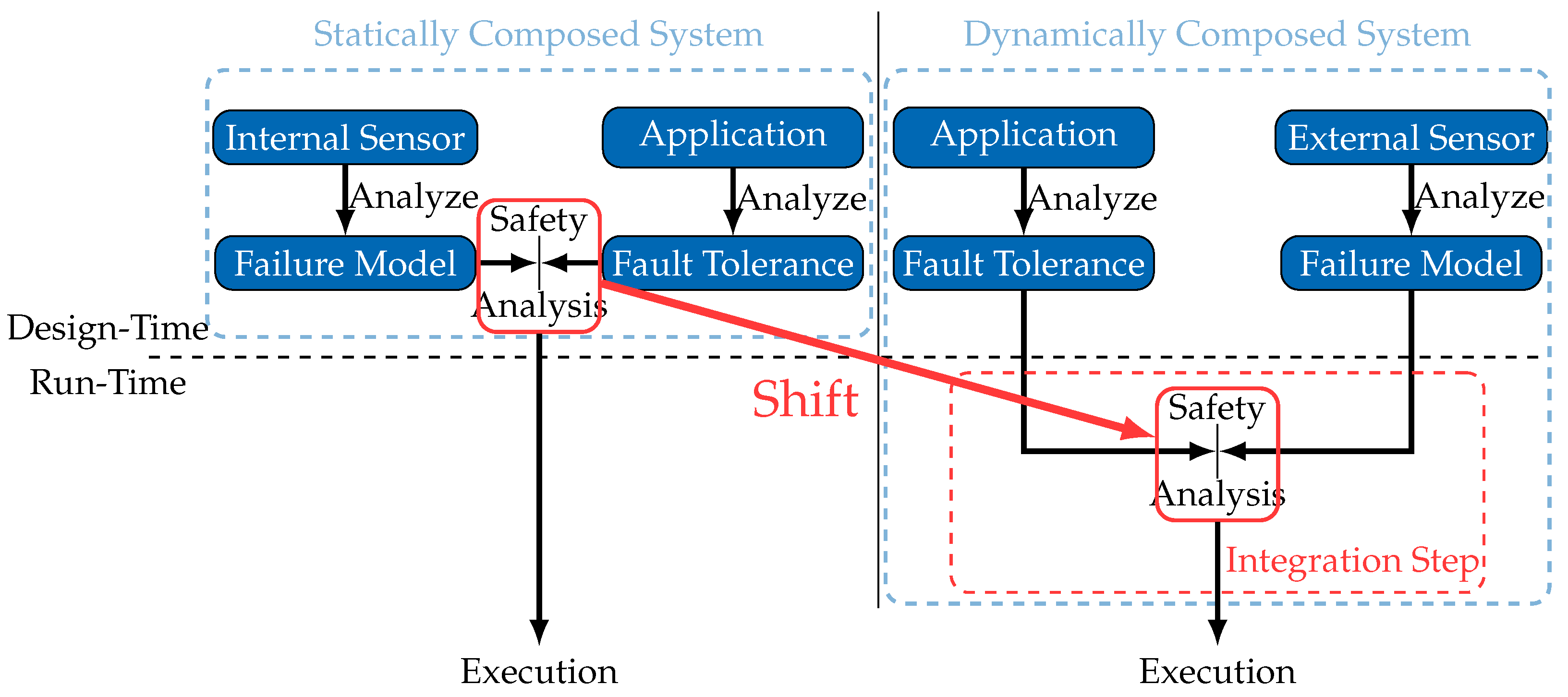
Figure 2 illustrates the inevitable shift of part of the safety analysis process to an integration step, which occurs at run-time whenever the system composition is about to change.
A consequence of this shift is that an external sensor is obligated to share not only its observations, but also its failure characteristics. This truly enables dynamically composed systems to conduct a safety analysis at run-time, in a sensor integration step, but requires an explicit and generic model of the sensor failure characteristics. Consequently, the following fundamental questions about such model must be answered. What requirements are posed on failure models of external sensors to be applicable in dynamically composed systems? Are there any suitable failure models already available? If not, how could one construct an appropriate failure model?
In the endeavor of answering these questions, we firstly derive and discuss requirements that have to be fulfilled by failure models to be suitable for such an approach. Then, and considering these requirements, in
Section 3, we review the state of the art on sensor failure modeling, which allows for concluding about the lack of appropriate failure models. Therefore, a fundamental contribution of this paper consists in the introduction of a generic failure model fulfilling the initially identified requirements, which we do in
Section 4. Furthermore, the second fundamental contribution of this paper is provided in
Section 5, where we propose and describe a processing chain to support the automated extraction of a parametrized failure model from raw sensor data. To evaluate this contribution, in
Section 6, we conduct experimental evaluations on raw data produced by a Sharp GP2D12 (Sensor manufactured by Sharp Cooperation, Osaka, Japan) [
7,
8] infrared distance sensor. The evaluation results allow not only to conclude that the processing chain is able to adequately generate generic failure models, but also that the generated failure models indeed fulfill the requirements to be applicable in
dynamically composed systems. The paper is concluded in
Section 7, where the key contributions are summarized and possible future lines of work are expressed.
2. Identifying Requirements on Failure Models
In the previous section, we clarified the need for explicit and generic sensor failure models in a dynamically composed system in order to maintain their safety when incorporating external sensors. As this differs from the traditional use of failure models in statically composed systems, different requirements also have to be fulfilled, which we identify in this section.
As shown in
Figure 2, a general approach for safety analysis in dynamically composed systems involves an integration step for each new external sensor whose data the application wants to use. A safety analysis is performed in this integration step, using the explicitly made available failure model of the external sensor. Given that the safety analysis performed in the integration step is completely in the hands of the application developer, one should not assume that a specific safety analysis methodology will be used. For generality, the widest possible range of safety analysis mechanisms should be applicable, each potentially implementing different failure representations. A
Generality requirement is thus expressed as follows.
Generality: An appropriate failure model is required to have a generic approach to the representation of failure characteristics. This shall enable an application independent description of failure characteristics that can be transformed into an application specific representation when needed.
The
Generality requirement ensures that a failure model is defined independently of a specific application. Further to that, for a successful deployment of the proposed scheme (
Figure 2) in various types of systems, an appropriate failure model has to be capable of representing failures of a wide range of sensor types (1D, 2D, 3D) to satisfy the needs of both sensor manufacturers and system engineers. Additionally, as external sensors may be virtual sensors [
9] or smart sensors [
10], they may provide not only raw sensor data, but also high-level features. Consequently, they may be affected by failures in a multitude of different ways. Due to this diversity of sensors and sensor failure types, a
Coverage requirement is thus defined as follows.
Coverage: An appropriate failure model must be capable of representing various failure characteristics in a versatile way.
Both of these requirements (
Generality and
Coverage) guarantee the applicability of a failure model to a broad set of systems and scenarios. However, for supporting its intended usage for safety analysis within an integration step, a third requirement ensuring an unambiguous interpretation of a failure model has to be fulfilled. A failure model transferred from an external sensor to an application can only be correctly analyzed when its interpretation is clear. This means that the failure characteristics described by the sensor’s manufacturer need to be extractable from the failure model unambiguously. Otherwise, an application could underestimate the severity of an external sensor’s failure characteristics and compromise safety. A
Clarity requirement for the representation of a failure model is defined as follows.
Clarity: The means used in a failure model to represent failure characteristics must be such that these characteristics will be interpreted unambiguously.
Fulfilling the previous requirements ensures that a semantically correct safety analysis of external sensors is possible. However, being done at run-time in a specific integration step, a final requirement related to its performance must be defined. In fact, this analysis may be subject to temporal restrictions (e.g., in Car-2-Car [
11] communication scenarios) or to computing resource restrictions (e.g., in the context of embedded robotic systems). Depending on the application and its context, it should be possible to perform the integration of external sensors in different ways, balancing the cost and the detail of the safety analysis in a suitable manner. In other words, when comparing the failure characteristics of an external sensor with the application needs, it should be possible to do this comparison with different degrees of detail, and naturally also with different degrees of performance and accuracy. A
Comparability requirement is thus defined as follows.
Comparability: For the flexible use of a failure model when comparing failure characteristics and application needs, the representation of failure characteristics must allow for interpretations with various levels of granularity.
In summary, fulfilling the presented requirements ensures the applicability of a failure model to the proposed safety analysis at run-time, in a specific integration step.
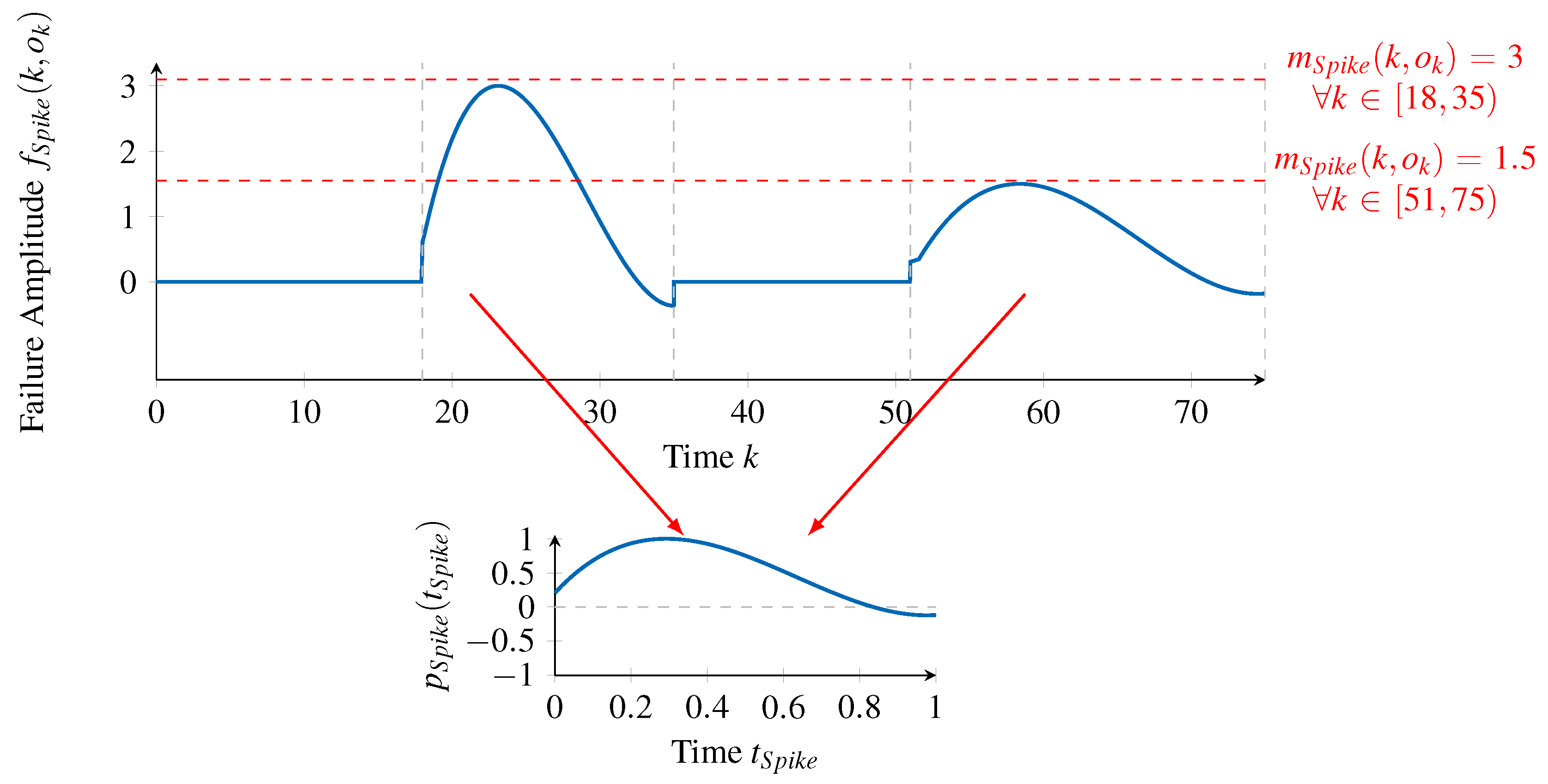
5. Automatic Designation of a Failure Model from Raw Sensor Data
Modeling failure characteristics of real sensors requires finding appropriate failure types by examining empirical observations of the sensor in question. Therefore, in this section, we propose a processing chain for converting a series of failure amplitudes into a parameterized failure model, doing this in an automated manner. An overview on the phases of the processing chain is given in
Figure 7.
The processing chain receives as input a series of failure amplitudes
, calculated by applying Equation (
1) to sensor observations and the corresponding reference values
(ground truth). The reference values
are also used in the processing chain. These inputs are converted by the processing chain into a set of failure types
constituting the generated failure model. The processing chain involves three phases.
Identifying Failure Types is the first phase, which identifies an intermediate set
of failure types representing the failure amplitudes
. We discuss this phase in
Section 5.1. Then,
Section 5.2 details the second phase,
Generalizing Failure Types, in which pairs of failure types in
that are similar to each other are identified and combined into a single failure type. The output of this phase is the set
, which holds all relevant failure types. Finally,
Section 5.3 discusses the last phase,
Parameterizing Failure Types, which uses the gathered information about each failure type in
to train RBF networks representing each failure types’ functions, as defined in
Section 4.2. In this manner, the final set of failure types
is determined.
5.1. Identifying Failure Patterns
The first phase of the processing chain exploits Equations (
2) and (
4), to decompose the failure amplitudes
received as input into a set of
failure types, as follows:
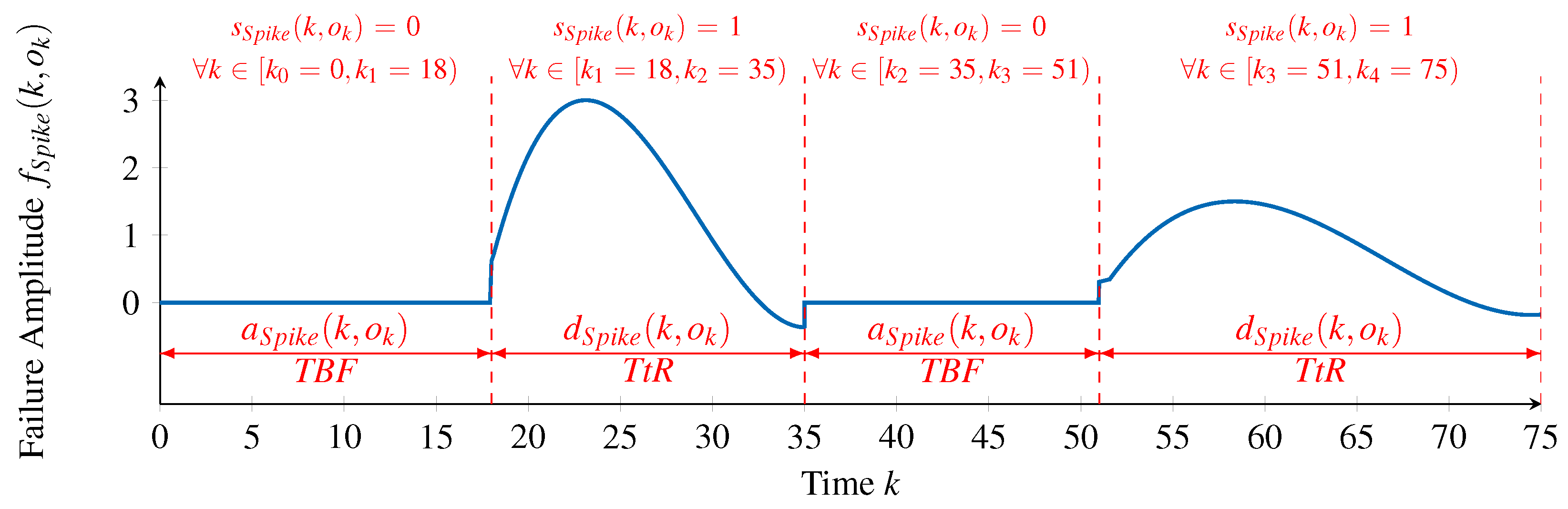
For each failure type, it is necessary to identify information about its occurrences (time steps at which ), the magnitude of each occurrence (value of ) and the failure type’s failure pattern (). This information will be passed to the next phase, along with the initial inputs of the processing chain.
In order to obtain this information from the given failure amplitudes, we firstly make two assumptions on the failure types to identify. The first assumption is that all occurrences of a single failure type have the same duration, that is, the same Time to Repair. Although it is known that the Time to Repair of a failure type may vary following a time- and value-correlated random distribution, this assumption simplifies the process of identifying appropriate failure patterns. If two occurrences of a failure type exist with different lengths of duration, in this phase, they will be classified as occurrences of different failure types. The second assumption is that failure patterns are defined only in the range of . This also simplifies identifying suitable failure patterns by restricting the search space to a positive range.
With these assumptions in place, we propose an iterative approach that, in each iteration, does the following:
Generates a pseudo random failure pattern with a duration ;
Looks for occurrences of that failure pattern in the entire series of failure amplitudes, whatever the scale of the occurrence;
If some occurrences are found, then a new failure type is identified and the occurrences are associated with it;
The observations in each failure pattern occurrence are removed from the set of failure amplitudes, that is, the initial failure amplitudes are reduced according to the identified occurrences of the failure pattern;
The duration is decreased and a new iteration takes place;
If , that is, if the pattern being searched corresponds to a single observation, then it will match all the remaining failure amplitudes, which will be grouped in a single failure type and interpreted as Noise.
While this brief enumeration of the iteration steps provides a global perspective of the approach, we now explain these steps in more detail.
In the first step, we generate a pseudo-random failure pattern
of a fixed duration
. The initial value of
has to be provided by the user, who knows the application context and hence the possible maximum duration of a failure pattern. Failure patterns are generated from a set of more usually observed patterns, and they are reshaped using an evolutionary algorithm [
40] while the series of failure amplitudes is being searched (in the second step) and similar patterns are found.
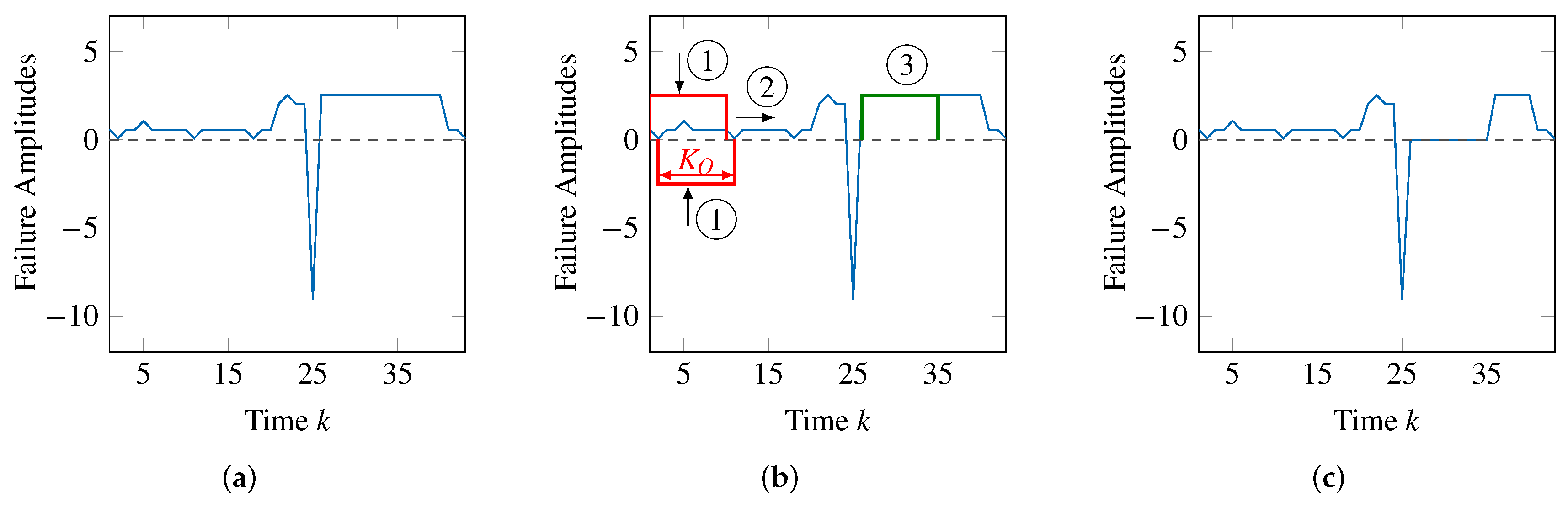
To search for a pattern in the second step, the whole series of failure amplitudes is sequentially parsed, shifting the pattern matching window of
observations (time steps) one observation at a time. This is illustrated in
Figure 8b, where the pattern matching window with size
(noted with ➀) is shifted to the right (noted with ➁). Therefore, at each step,
observations are compared with the failure pattern, which is scaled (the value of
is determined) positively and negatively to match the corresponding failure amplitudes. This scaling, illustrated by vertical arrows, is also shown in
Figure 8b at position ➀. Only if the pattern matches the failure amplitudes sufficiently, an occurrence of the failure type (time steps at which
) is identified. Since the pattern is shifted through the time steps of
, if some occurrences exist, they will be found.
If some occurrences are found, then, in the third step of the iterative approach, the information relative to all these occurrences will be associated to a failure type so that it will be used in the second phase of the processing chain.
In the fourth step of the iterative approach, the idea is to remove the amplitudes corresponding to the occurrences of the failure pattern from the initial series of failure amplitudes. This way, in the next iteration, different failure types may be identified, contributing to the remaining failure amplitudes. However, it may be the case that the identified failure type is not significant. This happens if it includes a very small number of occurrences or if these occurrences have a very small scaling. In this case, the failure type is ignored and the respective occurrences are not removed from the initial series of failure amplitudes.
Figure 8c also illustrates this step. The failure patterns noted with ➂ in
Figure 8b are removed from the series of failure amplitudes, which becomes as shown in
Figure 8c.
At the end of each iteration, the fixed duration , with which the evolutionary algorithm searches for occurrences of a suitable failure type, is decreased. On the one hand, this limits the number of iterations the algorithm is required to finish. On the other hand, the last duration, with which the evolutionary algorithm is applied, is . At this point, a failure pattern is assumed. As a consequence, the pattern can be scaled to match each of the remaining failure amplitudes by setting . Essentially, this means that the remaining failure amplitudes constitute occurrences of a failure type that may be interpreted as Noise.
5.2. Generalizing Failure Types
The output of the iterative algorithm of the previous phase is , a set of failure types, each described by a failure pattern , its occurrences (time steps k) in , and the scaling value of each occurrence. Given the initial assumption that the lengths of duration of all occurrences of a single failure type are fixed to a constant value , some information in might be redundant. This is the case when two failure types represented separately in have similar failure patterns and only differ in the duration of their occurrences. In this case, a single failure type could represent both by exploiting the fact that the Time to Repair may vary following a time- and value-correlated random distribution.
Therefore, in this section, we introduce the second phase of the processing chain, Generalizing Failure Types. It aims at identifying pairs of failure types () that are representable by a single, combined failure type (). By replacing the original failure types and with the combined failure type , redundancy is reduced and the failure types are generalized. This generalization also means that the simplifying assumptions made in the first phase no longer have any significance or impact.
In brief, an iterative approach is proposed that consists of the following. In each iteration, every pair of failure types is combined, forming a new tentative failure type. Then, since the combination of two failure types leads to some intrinsic loss of information, this loss is measured for all pairs. Finally, if some combination is found implying an acceptably small loss, the original failure types are replaced by the new one.
To combine two failure types, the occurrences of the original failure types
and
are superimposed to determine the occurrences of the combined failure type
. As explained in
Section 4.2, the occurrences of a failure type may vary regarding their scaling
, but the failure pattern
must be the same. Therefore, given that the failure patterns of
and
may be different, or they may lead to different patterns when being superimposed, it is necessary to determine a new failure pattern that resembles, as much as possible, the superimposed pattern. For this, an RBF network is trained with all occurrences of the combined failure type
, thus representing this new pattern.
Given the input set
of failure types, the generalization starts with assuming that the output set is the same as the input one,
. The described combination is thus applied to all the pairs in
. After that, it is then necessary to measure the information loss induced by each combination, for which we introduce
:
Here, denotes a series of failure amplitudes, similar to the initial series, but containing solely the occurrences of the failure types and . On the other hand, the series is constructed from the combined failure type, represented by the RBF network. For each time step in the series, a value for is calculated from the RBF network if the pattern is active in that time step. The resulting will be zero if the combined failure type faithfully represents the initial pair of failure types, that is, without loss of information. Otherwise, will be greater than zero.
Using , we define a stopping criteria for generalizing failure types by restricting the loss of information to . In that manner, is nothing but a threshold for restricting the loss of information.
With this criteria, it is then possible to replace the original failure types by the combined failure type. For that, the minimal assessment value over all pairs of failure types is determined. In case the loss of information is acceptable, that is, , the original failure types and are removed from while their combined failure type is appended to .
In summary, by applying this iterative process, the number of failure types is reduced by one in each iteration. Furthermore, by accepting the combined failure type only if the caused loss of information is less than a threshold (), the maximal loss of information is limited. As a result of the generalization, the intermediate set is transformed into the second intermediate set with a reduced number of failure types ().
It must also be noted that, after this generalization phase, the failure patterns for each failure type in are already represented by an RBF network. Furthermore, the pattern is now defined in the range and, as the superimposed occurrences may vary in their duration, of the combined failure type may vary too.
5.3. Parameterizing Failure Types
The previous phase produced the set containing all failure types comprising the final failure model. However, the failure types in this set are not yet fully represented by RBF networks (except for the failure patterns ), but in terms of individual occurrences relative to each failure type. Therefore, this phase aims at completing the parameterization of the failure types regarding their activation (), deactivation () and the scaling ().
All three of these functions are represented by time- and value-correlated random distributions (see
Section 4.2.1) and each of these random distributions is modeled using an ICDF and time- and value-correlated mean and standard deviation functions (i.e., three functions). Therefore, a total of nine RBF networks must be trained to represent the activation, deactivation and the scaling functions.
To briefly explain which training data is necessary and how it is obtained, we consider the specific case of the RBF network representing the standard deviation of the activation function . In this case, the basic measure of interest is the Time Between Failures (TBF) for the failure type under consideration. While it is possible to obtain measures of the TBF from the failure type occurrences and calculate an overall standard deviation relative to those measures, simply doing that does not inform us about how the standard deviation is correlated with the time k and with the value . What needs to be done is to partition the time and the value space into small ranges and obtain measures of interest (in this case the standard deviation of the TBF) within those ranges. Then, for training the RBF network, pairs (corresponding to the center of the considered ranges) will be used as input, while the corresponding value of interest (the standard deviation in that range) will be used as the output.
This reasoning has to be applied to all the time- and value-correlated functions to be represented by RBF networks. Concerning the representation of the random distribution using an ICDF, which is not time- or value-correlated, this can be done by considering the normalized values of interest in all ranges and determining the corresponding inverse cumulative distribution function.
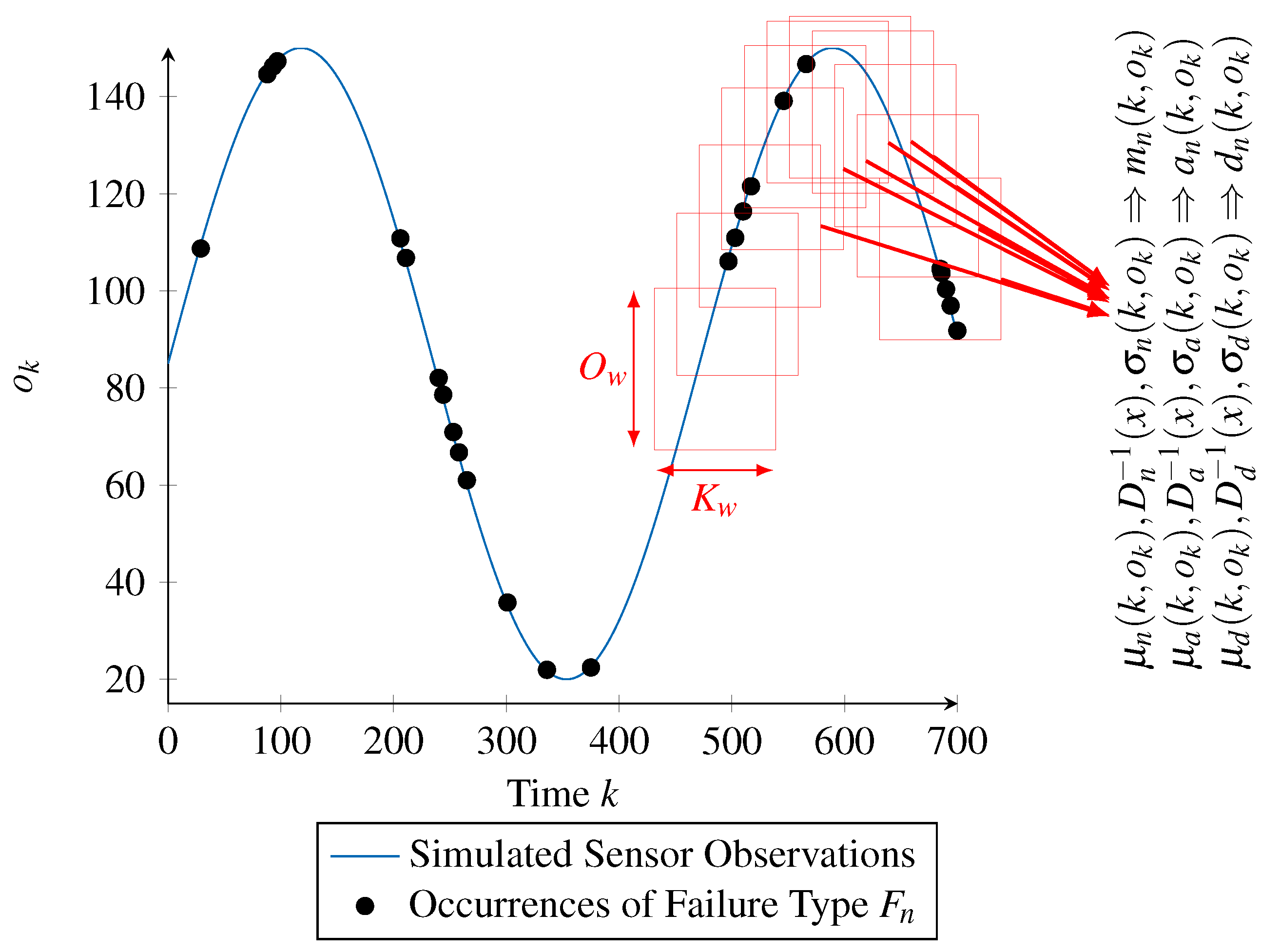
In a more generic way, the idea is to use a sliding window approach, with each window corresponding to the mentioned time and value range. This sliding window approach is illustrated in
Figure 9 and is detailed ahead.
The approach starts by associating the occurrences of a single failure type (depicted by the black dots in
Figure 9) to the series of reference values
(blue curve) obtained as an input to the processing chain. From this representation, we start the sliding window approach. For that, a window is defined as a range of
time steps as well as a range of
sensor values, corresponding to the red rectangles in
Figure 9. By shifting the window along the time axis with a step width of
and along the value axis with a step width of
, multiple subsets of the failure type’s occurrences are generated.
The generated subsets form the base on which the training data for parameterizing the RBF networks is calculated. Training data for supervised learning, as it is the case with RBF networks, consists of pairs of input and target values. The input values required for the time- and value-correlated functions (mean and standard deviation of the scaling function , activation function and deactivation function ) are already given by the sliding window approach, since the subsets are associated with a time step k and a sensor value for the corresponding window.
However, the target values, that is, the intended outputs of the functions, need to be determined. These values are dictated by the definition of a time- and value-correlated random distribution. According to this definition, the values of the mean (
) and standard deviation (
) are calculated using the Z-score normalization. Consequently, for the mean
and standard deviation
of the activation function
, we calculate the mean and standard deviation of the time between two occurrences of the failure type within each subset. Likewise, the target values of the functions
and
are calculated by considering the duration of the occurrences within each subset, while the target values of
and
are calculated by considering the scaling values of the occurrences within each subset (also illustrated in
Figure 9).
Finally, as explained in
Section 4.2.1, the remaining functions (
) representing the normalized random distributions are not correlated to the time
k or value
. Therefore, training data for these functions is generated by considering the normalized values of all subsets and determining the corresponding inverse cumulative distribution function.
By extracting this data, we can train the RBF networks to represent the individual functions of a failure type . In that way, the parameter matrices of all RBF networks are determined and the parameter sets , and for each failure type are generated. As these form the final failure model, the output of the processing chain is constructed.
6. Evaluation Using an Infra-Red Distance Sensor
To evaluate the introduced approach for generic failure modeling of sensor failures, and also to evaluate the proposed processing chain for automatically generating a failure model, in this section, we consider a real infra-red distance sensor and we conduct an extensive experimental analysis to show the following: firstly, that the processing chain is able to extract appropriate failure models and hence can be used as a valuable tool for automating the process of obtaining failure characteristics of any one-dimensional sensor; secondly, that the generated failure models are able to capture particular failure characteristics in a better way than any other approach that we know of, fulfilling the requirements for being used in cooperative sensor-based systems.
Section 6.1 discusses the experimental setup and the generation of the failure model. For comparison, we additionally parameterize a normal distribution, uniform distribution, inverse cumulative distribution function, and a neural network to represent the sensor’s failure characteristics. To assess the performance of the generated failure models and to compare them with each other,
Section 6.2 introduces two assessment measures. While both are based on the statistic of the Kolmogorov–Smirnov (KS) hypothesis test [
42], each focuses on a different aspect. The first assesses the overall fit of a failure model with the sensor’s failure characteristics, while the second focuses on the representation of failure amplitudes with high magnitudes. In particular, the second aspect is of special interest when it comes to safety. We discuss the results of applying the assessment measures to the designed failure models in
subsection 6.3.
6.1. Experimental Setup
To apply our methodology to real sensor data, an appropriate data acquisition is required. In this endeavor, we firstly describe the experimental setup using a Sharp GP2D12 [
7,
8] infra-red distance sensor, for acquiring sensor observations
relative to reference values
. Then, we provide details on using the obtained data for designing the envisioned failure models. Finally, to facilitate a subsequent comparison (in
Section 6.2) between the designed failure models, we generate series of failure amplitudes by performing Monte Carlo simulations.
6.1.1. Data Acquisition
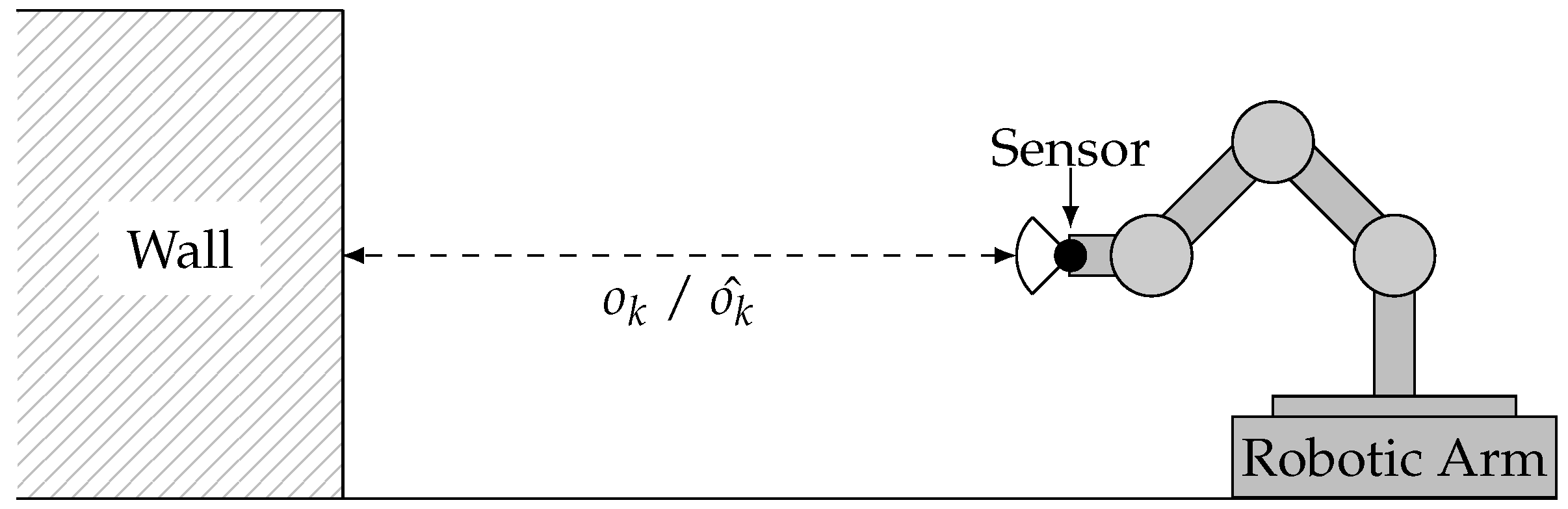
For the envisioned evaluation, real sensor observations
of a Sharp GP2D12 infra-red distance sensor and corresponding reference values
are obtained by mounting the distance sensor on a robotic arm and bringing it into defined distances to a wall, as illustrated in
Figure 10.
The arm was moved into five different distances ( in cm), which are measured manually to obtain the ground truth. In each of them, 50,000 observations are acquired with a periodicity of 39 ms while not changing the sensor’s distance to the wall.
To furthermore facilitate designing and validating failure models, we use the first half of the observations for training data (on which we can apply the processing chain) and the second half for validation data. Therefore, a total of 125,000 observations for each, training and validation data, are obtained.
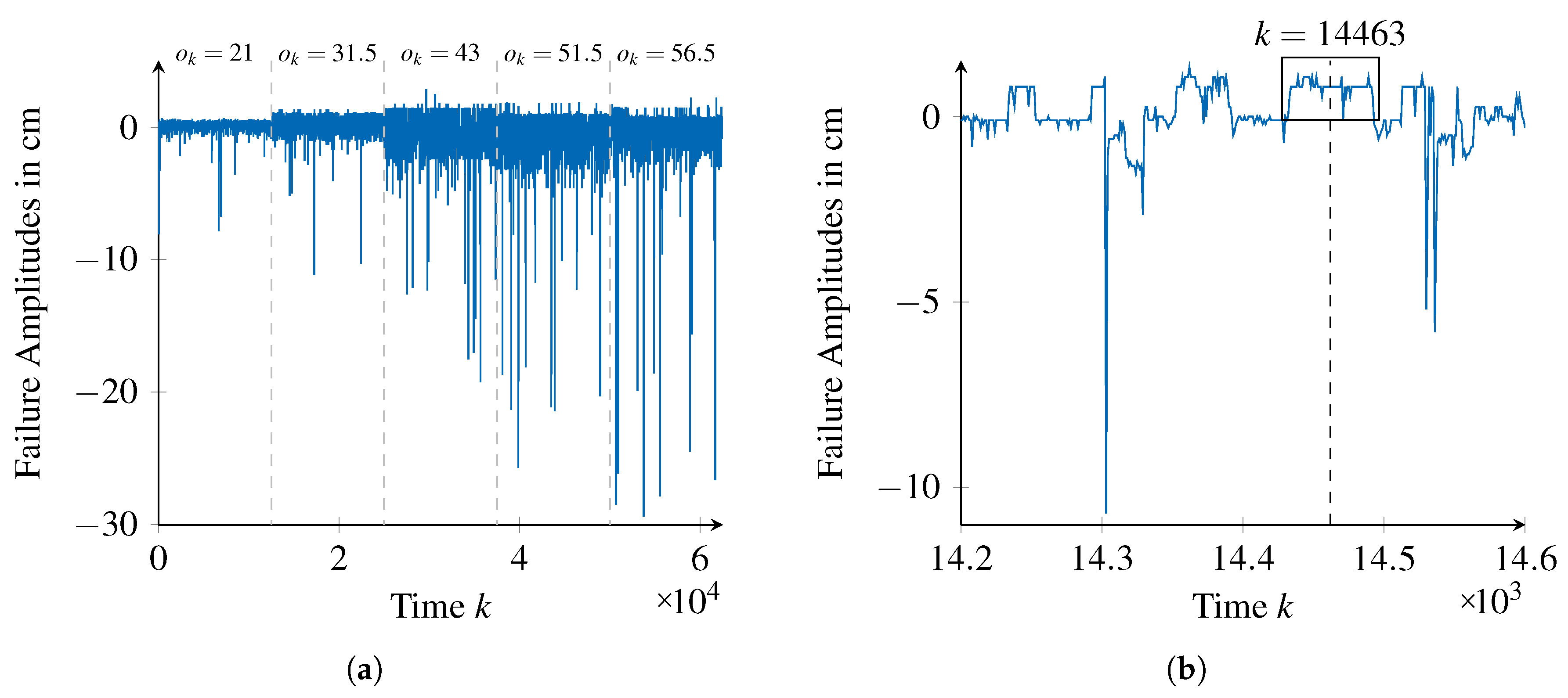
By calculating the difference between each observation and the reference value (ground truth), as stated in Equation (
1) to the data, the failure amplitudes shown exemplarily in
Figure 11 are obtained.
While
Figure 11a provides an overview on the failure amplitudes of the sensor for all the considered reference distances (data for each distance is shown in temporal sequence but were acquired as independent runs),
Figure 11b provides a segment of failure amplitudes for the distance of
cm.
6.1.2. Designing Failure Models
The obtained failure amplitudes and reference values enable us to design the envisioned failure models. We firstly apply the processing chain to extract a generic failure model before we discuss the parameterization of the traditional techniques (normal distribution, uniform distribution, ICDF). Finally, we provide details on the training of a feed-forward neural network [
40]. By training it to represent a time- and value-correlated ICDF, we enable the comparison of the generic failure model with another approach capable of representing such correlations.
For extracting a generic failure model from the obtained training data, we configure the processing chain as follows:
Identifying Failure Types: This phase is applied twice to facilitate identifying failure types with different failure patterns. At first, we apply the phase on the failure amplitudes
smoothed by a median filter with a window size of
:
In this way, constant failure patterns, exemplarily shown in
Figure 11b around time step
14,463, can be identified. However, due to the smoothing constant, failure patterns in
that endure less than 50 time steps may deviate inappropriately from the actual failure amplitudes in
. Consequently, we fix the pattern length
to be in the range of
, which means that the search will start for patterns with length
, down to patterns with length
. This search results in 21 failure types being identified, explaining
of all the failure amplitudes.
When applying this phase for the second time, we consider the unfiltered failure amplitudes , from which we remove the occurrences of the failure types identified in the first application. Furthermore, we configure the pattern length to be in the range of . The appropriateness of this choice was confirmed later, as only failure types with could be found within the second search. From this search, 25 additional failure types with were identified, explaining of the failure amplitudes. One last failure type, corresponding to , accounts for the remaining failure amplitudes (). In summary, a total of 47 failure types were identified, which are passed to the next phase.
Generalizing Failure Types: The first parameter of this phase is the number of neurons of the RBF networks used to model the failure pattern . We set this parameter to 15 as the correspondingly trained networks yield acceptable error values while restricting the complexity of the training process. The second parameter is the stopping criteria , which we set to 250 cm. This limits the loss of information caused by a single combination of failure types to of the failure amplitudes of its corresponding original failure types. Therefore, the combined failure type represents the original failure types almost perfectly. With this parameterization, 29 of 47 failure types were combined, effectively reducing the number of failure types to 18. These were evaluated to explain of the initial failure amplitudes, which means that the generalization caused an overall loss of information of .
Parameterizing Failure Types: We configure the sliding window approach used within this phase with a window size of and a step size of . As we have 12,500 observations available for each reference value , this configuration enables identifying potential time-correlations. Likewise, to facilitate the identification of value-correlations, we set the window size in the value domain to cm and the step size to cm. Given the measurement range of the distance sensor ( [10 cm, 80 cm]), this configurations enables the identification of value-correlations in fine granularity.
Using this configuration, the processing chain extracts from the training data a parameterized generic failure model comprising 18 failure types.
For comparison, we parameterize a normal distribution
to represent the same failure characteristics, as this is a frequently reported approach for failure characterization [
12,
15,
16]. Using the training data, its mean
and standard deviation
is calculated over all time steps
k.
A more restrictive approach is to solely state the minimal and maximal failure amplitudes [
43,
44]. Given that in this case there is no information about the distribution of failure amplitudes (within the minimal and maximal amplitudes), we assume a uniform distribution
and calculate
and
using the failure amplitudes of the training data.
Similarly to both previous approaches, one can model the failure amplitudes using an inverse cumulative distribution function (ICDF) [
45]. We obtain its parameterization by integrating the distribution function of the failure amplitudes in the training data and by inverting the result.
In contrast to our proposed approach, these approaches are established means for stochastic modeling, but are not capable of explicitly representing time- or value-correlations. Therefore, to provide a more fair comparison and evaluation of our approach, we train a traditional feed-forward neural network [
40] to represent a time- and value-correlated inverse cumulative distribution function. In this endeavor, we calculate the inverse cumulative distribution function for each distance (
in cm) within the training data and associate it with the corresponding reference value
and the time
k. By sampling the obtained ICDFs to generate training data for the neural network, it learns not a static ICDF, but adjusts it corresponding to the provided time
k and reference value
.
6.1.3. Monte Carlo Simulation of Failure Models
The several failure models that we constructed in the previous section are not directly comparable with each other, that is, it is not possible to know how much better or worse they represent the failure characteristics of the distance sensor just by comparing the parameters describing them. Therefore, to support a comparison, in this section we sample the previously obtained failure models using Monte Carlo simulations. The obtained series of failure amplitudes, one for each failure model, constitute expressions of what the failure model actually represents. Therefore, they allow their comparison by observing how closely the respective failure amplitudes resemble the ones originally obtained from the distance sensor. They also facilitate a comparison with the validation data (i.e., the originally obtained failure amplitudes that were not used for obtaining the failure models), which is done in
Section 6.3 using the assessment measures introduced in
Section 6.2.
The generation of a series of failure amplitudes using a Monte Carlo simulation is directly supported by the generic failure model as a consequence of using inverse cumulative distribution functions within time- and value-correlated random distributions, as expressed in Equation (
3). Three arguments are required to evaluate this equation: a uniformly distributed random value
to evaluate the ICDF (
), a time step
k, and a value
to evaluate the mean
and standard deviation
. While
x is generated by a random number generator, time
k as well as the reference value
can be taken from the series of validation data obtained in
Section 6.1.1. The same inputs are required for the Monte Carlo simulation of the feed-forward neural network as it is trained to represent a time- and value-correlated ICDF.
On the other hand, since the approach representing the exact ICDF does not model the time- and value-correlations, a Monte Carlo simulation of this approach requires only uniformly distributed random numbers . In a similar way, Monte Carlo simulations for the normal distribution and the uniform distribution are facilitated by drawing random numbers from their respective standard distributions and scaling them afterwards. In the case of the normal distributions, a random number is scaled according to while a random number is scaled according to for sampling the uniform distributions.
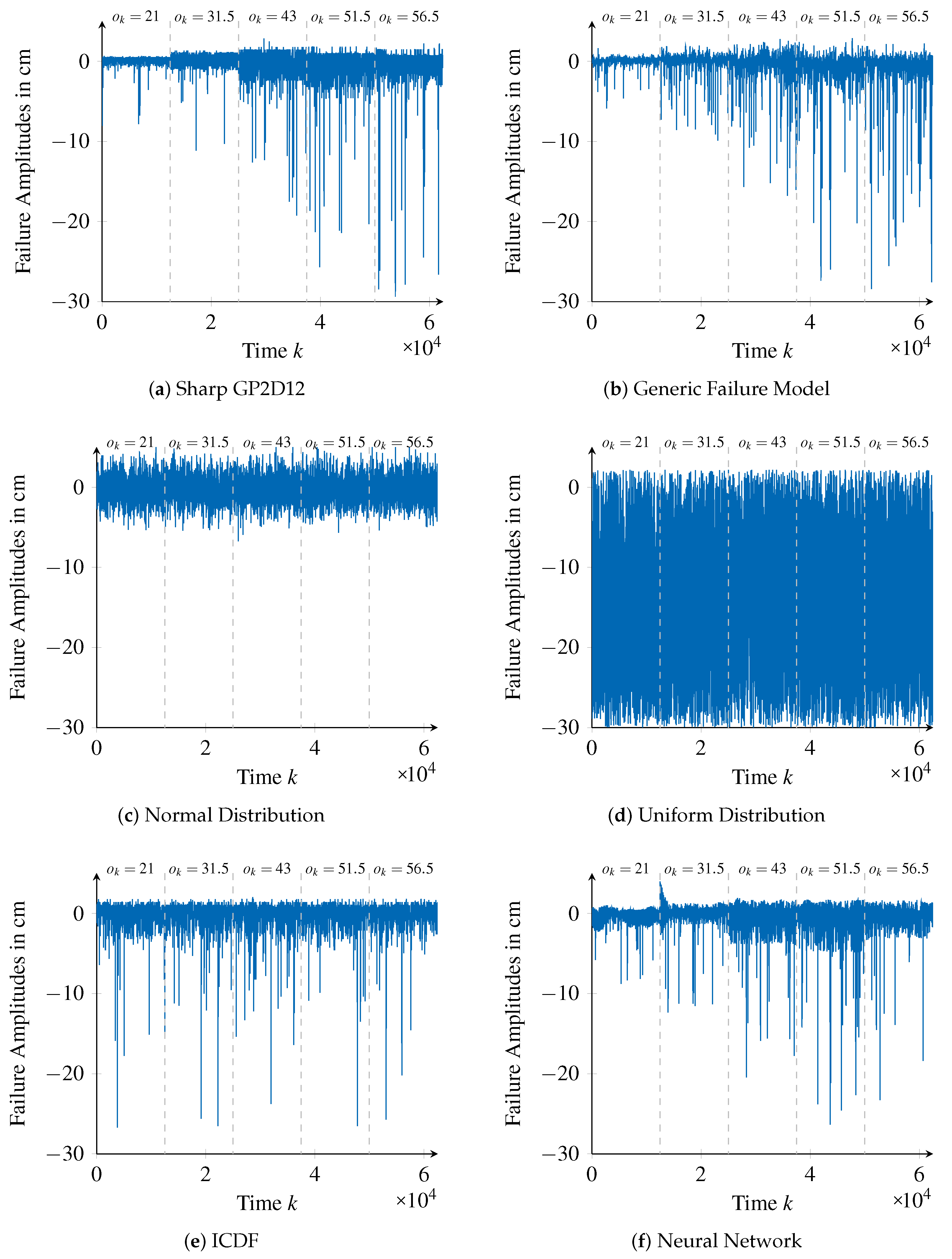
The generated failure amplitudes of different failure models are shown in
Figure 12 along with the validation data (
Figure 12a).
6.2. Introducing Assessment Measures Based on the Kolmogorov–Smirnov Statistic
For comparing the series of failure amplitudes generated in the previous section with the failure amplitudes of the distance sensor, we introduce two assessment measures. The first one considers the the overall match between the validation data and a failure model, in order to evaluate its appropriateness in general. The second is defined to specifically assess the appropriateness of the failure models with respect to safety concerns. Given that in this respect is is fundamental to ensure that worst case characteristics are well represented, the second measure focuses on the representation of failure amplitudes with high magnitudes.
6.2.1. Assessing the Goodness of Fit on Average
Due to their nature, failure amplitudes are subject to randomness, which prohibits comparing two series of failure amplitudes directly, time step by time step. Instead, we apply a stochastic approach, the Kolmogorov–Smirnov (KS) statistic [
42]. The statistic is used as a basis for the KS hypothesis test that is commonly applied to test whether or not two random variables
H and
G are following the same distribution. In that endeavor, the KS statistic compares their cumulative distribution functions
and
by calculating the maximal differences between them:
As this statistic does not restrict the underlaying distributions of
H or
G and can be applied to empirical data sets, it is well-suited for comparing the series of failure amplitudes in this evaluation. However, as it considers only the maximal difference between two cumulative distribution functions, only a global statement about the considered series of failure amplitudes is provided. In contrast, the failure amplitudes of the distance sensor exhibit time- and value-correlations, as visible in
Figure 12a. To assess whether or not these are represented by the individual failure models, we need to adapt the measure to generate a more local statement.
We thus apply a sliding window approach similar to the one described in
Section 5.3 so that, instead of comparing all failure amplitudes of
H and
G at once, we consider only failure amplitudes within a local interval covering
time steps. By calculating the value of
over the failure amplitudes in this window, a local statement about the goodness of fit is obtained and time- or value-correlations are considered. To successively cover all failure amplitudes, the window is shifted through time by a step width of
. As this generates a value of
for each window, another series of assessment values is calculated. For the sake of simplicity, we sacrifice some of the locality of the statement by averaging over all calculated values of
. In this way, a scalar value
assessing the fit of a failure model with the validation data is calculated.
6.2.2. Assessing the Goodness of Fit for Failure Amplitudes with High Magnitudes
The previously introduced measure assesses the goodness of fit considering all failure amplitudes within a certain time range. It therefore assesses to which degree a failure model matches the time- and value-correlations of failure characteristics in general. However, when it comes to safety, the representation of failure amplitudes with high magnitudes by a failure model is even more important. To explicitly assess this property, we adapt the first measure to consider only failure amplitudes with high magnitudes.
The idea is to filter the failure amplitudes for each window within the sliding window approach, for which we utilize the
Three Sigma Rule [
46]. This rule states that
of a normally distributed random variable’s values are within the range of
. Consequently, values outside this range can be considered to have a high magnitude. Although the failure amplitudes of the considered Sharp sensor are not normally distributed, this rule still provides appropriate criteria for deciding whether or not failure amplitudes have a high magnitude, at least for the purpose of the intended evaluation. Nevertheless, we relax this criteria by a factor of 2, meaning that a higher number of high failure amplitudes will be considered for the KS statistic and hence the assessment will be more encompassing with respect to the intended safety-related purpose. We also use the sliding window approach to produce a series of assessment values, which we average to obtain the final value of
.
With both measures in place, we can assess the goodness of fit of the designed failure models regarding the validation data. Furthermore, by comparing the assessment values between the different failure models, a comparison between them is facilitated.
6.3. Results
To calculate the proposed assessment values for the designed failure models, the underlying sliding window approach needs to be parameterized regarding its window size
and step size
. As the validation data comprises 12,500 observations for each reference value
, a window size of
12,500 is appropriate. However, to show that the effect of varying window sizes is limited and the conclusions drawn from the assessment values are therefore robust to it, we vary the values of
12,500}. Furthermore, we set the step size to
, which ensures overlapping windows while maintaining significant changes between subsequent windows. The obtained assessment values
and
are listed in
Table 2.
The considered failure models are listed row-wise while the varying window sizes are listed column-wise. Each cell holds either the assessment value (for the first four columns) or (for the last four columns). Values close to zero indicate well-fitting failure models while higher values imply the opposite. For reference, we also list the assessment values obtained by comparing the training data with the validation data in the first row (white cells). Furthermore, for a visual comparison, we colored the cells as follows. The cells associated with the generic failure model are colored blue. Cells holding assessment values better (lower) than the corresponding value of the generic failure model are colored green, while cells with worse (higher) assessment values are colored red. In the single case of equality, the cell is colored yellow.
To compare the proposed generic failure model approach with the remaining ones, the failure amplitudes presented in
Figure 12 provide an important visual complement to the assessment values
and
listed in
Table 2. Therefore, we often refer to this figure in the following discussion.
The approach using the uniform distribution is clearly the worst one. This is because only the minimal and maximal possible failure amplitudes are considered and hence the distribution of failure amplitudes in between is not represented. Therefore, the distribution of the validation data is not met, which is also shown in
Figure 12d. Furthermore, in this case, no value-correlations are represented, which can also be seen in
Figure 12d. Concretely, neither the value-correlated increase of the variance of frequently occurring failure amplitudes nor the value-correlated increase of high magnitudes of infrequently occurring failure amplitudes are represented by the uniform distribution approach.
When comparing the generic failure model and the normal distribution approaches,
values show that they provide similar performances. However, this is only with respect to the representation of frequently occurring failure amplitudes. In this case, the normal distribution’s mean
and standard deviation
are calculated to match failure amplitudes on average, thus leading to good results. On the other hand, the bad performance of the normal distribution approach to represent rarely occurring failure amplitudes with high magnitudes is not only made evident by the assessment values of
, but also by
Figure 12c.
In contrast to the normal distribution approach, the approach using an ICDF represents the exact distribution of failure amplitudes of the training data. Therefore, it achieves better assessment values compared to the generic failure model for the first assessment measure
. However, the results compare worse when considering the second assessment measure
. This means that this approach is not as good in representing high (and rare) failure amplitudes, which is particularly visible when considering the smallest window size (
), for which inability to represent the value-correlation of higher failure amplitudes is exacerbated. This inability becomes apparent in
Figure 12b, where it is possible to see that failure amplitudes with high magnitudes occur unrelated to the reference value
.
It is interesting to observe the results relative to the neural network approach, which, differently from the ICDF approach, are supposedly able to correctly represent time- and value-correlations. However, the values of
for the neural network underline that failure amplitudes with high magnitudes are still not represented as well as by the generic failure model. Furthermore, increasing the window size
plays favorably to our approach, whose performance is almost not affected. The performance degradation of the neural network approach for higher window sizes may be explained by uncertainties and artifacts introduced during the training of the network, also with relevance when considering high failure amplitudes. For instance, some deviations towards the positive range of failure amplitudes in the beginning of
, visible in
Figure 12c, end up degrading the assessment values for windows including this range. If few large windows are considered for calculating the final assessment value (which is averaged over all windows), then a single artifact will have a more significant impact.
When considering
values, the neural network approach performs sightly better than our approach. This indicates a better fit of frequently occurring failure amplitudes, which is underlined by
Figure 12c. Still, from a safety perspective, we believe that out approach is better as it provides almost the same performance as the neural network with respect to
assessment values, while it performs significantly better when it comes to represent failures with high amplitudes.
Nevertheless, in both cases, it is likely that optimizing the training procedure for designing a neural network, as well as optimizing the configuration and usage of the processing chain for extracting a generic failure model, enables better results.
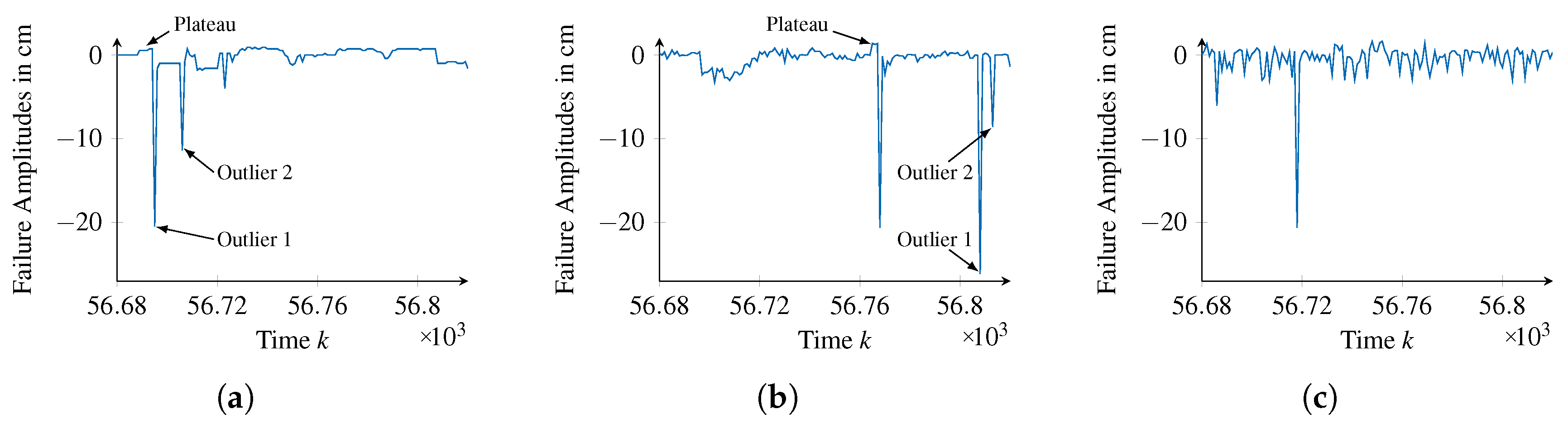
A more fundamental difference between both approaches becomes apparent when comparing their generated series of failure amplitudes with the validation data at a detailed level, which are shown in
Figure 13.
At about time step 56,690, the validation data show a small plateau before decreasing severely and thereby forming an Outlier. A similar shape can be found within the failure amplitudes of the generic failure model, near time step 56,770. Contrarily, the failure amplitudes of the neural network are exhibiting Outliers, but lack the plateau before. Furthermore, while the validation data and the generic failure model show two Outliers in sequence, as illustrated in
Figure 13d,e, a similar pattern can not be found in the data of the neural network. Although these are very particular examples, they clarify that the generic failure model is capable of representing the time behavior of failure amplitudes using failure pattern
, whereas the neural network solely represents their distribution.
Finally, we can compare both approaches with respect to the requirements defined in
Section 2. As the
Generality,
Clarity, and
Coverage requirements are fulfilled by both approaches due to their use of neural networks and mathematical expressions, the
Comparability requirement is of most interest. With respect to the neural network, this requirement is only partially fulfilled. For comparing a failure model, the neural network has to be sampled to either obtain an application specific representation of the ICDF or a Monte Carlo simulation has to be performed. To obtain any further information, an application has to apply corresponding calculations. On the other hand, the generic failure model supports more flexible evaluations. For instance, for calculating the maximal duration of a failure type, only the deactivation function has to be evaluated. Similarly, to determine the average scaling of a failure type, only the mean function
has to be evaluated. Finally, when performing a Monte Carlo simulation on the generic failure model, not only a series of failure amplitudes is obtained, but also detailed information about the activation, deactivation and failure amplitudes of individual failure types is acquired. This flexibility renders the
Comparability requirement to be fulfilled by the generic failure model.
7. Conclusions
The work presented in this paper is motivated by the question on how to maintain safety in dynamically composed systems. As an answer, we proposed an integration step to take place in the application context, for analyzing at run-time the failure model of an external sensor with respect to the application’s fault tolerance capacities. By rejecting or integrating the external sensor’s observations depending on the outcome of this run-time safety analysis, the safety of dynamically composed systems is maintained.
For applying this concept, we identified four requirements (Generality, Coverage, Clarity and Comparability) that have to be fulfilled by appropriate failure models of external sensors. In addition, by reviewing the state of the art on sensor failure modeling in different research areas, we showed that no current approach meets the listed requirements.
Then, as a fundamental novel contribution of this paper, we introduced a mathematically defined, generic failure model. It utilizes not only the concept of failure types, but also explicitly supports representing time- and value-correlated random distributions. As the second major contribution, we introduced a processing chain capable of automatically extracting appropriate failure models from a series of failure amplitudes.
To validate both contributions, we used the processing chain to extract a generic failure model for representing the failure characteristics of a Sharp GP2D12 infra-red distance sensor, which we then used to perform a detailed comparative analysis with a set of other approaches. This comparative analysis underlined the applicability of the approach as well as the fulfillment of the predefined requirements.
Nevertheless, the generic failure model was evaluated solely with respect to one-dimensional failure characteristics. To confirm the fulfillment of the Coverage requirement and simultaneously facilitate the adoption of the generic failure model, representing failure characteristics of multidimensional sensors is required in future work. Similarly, while Comparability is given due to the structure and composition of the proposed failure model, an empirical evaluation with respect to a real dynamically composed system is planned. In this manner, the representation of an application’s fault tolerance using the same methodology shall be investigated and an approach for matching it with a failure model shall be determined. This will underline not only the fulfillment of this requirement, but also the applicability of the proposed integration step.
Furthermore, to increase the applicability of the generic failure model to safety-critical systems in general, the processing chain shall be extended in such a way that certain properties (e.g., completeness, no under-estimation of failure characteristics) for extracted failure models can be guaranteed.
Besides dynamically composed systems, versatile applications of the generic failure model are feasible. Due to its mathematical and structural definition, its interpretation is not only clear, but can be automated too. Therefore, using it for automatically parameterizing appropriate failure detectors and filters facilitates a promising research direction too. This idea can be extended to the usage of the generic failure model within approaches for online monitoring of the quality of sensor observations, e.g., the validity concept [
47].

























































 —not fulfilled,
—not fulfilled,  —partially fulfilled,
—partially fulfilled,  —fulfilled.
—fulfilled.




