Parameter Estimation of the Thermal Network Model of a Machine Tool Spindle by Self-made Bluetooth Temperature Sensor Module
Abstract
:1. Introduction
2. Theoretical Background
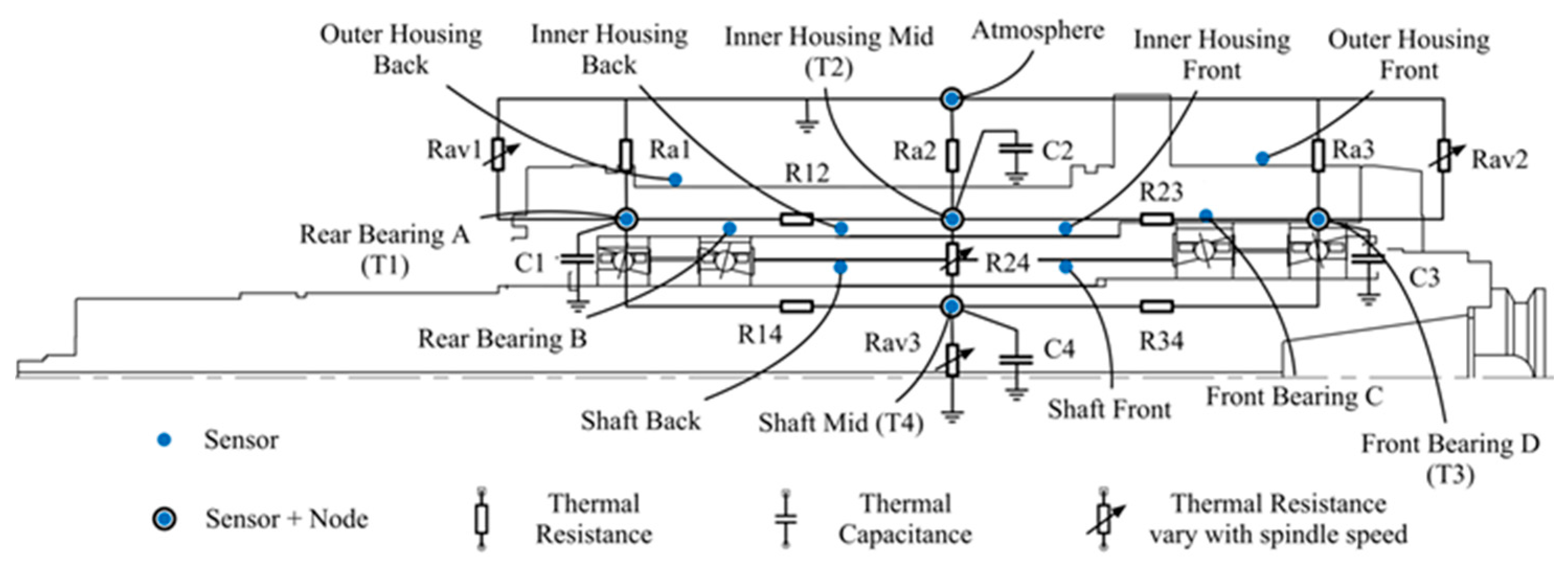
2.1. Thermal Characteristics of Spindle
2.2. System Identification Technique
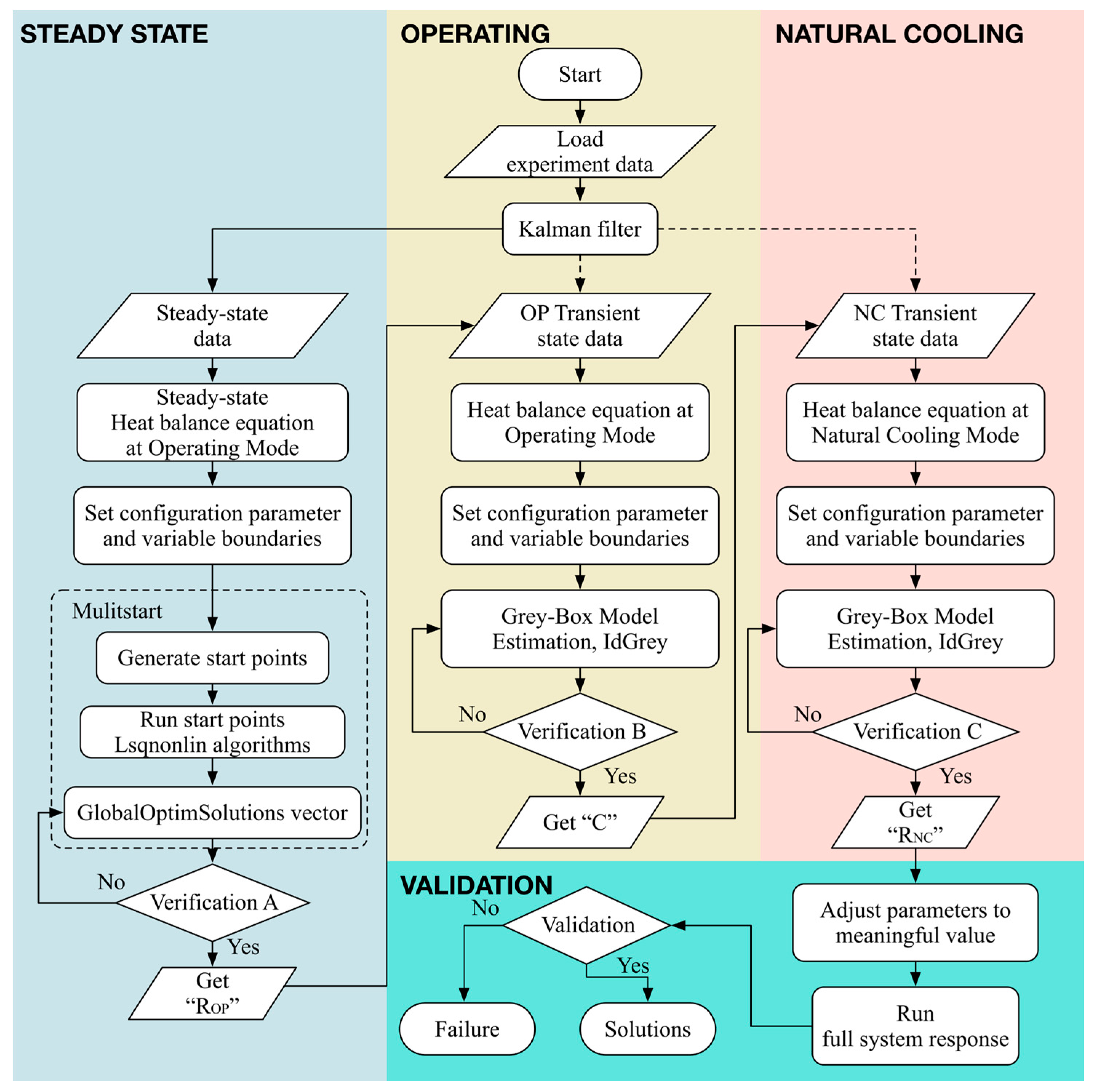
3. Parameterization Methodology for the Thermal Network Model of Spindle
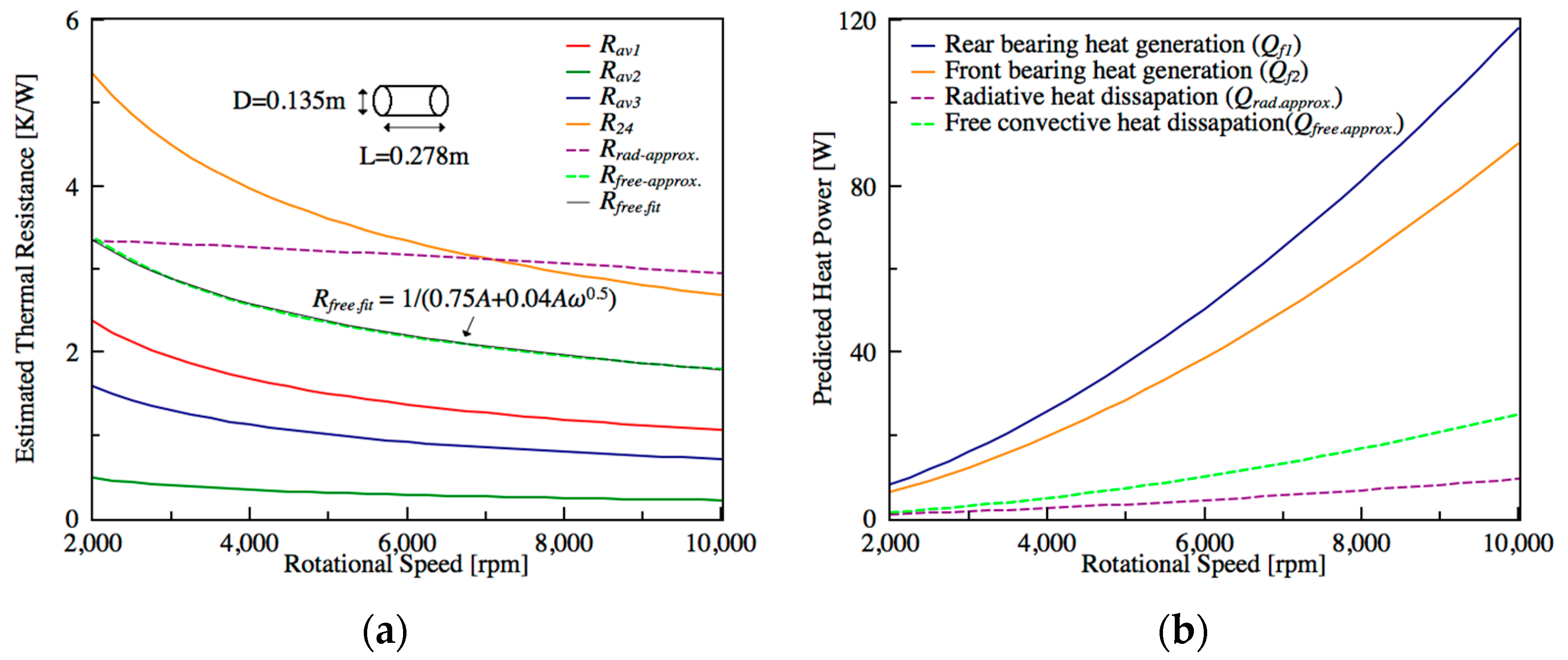
3.1. Parameterization Strategy
- (1)
- lumped element model assumption is valid, Bi << 0.1;
- (2)
- temperature distribution of spindle is axisymmetric;
- (3)
- heat generation and forced convective resistance are assumed according to the theoretical and empirical Equations (5), (9), and (12);
- (4)
- heat transfer through radiation and conduction are considered as a constant thermal resistance, including thermal contact resistance; and,
- (5)
- free convection coefficient is assumed as a function of .
3.2. Estimated Thermal Network Model in State-Space
4. Experiment Setup
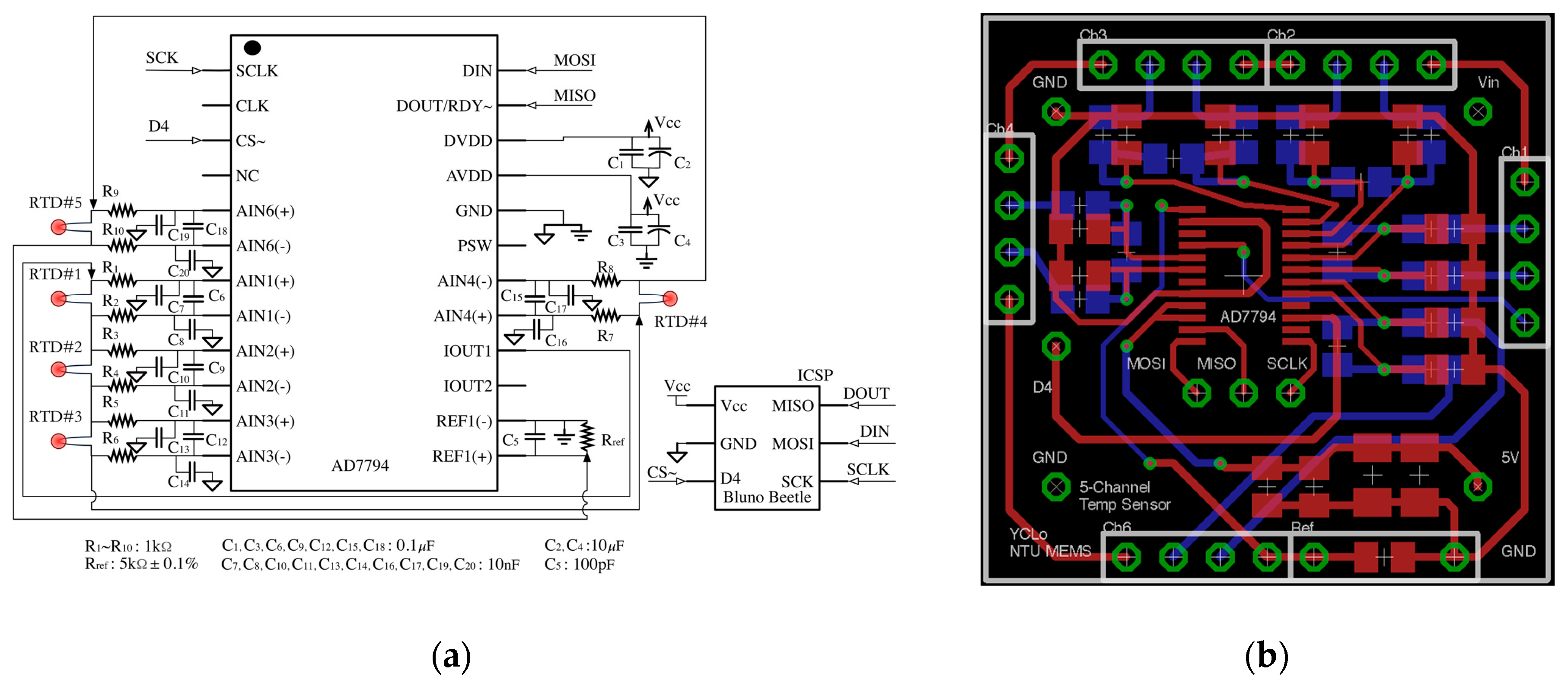
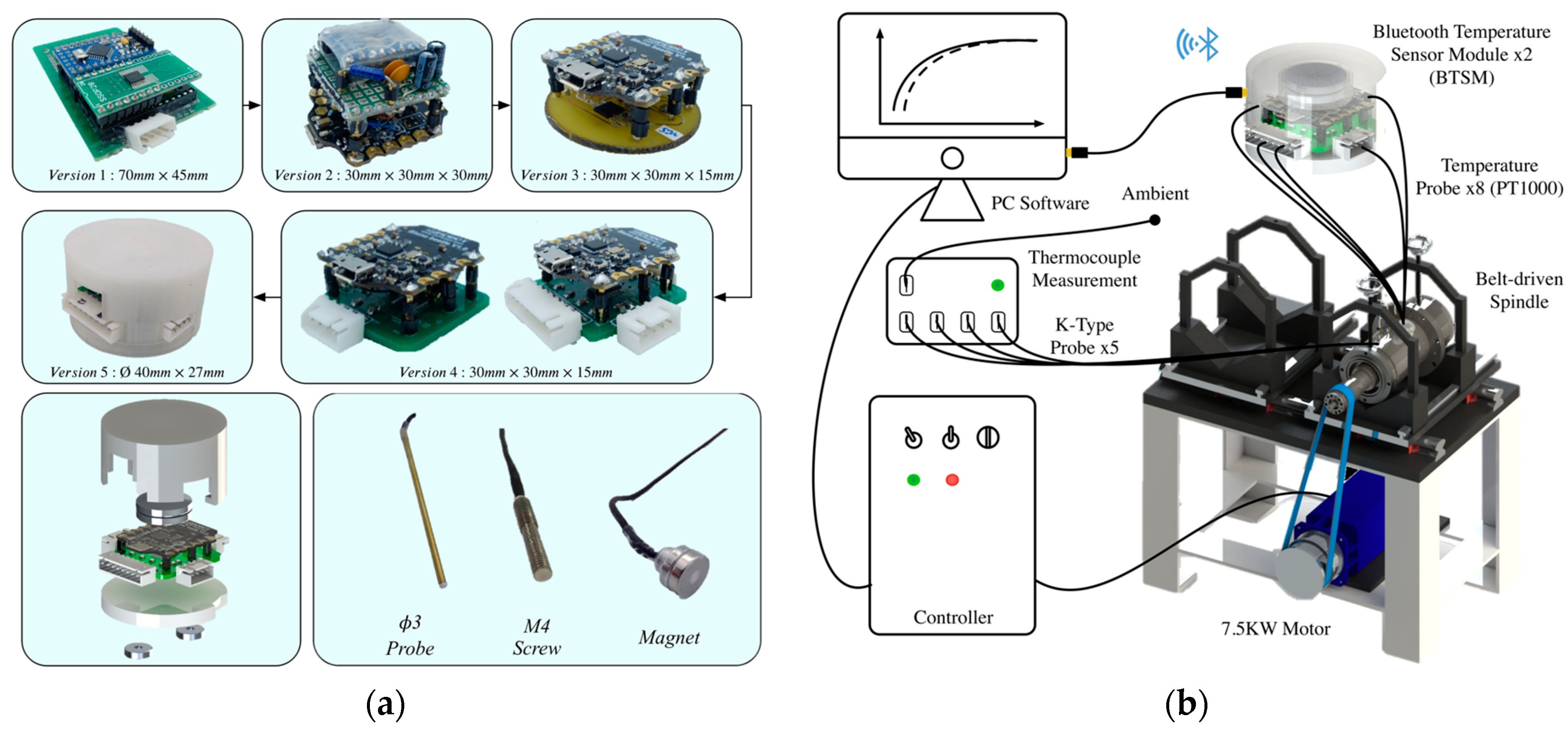
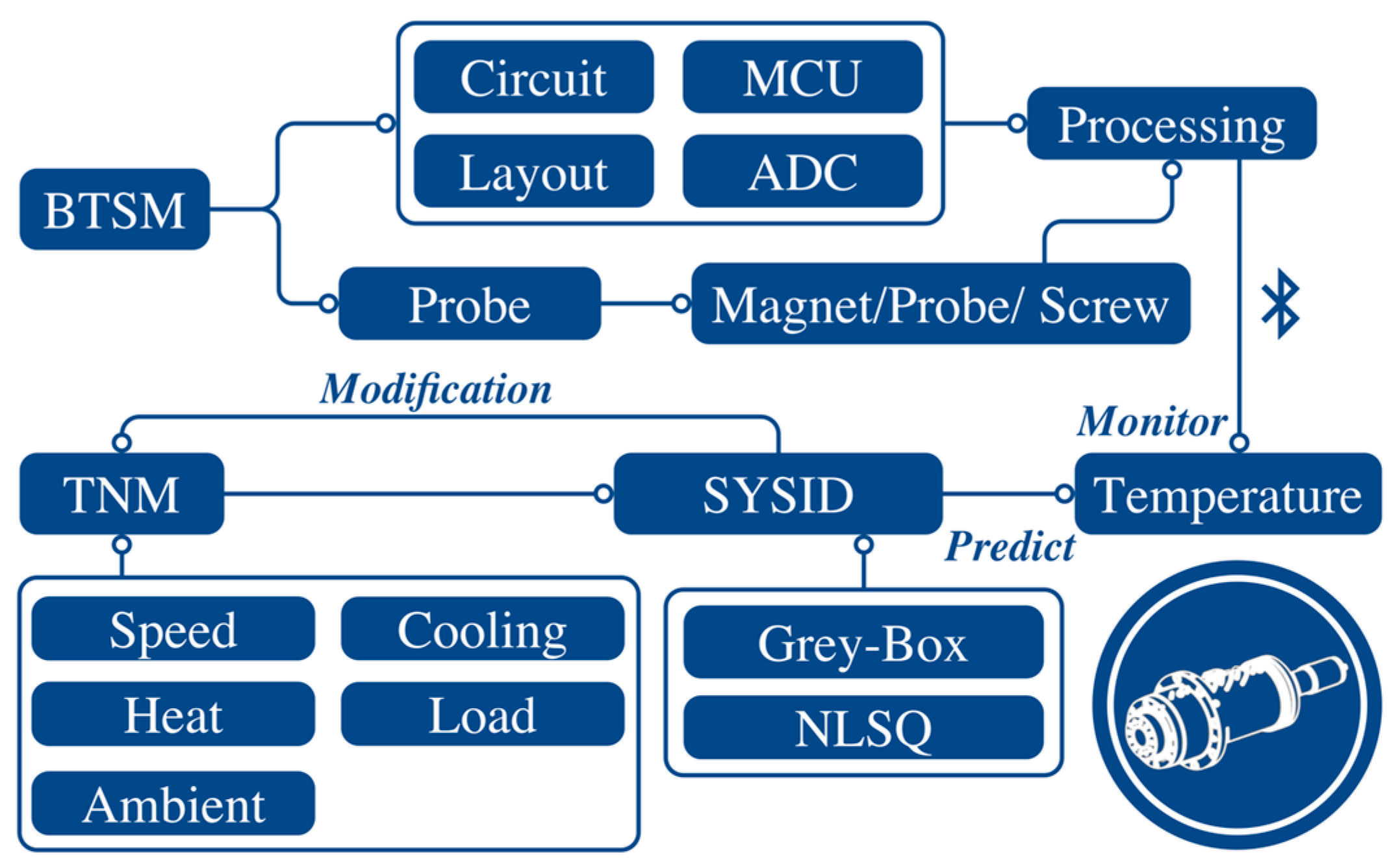
4.1. Self-Made Bluetooth Temperature Sensor Module
4.2. Experiment Setup
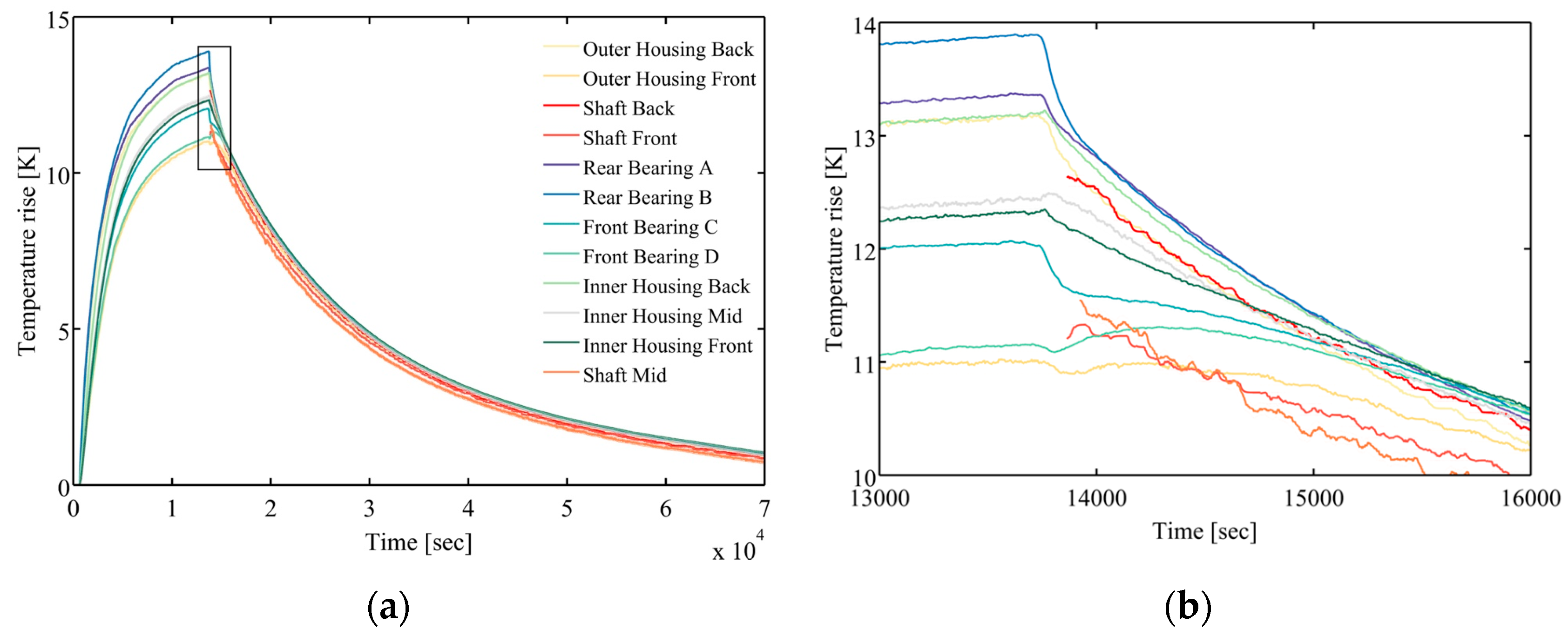
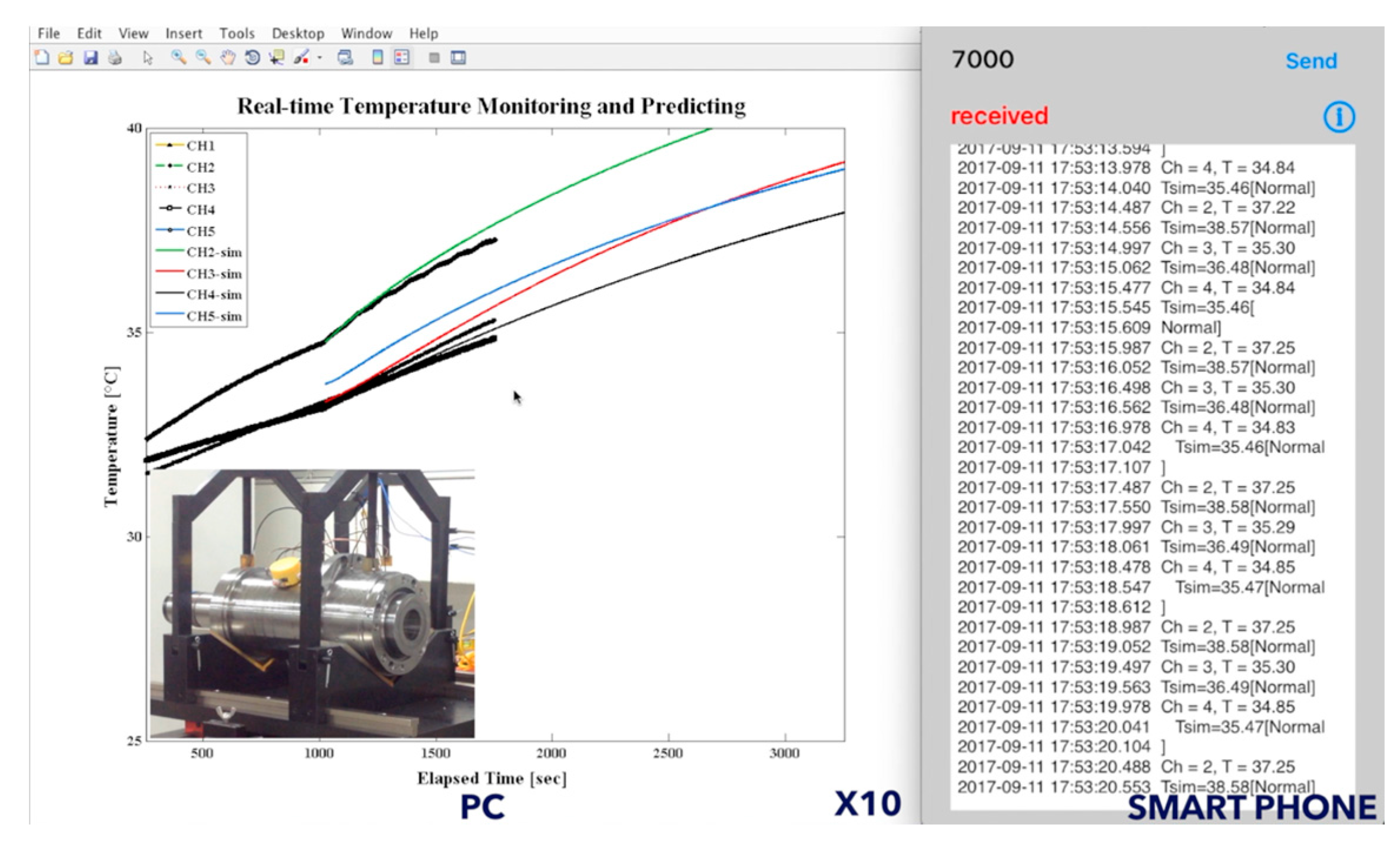
5. Results
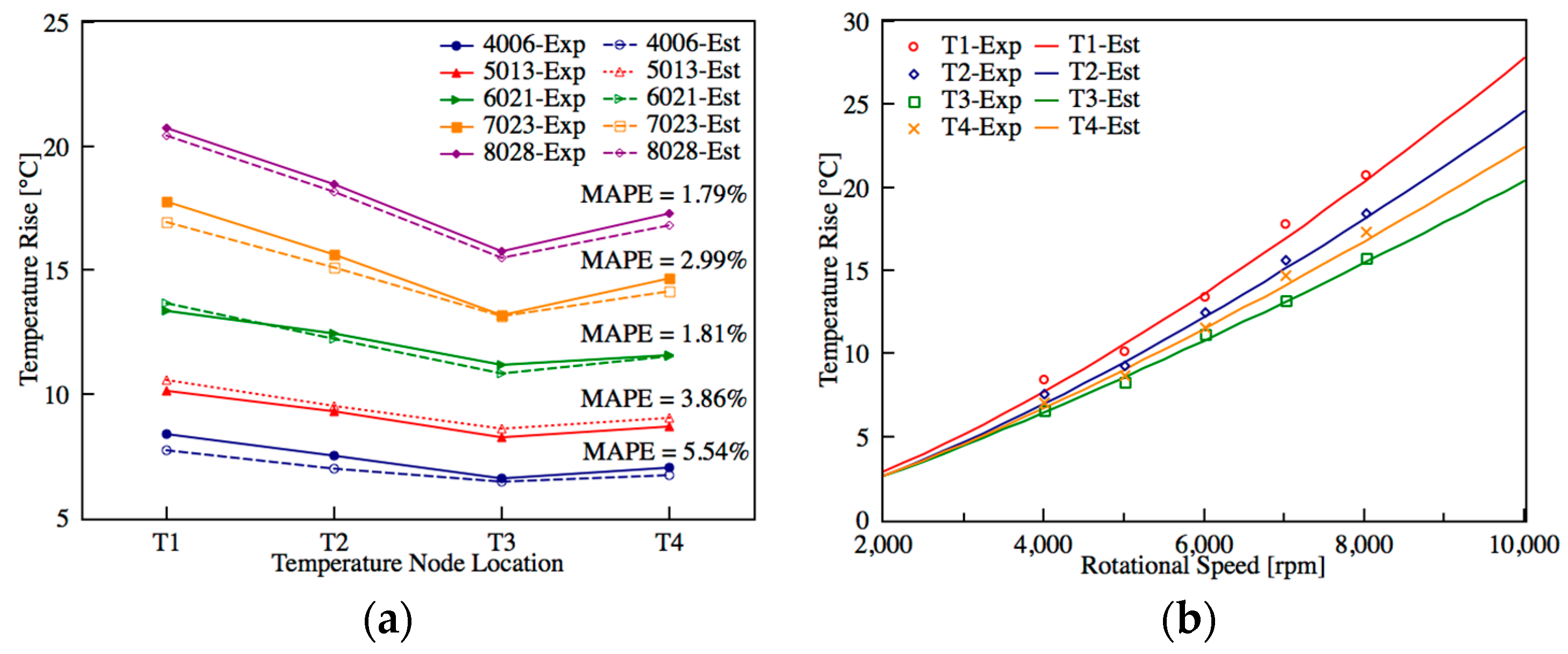
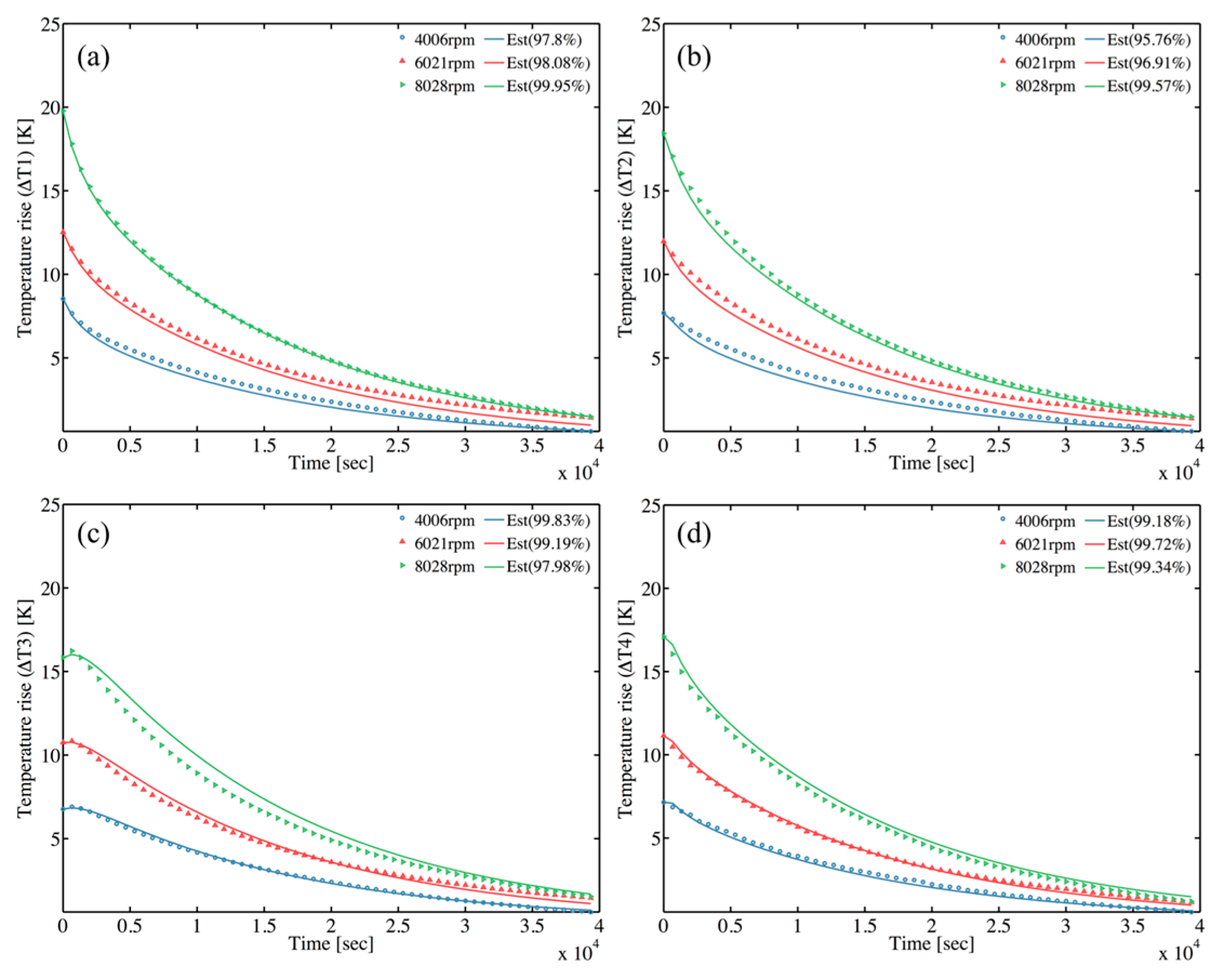
5.1. Steady State Self-Validation
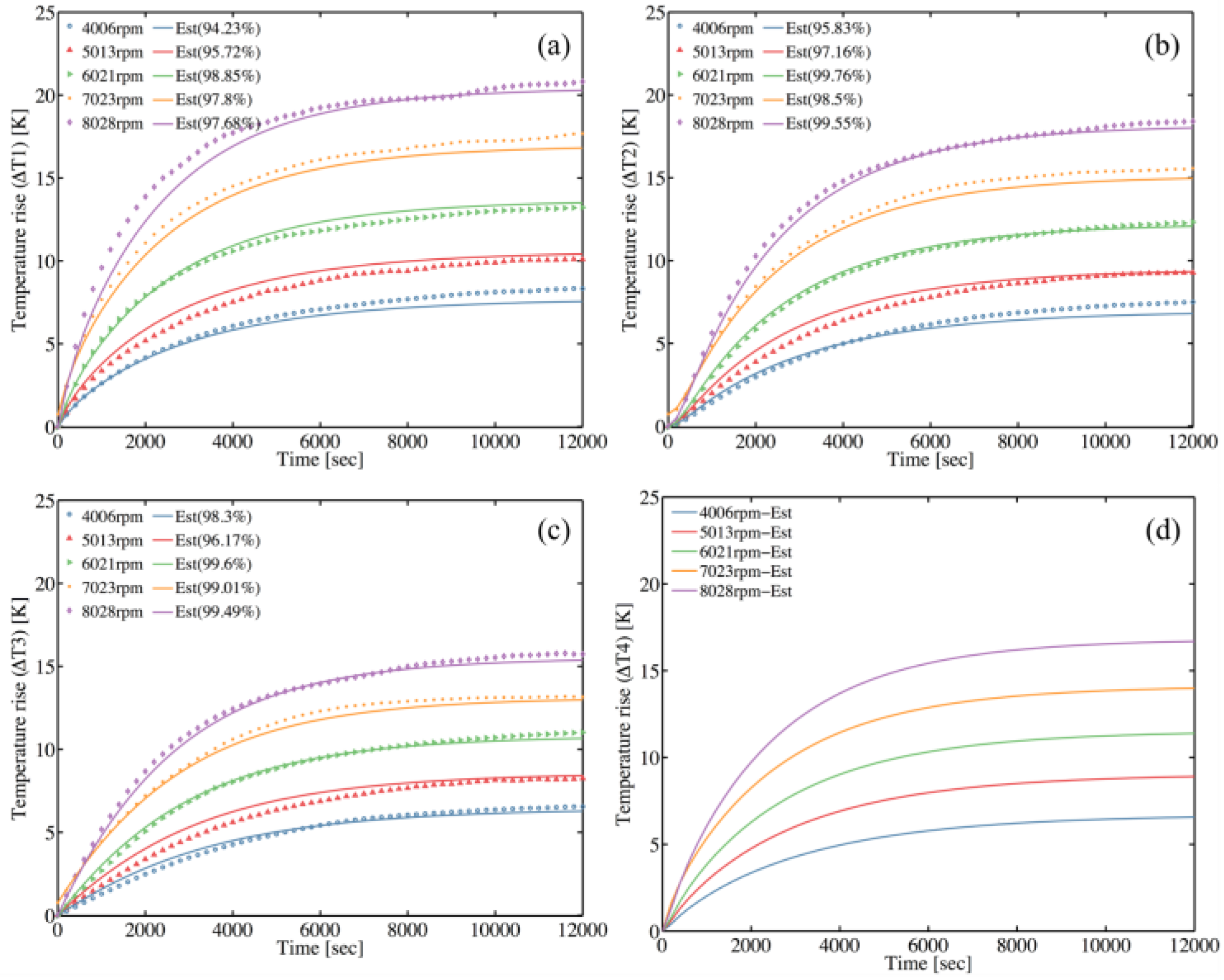
5.2. Transient State Self-Validation
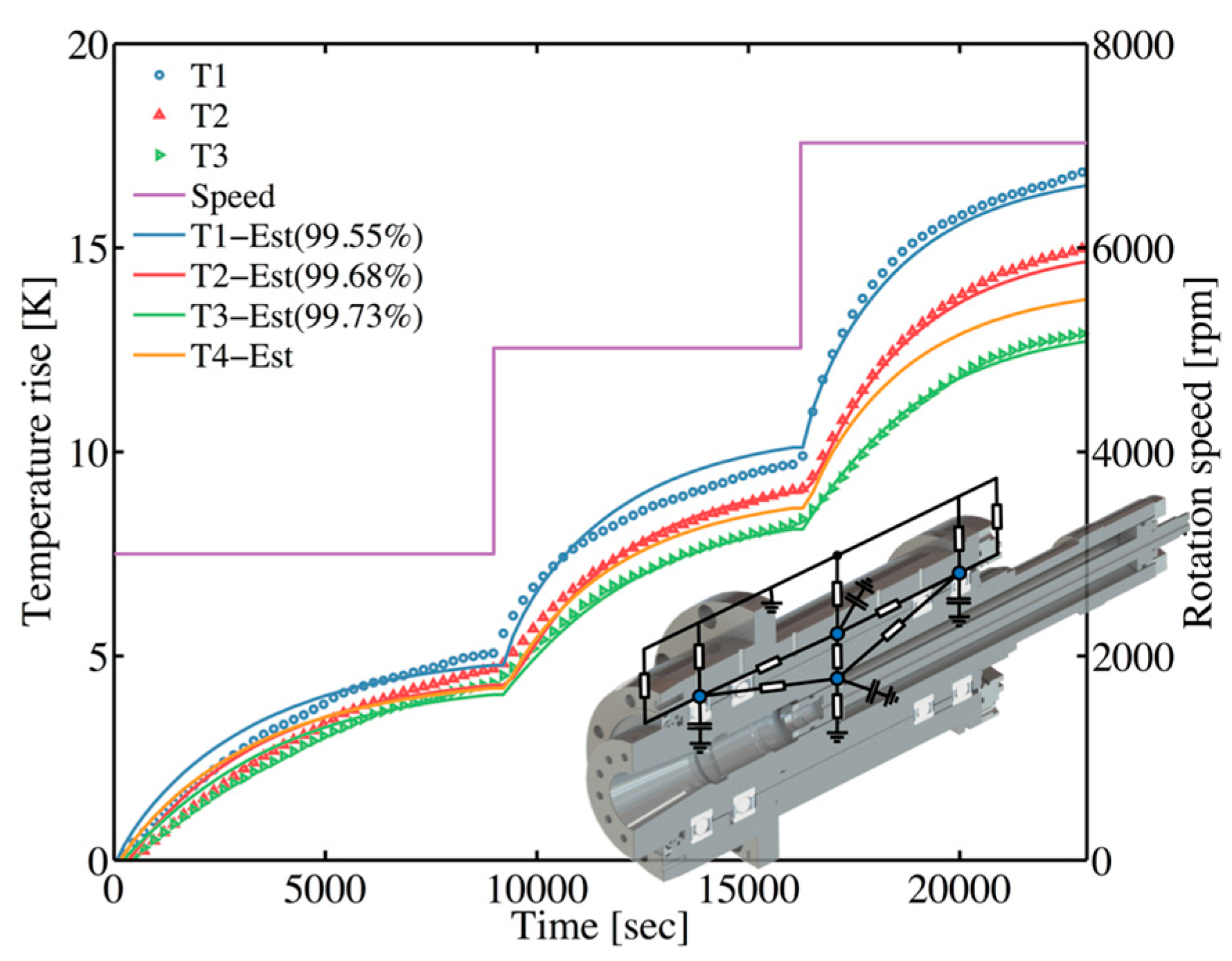
5.3. External Validation
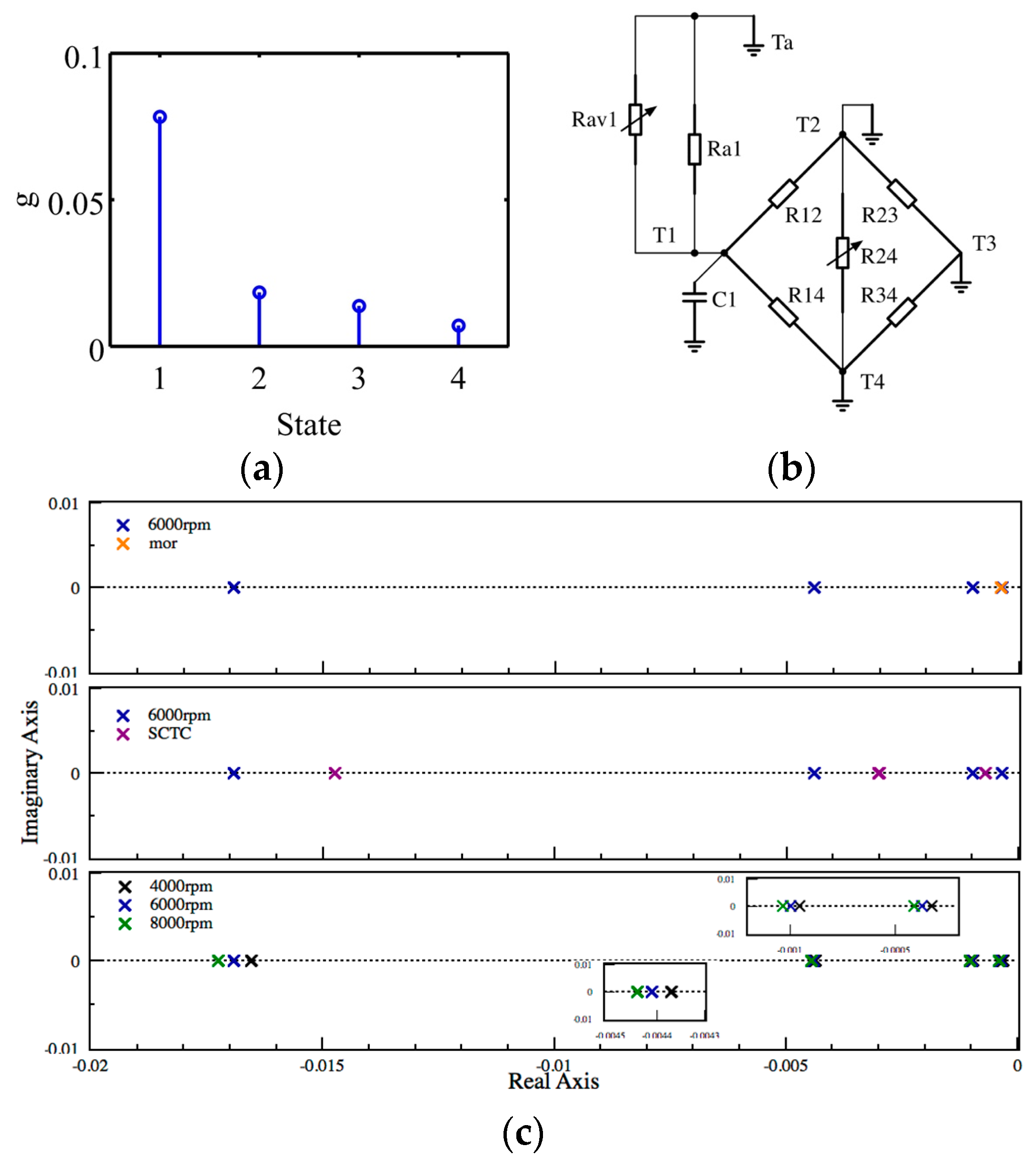
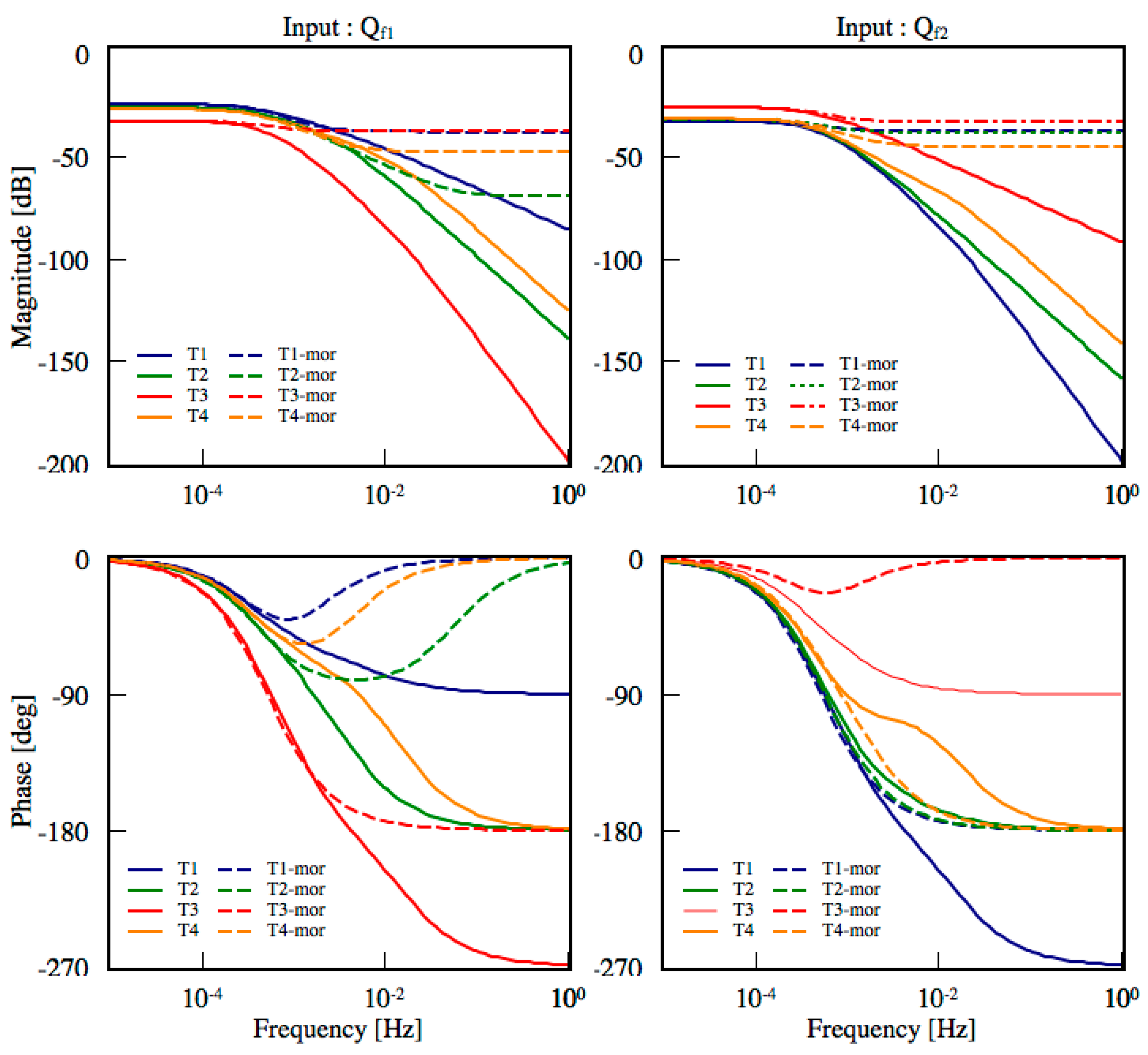
5.4. Model Order Reduction
5.5. Short Circuit Time Constant
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. System Parameter Matrices
References
- Mayr, J.; Jedrzejewski, J.; Uhlmann, E.; Donmez, A.; Knapp, W.; Härtig, F.; Wendt, K.; Moriwaki, T.; Shore, P.; Schmitt, R.; et al. Thermal issues in machine tools. CIRP Ann. Manuf. Technol. 2012, 61, 771–791. [Google Scholar] [CrossRef]
- Ramesh; Mannan, M.; Poo, A. Error compensation in machine tools—A review. Part II: Thermal errors. Int. J. Mach. Tools Manuf. 2000, 40, 1257–1284. [Google Scholar] [CrossRef]
- Bossmanns, B.; Tu, J. A thermal model for high speed motorized spindles. Int. J. Mach. Tools Manuf. 1999, 39, 1345–1366. [Google Scholar] [CrossRef]
- Bossmanns, B.; Tu, J. A Power Flow Model for High Speed Motorized Spindles—Heat Generation Characterization. J. Manuf. Sci. Eng. 2001, 123, 494. [Google Scholar]
- Lin, C.-W.; Tu, J.; Kamman, J. An integrated thermo-mechanical-dynamic model to characterize motorized machine tool spindles during very high speed rotation. Int. J. Mach. Tools Manuf. 2003, 43, 1035–1050. [Google Scholar]
- Ma, C.; Yang, J.; Zhao, L.; Mei, X.; Shi, H. Simulation and experimental study on the thermally induced deformations of high-speed spindle system. Appl. Therm. Eng. 2015, 86, 251–268. [Google Scholar] [CrossRef]
- Zivkovic, A.; Zeljkovic, M.; Tabakovic, S.; Milojevic, Z. Mathematical modeling and experimental testing of high-speed spindle behavior. Int. J. Adv. Manuf. Technol. 2015, 77, 1071–1086. [Google Scholar] [CrossRef]
- Huang, Y.-H.; Huang, C.-W.; Chou, Y.-D.; Ho, C.-C.; Lee, M.-T. An Experimental and Numerical Study of the Thermal Issues of a High-speed Built-in Motor Spindle. Smart Sci. 2016, 4, 1–7. [Google Scholar] [CrossRef]
- Liu, Z.; Pan, M.; Zhang, A.; Zhao, Y.; Yang, Y.; Ma, C. Thermal characteristic analysis of high-speed motorized spindle system based on thermal contact resistance and thermal-conduction resistance. Int. J. Adv. Manuf. Technol. 2015, 76, 1913–1926. [Google Scholar]
- Brecher, C.; Shneor, Y.; Neus, S.; Bakarinow, K.; Fey, M. Thermal Behavior of Externally Driven Spindle: Experimental Study and Modelling. Engineering 2015, 7, 73–92. [Google Scholar]
- Min, X.; Shuyun, J.; Ying, C. An improved thermal model for machine tool bearings. Int. J. Mach. Tools Manuf. 2007, 47, 53–62. [Google Scholar] [CrossRef]
- Takabi, J.; Khonsari, M.M. Experimental testing and thermal analysis of ball bearings. Tribol. Int. 2013, 60, 93–103. [Google Scholar] [CrossRef]
- Wu, L.; Tan, Q. Thermal Characteristic Analysis and Experimental Study of a Spindle-Bearing System. Entropy 2016, 18, 271. [Google Scholar] [CrossRef]
- Noh, J.-H.; Cha, K.-U.; Ahn, S.-T.; Yook, S.-J. Prediction of time-varying heat flux along a hollow cylindrical tube wall using recursive input estimation algorithm and thermal resistance network method. Int. J. Heat Mass Trans. 2016, 97, 232–241. [Google Scholar] [CrossRef]
- Than, V.-T.; Wang, C.-C.; Ngo, T.-T.; Huang, J. Estimating time-varying heat sources in a high speed spindle based on two measurement temperatures. Int. J. Therm. Sci. 2017, 111, 50–65. [Google Scholar] [CrossRef]
- Lin, X.; Perez, H.; Siegel, J.; Stefanopoulou, A.; Li, Y.; Anderson, R.; Ding, Y.; Castanier, M. Online Parameterization of Lumped Thermal Dynamics in Cylindrical Lithium Ion Batteries for Core Temperature Estimation and Health Monitoring. IEEE Trans. Control Syst. Technol. 2013, 21, 1745–1755. [Google Scholar]
- Kral, C.; Habetler, T.; Harley, R.; Pirker, F.; Pascoli, G.; Oberguggenberger, H.; Fenz, C. Rotor Temperature Estimation of Squirrel-Cage Induction Motors by Means of a Combined Scheme of Parameter Estimation and a Thermal Equivalent Model. IEEE Trans. Ind. Appl. 2004, 40, 1049–1057. [Google Scholar] [CrossRef]
- Kim, D.; Cai, J.; Ariyur, K.; Braun, J. System Identification for Building Thermal Systems under the Presence of Unmeasured Disturbances in Closed Loop Operation: Lumped Disturbance Modeling Approach. Build. Environ. 2016, 107, 169–180. [Google Scholar] [CrossRef]
- Skibinski, G.L.; Sethares, W.A. Thermal parameter estimation using recursive identification. IEEE Trans. Power Electron. 1991, 6, 228–239. [Google Scholar] [CrossRef]
- Huber, T.; Peters, W.; Böcker, J. Monitoring critical temperatures in permanent magnet synchronous motors using low-order thermal models. In Proceedings of the International Power Electronics Conference (IPEC-Hiroshima 2014-ECCE ASIA), Hiroshima, Japan, 18–21 May 2014. [Google Scholar]
- Wallscheid, O.; Böcker, J. Global Identification of a Low-Order Lumped-Parameter Thermal Network for Permanent Magnet Synchronous Motors. IEEE Trans. Energy Convers. 2016, 31, 354–365. [Google Scholar] [CrossRef]
- Gaona, D.; Wallscheid, O.; Böcker, J. Glocal Identification Methods for Low-Order Lumped-Parameter Thermal Networks Used in Permanent Magnet Synchronous Motors. In Proceedings of the IEEE International Conference on Power Electronics and Drive Systems, Honolulu, HI, USA, 12–15 December 2017. [Google Scholar]
- Harris, T.A.; Kotzalas, M.N. Essential Concepts of Bearing Technology; Taylor & Francis: New York, NY, USA, 2006. [Google Scholar]
- Stein, J.L.; Tu, J.F. A state-space model for monitoring thermally induced preload in anti-friction spindle bearings of high-speed machine tools. ASME J. Dyn. Syst. Meas. Control 1994, 116, 372–386. [Google Scholar] [CrossRef]
- Harris, T.A.; Kotzalas, M.N. Advanced Concepts of Bearing Technology: Rolling Bearing Analysis; Taylor & Francis: New York, NY, USA, 2006. [Google Scholar]
- Kendoush, A. An Approximate Solution of the Convective Heat Transfer from an Isothermal Rotating Cylinder. Int. J. Heat Fluid Fl. 1996, 17, 439–441. [Google Scholar] [CrossRef]
- Childs, P.; Long, C. A Review of Forced Convective Heat Transfer in Stationary and Rotating Annuli. Proc. Inst. Mech. Eng. Part. C J. Mech. Eng. Sci. 1996, 210, 123–134. [Google Scholar] [CrossRef]
- Kothandaraman, C.P. Fundamentals of Heat and Mass Transfer; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Ljung, L. System Identification Toolbox—User’s Guide; MathWorks: Natick, MA, USA, 1999. [Google Scholar]
- Bluno Beetle SKU:DFR0339. Available online: https://www.dfrobot.com/wiki/index.php/Bluno_Beetle_SKU:DFR0339 (accessed on 12 December 2017).
- AD7794, 6-Channel, Low Noise, Low Power, 24-Bit Sigma Delta ADC. Available online: http://www.analog.com/en/products/analog-to-digital-converters/ad7794.html#product-overview (accessed on 12 December 2017).
- Bluno Terminal. Available online: https://itunes.apple.com/tw/app/bluno-terminal/id794109935?mt=8 (accessed on 12 December 2017).

| Sensor Element | Accuracy [°C] | Resolution [°C] | Measurement Range [°C] | Power [mW] | Module Size [mm3] |
|---|---|---|---|---|---|
| RTD | ±(0.1 + 0.0029|ϑ|) | 0.00489 | −40~150 | 7 | Ø40× |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| R12 [KW−1] | 0.1263 | Ra1 [KW−1] | 0.884 | Rav3 [KW−1] | 1.0032 |
| R14 [KW−1] | 0.1537 | Ra2 [KW−1] | 1.393 | qf1 [W] | 37.162 |
| R23 [KW−1] | 0.5954 | Ra3 [KW−1] | 3.071 | qf2 [W] | 28.406 |
| R24 [KW−1] | 3.609 | Rav1 [KW−1] | 1.498 | qf3 [W] | 0.0043 |
| R34 [KW−1] | 0.48 | Rav2 [KW−1] | 0.303 | qf4 [W] | 0.0073 |
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| R12 [KW−1] | 0.1263 | R′a1 [KW−1] | 18.765 | C1 [JK−1] | 5375.8 |
| R14 [KW−1] | 0.1537 | Ra2 [KW−1] | 1.393 | C2 [JK−1] | 3545.8 |
| R23 [KW−1] | 0.5954 | R′a3 [KW−1] | 6.496 | C3 [JK−1] | 10,931.7 |
| R′24 [KW−1] | 6.737 | R′a4 [KW−1] | 2.497 | C4 [JK−1] | 625.4 |
| R34 [KW−1] | 0.48 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lo, Y.-C.; Hu, Y.-C.; Chang, P.-Z. Parameter Estimation of the Thermal Network Model of a Machine Tool Spindle by Self-made Bluetooth Temperature Sensor Module. Sensors 2018, 18, 656. https://doi.org/10.3390/s18020656
Lo Y-C, Hu Y-C, Chang P-Z. Parameter Estimation of the Thermal Network Model of a Machine Tool Spindle by Self-made Bluetooth Temperature Sensor Module. Sensors. 2018; 18(2):656. https://doi.org/10.3390/s18020656
Chicago/Turabian StyleLo, Yuan-Chieh, Yuh-Chung Hu, and Pei-Zen Chang. 2018. "Parameter Estimation of the Thermal Network Model of a Machine Tool Spindle by Self-made Bluetooth Temperature Sensor Module" Sensors 18, no. 2: 656. https://doi.org/10.3390/s18020656
APA StyleLo, Y.-C., Hu, Y.-C., & Chang, P.-Z. (2018). Parameter Estimation of the Thermal Network Model of a Machine Tool Spindle by Self-made Bluetooth Temperature Sensor Module. Sensors, 18(2), 656. https://doi.org/10.3390/s18020656





