Structural Designing of a MEMS Capacitive Accelerometer for Low Temperature Coefficient and High Linearity
Abstract
:1. Introduction
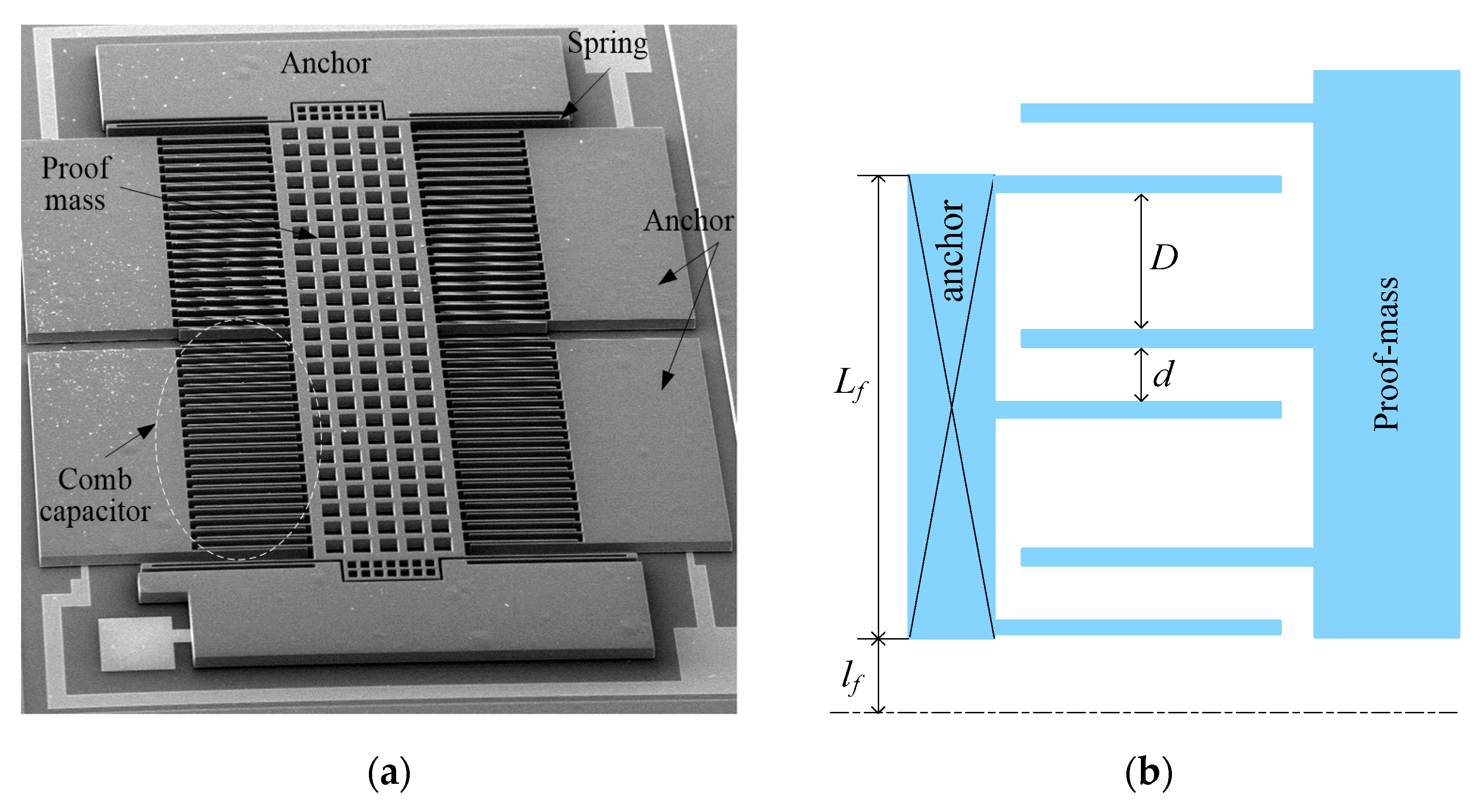
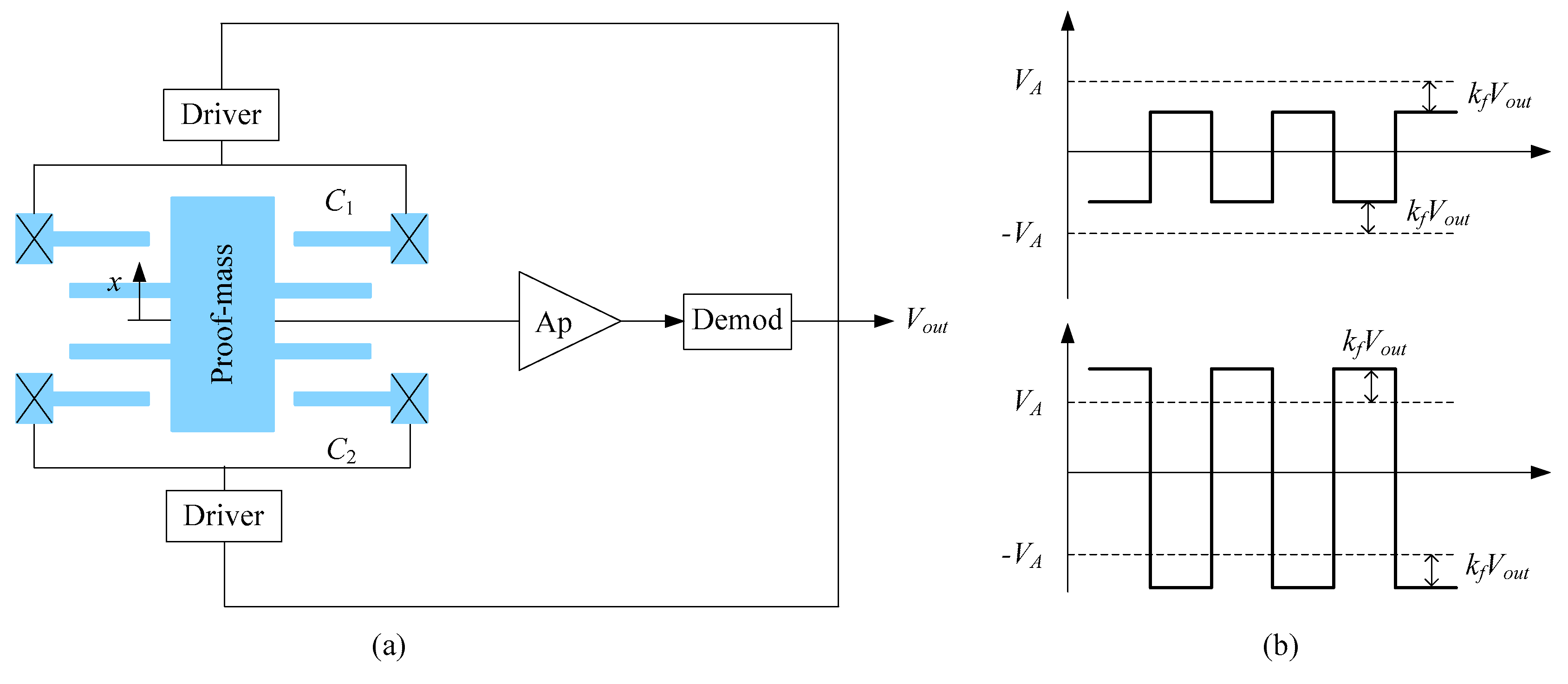
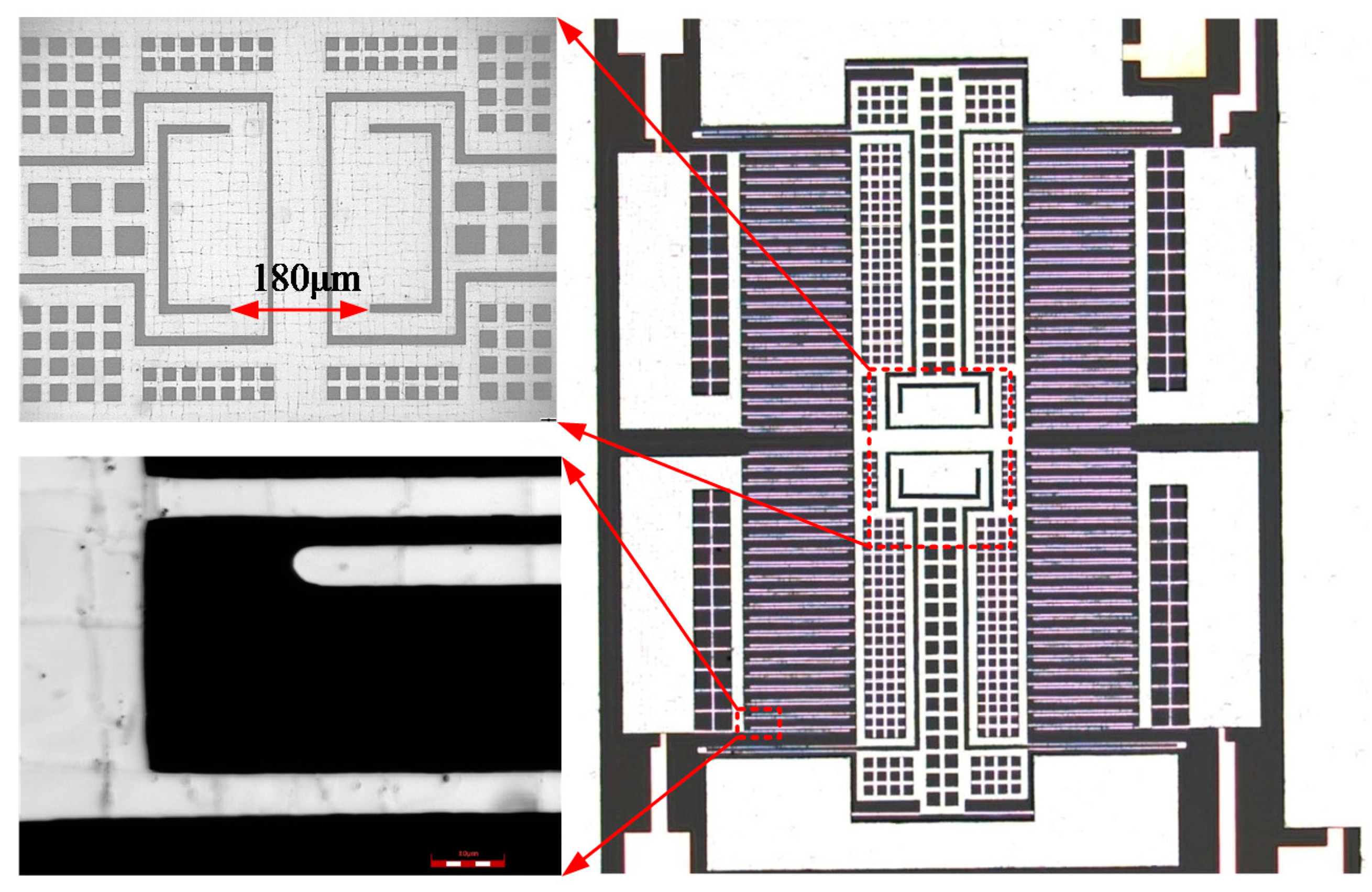
2. Fabrication and Detection Principle
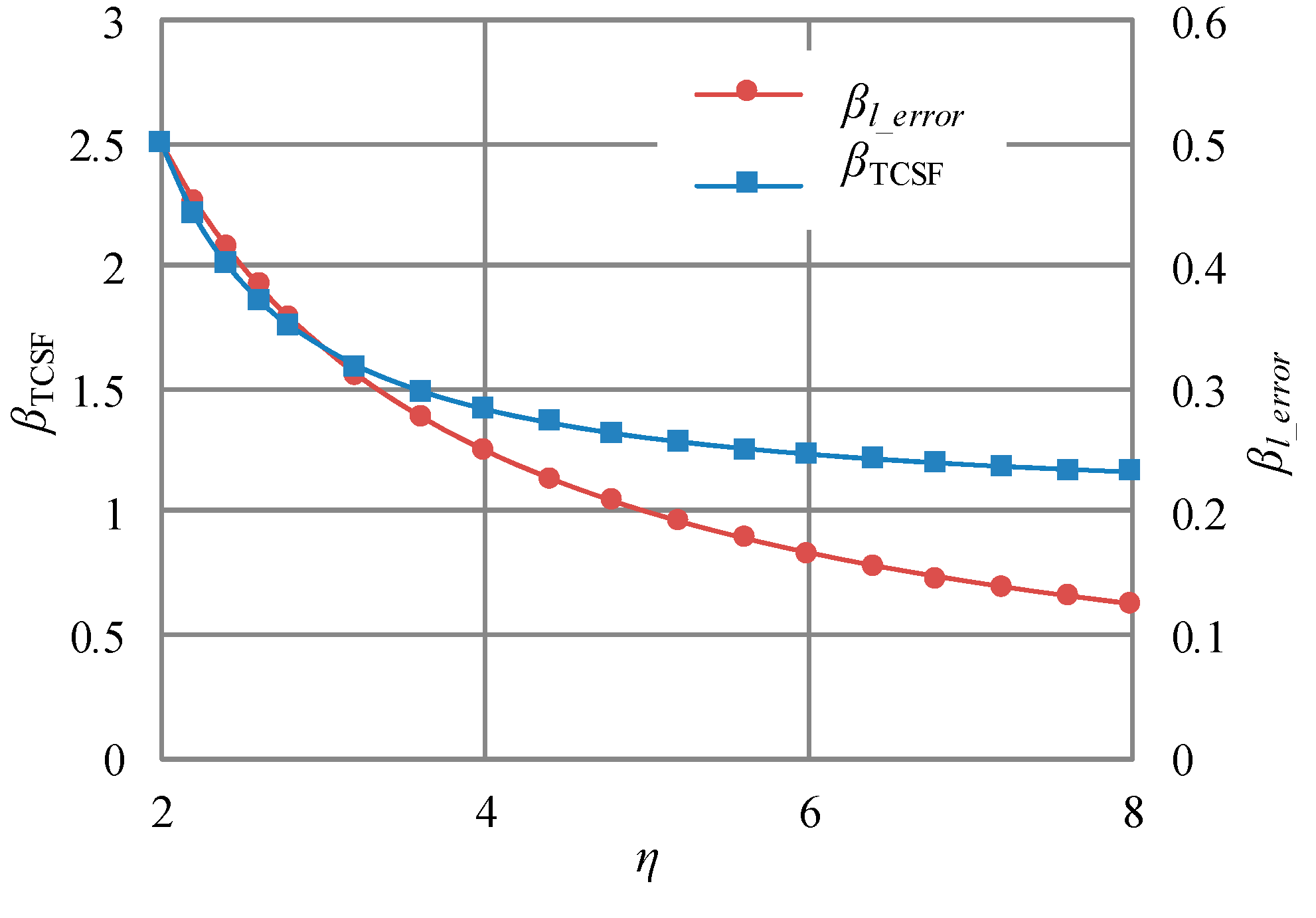
3. Contrary Effect of the WNGR on TCSF and Linearity Error
3.1. Analytical Model for the Linearity Error
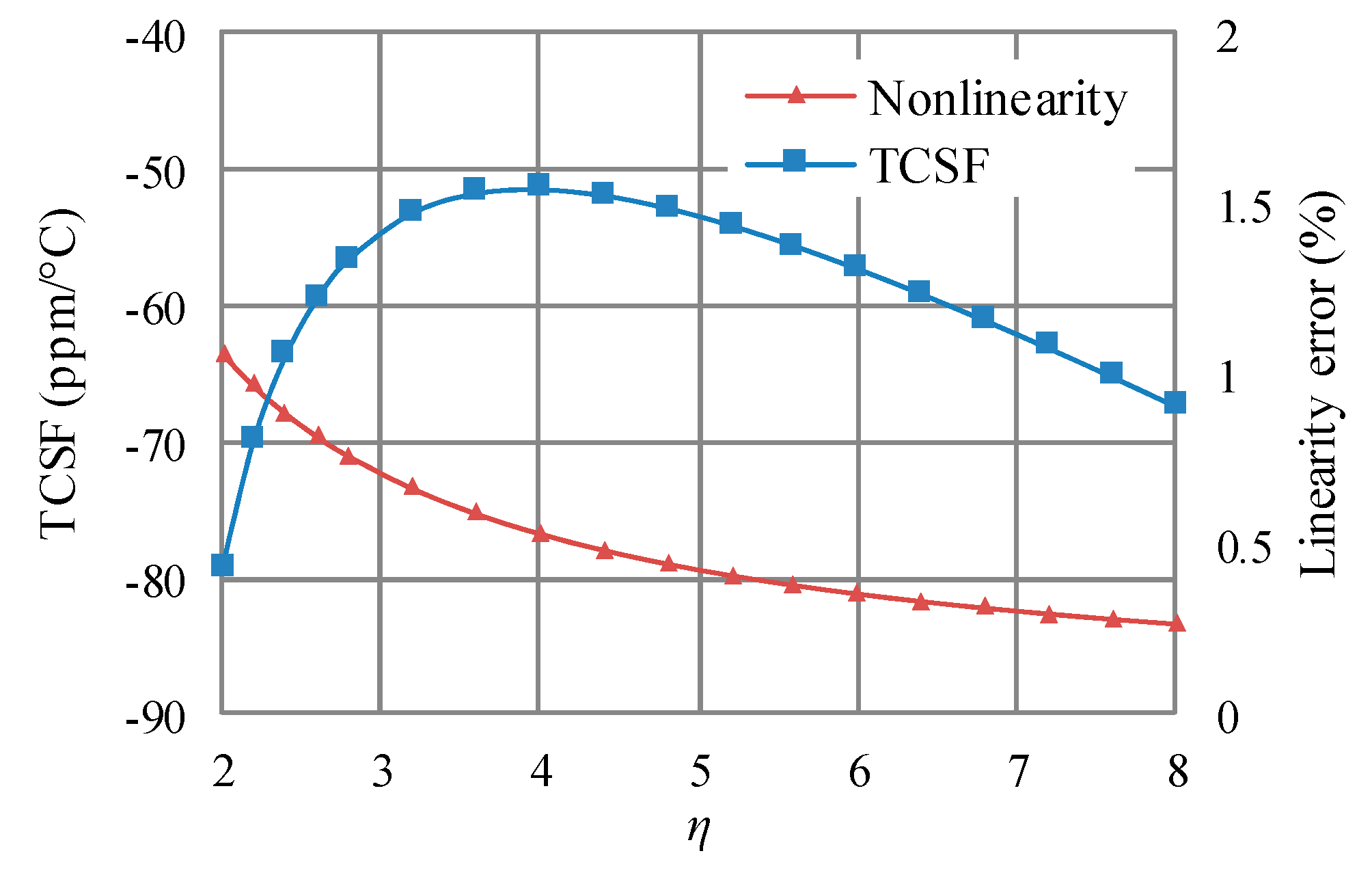
3.2. Illustration of the Contrary Effect
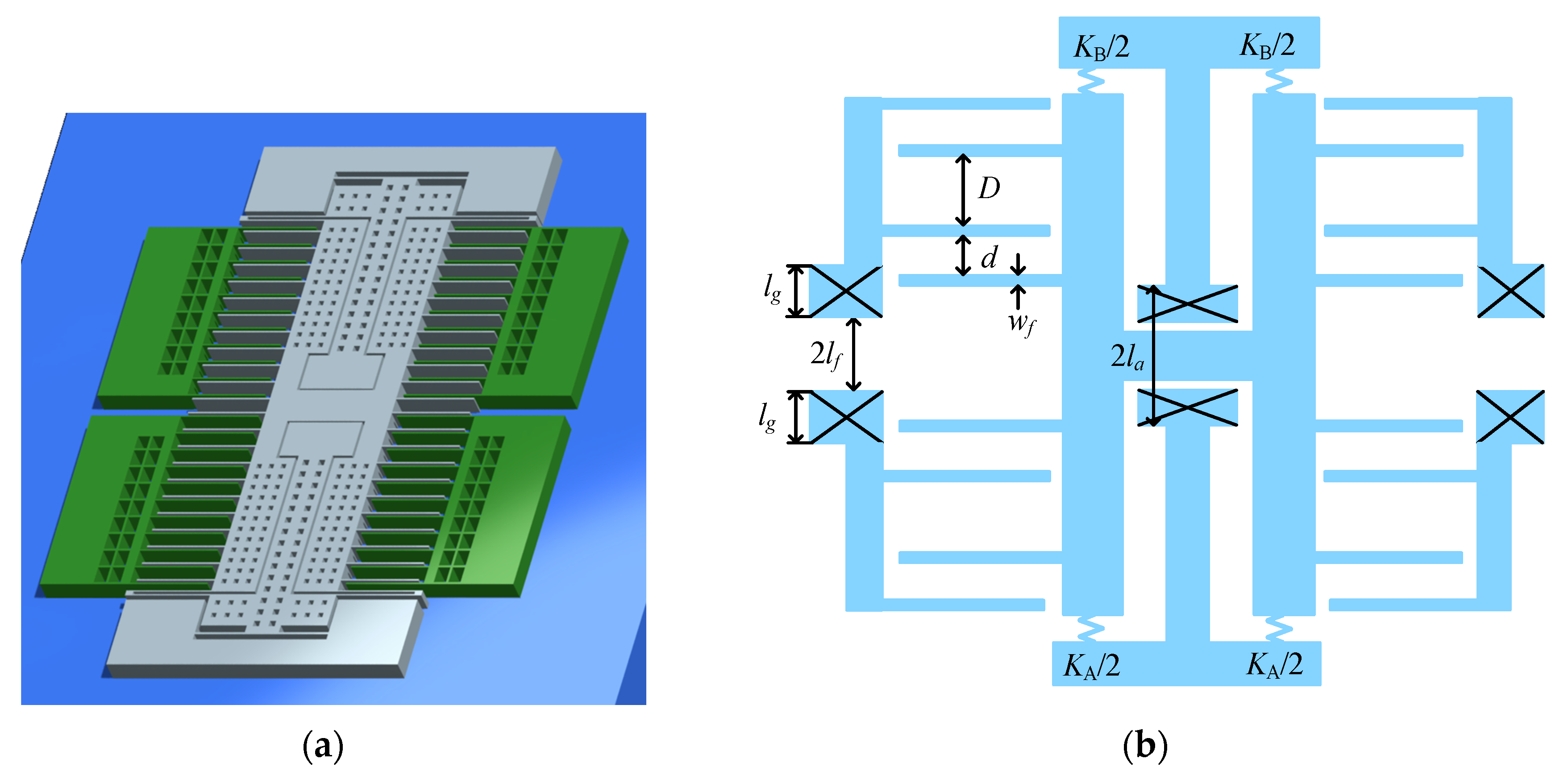
3.3. Structural Designing for Avoiding the Contrary Effect
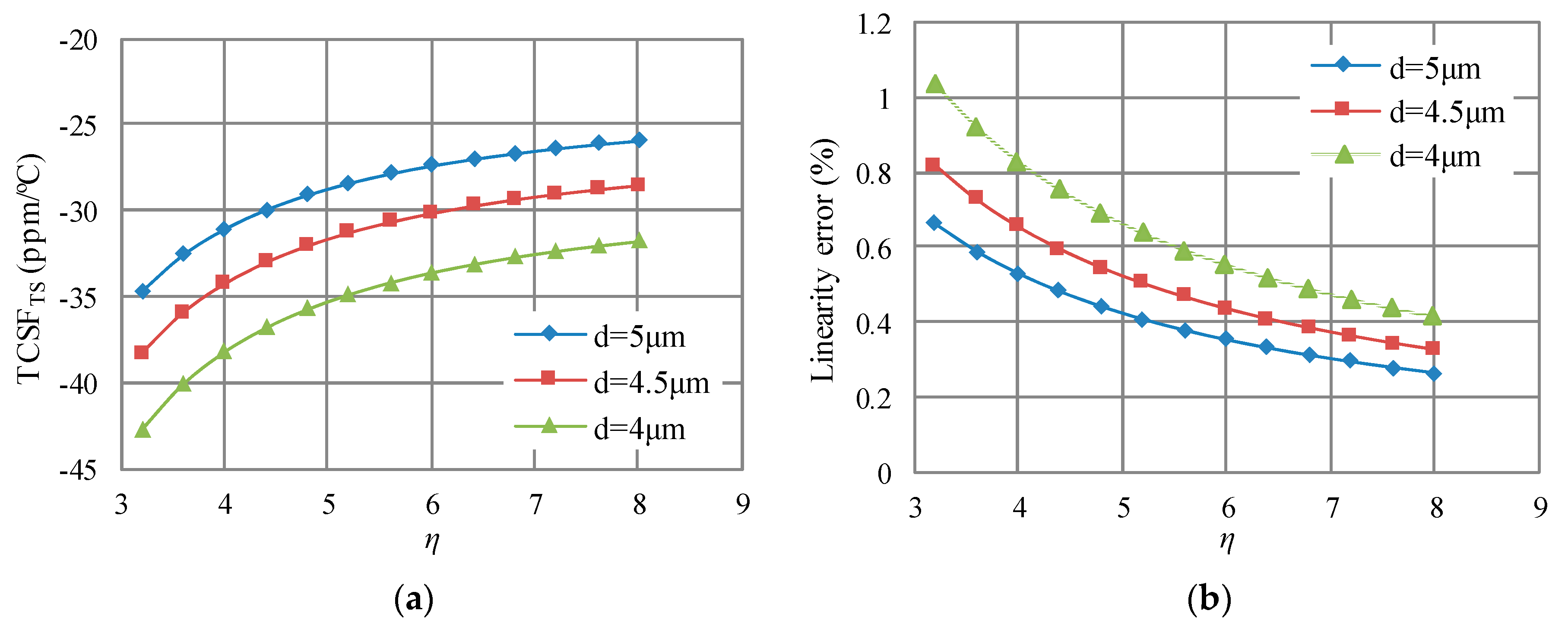
4. Precise Design for both Low Temperature Coefficient and Linearity Error
4.1. Design for Low TCSF and Linearity Error
4.2. Designing for Low TCB
- (1)
- In order to achieve the minimum αeq, a soft adhesive is employed for the die-attach.
- (2)
- The narrow gap d is decreased from 5 μm to 4.5 μm.
- (3)
- In order to make WNGR be 6.5, the wide gap D is modified to be 29.3 μm.
- (4)
- The distance from the anchor for moving electrodes to midline la is decreased from 190 μm to 90 μm.
5. Experiments
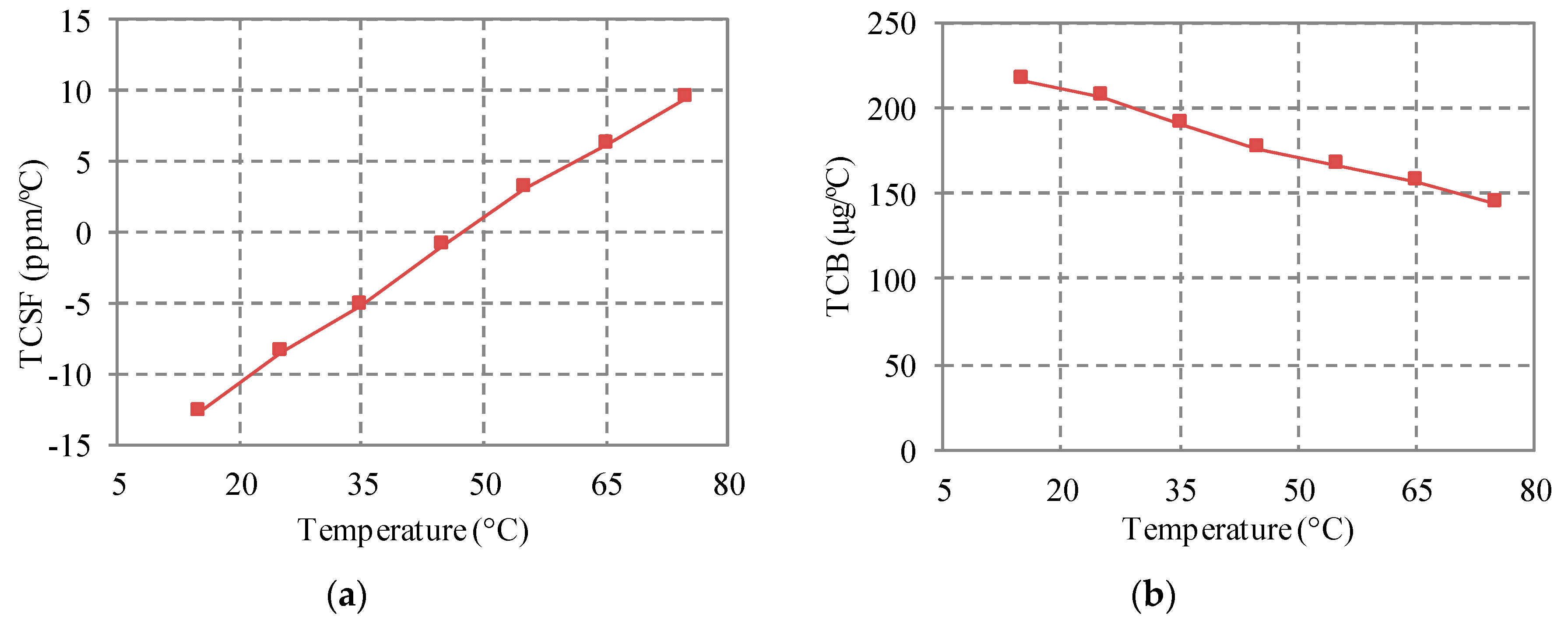
5.1. Temperature Coefficients
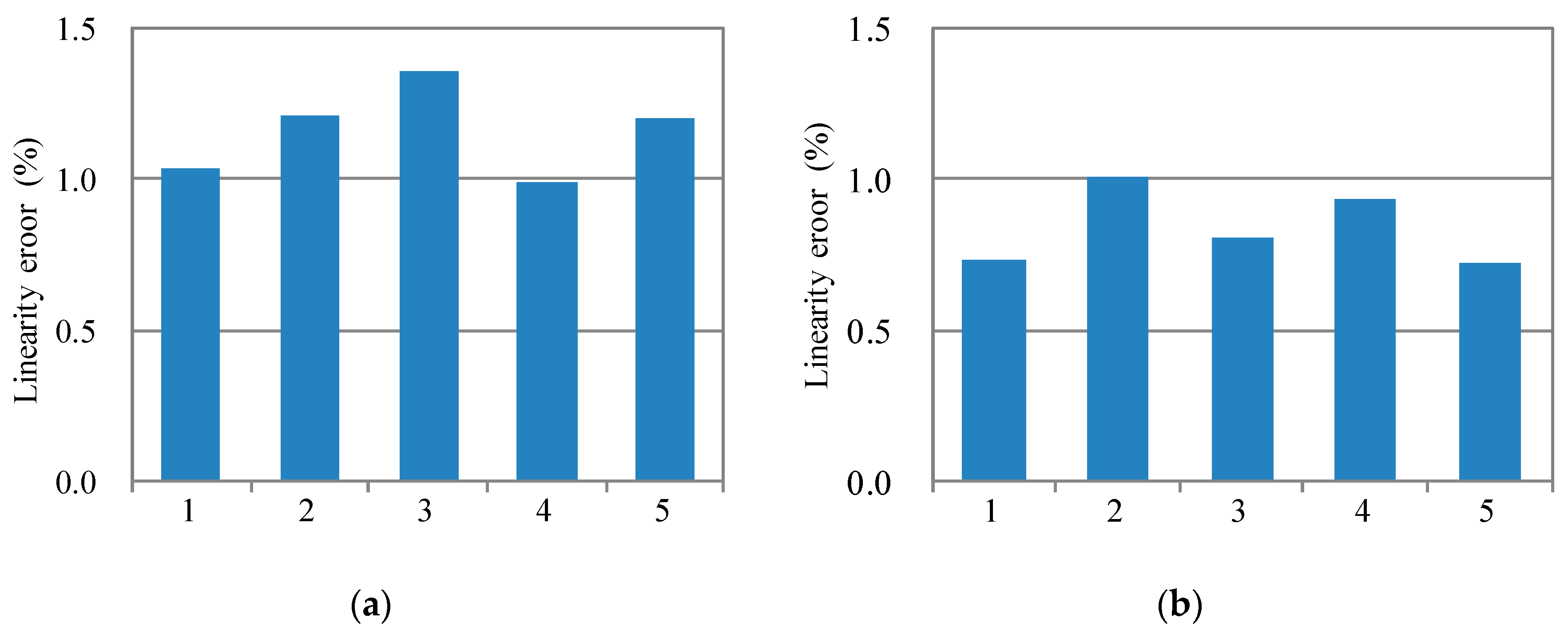
5.2. Linearity Error
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fan, C.; Hu, X.; He, X.; Tang, K.; Luo, B. Observability Analysis of a MEMS INS/GPS Integration System with Gyroscope G-Sensitivity Errors. Sensors 2014, 14, 16003–16016. [Google Scholar] [CrossRef] [PubMed]
- Yan, S.; Xie, Y.; Zhang, M.; Deng, Z.; Tu, L. A Subnano-g Electrostatic Force-Rebalanced Flexure Accelerometer for Gravity Gradient Instruments. Sensors 2017, 17, 2669. [Google Scholar] [CrossRef] [PubMed]
- Colibrys VIBRATION-Vibration Sensor. Available online: http://www.colibrys.com/product/vs1000-vibration-sensor/ (accessed on 20 February 2018).
- Dong, Y.; Zwahlen, P.; Nguyen, A.M.; Frosio, R.; Rudolf, F. Ultra-high precision MEMS accelerometer. In Proceedings of the IEEE Conference on Solid-State Sensors, Actuators and Microsystems, Beijing, China, 5–9 June 2011; pp. 695–698. [Google Scholar]
- Wei, T.A.; Khosla, P.K.; Riviere, C.N. Nonlinear Regression Model of a Low-g MEMS Accelerometer. IEEE Sens. J. 2007, 7, 81–88. [Google Scholar]
- He, J.; Xie, J.; He, X.; Du, L.; Zhou, W. Analytical study and compensation for temperature coefficients of a bulk silicon MEMS capacitive accelerometer. Sens. Actuators A 2016, 239, 174–184. [Google Scholar] [CrossRef]
- Dai, G.; Li, M.; He, X.; Du, L.; Shao, B.; Su, W. Thermal drift analysis using a multiphysics model of bulk silicon MEMS capacitive accelerometer. Sens. Actuators A 2011, 172, 369–378. [Google Scholar] [CrossRef]
- Peng, P.; Zhou, W.; Yu, H.; Peng, B.; Qu, H.; He, X. Investigation of the Thermal Coefficient of MEMS Capacitive Accelerometers Induced by the Overflow of Die Attachment Adhesive. IEEE Trans. Compon. Packag. Manuf. Technol. 2016, 6, 822–830. [Google Scholar] [CrossRef]
- Li, B.; Lu, D.; Wang, W. Micromachined accelerometer with area-changed capacitance. Mechatronics 2001, 11, 811–819. [Google Scholar] [CrossRef]
- Wan, C.; Dong, J.; Liu, Y.; Zhao, C. Nonlinearity of a Closed-Loop Micro-accelerometer. In Proceedings of the IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 1260–1265. [Google Scholar]
- Ko, H.; Cho, D.I. Highly programmable temperature compensated readout circuit for capacitive microaccelerometer. Sens. Actuators A 2010, 158, 72–83. [Google Scholar] [CrossRef]
- Colibrys, Product Range MS9000. Available online: http://www.colibrys.com/ (accessed on 20 February 2018).
- Pastre, M.; Kayal, M.; Schmid, H.; Zwahlen, P.; Dong, Y.; Nguyen, A.M. A navigation-grade MEMS accelerometer based on a versatile front end. In Proceedings of the 37th Annual Conference on IEEE Industrial Electronics Society (IECON), Melbourne, Australia, 7–10 November 2011; pp. 4038–4043. [Google Scholar]
- Zwahlen, P.; Nguyen, A.M.; Dong, Y.; Rudolf, F.; Pastre, M.; Schmid, H. Navigation grade MEMS accelerometer. In Proceedings of the IEEE 23rd International Conference on Micro Electro Mechanical Systems (MEMS), Hong Kong, China, 24–28 January 2010; pp. 631–634. [Google Scholar]
- Zwahlen, P.; Dong, Y.; Nguyen, A.M.; Rudolf, F. Breakthrough in high performance inertial navigation grade sigma–delta MEMS accelerometer. In Proceedings of the Position Location and Navigation Symposium (PLANS), Myrtle Beach, SC, USA, 23–26 April 2012; pp. 15–19. [Google Scholar]
- Dias, R.A.; Alves, F.S.; Costa, M.; Fonseca, H.; Cabral, J.; Gaspar, J.; Rocha, L.A. Real-time operation and characterization of a high-performance time-based accelerometer. J. Microelectromech. Syst. 2015, 24, 1703–1711. [Google Scholar] [CrossRef]
- Hollocher, D.C.; Memishian, J. Feedback Circuit for Micromachined Accelerometer. U.S. Patent 6530275, 11 March 2003. [Google Scholar]
- IEEE Standard for Inertial Sensor Terminology; IEEE: Piscataway, NJ, USA, 2001; pp. 10–11. [CrossRef]
- Ng, E.J.; Hong, V.A.; Yang, Y.; Ahn, C.H.; Everhart, C.L.M.; Kenny, T.W. Temperature Dependence of the Elastic Constants of Doped Silicon. J. Microelectromech. Syst. 2015, 24, 730–741. [Google Scholar] [CrossRef]
- SD-2–Glass Substrate for Silicon Sensors. Available online: http://www.hoyaoptics.com/pdf/silicon sensor.pdf (accessed on 20 February 2018).
- Okada, Y.; Tokumaru, Y. Precise determination of lattice parameter and thermal expansion coefficient of silicon between 300 and 1500 K. J. Appl. Phys. 1984, 56, 314. [Google Scholar] [CrossRef]
- He, J.; Xie, J.; He, X.; Du, L.; Zhou, W.; Wang, L. Calculating capacitance and analyzing nonlinearity of micro-accelerometers by Schwarz–Christoffel mapping. Microsyst. Technol. 2014, 20, 1195–1203. [Google Scholar] [CrossRef]

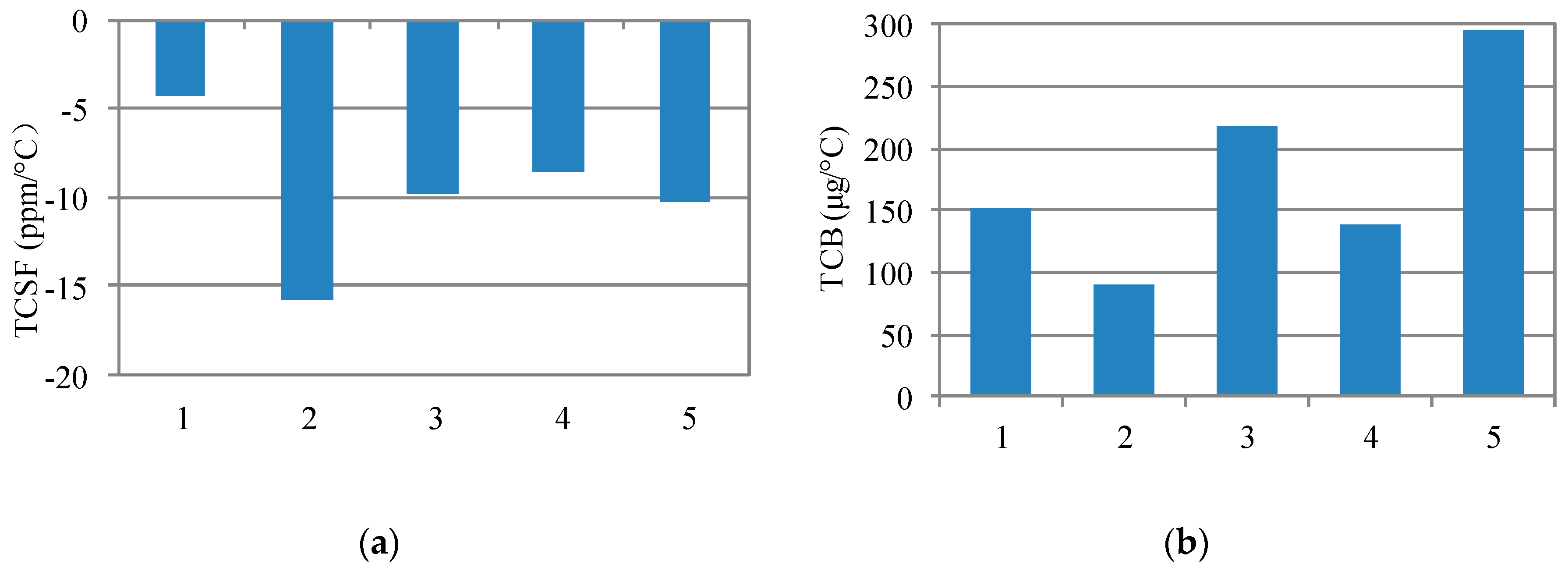
| Parameter | Value | Units | Parameter | Value | Units |
|---|---|---|---|---|---|
| Mass (m) | 59.4 | μg | Electrode width (wf) | 6.5 | μm |
| Fixed electrodes number in a comb structure (N) | 21 | Distance from the first fixed electrode to midline (lf) | 45 | μm | |
| Stiffness of springs (K) | 16 | N/m | Equivalent CTE (αeq) | 3.25 | ppm/°C |
| maximum acceleration (amax) | 20 | g | Silicon CTE (αs) [6] | 2.6 | ppm/°C |
| Narrow gap (d) | 5 | μm | TCS [6] | −30 | ppm/°C |
| WNGR (η) | 5 |
| Parameter | In This Work | In Previous Work | Units |
|---|---|---|---|
| Narrow gap (d) | 4.5 | 5 | μm |
| Wide gap (D) | 29.3 | 25 | μm |
| Distance from anchors for moving electrodes to midline (la) | 90 | 190 | μm |
| Equivalent CTE (αeq) | 3.25 | 4.2 | ppm/°C |
| Linearity error | 0.4% | 0.42% | |
| TCSF | almost zero | 37 | ppm/°C |
| TCB | The estimated TCB in this work is about 20% of that in the previous work | ||
| Parameter | In This Work | In Previous Work | Units |
|---|---|---|---|
| TCSF | average: −9.8 | average: −50.8 | ppm/°C |
| max: −16.1 | max: −62.6 | ||
| TCB | average: 179 | average: 520 | μg/°C |
| max: 294 | max: 1033 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Zhou, W.; Yu, H.; He, X.; Peng, P. Structural Designing of a MEMS Capacitive Accelerometer for Low Temperature Coefficient and High Linearity. Sensors 2018, 18, 643. https://doi.org/10.3390/s18020643
He J, Zhou W, Yu H, He X, Peng P. Structural Designing of a MEMS Capacitive Accelerometer for Low Temperature Coefficient and High Linearity. Sensors. 2018; 18(2):643. https://doi.org/10.3390/s18020643
Chicago/Turabian StyleHe, Jiangbo, Wu Zhou, Huijun Yu, Xiaoping He, and Peng Peng. 2018. "Structural Designing of a MEMS Capacitive Accelerometer for Low Temperature Coefficient and High Linearity" Sensors 18, no. 2: 643. https://doi.org/10.3390/s18020643
APA StyleHe, J., Zhou, W., Yu, H., He, X., & Peng, P. (2018). Structural Designing of a MEMS Capacitive Accelerometer for Low Temperature Coefficient and High Linearity. Sensors, 18(2), 643. https://doi.org/10.3390/s18020643





