Design, Implementation and Validation of a GNSS Measurement Exclusion and Weighting Function with a Dual Polarized Antenna †
Abstract
:1. Introduction
1.1. Related Work
1.2. Contributions
2. Set-Up and Hardware Description
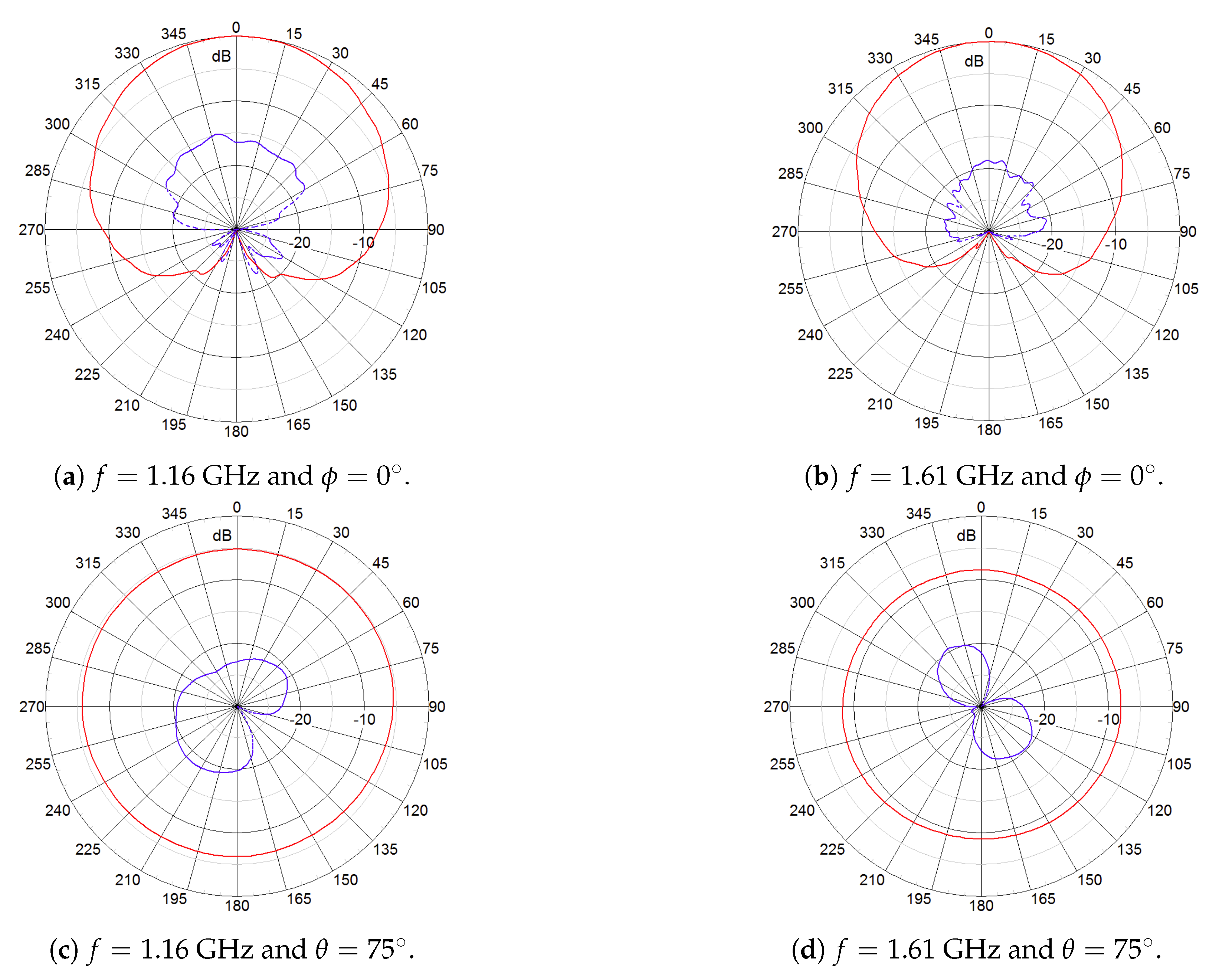
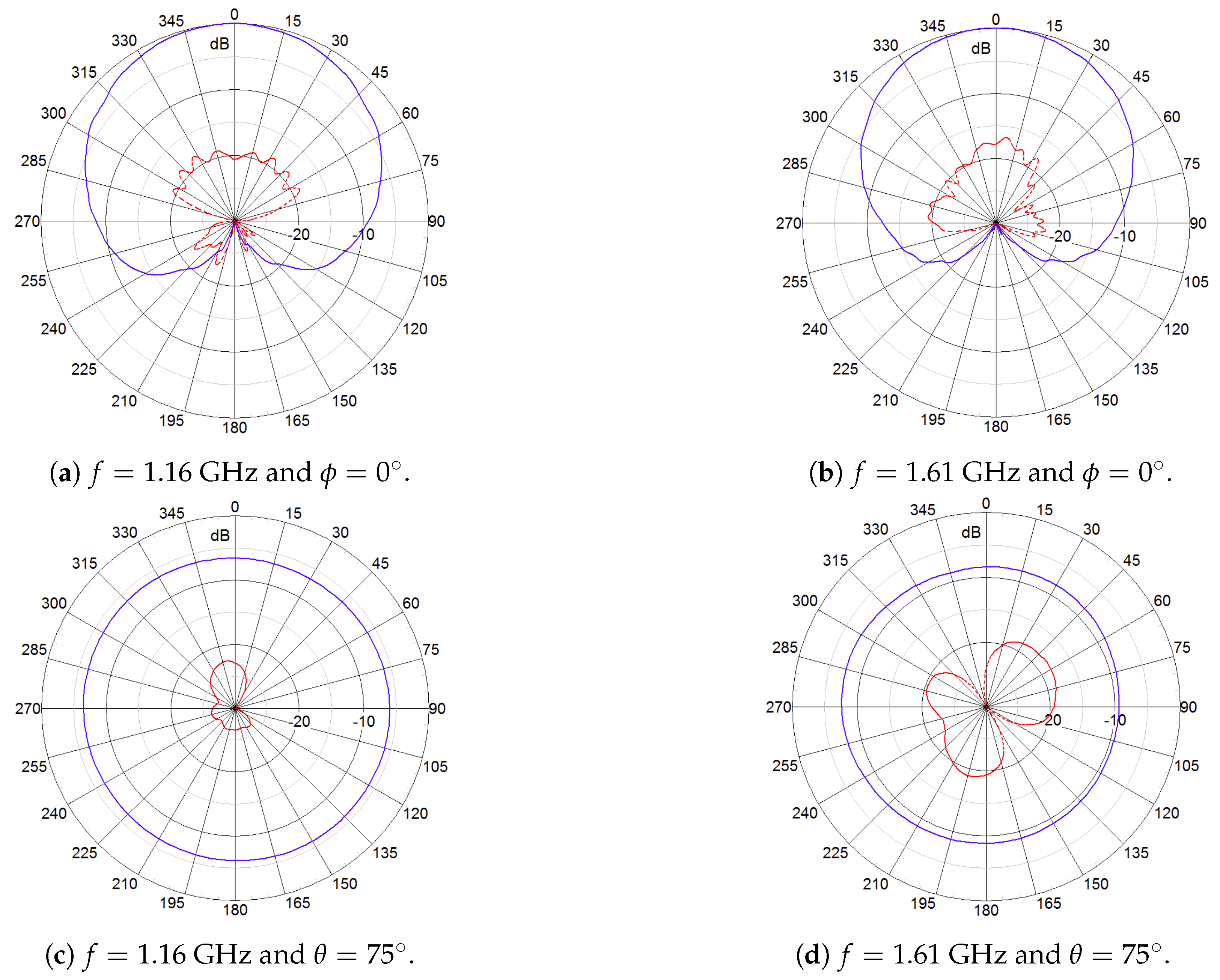
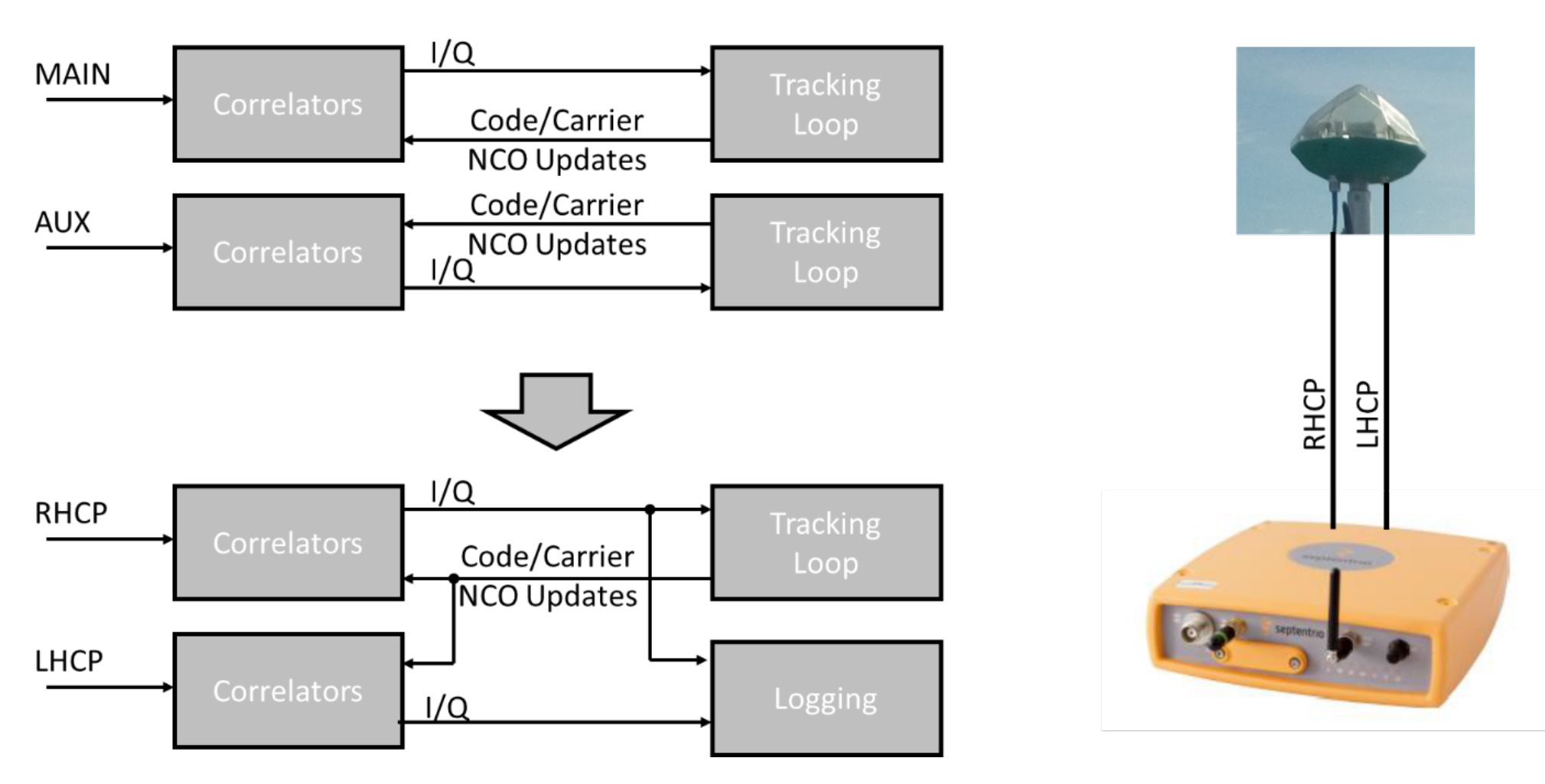
2.1. Dual-Polarized Antenna
2.2. Receiver
2.3. Data Collection Campaign
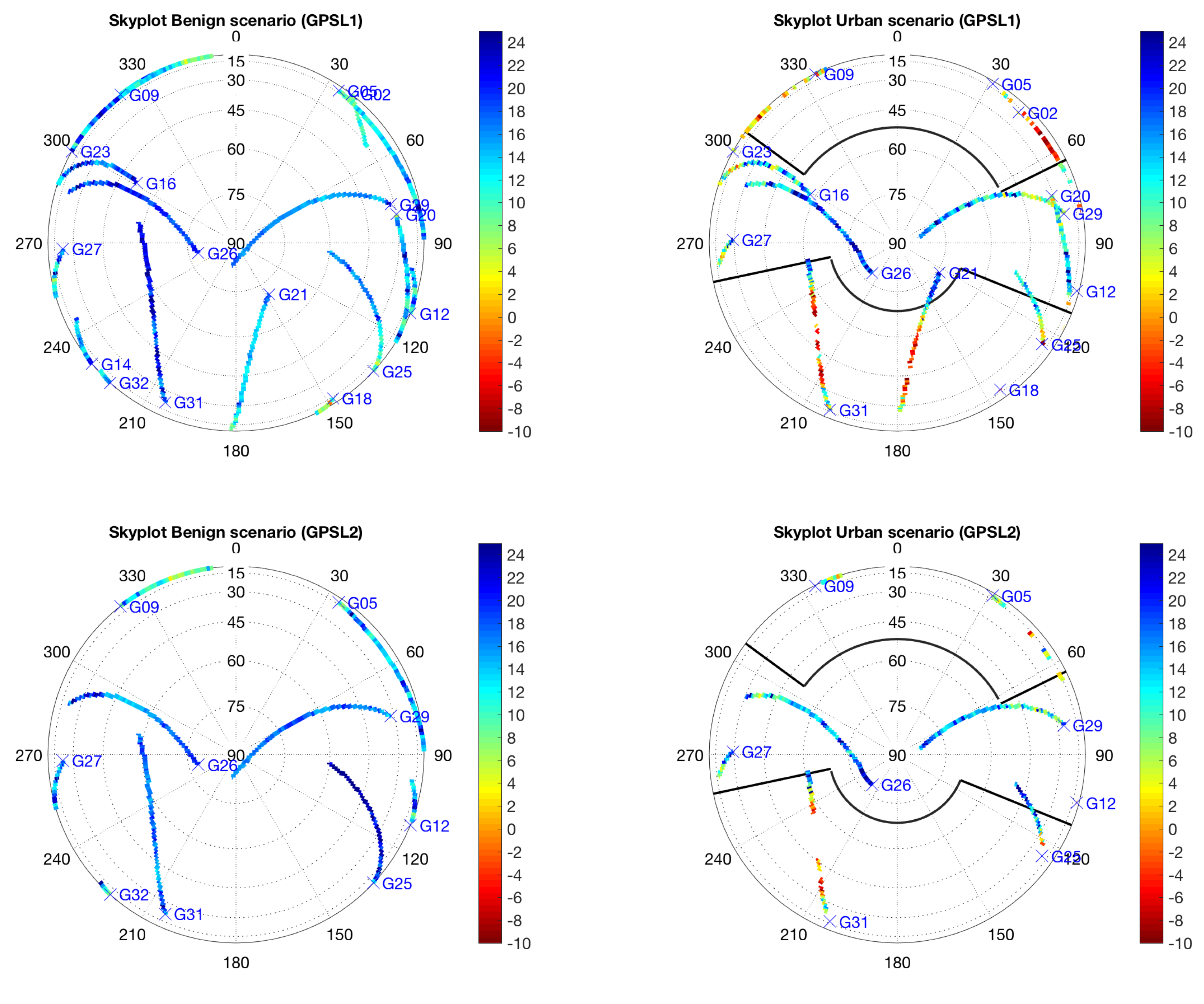
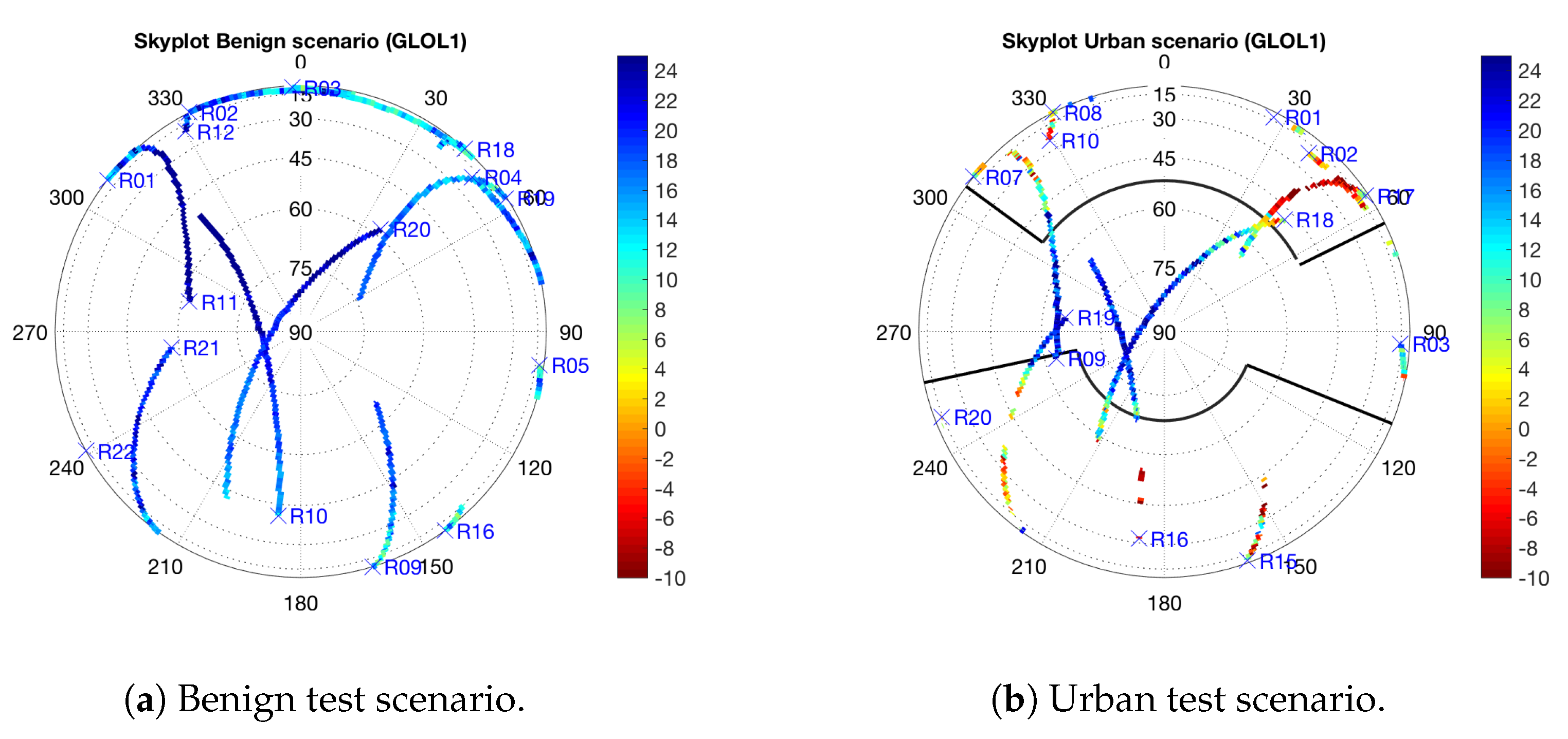
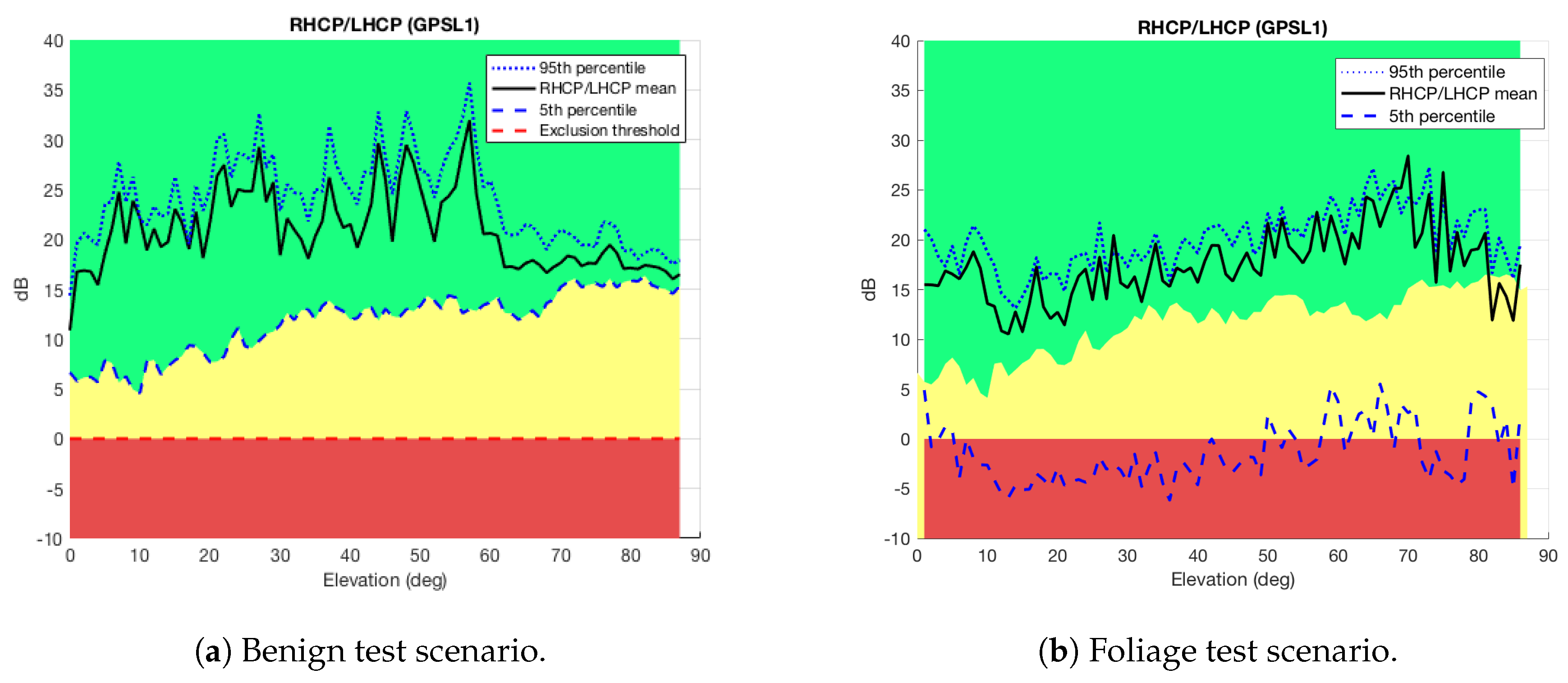
- Benign: Static recording at the open sky scenario shown in Figure 5a. The antenna was placed on a tripod on a farmer’s field with dry soil and no objects anywhere nearby. This test is attempted to minimize multipath and to be the reference file for calibration purposes.
- Foliage: Static recording under dense tree canopy to capture multipath and/or diffraction, shown in Figure 5b.
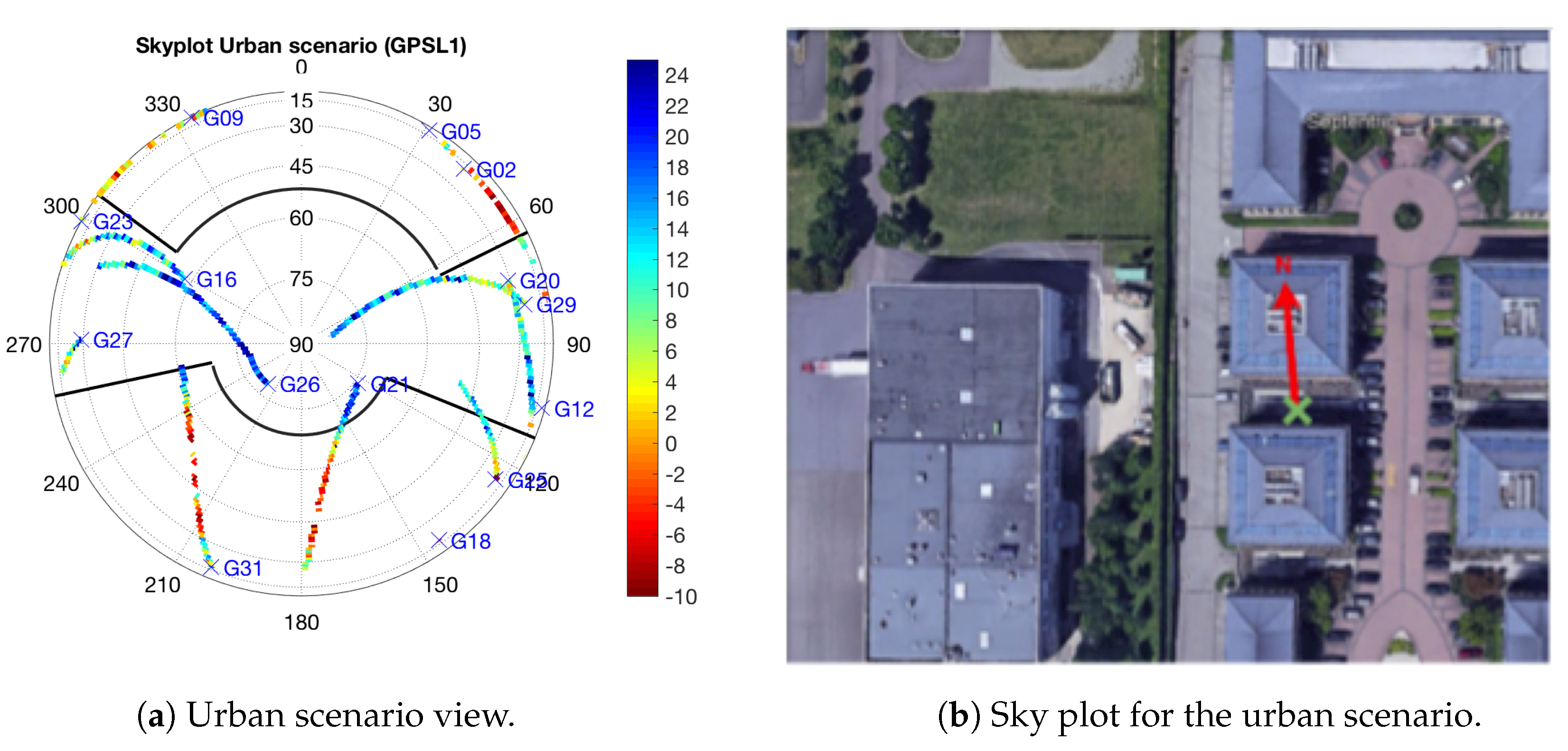
- Urban: Static recording between two buildings (see Figure 5c). This test is attempted to capture multipath and NLOS conditions.
- Dynamic: Dynamic recording with a moving car in a mixed environment including open sky, forests and deep urban scenarios. Figure 5d shows the truth trajectory of the moving car around Leuven, Belgium.
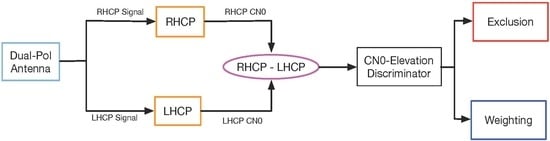
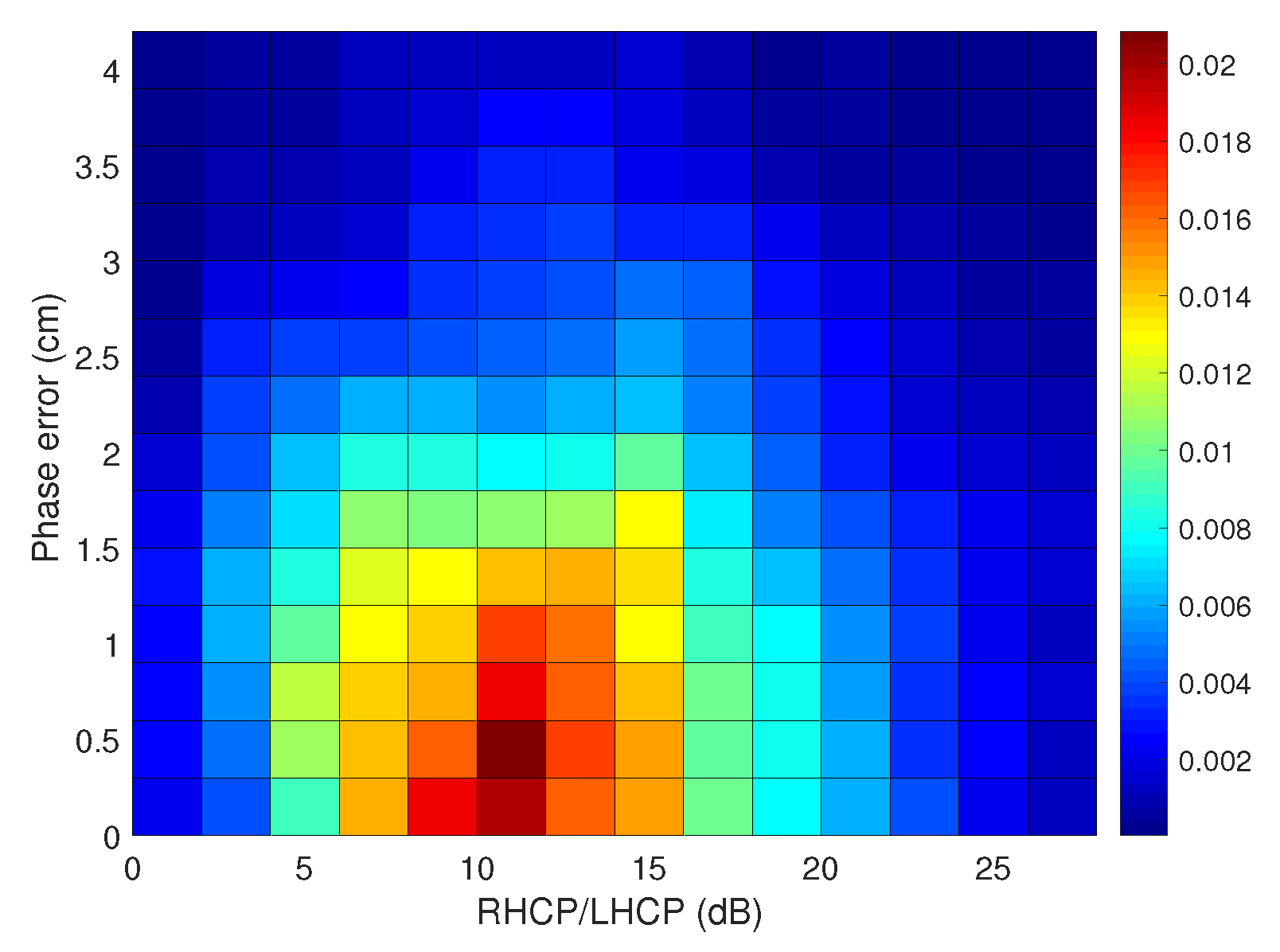
3. Measurement Weighting and Exclusion (WE)
3.1. Measurement Exclusion
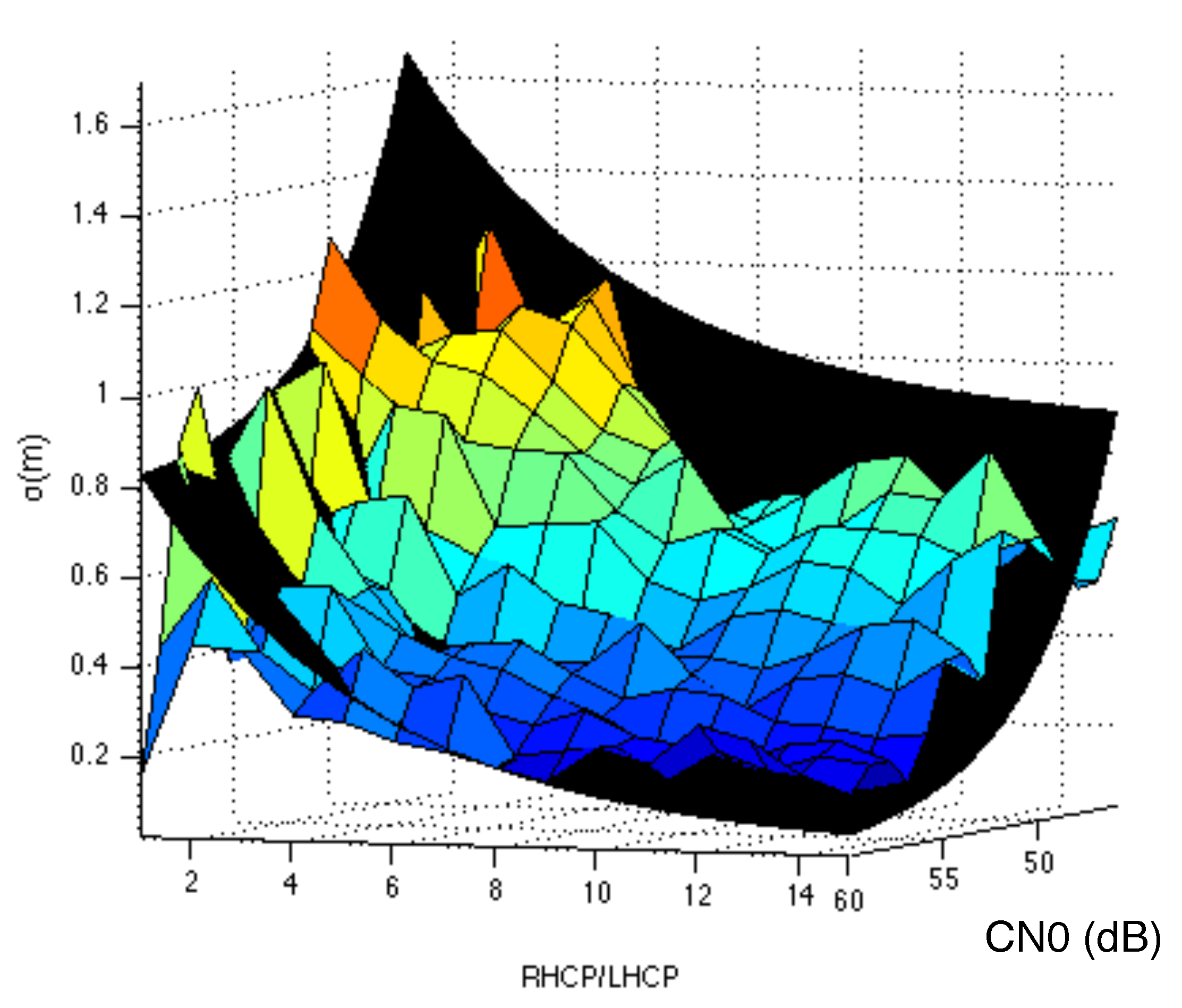
- Nominal (green area): Above the fifth percentile of the RLR in the benign scenario. In this area the received multipath is considered to be the one received under nominal conditions and the measurements should be considered by themselves (or traditional weighting).
- Weighting area (yellow area): In the range from 0 dB to the fifth percentile of the RLR in the benign scenario. In this area the received multipath is considered to be moderate (subject to a more severe multipath than in the benign scenario) and the measurements should be weighted down.
- Exclusion area (red area): Below the exclusion threshold. Theoretically, the exclusion threshold should be a ratio equal to 0 dB. In practice, this threshold must be calibrated. In this area, the received measurements can be considered to be obtained under NLOS conditions, thus they should be excluded.
3.2. Measurement Weighting
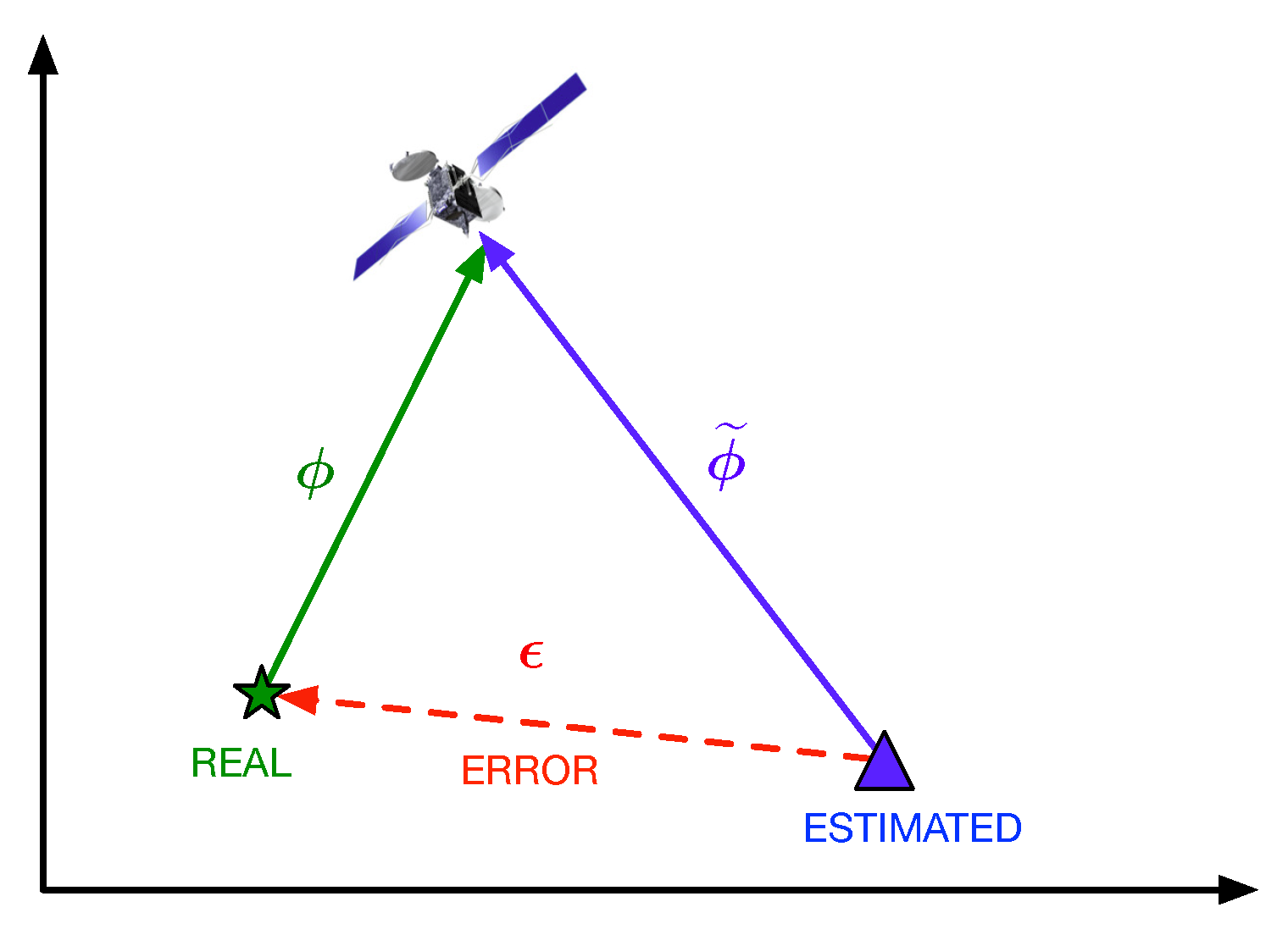
- Range correction: The idea is to estimate the offset included by multipath into the range measurements and apply them directly into the provided measurements [21].
- Tracking correction: The idea here is to use a common tracking loop for both RHCP and LHCP components that is closed using together the outputs of both the RHCP and LHCP tracking outputs to mitigate multipath [6].
4. PVT Results
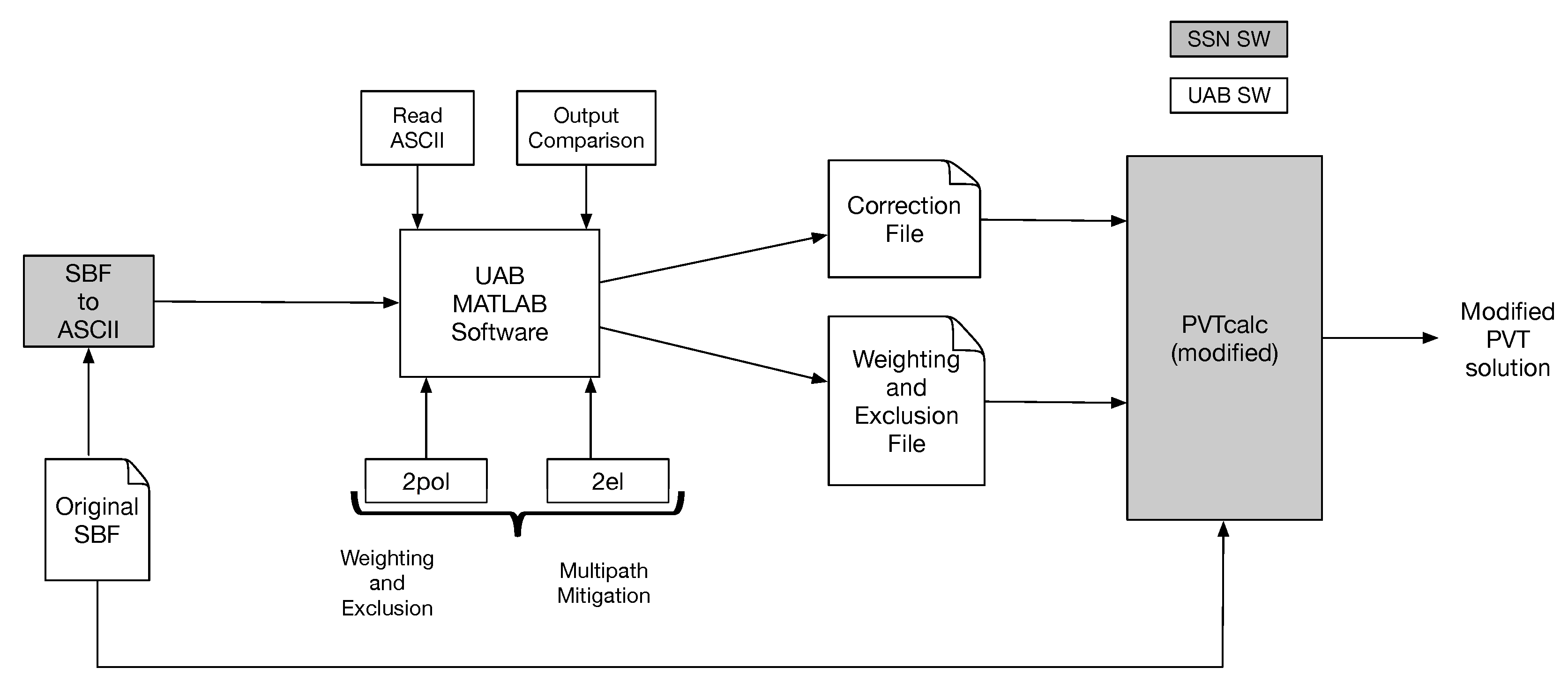
4.1. Processing of the Collected Data
4.2. Fine-Tuning of the WE Function
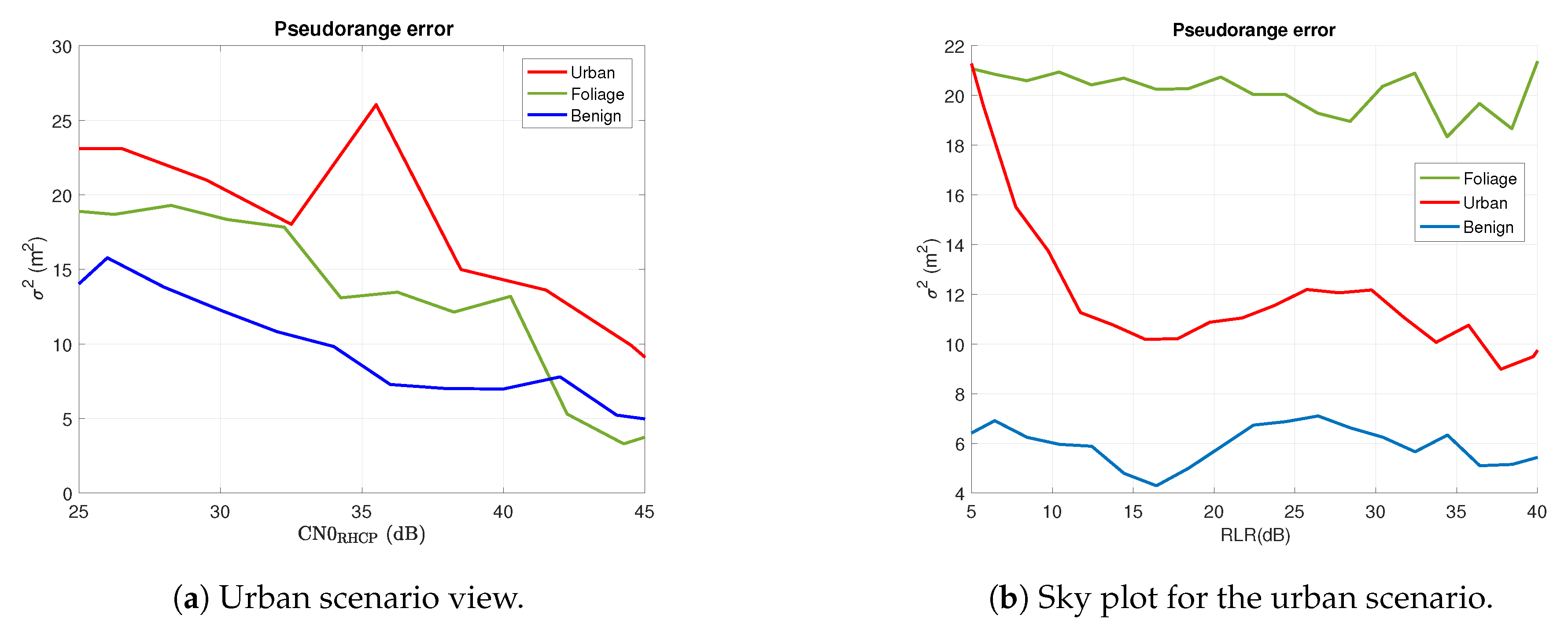
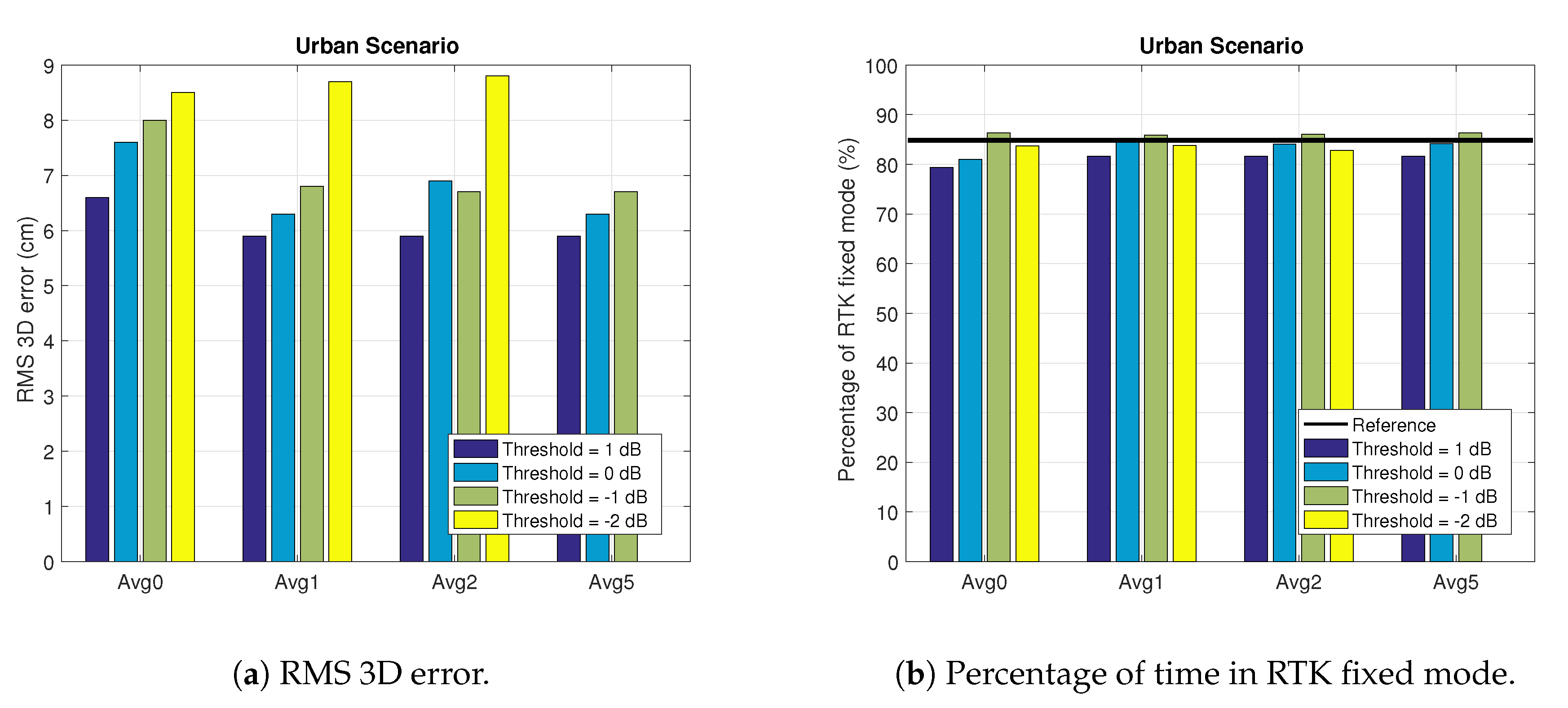
4.2.1. Static Urban Scenario
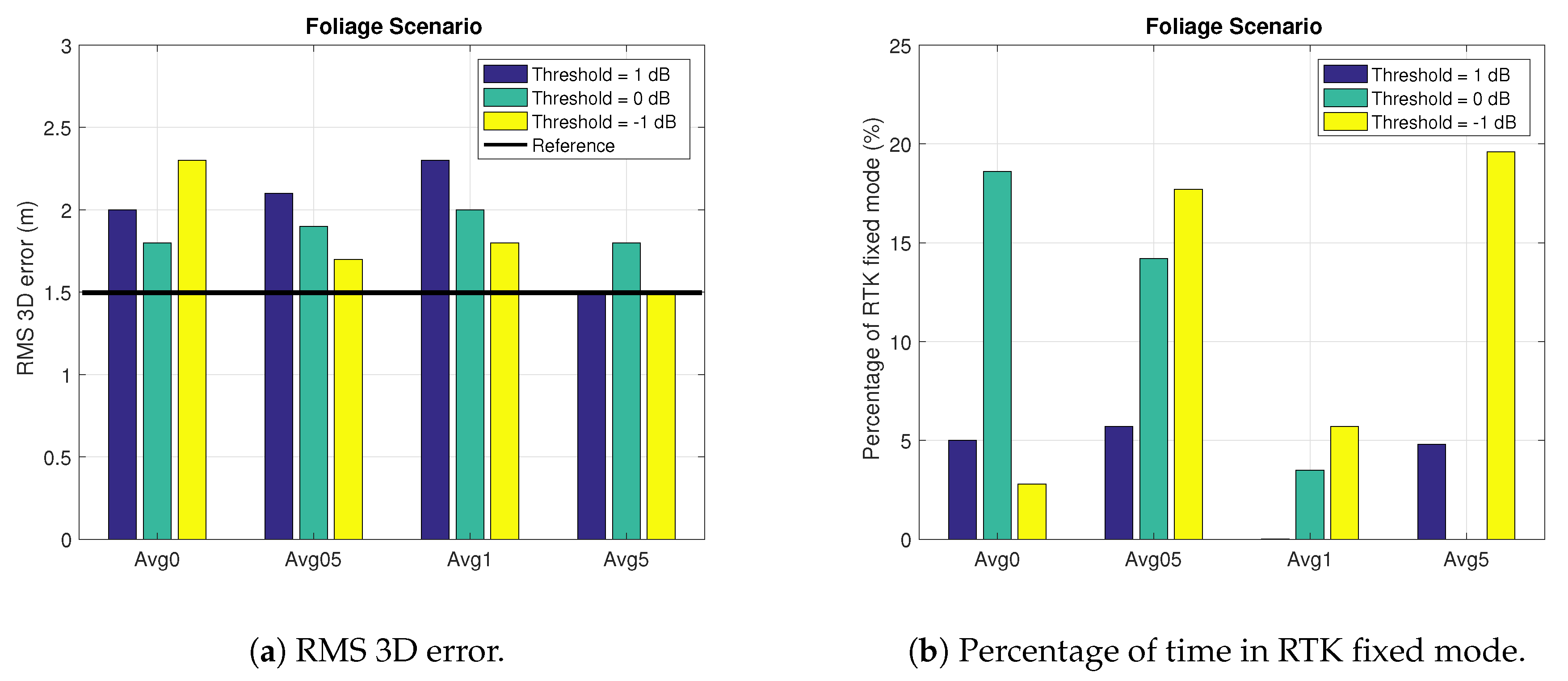
4.2.2. Foliage Scenario
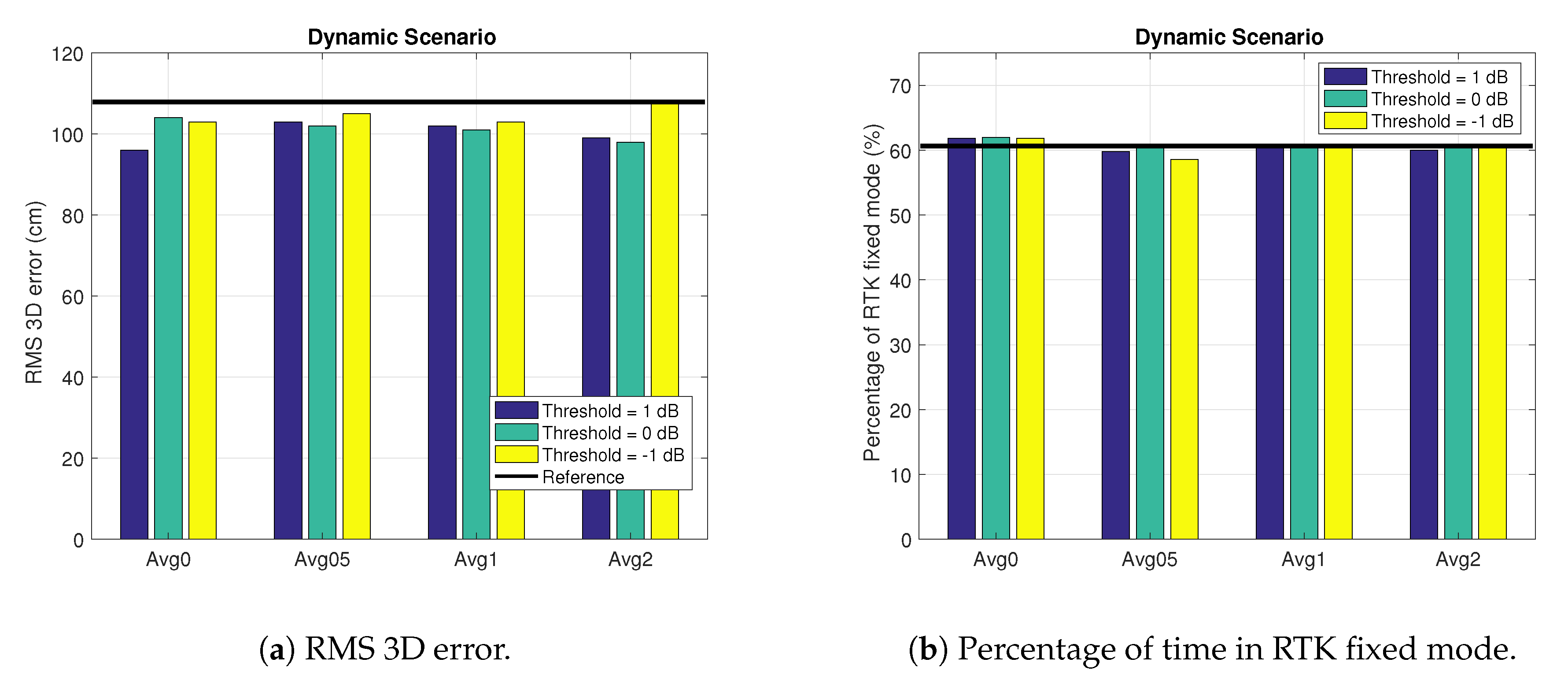
4.2.3. Dynamic Scenario
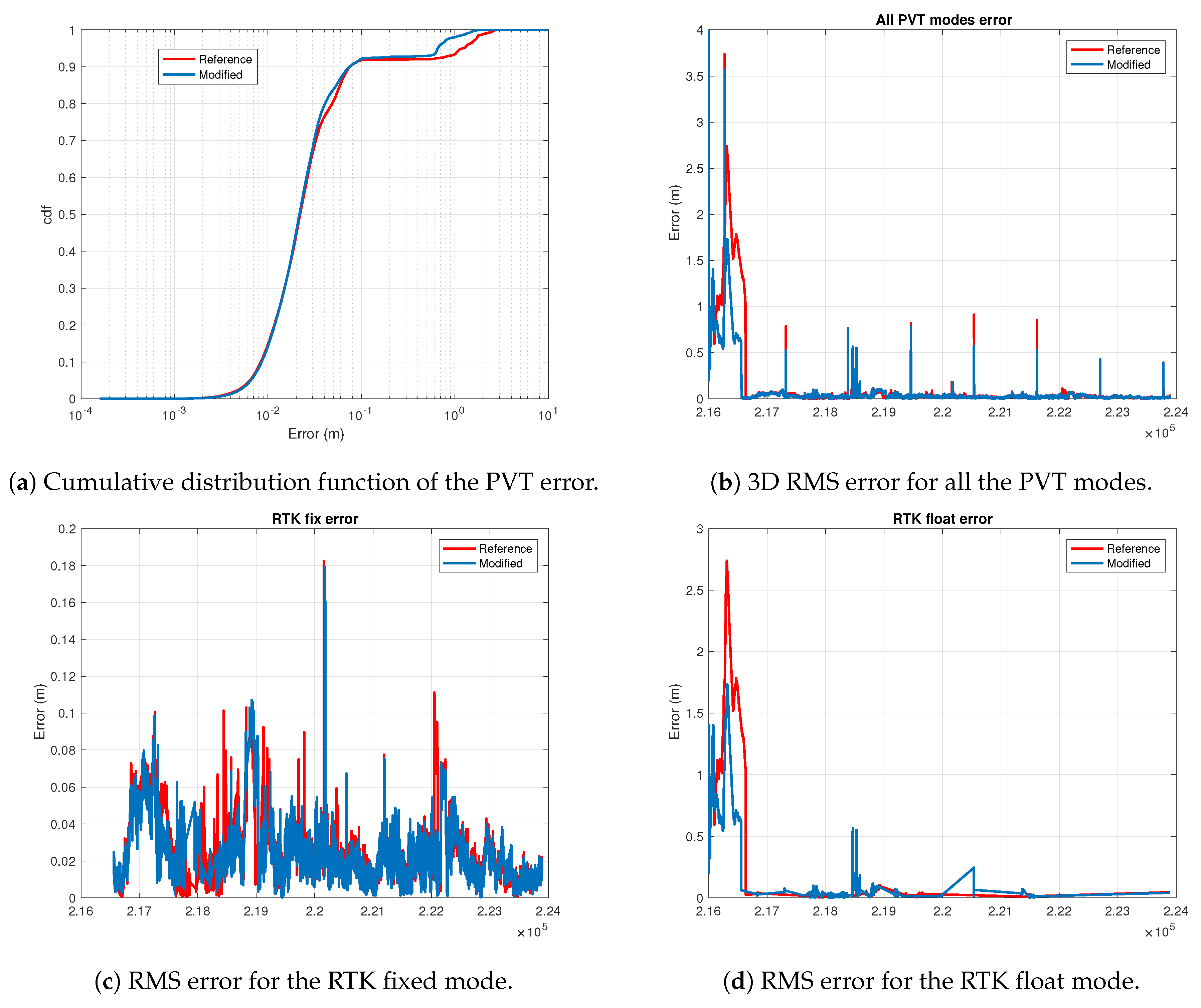
4.3. PVT Results Summary
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| 2pol | dual-circularly-polarized |
| CMC | Code-Minus-Carrier |
| CN0 | carrier-to-noise ratio |
| GNSS | Global Navigation Satellite System |
| GSA | European GNSS Agency |
| IMU | Inertial Measurement Unit |
| INS | Inertial Navigation System |
| LHCP | Left-Hand Circular Polarization |
| LOS | Line-of-Sight |
| NLOS | Non-Line-of-Sight |
| PVT | Position, Velocity and Time |
| RHCP | Right-Hand Circular Polarization |
| RLR | RHCP to LHCP Ratio |
| RMS | Root Mean Square |
| RTK | Real-Time Kinematics |
| SSN | Septentrio |
| SW | SoftWare |
| UAB | Universitat Autònoma de Barcelona |
| WE | Weighting and Exclusion |
References
- Braasch, M.S. Performance comparison of multipath mitigating receiver architectures. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 10–17 March 2001; Volume 3, pp. 3/1309–3/1315. [Google Scholar]
- Bhuiyan, M.Z.H.; Lohan, E.S.; Renfors, M. Code tracking algorithms for mitigating multipath effects in fading channels for satellite-based positioning. EURASIP J. Adv. Signal Process. 2007, 2008, 1–17. [Google Scholar] [CrossRef]
- Lau, L.; Cross, P. Development and testing of a new ray-tracing approach to GNSS carrier-phase multipath modelling. J. Geodesy 2007, 81, 713–732. [Google Scholar] [CrossRef]
- Shytenneja, E.; Garcia-Pena, A.; Julien, O. Proposed architecture for integrity monitoring of a GNSS / MEMS system with a fisheye camera in urban environment. In Proceedings of the International Conference on Localization and GNSS (ICL-GNSS), Helsinki, Finland, 24–26 June 2014; pp. 1–6. [Google Scholar]
- Vagle, N.; Broumandan, A.; Jafarnia-Jahromi, A.; Lachapelle, G. Performance analysis of GNSS multipath mitigation using antenna arrays. J. Glob. Position. Syst. 2016, 14, 4. [Google Scholar] [CrossRef]
- Yang, C.; Porter, C.A. GPS Multipath Estimation and Mitigation Via Polarization Sensing Diversity: Parallel Iterative Cross Cancellation. In Proceedings of the 18th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 13–16 September 2005; pp. 2707–2719. [Google Scholar]
- Manandhar, D.; Shibasaki, R.; Torimoto, H. GPS Reflected Signal Analysis using Software Receiver. J. Glob. Position. Syst. 2006, 5, 29–34. [Google Scholar] [CrossRef]
- Brenneman, M.; Morton, J.; Yang, C.; van Graas, F. Mitigation of GPS multipath using polarization and spatial diversities. In Proceedings of the 20th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 1221–1229. [Google Scholar]
- Groves, P.D.; Jiang, Z.; Skelton, B.; Cross, P.A.; Lau, L.; Adane, Y.; Kale, I. Novel multipath mitigation methods using a dual-polarization antenna. In Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2010), Portland, OR, USA, 21–24 September 2010; pp. 140–151. [Google Scholar]
- Groves, P.D.; Jiang, Z.; Rudi, M.; Strode, P. A portfolio approach to NLOS and multipath mitigation in dense urban areas. In Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2013), Nashville, TN, USA, 16–20 September 2013; pp. 3231–3247. [Google Scholar]
- Jiang, Z.; Groves, P.D. NLOS GPS signal detection using a dual-polarisation antenna. GPS Solut. 2014, 18, 15–26. [Google Scholar] [CrossRef]
- Palamartchouk, K.; Clarke, P.; Edwards, S. Available online: https://www.google.com.tw/url?sa=trct=jq=esrc=ssource=webcd=1ved=2ahUKEwjy2Zuzu6jfAhVM62EKHUS-AH0QFjAAegQIAxACurl=https%3A%2F%2Fcommunities.rics.org%2Fgf2.ti%2Ff%2F200194%2F12563077.1%2FPDF%2F-%2FRICS_Research__mitigation_of_GNSS_multipath_by_the_use_of_dualpolarisation_observations_2014.pdfusg=AOvVaw09P7t99V-1OqAu5QV7Mlic (accessed on 17 December 2018).
- Egea-Roca, D.; Tripiana-Caballero, A.; López-Salcedo, J.A.; Seco-Granados, G.; De Wilde, W.; Bougard, B.; Sleewaegen, J.M.; Popugaev, A. GNSS measurement exclusion and weighting with a dual polarized antenna: The FANTASTIC project. In Proceedings of the 8th International Conference on Localization and GNSS (ICL-GNSS), Guimaraes, Portugal, 26–28 June 2018; pp. 1–6. [Google Scholar]
- Cosmen-Schortmann, J.; Azaola-Sáenz, M.; Martínez-Olagüe, M.Á.; Toledo-López, M. Integrity in urban and road environments and its use in liability critical applications. In Proceedings of the IEEE Position Location and Navigation Symposium (PLANS), Monterey, CA, USA, 5–8 May 2008; pp. 972–983. [Google Scholar]
- Toledo-Moreo, R.; Úbeda, B.; Santa, J.; Zamora-Izquierdo, M.A.; Gómez-Skarmeta, A.F. An analysis of positioning and map-matching issues for GNSS-based road user charging. In Proceedings of the IEEE Conference on Intelligent Transportation Systems (ITSC), Funchal, Portugal, 19–22 September 2010; pp. 1486–1491. [Google Scholar] [CrossRef]
- Seco-Granados, G.; López-Salcedo, J.A.; Jiménez-Baños, D.; López-Risueño, G. Challenges in indoor global navigation satellite systems. IEEE Signal Process. Mag. 2012, 29, 108–131. [Google Scholar] [CrossRef]
- Egea-Roca, D.; Seco-Granados, G.; López-Salcedo, J.A.; Dovis, F. Signal-Level integrity and metrics based on the application of quickest detection theory to multipath detection. In Proceedings of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2015), Tampa, FL, USA, 14–18 September 2015; pp. 3136–3147. [Google Scholar]
- Popugaev, A.E. A family of high-performance GNSS antennas. In Proceedings of the 2015 Radio and Antenna Days of the Indian Ocean (RADIO), Belle Mare, Mauritius, 21–24 September 2015; pp. 1–2. [Google Scholar]
- Popugaev, A.E.; Wansch, R. Multi-Band GNSS Antenna. Microelectronic Systems: Circuits, Systems and Applications; Heuberger, A., Elst, G., Hanke, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 69–75. [Google Scholar]
- Li, J.; Wu, M. The improvement of positioning accuracy with weighted least square based on SNR. In Proceedings of the 5th International Conference on Wireless Communications, Networking and Mobile Computing, WiCOM 2009, Beijing, China, 24–26 September 2009; pp. 9–12. [Google Scholar]
- Xie, L.; Cui, X.; Zhao, S.; Lu, M. Mitigating multipath bias using a dual-polarization antenna: Theoretical performance, algorithm design, and simulation. Sensors 2017, 17, 359. [Google Scholar] [CrossRef] [PubMed]
- Hartinger, H.; Brunner, F.K. Variances of GPS Phase Observations: The SIGMA-ϵ Model. GPS Solut. 1999, 2, 35–43. [Google Scholar] [CrossRef]
- Tay, S.; Marais, J. Weighting models for GPS Pseudorange observations for land transportation in urban canyons. In Proceedings of the 6th European Workshop on GNSS Signals and Signal Processing, Munich, Germany, 5–6 December 2013; pp. 1–6. [Google Scholar]
- Odijk, D. Weighting Ionospheric Corrections to Improve Fast GPS Positioning Over Medium Distances. In Proceedings of the ION GPS, Salt Lake City, UT, USA, 19–22 September 2000; pp. 1113–1123. [Google Scholar]
- Septentrio. Post-Processing Software Development Kit (PP-SDK). Available online: https://www.septentrio.com/products/software/other-post-processing-software (accessed on 15 November 2018).
- IXBLUE. ATLANS-C: MOBILE MAPPING POSITION AND ORIENTATION SOLUTION. Available online: https://www.ixblue.com/sites/default/files/downloads/ixblue-br-atlans-c-08-2014-web_0.pdf (accessed on 15 November 2018).


| Configuration | Total | RTK_Fixes | RTK Correct Fixes (Wrong Fix: Error > 10 cm) | RTK_Float | |||
|---|---|---|---|---|---|---|---|
| Error (m) | Error (cm) | % | Error (cm) | % | Error (cm) | % | |
| Reference | 14.0 | 2.5 | 85.2 | 2.5 | 85.1 | 79.9 | 14.7 |
| Threshold = 0 dB | |||||||
| Avg1 | 6.7 | 2.4 | 84.7 | 2.4 | 84.7 | 26.7 | 15.3 |
| Threshold = −1 dB | |||||||
| Avg5 | 6.7 | 2.6 | 86.3 | 2.6 | 86.3 | 31.6 | 13.7 |
| Configuration | Total | RTK_Fixes | RTK Correct Fixes (Wrong Fix: Error > 10 cm) | RTK_Float | |||
|---|---|---|---|---|---|---|---|
| Error (m) | Error (cm) | % | Error (cm) | % | Error (m) | % | |
| Reference | 1.5 | 5.9 | 32.8 | 5.0 | 29.6 | 2.1 | 63.7 |
| Avg5 + Th | 1.5 | 18.9 | 27.9 | 5.1 | 19.6 | 1.9 | 67.3 |
| Scenario | Relative Improvement RMS 3D Error | RTK Fixed (% of Time) | RTK Float RMS 3D Error (cm) | ||
|---|---|---|---|---|---|
| One Antenna | 2pol Exclusion | One Antenna | 2pol Exclusion | ||
| Static Urban | 50% | 85 | 85 | 80 | 37 |
| Static Foliage | 3% | 29 | 19 | 213 | 186 |
| Dynamic | 11% | 61 | 62 | 96 | 88 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Egea-Roca, D.; Tripiana-Caballero, A.; López-Salcedo, J.A.; Seco-Granados, G.; De Wilde, W.; Bougard, B.; Sleewaegen, J.-M.; Popugaev, A. Design, Implementation and Validation of a GNSS Measurement Exclusion and Weighting Function with a Dual Polarized Antenna. Sensors 2018, 18, 4483. https://doi.org/10.3390/s18124483
Egea-Roca D, Tripiana-Caballero A, López-Salcedo JA, Seco-Granados G, De Wilde W, Bougard B, Sleewaegen J-M, Popugaev A. Design, Implementation and Validation of a GNSS Measurement Exclusion and Weighting Function with a Dual Polarized Antenna. Sensors. 2018; 18(12):4483. https://doi.org/10.3390/s18124483
Chicago/Turabian StyleEgea-Roca, Daniel, Antonio Tripiana-Caballero, José A. López-Salcedo, Gonzalo Seco-Granados, Wim De Wilde, Bruno Bougard, Jean-Marie Sleewaegen, and Alexander Popugaev. 2018. "Design, Implementation and Validation of a GNSS Measurement Exclusion and Weighting Function with a Dual Polarized Antenna" Sensors 18, no. 12: 4483. https://doi.org/10.3390/s18124483
APA StyleEgea-Roca, D., Tripiana-Caballero, A., López-Salcedo, J. A., Seco-Granados, G., De Wilde, W., Bougard, B., Sleewaegen, J.-M., & Popugaev, A. (2018). Design, Implementation and Validation of a GNSS Measurement Exclusion and Weighting Function with a Dual Polarized Antenna. Sensors, 18(12), 4483. https://doi.org/10.3390/s18124483