An Improved Inverse Beamforming Method: Azimuth Resolution Analysis for Weak Target Detection
Abstract
1. Introduction
2. Analysis of IBF
2.1. Principle of IBF
2.2. Phase Compensation Analysis of IBF Theory
2.3. Cause of Side-Lobe Enhancement
3. DOA Estimation Principle of GIBF
3.1. GIBF Principle
3.2. Extension of GIBF Method
4. Simulation
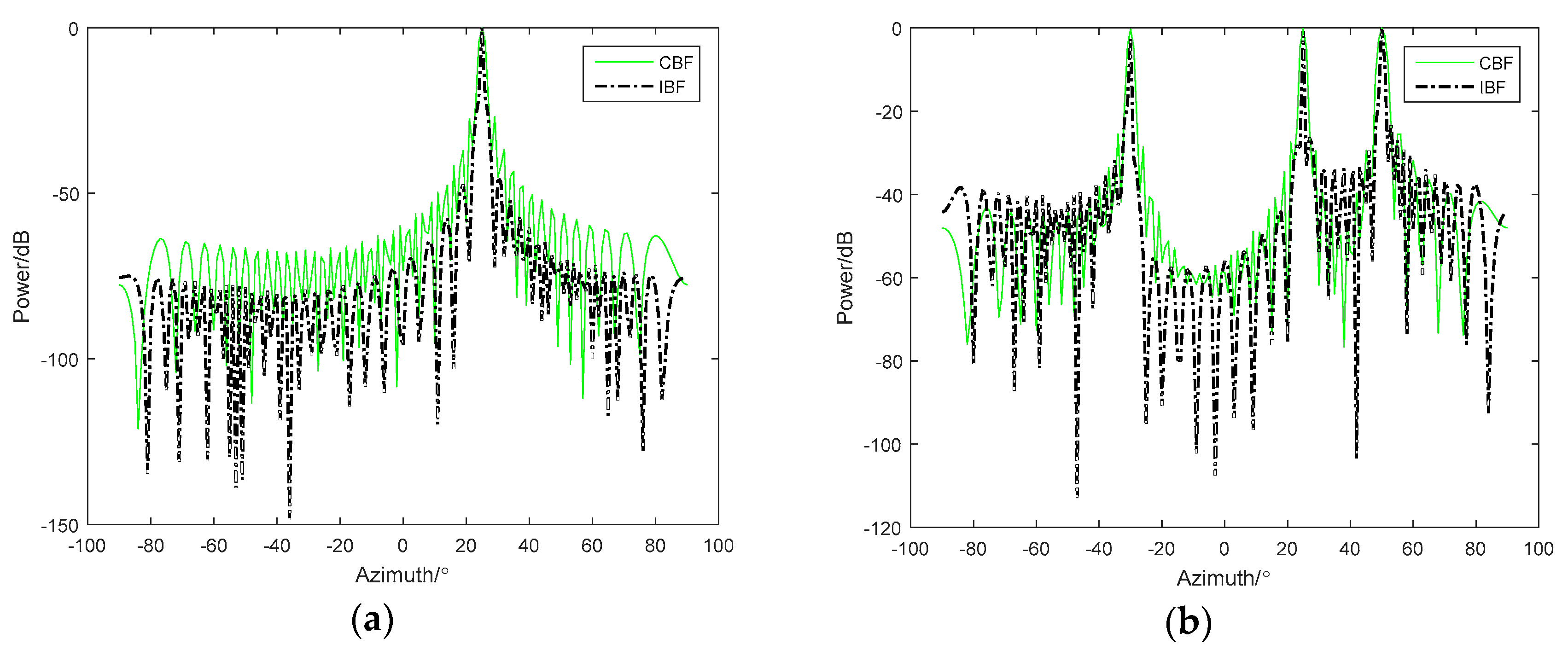
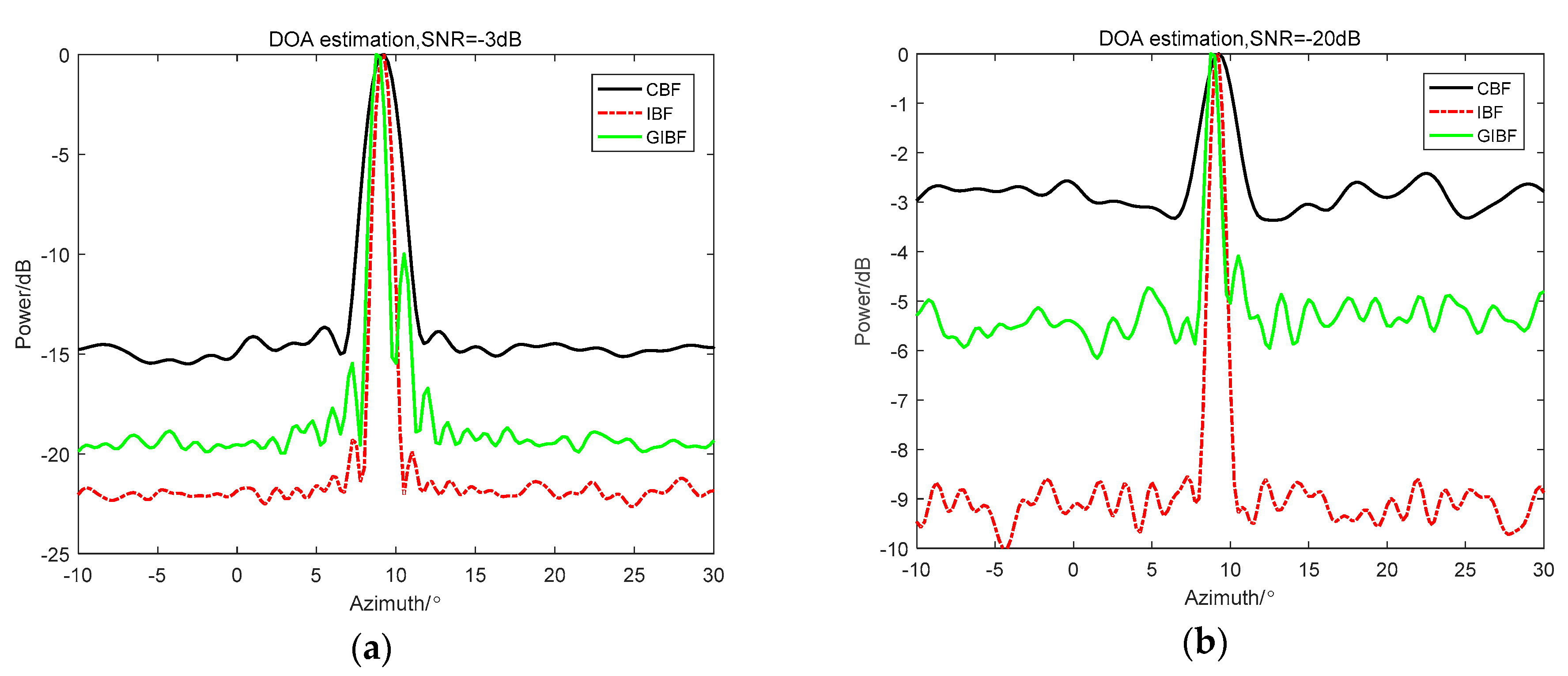
4.1. Weak Target Detection Capability of GIBF
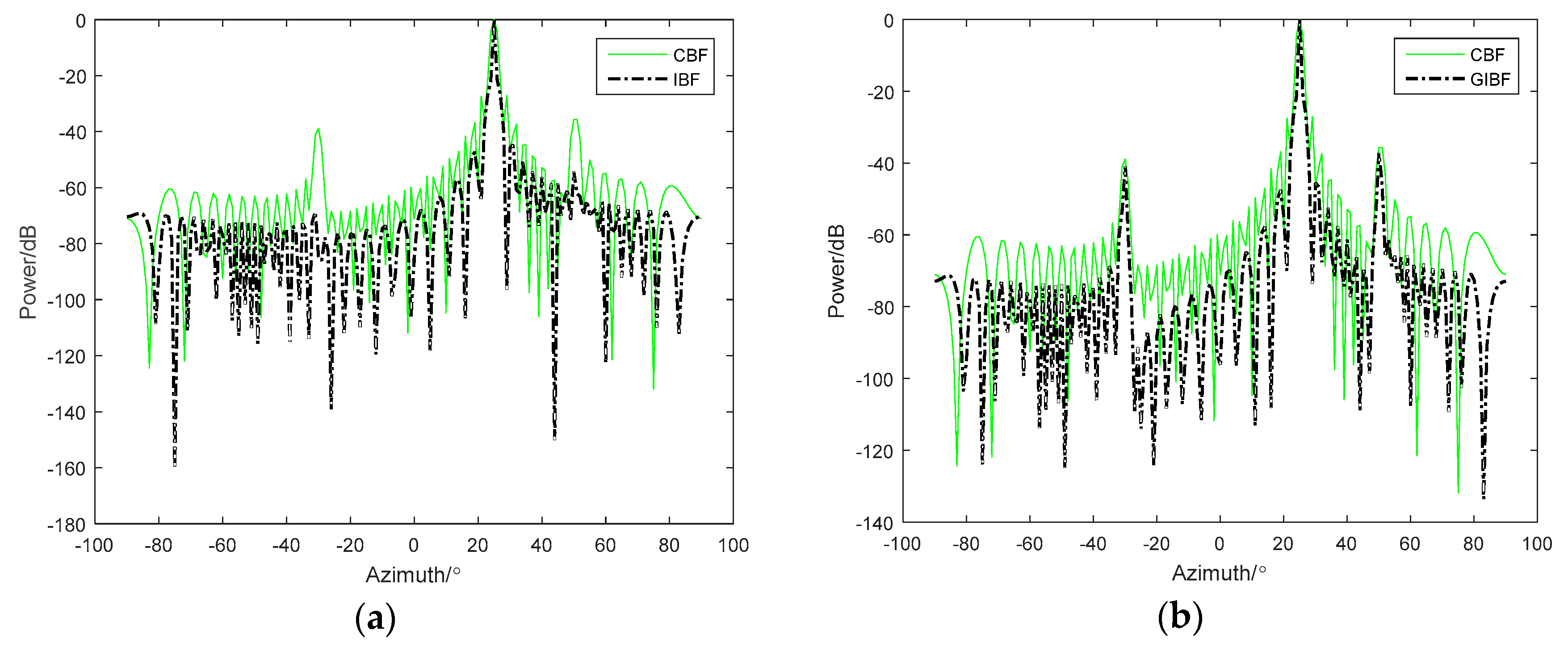
4.2. Azimuth Resolution of GIBF
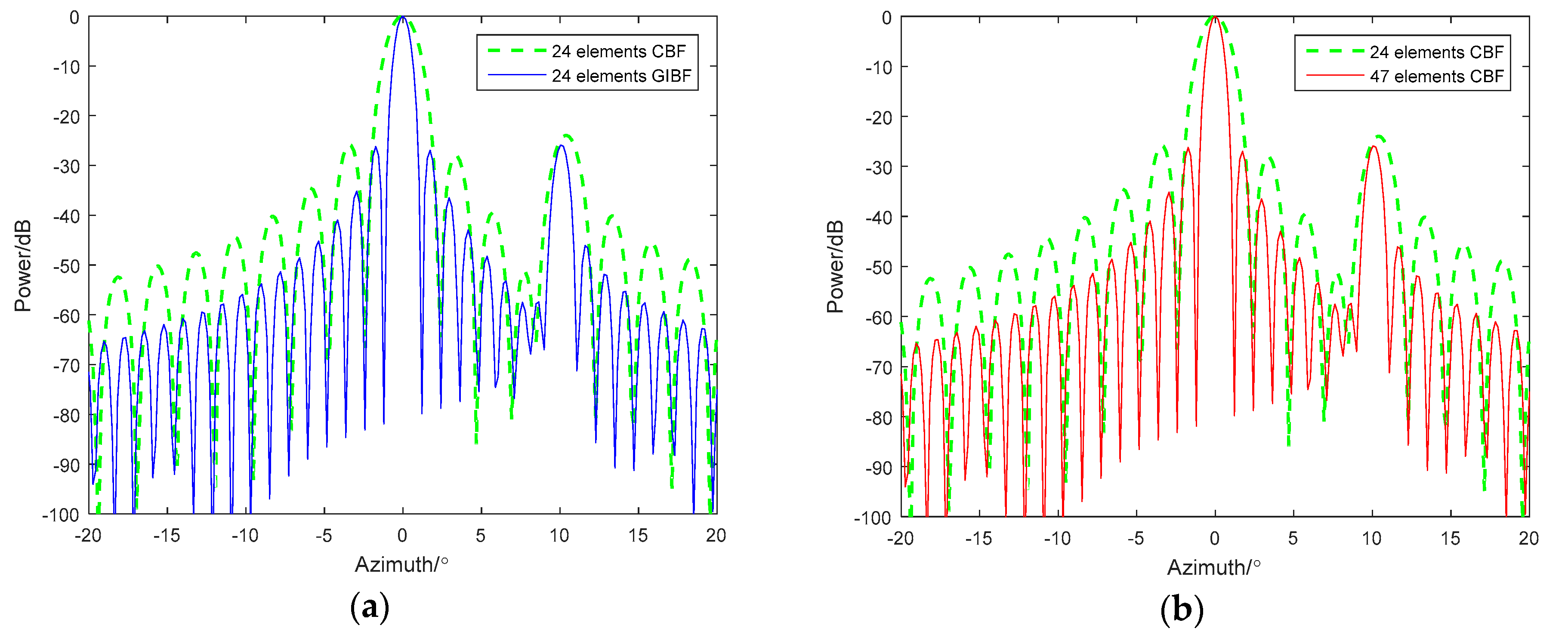
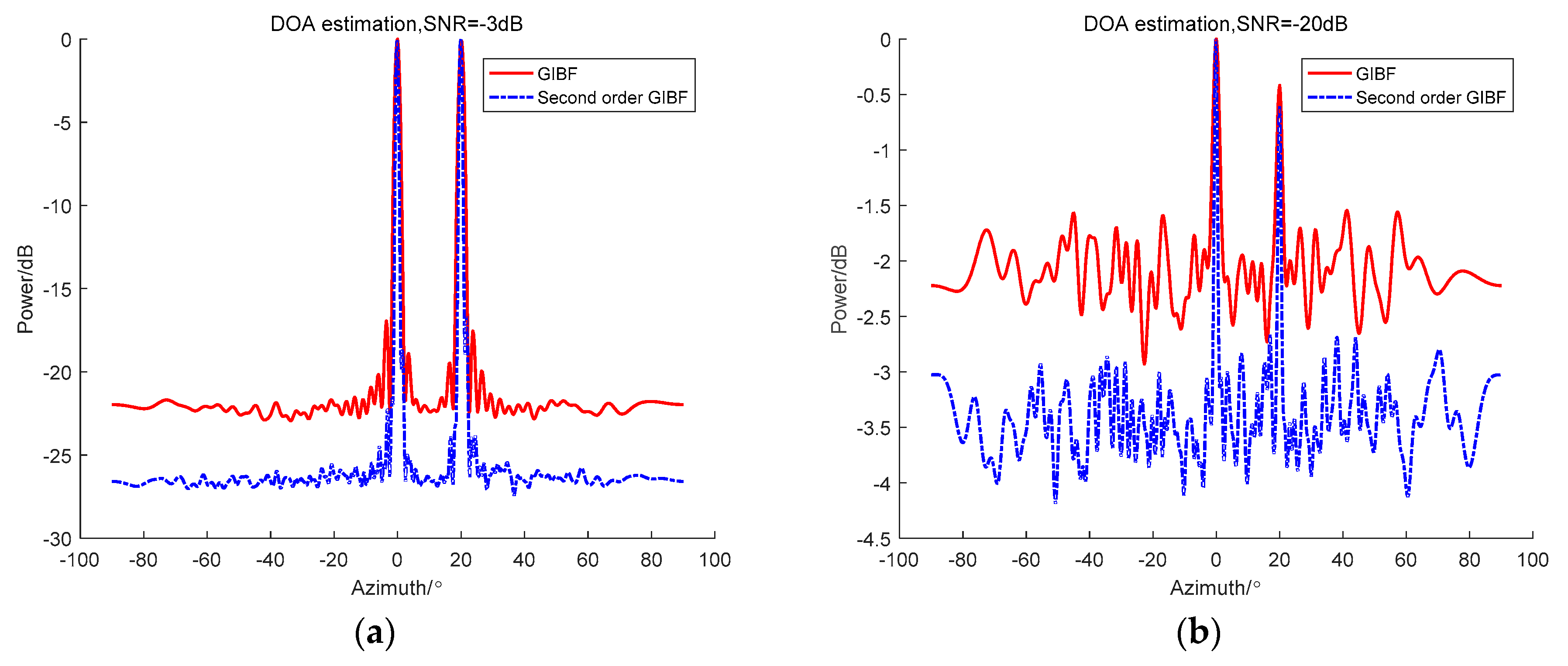
4.3. Second Order GIBF
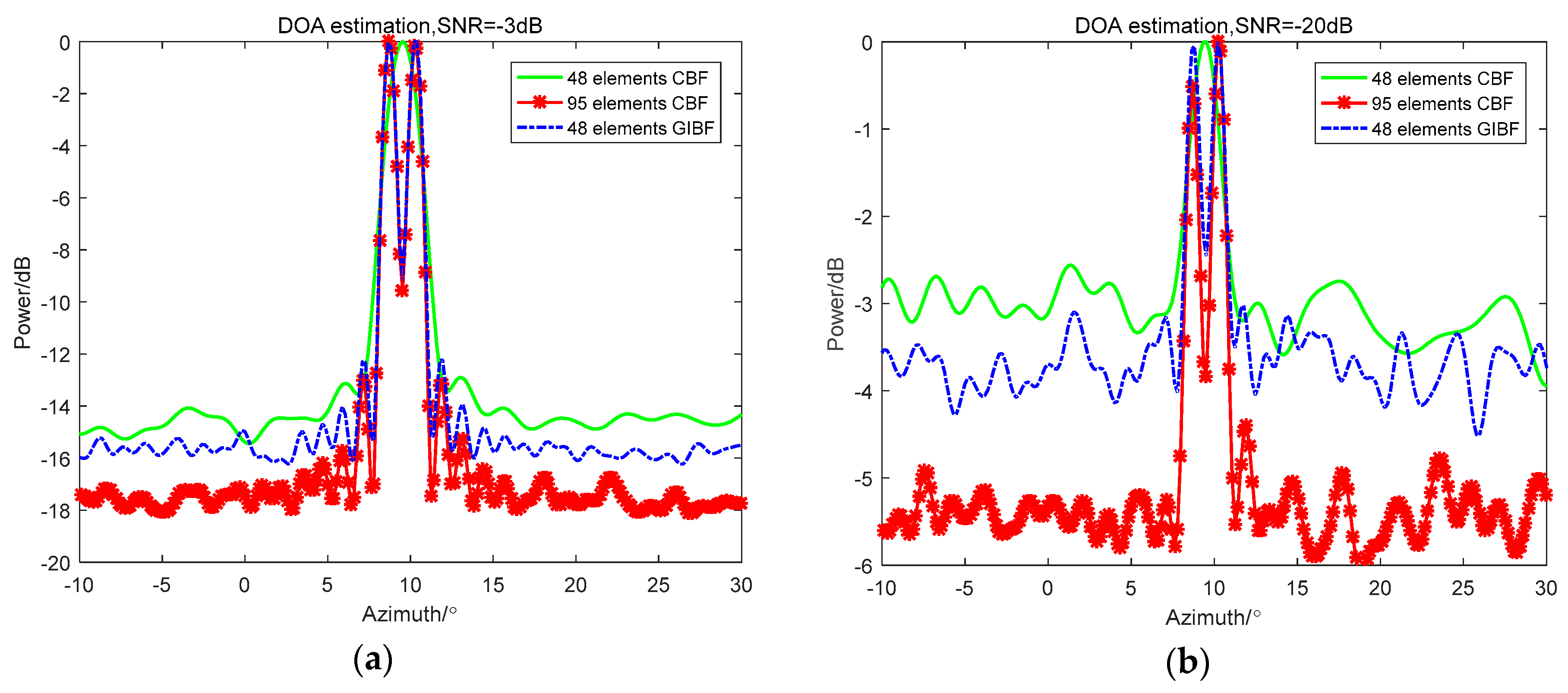
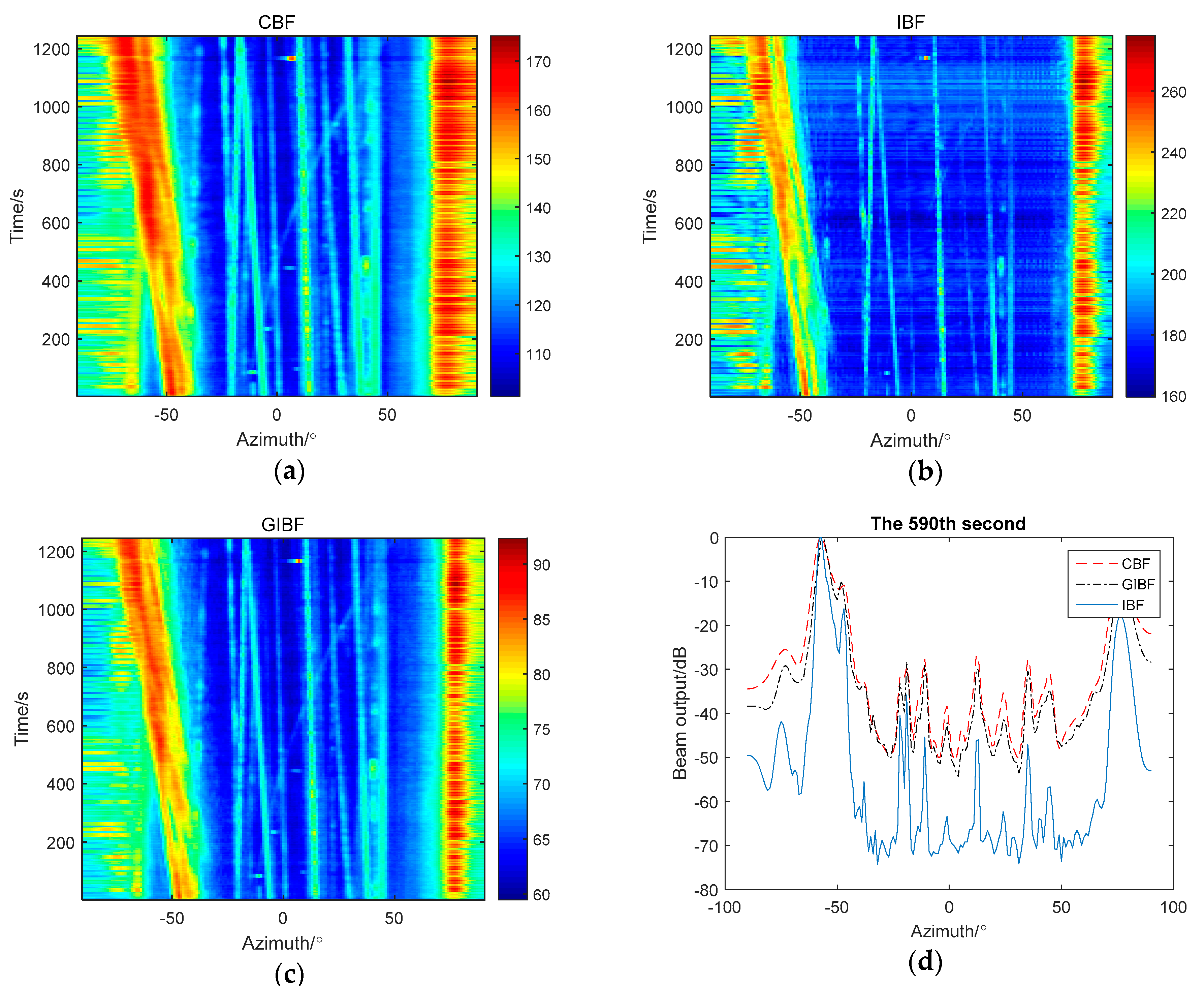
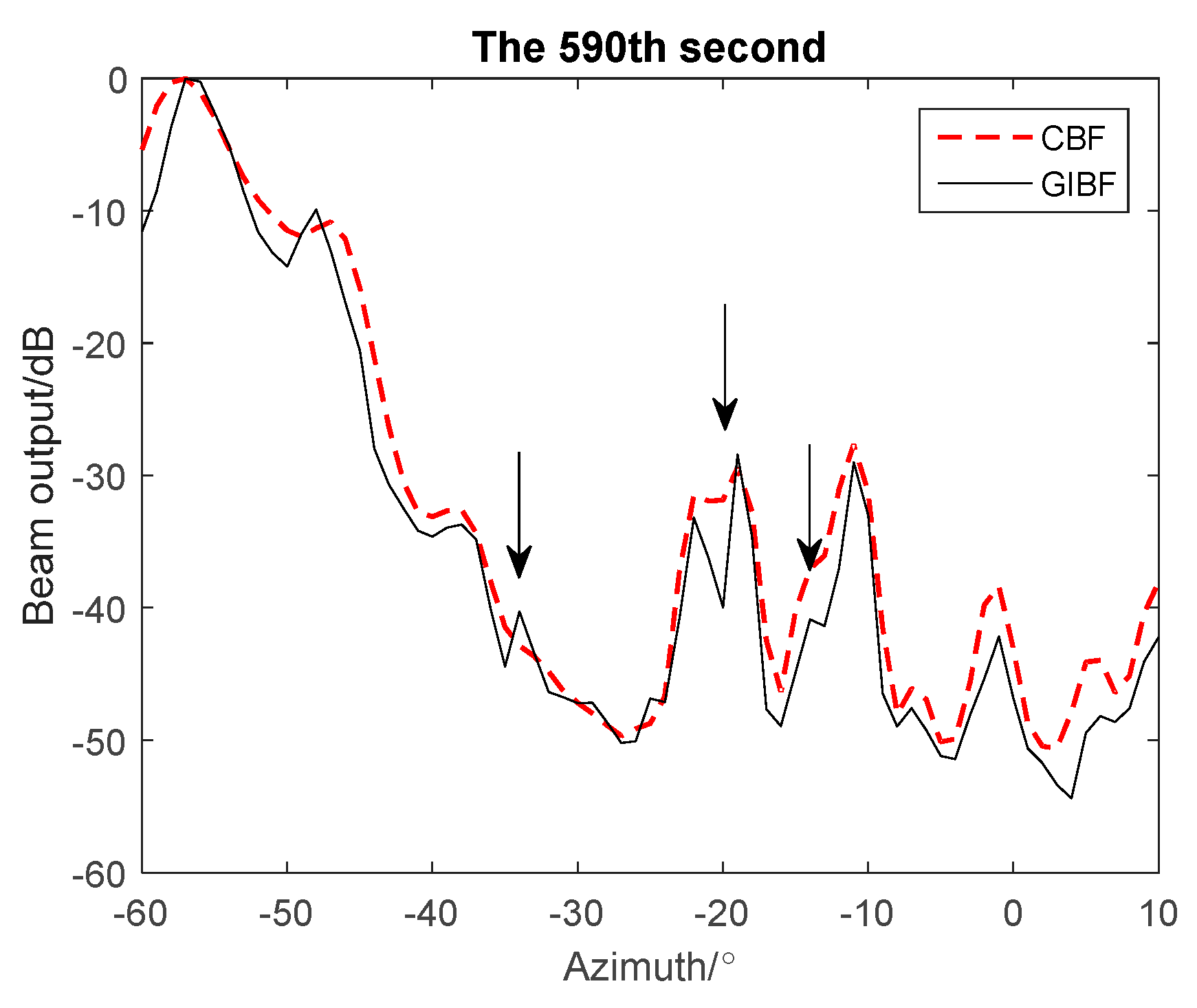
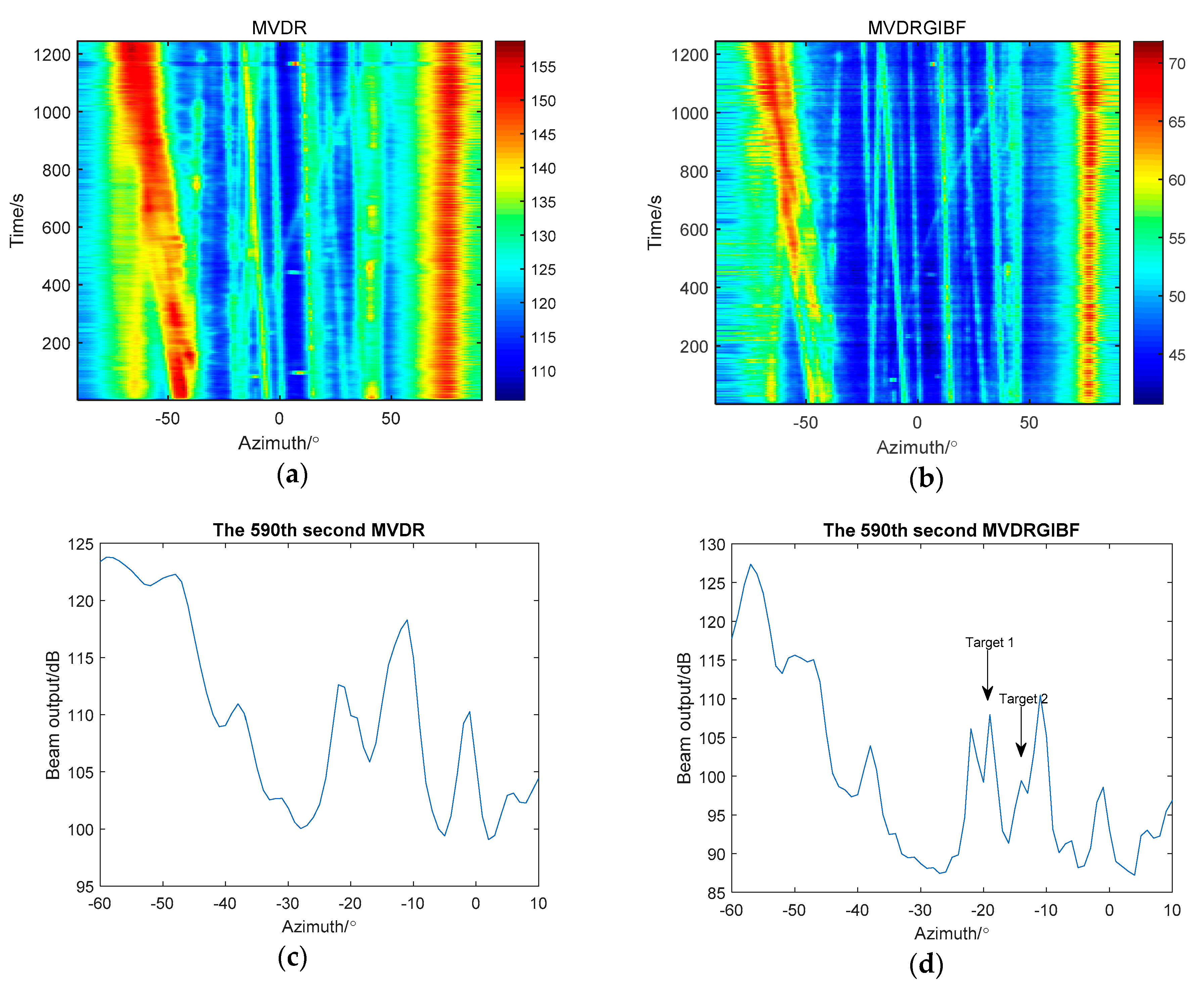
5. Experimental Data Verification
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Salama, A.A.; Ahmad, M.O.; Swamy, M.N.S. Underdetermined DOA Estimation Using MVDR-Weighted LASSO. Sensors 2016, 16, 1549. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Jin, G.; Li, Z.; Xu, H. A Nonlinear Adaptive Beamforming Algorithm Based on Least Squares Support Vector Regression. Sensors 2012, 12, 12424–12436. [Google Scholar] [CrossRef]
- Bucker, H.P. High-resolution cross-sensor beamforming for a uniform line array. J. Acoust. Soc. Am. 1978, 63, 420–424. [Google Scholar] [CrossRef]
- James, H.W. Signal detection and localization using the Fourier series method (FSM) and cross-sensor data. J. Acoust. Soc. Am. 1983, 73, 1648–1656. [Google Scholar] [CrossRef]
- James, H.W. Applications of inverse beamforming theory. J. Acoust. Soc. Am. 1995, 98, 3250–3567. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, H.Z.; Chen, F.H. Sidelobe controlling of the inverse beamforming. Appl. Acoust. 2009, 28, 372–377. [Google Scholar] [CrossRef]
- Wang, J.; Song, Z.J. Inverse beamforming on equispaced line array with moving average. Tech. Acoust. 2007, 26, 483–487. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, Y.; Wang, P. Wideband inverse beamforming technique with extended towed array. J. Appl. Acoust. 2015, 34, 142–147. [Google Scholar] [CrossRef]
- Wang, L. Research of Inverse Beam-Forming Method Based on Fourth-Order Cumulants; Ocean University: Qingdao, China, 2006. [Google Scholar]
- Zhou, W.; Hui, J.Y. Inverse Beamforming Based on Coherent Interference Vector Adaptive Canceling. Acta Mamentarii 2010, 31, 1188–1192. [Google Scholar]
- Liu, X.H.; Liu, Q.Y.; Yuan, Y.Y. On high-resolution adaptive beamforming based on Fourier integral method. In Proceedings of the 2016 National Acoustics Conference, Wuhan, China, 28 October 2016. [Google Scholar]
- Wang, L.; Song, Z.J.; Du, J.Y. High Resolution Algorithm for Passive Direction Finding Sonar Analysis Based on Fourth Order Cumulants. Period. Ocean Univ. China 2007, 37, 211–214. [Google Scholar] [CrossRef]
- Tian, T. Sonar Technology; Harbin Engineering University Press: Harbin, China, 2009. [Google Scholar]
- Tian, T.A.; Xue, L. Sonar technology. In Sonar Beamforming Technology, 2nd ed.; Tian, T., Ed.; Harbin Engineering University Press: Harbin, China, 2009; pp. 76–79. ISBN 978-7-81133-598-9. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Zhang, X.; Li, L.; Zhang, W. An Improved Inverse Beamforming Method: Azimuth Resolution Analysis for Weak Target Detection. Sensors 2018, 18, 4160. https://doi.org/10.3390/s18124160
Li P, Zhang X, Li L, Zhang W. An Improved Inverse Beamforming Method: Azimuth Resolution Analysis for Weak Target Detection. Sensors. 2018; 18(12):4160. https://doi.org/10.3390/s18124160
Chicago/Turabian StyleLi, Peng, Xinhua Zhang, Lanrui Li, and Wenlong Zhang. 2018. "An Improved Inverse Beamforming Method: Azimuth Resolution Analysis for Weak Target Detection" Sensors 18, no. 12: 4160. https://doi.org/10.3390/s18124160
APA StyleLi, P., Zhang, X., Li, L., & Zhang, W. (2018). An Improved Inverse Beamforming Method: Azimuth Resolution Analysis for Weak Target Detection. Sensors, 18(12), 4160. https://doi.org/10.3390/s18124160




