An Integrated Machine Learning Algorithm for Separating the Long-Term Deflection Data of Prestressed Concrete Bridges
Abstract
1. Introduction
2. Multiscale Characteristics of Long-Term Deflection Data
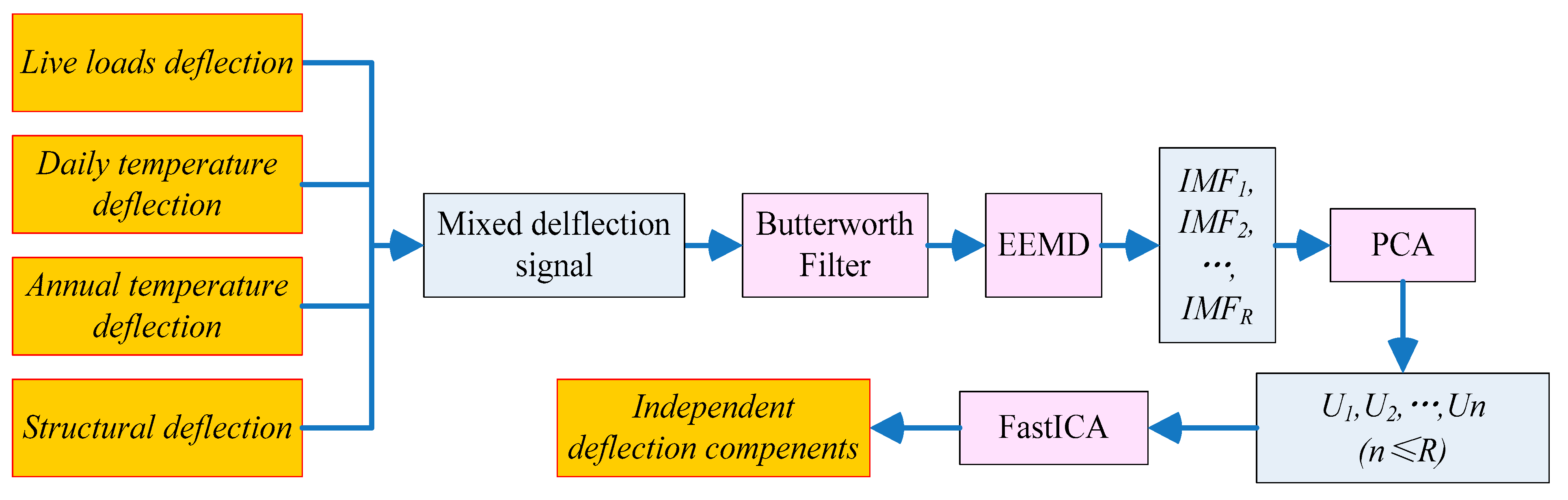
3. An Integrated Machine Learning Algorithm
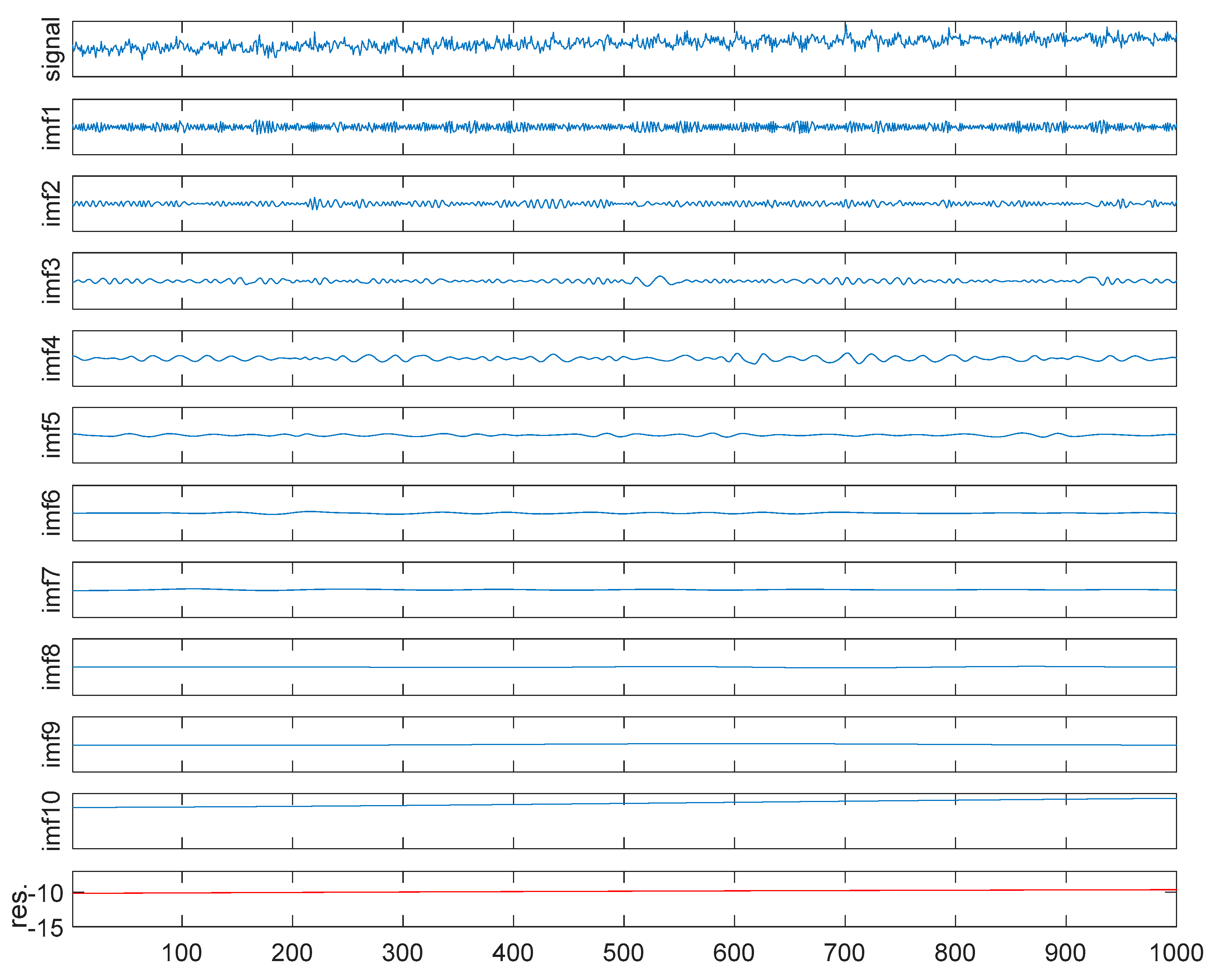
3.1. EEMD
- (1)
- Add a white-noise series to the targeted signal.where is the mixed signal to be analyzed. is the added white noise, which has a mean of zero and a standard deviation of , which is in the range of 0.1 to 0.4. The index m is the ensemble number with a preset maximum number (me), which starts from 1.
- (2)
- Decompose the signal into a series of IMFs, , and a residual, , using EMD. We can obtain:where N − 1 is the total number of IMFs produced in each EMD decomposition.
- (3)
- Repeat Step (1) and Step (2) for me trials.
- (4)
- The final IMFs are obtained by overall averaging the IMFs produced in each trial.
3.2. PCA
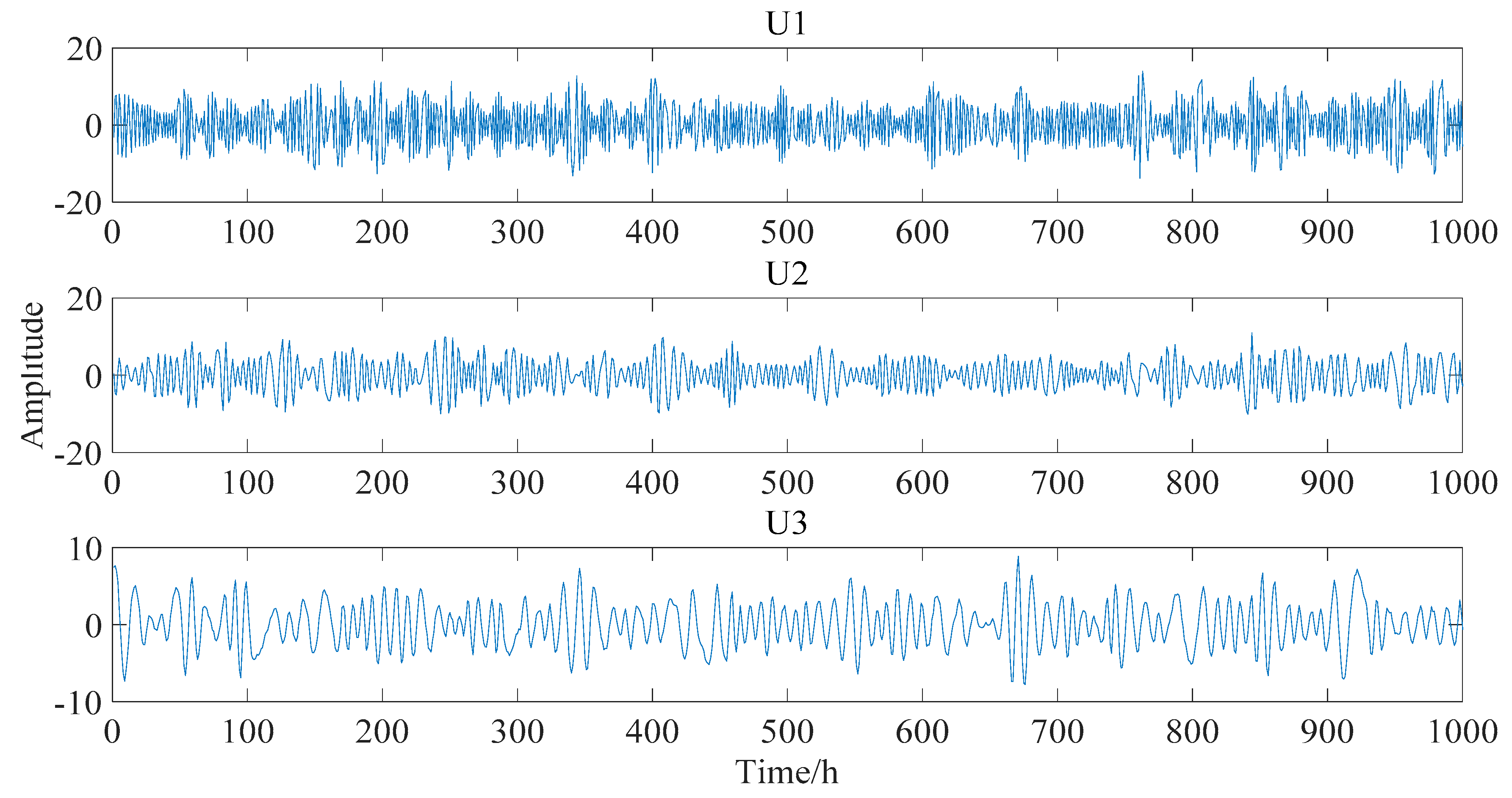
3.3. FastICA
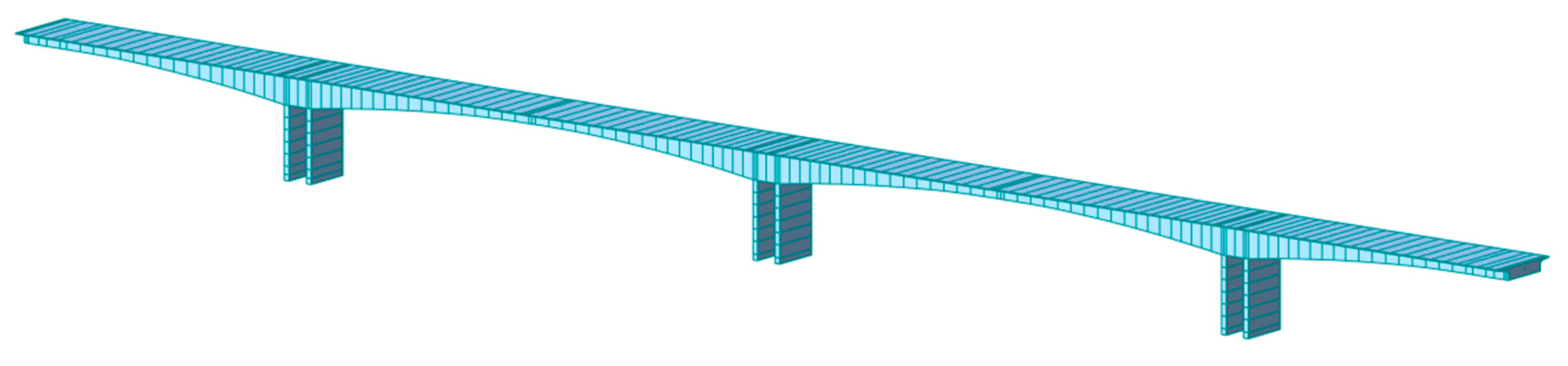
4. Numerical Simulation
4.1. Characteristic of the Individual Deflection Component of Different Effects
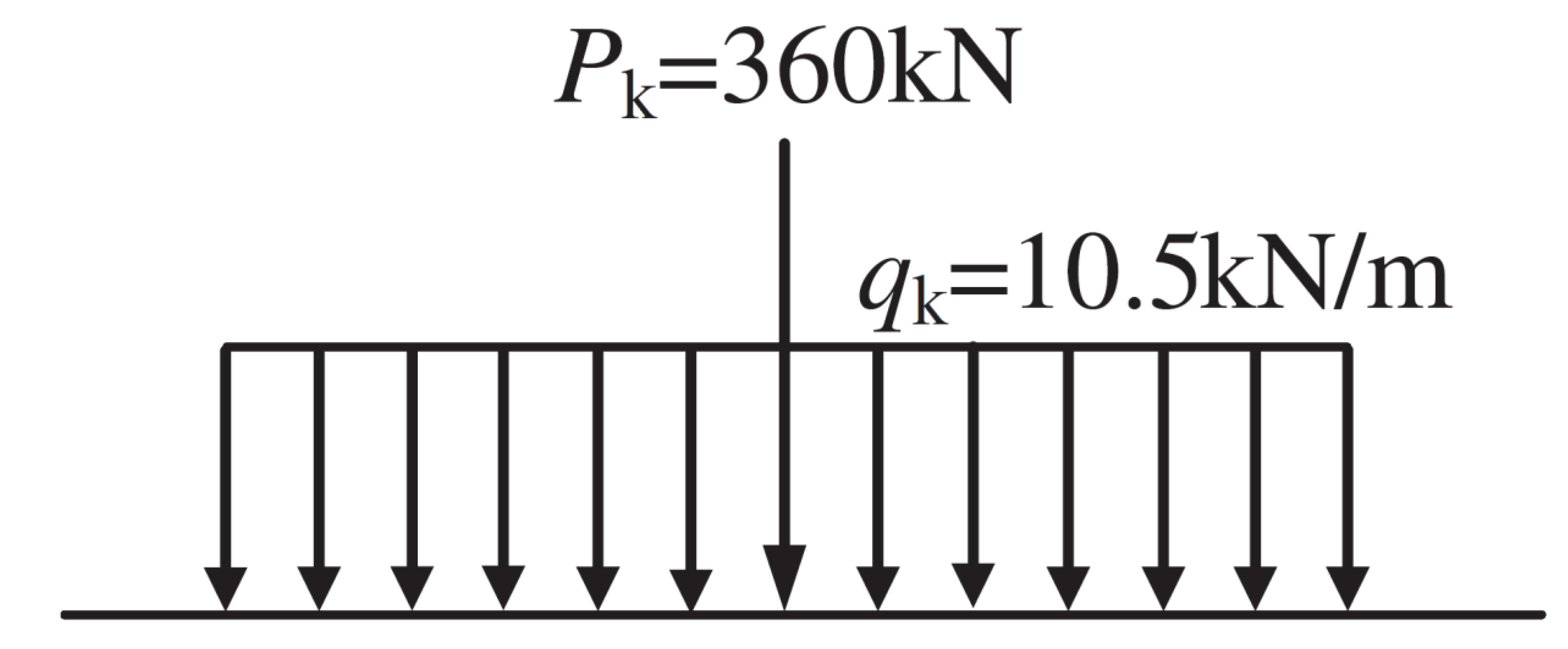
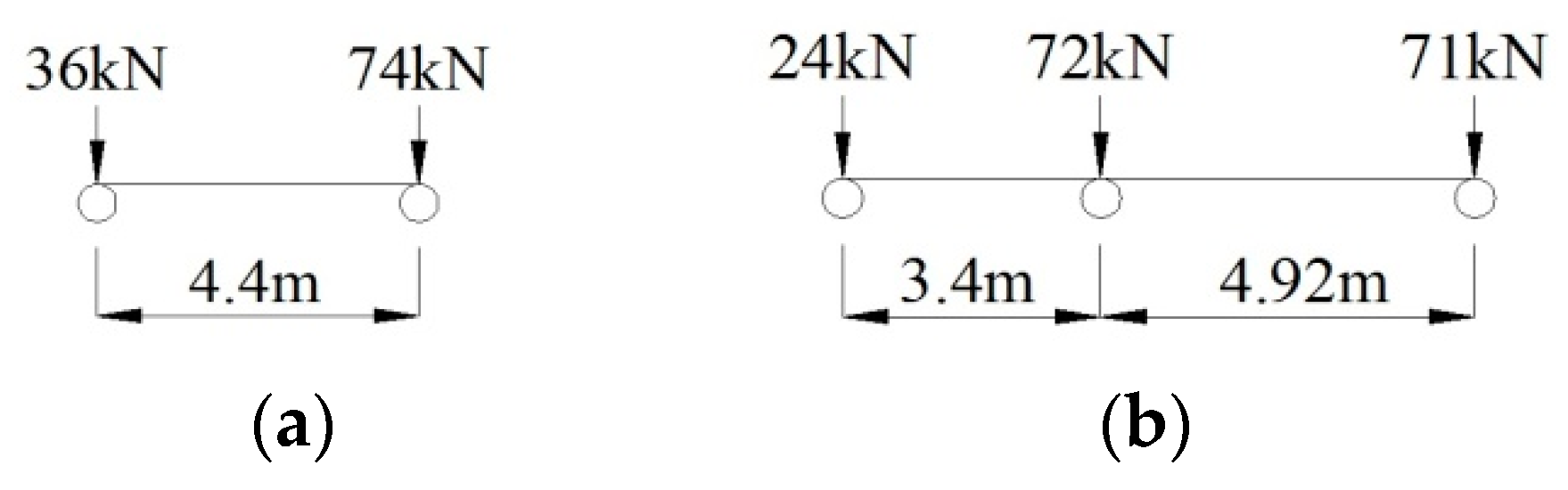
4.1.1. Live Load Effect
4.1.2. Temperature Effect
4.1.3. Effect of Concrete Shrinkage and Creep
4.1.4. Effect of Prestress Loss
4.2. Validation Result
4.2.1. Total Deflection
4.2.2. Procedure of Separation
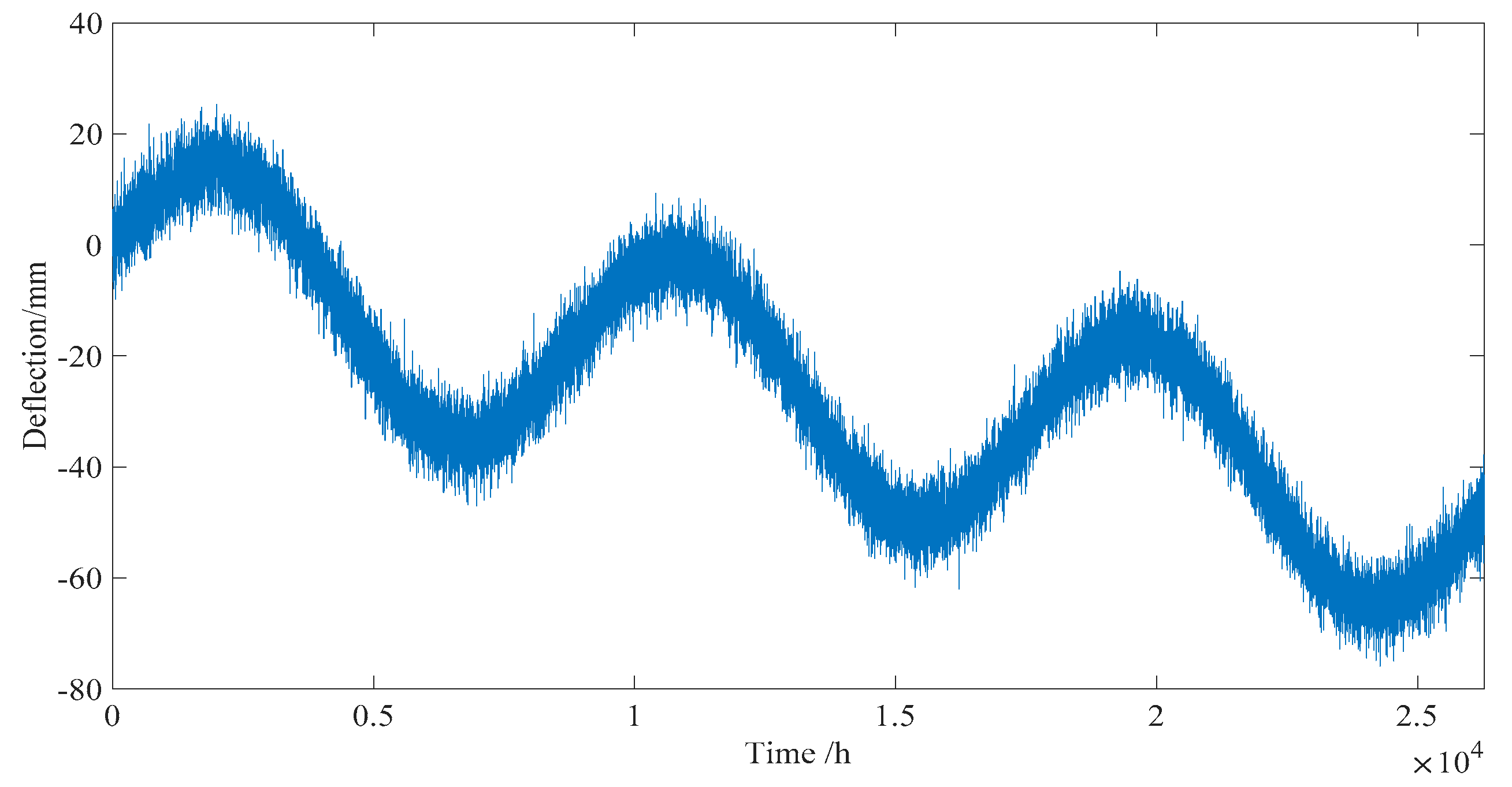
5. Practical Verification
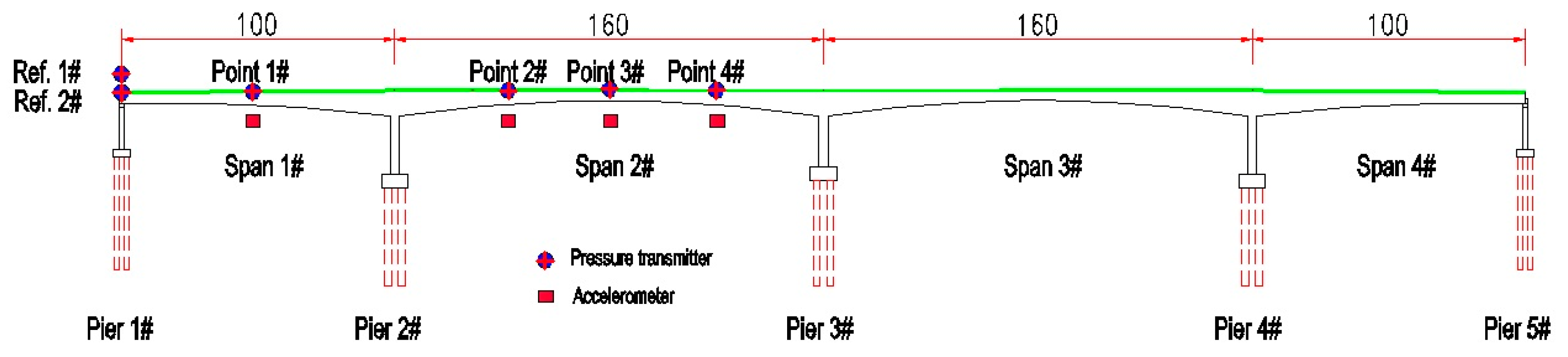
5.1. Description of the Structural Health Monitoring (SHM) System
5.2. Processing of the Monitored Deflection Data
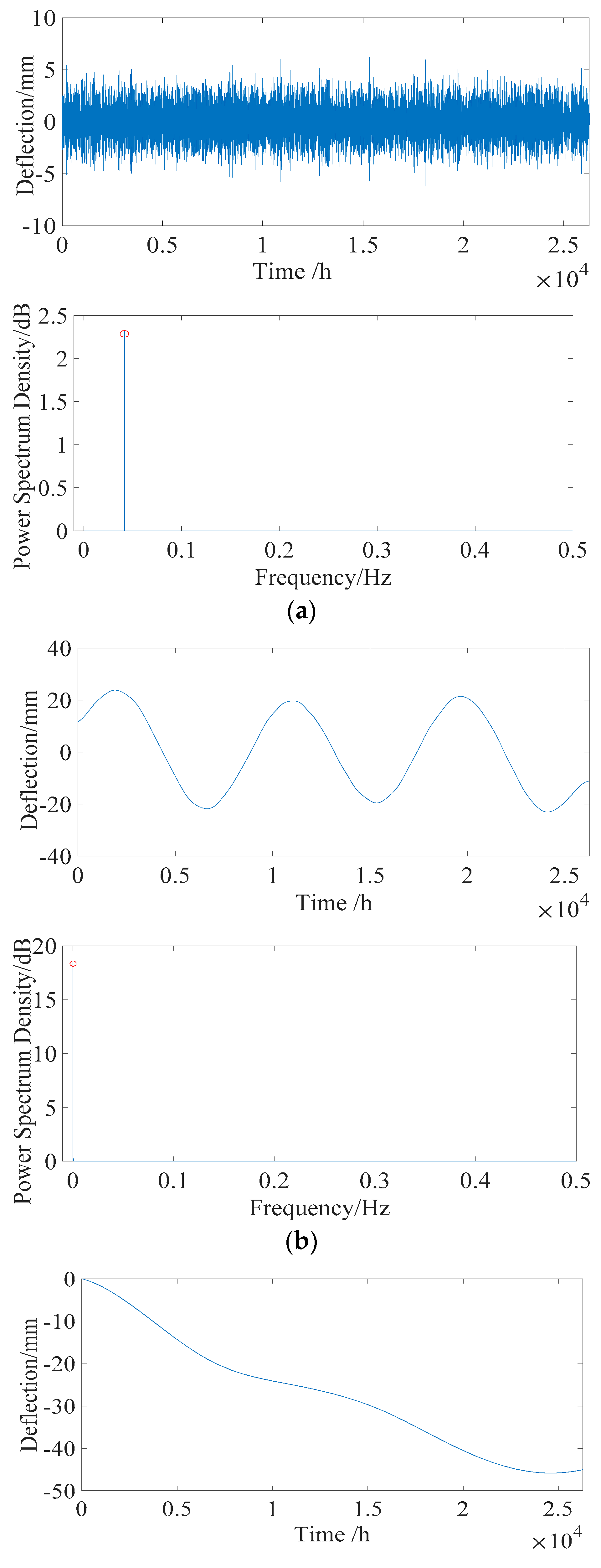
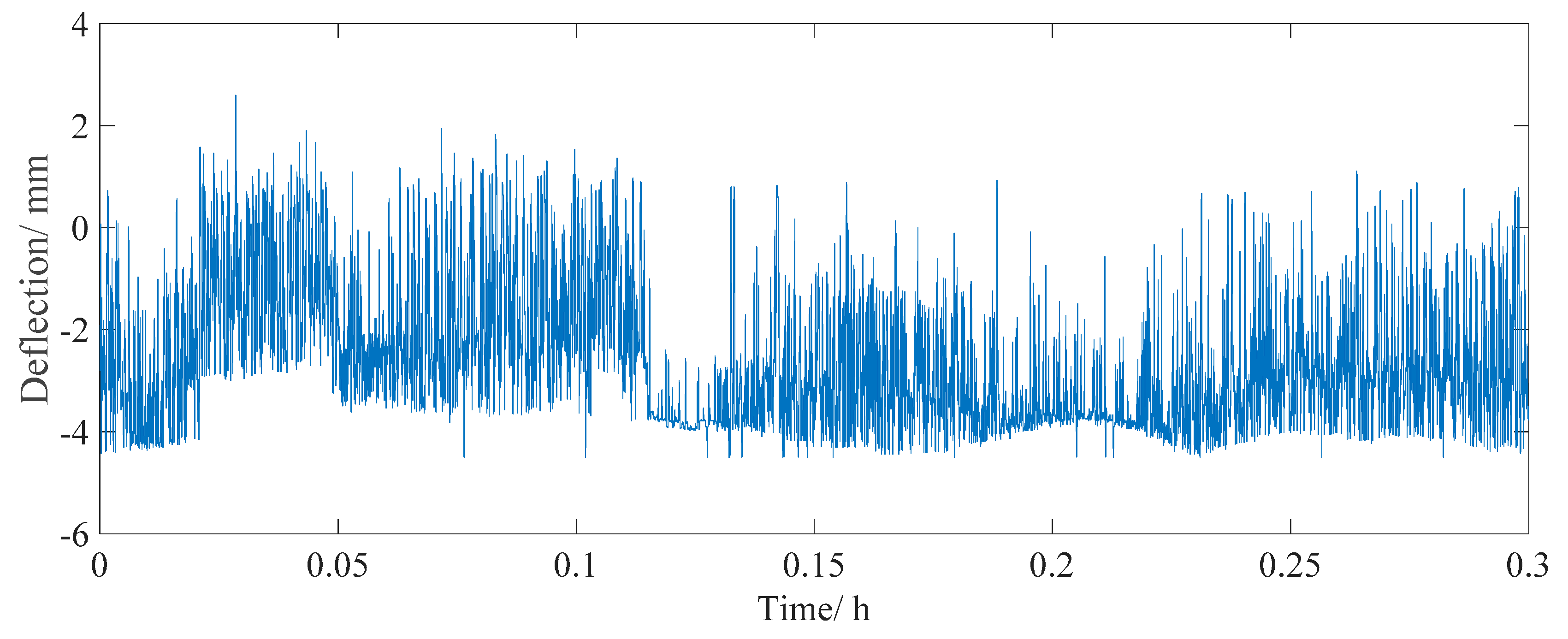
5.2.1. Live Loads Effect
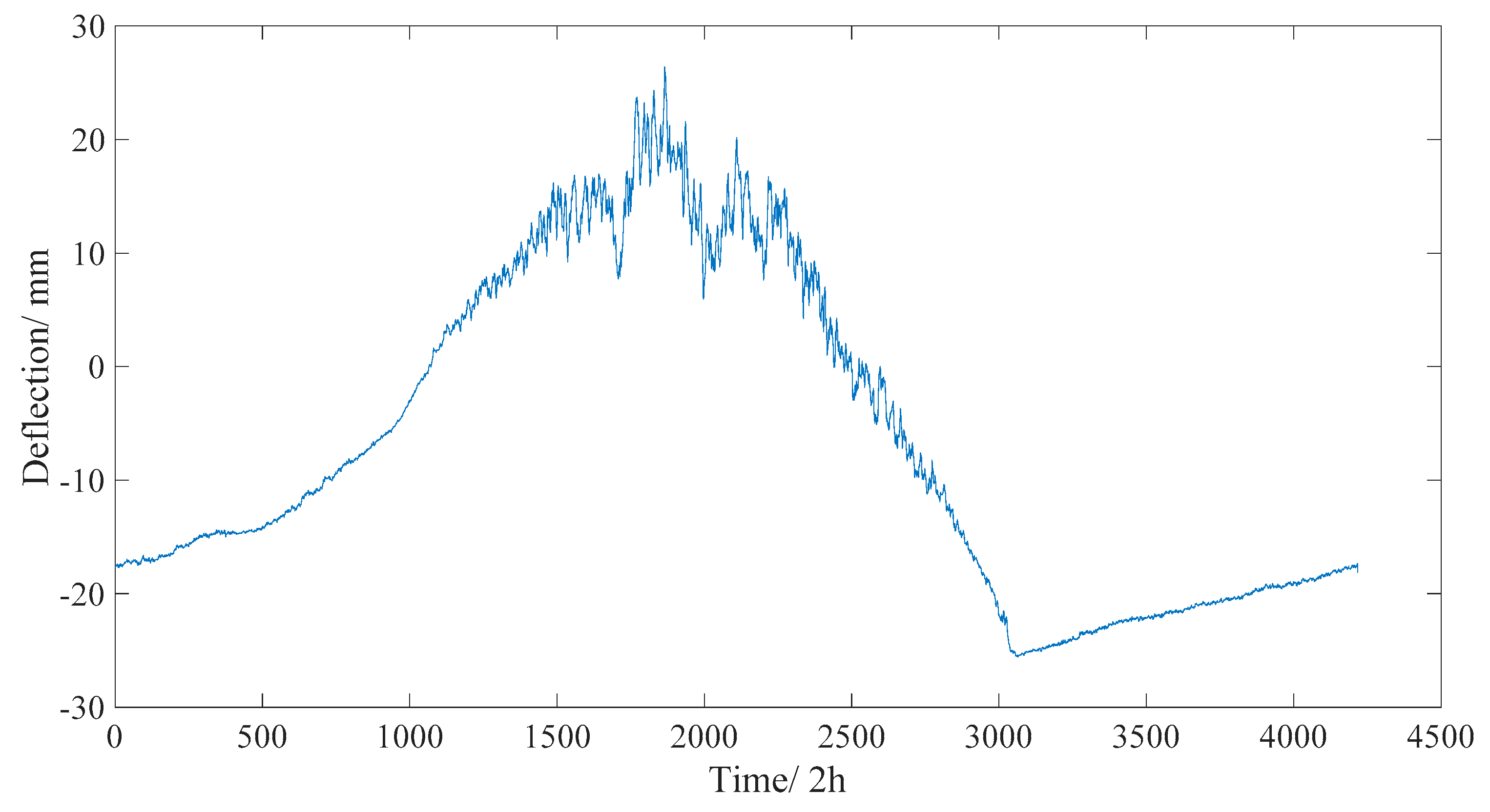
5.2.2. Temperature Effect
5.2.3. Structural Deflection
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chen, W.F.; Lian, D. (Eds.) Bridge Engineering Handbook: Construction and Maintenance; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Krístek, V.; Bažant, Z.P.; Zich, M.; Kohoutkova, A. Box girder bridge deflections: Why is the initial trend deceptive? ACI Concr. Int. 2006, 28, 55–63. [Google Scholar]
- Elbadry, M.; Ghali, A.; Gayed, R. Deflection control of prestressed box girder bridges. J. Bridge Eng. 2014, 19, 04013027. [Google Scholar] [CrossRef]
- Sousa, H.; Bento, J.; Figueiras, J. Construction assessment and long-term prediction of prestressed concrete bridges based on monitoring data. Eng. Struct. 2013, 52, 26–37. [Google Scholar] [CrossRef]
- Bažant, Z.; Yu, Q.; Li, G. Excessive Long-Time Deflections of Prestressed Box Girders I: Record-Span Bridge in Palau and Other Paradigms. J. Struct. Eng. 2012, 138, 676–689. [Google Scholar] [CrossRef]
- Bažant, Z.; Yu, Q.; Li, G. Excessive long-time deflections of prestressed box girders. II: Numerical analysis and lessons learned. J. Struct. Eng. 2012, 138, 687–696. [Google Scholar] [CrossRef]
- Benveniste, A. Multiscale signal processing: From QMF To wavelet. In International Series on Advances in Control and Dynamic Systems; Leondes, C.T., Ed.; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Pirner, M.; Fischer, O. Monitoring stresses in GRP extension of the Prague TV tower. In DAMAS 97: Structural Damage Assessment Using Advanced signal Processing Procedures; University of Sheffield: Sheffield, UK, 1997; pp. 451–460. [Google Scholar]
- Sohn, H. Effects of Environmental and Operational Variability on Structural Health Monitoring. Philos. Trans. R. Soc. A 2007, 365, 539–560. [Google Scholar] [CrossRef] [PubMed]
- Robertson, I.N. Prediction of vertical deflections for a long-span prestressed concrete bridge structure. Eng. Struct. 2005, 27, 1820–1827. [Google Scholar] [CrossRef]
- Sousa, C.; Sousa, H.; Neves, A.S.; Figueiras, J. Numerical Evaluation of the Long-Term Behavior of Precast Continuous Bridge Decks. J. Bridge Eng. 2012, 17, 89–96. [Google Scholar] [CrossRef]
- Sousa, H.; Bento, J.; Figueiras, J. Assessment and Management of Concrete Bridges Supported by Monitoring Data-Based Finite-Element Modeling. J. Bridge Eng. 2014, 19, 05014002. [Google Scholar] [CrossRef]
- Tong, T.; Liu, Z.; Zhang, J.; Yu, Q. Long-term performance of prestressed concrete bridges under the intertwined effects of concrete damage, static creep and traffic-induced cyclic creep. Eng. Struct. 2016, 127, 510–524. [Google Scholar] [CrossRef]
- Guo, T.; Chen, Z. Deflection control of long-span PSC boxgirder bridge based on field monitoring and probabilistic FEA. J. Perform. Constr. Facil. 2016, 30, 04016053. [Google Scholar] [CrossRef]
- Huang, H.D.; Huang, S.S.; Pilakoutas, K. Modeling for Assessment of Long-Term Behavior of Prestressed Concrete Box-Girder Bridges. J. Bridge Eng. 2018, 23, 04018002. [Google Scholar] [CrossRef]
- Ghali, A.; Elbadry, M.; Megally, S. Two-year deflections of the Confederation Bridge. Can. J. Civ. Eng. 2000, 27, 1139–1149. [Google Scholar] [CrossRef]
- Cross, E.J.; Koo, K.Y.; Browniohn, J.M.W.; Worden, K. Long-term monitoring and data analysis of the Tamar Bridge. Mech. Syst. Signal Process. 2013, 35, 16–34. [Google Scholar] [CrossRef]
- Brownjohn, J.M.W.; Koo, K.Y.; Scullion, A.; List, D. Operational deformations in long-span bridges. Struct. Infrastruct. Eng. 2015, 11, 556–574. [Google Scholar] [CrossRef]
- Xia, Y.; Hao, H.; Zanardo, G. Long term vibration monitoring of an RC slab: Temperature and humidity effect. Eng. Struct. 2006, 28, 441–452. [Google Scholar] [CrossRef]
- Kim, J.T.; Park, J.H.; Lee, B.J. Vibration-based damage monitoring in model plate-girder bridges under uncertain temperature conditions. Eng. Struct. 2007, 29, 1354–1365. [Google Scholar] [CrossRef]
- Xia, H.W.; Ni, Y.Q.; Ko, J.M.; Wong, K.Y. Wavelet-based multi-resolution decomposition of long-term monitoring signal of in-service strain. In Proceedings of the 2nd International Postgraduate Conference on Infrastructure and Environment, Hong Kong, China, 10–12 January 2010; pp. 278–285. [Google Scholar]
- Xia, H.W.; Ni, Y.Q.; Wong, K.Y.; Ko, J.M. Reliability-based condition assessment of in-service bridges using mixture distribution models. Comput. Struct. 2012, 106–107, 204–213. [Google Scholar] [CrossRef]
- Ye, X.W.; Su, Y.H.; Xi, P.S. Statistical Analysis of Stress Signals from Bridge Monitoring by FBG System. Sensors 2018, 18, 491. [Google Scholar]
- Smarsly, K.; Dragos, K.; Wiggenbrock, J. Machine learning techniques for structural health monitoring. In Proceedings of the 8th European Workshop on Structural Health Monitoring (EWSHM 2016), Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- Liu, X.P.; Yang, H.; Sun, Z.; Yang, J.; Liu, A. Separation study of bridge deflection based on singular value decomposition. Acta Sci. Nat. Univ. Sunyatseni 2013, 52, 11–16. (In Chinese) [Google Scholar]
- Liu, G.; Shao, Y.M.; Huang, Z.M.; Zhou, X. A new method to separate temperature effect from long-term structural health monitoring data. Eng. Mech. 2010, 27, 55–61. (In Chinese) [Google Scholar]
- Yang, H.; Liu, X.P.; Sun, Z.; He, Q.; Wang, Y. Study on separation of bridge deflection temperature effect based on LS-SVM. J. Chin. Railway Soc. 2012, 34, 91–96. (In Chinese) [Google Scholar]
- Yang, H.; Sun, Z.; Liu, X.P.; Zhu, W.; Wang, Y. Separation of bridge temperature deflection effect based on M-LS-SVM. J. Vib. Shock 2014, 33, 71–75. (In Chinese) [Google Scholar]
- Peng, L.; Niu, R.Q.; Wu, T. Time series analysis and support vector machine for landslide displacement prediction. J. Zhejiang Univ. Eng. Sci. 2013, 47, 1672. (In Chinese) [Google Scholar]
- Yan, A.M.; Kerschen, G.; De Boe, P.; Golinval, J.-C. Structural damage diagnosis under varying environmental conditions-Part I: A linear analysis. Mech. Syst. Signal Process. 2005, 19, 847–864. [Google Scholar] [CrossRef]
- Sohn, H.; Worden, K.; Farrar, C.R. Statistical damage classification under changing environmental and operational conditions. J. Intell. Mater. Syst. Struct. 2003, 13, 561–574. [Google Scholar] [CrossRef]
- Abdelgawad, A.; Mahmud, M.A.; Yelamarthi, K. Butterworth Filter Application for Structural Health Monitoring. Int. J. Handheld Comput. Res. 2016, 7, 15–29. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Peng, Z.; Tse, P.; Chu, F. An improved Hilbert Huang transform and its application in vibration signal analysis. J. Sound Vib. 2005, 286, 187–205. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, Na.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for non-linear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Feldman, M. Analytical basics of the EMD: Two harmonics decomposition. Mech. Syst. Signal Process. 2009, 23, 2059–2071. [Google Scholar] [CrossRef]
- Pearson, K. On Lines and Planes of Closest Fit to Systems of Points in Space. Philos. Mag. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Anaya, M.; Tibaduiza, D.A.; Pozo, F. A bioinspired methodology based on an artiicial immune system for damage detection in structural health monitoring. Shock Vib. 2015, 501, 648097. [Google Scholar]
- Tibaduiza, D.A.; Mujica, L.E.; Rodellar, J. Damage classification in structural health monitoring using principal component analysis and self organizing maps. Struct. Control Health Monit. 2012, 20, 1303–1316. [Google Scholar] [CrossRef]
- Comon, P. Independent component analysis: A new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Hyvarinen, A.; Oja, E. Independent Component Analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. A Fast Fixed-Point Algorithm for Independent Component Analysis. Neural Comput. 1997, 9, 1483–1492. [Google Scholar] [CrossRef]
- Ye, X.J.; Chen, B.C. Condition assessment of bridge structures based on a liquid level sensing system: Theory, verification and application. Arabian J. Sci. Eng. 2018. [CrossRef]
- Ministry of Transport of the People’s Republic of China. General Specifications for Design of Highway Bridges and Culverts; China Communications Press: Beijing, China, 2015.
- Wang, R.H.; Chi, C.; Chen, Q.Z.; Zhen, X. Study on the model of the fatigue-loaded vehicles in Guangzhou trestle bridges. J. South China Univ. Technol. (Nat. Sci. Ed.) 2004, 32, 94–96. (In Chinese) [Google Scholar]
- Priestley, M.J.N. Design of concrete bridges for temperature gradients. ACI J. 1978, 75, 209–217. [Google Scholar]
- Ministry of Transport of the People’s Republic of China. Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts; China Communications Press: Beijing, China, 2018.
- Niu, Y.W.; Shi, X.F.; Ruan, X. Measured sustained deflection analysis of long-span prestressed concrete beam bridges. Eng. Mech. 2008, 6, 116–119. (In Chinese) [Google Scholar]

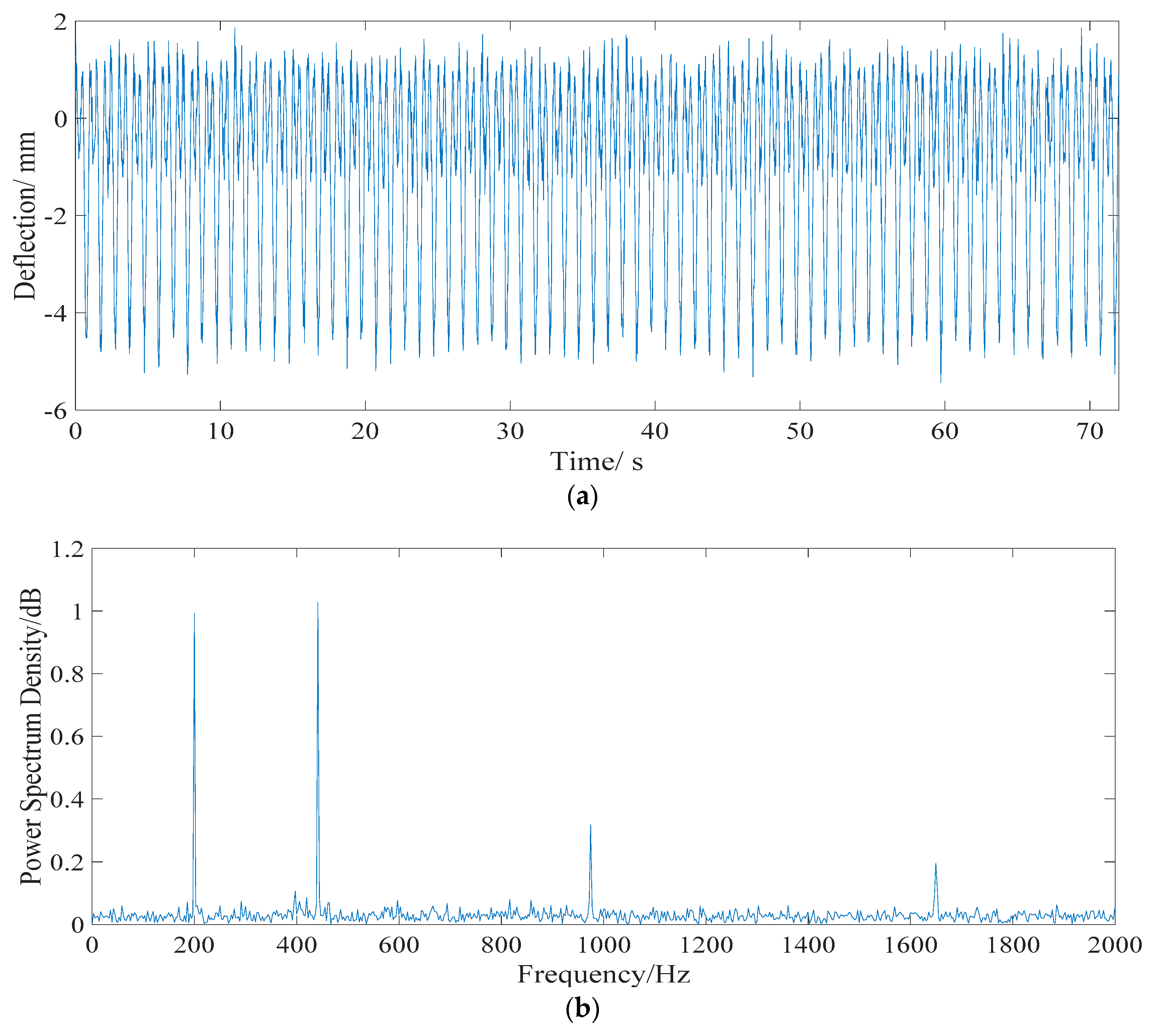
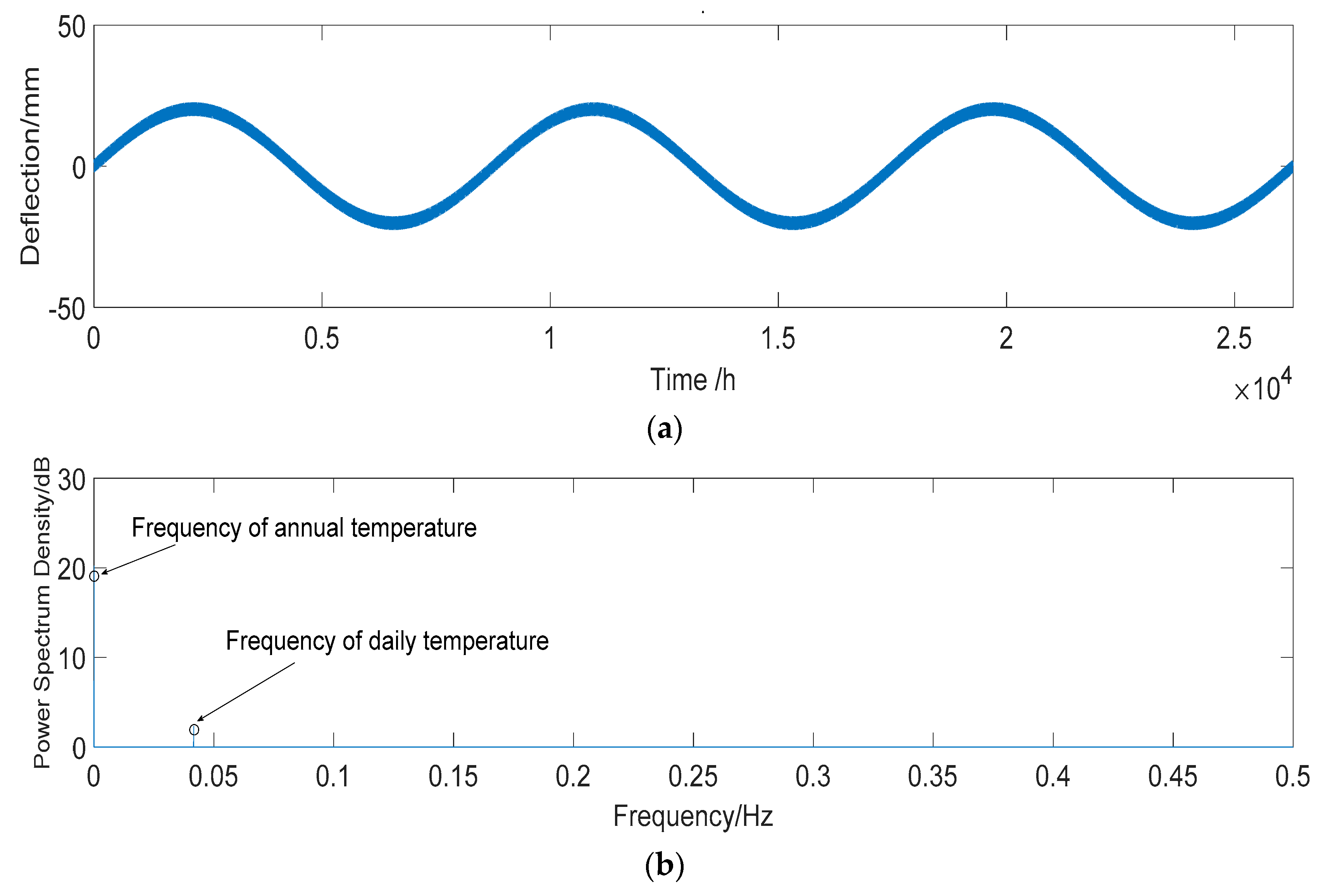
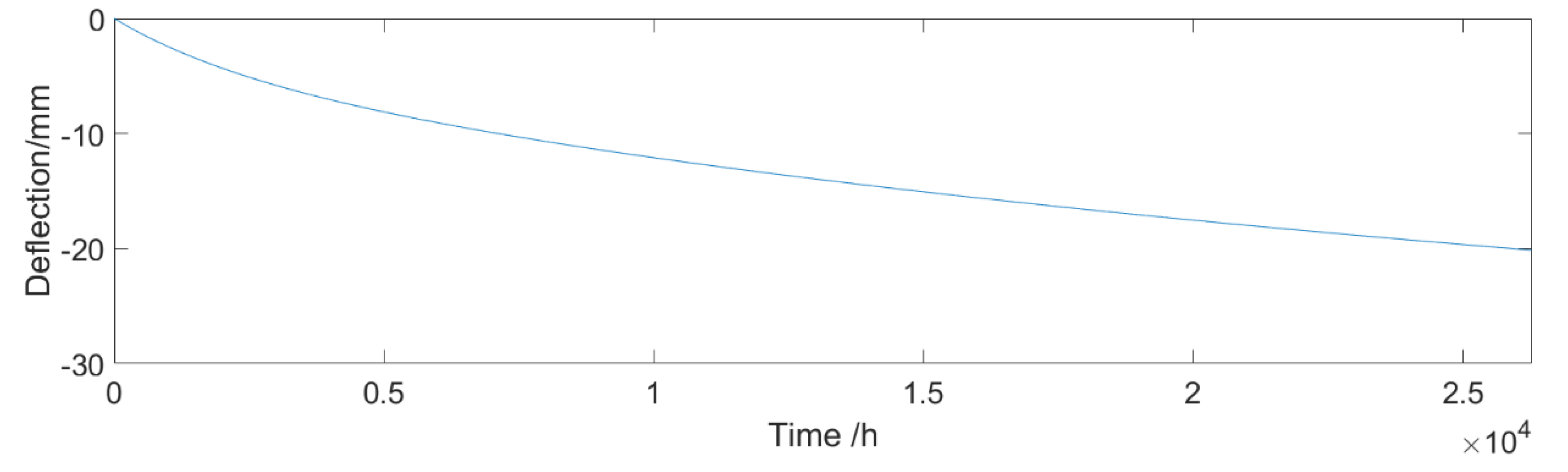
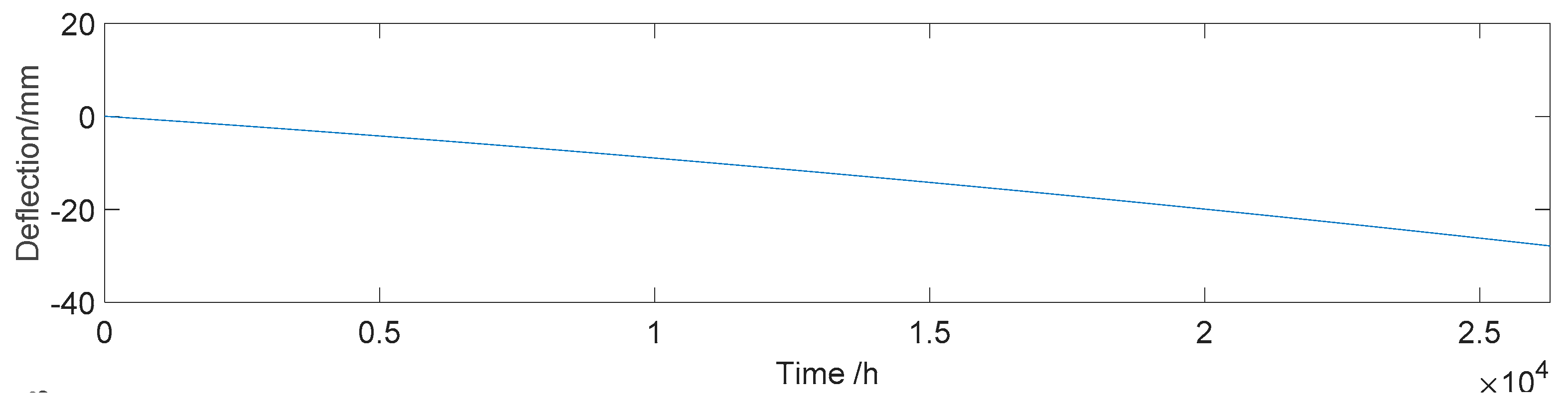
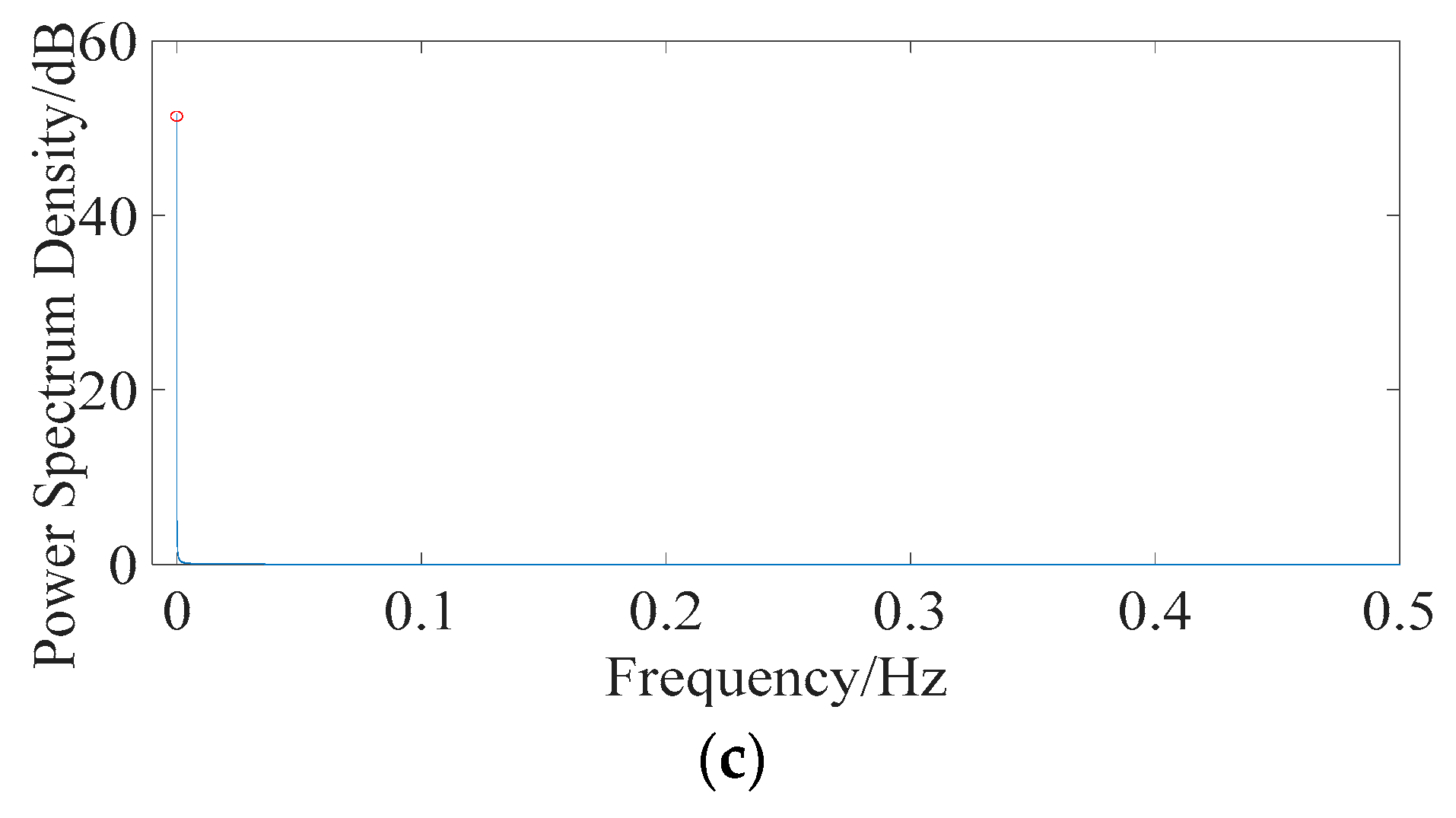
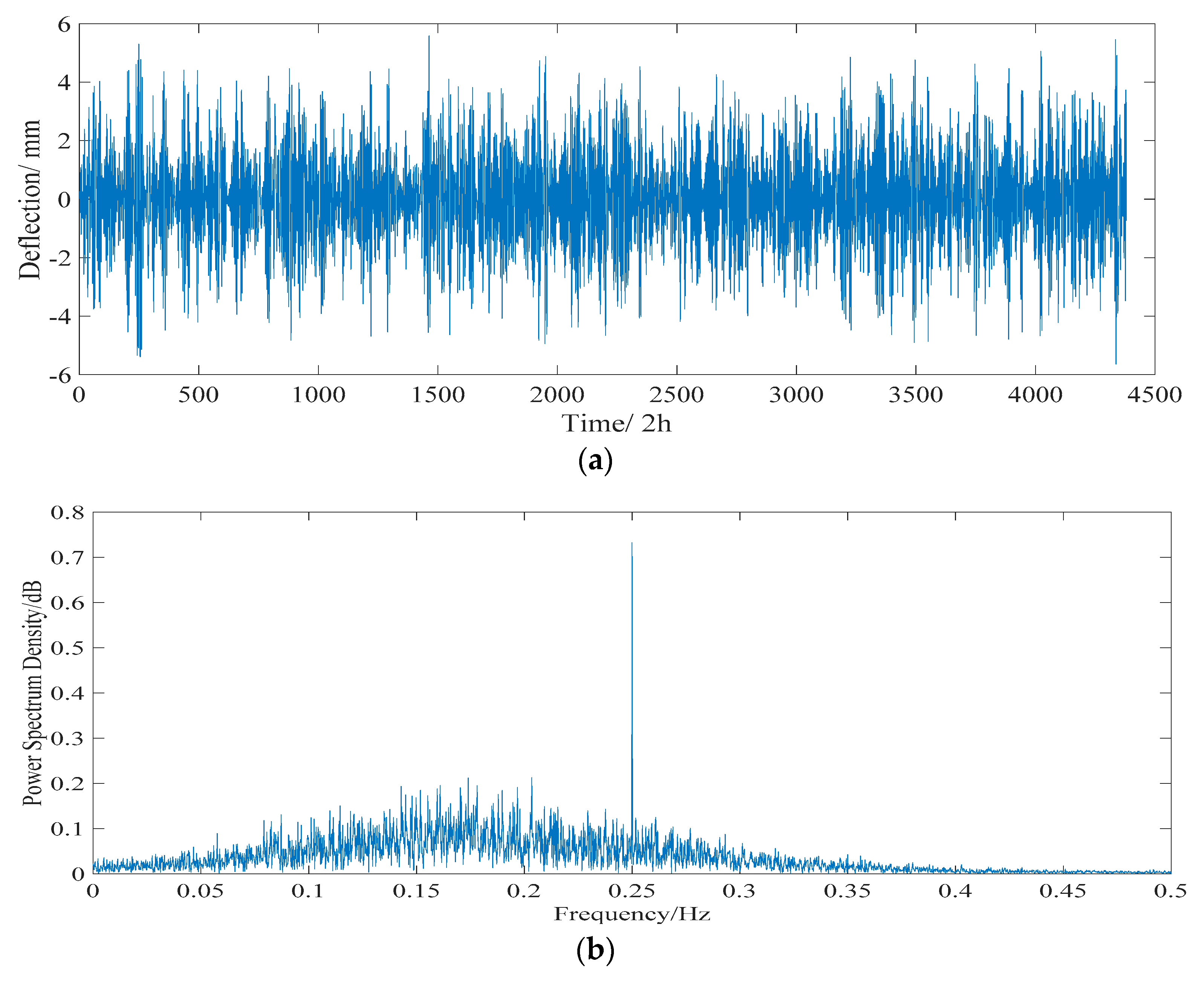
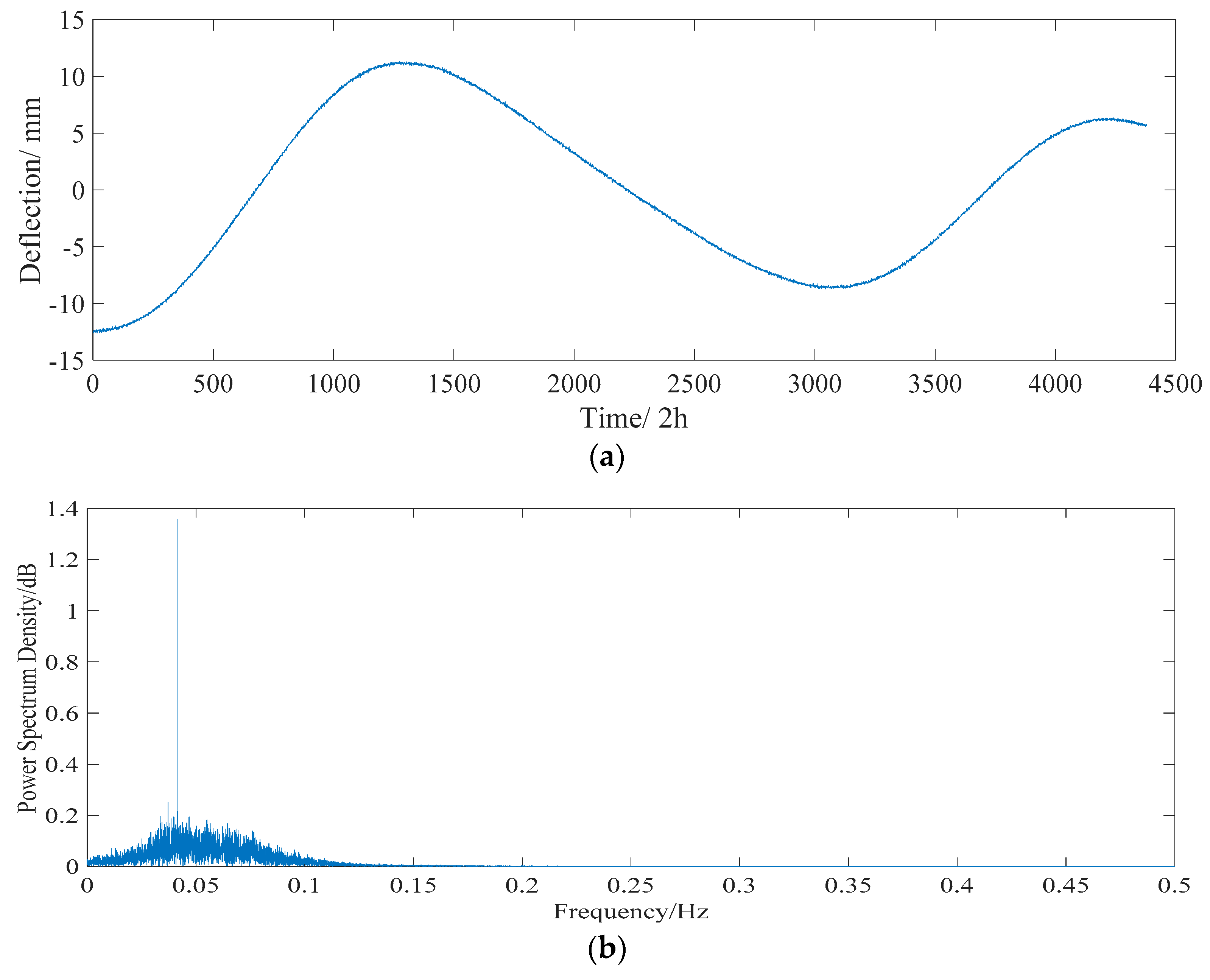
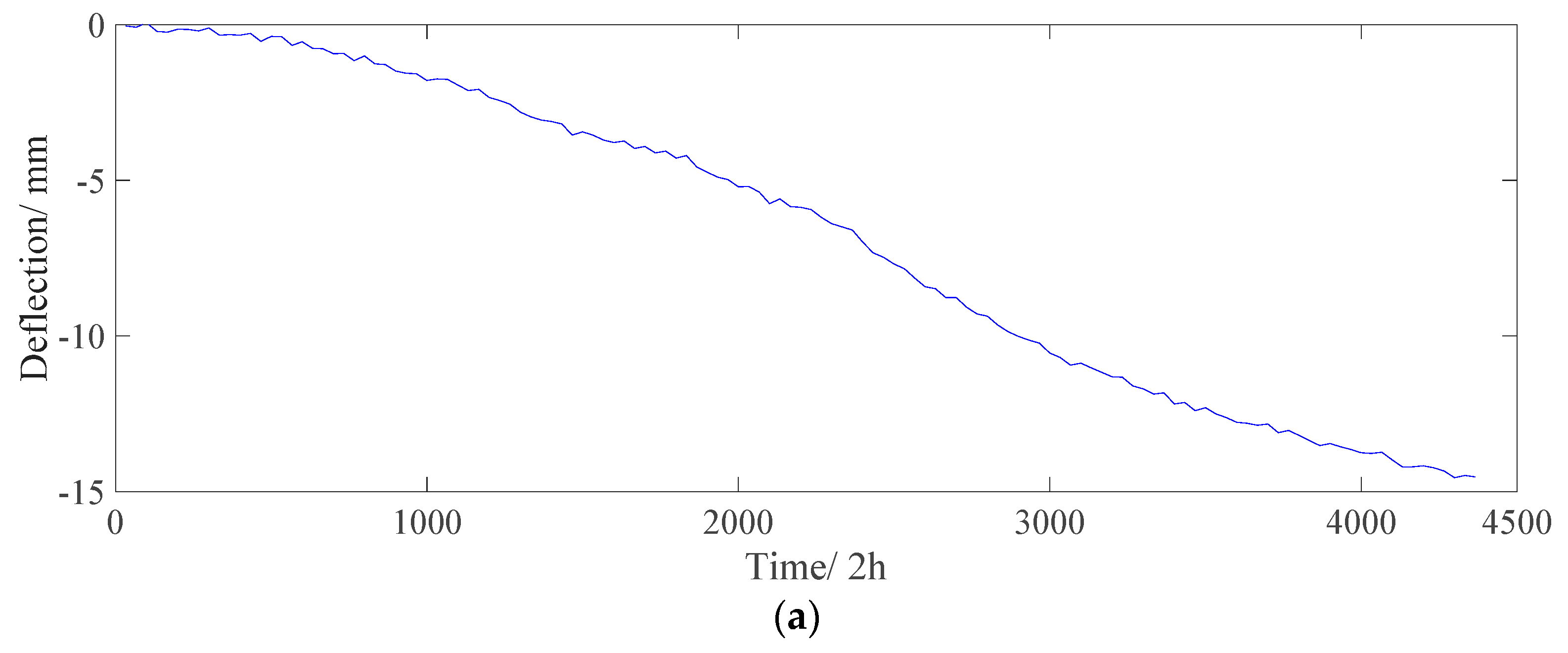
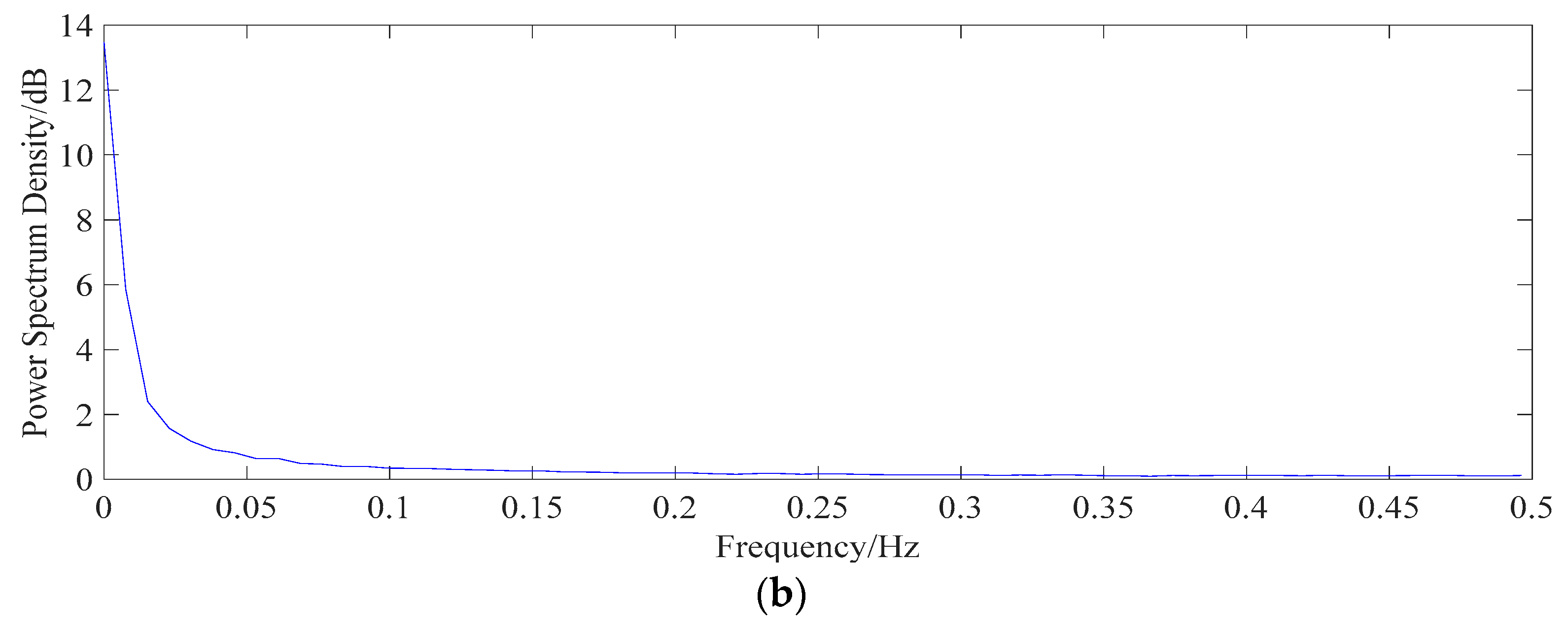
| Effects | Frequency Domain | |||
|---|---|---|---|---|
| Low | Medium | High | ||
| Live loads | DL | |||
| Daily temperature variation (DT1) | DT | |||
| Annual temperature variation (DT2) | ||||
| creep | Dv | |||
| shrinkage | ||||
| material deterioration | ||||
| noise | - | |||
| Noise Level (SNR) | Daily Temperature Effect DT1 | Annual Temperature Deflection Effect DT2 | Structural Deflection DV |
|---|---|---|---|
| 5% | 0.921 | 0.937 | 0.916 |
| 10% | 0.822 | 0.837 | 0.804 |
| 15% | 0.691 | 0.728 | 0.703 |
| 20% | 0.413 | 0.506 | 0.398 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, X.; Chen, X.; Lei, Y.; Fan, J.; Mei, L. An Integrated Machine Learning Algorithm for Separating the Long-Term Deflection Data of Prestressed Concrete Bridges. Sensors 2018, 18, 4070. https://doi.org/10.3390/s18114070
Ye X, Chen X, Lei Y, Fan J, Mei L. An Integrated Machine Learning Algorithm for Separating the Long-Term Deflection Data of Prestressed Concrete Bridges. Sensors. 2018; 18(11):4070. https://doi.org/10.3390/s18114070
Chicago/Turabian StyleYe, Xijun, Xueshuai Chen, Yaxiong Lei, Jiangchao Fan, and Liu Mei. 2018. "An Integrated Machine Learning Algorithm for Separating the Long-Term Deflection Data of Prestressed Concrete Bridges" Sensors 18, no. 11: 4070. https://doi.org/10.3390/s18114070
APA StyleYe, X., Chen, X., Lei, Y., Fan, J., & Mei, L. (2018). An Integrated Machine Learning Algorithm for Separating the Long-Term Deflection Data of Prestressed Concrete Bridges. Sensors, 18(11), 4070. https://doi.org/10.3390/s18114070





