Accuracy Assessment of Semi-Automatic Measuring Techniques Applied to Displacement Control in Self-Balanced Pile Capacity Testing Appliance
Abstract
1. Introduction
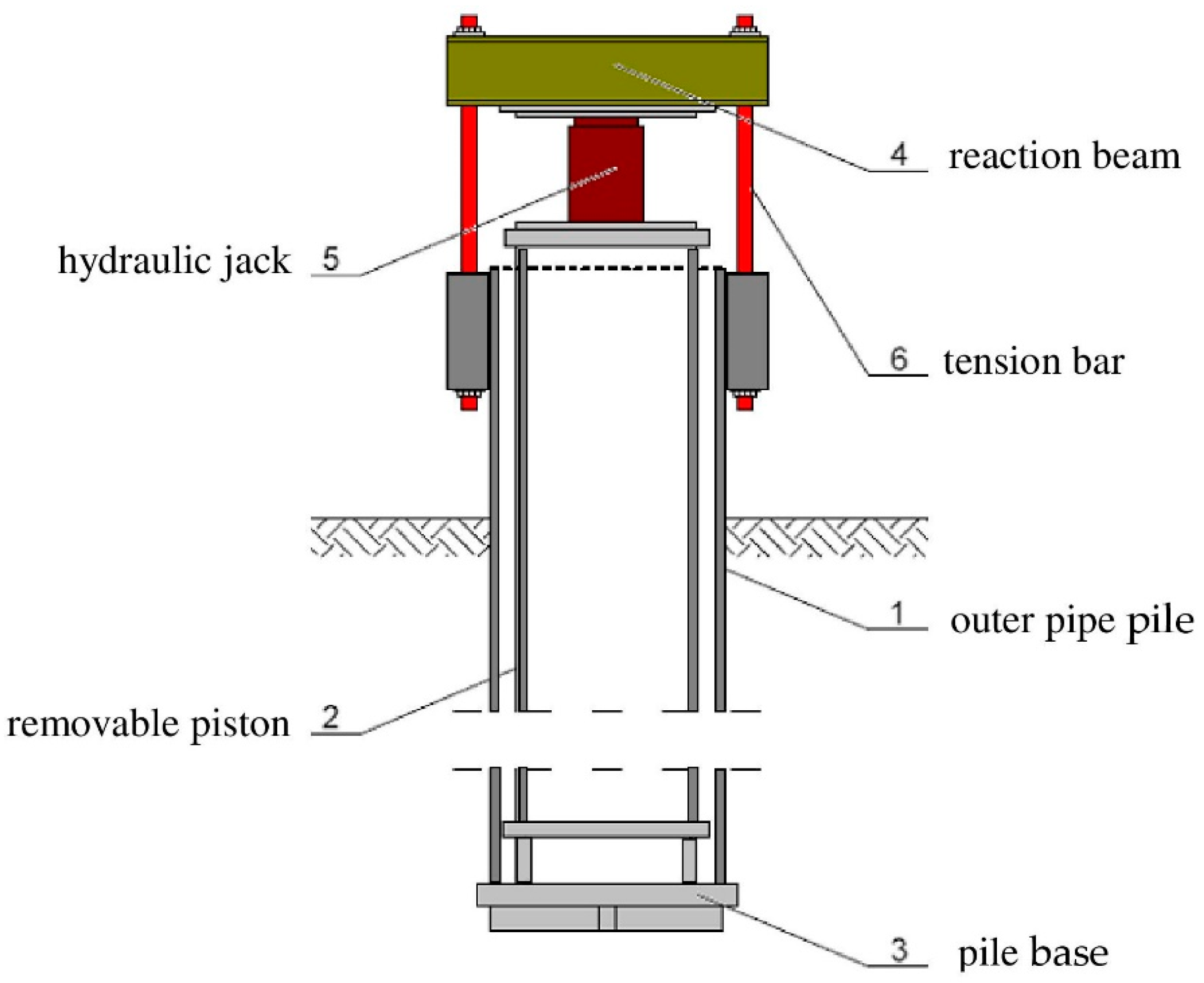
1.1. Principles of the Tubular Pile Testing Method
1.2. Principles of Independent Measuring Techniques
- providing a reference system that is not associated with a testing structure; thus allowing us to determine the values of absolute displacements;
- the possibility of acquisition of many data in a short time;
- the limitation of contact between staff and the testing structure which increases the safety of the test and eliminates the accidental movement of the gauges;
- ensuring the accuracy of the measured values, however, generally, this accuracy is lower than the one obtained from gauges.
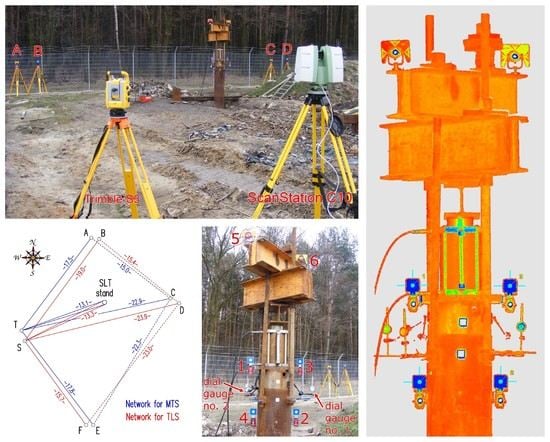
2. Materials and Methods
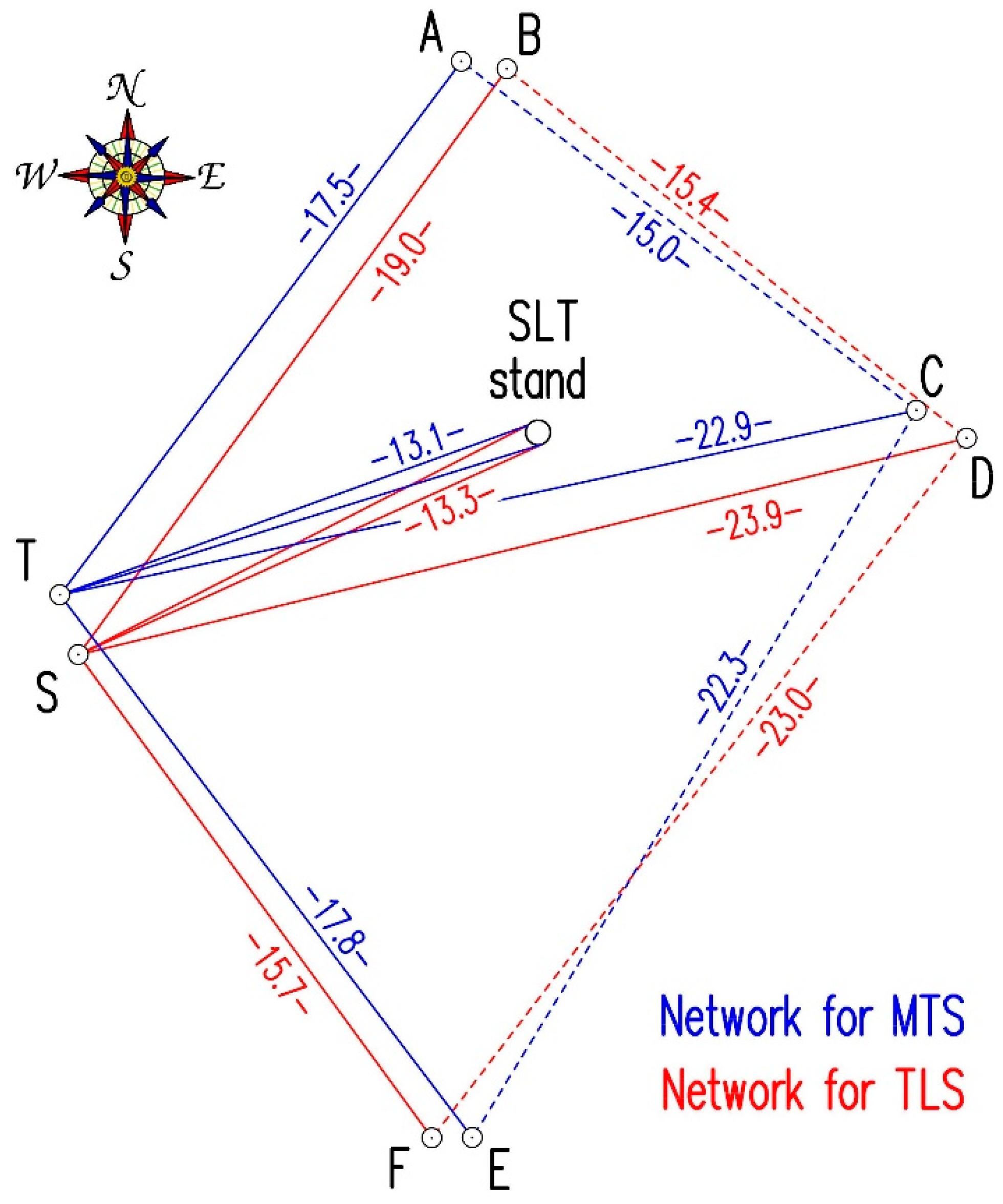
2.1. Semi-Automatic Geodetic Measuring Techniques for Determination of Displacement
2.2. Evaluation of Measurement Uncertainty
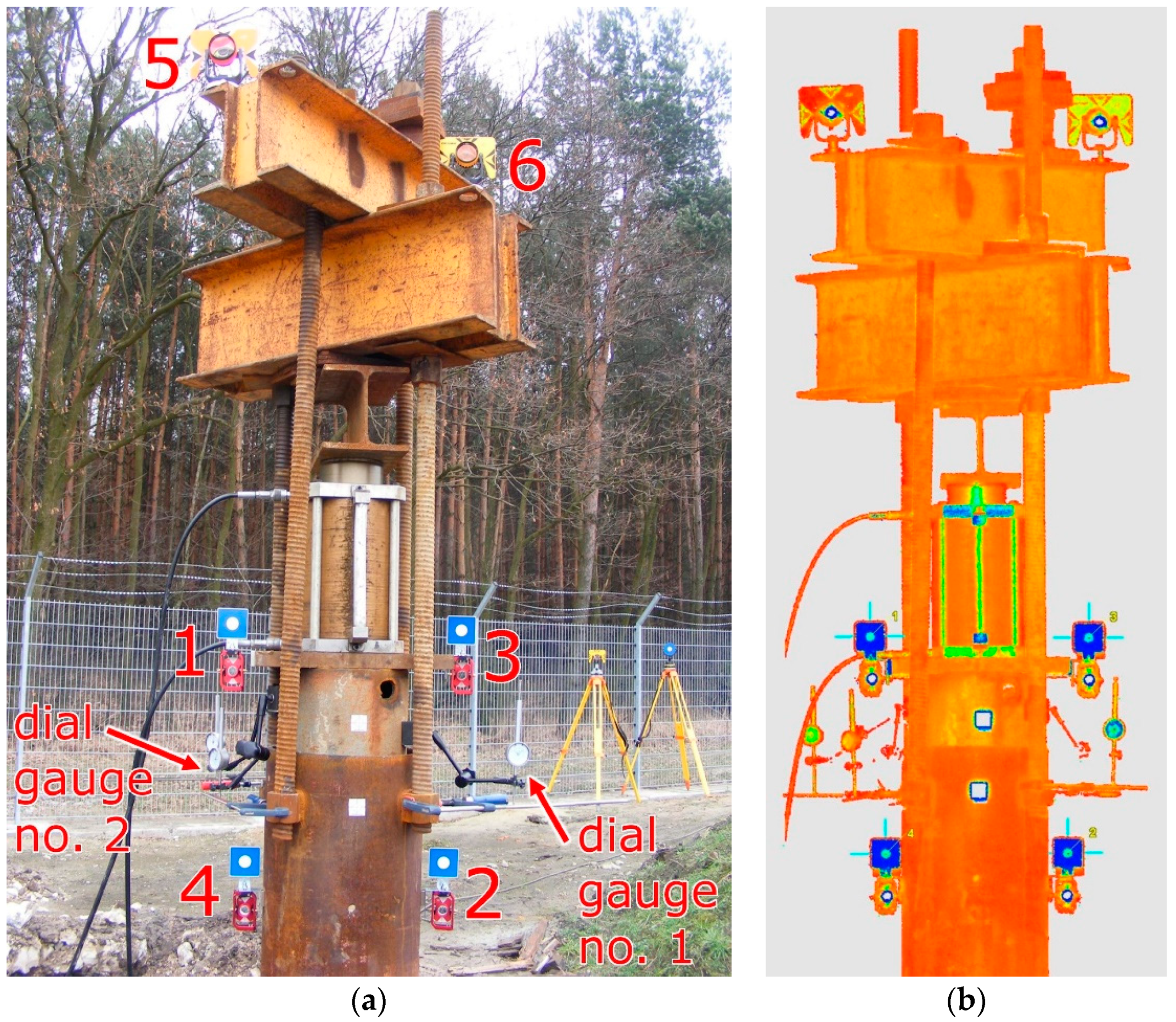
2.3. Description of Self-Balanced Pile Capacity Testing Appliance
2.4. Acquisition and Pre-Processing of Data
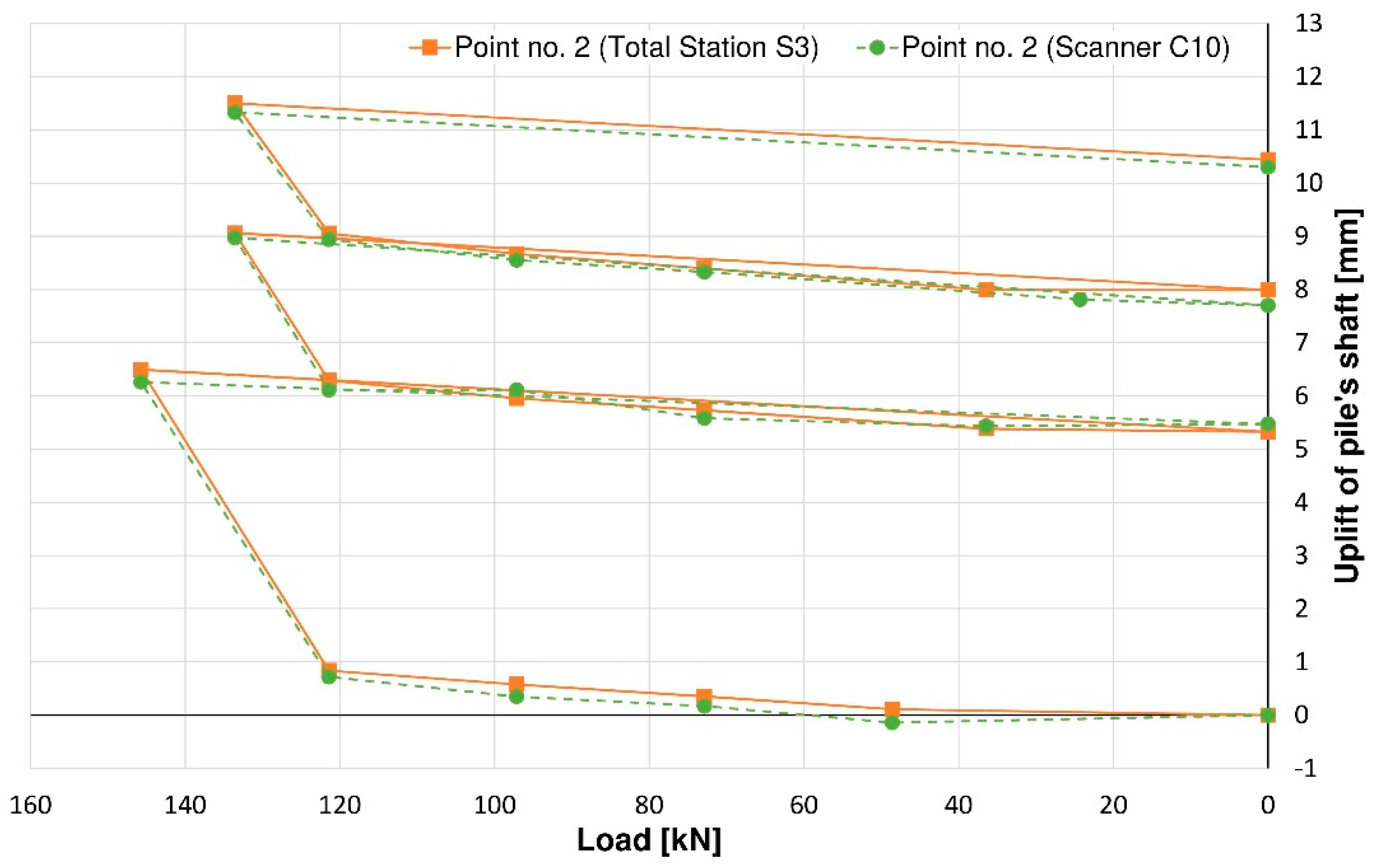
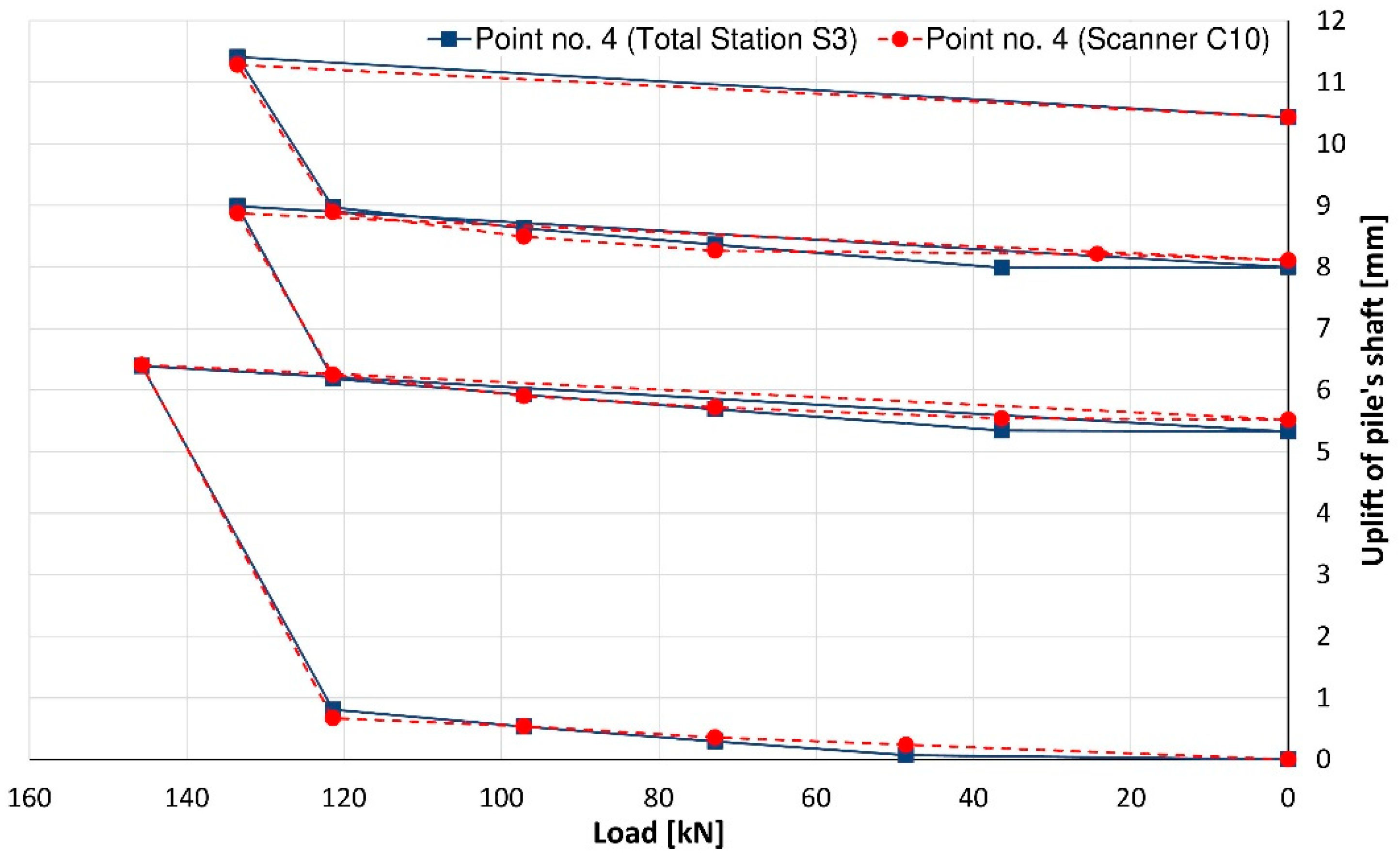
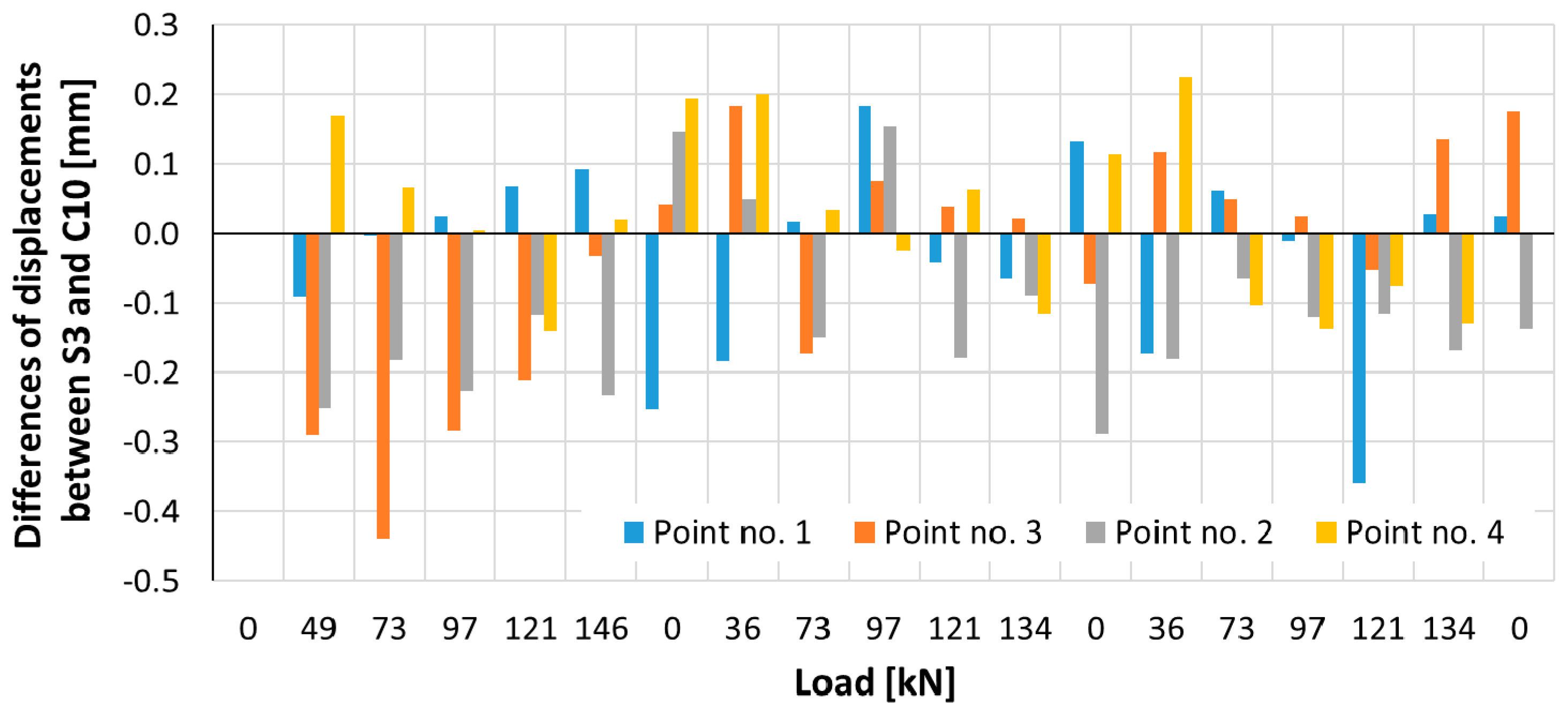
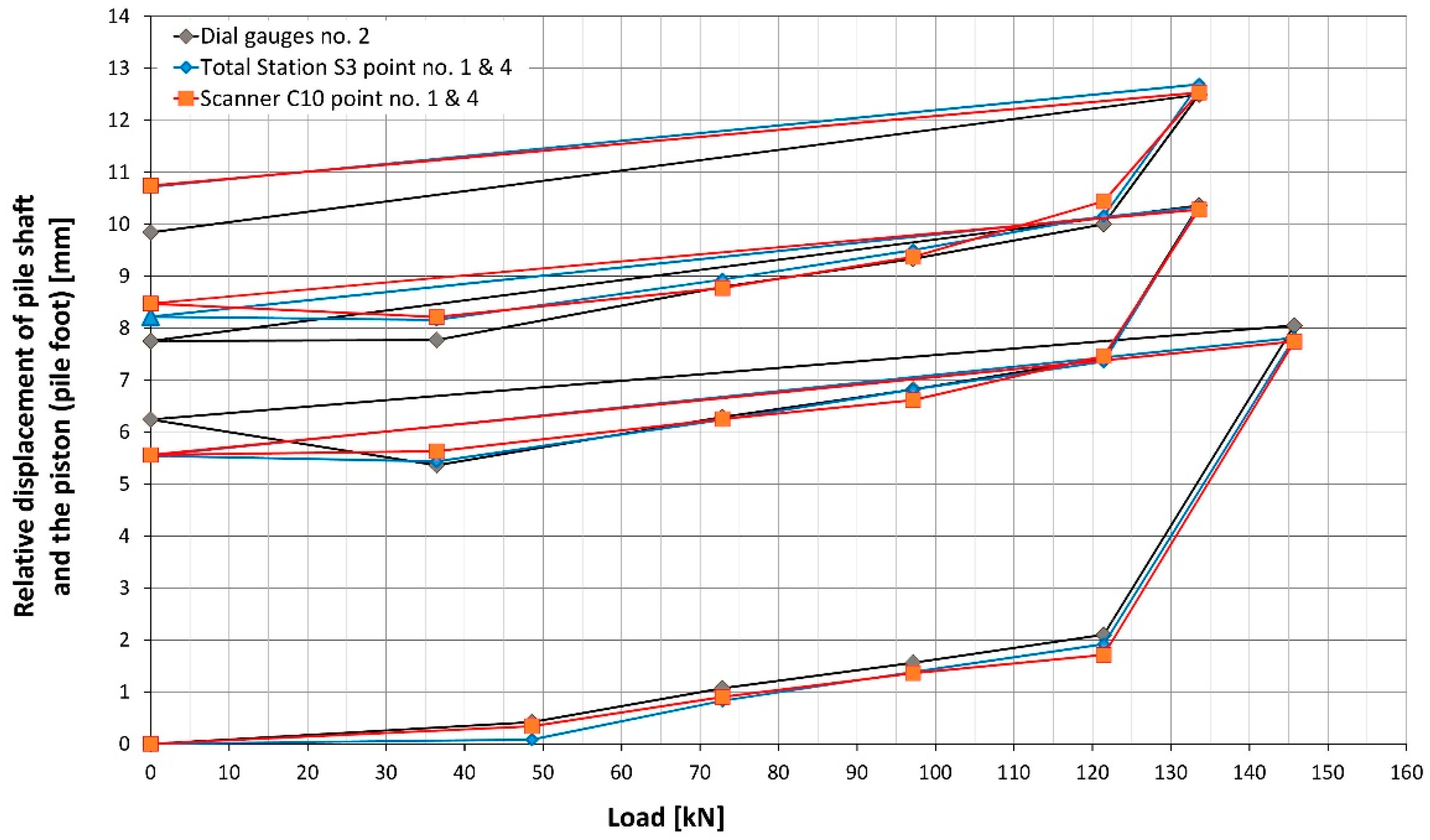
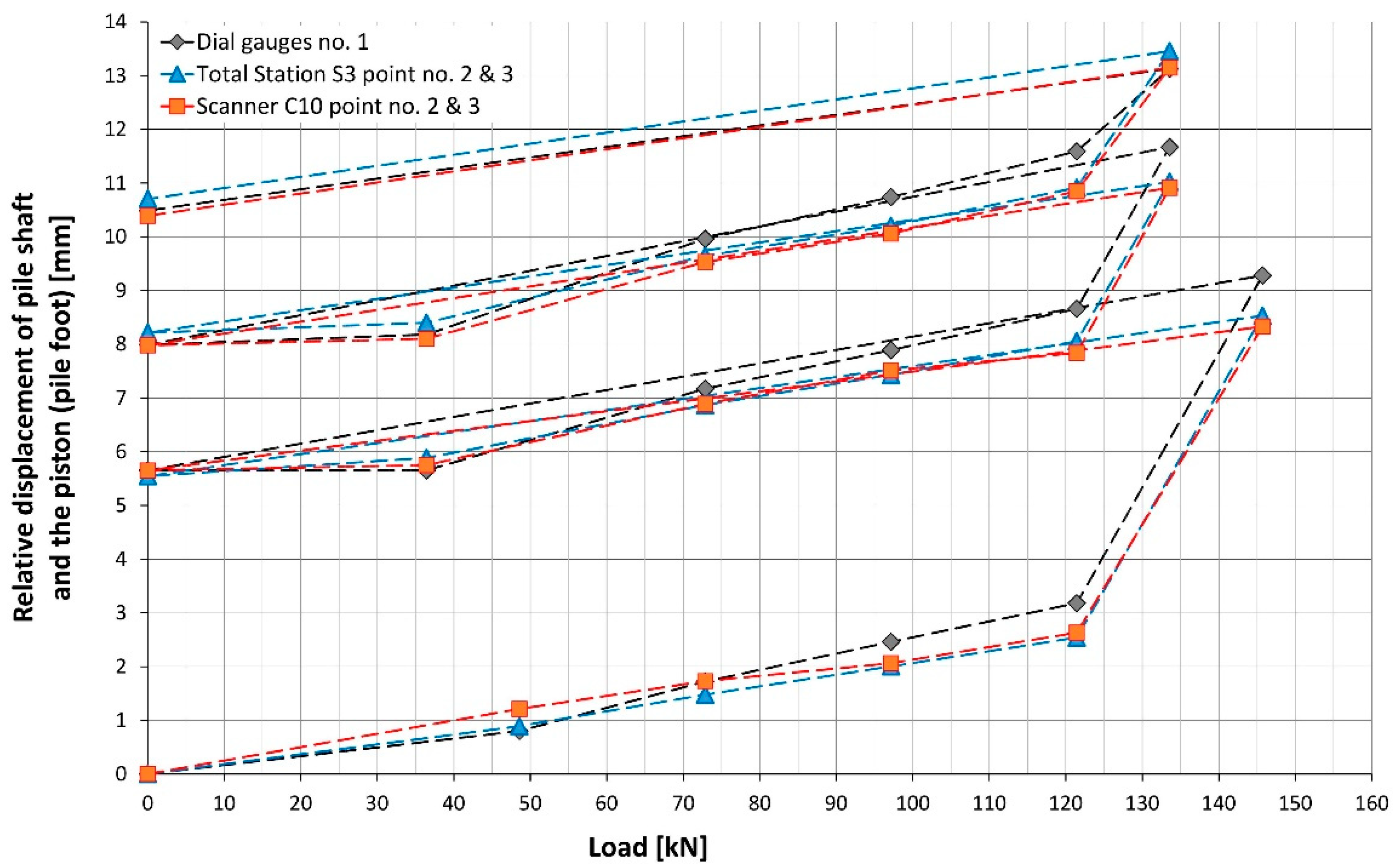
3. Results
4. Discussion
- there was some time offset which cannot be eliminated between the first and second readings from the dial gauges (averaged in further calculations) and the duration of surveying measurements (3 min for the total station and 7.5 min for the scanner);
- the location of the dial gauges and geodetic prisms/targets was slightly offset due to the limited amount of available space;
- during the unloading of the test stand and during the first reloading step, the internal pipe may tilt slightly, which may disturb the correct registration of relative displacement by dial gauges. The presented geodetic methods also enable the registration of the horizontal displacements of the loading appliance.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kozubal, J.; Pula, W.; Wyjadlowski, M.; Bauer, J. Influence of varying soil properties on evaluation of pile reliability under lateral loads. J. Civ. Eng. Manag. 2013, 19, 272–284. [Google Scholar] [CrossRef]
- Zhussupbekov, A.; Omarov, A.; Zhukenova, G.; Tanyrbergenova, G. Pile Foundations of Mega Projects: New Railway Station and LRT in Problematical Soil Ground of Astana. In Procedia Engineering, Proceedings of the International Scientific Conference Transportation Geotechnics and Geoecology (TGG 2017), St. Petersburg, Russia, 17 May 2017; Elsevier Ltd.: Amsterdam, The Netherlands, 2017; pp. 511–518. [Google Scholar]
- Liu, C.; Soltani, H.; Muraleetharan, K.K.; Cerato, A.B.; Miller, G.A.; Sritharan, S. Cyclic and seismic response of single piles in improved and unimproved soft clays. Acta Geotech. 2016, 11, 1431–1444. [Google Scholar] [CrossRef]
- Zhang, B.-J.; Huang, B.; Mei, C.; Fu, X.-D.; Luo, G.; Yang, Z.-J. Dynamic Behaviours of a Single Soft Rock-Socketed Shaft Subjected to Axial Cyclic Loading. Adv. Mater. Sci. Eng. 2016, 2016, 7457086. [Google Scholar] [CrossRef]
- Muszyński, Z.; Rybak, J. Some remarks on geodetic survey methods application in displacement measurements and capacity testing of injected and driven piles. In Proceedings of the 14th International Multidisciplinary Scientific Geoconference and EXPO (SGEM 2014), Albena, Bulgaria, 17–26 June 2014; pp. 451–458. [Google Scholar]
- Baca, M.; Muszyński, Z.; Rybak, J.; Zyrek, T. The application of geodetic methods for displacement control in the self-balanced pile capacity testing instrument. In Advances and Trends in Engineering Sciences and Technologies, Proceedings of the International Conference on Engineering Sciences and Technologies (ESaT 2015), Tatranská Štrba, High Tatras Mountains, Slovak Republic, 27–29 May 2015; Ali, M.A., Platko, P., Eds.; CRC Press/Balkema: Leiden, The Netherlands, 2016; pp. 15–20. [Google Scholar]
- Muszyński, Z.; Rybak, J. Horizontal Displacement Control in Course of Lateral Loading of a Pile in a Slope. In IOP Conference Series: Materials Science and Engineering, Proceedings of the World Multidisciplinary Civil Engineering-Architecture-Urban Planning Symposium 2017 (WMCAUS 2017), Prague, Czech Republic, 12–16 June 2017; Drusa, M., Yilmaz, I., Marschalko, M., Coisson, E., Rybak, J., Segalini, A., Eds.; Institute of Physics Publishing: Bristol, UK, 2017. [Google Scholar] [CrossRef]
- Muszyński, Z. Assessment of suitability of terrestrial laser scanning for determining horizontal displacements of cofferdam during modernization works on the redzin sluice. In Proceedings of the 14th International Multidisciplinary Scientific Geoconference and EXPO (SGEM 2014), Albena, Bulgaria, 17–26 June 2014; pp. 81–88. [Google Scholar]
- Muszyński, Z.; Rybak, J. Evaluation of Terrestrial Laser Scanner Accuracy in the Control of Hydrotechnical Structures. Stud. Geotech. Mech. 2017, 39, 45–57. [Google Scholar] [CrossRef]
- Bauer, J.; Kozubal, J.; Puła, W.; Wyjadłowski, M. Application of HDMR method to reliability assessment of a single pile subjected to lateral load. Studia Geotechnica Mechanica 2012, 34, 37–51. [Google Scholar] [CrossRef]
- Cui, Y.; Chu, X.-G.; Dong, J.; Jin, Y.-Q.; Tan, D.-S. Prediction research on the vertical bearing capacity of pile foundation based on neural network. J. Railw. Eng. Soc. 2016, 33, 65–69. [Google Scholar]
- Rybak, J. Some Remarks on Foundation Pile Testing Procedures. In IOP Conference Series: Materials Science and Engineering, Proceedings of the World Multidisciplinary Civil Engineering-Architecture-Urban Planning Symposium 2017 (WMCAUS 2017), Prague, Czech Republic, 12–16 June 2017; Marschalko, M., Drusa, M., Rybak, J., Yilmaz, I., Segalini, A., Coisson, E., Eds.; Institute of Physics Publishing: Bristol, UK, 2017. [Google Scholar] [CrossRef]
- Rybak, J.; Król, M. Limitations and risk related to static capacity testing of piles—“unfortunate case” studies. In MATEC Web of Conferences, Proceedings of the 9th International Conference Building Defects, Building Defects 2017, České Budějovice, Czech Republic, 23–24 November 2017; Juhasova Senitkova, I., Ed.; EDP Sciences: Julius, France, 2018. [Google Scholar] [CrossRef]
- Rybak, J.; Baca, M.; Zyrek, T. Practical aspects of tubular pile axial capacity testing, International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management, SGEM. In Proceedings of the 15th International Multidisciplinary Scientific Geoconference and EXPO (SGEM 2015), Albena, Bulgaria, 18–24 June 2015; pp. 549–554. [Google Scholar]
- Baca, M.; Muszyński, Z.; Rybak, J.; Zyrek, T.; Tamrazyan, A.G. Cyclic load tests of driven pile base capacity. In Advances and Trends in Engineering Sciences and Technologies II, Proceedings of the 2nd International Conference on Engineering Sciences and Technologies (ESaT 2016), High Tatras Mountains, Tatranské Matliare, Slovak Republic, 29 June–1 July 2016; Al Ali, M., Platko, P., Eds.; CRC Press/Balkema: Leiden, The Netherlands, 2017; pp. 723–728. [Google Scholar]
- Baca, M.; Brzakala, W. Numerical modeling of pile installation influence on surrounding soil. In Proceedings of the 17th International Multidisciplinary Scientific Geoconference (SGEM 2017), Albena, Bulgaria, 29 June–5 July 2017; pp. 619–626. [Google Scholar]
- England, M. Review of methods of analysis of test results from bi-directional static load tests. In Proceedings of the 5th International Symposium on Deep Foundations on Bored and Auger Piles (BAP V), Ghent, Belgium, 8–10 September 2008; pp. 235–239. [Google Scholar]
- Muszyński, Z.; Rybak, J.; Szot, A. Monitoring of structures adjacent to deep excavations. In Underground Infrastructure of Urban Areas 2; CRC Press/Balkema: Leiden, The Netherlands, 2011; pp. 168–174. [Google Scholar]
- Ma, L.; Wang, L.; Guo, Z.; Jiang, H.; Gao, Y. Time development of scour around pile groups in tidal currents. Ocean Eng. 2018, 163, 400–418. [Google Scholar] [CrossRef]
- Gazetas, G.; Zarzouras, O.; Drosos, V.; Anastasopoulos, I. Bridge-Pier Caisson foundations subjected to normal and thrust faulting: Physical experiments versus numerical analysis. Meccanica 2014, 50, 341–354. [Google Scholar] [CrossRef]
- Park, S.W.; Oh, B.K.; Park, H.S. Terrestrial laser scanning-based stress estimation model using multi-dimensional double layer lattices. Integr. Comput. Aided Eng. 2017, 24, 367–383. [Google Scholar] [CrossRef]
- Olsen, M.J. In situ change analysis and monitoring through terrestrial laser scanning. J. Comput. Civ. Eng. 2015, 29. [Google Scholar] [CrossRef]
- Marino, G. Analysis of Performance of Automatic Target Recognition Systems. Ph.D. Thesis, Cranfield University, Bedford, UK, 2011. [Google Scholar]
- Roy, D.S.; Gouvin, P. Applications and limitations of automated motorized total stations. In Proceedings of the 7th International Symposium on Field Measurements in Geomechanics (FMGM 2007), Boston, MA, USA, 24–27 September 2007; p. 103. [Google Scholar]
- Chmelina, K.; Jansa, J.; Hesina, G.; Traxler, C. A 3-d laser scanning system and scan data processing method for themonitoring of tunnel deformations. J. Appl. Geod. 2012, 6, 177–185. [Google Scholar] [CrossRef]
- Wang, H.; Liu, X.; Yuan, X.; Liang, D. Multi-perspective terrestrial LiDAR point cloud registration using planar primitives. In International Geoscience and Remote Sensing Symposium (IGARSS), Proceedings of the 36th IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2016), Beijing, China, 10–15 July 2016; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA; pp. 6722–6725.
- Fan, L.; Smethurst, J.A.; Atkinson, P.M.; Powrie, W. Error in target-based georeferencing and registration in terrestrial laser scanning. Comput. Geosci. 2015, 83, 54–64. [Google Scholar] [CrossRef]
- Pandžic, J.; Pejic, M.; Božic, B.; Eric, V. Error model of direct georeferencing procedure of terrestrial laser scanning. Autom. Constr. 2017, 78, 13–23. [Google Scholar] [CrossRef]
- Osada, E.; Sośnica, K.; Borkowski, A.; Owczarek-Wesołowska, M.; Gromczak, A. A Direct Georeferencing Method for Terrestrial Laser Scanning Using GNSS Data and the Vertical Deflection from Global Earth Gravity Models. Sensors 2017, 17, 1489. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Yao, W.; Polewski, P. Mapping individual tree species and vitality along urban road corridors with LiDAR and imaging sensors: Point density versus view perspective. Remote Sens. 2018, 10, 1403. [Google Scholar] [CrossRef]
- Amiri, N.; Heurich, M.; Krzystek, P.; Skidmore, A.K. Feature relevance assessment of multispectral airborne LiDAR data for tree species classification, International Archives of the Photogrammetry. In Remote Sensing and Spatial Information Sciences—ISPRS Archives, Proceedings of the 2018 ISPRS TC III Mid-Term Symposium on Developments, Technologies and Applications in Remote Sensing, Beijing, China, 7–10 May 2018; Liang, X., Osmanoglu, B., Soergel, U., Honkavaara, E., Scaioni, M., Peled, A., Shaker, A., Wu, L., Abdulmuttalib, H.M., Zhang, H., et al., Eds.; International Society for Photogrammetry and Remote Sensing: Christian Heipke, Germany, 2018; pp. 31–34. [Google Scholar]
- Pearse, G.D.; Dash, J.P.; Persson, H.J.; Watt, M.S. Comparison of high-density LiDAR and satellite photogrammetry for forest inventory. ISPRS J. Photogramm. Remote Sens. 2018, 142, 257–267. [Google Scholar] [CrossRef]
- Gonzalez de Tanago, J.; Lau, A.; Bartholomeus, H.; Herold, M.; Avitabile, V.; Raumonen, P.; Martius, C.; Goodman, R.C.; Disney, M.; Manuri, S.; et al. Estimation of above-ground biomass of large tropical trees with terrestrial LiDAR. Methods Ecol. Evol. 2018, 9, 223–234. [Google Scholar] [CrossRef]
- Polat, N.; Uysal, M. An Experimental Analysis of Digital Elevation Models Generated with Lidar Data and UAV Photogrammetry. J. Indian Soc. Remote Sens. 2018, 46, 1135–1142. [Google Scholar] [CrossRef]
- Salach, A.; Bakula, K.; Pilarska, M.; Ostrowski, W.; Górski, K.; Kurczynski, Z. Accuracy assessment of point clouds from LidaR and dense image matching acquired using the UAV platform for DTM creation. ISPRS Int. J. Geo Inf. 2018, 7, 342. [Google Scholar] [CrossRef]
- Zheng, X.; Xiao, C. Typical applications of airborne lidar technolagy in geological investigation, International Archives of the Photogrammetry. In Remote Sensing and Spatial Information Sciences—ISPRS Archives, Proceedings of the 2018 ISPRS TC III Mid-Term Symposium on Developments, Technologies and Applications in Remote Sensing, Beijing, China, 7–10 May 2018; Liang, X., Osmanoglu, B., Soergel, U., Honkavaara, E., Scaioni, M., Peled, A., Shaker, A., Wu, L., Abdulmuttalib, H.M., Zhang, H., Di, K., et al., Eds.; International Society for Photogrammetry and Remote Sensing: Christian Heipke, Germany, 2018; pp. 2459–2463. [Google Scholar]
- Wu, H.; Xu, X.; Zheng, F.; Qin, C.; He, X. Gully morphological characteristics in the loess hilly-gully region based on 3D laser scanning technique. Earth Surf. Process. Landf. 2018, 43, 1701–1710. [Google Scholar] [CrossRef]
- Goodwin, N.R.; Armston, J.D.; Muir, J.; Stiller, I. Monitoring gully change: A comparison of airborne and terrestrial laser scanning using a case study from Aratula, Queensland. Geomorphology 2017, 282, 195–208. [Google Scholar] [CrossRef]
- Invernizzi, S.; Spanò, A.; Chiabrando, F. Survey, Assessment and Conservation of Post-industrial Cultural Heritage: The Case of the Thin Concrete Vault in Casale, Italy. In Structural Analysis of Historical Constructions; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Kedzierski, M.; Fryskowska, A. Methods of laser scanning point clouds integration in precise 3D building modelling. Measurement 2015, 74, 221–232. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Q.; Liu, L.; Li, X.; Sangaiah, A.K.; Li, K. Systematic comparison of power line classification methods from ALS and MLS point cloud data. Remote Sens. 2018, 10, 1222. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, X. Tunnel Deformation Analysis Based on Lidar Points. Chin. J. Lasers. 2018, 45. [Google Scholar] [CrossRef]
- Muszyński, Z.; Milczarek, W. Application of Terrestrial Laser Scanning to Study the Geometry of Slender Objects. In IOP Conference Series: Earth and Environmental Science, Proceedings of the 3rd World Multidisciplinary Earth Sciences Symposium (WMESS 2017), Prague, Czech Republic, 11–15 September 2017; Drusa, M., Torok, I., Ferrero, A.M., Yilmaz, I., Marschalko, M., Karaca, O., Eds.; Institute of Physics Publishing: Bristol, UK, 2017. [Google Scholar] [CrossRef]
- EA Laboratory Committee. Evaluation of the Uncertainty of Measurement in Calibration; EA-4/02 M; European Co-operation for Accreditation: Paris, Fance, 2013. [Google Scholar]
- Polish Committee for Standardization (PKN). Optics and Optical Instruments—Field Procedures for Testing Geodetic and Surveying Instruments—Part 3: Theodolites (in Polish); PN-ISO 17123:3-2005; PKN: Warsaw, Poland, 2005. [Google Scholar]
- Taylor, J.R. An Introduction to Error Analysis, 2nd ed.; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Osterberg, J.O. The Osterberg load test method for bored and driven piles the first ten years. In Proceedings of the Seventh International Conference & Exhibition on Piling and Deep Foundations, Vienna, Austria, 15–17 June 1998; pp. 1–17. [Google Scholar]
- Schmertmann, J.H.; Hayes, J.A. The Osterberg cell and bored pile testing—A symbiosis. In Proceedings of the 3rd International Geotechnical Engineering Conference, Cairo, Egypt, 5–8 January 1997; pp. 3–12. [Google Scholar]





| Step No. | Load (kN) | Time of Load Application and Delay in Starting Geodetic Meas. and First Readings of Dial Gauges | Duration of Geodetic Measurements S3/C10 | Delay in the Second Reading of the Dial Gauges | Remarks |
|---|---|---|---|---|---|
| 1 | 0 | 13:22 + 1 min | 3 min/7.5 min | - | |
| 2 | 49 | 13:25 + 1 min | 3 min/7.5 min | +7 min | |
| 3 | 73 | 13:34 + 1 min | 3 min/7.5 min | +8 min | |
| 4 | 97 | 13:43 + 1 min | 3 min/7.5 min | +8 min | |
| 5 | 121 | 13:51 + 1 min | 3 min/7.5 min | +9 min | |
| 6 | 146 | 14:19 + 1 min | 3 min/7.5 min | +8 min | |
| 7 | 0 | 14:30 + 1 min | 3 min/7.5 min | +8 min | unloading |
| 8 | 36 | 14:41 + 1 min | 3 min/7.5 min | +25 min | battery change |
| 9 | 73 | 15:08 + 1 min | 3 min/7.5 min | +8 min | |
| 10 | 97 | 15:17 + 1 min | 3 min/7.5 min | +7 min | |
| 11 | 121 | 15:25 + 1 min | 3 min/7.5 min | +8 min | |
| 12 | 134 | 15:43 + 1 min | 3 min/7.5 min | +9 min | |
| 13 | 0 | 15:53 + 1 min | 3 min/7.5 min | +13 min | unloading |
| 14 | 36 | 16:07 + 1 min | 3 min/7.5 min | +9 min | |
| 15 | 73 | 16:17 + 1 min | 3 min/7.5 min | +7 min | |
| 16 | 97 | 16:25 + 1 min | 3 min/7.5 min | +7 min | |
| 17 | 121 | 16:33 + 1 min | 3 min/7.5 min | 7 min | |
| 18 | 134 | 16:51 + 1 min | 3 min/7.5 min | +8 min | |
| 19 | 0 | 17:00 + 1 min | 3 min/7.5 min | +10 min | unloading |
| Load | Total Station S3 | Scanner C10 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| mx | my | mt | sh | dh | mx | my | mt | sh | dh | |
| (kN) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) |
| 0 | - | - | - | - | - | - | - | - | - | - |
| 49 | 0.2 | 0.1 | 0.3 | 0.1 | −0.1 | 0.5 | 0.3 | 0.6 | 0.1 | −0.2 |
| 73 | 0.2 | 0.2 | 0.3 | 0.0 | 0.0 | 0.7 | 0.5 | 0.8 | 0.1 | −0.2 |
| 97 | 0.2 | 0.1 | 0.3 | 0.1 | −0.1 | 0.6 | 0.6 | 0.9 | 0.1 | −0.2 |
| 121 | 0.3 | 0.2 | 0.3 | 0.1 | −0.1 | 0.2 | 0.3 | 0.4 | 0.1 | −0.3 |
| 146 | 0.3 | 0.2 | 0.4 | 0.0 | −0.1 | 0.3 | 0.5 | 0.6 | 0.0 | −0.3 |
| 0 | 0.3 | 0.2 | 0.3 | 0.1 | −0.1 | 0.5 | 0.3 | 0.6 | 0.1 | −0.3 |
| 36 | 0.6 | 0.3 | 0.7 | 0.0 | −0.1 | 0.7 | 0.4 | 0.9 | 0.1 | −0.2 |
| 73 | 0.3 | 0.1 | 0.3 | 0.0 | −0.1 | 0.6 | 0.5 | 0.7 | 0.1 | −0.3 |
| 97 | 0.4 | 0.2 | 0.4 | 0.0 | 0.0 | 0.5 | 0.8 | 0.9 | 0.1 | −0.4 |
| 121 | 0.4 | 0.2 | 0.4 | 0.0 | 0.0 | 0.4 | 0.5 | 0.6 | 0.1 | −0.4 |
| 134 | 0.1 | 0.4 | 0.4 | 0.0 | 0.0 | 0.5 | 0.6 | 0.8 | 0.2 | −0.3 |
| 0 | 0.5 | 0.2 | 0.6 | 0.0 | 0.0 | 0.4 | 0.5 | 0.6 | 0.1 | −0.3 |
| 36 | 0.6 | 0.3 | 0.6 | 0.0 | 0.0 | 0.5 | 0.6 | 0.8 | 0.1 | −0.3 |
| 73 | 0.3 | 0.3 | 0.4 | 0.0 | 0.0 | 0.7 | 0.4 | 0.8 | 0.1 | −0.2 |
| 97 | 0.3 | 0.1 | 0.3 | 0.0 | 0.0 | 0.7 | 0.6 | 0.9 | 0.1 | −0.2 |
| 121 | 0.2 | 0.2 | 0.3 | 0.0 | 0.0 | 0.6 | 0.8 | 1.0 | 0.2 | −0.2 |
| 134 | 0.3 | 0.2 | 0.4 | 0.0 | 0.0 | 0.9 | 0.8 | 1.2 | 0.0 | −0.2 |
| 0 | 0.5 | 0.3 | 0.5 | 0.0 | 0.0 | 0.8 | 0.8 | 1.1 | 0.2 | −0.1 |
| Instrument | Uncertainty of B type | Uncertainty of A Type | Standard Direct Uncertainty | |||
|---|---|---|---|---|---|---|
| Zenith Angle | Spatial Distance | Zenith Angle | Spatial Distance | Zenith Angle | Spatial Distance | |
| (cc) | (mm) | (cc) | (mm) | [cc] | (mm) | |
| Trimble S3 | 10.4 | 3.5 | 1.2 | 0.3 | 10.5 | 3.5 |
| Leica C10 | 66.2 | 6.9 | 0.3 | 0.4 | 66.2 | 6.9 |
| Point No. | Maximum Values of Indirect Uncertainty for Determination | |||
|---|---|---|---|---|
| Height | Vertical Displacement | Height | Vertical Displacement | |
| Trimble S3 | Leica C10 | |||
| (mm) | (mm) | (mm) | (mm) | |
| 1 | 0.2 | 0.3 | 1.4 | 1.9 |
| 2 | 0.2 | 0.3 | 1.4 | 2.0 |
| 3 | 0.2 | 0.3 | 1.4 | 2.0 |
| 4 | 0.2 | 0.3 | 1.4 | 2.0 |
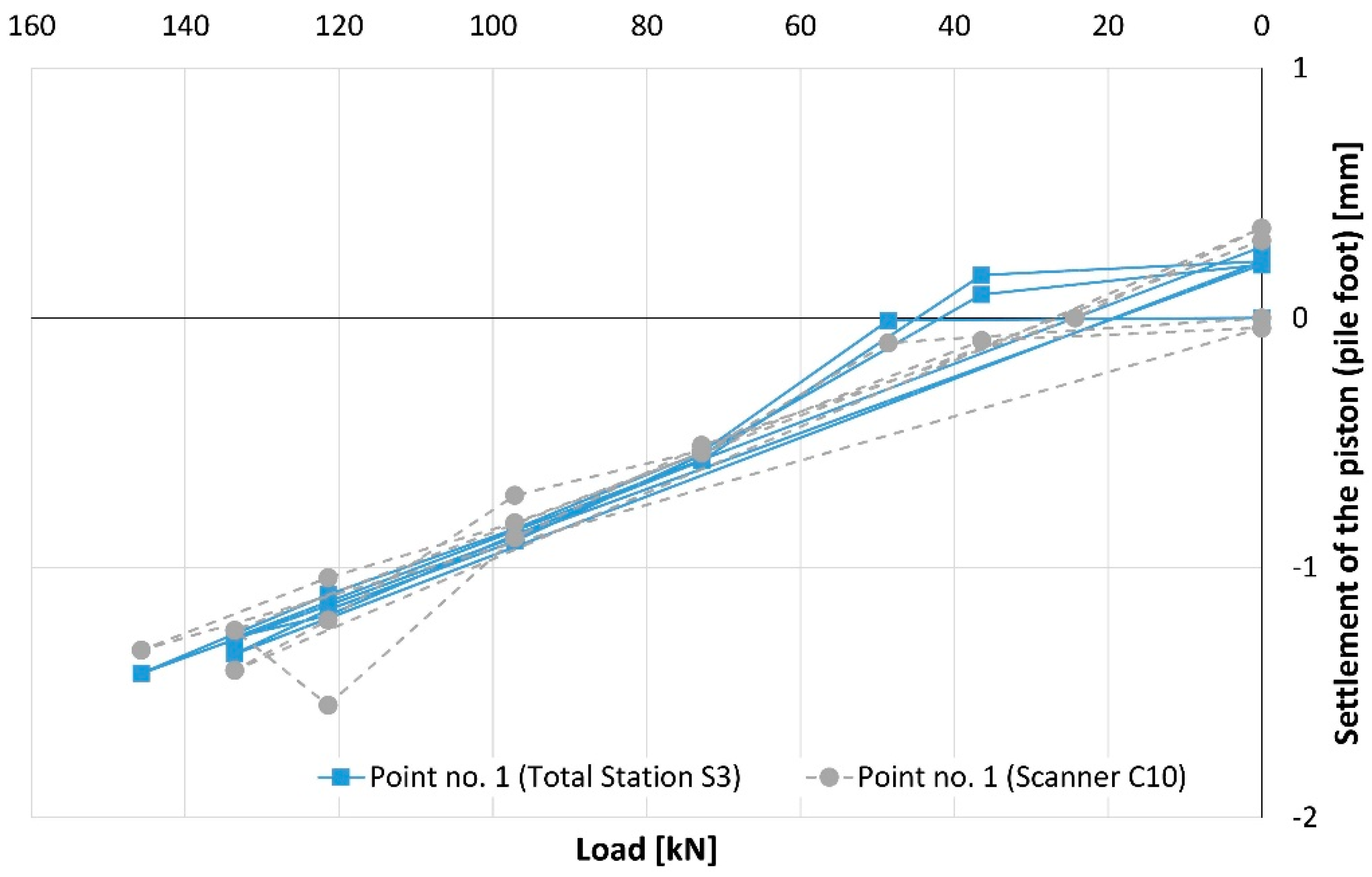
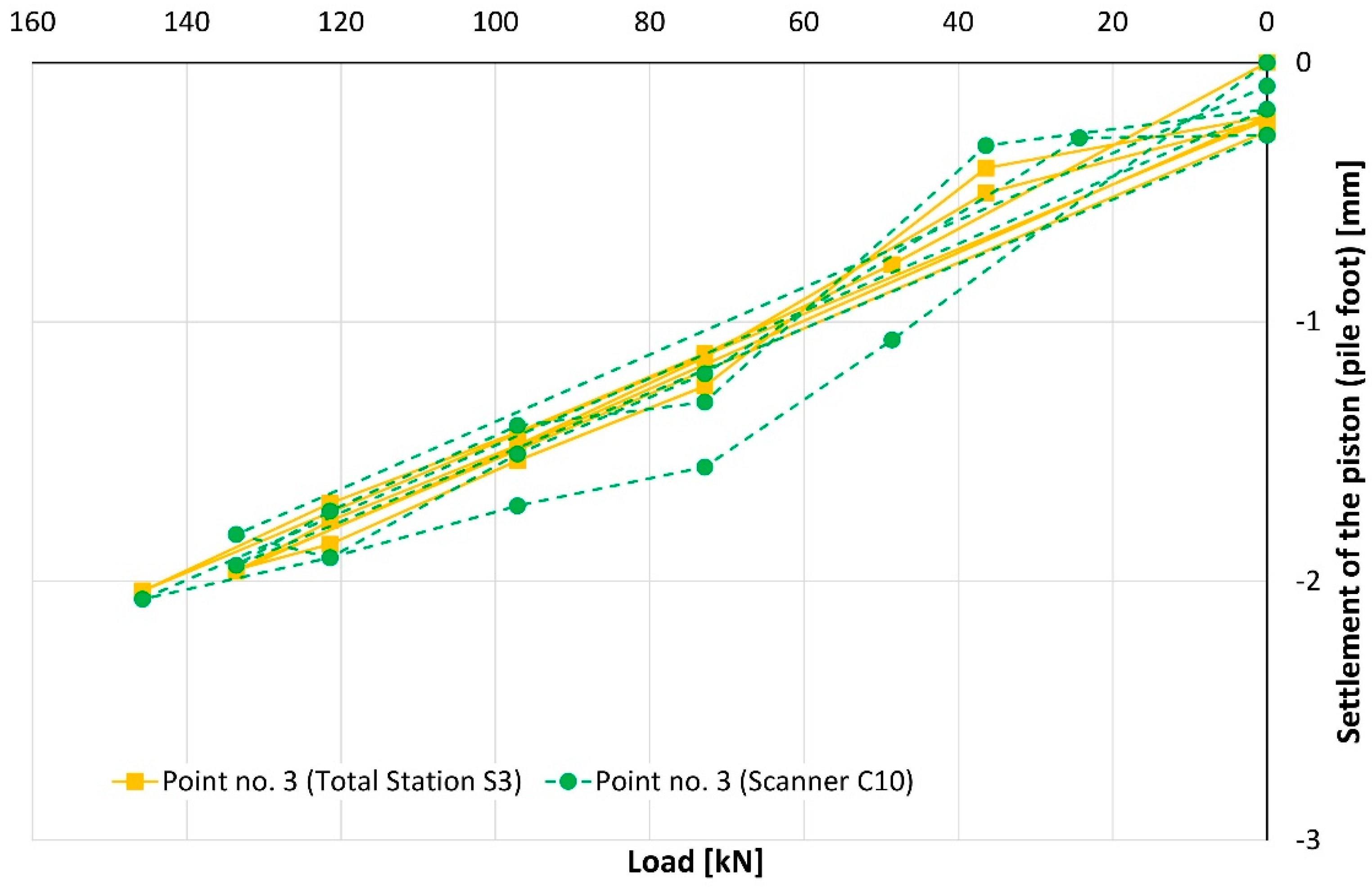
| Load | Settlement of the Piston (Pile Foot) (mm) | |||||
|---|---|---|---|---|---|---|
| Point No. 1 | Point No.3 | |||||
| (kN) | TLS | MTS | Differences | TLS | MTS | Differences |
| 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 49 | −0.1 | 0.0 | −0.1 | −1.1 | −0.8 | −0.3 |
| 73 | −0.5 | −0.5 | 0.0 | −1.6 | −1.1 | −0.4 |
| 97 | −0.8 | −0.8 | 0.0 | −1.7 | −1.4 | −0.3 |
| 121 | −1.0 | −1.1 | 0.1 | −1.9 | −1.7 | −0.2 |
| 146 | −1.3 | −1.4 | 0.1 | −2.1 | −2.0 | 0.0 |
| 0 | 0.0 | 0.2 | −0.3 | −0.2 | −0.2 | 0.0 |
| 36 | −0.1 | 0.1 | −0.2 | −0.3 | −0.5 | 0.2 |
| 73 | −0.5 | −0.5 | 0.0 | −1.3 | −1.1 | −0.2 |
| 97 | −0.7 | −0.9 | 0.2 | −1.4 | −1.5 | 0.1 |
| 121 | −1.2 | −1.2 | 0.0 | −1.7 | −1.8 | 0.0 |
| 134 | −1.4 | −1.3 | −0.1 | −1.9 | −2.0 | 0.0 |
| 0 | 0.4 | 0.2 | 0.1 | −0.3 | −0.2 | −0.1 |
| 24 | 0.0 | 0.2 | −0.2 | −0.3 | −0.4 | 0.1 |
| 73 | −0.5 | −0.6 | 0.1 | −1.2 | −1.2 | 0.0 |
| 97 | −0.9 | −0.9 | 0.0 | −1.5 | −1.5 | 0.0 |
| 121 | −1.6 | −1.2 | −0.4 | −1.9 | −1.9 | −0.1 |
| 134 | −1.3 | −1.3 | 0.0 | −1.8 | −2.0 | 0.1 |
| 0 | 0.3 | 0.3 | 0.0 | −0.1 | −0.3 | 0.2 |
| Min. | −1.6 | −1.4 | −0.4 | −2.1 | −2.0 | −0.4 |
| Max. | 0.4 | 0.3 | 0.2 | 0.0 | 0.0 | 0.2 |
| Mean | −0.6 | −0.6 | 0.0 | −1.2 | −1.1 | 0.0 |
| Std. dev. | 0.6 | 0.6 | 0.1 | 0.7 | 0.7 | 0.2 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muszyński, Z.; Rybak, J.; Kaczor, P. Accuracy Assessment of Semi-Automatic Measuring Techniques Applied to Displacement Control in Self-Balanced Pile Capacity Testing Appliance. Sensors 2018, 18, 4067. https://doi.org/10.3390/s18114067
Muszyński Z, Rybak J, Kaczor P. Accuracy Assessment of Semi-Automatic Measuring Techniques Applied to Displacement Control in Self-Balanced Pile Capacity Testing Appliance. Sensors. 2018; 18(11):4067. https://doi.org/10.3390/s18114067
Chicago/Turabian StyleMuszyński, Zbigniew, Jarosław Rybak, and Paulina Kaczor. 2018. "Accuracy Assessment of Semi-Automatic Measuring Techniques Applied to Displacement Control in Self-Balanced Pile Capacity Testing Appliance" Sensors 18, no. 11: 4067. https://doi.org/10.3390/s18114067
APA StyleMuszyński, Z., Rybak, J., & Kaczor, P. (2018). Accuracy Assessment of Semi-Automatic Measuring Techniques Applied to Displacement Control in Self-Balanced Pile Capacity Testing Appliance. Sensors, 18(11), 4067. https://doi.org/10.3390/s18114067