NLOS Identification in WLANs Using Deep LSTM with CNN Features
Abstract
1. Introduction
2. Related Works
3. Preliminaries
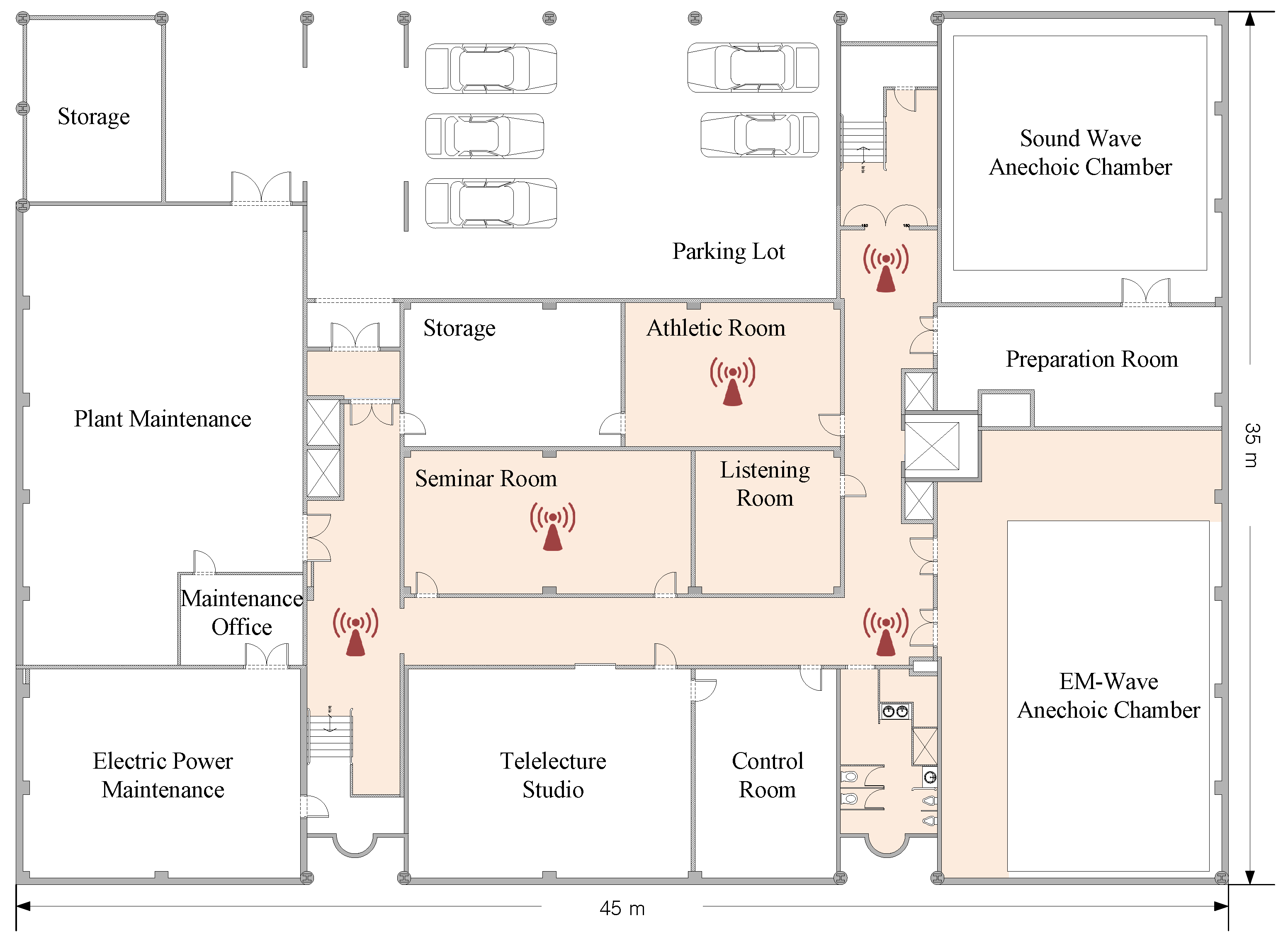
3.1. System Model
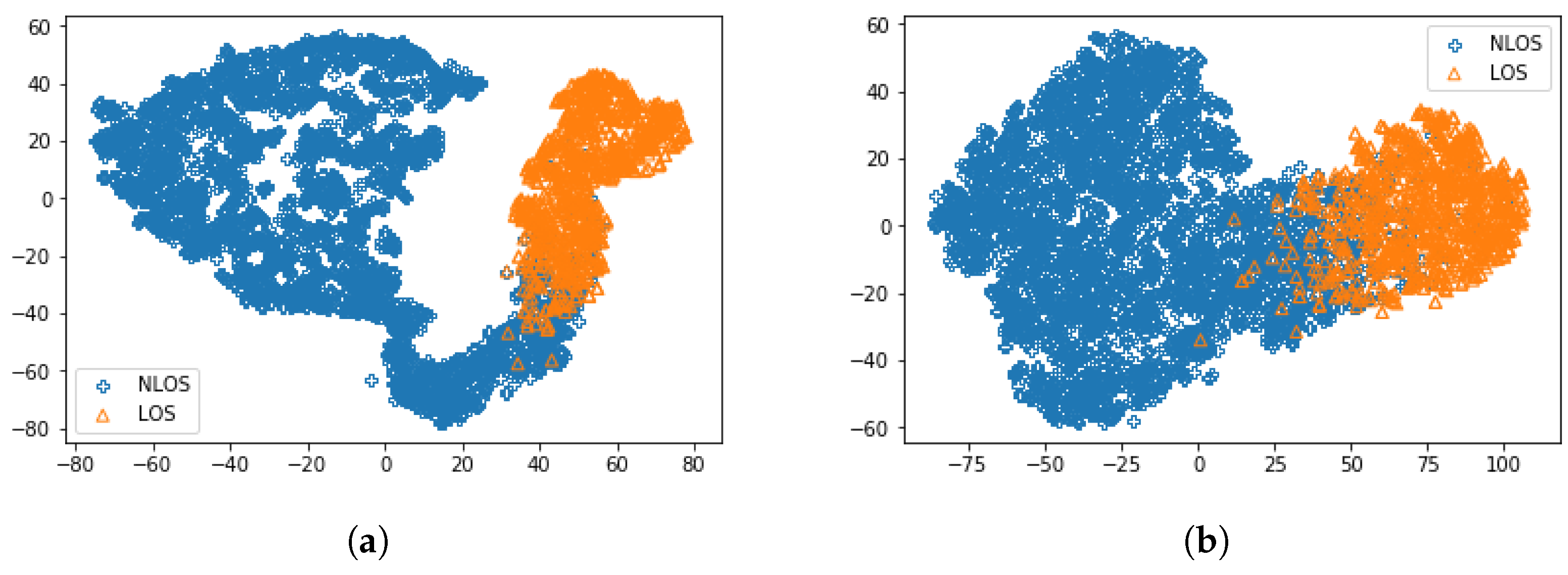
3.2. Experimental Data
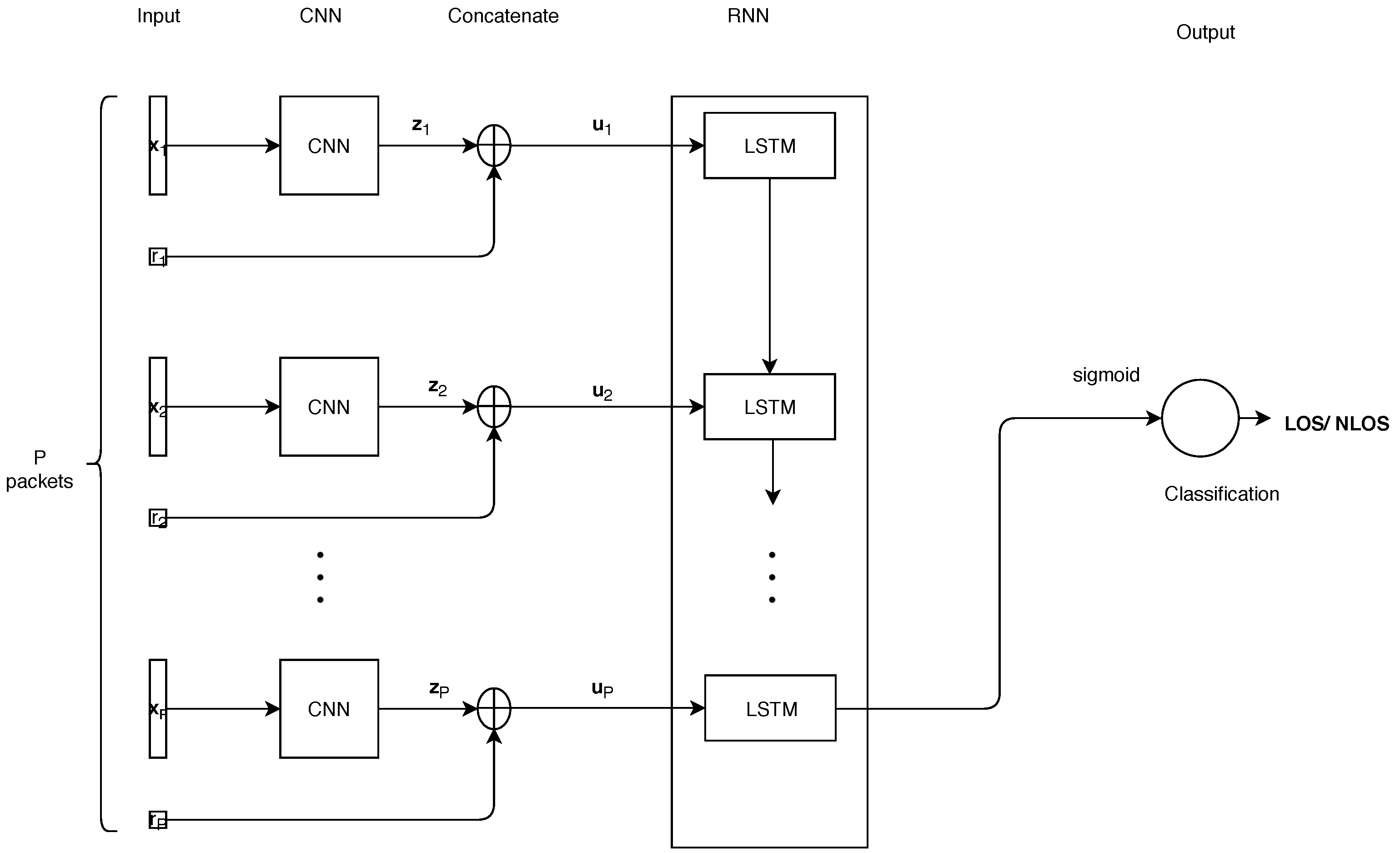
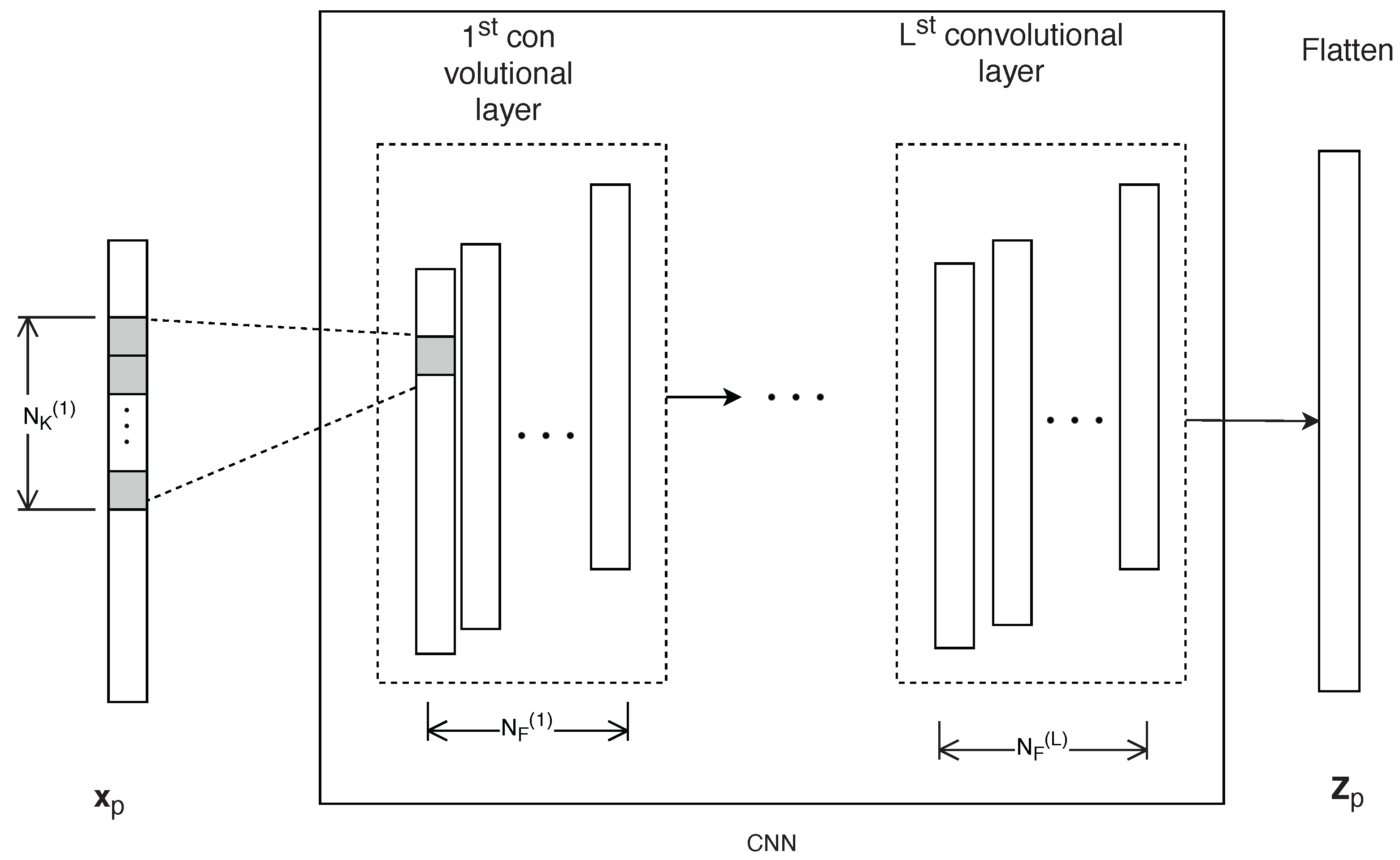
4. Proposed CNNLSTM Model
4.1. CNN Part
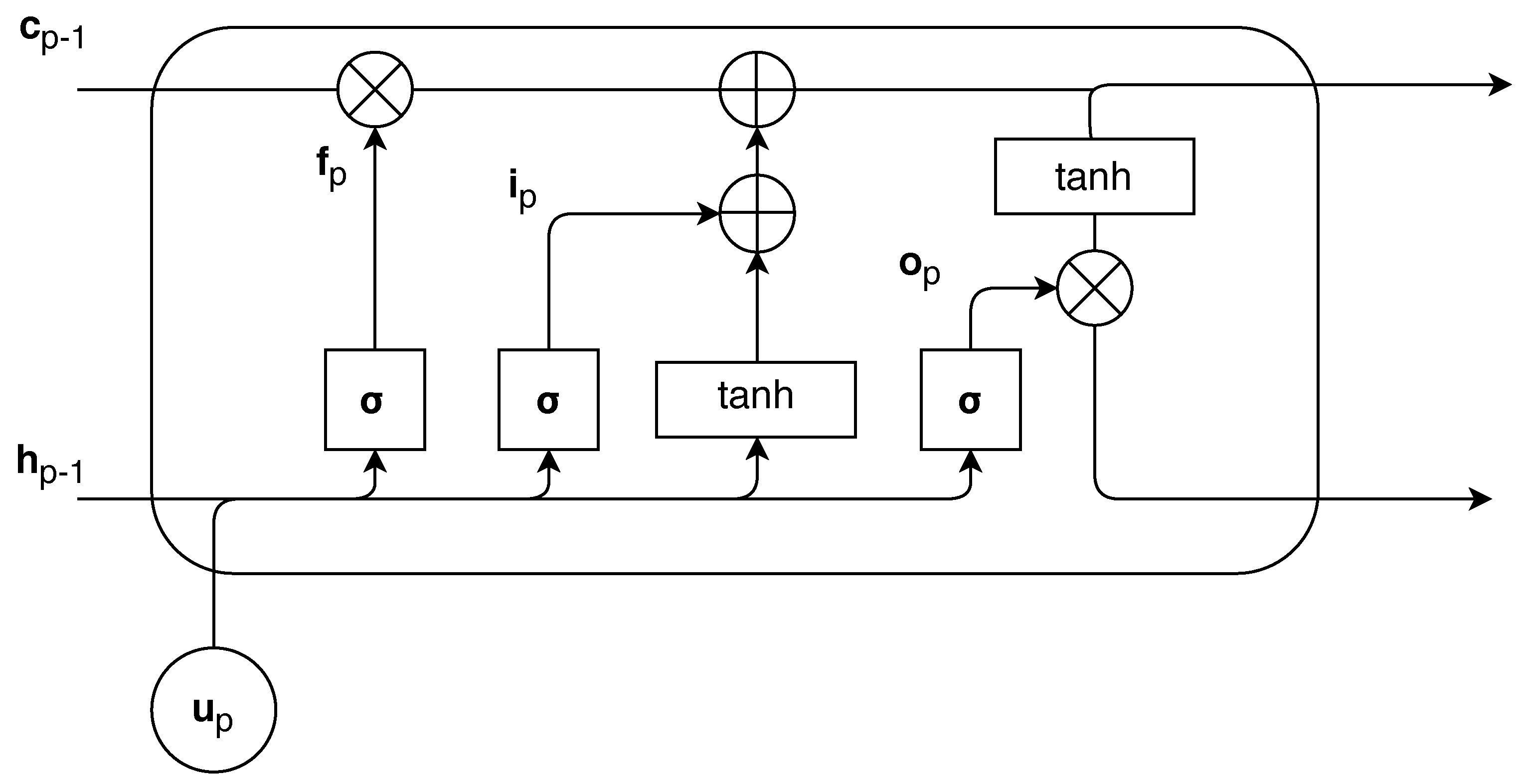
4.2. RNN Part
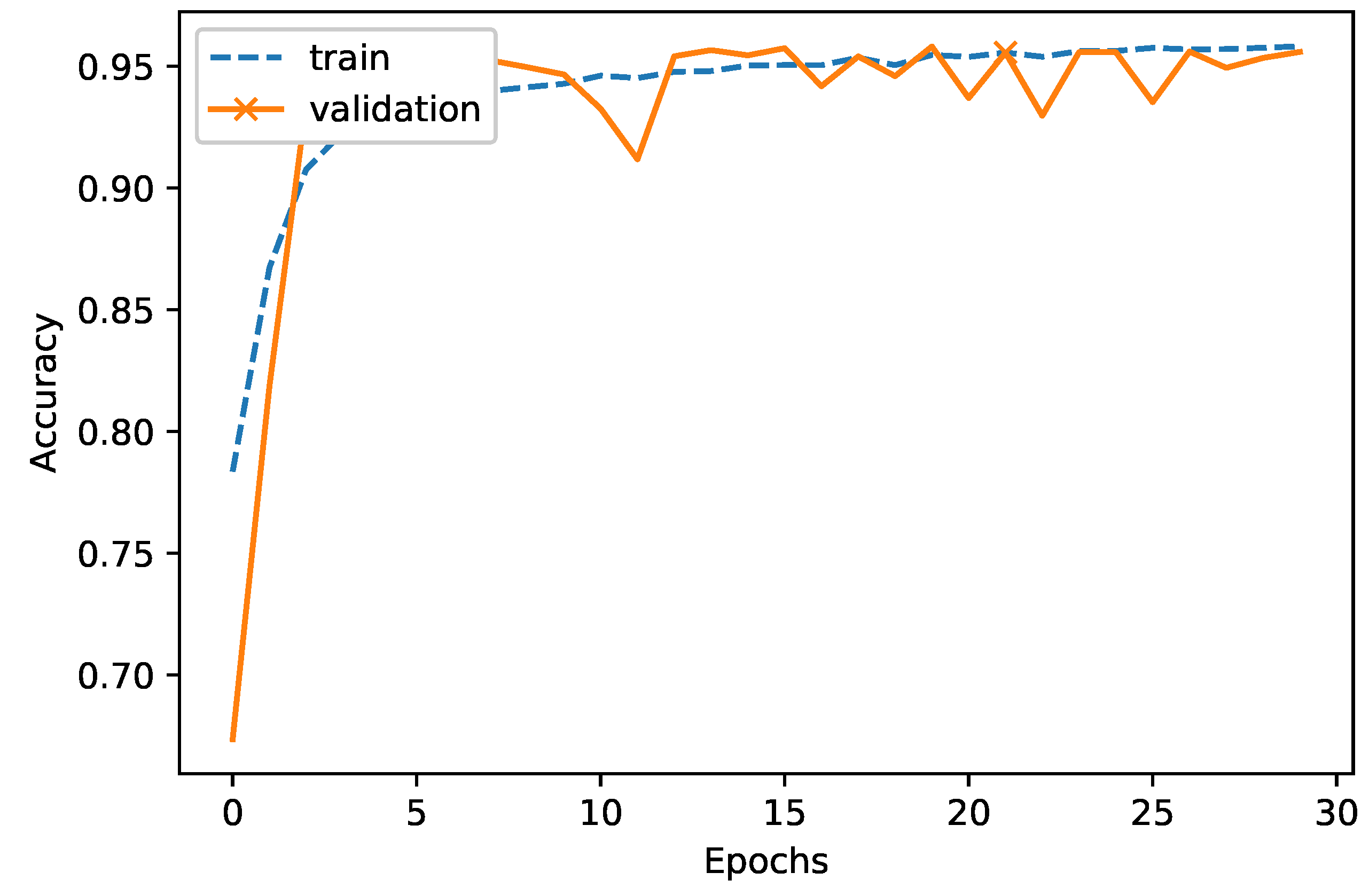
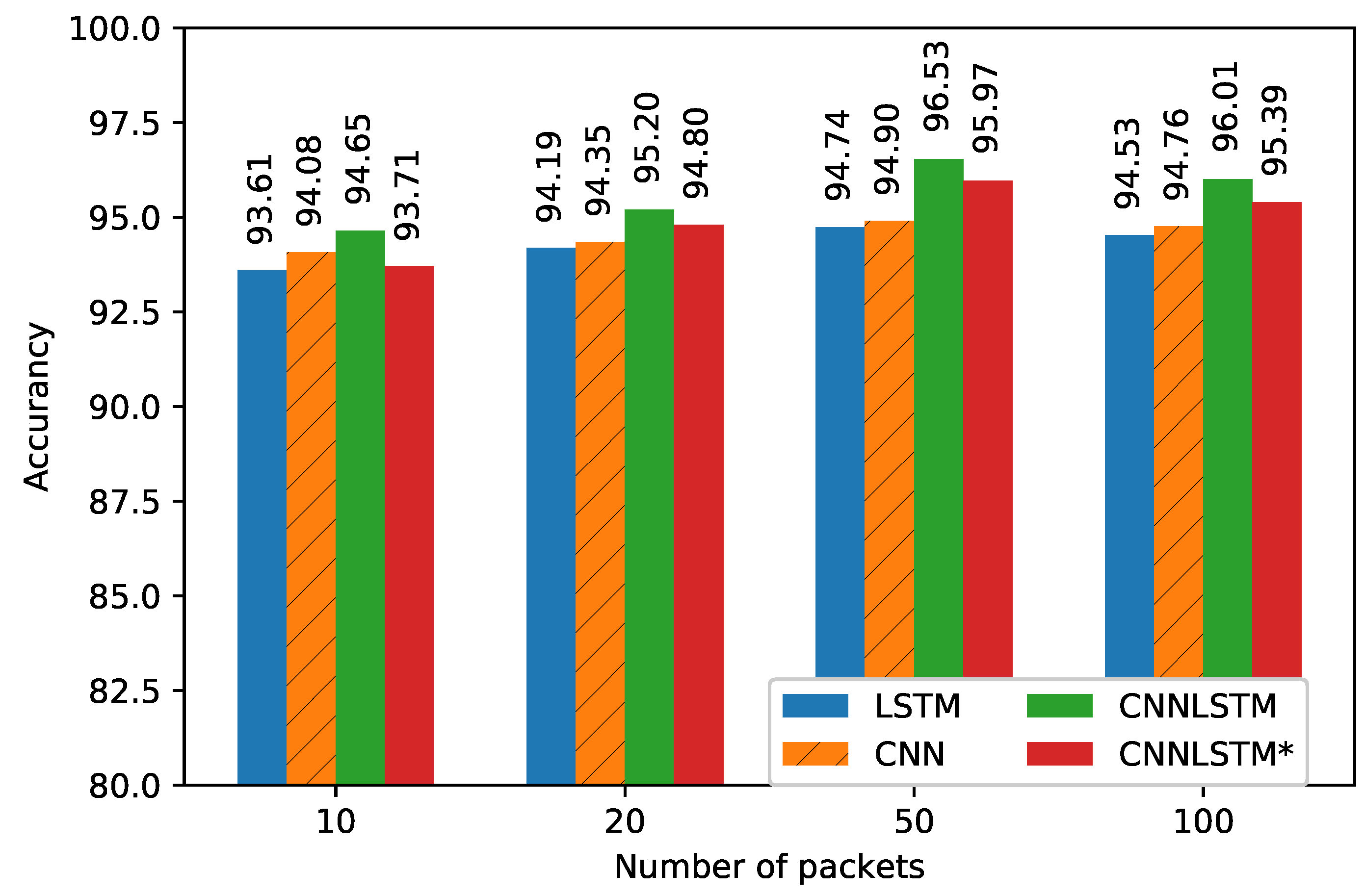
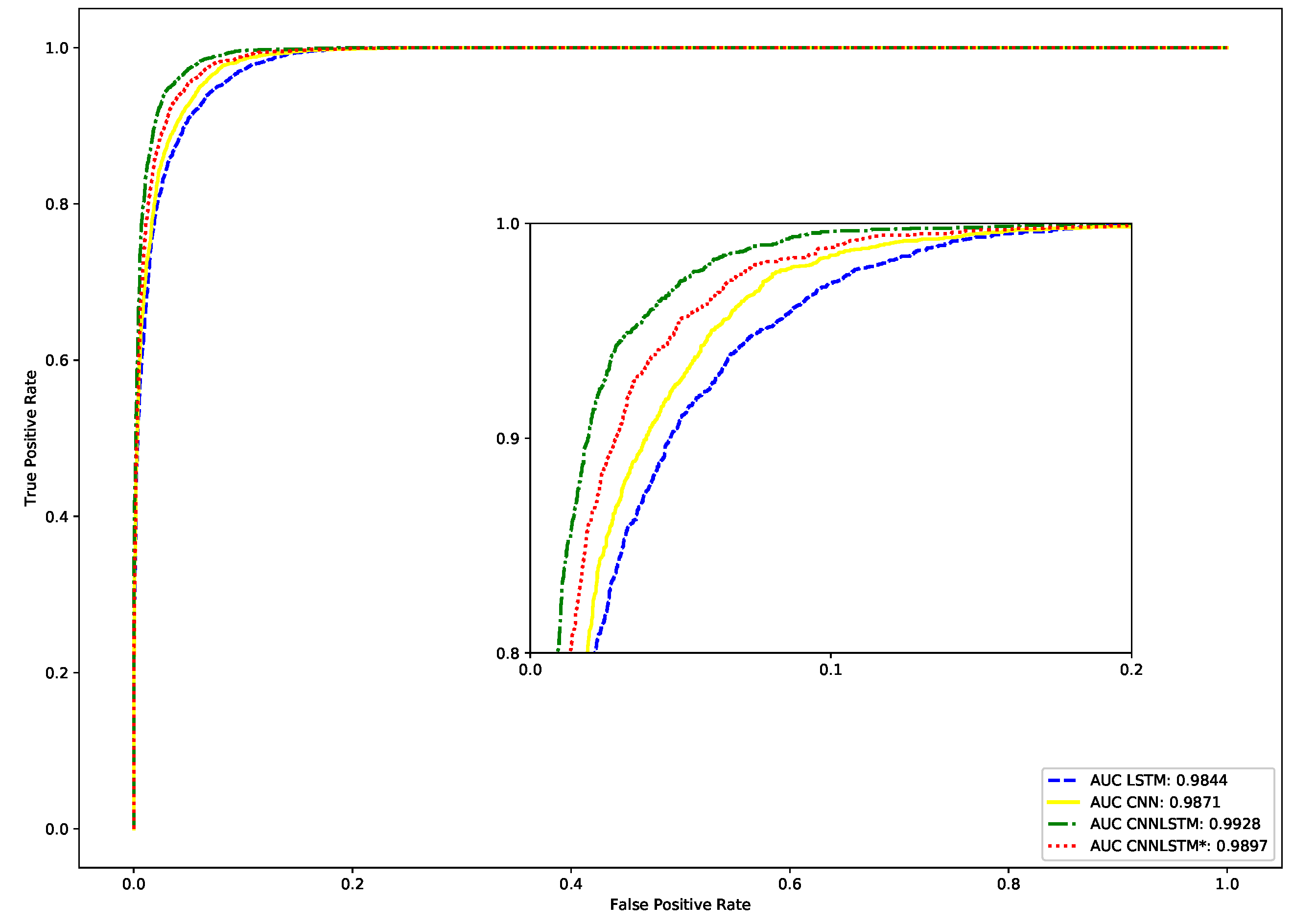
5. Performance Evaluation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- McNeff, J.G. The global positioning system. IEEE Trans. Microw. Theory Tech. 2008, 50, 645–652. [Google Scholar] [CrossRef]
- Cui, K.; Chen, G.; Xu, Z.; Richard, D.R. Line-of-sight visible light communication system design and demonstration. In Proceedings of the 7th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP 2010), Newcastle upon Tyne, UK, 21–23 July 2010; pp. 621–625. [Google Scholar]
- Dialani, J.C.; Patel, A.; Jindal, R.P. Performance measurements of IEEE 802.11 a wireless LANs in presence of ultrawideband interference. In Proceedings of the 2006 IEEE Sarnoff Symposium, Princeton, NJ, USA, 27–28 March 2006; pp. 1–4. [Google Scholar]
- Aiello, G.R.; Rogerson, G.D. Ultra-wideband wireless systems. IEEE Microw. Mag. 2003, 2, 36–47. [Google Scholar] [CrossRef]
- Kaemarungsi, K. Distribution of WLAN received signal strength indication for indoor location determination. In Proceedings of the 1st International Symposium on Wireless Pervasive Computing, Phuket, Thailand, 16–18 January 2006. [Google Scholar]
- Seshadri, V.; Zaruba, G.V.; Huber, M. A bayesian sampling approach to in-door localization of wireless devices using received signal strength indication. In Proceedings of the Third IEEE International Conference on Pervasive Computing and Communications, Kauai Island, HI, USA, 8–12 March 2005; pp. 75–84. [Google Scholar]
- Wang, X.; Wang, Z.; O’Dea, B. A TOA-based location algorithm reducing the errors due to non-line-of-sight (NLOS) propagation. IEEE Trans. Veh. Technol. 2003, 1, 112–116. [Google Scholar] [CrossRef]
- Guvenc, I.; Chong, C.-C. A survey on TOA based wireless localization and NLOS mitigation techniques. IEEE Commun. Surv. Tutor. 2009, 11, 107–124. [Google Scholar] [CrossRef]
- Chan, Y.-T.; Tsui, W.-Y.; So, H.-C.; Ching, P.-C. Time-of-arrival based localization under NLOS conditions. IEEE Trans. Veh. Technol. 2006, 1, 17–24. [Google Scholar] [CrossRef]
- Venkatraman, S.; Caffery, J.; You, H.-R. A novel TOA location algorithm using LOS range estimation for NLOS environments. IEEE Trans. Veh. Technol. 2004, 5, 1515–1524. [Google Scholar] [CrossRef]
- Caire, G.; Shamai, S. On the capacity of some channels with channel state information. IEEE Trans. Inf. Theory 1999, 6, 2007–2019. [Google Scholar] [CrossRef]
- Marzetta, T.L.; Hochwald, B.M. Fast transfer of channel state information in wireless systems. IEEE Trans. Sign. Process. 2006, 4, 1268–1278. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, Z.; Wu, C.; Sun, W.; Liu, Y. LiFi: Line-of-sight identification with WiFi. In Proceedings of the IEEE INFOCOM 2014–IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 2688–2696. [Google Scholar]
- Zhou, Z.; Yang, Z.; Wu, C.; Shangguan, L.; Cai, H.; Liu, Y.; Ni, L.M. WiFi-based indoor line-of-sight identification. IEEE Trans. Wirel. Commun. 2015, 11, 6125–6136. [Google Scholar] [CrossRef]
- Wu, C.; Yang, Z.; Zhou, Z.; Qian, K.; Liu, Y.; Liu, M. PhaseU: Real-time LOS identification with WiFi. IEEE Trans. Wirel. Commun. 2015, 14, 2038–2046. [Google Scholar]
- Choi, J.S.; Lee, W.H.; Lee, J.H.; Lee, J.H.; Kim, S.C. Deep Learning Based NLOS Identification with Commodity WLAN Devices. IEEE Trans. Veh. Technol. 2018, 4, 3295–3303. [Google Scholar] [CrossRef]
- Kim, K.S.; Lee, S.; Huang, K. A scalable deep neural network architecture for multi-building and multi-floor indoor localization based on Wi-Fi fingerprinting. Big Data Anal. 2018, 3, 4. [Google Scholar] [CrossRef]
- Abbas, R.; Hussain, A.J.; Al-Jumeily, D.; Baker, T.; Khattak, A. Classification of Foetal Distress and Hypoxia Using Machine Learning Approaches. Int. Conf. Intell. Comput. 2018, 767–776. [Google Scholar]
- Amin, A.; Shah, B.; Khattak, A.M.; Baker, T.; Anwar, S. Just-in-time Customer Churn Prediction: With and Without Data Transformation. In Proceedings of the IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–6. [Google Scholar]
- Alshabandar, R.; Hussain, A.; Keight, R.; Laws, A.; Baker, T. The Application of Gaussian Mixture Models for the Identification of At-Risk Learners in Massive Open Online Courses. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Cireşan, D.C.; Meier, U.; Gambardella, L.M.; Schmidhuber, J. Deep, big, simple neural nets for handwritten digit recognition. Neural Comput. 2010, 22, 3207–3220. [Google Scholar] [CrossRef] [PubMed]
- Sharif Razavian, A.; Azizpour, H.; Sullivan, J.; Carlsson, S. CNN features off-the-shelf: An astounding baseline for recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition workshops, Columbus, OH, USA, 24–27 June 2014; pp. 806–813. [Google Scholar]
- Yin, W.; Kann, K.; Yu, M.; Schütze, H. Comparative study of cnn and rnn for natural language processing. arXiv, 2017; arXiv:1702.01923. Available online: https://arxiv.org/abs/1702.01923 (accessed on 7 February 2017).
- Chen, H.; Zhang, Y.; Li, W.; Tao, X.; Zhang, P. ConFi: Convolutional neural networks based indoor wi-fi localization using channel state information. IEEE Access 2017, 5, 18066–18074. [Google Scholar] [CrossRef]
- Graves, A.; Mohamed, A.R.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the Acoustics, speech and signal processing (icassp), 2013 ieee international conference, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- Pascanu, R.; Gulcehre, C.; Cho, K.; Bengio, Y. How to construct deep recurrent neural networks. arXiv, 2013; arXiv:1312.6026. Available online: https://arxiv.org/abs/1312.6026 (accessed on 24 April 2014).
- Hochreiter, S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Tsironi, E.; Barros, P.; Weber, C.; Wermter, S. An analysis of convolutional long short-term memory recurrent neural networks for gesture recognition. Neurocomputing 2017, 268, 76–86. [Google Scholar] [CrossRef]
- Tzirakis, P.; Trigeorgis, G.; Nicolaou, M.A.; Schuller, B.W.; Zafeiriou, S. End-to-end multimodal emotion recognition using deep neural networks. IEEE J. Sel. Top. Sign. Process. 2017, 11, 1301–1309. [Google Scholar] [CrossRef]
- Sainath, T.N.; Vinyals, O.; Senior, A.; Sak, H. Convolutional, long short-term memory, fully connected deep neural networks. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 4580–4584. [Google Scholar]
- Mishkin, D.; Sergievskiy, N.; Matas, J. Systematic evaluation of CNN advances in the ImageNet. Comput. Vis. Image Underst. 2017, 161, 11–19. [Google Scholar] [CrossRef]
- Sergey Ioffe and Christian Szegedy, Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv, 2015; arXiv:1502.03167. Available online: https://arxiv.org/abs/1502.03167 (accessed on 2 March 2015).
- Werbos, P.J. Backpropagation through time: What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv, 2014; arXiv:1412.6980. Available online: https://arxiv.org/abs/1412.6980 (accessed on 30 January 2017).
- Cotter, A.; Shamir, O.; Srebro, N.; Sridharan, K. Better mini-batch algorithms via accelerated gradient methods. Adv. Neural Inf. Process. Syst. 2011, 1647–1655. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a Receiver Operating Characteristic (ROC) Curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Maaten, L.V.D.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
| Layer Type | Activation | Kernel Size | Stride | Filter | Output Shape |
|---|---|---|---|---|---|
| Input | 50 × 112 × 1 | ||||
| Convolution | softplus | 8 | 2 | 32 | 50 × 53 × 32 |
| Convolution | softplus | 2 | 1 | 16 | 50 × 52 × 16 |
| Convolution | reLU | 2 | 1 | 8 | 50 × 51 × 8 |
| Flatten | _ | _ | _ | _ | 50 × 408 |
| Concatenate with RSSI | _ | _ | _ | _ | 50 × 409 |
| LSTM | _ | _ | _ | 10 | 10 |
| FC | sigmoid | _ | _ | 1 | 1 |
| Model | Decision Threshold | Avg Detection Rate | Accuracy |
|---|---|---|---|
| LSTM | 0.332970 | 0.94920 | 94.57 |
| CNN | 0.372340 | 0.94310 | 94.90 |
| CNNLSTM | 0.302848 | 0.95989 | 96.53 |
| CNNLSTM* | 0.225334 | 0.95141 | 95.97 |
| Model | Time (s) | Epochs | Total Training Time (s) | Number of Parameters |
|---|---|---|---|---|
| LSTM | 9 | 37 | 333 | 5011 |
| CNN | 16 | 25 | 400 | 22,463 |
| CNNLSTM | 17.5 | 21 | 367.5 | 18,863 |
| CNNLSTM* | 15 | 23 | 345 | 9679 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, V.-H.; Nguyen, M.-T.; Choi, J.; Kim, Y.-H. NLOS Identification in WLANs Using Deep LSTM with CNN Features. Sensors 2018, 18, 4057. https://doi.org/10.3390/s18114057
Nguyen V-H, Nguyen M-T, Choi J, Kim Y-H. NLOS Identification in WLANs Using Deep LSTM with CNN Features. Sensors. 2018; 18(11):4057. https://doi.org/10.3390/s18114057
Chicago/Turabian StyleNguyen, Viet-Hung, Minh-Tuan Nguyen, Jeongsik Choi, and Yong-Hwa Kim. 2018. "NLOS Identification in WLANs Using Deep LSTM with CNN Features" Sensors 18, no. 11: 4057. https://doi.org/10.3390/s18114057
APA StyleNguyen, V.-H., Nguyen, M.-T., Choi, J., & Kim, Y.-H. (2018). NLOS Identification in WLANs Using Deep LSTM with CNN Features. Sensors, 18(11), 4057. https://doi.org/10.3390/s18114057





