A Novel Recovery Method of Soft X-ray Spectrum Unfolding Based on Compressive Sensing
Abstract
1. Introduction
- (1)
- The spectrum recovery is formulated as a problem of an accurate signal recovering from a few measurements (i.e., compressive sensing), which applies the measurement matrix to convert the spectrum signal into a voltage signal, and enables the signal be reconstructed with a small amount of measured data.
- (2)
- The proper basis atoms are selected adaptively over the Legendre orthogonal basis dictionary with a large size and Lasso regression in the sense of the ℓ1 norm, which enables the spectrum to be recovered with high accuracy from the small amount of measured data of the limited detection channels.
- (3)
- By employing this method, since the soft X-ray spectrometer may recover the spectrum with limited detection channel data, it provides the possibility of saving space for other detectors.
2. Soft X-ray Spectrometer and Compressive Sensing
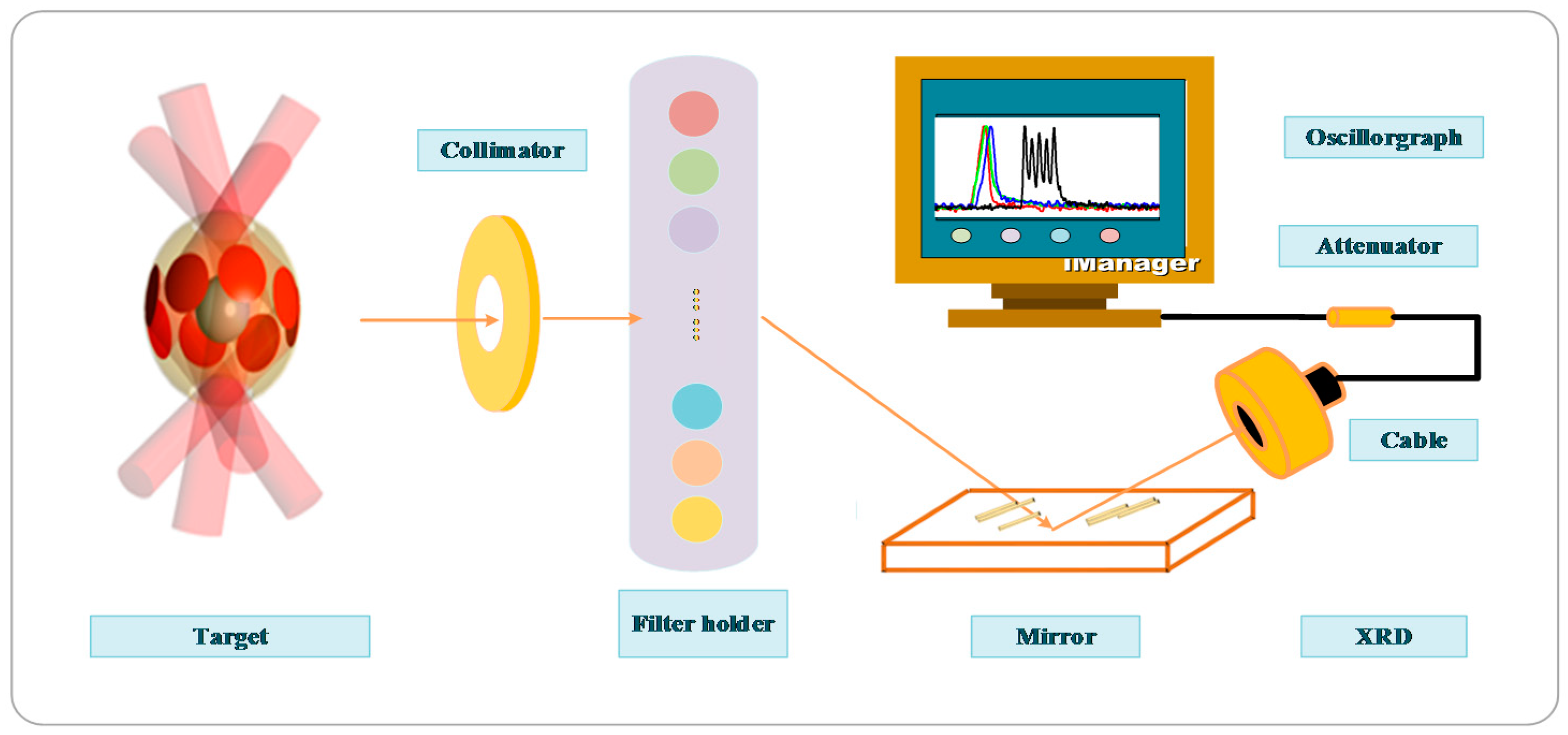
2.1. Soft X-ray Spectrometer
2.2. Compressive Sensing Method
2.2.1. Sparse Representation
2.2.2. Measurement Matrix
2.2.3. Sparse Coefficients Reconstruction
3. Spectrum Unfolding based on Compressive Sensing
3.1. Sparse Representation of Spectrum with Legendre Polynomial
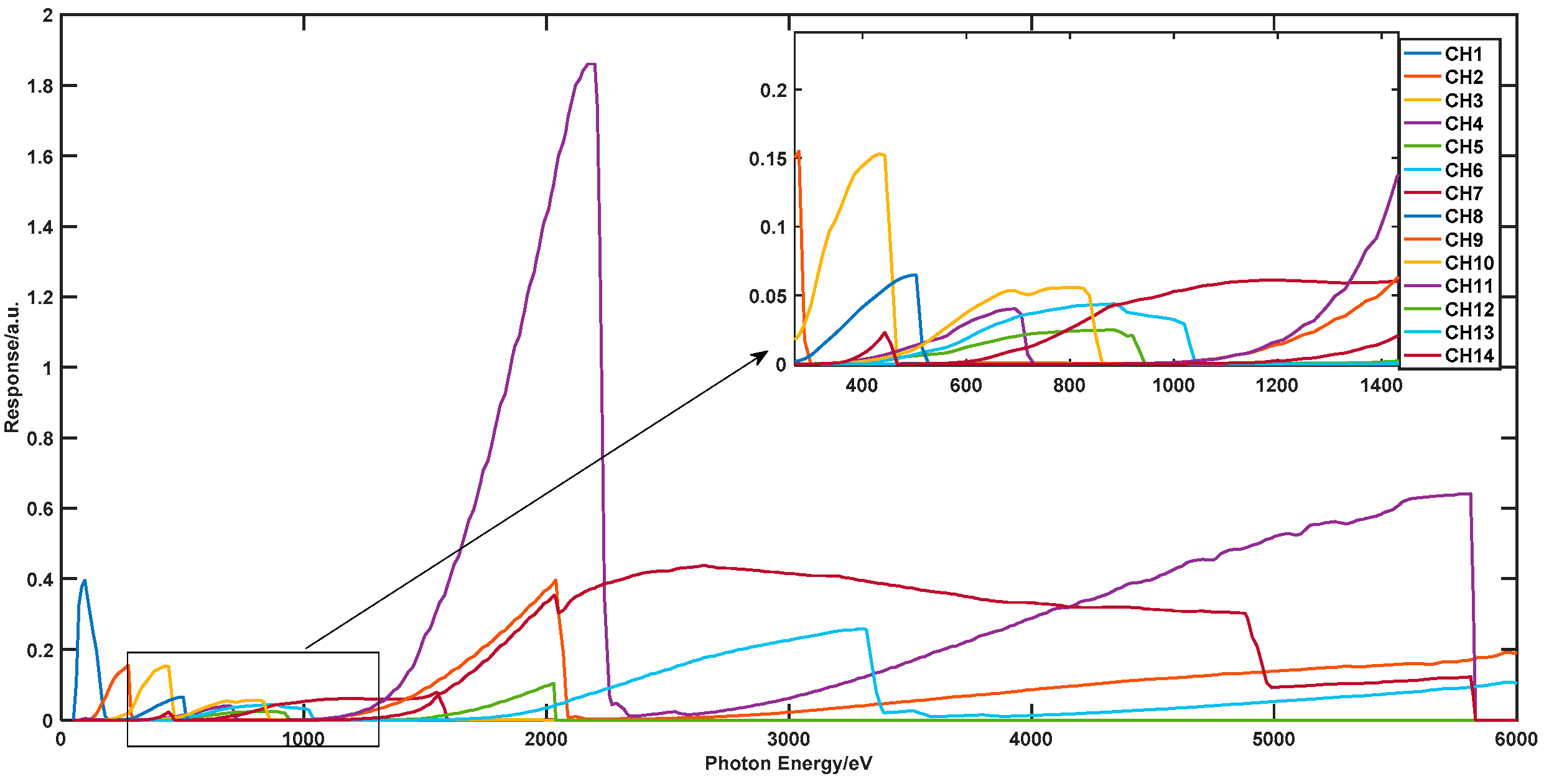
3.2. Measurement Data for Sparse Spectrum Reconstruction
3.3 Sparse Coefficient Recovery for the Soft X-ray Spectrum
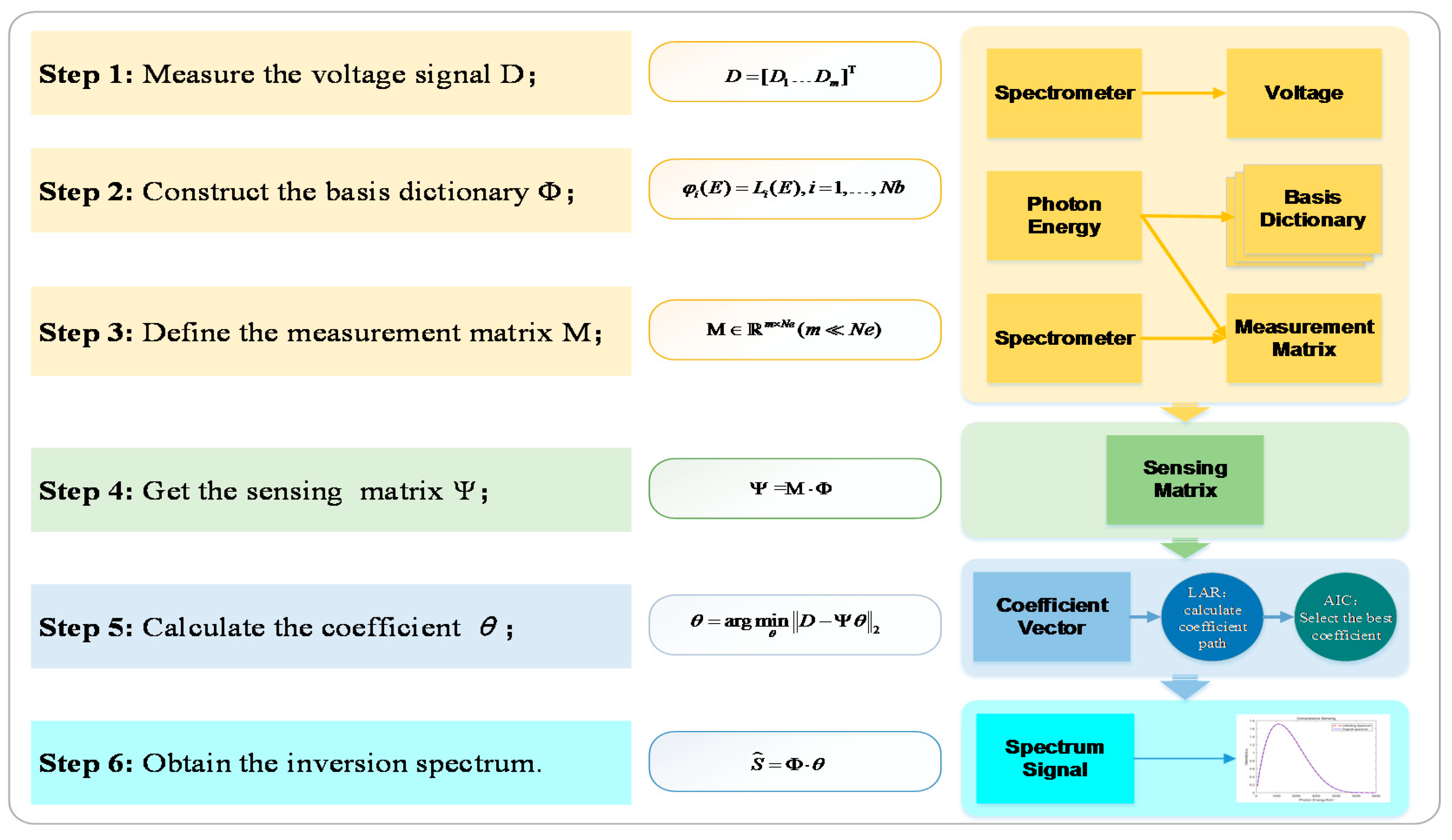
3.4. Overview of the Soft X-ray Spectrum Unfolding Process
4. Numerical Experiments
4.1. Accuracy Assessment Criteria
4.2. Experimental Settings
4.3. Experimental Results and Analysis
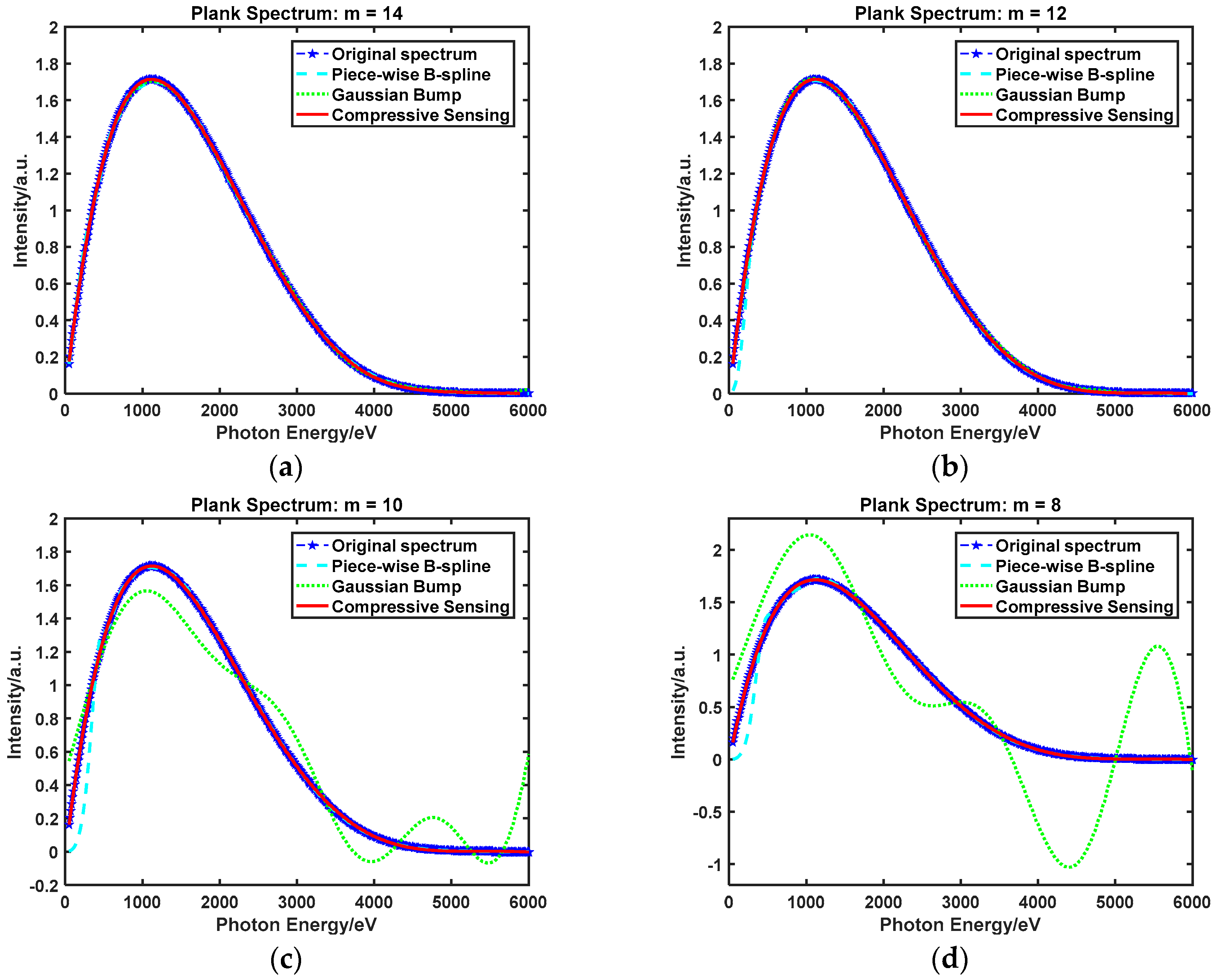
4.3.1. Spectrum Unfolding Method Contrast: Plank Spectrum
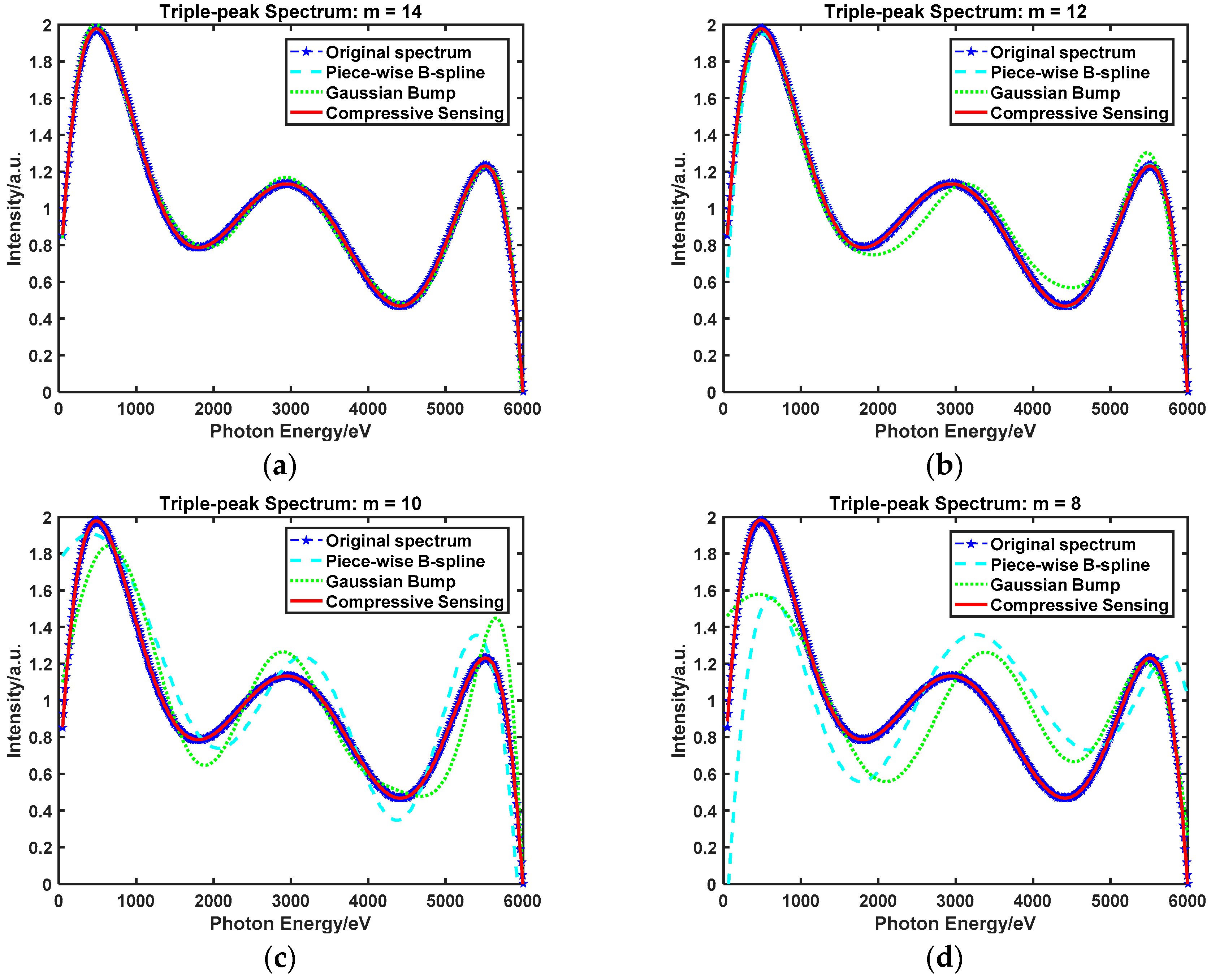
4.3.2. Spectrum Unfolding Method Contrast: Triple-Peak Spectrum
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Atzeni, S.; Meyertervehn, J. The Physics of Inertial Fusion. Plasma Phys. Control. Fusion 2004, 46, 1805. [Google Scholar]
- Li, H.; Huang, Y.; Jiang, S.; Jing, L.; Ding, Y. An efficient computational approach for evaluating radiation flux for laser driven inertial confinement fusion targets. Comput. Phys. Commun. 2015, 193, 49–54. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, C.; Yan, T.; Chen, Z. Spectrum Reconstruction for Five-Channel Autocorrelation Function of Spectropolarimeter. Optik 2017, 157, 1259–1266. [Google Scholar] [CrossRef]
- Fernandez, J.E.; Scot, V.; Giulio, E.D. Spectrum unfolding in X-ray spectrometry using the maximum entropy method. Radiat. Phys. Chem. 2014, 95, 154–157. [Google Scholar] [CrossRef]
- Reginatto, M. Overview of spectral unfolding techniques and uncertainty estimation. Radiat. Meas. 2010, 45, 1323–1329. [Google Scholar] [CrossRef]
- Gallardo, S.; Ródenas, J.; Querol, A.; Verdú, G. Application of the MTSVD unfolding method for reconstruction of primary X-ray spectra using semiconductor detectors. Prog. Nucl. Energy 2011, 53, 1136–1139. [Google Scholar] [CrossRef]
- Hosseini, S.A. Neutron spectrum unfolding using artificial neural network and modified least square method. Radiat. Phys. Chem. 2016, 126, 75–84. [Google Scholar] [CrossRef]
- Fehl, D.L.; Stygar, W.A.; Chandler, G.A.; Cuneo, M.E.; Ruiz, C.L. X-ray flux from filtered arrays of detectors without unfolding. Rev. Sci. Instrum. 2005, 76, 561. [Google Scholar] [CrossRef]
- Tianming, S.; Jiamin, Y.; Rongqing, Y. Recover soft x-ray spectrum using virtual flat response channels with filtered x-ray diode array. Rev. Sci. Instrum. 2012, 83, 113102. [Google Scholar]
- Song, T.; Yang, J.; Yi, R. Unfolding soft X-ray spectra in ICF experiments with base function method. High Power Laser Part. Beams 2010, 22, 2905–2910. [Google Scholar] [CrossRef]
- Jiang, S.E.; Zheng, Z.J.; Sun, K.X. A New Method Unfolding Spectra for the Soft X-ray Spectrometer. Chin. J. Comput. Phys. 2001, 18, 276–280. [Google Scholar]
- Delamater, N.D.; Wilson, D.C.; Kyrala, G.A.; Seifter, A.; Hoffman, N.M.; Dodd, E.; Singleton, R.; Glebov, V.; Stoeckl, C.; Li, C.K. Use of d-H3e proton spectroscopy as a diagnostic of shell ρr in capsule implosion experiments with ~0.2 NIF scale high temperature Hohlraums at Omegaa). Rev. Sci. Instrum. 2008, 79, 75. [Google Scholar] [CrossRef] [PubMed]
- May, M.J.; Widmann, K.; Sorce, C.; Park, H.S.; Schneider, M. Uncertainty analysis technique for OMEGA Dante measurements. Rev. Sci. Instrum. 2010, 81, 2179. [Google Scholar] [CrossRef] [PubMed]
- Fehl, D.L.; Leeper, R.J.; Kensek, R.P. A simple unfold method for Rutherford scattering, intense ion-beam spectrographs. Rev. Sci. Instrum. 1992, 63, 4786–4788. [Google Scholar] [CrossRef]
- Reginatto, M.; Goldhagen, P.; Neumann, S. Spectrum unfolding, sensitivity analysis and propagation of uncertainties with the maximum entropy deconvolution code MAXED. Nucl. Instrum. Methods Phys. Res. Sect. A 2002, 476, 242–246. [Google Scholar] [CrossRef]
- Reginatto, M.; Zimbal, A. Bayesian and maximum entropy methods for fusion diagnostic measurements with compact neutron spectrometers. Rev. Sci. Instrum. 2008, 79, 023505. [Google Scholar] [CrossRef] [PubMed]
- Candes, E.J.; Wakin, M.B.; Wakin, M.B. An introduction to compressive sampling. IEEE Signal Process. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Lustig, M.; Santos, J.M.; Lee, J.H.; Donoho, D.L.; Pauly, J.M. Application of “Compressed Sensing” for Rapid MR Imaging. Spars 2010, 58, 1182–1195. [Google Scholar]
- Davenport, M.A.; Laska, J.N.; Treichler, J.R.; Baraniuk, R.G. The Pros and Cons of Compressive Sensing for Wideband Signal Acquisition: Noise Folding versus Dynamic Range. IEEE Trans. Signal Process. 2011, 60, 4628–4642. [Google Scholar] [CrossRef]
- Sheikh, M.A.; Milenkovic, O.; Baraniuk, R.G. Designing Compressive Sensing DNA Microarrays. In Proceedings of the 2nd IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, St. Thomas, VI, USA, 12–14 December 2007; pp. 141–144. [Google Scholar]
- Sen, P.; Darabi, S. Compressive Rendering: A Rendering Application of Compressed Sensing. IEEE Trans. Vis. Comput. Graph. 2011, 17, 487–499. [Google Scholar] [CrossRef] [PubMed]
- Lindl, J. Development of the indirect-drive approach to inertial confinement fusion and the target physics basis for ignition and gain. Phys. Plasma 1995, 2, 3933–4024. [Google Scholar] [CrossRef]
- Kornblum, H.N.; Kauffman, R.L.; Smith, J.A. Measurement of 0.1–3-keV x rays from laser plasmas. Rev. Sci. Instrum. 1986, 57, 2179–2181. [Google Scholar] [CrossRef]
- Sorce, C.; Schein, J.; Weber, F.; Widmann, K.; Campbell, K.; Dewald, E.; Turner, R.; Landen, O.; Jacoby, K.; Torres, P. Soft X-ray power diagnostic improvements at the Omega Laser Facility. Rev. Sci. Instrum. 2006, 77, 508. [Google Scholar] [CrossRef]
- Dewald, E.L.; Campbell, K.M.; Turner, R.E.; Holder, J.P.; Landen, O.L.; Glenzer, S.H.; Kauffman, R.L.; Suter, L.J.; Landon, M.; Rhodes, M. Dante soft X-ray power diagnostic for National Ignition Facility. Rev. Sci. Instrum. 2004, 75, 3759–3761. [Google Scholar] [CrossRef]
- Bourgade, J.L.; Villette, B.; Bocher, J.L.; Boutin, J.Y.; Chiche, S.; Dague, N.; Gontier, D.; Jadaud, J.P.; Savale, B.; Wrobel, R. DMX: An absolutely calibrated time-resolved broadband soft x-ray spectrometer designed for MJ class laser-produced plasmas (invited). Rev. Sci. Instrum. 2001, 72, 1173–1182. [Google Scholar] [CrossRef]
- Hou, L.; Li, J.; Du, H.; Cui, Y.; Song, T.; Wei, M.; Yang, Y.; Li, S.; Yi, R.; Yi, T. Development of soft X-ray energy spectrometer on Shenguang II-up equipment. High Power Laser Part. Beam 2013, 25, 3139–3144. [Google Scholar]
- Lustig, M.; Donoho, D.L.; Santos, J.M.; Pauly, J.M. Compressed Sensing MRI. IEEE Signal Processing. Mag. 2008, 25, 72–82. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Tsaig, Y.; Donoho, D.L. Extensions of Compressed Sensing; Elsevier North-Holland, Inc.: Amsterdam, The Netherlands, 2006; pp. 549–571. [Google Scholar]
- Arjoune, Y.; Kaabouch, N.; El Ghazi, H.; Tamtaoui, A. A performance comparison of measurement matrices in compressive sensing. Int. J. Commun. Syst. 2018, 31, e3576. [Google Scholar] [CrossRef]
- Abo-Zahhad, M.M.; Hussein, A.I.; Mohamed, A.M. Compressive Sensing Algorithms for Signal Processing Applications: A Survey. Int. J. Commun. Netw. Syst. Sci. 2015, 8, 197–216. [Google Scholar]
- Nguyen, T.L.; Shin, Y. Deterministic sensing matrices in compressive sensing: A survey. Sci. World. J. 2013, 2013, 192795. [Google Scholar] [CrossRef] [PubMed]
- Babacan, S.D.; Molina, R.; Katsaggelos, A.K. Bayesian Compressive Sensing Using Laplace Priors. IEEE Trans. Image Process. 2009, 19, 53–63. [Google Scholar] [CrossRef] [PubMed]
- Cotter, S.F.; Rao, B.D. Sparse channel estimation via matching pursuit with application to equalization. IEEE Trans. Wirel. Commun. 2002, 50, 374–377. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Baron, D.; Sarvotham, S.; Baraniuk, R.G. Bayesian Compressive Sensing Via Belief Propagation. IEEE Trans. Signal Process. 2009, 58, 269–280. [Google Scholar] [CrossRef]
- Arjoune, Y.; Kaabouch, N.; Ghazi, H.E.; Tamtaoui, A. Compressive sensing: Performance comparison of sparse recovery algorithms. In Proceedings of the Computing and Communication Workshop and Conference, Las Vegas, NV, USA, 9–11 January 2017; pp. 1–7. [Google Scholar]
- Chen, S.S.; Saunders, M.A. Atomic Decomposition by Basis Pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–451. [Google Scholar]
- Iturbide, E.; Cerda, J.; Graff, M. A Comparison between LARS and LASSO for Initialising the Time-Series Forecasting Auto-Regressive Equations. Procedia Technol. 2013, 7, 282–288. [Google Scholar] [CrossRef]
- Zou, H.; Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. 2005, 67, 301–320. [Google Scholar]
- Gribonval, R.; Cevher, V.; Davies, M.E. Compressible Distributions for High-Dimensional Statistics. IEEE Trans. Inf. Theory 2012, 58, 5016–5034. [Google Scholar] [CrossRef]
- Hesterberg, T.; Choi, N.H.; Meier, L.; Fraley, C. Least angle and ℓ1 penalized regression: A review. Stat. Surv. 2008, 2, 61–93. [Google Scholar] [CrossRef]
- Sjöstrand, K.; Clemmensen, L.H.; Larsen, R.; Ersbøll, B.; Einarsson, G. SpaSM: A MATLAB toolbox for sparse statistical modeling. J. Stat. Softw. 2018, 84, 37. [Google Scholar]

| M | RMSE | MAE | ||||
|---|---|---|---|---|---|---|
| Piece-Wise B-Spline | Gaussian Bump | Compressive Sensing | Piece-Wise B-Spline | Gaussian Bump | Compressive Sensing | |
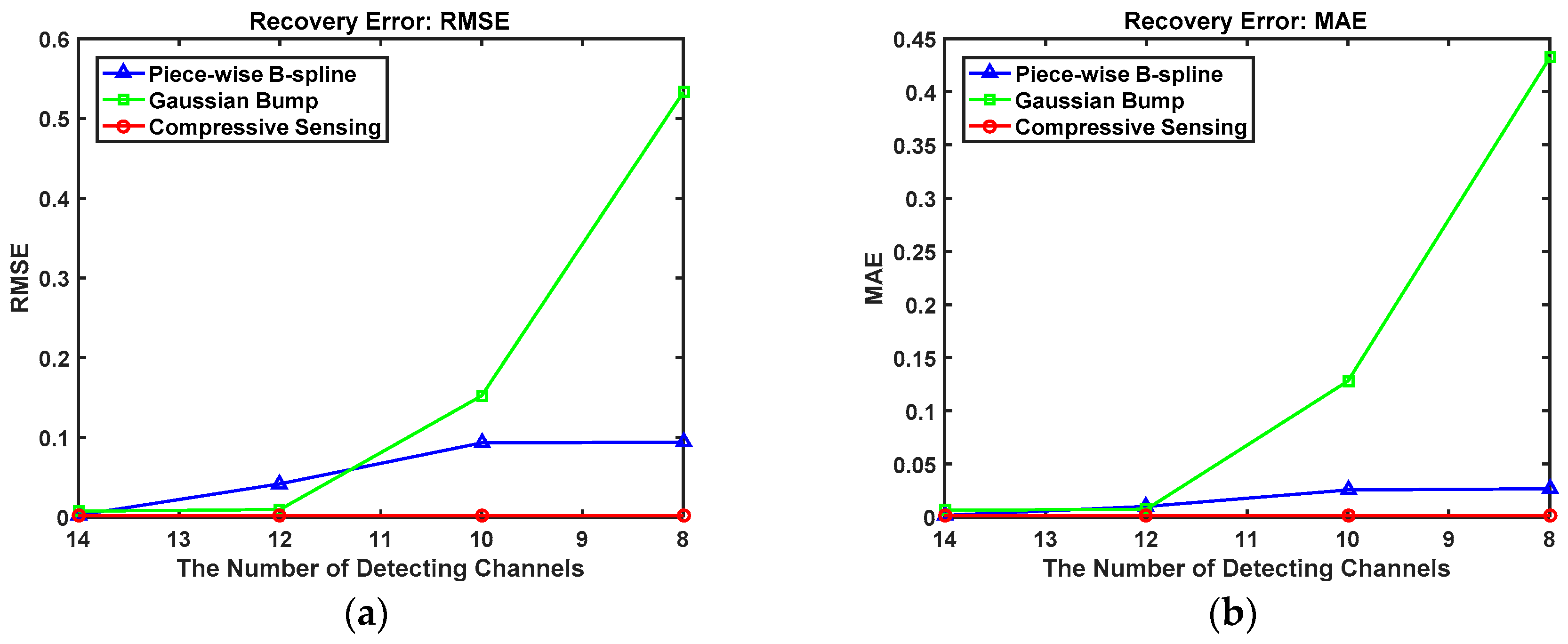
| 14 | 0.002647 | 0.007489 | 0.001992 | 0.001740 | 0.006479 | 0.001293 |
| 12 | 0.041785 | 0.009726 | 0.002006 | 0.010048 | 0.007416 | 0.001305 |
| 10 | 0.093317 | 0.152139 | 0.002010 | 0.025542 | 0.128225 | 0.001311 |
| 8 | 0.094138 | 0.532886 | 0.002013 | 0.026802 | 0.432161 | 0.001315 |
| M | RMSE | MAE | ||||
|---|---|---|---|---|---|---|
| Piece-Wise B-Spline | Gaussian Bump | Compressive Sensing | Piece-Wise B-Spline | Gaussian Bump | Compressive Sensing | |
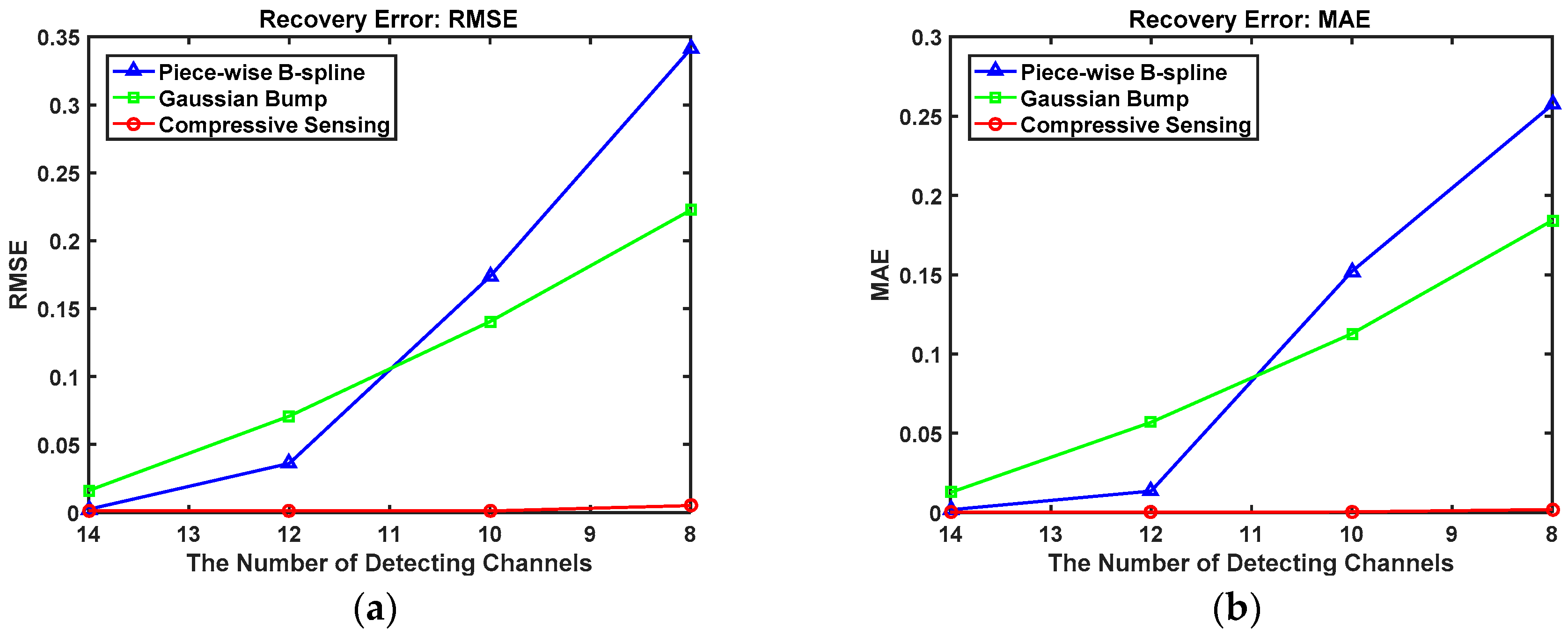
| 14 | 0.002298 | 0.016160 | 0.001137 | 0.001734 | 0.012620 | 0.000116 |
| 12 | 0.036192 | 0.070879 | 0.001179 | 0.013579 | 0.056895 | 0.000170 |
| 10 | 0.173786 | 0.140535 | 0.001245 | 0.152061 | 0.112756 | 0.000428 |
| 8 | 0.341228 | 0.222501 | 0.005037 | 0.257305 | 0.184214 | 0.001917 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, N.; Huang, Y.; Li, H.; Li, P.; Wang, K.; Wang, F. A Novel Recovery Method of Soft X-ray Spectrum Unfolding Based on Compressive Sensing. Sensors 2018, 18, 3725. https://doi.org/10.3390/s18113725
Xia N, Huang Y, Li H, Li P, Wang K, Wang F. A Novel Recovery Method of Soft X-ray Spectrum Unfolding Based on Compressive Sensing. Sensors. 2018; 18(11):3725. https://doi.org/10.3390/s18113725
Chicago/Turabian StyleXia, Nan, Yunbao Huang, Haiyan Li, Pu Li, Kefeng Wang, and Feng Wang. 2018. "A Novel Recovery Method of Soft X-ray Spectrum Unfolding Based on Compressive Sensing" Sensors 18, no. 11: 3725. https://doi.org/10.3390/s18113725
APA StyleXia, N., Huang, Y., Li, H., Li, P., Wang, K., & Wang, F. (2018). A Novel Recovery Method of Soft X-ray Spectrum Unfolding Based on Compressive Sensing. Sensors, 18(11), 3725. https://doi.org/10.3390/s18113725




