Urban Land Use and Land Cover Classification Using Novel Deep Learning Models Based on High Spatial Resolution Satellite Imagery
Abstract
1. Introduction
2. Methods
2.1. Network Architecture
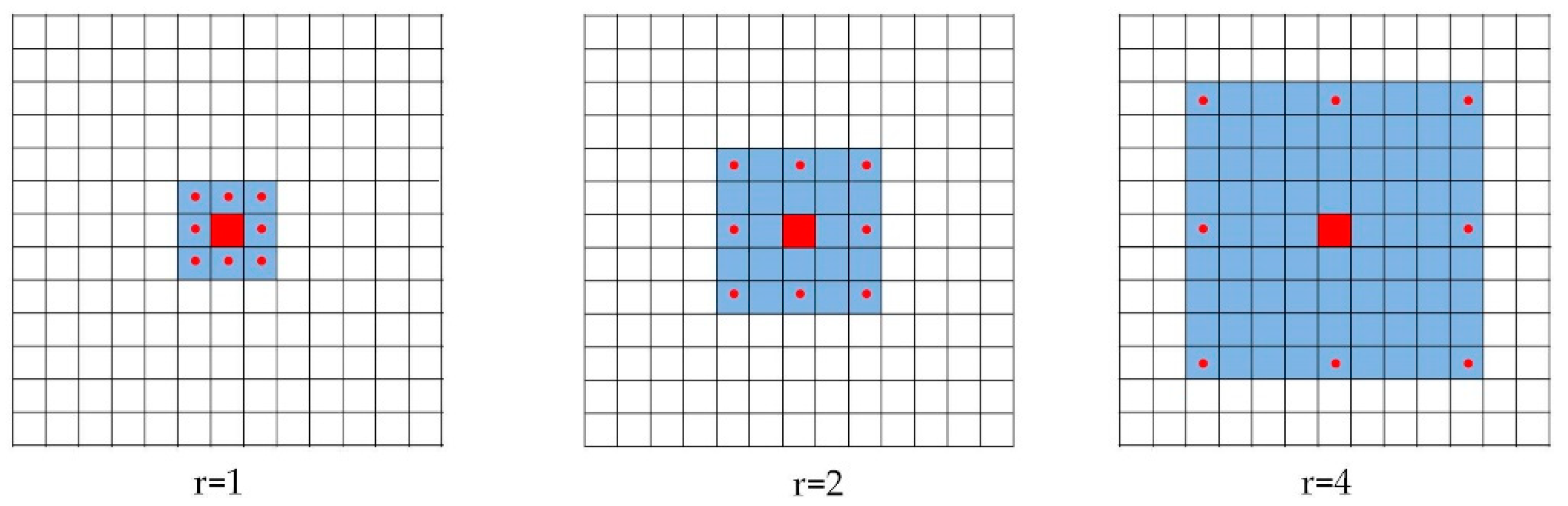
2.1.1. ASPP for Multi-Scale Feature Extraction
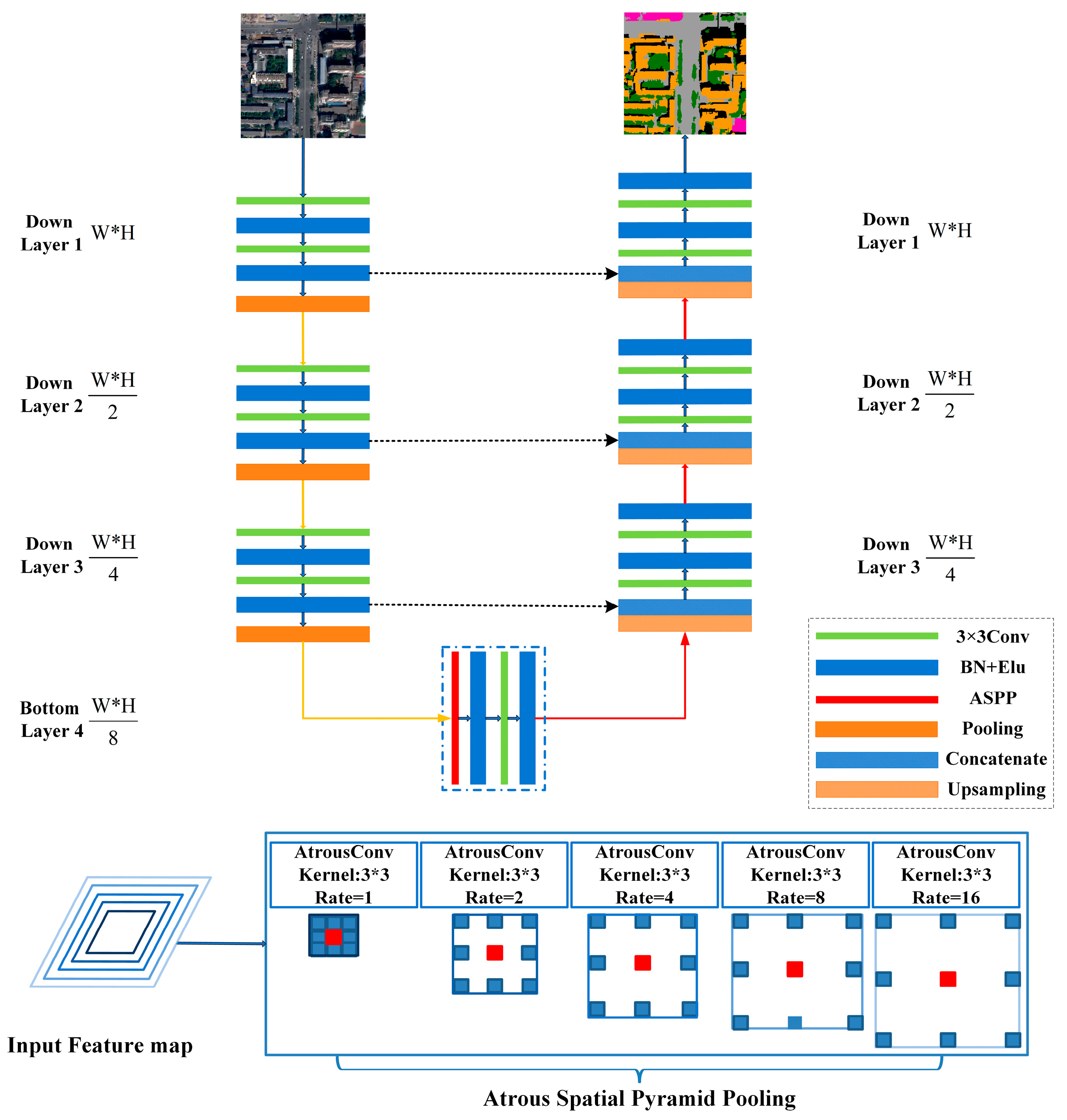
2.1.2. ASPP-Unet Architecture
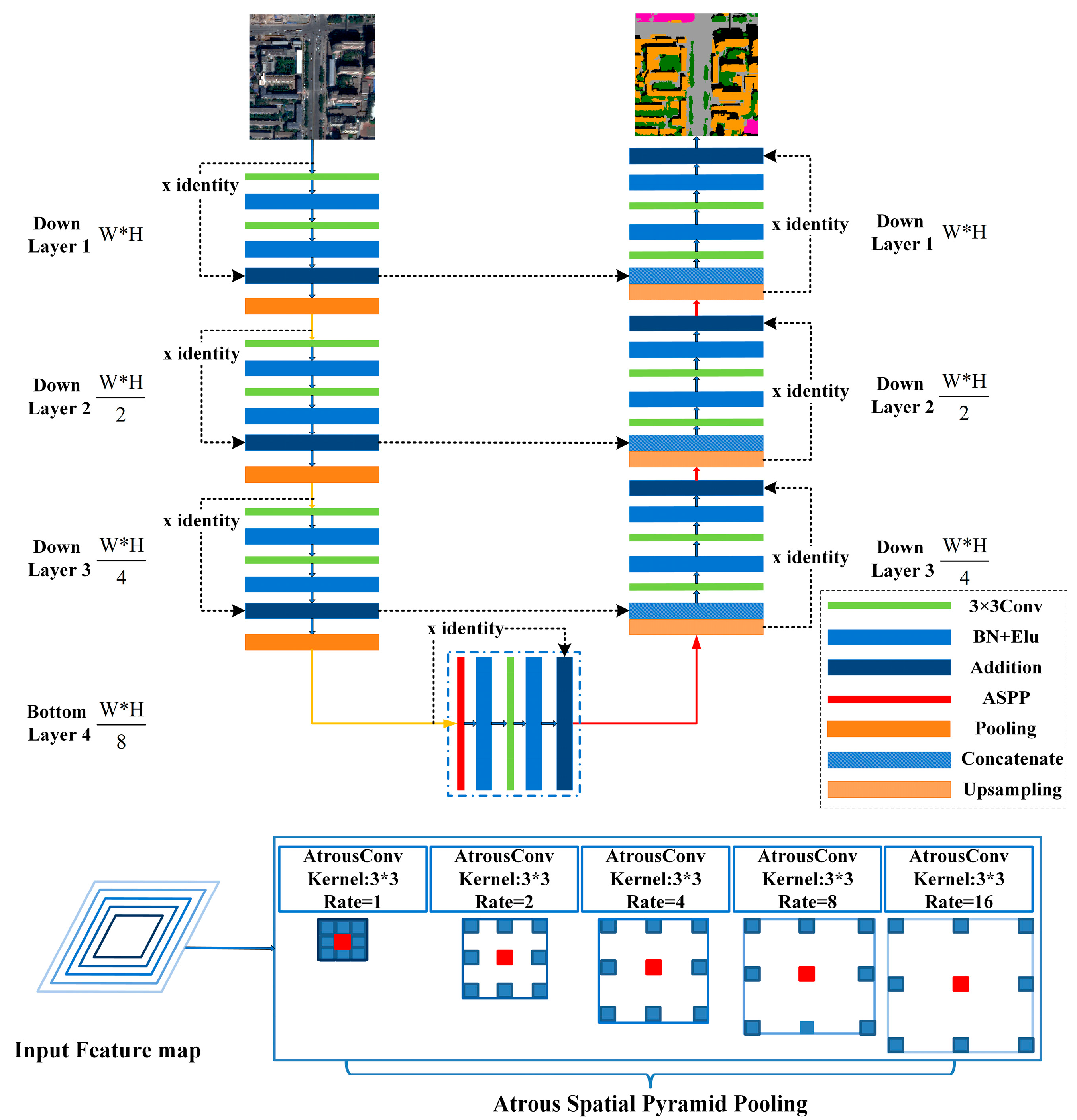
2.1.3. ResASPP-Unet Architecture
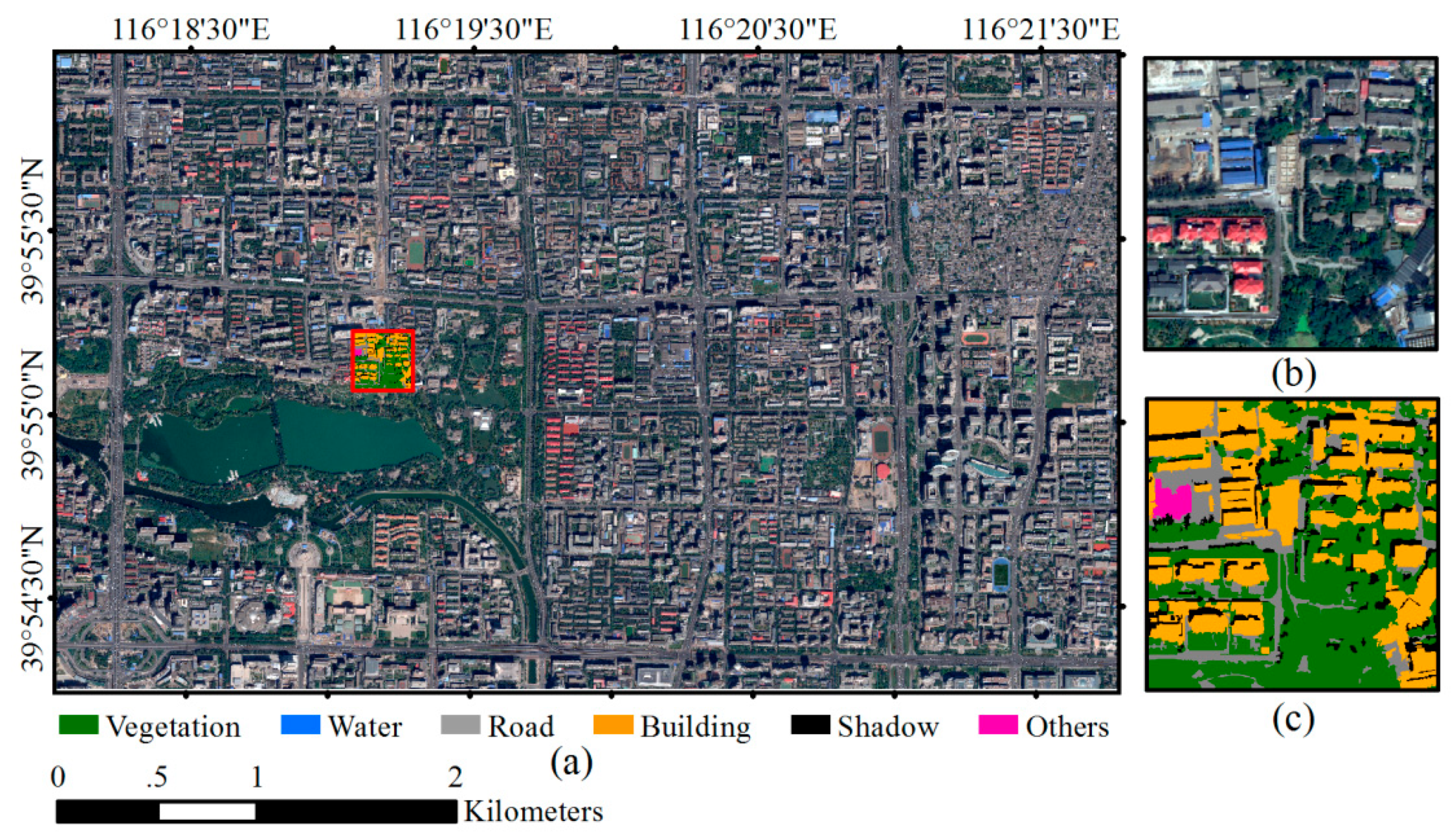
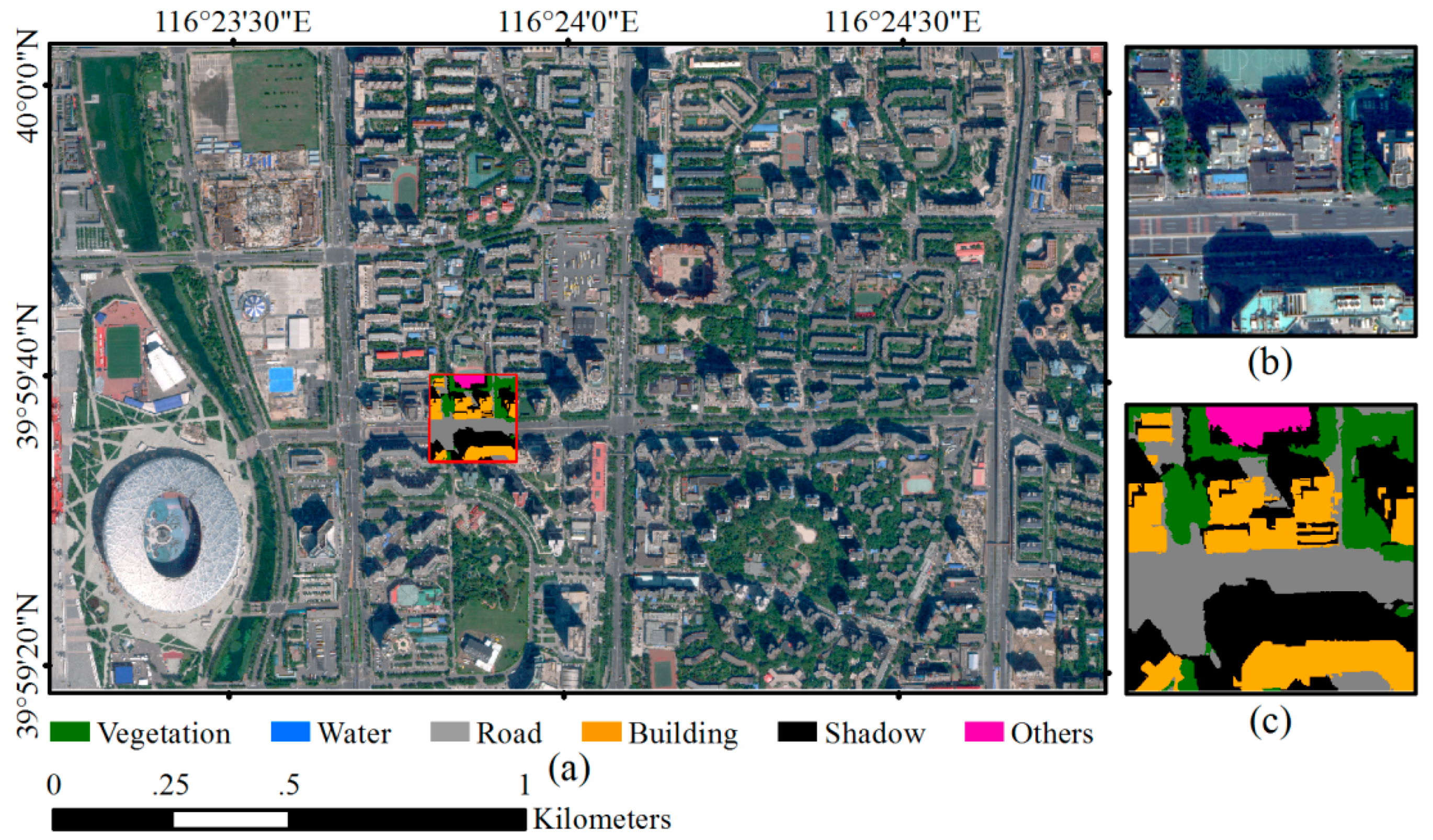
2.2. Datasets and Network Training
2.3. Classification Using the Trained Network
3. Experiments and Comparisons
3.1. Experiments
3.2. Comparison Setup
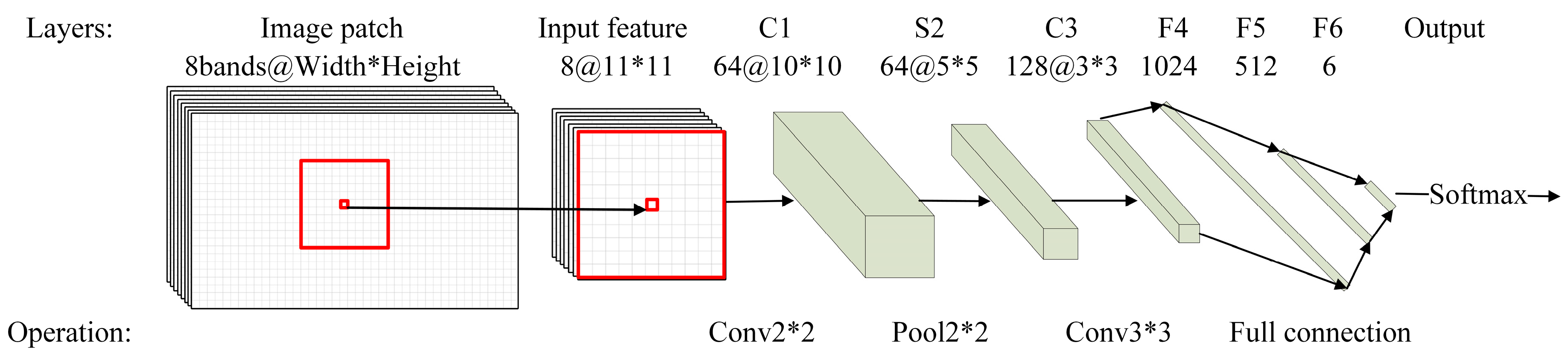
3.2.1. CNN
3.2.2. SVM
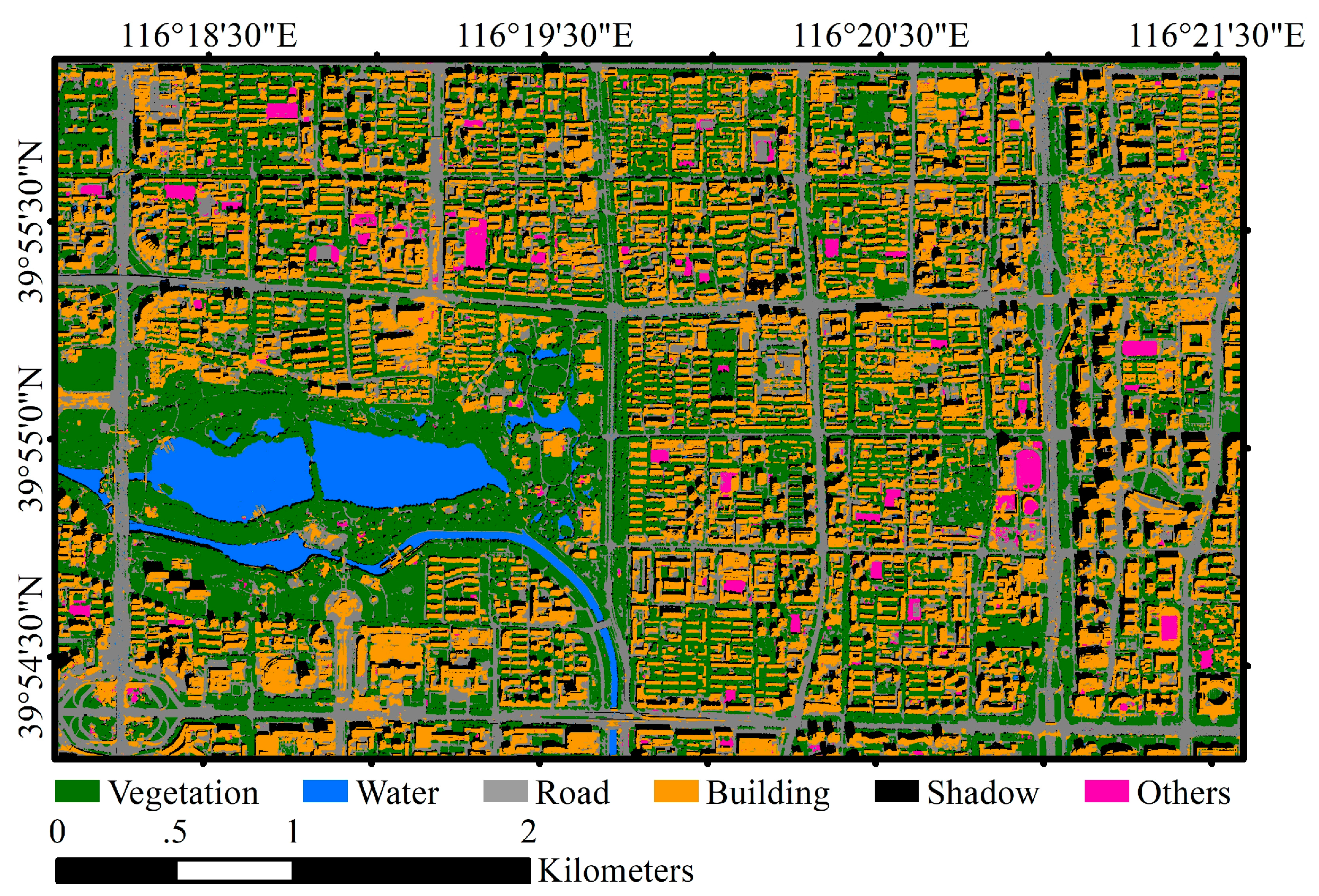
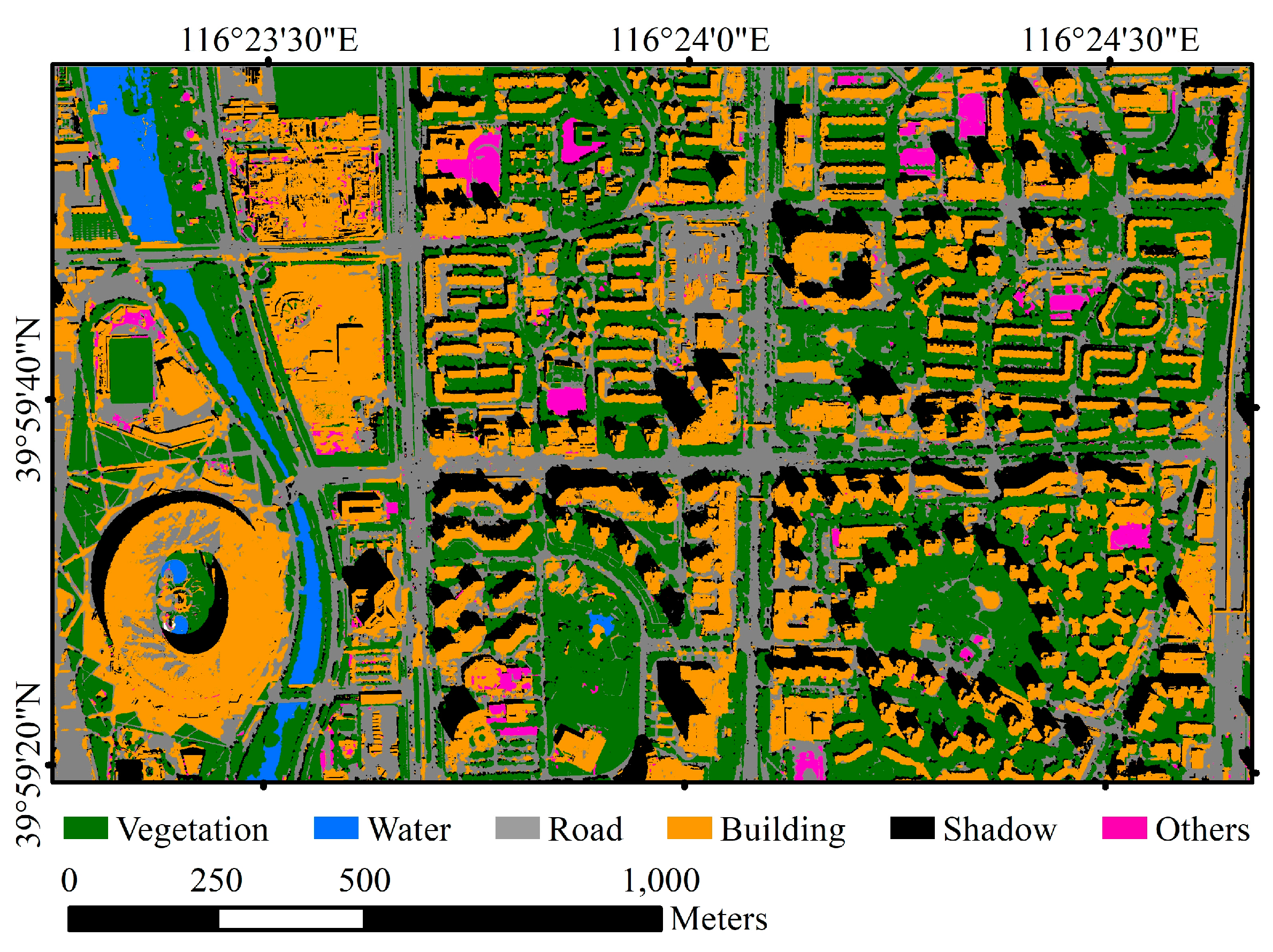
3.3. Results
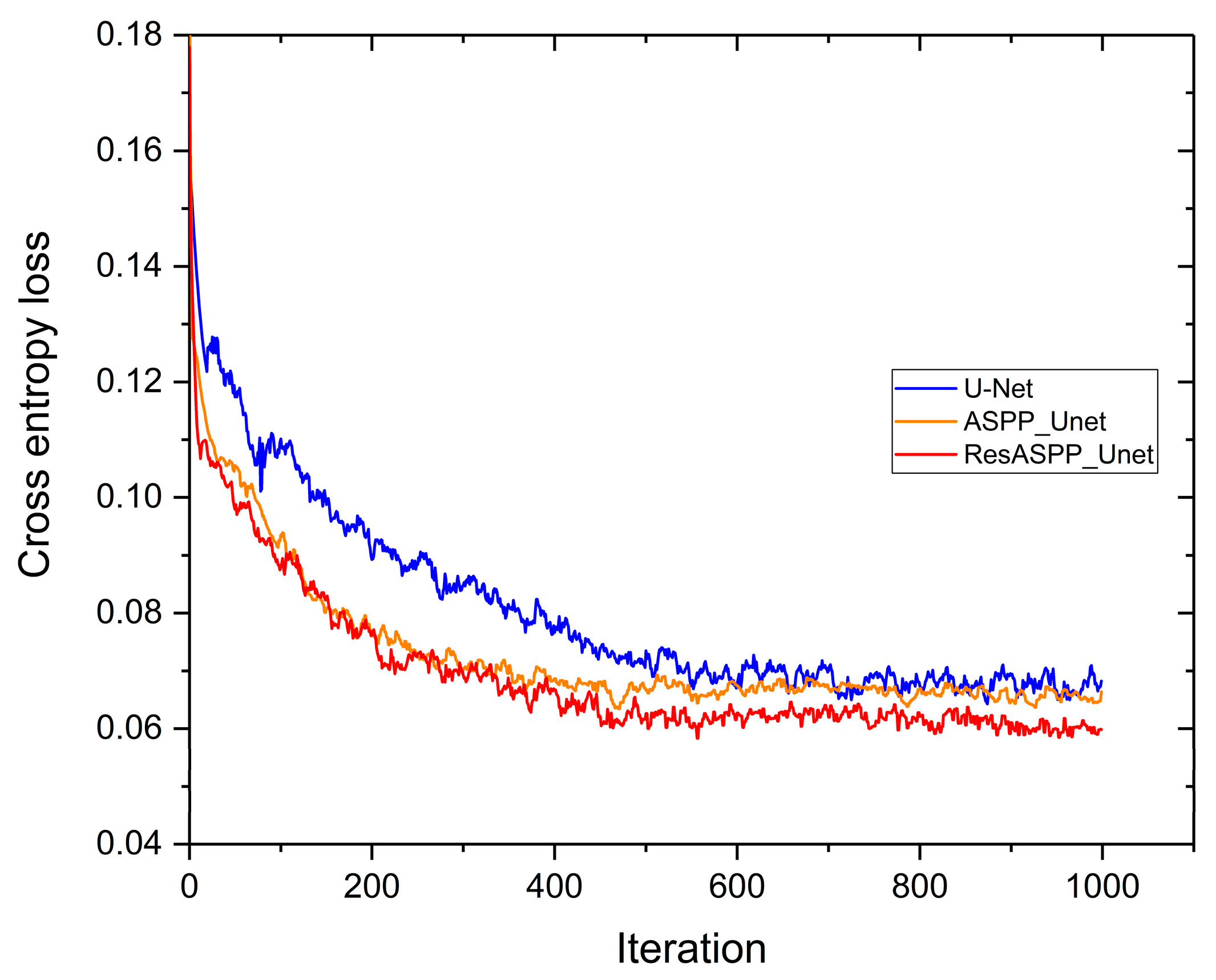
3.3.1. Performances of Res-ASPP-Unet, ASPP-Unet and U-Net
3.3.2. Comparisons with CNN and SVM Models
4. Discussion
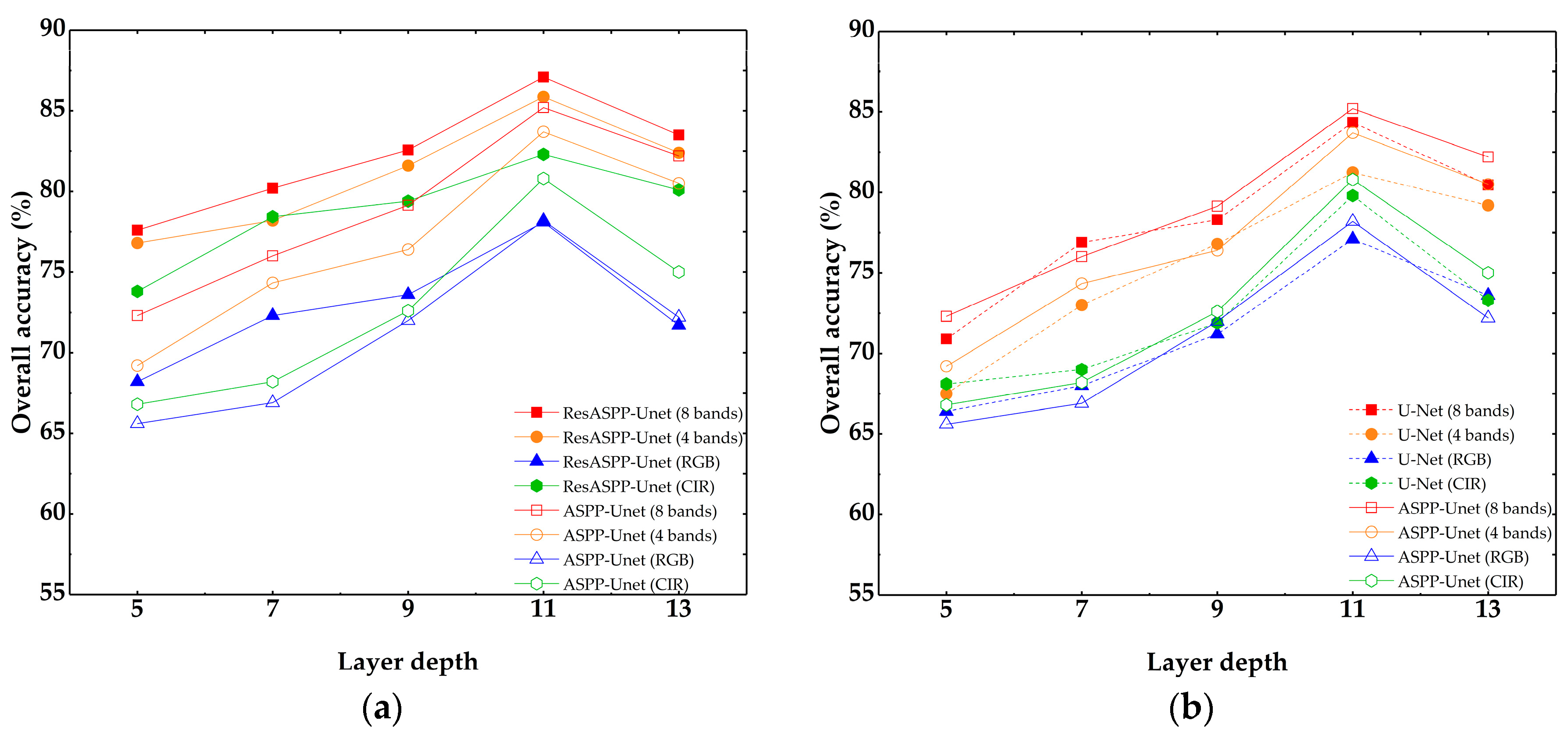
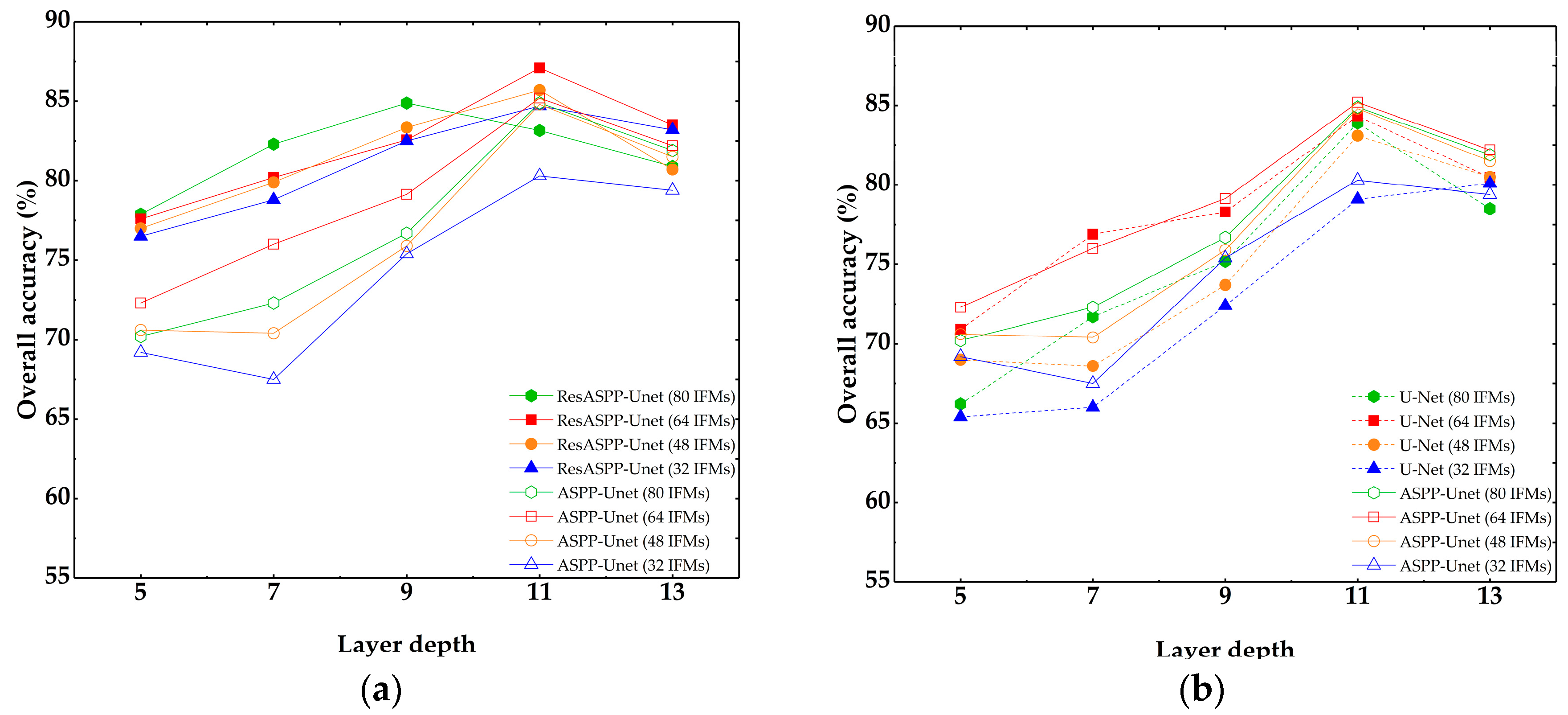
4.1. Parameter Sensitivities of Res-ASPP-Unet, ASPP-Unet and U-Net
4.2. Res-ASPP-Unet and ASPP-Unet vs. U-Net, CNN and SVM
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hussain, E.; Shan, J. Object-based urban land cover classification using rule inheritance over very high-resolution multisensor and multitemporal data. GISci. Remote Sens. 2016, 53, 164–182. [Google Scholar] [CrossRef]
- Myint, S.W.; Gober, P.; Brazel, A.; Grossman-Clarke, S.; Weng, Q. Per-pixel vs. object-based classification of urban land cover extraction using high spatial resolution imagery. Remote Sens. Environ. 2011, 115, 1145–1161. [Google Scholar] [CrossRef]
- Landry, S. Object-based urban detailed land cover classification with high spatial resolution IKONOS imagery. Int. J. Remote Sens. 2011, 32, 3285–3308. [Google Scholar]
- Li, X.; Shao, G. Object-based urban vegetation mapping with high-resolution aerial photography as a single data source. Int. J. Remote Sens. 2013, 34, 771–789. [Google Scholar] [CrossRef]
- Ke, Y.; Quackenbush, L.J.; Im, J. Synergistic use of QuickBird multispectral imagery and LIDAR data for object-based forest species classification. Remote Sens. Environ. 2010, 114, 1141–1154. [Google Scholar] [CrossRef]
- Li, D.; Ke, Y.; Gong, H.; Li, X. Object-based urban tree species classification using bi-temporal WorldView-2 and WorldView-3 images. Remote Sens. 2015, 7, 16917–16937. [Google Scholar] [CrossRef]
- Baatz, M.; Schäpe, A. Multiresolution Segmentation: An Optimization Approach for High Quality Multi-scale Image Segmentation. In Angewandte Geographische Information Sverarbeitung XII; Herbert Wichmann Verlag: Heidelberg, Germany, 2000; pp. 12–23. [Google Scholar]
- Cheng, Y. Mean shift, mode seeking, and clustering. IEEE Trans. Pattern 1995, 17, 790–799. [Google Scholar] [CrossRef]
- Fu, G.; Zhao, H.; Li, C.; Shi, L. Segmentation for High-Resolution Optical Remote Sensing Imagery Using Improved Quadtree and Region Adjacency Graph Technique. Remote Sens. 2013, 5, 3259–3279. [Google Scholar] [CrossRef]
- Hinton, G.; Osindero, S.; Welling, M.; Teh, Y.-W. Unsupervised Discovery of Nonlinear Structure Using Contrastive Backpropagation. Science 2006, 30, 725–732. [Google Scholar] [CrossRef] [PubMed]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the Neural Information Processing Systems (NIPS) Conference, La Jolla, CA, USA, 3–8 December 2012. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, W.; Roth, S.; Schiele, B. The cityscapes dataset for semantic urban scene understanding. In Proceedings of the IEEE conference on computer vision and pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 3213–3223. [Google Scholar]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Mnih, V.; Hinton, G.E. Learning to detect roads in high-resolution aerial images. In Computer Vision—ECCV 2010, Lecture Notes in Computer Science; Daniilidis, K., Maragos, P., Paragios, N., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6316, pp. 210–223. [Google Scholar]
- Wang, J.; Song, J.; Chen, M.; Yang, Z. Road network extraction: A neural-dynamic framework based on deep learning and a finite state machine. Int. J. Remote Sens. 2015, 36, 3144–3169. [Google Scholar] [CrossRef]
- Hu, F.; Xia, G.S.; Hu, J.; Zhang, L. Transferring deep convolutional neural networks for the scene classification of high-resolution remote sensing imagery. Remote Sens. 2015, 7, 14680–14707. [Google Scholar] [CrossRef]
- Längkvist, M.; Kiselev, A.; Alirezaie, M.; Loutfi, A. Classification and segmentation of satellite orthoimagery using convolutional neural networks. Remote Sens. 2016, 8, 329. [Google Scholar] [CrossRef]
- Maltezos, E. Deep convolutional neural networks for building extraction from orthoimages and dense image matching point clouds. J. Appl. Remote Sens. 2017, 11, 1–22. [Google Scholar] [CrossRef]
- Pan, X.; Zhao, J. A central-point-enhanced convolutional neural network for high-resolution remote-sensing image classification. Int. J. Remote Sens. 2017, 38, 6554–6581. [Google Scholar] [CrossRef]
- Zhang, C.; Pan, X.; Li, H.; Gardiner, A.; Sargent, I.; Hare, J.; Atkinson, P.M. A hybrid MLP-CNN classifier for very fine resolution remotely sensed image classification. ISPRS J. Photogramm. Remote Sens. 2018, 140, 133–144. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 5–7 June 2015; pp. 3431–3440. [Google Scholar]
- Sherrah, J. Fully convolutional networks for dense semantic labeling of high-resolution aerial imagery. arXiv, 2016; arXiv:1606.02585. [Google Scholar]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Beyond RGB: Very high resolution urban remote sensing with multimodal deep networks. ISPRS J. Photogramm. Remote Sens. 2018, 140, 20–32. [Google Scholar] [CrossRef]
- Sun, X.; Shen, S.; Lin, X.; Hu, Z. Semantic Labeling of High Resolution Aerial Images Using an Ensemble of Fully Convolutional Networks. J. Appl. Remote Sens. 2017, 11, 042617. [Google Scholar] [CrossRef]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Fully Convolutional Neural Networks for Remote Sensing Image Classification. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 5071–5074. [Google Scholar]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional Neural Networks for Large-Scale Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 645–657. [Google Scholar] [CrossRef]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. High-resolution aerial image labeling with convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7092–7103. [Google Scholar] [CrossRef]
- Fu, G.; Liu, C.; Zhou, R.; Sun, T.; Zhang, Q. Classification for High Resolution Remote Sensing Imagery Using a Fully Convolutional Network. Remote Sens. 2017, 9, 498. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Kestur, R.; Farooq, S.; Abdal, R.; Mehraj, E.; Narasipura, O.; Mudigere, M. UFCN: A fully convolutional neural network for road extraction in RGB imagery acquired by remote sensing from an unmanned aerial vehicle. J. Appl. Remote Sens. 2018, 12, 016020. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, Q.; Wang, Y. Road extraction by deep residual u-net. IEEE Geosci. Remote Sens. Lett. 2018, 15, 749–753. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, L.; Xie, Z.; Chen, Z. Building Extraction in Very High Resolution Remote Sensing Imagery Using Deep Learning and Guided Filters. Remote Sens. 2018, 10, 144. [Google Scholar] [CrossRef]
- Li, R.; Liu, W.; Yang, L.; Sun, S.; Hu, W.; Zhang, F.; Li, W. DeepUnet: A deep fully convolutional network for pixel-level sea-land segmentation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 99, 1–9. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv, 2017; arXiv:1706.05587. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. arXiv, 2018; arXiv:1802.02611. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Clevert, D.; Unterthiner, T.; Hochreiter, S. Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs). arXiv, 2015; arXiv:1511.07289. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv, 2015; arXiv:1502.03167. [Google Scholar]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Sun, W.; Messinger, D. Nearest-neighbor diffusion-based pan-sharpening algorithm for spectral images. Opt. Eng. 2013, 53, 013107. [Google Scholar] [CrossRef]
- Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; Wiley: Indianapolis, IN, USA, 2011; pp. 154–196. ISBN 9780470458365. [Google Scholar]
- Definients Image. eCognition User’s Guide 4; Definients Image: Bernhard, Germany, 2004. [Google Scholar]
- Collobert, R.; Weston, J.; Bottou, L.; Karlen, M.; Kavukcuoglu, K.; Kuksa, P. Natural language processing (almost) from scratch. J. Mach. Learn. Res. 2011, 12, 2493–2537. [Google Scholar]
- Ning, Q. On the momentum term in gradient descent learning algorithms. Neural Netw. 1999, 12, 145–151. [Google Scholar]
- Srivastava, N.; Hinton, G.E.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Ciresan, D.; Giusti, A.; Gambardella, L.M.; Schmidhuber, J. Deep neural networks segment neuronal membranes in electron microscopy images. In Proceedings of the Neural Information Processing Systems 2012, Lake Tahoe, NV, USA, 3 December 2012; pp. 2843–2851. [Google Scholar]
- Cortes, C.; Vapnik, V. Support vector network. Mach. Learn. 1995, 3, 273–297. [Google Scholar] [CrossRef]
- Paisitkriangkrai, S.; Sherrah, J.; Janney, P.; Hengel, V.D. Effective semantic pixel labelling with convolutional networks and conditional random fields. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 5–7 June 2015; pp. 36–43. [Google Scholar]
- Huang, X.; Hu, T.; Li, J.; Wang, Q.; Benediktsson, J.A. Mapping Urban Areas in China Using Multisource Data with a Novel Ensemble SVM Method. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4258–4273. [Google Scholar] [CrossRef]
- Ke, Y.; Im, J.; Park, S.; Gong, H. Spatiotemporal downscaling approaches for monitoring 8-day 30 m actual evapotranspiration. ISPRS J. Photogramm. Remote Sens. 2017, 126, 79–93. [Google Scholar] [CrossRef]
- Ke, Y.; Im, J.; Park, S.; Gong, H. Downscaling of MODIS One kilometer evapotranspiration using Landsat-8 data and machine learning approaches. Remote Sens. 2016, 8, 215. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Learning multiscale and deep representations for classifying remotely sensed imagery. ISPRS J. Photogramm. Remote Sens. 2016, 113, 155–165. [Google Scholar] [CrossRef]

| Fixed Parameters | Varying Input/Parameters | ||
|---|---|---|---|
| Initial learning rate | 0.1 | Input training samples | 8 bands, 4 bands (IR + RGB), RGB and CIR |
| Number of epoch | 100 | Number of IFMs | 16, 32, 48, 64 |
| Filter size | 3 × 3 | Layer depth | 5, 7, 9, 11, 13 |
| Pooling size | 2 × 2 | ||
| Activation function | Elu | ||
| WV2 | SVM | CNN | U-Net | ASPP-Unet | Res_ASPP_Unet | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PA (%) | UA (%) | F1 | PA (%) | UA (%) | F1 | PA (%) | UA (%) | F1 | PA (%) | UA (%) | F1 | PA (%) | UA (%) | F1 | |
| Vegetation | 91.9 | 91.1 | 0.915 | 92.4 | 93.2 | 0.928 | 91.8 | 93.3 | 0.926 | 91.7 | 94.1 | 0.929 | 91.8 | 94.3 | 0.930 |
| Water | 98.9 | 55.9 | 0.714 | 97.8 | 90.8 | 0.942 | 97.5 | 79.4 | 0.875 | 98.5 | 87.7 | 0.928 | 90.2 | 91.0 | 0.906 |
| Road | 45.6 | 52.4 | 0.488 | 67.7 | 74.4 | 0.709 | 71.8 | 74.5 | 0.731 | 78.0 | 70.1 | 0.738 | 78.5 | 79.9 | 0.792 |
| Building | 58.9 | 49.1 | 0.536 | 83.5 | 71.9 | 0.773 | 83.1 | 81.3 | 0.822 | 81.3 | 84.5 | 0.830 | 85.1 | 85.9 | 0.856 |
| Shadow | 67.7 | 86.7 | 0.796 | 81.1 | 87.8 | 0.843 | 81.8 | 81.7 | 0.817 | 79.0 | 80.3 | 0.796 | 89.0 | 74.9 | 0.814 |
| Others | 41.1 | 72.7 | 0.525 | 13.1 | 79.2 | 0.224 | 0 | 0 | 0 | 0 | 0 | 0 | 39.2 | 84.4 | 0.536 |
| Test OA (%) | 71.4 | 83.6 | 84.7 | 85.2 | 87.1 | ||||||||||
| kappa | 0.606 | 0.774 | 0.788 | 0.793 | 0.820 | ||||||||||
| Training OA (%) | 79.3 | 89.5 | 85.5 | 86.4 | 87.6 | ||||||||||
| WV3 | SVM | CNN | U-Net | ASPP-Unet | Res_ASPP_Unet | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PA (%) | UA (%) | F1 | PA (%) | UA (%) | F1 | PA (%) | UA (%) | F1 | PA (%) | UA (%) | F1 | PA (%) | UA (%) | F1 | |
| Vegetation | 69.4 | 44.5 | 0.542 | 94.8 | 91.5 | 0.931 | 93.7 | 91.7 | 0.927 | 94.6 | 92.1 | 0.933 | 93.1 | 93.0 | 0.931 |
| Water | 0.12 | 0.01 | 0.001 | 97.0 | 82.7 | 0.892 | 79.1 | 94.3 | 0.860 | 78.4 | 95.5 | 0.861 | 76.8 | 91.4 | 0.835 |
| Road | 44.9 | 57.7 | 0.505 | 61.9 | 65.3 | 0.635 | 63.9 | 52.6 | 0.577 | 75.2 | 63.7 | 0.690 | 75.2 | 75.9 | 0.755 |
| Building | 29.4 | 32.7 | 0.310 | 67.4 | 60.2 | 0.636 | 69.1 | 81.0 | 0.746 | 69.7 | 83.7 | 0.761 | 74.8 | 80.0 | 0.773 |
| Shadow | 63.8 | 79.3 | 0.706 | 84.7 | 91.9 | 0.882 | 89.3 | 87.2 | 0.882 | 88.5 | 90.0 | 0.897 | 89.5 | 80.7 | 0.849 |
| Others | 0 | 0 | 0 | 49.6 | 78.9 | 0.609 | 0 | 0 | 0 | 0 | 0 | 0 | 75.8 | 97.0 | 0.851 |
| Test OA (%) | 51.3 | 79.2 | 81.0 | 83.2 | 84.0 | ||||||||||
| kappa | 0.359 | 0.722 | 0.740 | 0.774 | 0.787 | ||||||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Ke, Y.; Zhang, Z.; Wang, M.; Li, P.; Zhang, S. Urban Land Use and Land Cover Classification Using Novel Deep Learning Models Based on High Spatial Resolution Satellite Imagery. Sensors 2018, 18, 3717. https://doi.org/10.3390/s18113717
Zhang P, Ke Y, Zhang Z, Wang M, Li P, Zhang S. Urban Land Use and Land Cover Classification Using Novel Deep Learning Models Based on High Spatial Resolution Satellite Imagery. Sensors. 2018; 18(11):3717. https://doi.org/10.3390/s18113717
Chicago/Turabian StyleZhang, Pengbin, Yinghai Ke, Zhenxin Zhang, Mingli Wang, Peng Li, and Shuangyue Zhang. 2018. "Urban Land Use and Land Cover Classification Using Novel Deep Learning Models Based on High Spatial Resolution Satellite Imagery" Sensors 18, no. 11: 3717. https://doi.org/10.3390/s18113717
APA StyleZhang, P., Ke, Y., Zhang, Z., Wang, M., Li, P., & Zhang, S. (2018). Urban Land Use and Land Cover Classification Using Novel Deep Learning Models Based on High Spatial Resolution Satellite Imagery. Sensors, 18(11), 3717. https://doi.org/10.3390/s18113717





