3D Imaging Based on Depth Measurement Technologies
Abstract
1. Introduction
2. Theory of 3D Imaging and Progress of Its Development
2.1. Ray-Based Light Field Imaging
2.2. Wavefront-Based Light Field Imaging
3. Ray-Based Light Field Imaging from Depth Measurements
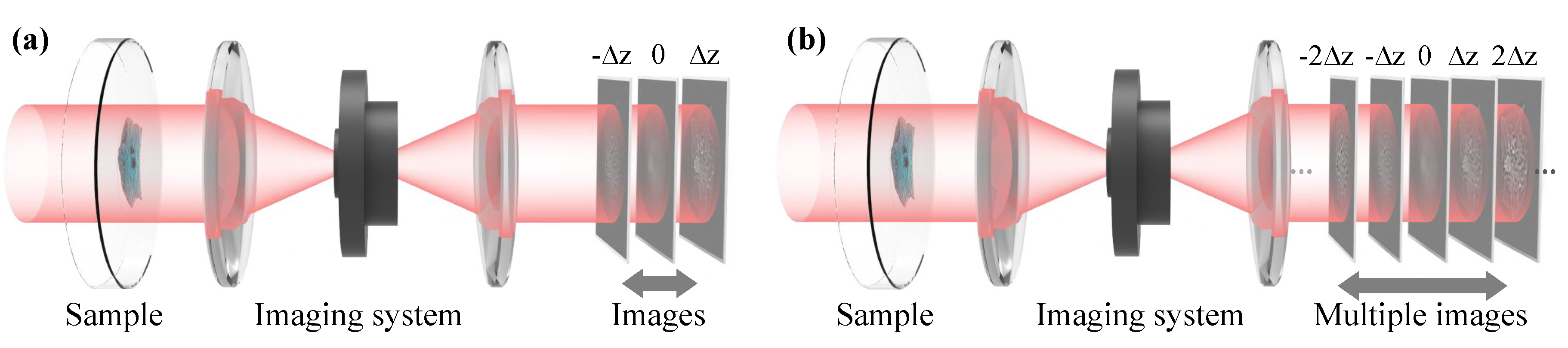
3.1. Focal Sweeping Measurement with a Conventional Camera
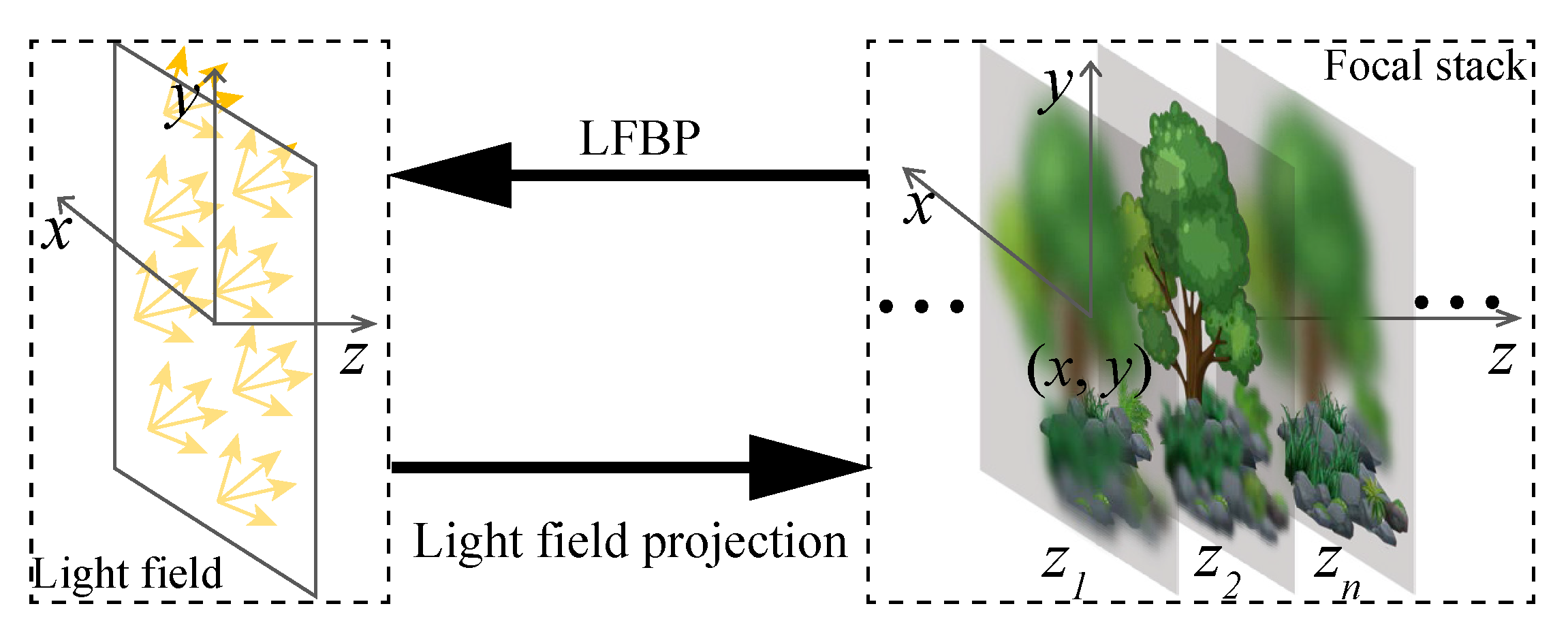
3.2. Light Ray Field Reconstruction by Back-Projection
3.3. Iterative Light Ray Field Reconstruction Based on Back-Projection
3.4. Light Field Moment Imaging
3.5. Issues
4. Wavefront-Based Light Field Imaging from Depth Measurements
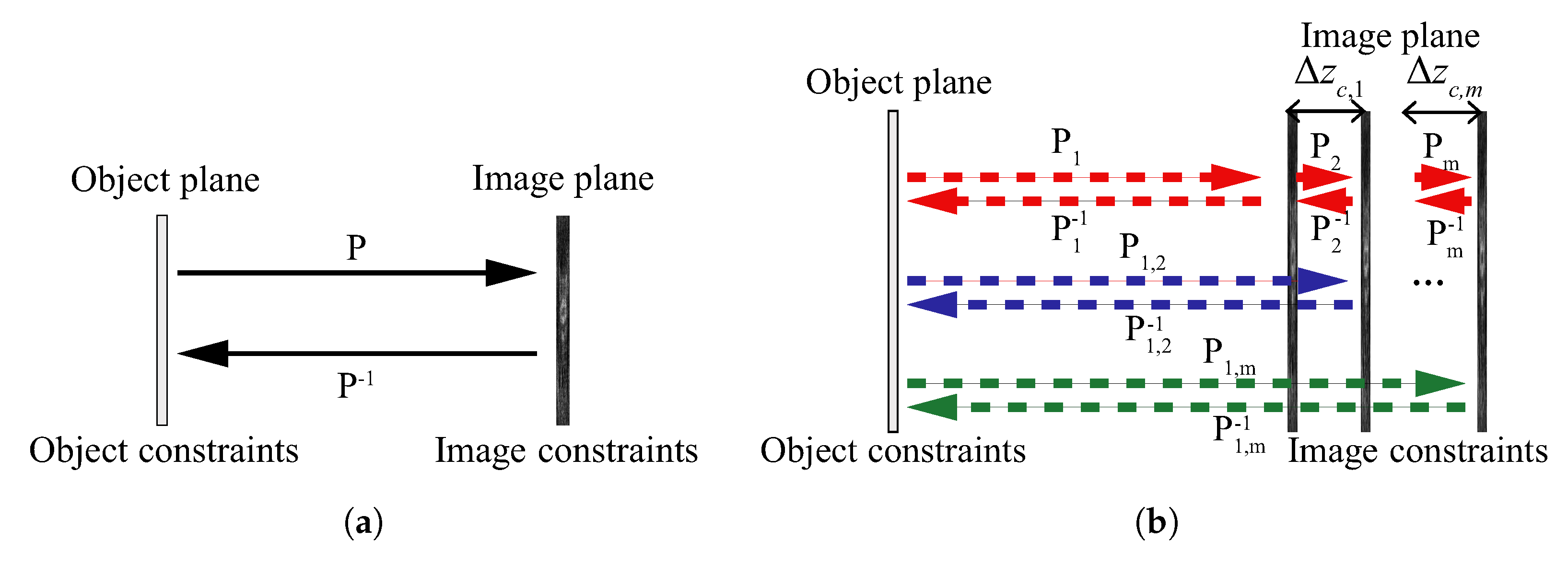
4.1. Iterative Phase Retrieval
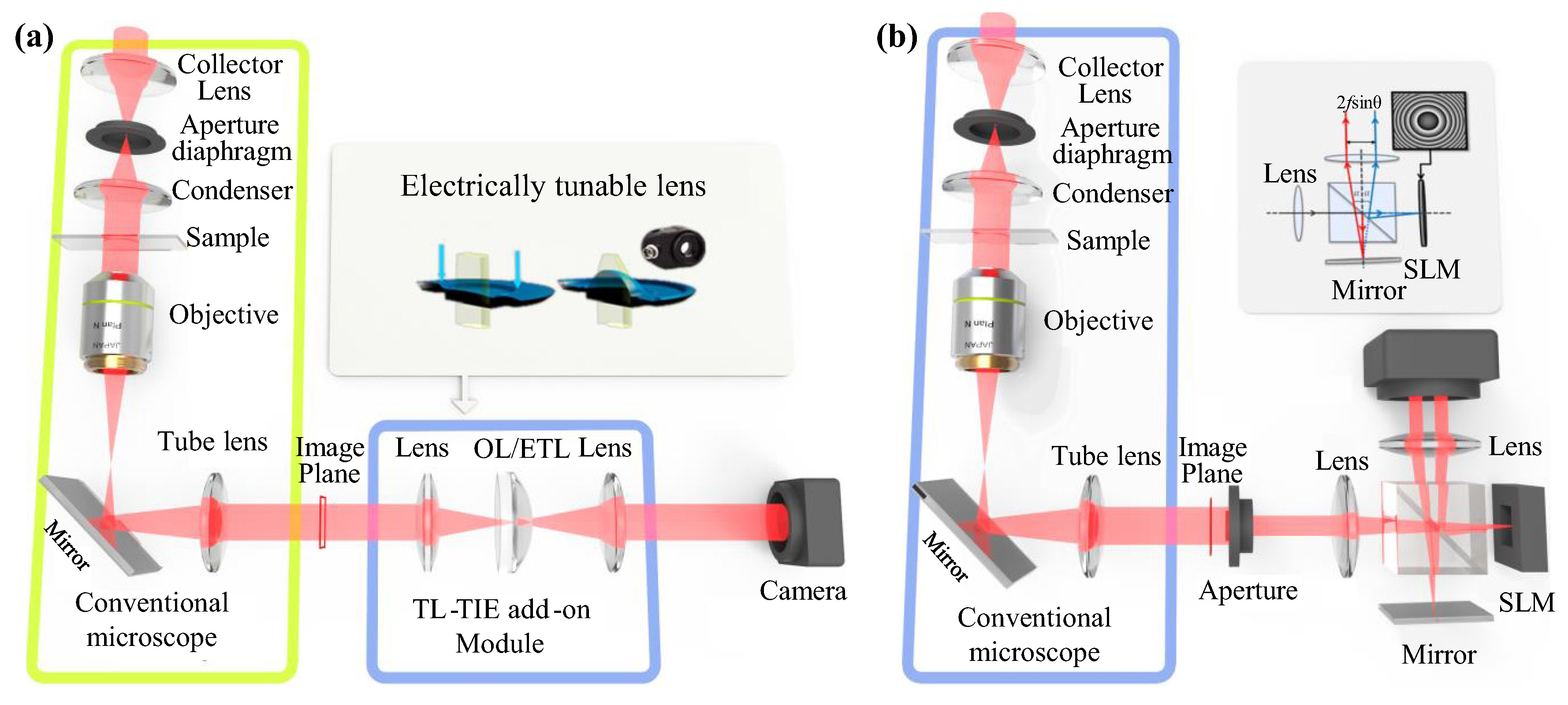
4.2. Transport of Intensity Equation
4.2.1. Solutions to Transport of Intensity Equation
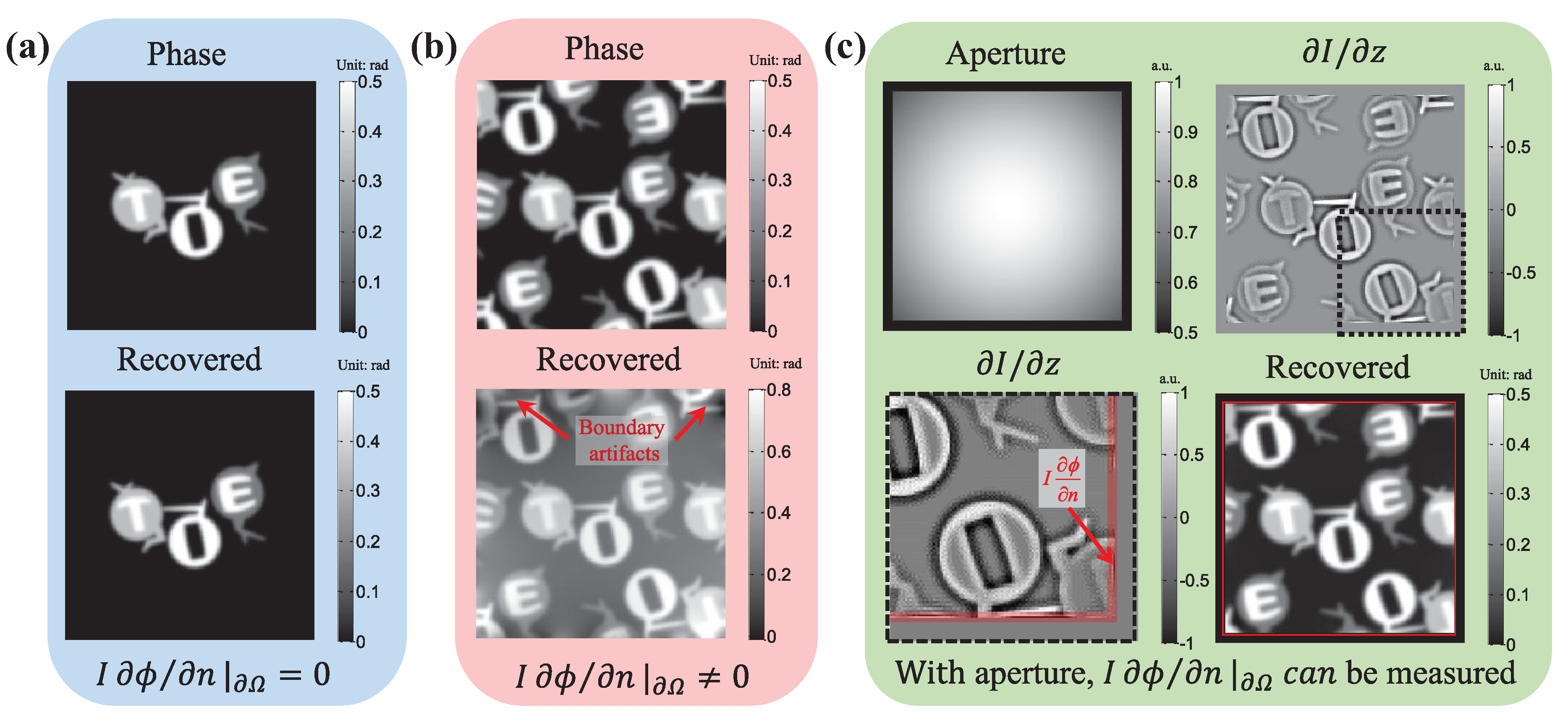
4.2.2. Phase Discrepancy and Compensation
4.2.3. Axial Intensity Derivative Estimation
4.3. Discussion
5. Connection between Ray-Based and Wave-Based Light Field Imaging
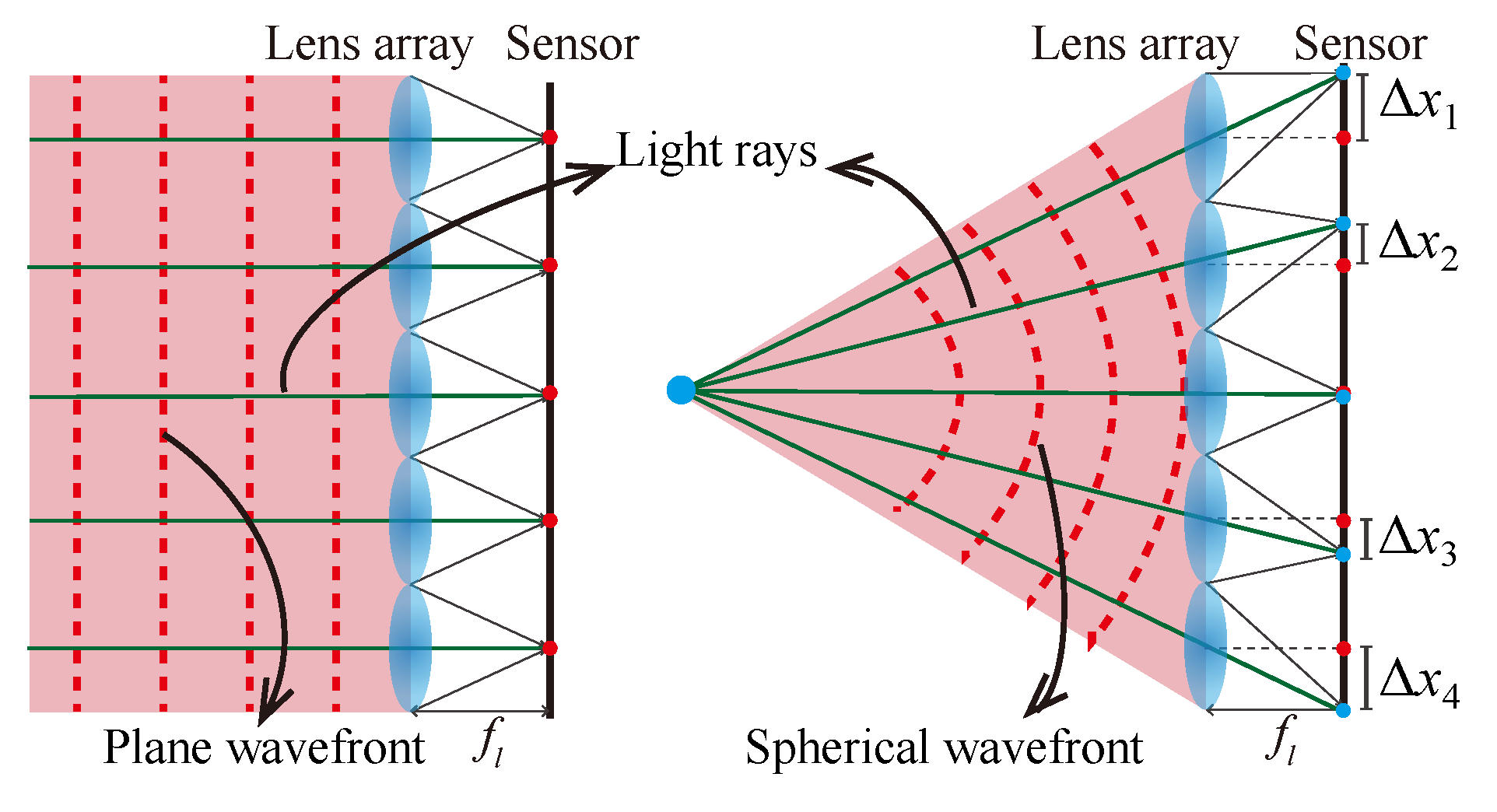
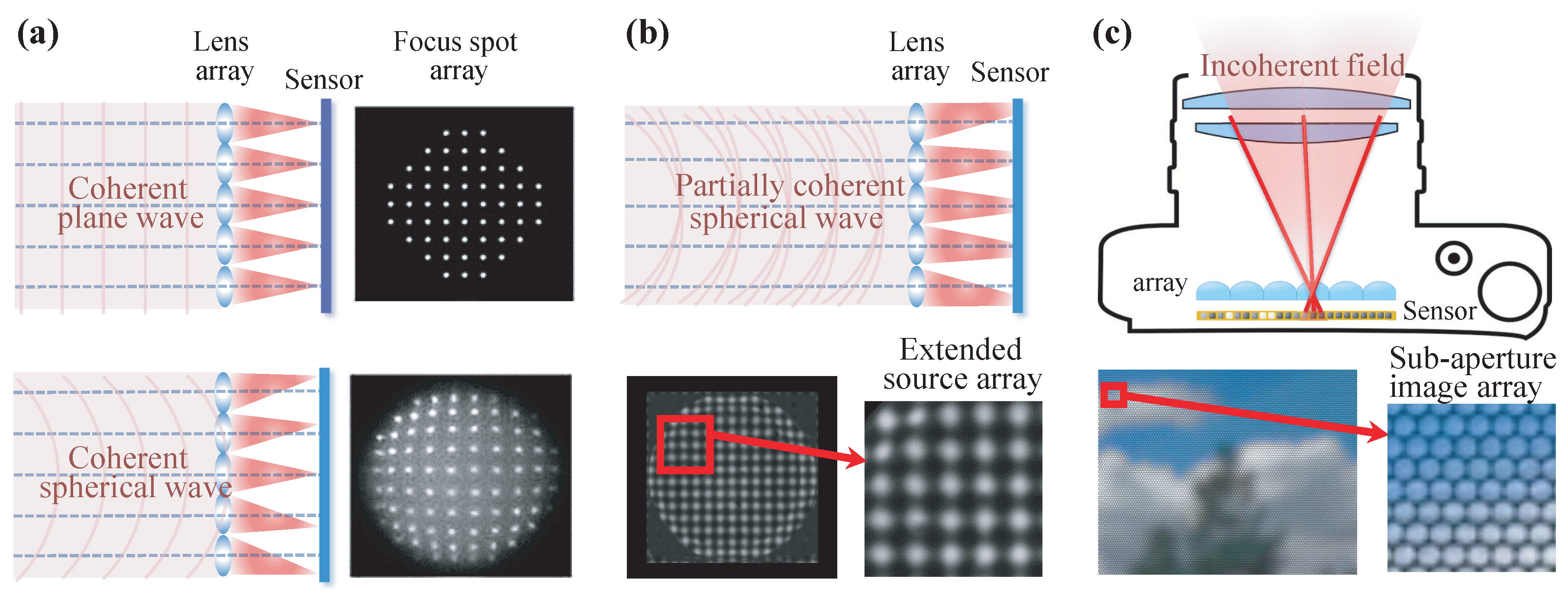
5.1. Shack–Hartmann Wavefront Sensor and Light Ray Field Camera
5.2. Transport of Intensity Equation and Light Field Moment Imaging
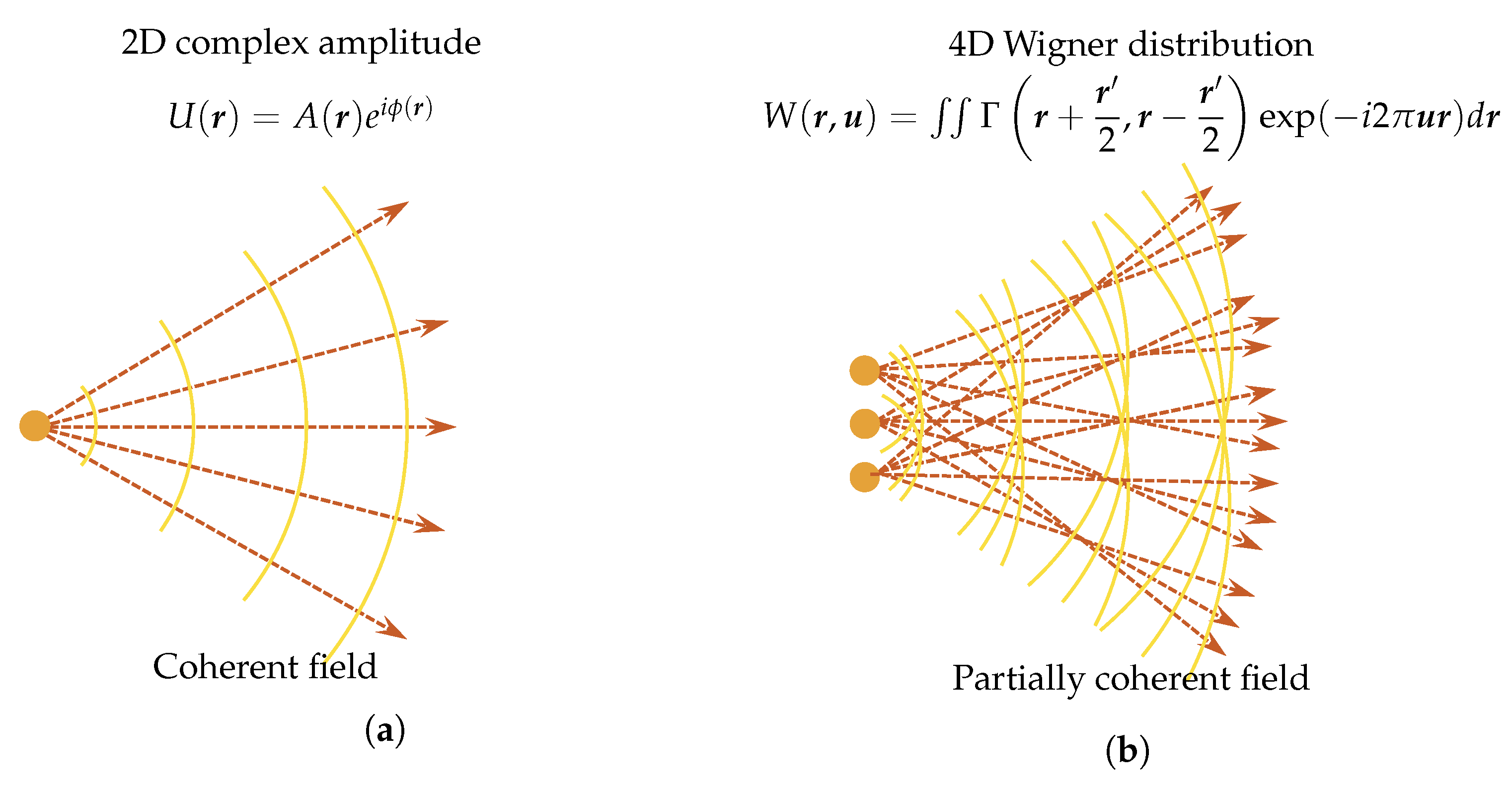
5.2.1. Generalized Transport of Intensity Equation for Partially Coherent Field
5.2.2. Generalized Definition of “Phase” in Phase Space
5.2.3. Light Field Moment Imaging Using Transport of Intensity Equation
5.3. Hologram Synthesis from Focal Stack Measurements
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Watanabe, T.M.; Sato, T.; Gonda, K.; Higuchi, H. Three-dimensional nanometry of vesicle transport in living cells using dual-focus imaging optics. Biochem. Biophys. Res. Commun. 2007, 359, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Tanida, J.; Kumagai, T.; Yamada, K.; Miyatake, S.; Ishida, K.; Morimoto, T.; Kondou, N.; Miyazaki, D.; Ichioka, Y. Thin observation module by bound optics (TOMBO): concept and experimental verification. Appl. Opt. 2001, 40, 1806–1813. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, M. Light-field and holographic three-dimensional displays. J. Opt. Soc. Am. A 2016, 33, 2348–2364. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Corral, M.; Javidi, B. Fundamentals of 3D imaging and displays: A tutorial on integral imaging, light-field, and plenoptic systems. Adv. Opt. Photonics 2018, 10, 512–566. [Google Scholar] [CrossRef]
- Bruning, J.H.; Herriott, D.R.; Gallagher, J.E.; Rosenfeld, D.P.; White, A.D.; Brangaccio, D.J. Digital wavefront measuring interferometer for testing optical surfaces and lenses. Appl. Opt. 1974, 13, 2693–2703. [Google Scholar] [CrossRef] [PubMed]
- Wolf, E. Three-dimensional structure determination of semi-transparent objects from holographic data. Opt. Commun. 1969, 1, 153–156. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar] [CrossRef]
- Saleh, B.E.; Teich, M.C.; Saleh, B.E. Fundamentals of Photonics, 2nd ed.; Wiley: New York, NY, USA, 2007; Volume 22. [Google Scholar]
- Gershun, A. The light field. J. Math. Phys. 1939, 18, 51–151. [Google Scholar] [CrossRef]
- Lam, E.Y. Computational photography with plenoptic camera and light field capture: Tutorial. J. Opt. Soc. Am. 2015, 32, 2021–2032. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Micó, V.; Gao, P. Resolution enhancement in phase microscopy: A review. Preprints 2018. [Google Scholar] [CrossRef]
- Hong, J.; Kim, Y.; Choi, H.J.; Hahn, J.; Park, J.H.; Kim, H.; Min, S.W.; Chen, N.; Lee, B. Three-Dimensional display technologies of recent interest: principles, status, and issues. Appl. Opt. 2011, 50, H87–H115. [Google Scholar] [CrossRef] [PubMed]
- Park, S.G.; Yeom, J.; Jeong, Y.; Chen, N.; Hong, J.Y.; Lee, B. Recent issues on integral imaging and its applications. J. Inf. Dis. 2014, 15, 37–46. [Google Scholar] [CrossRef]
- Zhao, Y.; Kwon, K.C.; Piao, Y.L.; Jeon, S.H.; Kim, N. Depth-layer weighted prediction method for a full-color polygon-based holographic system with real objects. Opt. Lett. 2017, 42, 2599–2602. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Hong, K.; Yeom, J.; Chen, N.; Park, J.H.; Kim, N.; Lee, B. Acceleration method for computer generated spherical hologram calculation of real objects using graphics processing unit. Chin. Opt. Lett. 2014, 12, 060016. [Google Scholar] [CrossRef]
- Mait, J.N.; Euliss, G.W.; Athale, R.A. Computational imaging. Adv. Opt. Photonics 2018, 10, 409–483. [Google Scholar] [CrossRef]
- Horisaki, R.; Ogura, Y.; Aino, M.; Tanida, J. Single-shot phase imaging with a coded aperture. Opt. Lett. 2014, 39, 6466–6469. [Google Scholar] [CrossRef] [PubMed]
- Fienup, J.R. Phase retrieval algorithms: A comparison. Appl. Opt. 1982, 21, 2758–2769. [Google Scholar] [CrossRef] [PubMed]
- Testorf, M.; Hennelly, B.; Ojeda-Castañeda, J. Phase-Space Optics; McGraw-Hill Professional Publishing: New York, NY, USA, 2009. [Google Scholar]
- Teague, M.R. Deterministic phase retrieval: A Green’s function solution. J. Opt. Soc. Am. 1983, 73, 1434–1441. [Google Scholar] [CrossRef]
- Gabor, D. A new microscopic principle. Nature 1948, 161, 777–778. [Google Scholar] [CrossRef] [PubMed]
- Poon, T.C. Digital Holography and Three-Dimensional Display: Principles and Applications; Springer: London, UK, 2006. [Google Scholar]
- Boesl, U. Time-of-flight mass spectrometry: Introduction to the basics. Mass Spectrom. Rev. 2016, 36, 86–109. [Google Scholar] [CrossRef] [PubMed]
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photonics 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Banks, M.S.; Read, J.C.A.; Allison, R.S.; Watt, S.J. Stereoscopy and the Human Visual System. SMPTE Motion Imaging J. 2012, 121, 24–43. [Google Scholar] [CrossRef] [PubMed]
- Orth, A.; Crozier, K.B. Light field moment imaging. Opt. Lett. 2013, 38, 2666–2668. [Google Scholar] [CrossRef] [PubMed]
- Levoy, M. Light fields and computational imaging. Computer 2006, 39, 46–55. [Google Scholar] [CrossRef]
- Levoy, M.; Ng, R.; Adams, A.; Footer, M.; Horowitz, M. Light field microscopy. ACM Trans. Gr. 2006, 25, 924–934. [Google Scholar] [CrossRef]
- Ng, R. Fourier slice photography. ACM Trans. Gr. 2005, 24, 735–744. [Google Scholar] [CrossRef]
- Levoy, M.; Hanrahan, P. Light field rendering. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques; ACM: New York, NY, USA, 1996; pp. 31–42. [Google Scholar] [CrossRef]
- Ng, R.; Levoy, M.; Brédif, M.; Duval, G.; Horowitz, M.; Hanrahan, P. Light field photography with a hand-held plenoptic camera. Comput. Sci. Tech. Rep. CSTR 2005, 2, 1–11. [Google Scholar] [CrossRef]
- Xiao, X.; Javidi, B.; Martinez-Corral, M.; Stern, A. Advances in three-dimensional integral imaging: Sensing, display, and applications. Appl. Opt. 2013, 52, 546–560. [Google Scholar] [CrossRef] [PubMed]
- Wilburn, B.; Joshi, N.; Vaish, V.; Talvala, E.V.; Antunez, E.; Barth, A.; Adams, A.; Horowitz, M.; Levoy, M. High performance imaging using large camera arrays. ACM Trans. Gr. 2005, 24, 765–776. [Google Scholar] [CrossRef]
- Lin, X.; Wu, J.; Zheng, G.; Dai, Q. Camera array based light field microscopy. Biomed. Opt. Express 2015, 6, 3179–3189. [Google Scholar] [CrossRef] [PubMed]
- Georgiev, T.; Zheng, K.C.; Curless, B.; Salesin, D.; Nayar, S.; Intwala, C. Spatio-angular resolution tradeoffs in integral photography. Render. Tech. 2006, 263–272. [Google Scholar] [CrossRef]
- Veeraraghavan, A.; Raskar, R.; Agrawal, A.; Mohan, A.; Tumblin, J. Dappled photography: Mask enhanced cameras for heterodyned light fields and coded aperture refocusing. ACM Trans. Gr. 2007, 26, 69. [Google Scholar] [CrossRef]
- Liang, C.K.; Lin, T.H.; Wong, B.Y.; Liu, C.; Chen, H.H. Programmable aperture photography: Multiplexed light field acquisition. ACM Trans. Gr. 2008, 27, 55:1–55:10. [Google Scholar] [CrossRef]
- Fuchs, M.; Kachele, M.; Rusinkiewicz, S. Design and fabrication of faceted mirror arrays for light field capture. Comput. Gr. Forum 2013, 32, 246–257. [Google Scholar] [CrossRef]
- Manakov, A.; Restrepo, J.F.; Klehm, O.; Hegedüs, R.; Eisemann, E.; Seidel, H.P.; Ihrke, I. A reconfigurable camera add-on for high dynamic range, multispectral, polarization, and light-field imaging. ACM Trans. Gr. 2013, 32, 1–47. [Google Scholar] [CrossRef]
- Levoy, M.; Zhang, Z.; Mcdowall, I. Recording and controlling the 4D light field in a microscope using microlens arrays. J. Microsc. 2009, 235, 144–162. [Google Scholar] [CrossRef] [PubMed]
- Ng, R. Digital Light Field Photography. Ph.D. Thesis, Standford University, Stanford, CA, USA, 2006. [Google Scholar] [CrossRef]
- Park, J.H.; Hong, K.; Lee, B. Recent progress in three-dimensional information processing based on integral imaging. Appl. Opt. 2009, 48, H77–H94. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Park, J.H.; Kim, N. Parameter analysis of integral Fourier hologram and its resolution enhancement. Opt. Express 2010, 18, 2152–2167. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Yeom, J.; Jung, J.H.; Park, J.H.; Lee, B. Resolution comparison between integral-imaging-based hologram synthesis methods using rectangular and hexagonal lens arrays. Opt. Express 2011, 19, 26917–26927. [Google Scholar] [CrossRef] [PubMed]
- Denisyuk, Y.N. On the reflection of optical properties of an object in a wave field of light scattered by it. Dokl. Akad. Nauk. SSSR 1962, 144, 1275–1278. [Google Scholar] [CrossRef]
- Leith, E.N.; Upatnieks, J. Wavefront reconstruction with continuous-tone objects. J. Opt. Soc. Am. 1963, 53, 1377–1381. [Google Scholar] [CrossRef]
- Ren, Z.; Xu, Z.; Lam, E.Y. Learning-based nonparametric autofocusing for digital holography. Optica 2018, 5, 337–344. [Google Scholar] [CrossRef]
- Hariharan, P.; Oreb, B.F.; Eiju, T. Digital phase-shifting interferometry: A simple error-compensating phase calculation algorithm. Appl. Opt. 1987, 26, 2504–2506. [Google Scholar] [CrossRef] [PubMed]
- Chan, A.C.; Tsia, K.K.; Lam, E.Y. Subsampled scanning holographic imaging (SuSHI) for fast, non-adaptive recording of three-dimensional objects. Optica 2016, 3, 911–917. [Google Scholar] [CrossRef]
- Nugent, K.A. X-ray non-interferometric phase imaging: A unified picture. J. Opt. Soc. Am. A 2007, 24, 536–547. [Google Scholar] [CrossRef]
- Chen, N.; Ren, Z.; Li, D.; Lam, E.Y.; Situ, G. Analysis of the noise in back-projection light field acquisition and its optimization. Appl. Opt. 2017, 56, F20–F26. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W. Introduction to Fourier Optics, 3rd ed.; Roberts & Company: Dunedin, New Zealand, 2005. [Google Scholar] [CrossRef]
- Park, J.H.; Seo, S.W.; Chen, N.; Kim, N. Fourier hologram generation from multiple incoherent defocused images. In Proceedings of the Three-Dimensional Imaging, Visualization, and Display 2010 and Display Technologies and Applications for Defense, Security, and Avionics IV, Orlando, FL, USA, 5 May 2010; pp. 7690–7698. [Google Scholar] [CrossRef]
- Park, J.H.; Seo, S.W.; Chen, N.; Kim, N. Hologram synthesis from defocused images captured under incoherent illumination. In Proceedings of the Digital Holography and Three-Dimensional Imaging 2010, Miami, FL, USA, 12–14 April 2010. [Google Scholar] [CrossRef]
- Levin, A.; Durand, F. Linear view synthesis using a dimensionality gap light field prior. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1831–1838. [Google Scholar] [CrossRef]
- Xu, Z.; Ke, J.; Lam, E.Y. High-resolution lightfield photography using two masks. Opt. Express 2012, 20, 10971–10983. [Google Scholar] [CrossRef] [PubMed]
- Marwah, K.; Wetzstein, G.; Bando, Y.; Raskar, R. Compressive light field photography using overcomplete dictionaries and optimized projections. ACM Trans. Gr. 2013, 32, 46:1–46:12. [Google Scholar] [CrossRef]
- Bailey, S.W.; Echevarria, J.I.; Bodenheimer, B.; Gutierrez, D. Fast depth from defocus from focal stacks. Vis. Comput. 2014, 31, 1697–1708. [Google Scholar] [CrossRef]
- Kuthirummal, S.; Nagahara, H.; Zhou, C.; Nayar, S.K. Flexible depth of field photography. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 58–71. [Google Scholar] [CrossRef] [PubMed]
- Zeng, G.L. One-angle fluorescence tomography with in-and-out motion. J. Electron. Imaging 2013, 22, 043018. [Google Scholar] [CrossRef] [PubMed]
- McMillan, L.; Bishop, G. Plenoptic modeling: An image-based rendering system. In Proceedings of the 22nd Annual Conference on Computer Graphics and Interactive Techniques; ACM: New York, NY, USA, 1995; pp. 39–46. [Google Scholar] [CrossRef]
- Park, J.H.; Lee, S.K.; Jo, N.Y.; Kim, H.J.; Kim, Y.S.; Lim, H.G. Light ray field capture using focal plane sweeping and its optical reconstruction using 3D displays. Opt. Express 2014, 22, 25444–25454. [Google Scholar] [CrossRef] [PubMed]
- Mousnier, A.; Vural, E.; Guillemot, C. Partial Light Field Tomographic Reconstruction from a Fixed-Camera Focal Stack. arXiv, 2015; arXiv:1503.01903. [Google Scholar]
- Wang, H.; Chen, N.; Zheng, S.; Liu, J.; Situ, G. Fast and high-resolution light field acquisition using defocus modulation. Appl. Opt. 2018, 57, A250–A256. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Chen, N.; Liu, J.; Situ, G. Light field imaging based on defocused photographic images. Digital Holography and Three-Dimensional Imaging; Optical Society of America: Jeju, Korea, 2017; p. W3A–3. [Google Scholar] [CrossRef]
- Chen, N.; Ren, Z.; Lam, E.Y. High-resolution Fourier hologram synthesis from photographic images through computing the light field. Appl. Opt. 2016, 55, 1751–1756. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Xu, T.; Yue, W.; Sun, J.; Situ, G. Light-field moment microscopy with noise reduction. Opt. Express 2015, 23, 29154–29162. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Levoy, M. Wigner distributions and how they relate to the light field. In Proceedings of the 2009 IEEE International Conference on Computational Photography (ICCP), San Francisco, CA, USA, 16–17 April 2009; pp. 1–10. [Google Scholar] [CrossRef]
- Sun, X.; Meng, N.; Xu, Z.; Lam, E.Y.; So, H.K.H. Sparse hierarchical nonparametric Bayesian learning for light field representation and denoising. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 3272–3279. [Google Scholar] [CrossRef]
- Sun, X.; Xu, Z.; Meng, N.; Lam, E.Y.; So, H.K.H. Data-driven light field depth estimation using deep convolutional neural networks. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 367–374. [Google Scholar] [CrossRef]
- Liu, C.; Qiu, J.; Jiang, M. Light field reconstruction from projection modeling of focal stack. Opt. Express 2017, 25, 11377–11388. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Wang, G.; Li, W.; Liao, Q. Iteratively reconstructing 4D light fields from focal stacks. Appl. Opt. 2016, 55, 8457–8463. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Z.; Pan, X.; Liu, C.; Wang, L.; Zhu, J. Light field moment imaging with the ptychographic iterative engine. AIP Adv. 2014, 4, 107108. [Google Scholar] [CrossRef]
- Teague, M.R. Irradiance moments: their propagation and use for unique retrieval of phase. J. Opt. Soc. Am. 1982, 72, 1199–1209. [Google Scholar] [CrossRef]
- Falaggis, K.; Kozacki, T.; Kujawińska, M.; Józwik, M.; Kuś, A. Optimum plane selection criteria for single-beam phase retrieval techniques based on the contrast transfer function. Opt. Lett. 2014, 39, 30–33. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Carranza, J.; Falaggis, K.; Kozacki, T. Optimum measurement criteria for the axial derivative intensity used in transport of intensity-equation-based solvers. Opt. Lett. 2014, 39, 182–185. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Qiu, J.; Zhao, S. Iterative reconstruction of scene depth with fidelity based on light field data. Appl. Opt. 2017, 56, 3185–3192. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Chen, Q.; Qu, W.; Asundi, A. High-speed transport-of-intensity phase microscopy with an electrically tunable lens. Opt. Express 2013, 21, 24060–24075. [Google Scholar] [CrossRef] [PubMed]
- Gerchberg, R.W.; Saxton, W.O. A practical algorithm for the determination of the phase from image and diffraction plane pictures. J. Phys. D Appl. Phys. 1972, 35, 237–246. [Google Scholar] [CrossRef]
- Gureyev, T.E.; Roberts, A.; Nugent, K.A. Partially coherent fields, the transport-of-intensity equation, and phase uniqueness. J. Opt. Soc. Am. A 1995, 12, 1942–1946. [Google Scholar] [CrossRef]
- Paganin, D.; Nugent, K.A. Noninterferometric phase imaging with partially coherent light. Phys. Rev. Lett. 1998, 80, 2586–2589. [Google Scholar] [CrossRef]
- Yang, G.Z.; Dong, B.Z.; Gu, B.Y.; Zhuang, J.Y.; Ersoy, O.K. Gerchberg–Saxton and Yang-Gu algorithms for phase retrieval in a nonunitary transform system: A comparison. Appl. Opt. 1994, 33, 209–218. [Google Scholar] [CrossRef] [PubMed]
- Fienup, J.R. Reconstruction of an object from the modulus of its Fourier transform. Opt. Lett. 1978, 3, 27–29. [Google Scholar] [CrossRef] [PubMed]
- Cederquist, J.N.; Fienup, J.R.; Wackerman, C.C.; Robinson, S.R.; Kryskowski, D. Wave-front phase estimation from Fourier intensity measurements. J. Opt. Soc. Am. A 1989, 6, 1020–1026. [Google Scholar] [CrossRef]
- Devaney, A.J.; Chidlaw, R. On the uniqueness question in the problem of phase retrieval from intensity measurements. J. Opt. Soc. Am. 1978, 68, 1352–1354. [Google Scholar] [CrossRef]
- Fienup, J.R. Reconstruction of a complex-valued object from the modulus of its Fourier transform using a support constraint. J. Opt. Soc. Am. A 1987, 4, 118–123. [Google Scholar] [CrossRef]
- Guo, C.; Liu, S.; Sheridan, J.T. Iterative phase retrieval algorithms I: Optimization. Appl. Opt. 2015, 54, 4698–4708. [Google Scholar] [CrossRef] [PubMed]
- Rolleston, R.; George, N. Image reconstruction from partial Fresnel zone information. Appl. Opt. 1986, 25, 178–183. [Google Scholar] [CrossRef] [PubMed]
- Misell, D.L. An examination of an iterative method for the solution of the phase problem in optics and electron optics: I. Test calculations. J. Phys. D Appl. Phys. 1973, 6, 2200–2216. [Google Scholar] [CrossRef]
- Fienup, J.R. Lensless coherent imaging by phase retrieval with an illumination pattern constraint. Opt. Express 2006, 14, 498–508. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.; Shen, C.; Li, Q.; Tan, J.; Liu, S.; Kan, X.; Liu, Z. A fast-converging iterative method based on weighted feedback for multi-distance phase retrieval. Sci. Rep. 2018, 8. [Google Scholar] [CrossRef] [PubMed]
- Konijnenberg, A.; Coene, W.; Pereira, S.; Urbach, H. Combining ptychographical algorithms with the Hybrid Input-Output (HIO) algorithm. Ultramicroscopy 2016, 171, 43–54. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Gao, W.; Zuo, J.M.; Yuan, J. Atomic resolution tomography reconstruction of tilt series based on a GPU accelerated hybrid input–output algorithm using polar Fourier transform. Ultramicroscopy 2015, 149, 64–73. [Google Scholar] [CrossRef] [PubMed]
- Rolleston, R.; George, N. Stationary phase approximations in Fresnel-zone magnitude-only reconstructions. J. Opt. Soc. Am. A 1987, 4, 148–153. [Google Scholar] [CrossRef]
- Dean, B.H.; Bowers, C.W. Diversity selection for phase-diverse phase retrieval. J. Opt. Soc. Am. A 2003, 20, 1490–1504. [Google Scholar] [CrossRef]
- Mayo, S.C.; Miller, P.R.; Wilkins, S.W.; Davis, T.J.; Gao, D.; Gureyev, T.E.; Paganin, D.; Parry, D.J.; Pogany, A.; Stevenson, A.W. Quantitative X-ray projection microscopy: Phase-contrast and multi-spectral imaging. J. Microsc. 2002, 207, 79–96. [Google Scholar] [CrossRef] [PubMed]
- Anand, A.; Pedrini, G.; Osten, W.; Almoro, P. Wavefront sensing with random amplitude mask and phase retrieval. Opt. Lett. 2007, 32, 1584–1586. [Google Scholar] [CrossRef] [PubMed]
- Almoro, P.F.; Hanson, S.G. Random phase plate for wavefront sensing via phase retrieval and a volume speckle field. Appl. Opt. 2008, 47, 2979–2987. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Chen, B.; Morrison, G.R.; Vila-Comamala, J.; Guizar-Sicairos, M.; Robinson, I.K. Phase retrieval by coherent modulation imaging. Nat. Commun. 2016, 7, 13367. [Google Scholar] [CrossRef] [PubMed]
- Brady, G.R.; Guizar-Sicairos, M.; Fienup, J.R. Optical wavefront measurement using phase retrieval with transverse translation diversity. Opt. Express 2009, 17, 624–639. [Google Scholar] [CrossRef] [PubMed]
- Rodenburg, J.M.; Faulkner, H.M.L. A phase retrieval algorithm for shifting illumination. Appl. Phys. Lett. 2004, 85, 4795–4797. [Google Scholar] [CrossRef]
- Pedrini, G.; Osten, W.; Zhang, Y. Wave-front reconstruction from a sequence of interferograms recorded at different planes. Opt. Lett. 2005, 30, 833–835. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Yeom, J.; Hong, K.; Li, G.; Lee, B. Fast converging algorithm for wavefront reconstruction based on a sequence of diffracted intensity images. J. Opt. Soc. Korea 2014, 18, 217–224. [Google Scholar] [CrossRef]
- Bao, P.; Zhang, F.; Pedrini, G.; Osten, W. Phase retrieval using multiple illumination wavelengths. Opt. Lett. 2008, 33, 309–311. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Hong, J.-Y.; Yoo, D.; Cho, J.; Jeong, Y.; Moon, S.; Lee, B. Single-shot phase retrieval via Fourier ptychographic microscopy. Optica 2018, 5, 976–983. [Google Scholar] [CrossRef]
- Zheng, G.; Horstmeyer, R.; Yang, C. Wide-field, high-resolution Fourier ptychographic microscopy. Nat. Photonics 2013, 7, 739–745. [Google Scholar] [CrossRef] [PubMed]
- Zhou, A.; Chen, N.; Wang, H.; Situ, G. Analysis of Fourier ptychographic microscopy with half of the captured images. J. Opt. 2018, 20, 095701. [Google Scholar] [CrossRef]
- Zhou, A.; Wang, W.; Chen, N.; Lam, E.Y.; Lee, B.; Situ, G. Fast and robust misalignment correction of Fourier ptychographic microscopy for full field of view reconstruction. Opt. Express 2018, 26, 23661–23674. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Pedrini, G.; Osten, W. Phase retrieval with resolution enhancement by using structured illumination. Opt. Lett. 2013, 38, 5204–5207. [Google Scholar] [CrossRef] [PubMed]
- Gao, P.; Pedrini, G.; Zuo, C.; Osten, W. Phase retrieval using spatially modulated illumination. Opt. Lett. 2014, 39, 3615–3618. [Google Scholar] [CrossRef] [PubMed]
- Almoro, P.; Pedrini, G.; Osten, W. Complete wavefront reconstruction using sequential intensity measurements of a volume speckle field. Appl. Opt. 2006, 45, 8596–8605. [Google Scholar] [CrossRef] [PubMed]
- Camacho, L.; Micó, V.; Zalevsky, Z.; García, J. Quantitative phase microscopy using defocussing by means of a spatial light modulator. Opt. Express 2010, 18, 6755–6766. [Google Scholar] [CrossRef] [PubMed]
- Agour, M.; Almoro, P.F.; Falldorf, C. Investigation of smooth wave fronts using SLM-based phase retrieval and a phase diffuser. J. Eur. Opt. Soc. Rapid Publ. 2012, 7. [Google Scholar] [CrossRef]
- Almoro, P.F.; Glückstad, J.; Hanson, S.G. Single-plane multiple speckle pattern phase retrieval using a deformable mirror. Opt. Express 2010, 18, 19304–19313. [Google Scholar] [CrossRef] [PubMed]
- Roddier, F.; Roddier, C.; Roddier, N. Curvature sensing: A new wavefront sensing method. In Proceedings of the 32nd Annual International Technical Symposium on Optical and Optoelectronic Applied Science and Engineering, San Diego, CA, USA, 2 December 1988. [Google Scholar] [CrossRef]
- Bajt, S.; Barty, A.; Nugent, K.; McCartney, M.; Wall, M.; Paganin, D. Quantitative phase-sensitive imaging in a transmission electron microscope. Ultramicroscopy 2000, 83, 67–73. [Google Scholar] [CrossRef]
- Nugent, K.A. Coherent methods in the X-ray sciences. Adv. Phys. 2010, 59, 1–99. [Google Scholar] [CrossRef]
- Allman, B.; McMahon, P.; Nugent, K.; Paganin, D.; Jacobson, D.; Arif, M.; Werner, S. Phase radiography with neutrons. Nature 2000, 408, 158–159. [Google Scholar] [CrossRef] [PubMed]
- Streibl, N. Phase imaging by the transport equation of intensity. Opt. Commun. 1984, 49, 6–10. [Google Scholar] [CrossRef]
- Barty, A.; Nugent, K.A.; Paganin, D.; Roberts, A. Quantitative optical phase microscopy. Opt. Lett. 1998, 23, 817–819. [Google Scholar] [CrossRef] [PubMed]
- Kou, S.S.; Waller, L.; Barbastathis, G.; Marquet, P.; Depeursinge, C.; Sheppard, C.J.R. Quantitative phase restoration by direct inversion using the optical transfer function. Opt. Lett. 2011, 36, 2671–2673. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Chen, Q.; Qu, W.; Asundi, A. Noninterferometric single-shot quantitative phase microscopy. Opt. Lett. 2013, 38, 3538–3541. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Chen, Q.; Asundi, A. Light field moment imaging: Comment. Opt. Lett. 2014, 39, 654. [Google Scholar] [CrossRef] [PubMed]
- Woods, S.C.; Greenaway, A.H. Wave-front sensing by use of a Green’s function solution to the intensity transport equation. J. Opt. Soc. Am. A 2003, 20, 508–512. [Google Scholar] [CrossRef]
- Allen, L.; Oxley, M. Phase retrieval from series of images obtained by defocus variation. Opt. Commun. 2001, 199, 65–75. [Google Scholar] [CrossRef]
- Pinhasi, S.V.; Alimi, R.; Perelmutter, L.; Eliezer, S. Topography retrieval using different solutions of the transport intensity equation. J. Opt. Soc. Am. A 2010, 27, 2285–2292. [Google Scholar] [CrossRef] [PubMed]
- Gureyev, T.E.; Roberts, A.; Nugent, K.A. Phase retrieval with the transport-of-intensity equation: Matrix solution with use of Zernike polynomials. J. Opt. Soc. Am. A 1995, 12, 1932–1941. [Google Scholar] [CrossRef]
- Gureyev, T.E.; Nugent, K.A. Phase retrieval with the transport-of-intensity equation. II. Orthogonal series solution for nonuniform illumination. J. Opt. Soc. Am. A 1996, 13, 1670–1682. [Google Scholar] [CrossRef]
- Gureyev, T.E.; Nugent, K.A. Rapid quantitative phase imaging using the transport of intensity equation. Opt. Commun. 1997, 133, 339–346. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Asundi, A. Boundary-artifact-free phase retrieval with the transport of intensity equation: Fast solution with use of discrete cosine transform. Opt. Express 2014, 22, 9220–9244. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Chen, Q.; Li, H.; Qu, W.; Asundi, A. Boundary-artifact-free phase retrieval with the transport of intensity equation II: Applications to microlens characterization. Opt. Express 2014, 22, 18310–18324. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Zuo, C.; Idir, M.; Qu, W.; Asundi, A. Phase retrieval with the transport-of-intensity equation in an arbitrarily shaped aperture by iterative discrete cosine transforms. Opt. Lett. 2015, 40, 1976–1979. [Google Scholar] [CrossRef] [PubMed]
- Volkov, V.; Zhu, Y.; Graef, M.D. A new symmetrized solution for phase retrieval using the transport of intensity equation. Micron 2002, 33, 411–416. [Google Scholar] [CrossRef]
- Martinez-Carranza, J.; Falaggis, K.; Kozacki, T.; Kujawinska, M. Effect of imposed boundary conditions on the accuracy of transport of intensity equation based solvers. In Proceedings of the Modeling Aspects in Optical Metrology IV, Munich, Germany, 13 May 2013; p. 87890N. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Huang, L.; Asundi, A. Phase discrepancy analysis and compensation for fast Fourier transform based solution of the transport of intensity equation. Opt. Express 2014, 22, 17172–17186. [Google Scholar] [CrossRef] [PubMed]
- Ishizuka, K.; Allman, B. Phase measurement of atomic resolution image using transport of intensity equation. Microscopy 2005, 54, 191–197. [Google Scholar] [CrossRef] [PubMed]
- Soto, M.; Acosta, E. Improved phase imaging from intensity measurements in multiple planes. Appl. Opt. 2007, 46, 7978–7981. [Google Scholar] [CrossRef] [PubMed]
- Cong, W.; Wang, G. Higher-order phase shift reconstruction approach: Higher-order phase shift reconstruction approach. Med. Phys. 2010, 37, 5238–5242. [Google Scholar] [CrossRef] [PubMed]
- Waller, L.; Tian, L.; Barbastathis, G. Transport of intensity phase-amplitude imaging with higher order intensity derivatives. Opt. Express 2010, 18, 12552–12561. [Google Scholar] [CrossRef] [PubMed]
- Bie, R.; Yuan, X.H.; Zhao, M.; Zhang, L. Method for estimating the axial intensity derivative in the TIE with higher order intensity derivatives and noise suppression. Opt. Express 2012, 20, 8186–8191. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Chen, Q.; Yu, Y.; Asundi, A. Transport-of-intensity phase imaging using Savitzky-Golay differentiation filter-theory and applications. Opt. Express 2013, 21, 5346–5362. [Google Scholar] [CrossRef] [PubMed]
- Gureyev, T.; Pogany, A.; Paganin, D.; Wilkins, S. Linear algorithms for phase retrieval in the Fresnel region. Opt. Commun. 2004, 231, 53–70. [Google Scholar] [CrossRef]
- Martinez-Carranza, J.; Falaggis, K.; Kozacki, T. Multi-filter transport of intensity equation solver with equalized noise sensitivity. Opt. Express 2015, 23, 23092–23107. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.; Zuo, C.; Chen, Q. Iterative optimum frequency combination method for high efficiency phase imaging of absorptive objects based on phase transfer function. Opt. Express 2015, 23, 28031–28049. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, M.H.; Long, J.M.; Gaylord, T.K. Multifilter phase imaging with partially coherent light. Appl. Opt. 2014, 53, D29–D39. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.; Claus, R.A.; Dauwels, J.; Tian, L.; Waller, L. Transport of intensity phase imaging by intensity spectrum fitting of exponentially spaced defocus planes. Opt. Express 2014, 22, 10661–10674. [Google Scholar] [CrossRef]
- Frank, J.; Altmeyer, S.; Wernicke, G. Non-interferometric, non-iterative phase retrieval by Green’s functions. J. Opt. Soc. Am. A 2010, 27, 2244–2251. [Google Scholar] [CrossRef] [PubMed]
- Ishizuka, A.; Mitsuishi, K.; Ishizuka, K. Direct observation of curvature of the wave surface in transmission electron microscope using transport intensity equation. Ultramicroscopy 2018, 194, 7–14. [Google Scholar] [CrossRef] [PubMed]
- Ishizuka, A.; Ishizuka, K.; Mitsuishi, K. Boundary-artifact-free observation of magnetic materials using the transport of intensity equation. Microsc. Microanal. 2018, 24, 924–925. [Google Scholar] [CrossRef]
- Schmalz, J.A.; Gureyev, T.E.; Paganin, D.M.; Pavlov, K.M. Phase retrieval using radiation and matter-wave fields: Validity of Teague’s method for solution of the transport-of-intensity equation. Phys. Rev. A 2011, 84, 023808. [Google Scholar] [CrossRef]
- Ferrari, J.A.; Ayubi, G.A.; Flores, J.L.; Perciante, C.D. Transport of intensity equation: Validity limits of the usually accepted solution. Opt. Commun. 2014, 318, 133–136. [Google Scholar] [CrossRef]
- Paganin, D.; Barty, A.; McMahon, P.J.; Nugent, K.A. Quantitative phase-amplitude microscopy. III. The effects of noise. J. Microsc. 2004, 214, 51–61. [Google Scholar] [CrossRef] [PubMed]
- Martin, A.; Chen, F.R.; Hsieh, W.K.; Kai, J.J.; Findlay, S.; Allen, L. Spatial incoherence in phase retrieval based on focus variation. Ultramicroscopy 2006, 106, 914–924. [Google Scholar] [CrossRef] [PubMed]
- Xue, B.; Zheng, S.; Cui, L.; Bai, X.; Zhou, F. Transport of intensity phase imaging from multiple intensities measured in unequally-spaced planes. Opt. Express 2011, 19, 20244–20250. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Xue, B.; Xue, W.; Bai, X.; Zhou, F. Transport of intensity phase imaging from multiple noisy intensities measured in unequally-spaced planes. Opt. Express 2012, 20, 972–985. [Google Scholar] [CrossRef] [PubMed]
- Savitzky, A.; Golay, M.J.E. Smoothing and differentiation of data by dimplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Gorry, P.A. General least-squares smoothing and differentiation of nonuniformly spaced data by the convolution method. Anal. Chem. 1991, 63, 534–536. [Google Scholar] [CrossRef]
- Luo, J.; Ying, K.; He, P.; Bai, J. Properties of Savitzky-Golay digital differentiators. Dig. Signal Process. 2005, 15, 122–136. [Google Scholar] [CrossRef]
- Zuo, C.; Sun, J.; Zhang, J.; Hu, Y.; Chen, Q. Lensless phase microscopy and diffraction tomography with multi-angle and multi-wavelength illuminations using a LED matrix. Opt. Express 2015, 23, 14314–14328. [Google Scholar] [CrossRef] [PubMed]
- Waller, L.; Kou, S.S.; Sheppard, C.J.R.; Barbastathis, G. Phase from chromatic aberrations. Opt. Express 2010, 18, 22817–22825. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.; Nehmetallah, G.; Tran, D.; Darudi, A.; Soltani, P. Fully automated, high speed, tomographic phase object reconstruction using the transport of intensity equation in transmission and reflection configurations. Appl. Opt. 2015, 54, 10443–10453. [Google Scholar] [CrossRef] [PubMed]
- Almoro, P.F.; Waller, L.; Agour, M.; Falldorf, C.; Pedrini, G.; Osten, W.; Hanson, S.G. Enhanced deterministic phase retrieval using a partially developed speckle field. Opt. Lett. 2012, 37, 2088–2090. [Google Scholar] [CrossRef] [PubMed]
- Gorthi, S.S.; Schonbrun, E. Phase imaging flow cytometry using a focus-stack collecting microscope. Opt. Lett. 2012, 37, 707–709. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Sun, J.; Li, J.; Zhang, J.; Asundi, A.; Chen, Q. High-resolution transport-of-intensity quantitative phase microscopy with annular illumination. Sci. Rep. 2017, 7, 7654. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chen, Q.; Zhang, J.; Zhang, Y.; Lu, L.; Zuo, C. Efficient quantitative phase microscopy using programmable annular LED illumination. Biomed. Opt. Express 2017, 8, 4687–4705. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, T.; Petruccelli, J.C. Source diversity for transport of intensity phase imaging. Opt. Express 2017, 25, 9122–9137. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, T.; Petruccelli, J.C. Optical convolution for quantitative phase retrieval using the transport of intensity equation. Appl. Opt. 2018, 57, A134–A141. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Chen, Q.; Qu, W.; Asundi, A. Direct continuous phase demodulation in digital holography with use of the transport-of-intensity equation. Opt. Commun. 2013, 309, 221–226. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Asundi, A. Comparison of digital holography and transport of intensity for quantitative phase contrast imaging. In Fringe 2013; Osten, W., Ed.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 137–142. [Google Scholar]
- Gureyev, T.E.; Paganin, D.M.; Stevenson, A.W.; Mayo, S.C.; Wilkins, S.W. Generalized Eikonal of partially coherent beams and its use in quantitative imaging. Phys. Rev. Lett. 2004, 93, 068103. [Google Scholar] [CrossRef] [PubMed]
- Zysk, A.M.; Schoonover, R.W.; Carney, P.S.; Anastasio, M.A. Transport of intensity and spectrum for partially coherent fields. Opt. Lett. 2010, 35, 2239–2241. [Google Scholar] [CrossRef] [PubMed]
- Petruccelli, J.C.; Tian, L.; Barbastathis, G. The transport of intensity equation for optical path length recovery using partially coherent illumination. Opt. Express 2013, 21, 14430–14441. [Google Scholar] [CrossRef] [PubMed]
- Zuo, C.; Chen, Q.; Tian, L.; Waller, L.; Asundi, A. Transport of intensity phase retrieval and computational imaging for partially coherent fields: The phase space perspective. Opt. Lasers Eng. 2015, 71, 20–32. [Google Scholar] [CrossRef]
- Langer, M.; Cloetens, P.; Guigay, J.P.; Peyrin, F. Quantitative comparison of direct phase retrieval algorithms in in-line phase tomography. Med. Phys. 2008, 35, 4556–4566. [Google Scholar] [CrossRef] [PubMed]
- Gureyev, T. Composite techniques for phase retrieval in the Fresnel region. Opt. Commun. 2003, 220, 49–58. [Google Scholar] [CrossRef]
- Guigay, J.P.; Langer, M.; Boistel, R.; Cloetens, P. Mixed transfer function and transport of intensity approach for phase retrieval in the Fresnel region. Opt. Lett. 2007, 32, 1617–1619. [Google Scholar] [CrossRef] [PubMed]
- Greenbaum, A.; Zhang, Y.; Feizi, A.; Chung, P.L.; Luo, W.; Kandukuri, S.R.; Ozcan, A. Wide-field computational imaging of pathology slides using lens-free on-chip microscopy. Sci. Transl. Med. 2014, 6, 267ra175. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Chen, Q.; Li, J.; Sun, J.; Zuo, C. Lensfree dynamic super-resolved phase imaging based on active micro-scanning. Opt. Lett. 2018, 43, 3714–3717. [Google Scholar] [CrossRef] [PubMed]
- Shaked, N.T.; Katz, B.; Rosen, J. Review of three-dimensional holographic imaging by multiple-viewpoint projection based methods. Appl. Opt. 2009, 48, H120–H136. [Google Scholar] [CrossRef] [PubMed]
- McCrickerd, J.T.; George, N. Holographic stereogram from sequential component photographs. Appl. Phys. Lett. 1968, 12, 10–12. [Google Scholar] [CrossRef]
- Benton, S.A. Survey of holographic stereograms. In Proceedings of the Processing and Display of Three-Dimensional Data, San Diego, CA, USA, 8 April 1983. [Google Scholar] [CrossRef]
- Tian, L.; Waller, L. 3D intensity and phase imaging from light field measurements in an LED array microscope. Optica 2015, 2, 104–111. [Google Scholar] [CrossRef]
- Park, J.H.; Baasantseren, G.; Kim, N.; Park, G.; Kang, J.M.; Lee, B. View image generation in perspective and orthographic projection geometry based on integral imaging. Opt. Express 2008, 16, 8800–8813. [Google Scholar] [CrossRef] [PubMed]
- Ko, J.; Davis, C.C. Comparison of the plenoptic sensor and the Shack–Hartmann sensor. Appl. Opt. 2017, 56, 3689–3698. [Google Scholar] [CrossRef] [PubMed]
- Adelson, E.H.; Bergen, J.R. The plenoptic function and the elements of early vision. In Computational Models of Visual Processing; MIT Press: Cambridge, MA, USA, 1991; pp. 3–20. [Google Scholar]
- Bastiaans, M.J. Application of the Wigner distribution function to partially coherent light. J. Opt. Soc. Am. A 1986, 3, 1227–1238. [Google Scholar] [CrossRef]
- Walther, A. Radiometry and coherence. J. Opt. Soc. Am. 1968, 58, 1256–1259. [Google Scholar] [CrossRef]
- Boashash, B. Estimating and interpreting the instantaneous frequency of a signal. I. Fundamentals. Proc. IEEE 1992, 80, 520–538. [Google Scholar] [CrossRef]
- Bastiaans, M.J. The Wigner distribution function applied to optical signals and systems. Opt. Commun. 1978, 25, 26–30. [Google Scholar] [CrossRef]
- Dragoman, D. Phase-space interferences as the source of negative values of the Wigner distribution function. J. Opt. Soc. Am. A 2000, 17, 2481–2485. [Google Scholar] [CrossRef]
- Bastiaans, M.J. Uncertainty principle for partially coherent light. J. Opt. Soc. Am. 1983, 73, 251–255. [Google Scholar] [CrossRef]
- Paganin, D.; Gureyev, T.E.; Mayo, S.C.; Stevenson, A.W.; Nesterets, Y.I.; Wilkins, S.W. X-ray omni microscopy. J. Microsc. 2004, 214, 315–327. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chen, Q.; Sun, J.; Zhang, J.; Zuo, C. Multimodal computational microscopy based on transport of intensity equation. J. Biomed. Opt. 2016, 21, 126003. [Google Scholar] [CrossRef] [PubMed]
- Friberg, A.T. On the existence of a radiance function for finite planar sources of arbitrary states of coherence. J. Opt. Soc. Am. 1979, 69, 192–198. [Google Scholar] [CrossRef]
- Oh, S.B.; Kashyap, S.; Garg, R.; Chandran, S.; Raskar, R. Rendering wave effects with augmented light field. Comput. Gr. Forum 2010, 29, 507–516. [Google Scholar] [CrossRef]
- Schwiegerling, J. Wavefront Sensing: Shack-Hartmann sensing. J. Refract. Surg. 2001, 17, 573–577. [Google Scholar] [CrossRef]
- Waller, L. Phase imaging with partially coherent light. In Proceedings of the Three-dimensional and multidimensional microscopy: Image acquisition and processing XX, San Francisco, CA, USA, 22 February 2013. [Google Scholar] [CrossRef]
- Iaconis, C.; Walmsley, I.A. Direct measurement of the two-point field correlation function. Opt. Lett. 1996, 21, 1783–1785. [Google Scholar] [CrossRef] [PubMed]
- Marks, D.L.; Stack, R.A.; Brady, D.J. Three-dimensional coherence imaging in the Fresnel domain. Appl. Opt. 1999, 38, 1332–1342. [Google Scholar] [CrossRef] [PubMed]
- Nugent, K.A. Wave field determination using three-dimensional intensity information. Phys. Rev. Lett. 1992, 68, 2261–2264. [Google Scholar] [CrossRef] [PubMed]
- Raymer, M.G.; Beck, M.; McAlister, D. Complex wave-field reconstruction using phase-space tomography. Phys. Rev. Lett. 1994, 72, 1137–1140. [Google Scholar] [CrossRef] [PubMed]
- Rydberg, C.; Bengtsson, J. Numerical algorithm for the retrieval of spatial coherence properties of partially coherent beams from transverse intensity measurements. Opt. Express 2007, 15, 13613–13623. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Chen, Z.; Rehman, S.; Barbastathis, G. Factored form descent: A practical algorithm for coherence retrieval. Opt. Express 2013, 21, 5759. [Google Scholar] [CrossRef] [PubMed]
- Tian, L.; Zhang, Z.; Petruccelli, J.C.; Barbastathis, G. Wigner function measurement using a lenslet array. Opt. Express 2013, 21, 10511–10525. [Google Scholar] [CrossRef] [PubMed]
- Waller, L.; Situ, G.; Fleischer, J.W. Phase-space measurement and coherence synthesis of optical beams. Nat. Photonics 2012, 6, 474–479. [Google Scholar] [CrossRef]
- Park, J.H.; Kim, M.S.; Baasantseren, G.; Kim, N. Fresnel and Fourier hologram generation using orthographic projection images. Opt. Express 2009, 17, 6320–6334. [Google Scholar] [CrossRef] [PubMed]
- Shaked, N.T.; Rosen, J.; Stern, A. Integral holography: White-light single-shot hologram acquisition. Opt. Express 2007, 15, 5754–5760. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.J.; Faulkner, H.M.L.; Nugent, K.A.; Oxley, M.P.; Paganin, D. Phase retrieval from images in the presence of first-order vortices. Phys. Rev. E 2001, 63, 037602. [Google Scholar] [CrossRef] [PubMed]
- Lubk, A.; Guzzinati, G.; Börrnert, F.; Verbeeck, J. Transport of intensity phase retrieval of arbitrary wave fields including vortices. Phys. Rev. Lett. 2013, 111. [Google Scholar] [CrossRef] [PubMed]






| Accuracy | Noise | Occlusion | Time Cost | |
|---|---|---|---|---|
| LFBP I | Moderate | High | Exists | Low |
| LFBP II | Moderate | Low | Exists partially e | High |
| iLFBP | High | Low | Exists less | High |
| LFMI | Low | High | Exists | Low |
| Techniques | Pros | Cons | |
|---|---|---|---|
| Algorithm | GS | 2 images | Error |
| Stagnation | |||
| Local minima | |||
| GDS | Moderate fast | low | |
| HIO | Effective | ||
| Contraints | Amplitude mask | Fewer iteration | Attenuation |
| Phase mask | Fewer iteration | Fabrication | |
| Known pattern | Fewer iteration | ||
| Multi-depth | Resolution | Time cost | |
| Single position/shot possible | Possible experimental complexity | ||
| Multi-wavelength | Resolution | Time cost | |
| Single position | Expensive | ||
| Multi-angular | Resolution | Experimental complexity | |
| Structure illumination | Resolution | Experimental complexity | |
| Synthetic aperture | Resolution | Experimental complexity |
| Issues | Techniques | Pros | Cons |
|---|---|---|---|
| TIE solvers | Green’s function | Theoretical analysis | Computation-extensive, memory-demanding |
| Multi-Grid | Simple and fast | Low-frequency noise, | |
| Zernike polynomials | Precisely represent the optical aberration | only for circular regions, difficult to follow details | |
| FFT | Fast, easy to implement, incorporate regularization in reconstruction | Imply periodic boundary conditions | |
| DCT e | Fast, inhomogeneous Neumann boundary condition | Rectangular aperture, required to limit FOV | |
| Iterative DCT | Inhomogeneous Neumann boundary condition, arbitrarily shaped apertures | Need several iterations | |
| Boundary conditions | Homogeneous Dirichlet/Neumann | Easy to apply, can be implemented by different solvers | “Flat” boundary phase |
| Periodic | Can be implemented by FFT-based solver | Periodic boundary phase | |
| Inhomogeneous Dirichlet | - | Boundary phase required | |
| Inhomogeneous Neumann | Can be measured by introducing a hard aperture | - | |
| Phase discrepancy | Picard-type iteration | Can compensate the phase discrepancy | Need 2-4 iterations |
| Axial derivative | 2-planes | Less intensity acquisition | Noise-resolution trade off |
| Multi-planes | Higher resolution, better noise tolerance | More measurements |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, N.; Zuo, C.; Lam, E.Y.; Lee, B. 3D Imaging Based on Depth Measurement Technologies. Sensors 2018, 18, 3711. https://doi.org/10.3390/s18113711
Chen N, Zuo C, Lam EY, Lee B. 3D Imaging Based on Depth Measurement Technologies. Sensors. 2018; 18(11):3711. https://doi.org/10.3390/s18113711
Chicago/Turabian StyleChen, Ni, Chao Zuo, Edmund Y. Lam, and Byoungho Lee. 2018. "3D Imaging Based on Depth Measurement Technologies" Sensors 18, no. 11: 3711. https://doi.org/10.3390/s18113711
APA StyleChen, N., Zuo, C., Lam, E. Y., & Lee, B. (2018). 3D Imaging Based on Depth Measurement Technologies. Sensors, 18(11), 3711. https://doi.org/10.3390/s18113711







