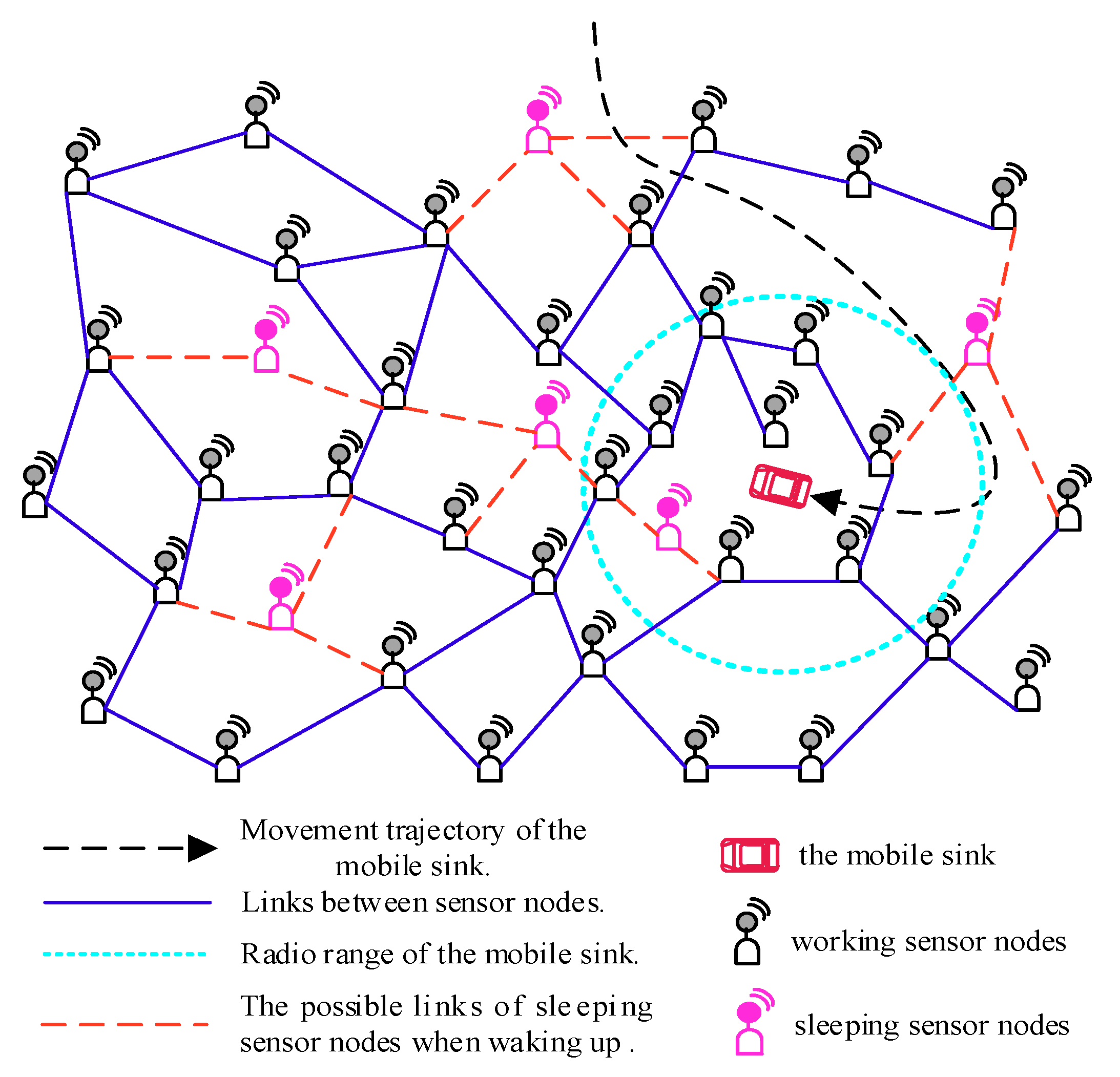
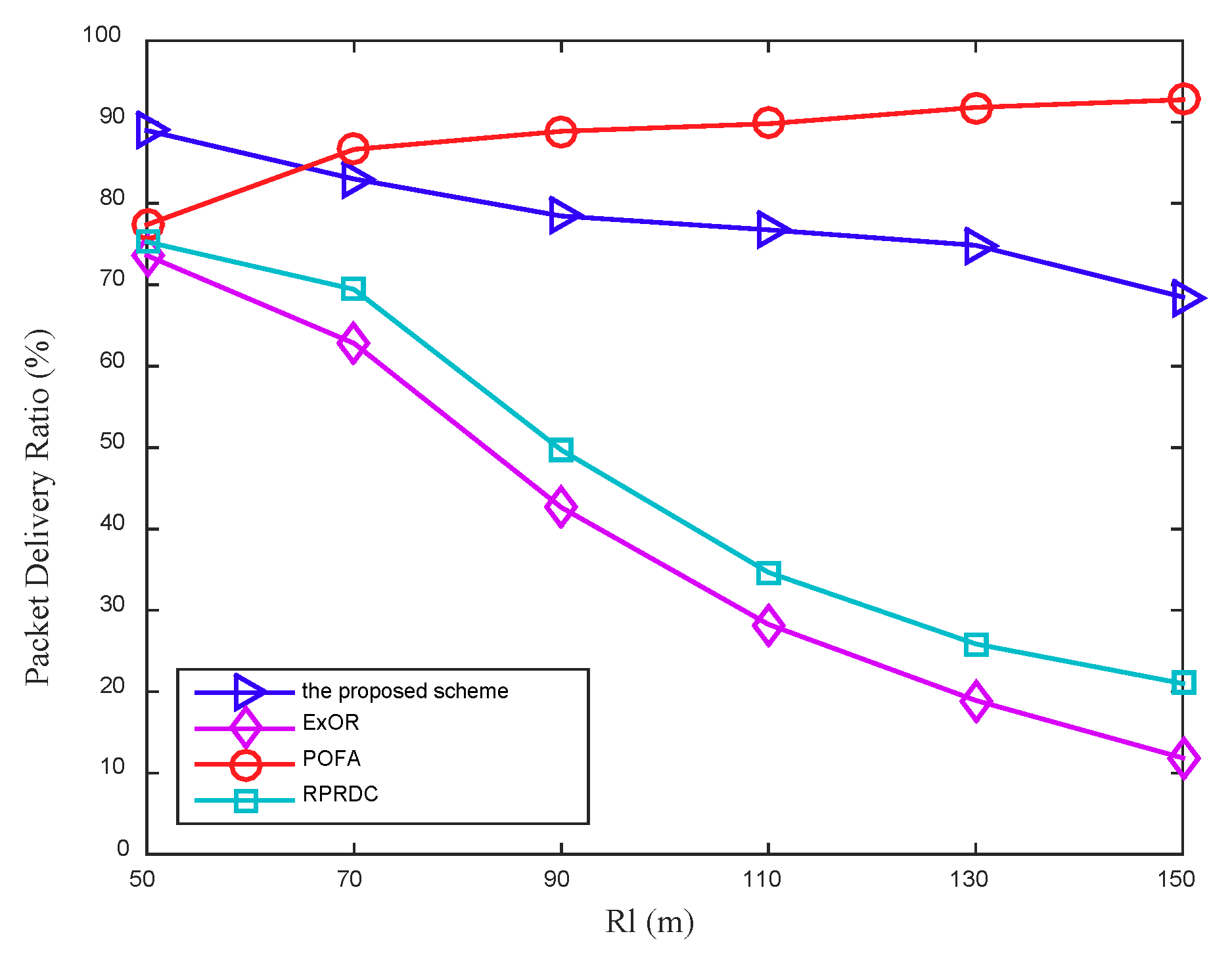
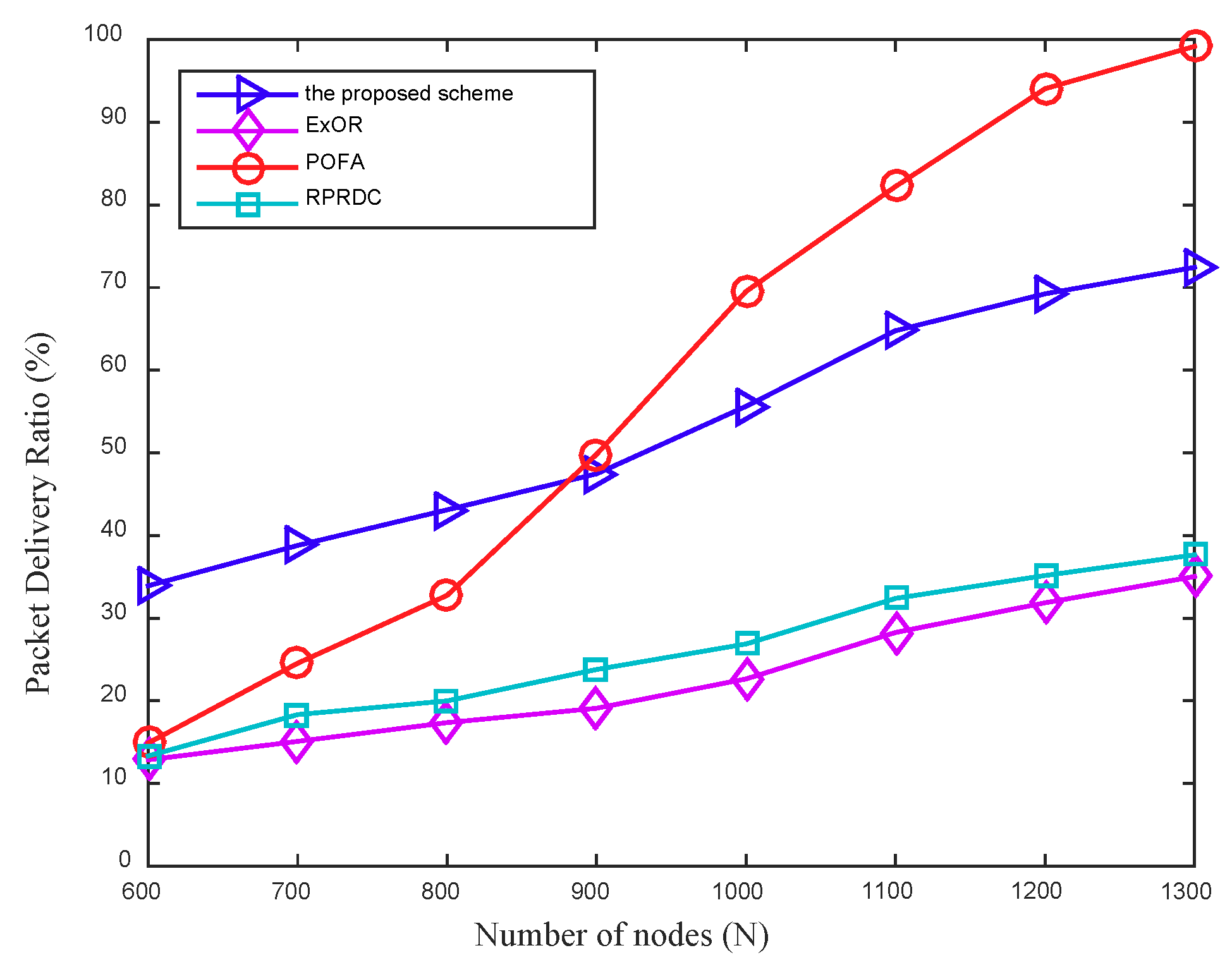
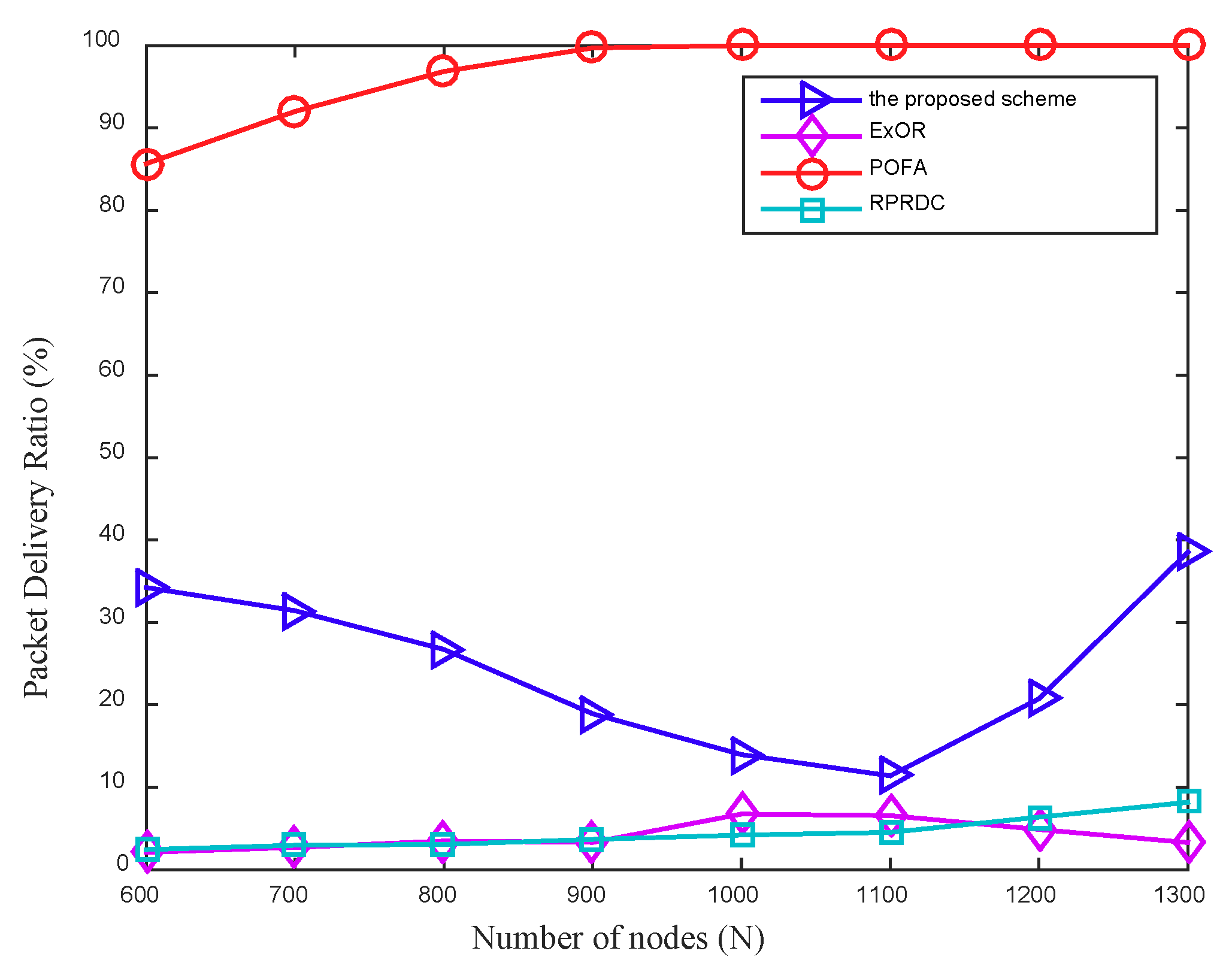
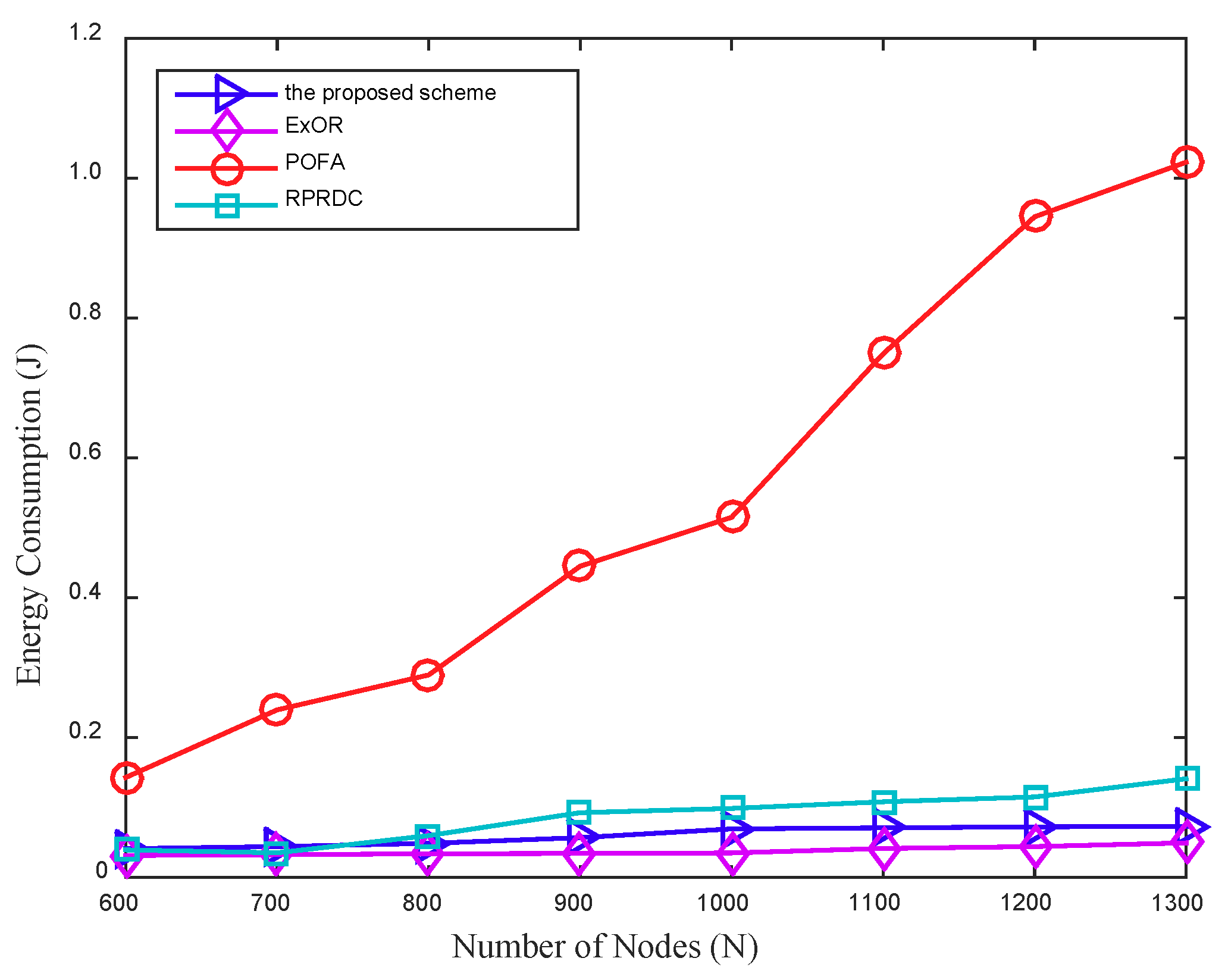
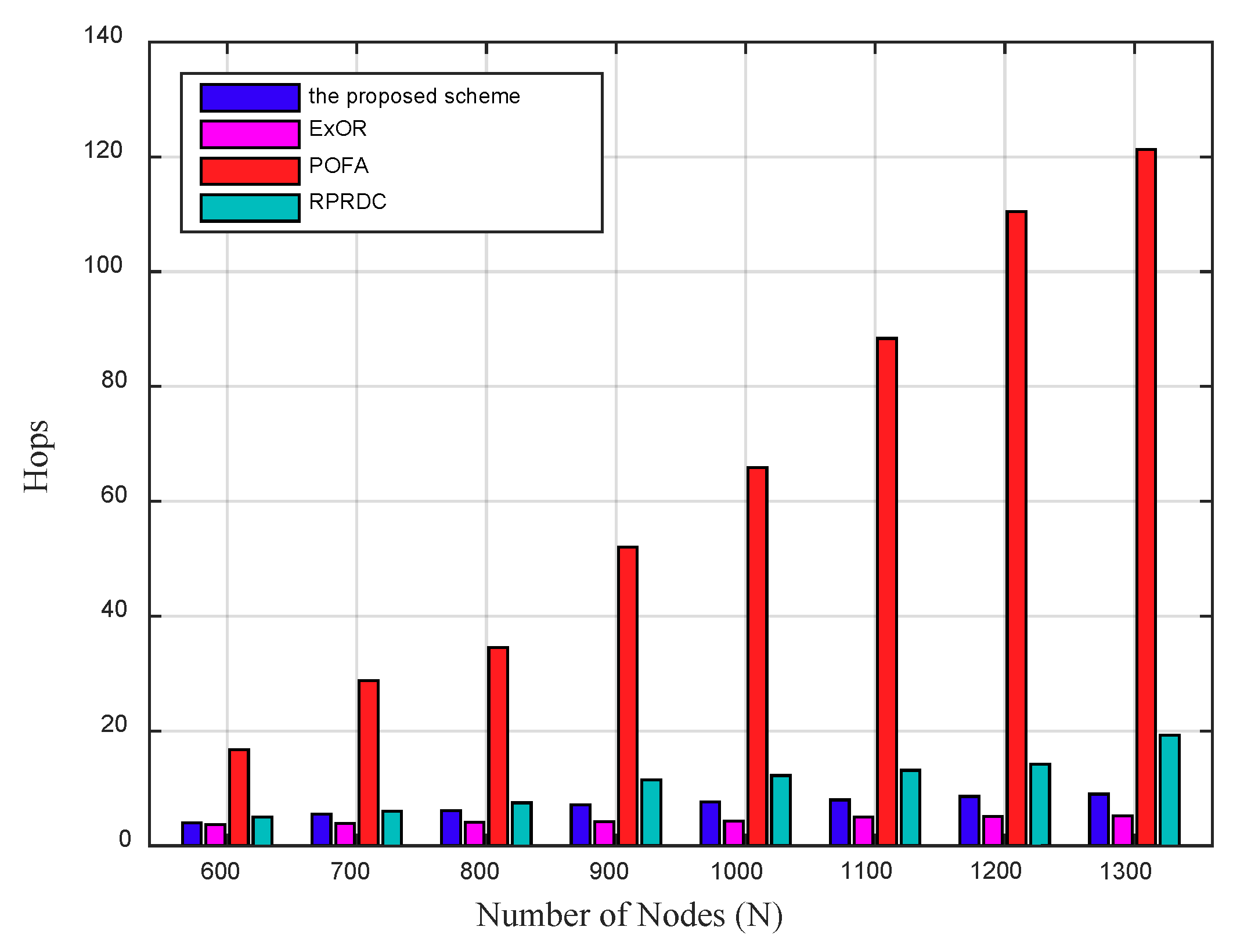
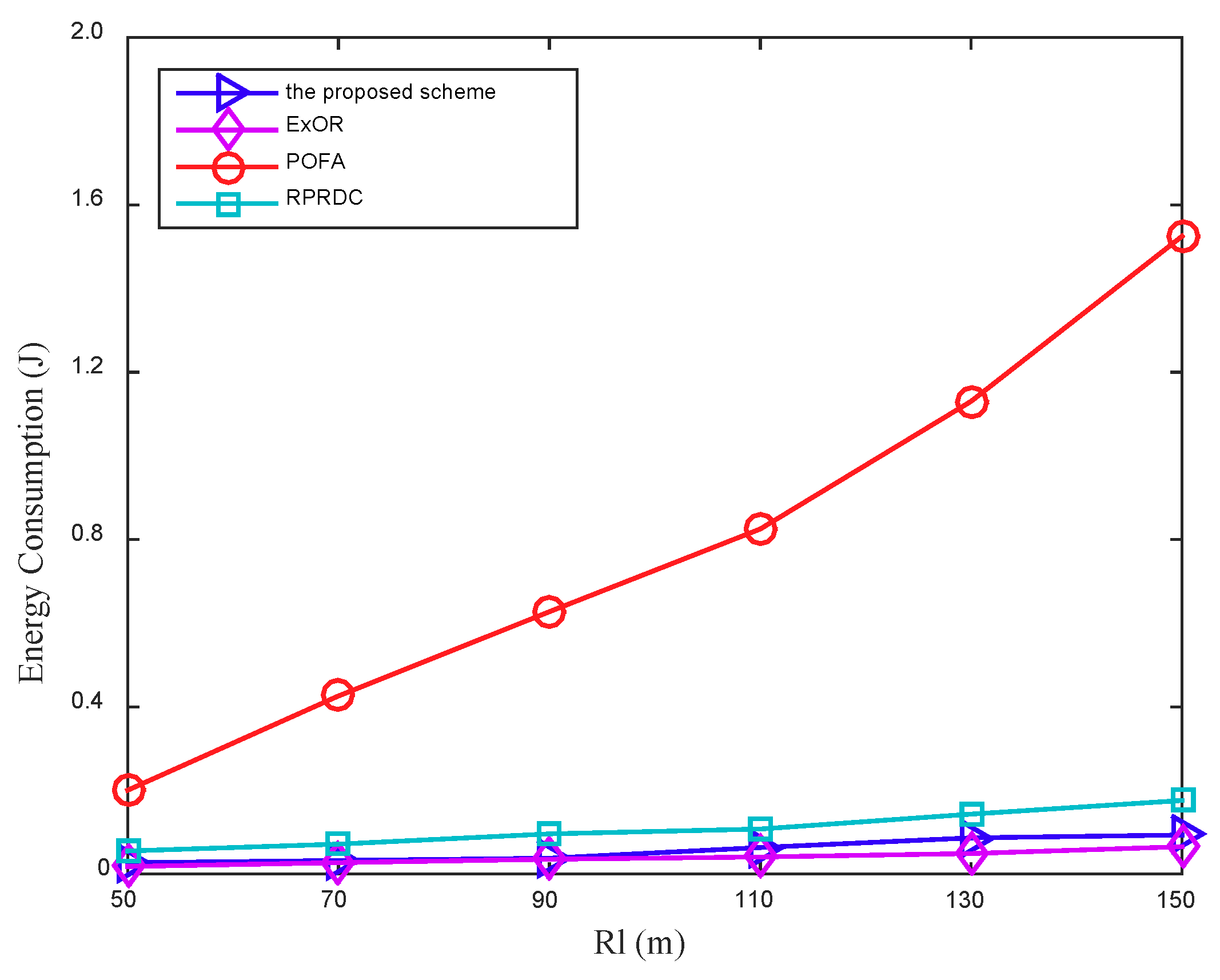
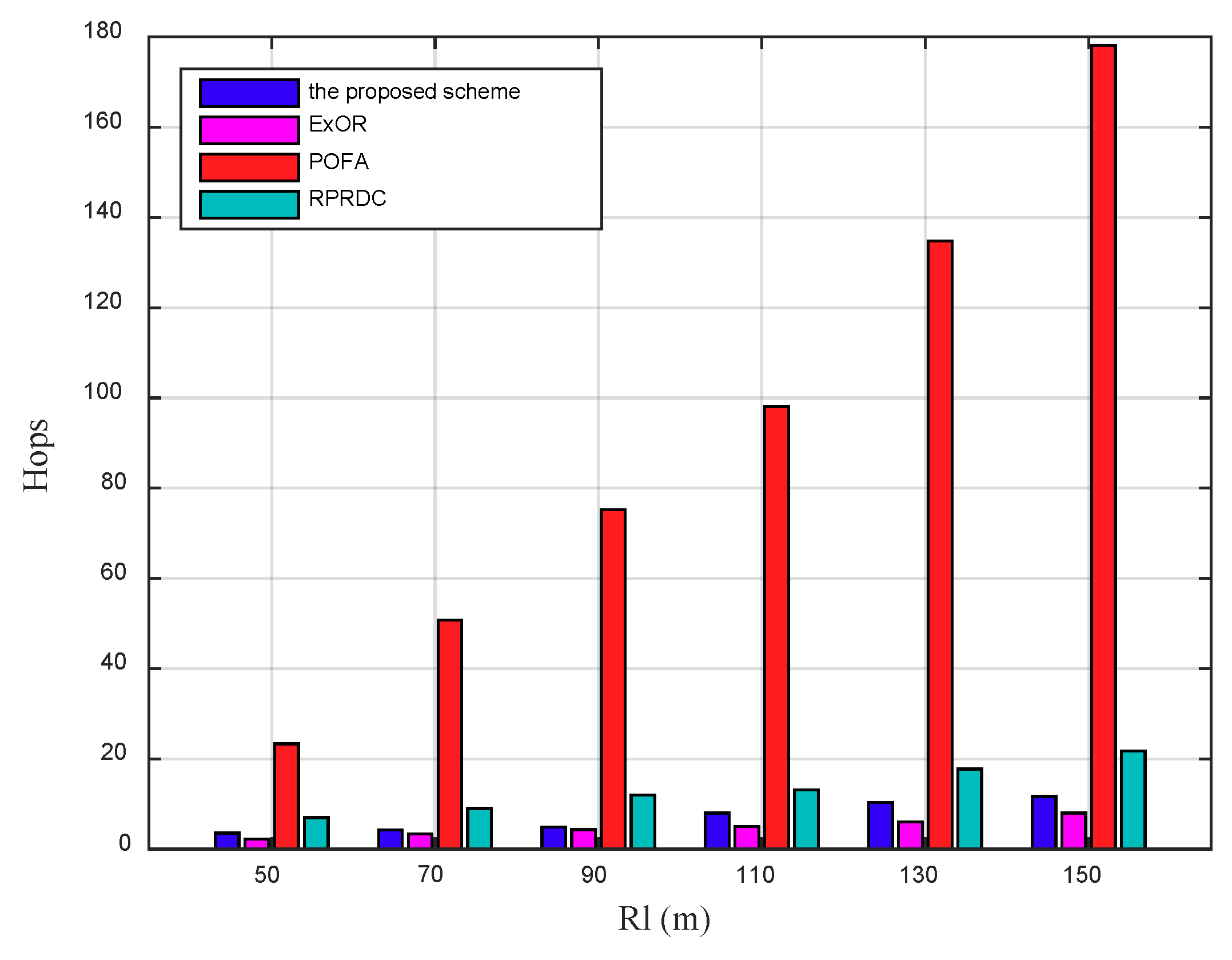
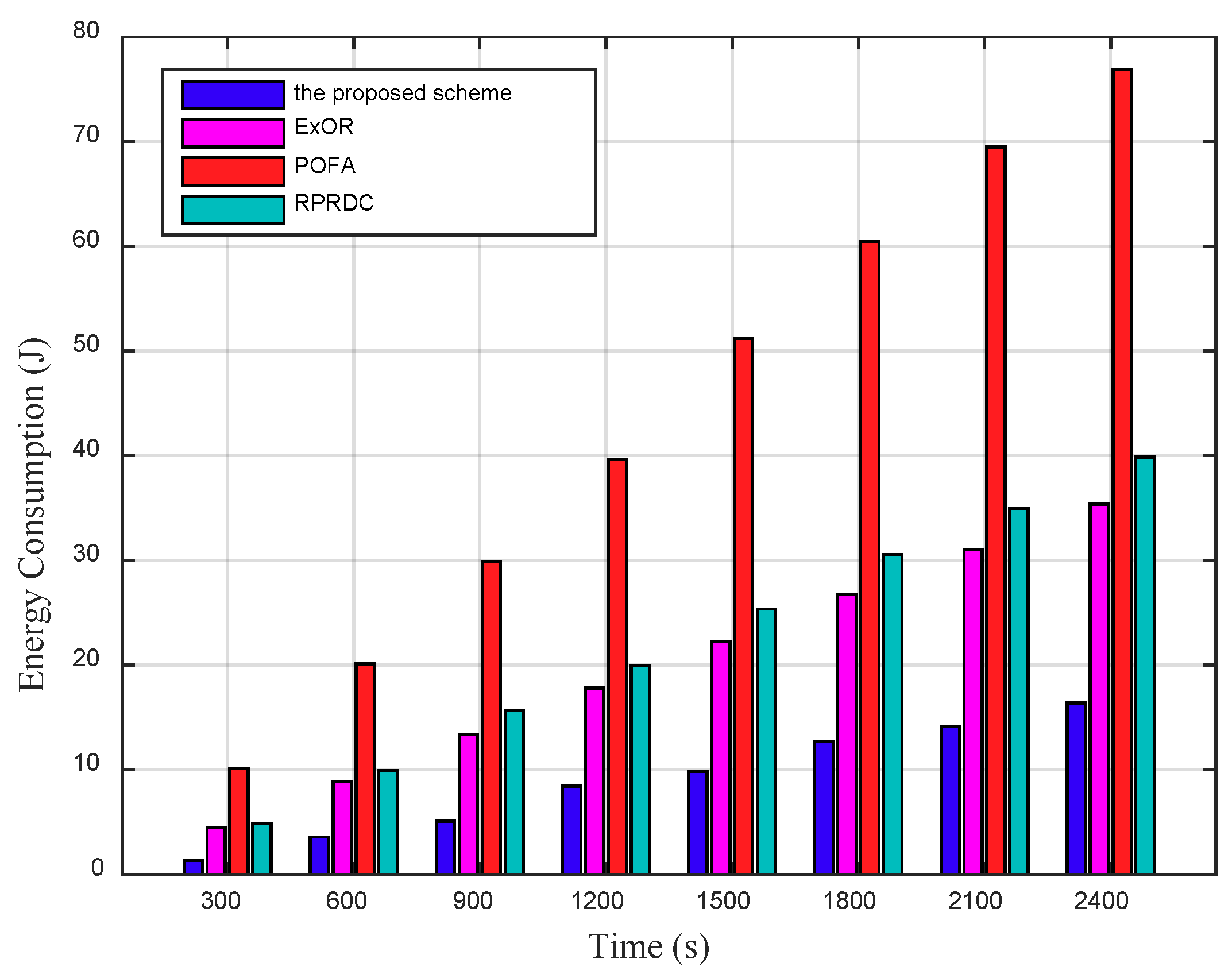
In the scheme, the mobile sink remains stationary and can determine the collection scope during the data collection. Once this data collection is completed, it can move in the network randomly and launch another data collection task anywhere in the network at any time. The proposed scheme can be presented in detail in the following four phases:
4.1. Initialization
To start a data collection period, the mobile sink can launch a data collection task anywhere in network at any time by broadcasting a tag message (including the duration for this data collection and the SID of the sink) by a long radio range Rl, and then it should keep stationary until accomplish this data collection task. Therefore, all nodes under this radio range Rl could receive this tag message.
On receiving a tag message, by obtaining the duration for this data collection included in this message, a node can calculate its whole working time (according to its own working–sleeping scheduling) and its status transition (from the working status to the sleeping status, or vice versa) frequency during this data collection period, which will be used to construct the OCRG in further.
For a node in current data collection scope, the method of Received Signal Strength Indication (RSSI) is used to estimate its distance to the mobile sink, the value of which is used to calculate its Expected Optimal Hops (EOH) (Definition 1) according to Lemma 1. The EOH of a node will be employed to select proper forwarders to minimize the overall energy consumption when forwarding the probe message to the mobile sink.
In order to facilitate the sleeping node to participate in data collection when it wakes up, the mobile sink can choose to re-broadcast the tag message randomly, and in this case, the nodes that have received the same tag message will not deal with it again.
Definition 1. Expected Optimal Hops (EOH). The Expected Optimal Hops denote the number of hops it takes to forward a probe message from any node to the mobile sink with the minimized energy consumption.
It should be noted that EOH is different from the shortest path, according to the energy model, the energy consumption for a node to transfer data to the mobile sink is not linearly related to the length of the data transmission path.
Lemma 1. For any node vi in a data collection scope, its EOH satisfies:where d(vi,vsink) is the distance between node vi and the mobile sink. Proof of Lemma 1. Assuming that there is
B-bit data from node
should be forwarded to the mobile sink
vsink along the path (
vi,
vsink,
k), where
k is the hops on the path and satisfies 1 ≤
k ≤ N − 1. To unify the path representation,
vsink is represented by
vi+k in the next proof process, from which it means that it needs
k hops to forward a probe message from
vi to
vsink. Then, the energy consumption function with respect to
k for this forwarding can be calculated as follows:
To get the minimum value of
Cvi(
k), we can use the average value inequality to derive inequality of
Cvi(
k) which can be described as follows:
Since the sum of the distances for any two adjacent nodes on the path (
vi,
vi+k,
k) satisfies the following inequality:
Therefore, the minimum energy consumption function
with respect to
k satisfies:
To get the value of
k that can minimize
, we can take the first derivative of
with respect to
k as follows:
Let
equal to 0, we can get a value of
k. By using
kexpected to denote this value, we have:
Next, taking the second derivative of
with respect to
k and comparing the value of it at
k = kexpected with 0 as follows:
Therefore, the
has a minimum value at
k =
, and since
vi+k represents
vsink, so we here define the EOH for node
vi is:
The proof is completed. □
4.2. Energy Efficient Probe Message Forwarding Mechanism
For each node in the data collection scope, it needs to send its source information (including its whole working time, its status transition frequency and all its neighbors’ IDs) included in the probe messages to the mobile sink. The format of the probe message is given in
Table 2.
The “Message Source” field is used to indicate the ID of the node sending this probe message. The “Source Information” field is used to store the whole working time, the status transition frequency, and the neighbors’ IDs of the message source. The “Sink ID” field indicates the SID of the mobile sink launching this data collection task, and which is also the forwarded destination for the probe messages. The “Forwarders ID” field is used to store the IDs of nodes that have forwarded this probe message in sequence. In the process of forwarding a probe message, each time the message is relayed by a node (forwarder), it should add its ID in the “Forwarders ID” field in the probe message. The “EOH” field is used to store the value of EOH for the message source.
Since a probe message can be generated from any node that received a tag message and the opportunistic node connections in the network decrease the efficiency of probe message forwarding, it is necessary to design an energy efficient probe message forwarding mechanism to minimize the overall energy consumption when forwarding them to the mobile sink.
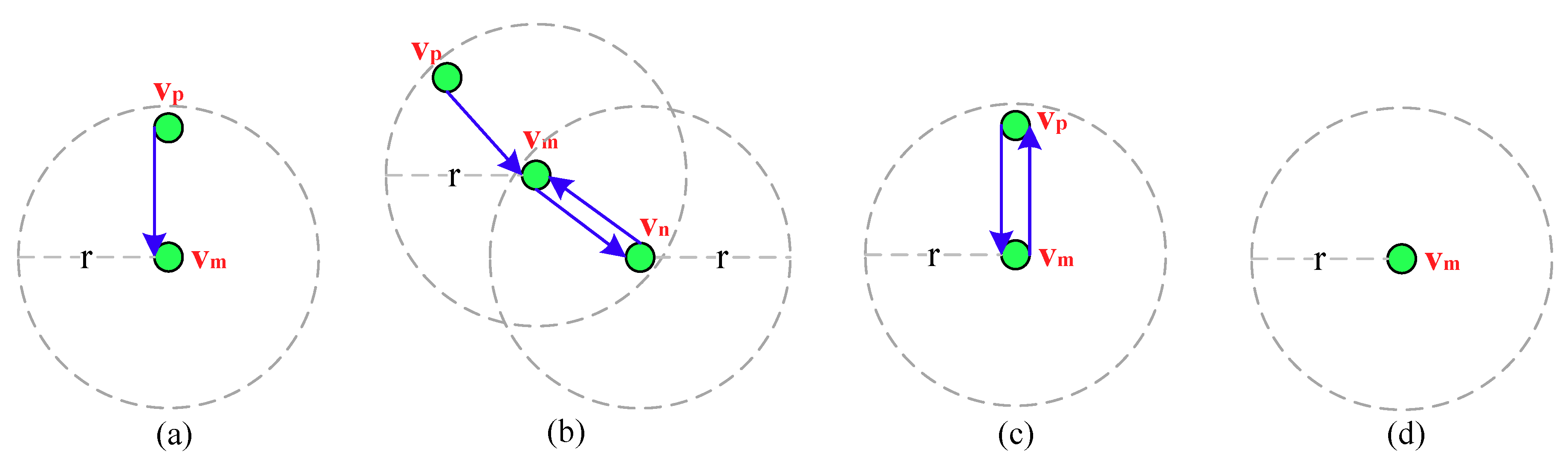
In the mechanism, only the nodes that have received this tag message can participate in the probe message forwarding. When an intermediate node vm receives a probe message, it will check the IDs stored in “Forwarders ID” field in this probe message to learn whether it has forwarded it or not.
Here if
vm has not forwarded this message, as shown in
Figure 3a, it first updates the “Forwarders ID” field by adding its ID in it and calculates the Number of Forwarders (NF) based on it, by obtaining the value of EOH in this message it then can further calculate (EOH–NF), to find a neighbor whose EOH is closest to it as an optimal forwarder. However, if
vm has forwarded this message, as shown in
Figure 3b, for sake of exposition, suppose that the IDs in the “Forwarders ID” field are denoted as {
,…,
,
,
}, it first explores the neighbors that have not forwarded this probe message by checking the IDs in this field, and then updates this field by deleting the IDs of
vm,
vn from it and adds its ID in it. In the next, by calculating NF based on this field and obtaining the value of EOH in this message,
vm can further calculate (EOH–NF) to find a neighbor whose EOH is closest to it from the explored neighbors as an optimal forwarder.
Considering the asynchronous working–sleeping cycle strategy for nodes, when
vm receives this probe message from
vp, if only the neighbor
vp is in working status, as shown in
Figure 3c, it forwards the message to
vp. However, if
vp is also in sleeping status, as shown in
Figure 3d,
vm stops forwarding it. Algorithm 1 gives the detailed energy efficient probe message forwarding mechanism.
| Algorithm 1. Energy efficient probe message forwarding mechanism |
- 1.
When an intermediate node vm receives a probe message: - 2.
if (vm has not forwarded the probe message) - 3.
Add its ID in the “Forwarders ID” field included in the probe message; - 4.
Calculate NF based on the “Forwarders ID” field; - 5.
Calculate (EOH–NF); // the EOH is obtained from the “EOH” field - 6.
if (vm has neighbors) //vp is not included - 7.
Select the neighbor whose EOH is closest to (EOH–NF) as an optimal forwarder; - 8.
Forward the probe message to it; - 9.
end if - 10.
else - 11.
//suppose that vm has forwarded the probe message to vn, but then receives this message again from it - 12.
Explore the neighbors that have not forwarded this probe message; - 13.
Delete the IDs of vm, vn from the “Forwarders ID” field; - 14.
Node vm adds its ID in the “Forwarders ID” field; - 15.
Calculate NF based on the “Forwarders ID” field; - 16.
Calculate (EOH–NF); - 17.
if (the explored neighbors exist) - 18.
Select the neighbor whose EOH is closest to (EOH–NF) as an optimal forwarder; - 19.
Forward the probe message to it; - 20.
end if - 21.
end if - 22.
if (only the neighbor vp of vm is in working status) - 23.
Forward the probe message to vp; - 24.
else //vm is in sleeping status - 25.
Stop forwarding this probe message; - 26.
end if
|
4.3. Opportunistic Connection Random Graph Construction
After receiving these probe messages, the mobile sink constructs an OCRG (Definition 2) by analyzing the included source information to reflect the opportunistic node connections in this data collection scope.
Definition 2. Opportunistic Connection Random Graph (OCRG). The OCRG is constructed based on the intermittent communication caused by asynchronous working–sleeping cycle strategy of nodes, which can be analyzed from all the source information, to reflect the opportunistic node connections in the data collection scope, denoted as G(V, E, Pe).
In an OCRG, V denotes a set of all message sources, E denotes a set of all opportunistic connections between any two adjacent nodes in set V, and Pe denotes the link connectivity between any two adjacent nodes in set V.
For sake of exposition, the link connectivity
Pe between any two adjacent nodes
vi and
vj is denoted as
. There are two factors affect the value of
, of which the first one is the whole working time of nodes
vi and
vj, the longer the nodes’ whole working time, the more likely they can communicate with each other. In addition, the second one is the status transition frequencies of nodes
vi and
vj, which can be explained by that, under the same duration for a data collection, sensor nodes with different status transition frequencies may produce the same whole working time, but nodes with higher status transition frequencies contribute more to improve the link connectivity. This phenomenon can be illustrated in
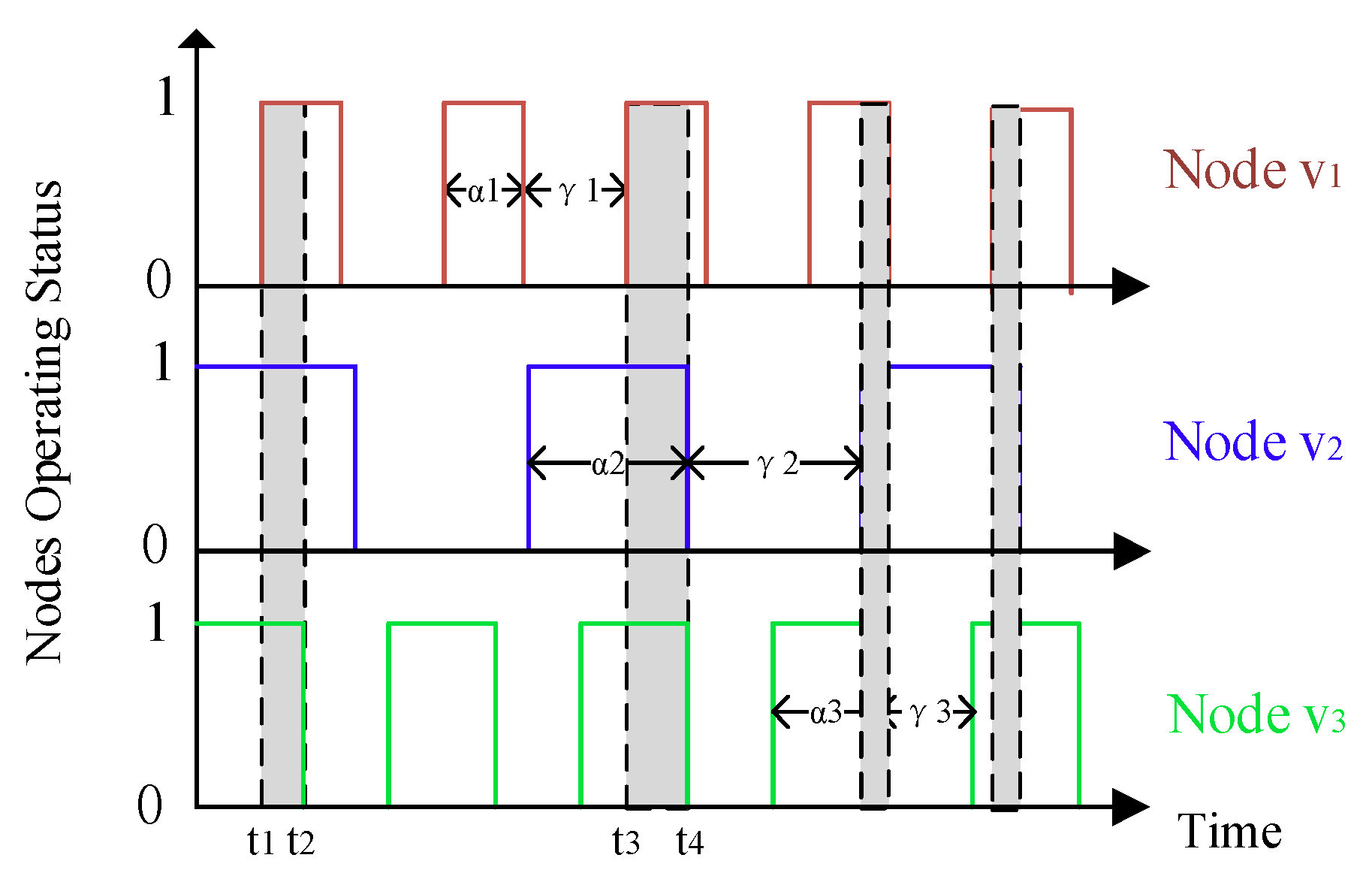
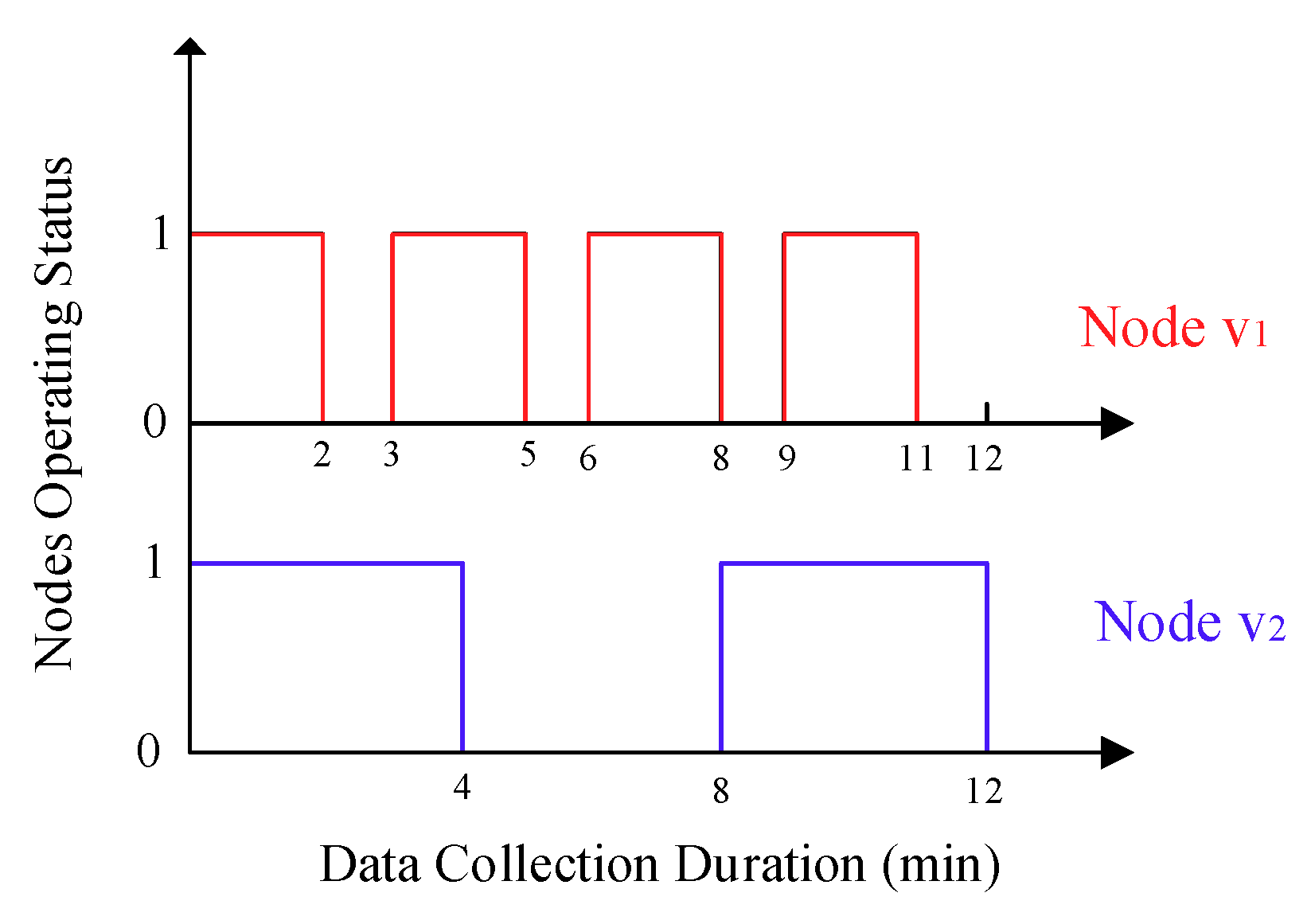
Figure 4, in which the duration for a data collection for the mobile sink is 12 min, and the working–sleeping cycle for node
and
is 3 min and 8 min, respectively, so both of them work 8 min during this process, but the status transition frequency for node
is about 2.3 times that of node
.
Based on the analysis above, the link connectivity (
) between any two adjacent nodes
vi and
vj can be calculated as follows:
where
and
is the whole working time of node
vi and
vj in a data collection period
, respectively, while
and
is the status transition frequencies of node
vi and
vj in this period, respectively. Here
is the max value of the status transition frequency obtained from all the probe messages, and it is used to achieve normalization of the node’s status transition frequency.
Noted that the mobile sink is always in working status, any of its adjacent node (under its short radio range
) that in working status can communicate with it at any time. Hence, for the mobile sink and any of its adjacent node
vi, their link connectivity (
) can be affected by the whole working time and the status transition frequency of node
vi, and accordingly,
can be calculated as follows:
By combing Equations (12) and (13),
Pe can be described as follows:
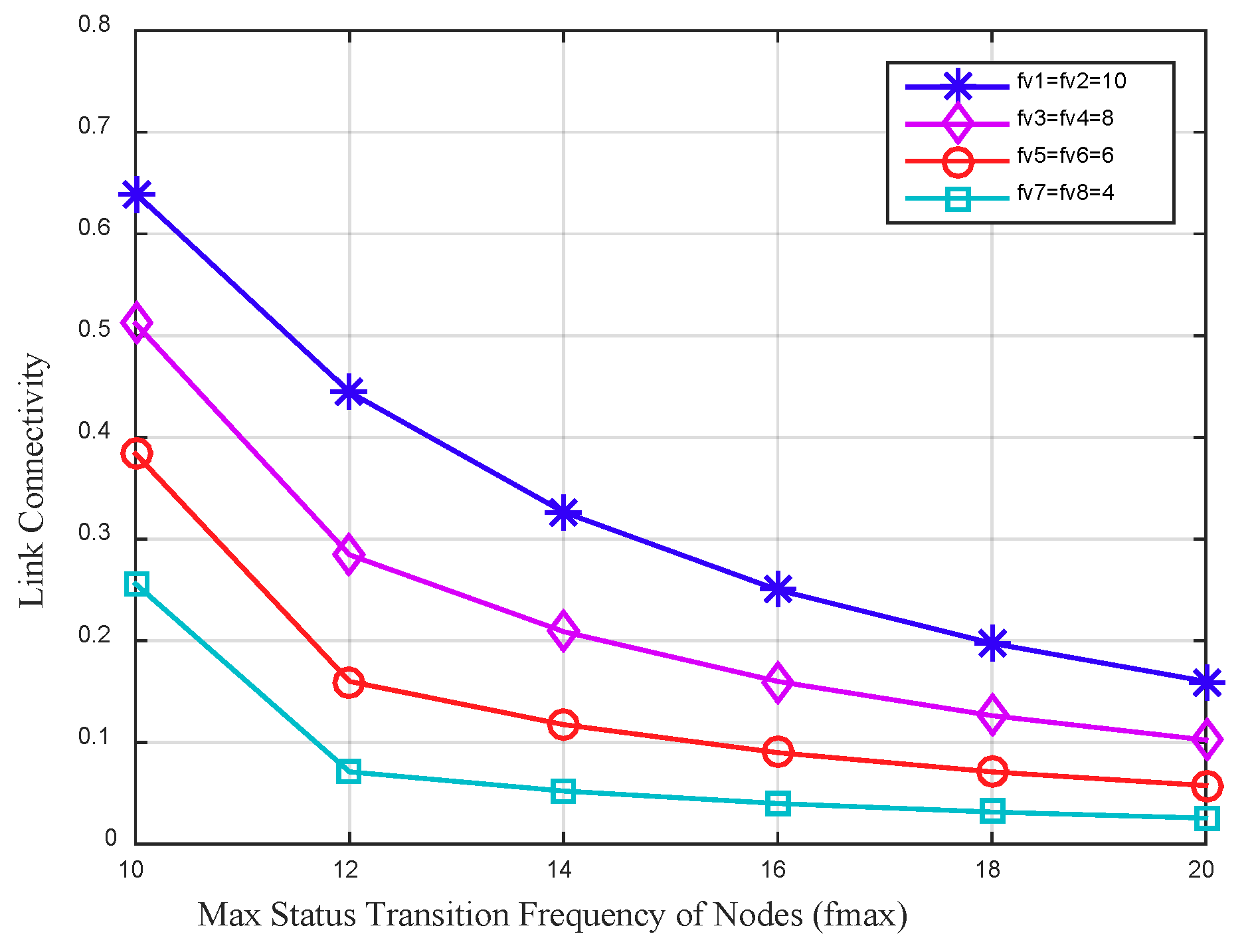
Figure 5 depicts the link connectivity between four node pairs varies by the max status transition frequency of nodes. The whole working time of nodes in this data collection period is set to a fixed value to explore the impact of different status transition frequency of nodes on the link connectivity. In the figure it can be seen that, with a fixed whole working time of the node, the link connectivity between nodes decreases as the max status transition frequency of nodes increases. For two adjacent nodes with higher status transition frequency, the link connectivity between them is higher. The main reason is that the higher status transition frequency of a node increases the communication opportunities with its neighbors, and further improves the link connectivity between them.
Based on the analysis above, the mobile sink can first obtain the message source set V by gathering their IDs stored in the “Message Source” field included in the probe messages, and then obtain the edge set E by analyzing the neighbors’ IDs of each message source that stored in the “Source Information” field, by gathering all message sources’ whole working time and status transition frequencies stored in the “Source Information” field it can calculate the link connectivity between any two adjacent nodes in set V according to Equation (14), thus constructing an OCRG.
By constructing OCRG, the mobile sink models the opportunistic node connections in the data collection scope, based on which, it could calculate the optimal data forwarding path in advance for each node to send their sensing data to improve the reliability of data transmission. Furthermore, the source node could obtain its data forwarding path in advance therefore reduce the delay in each hop, and due to the intermittent communication mode of the nodes, it could also improve the success rate of the data transmission.
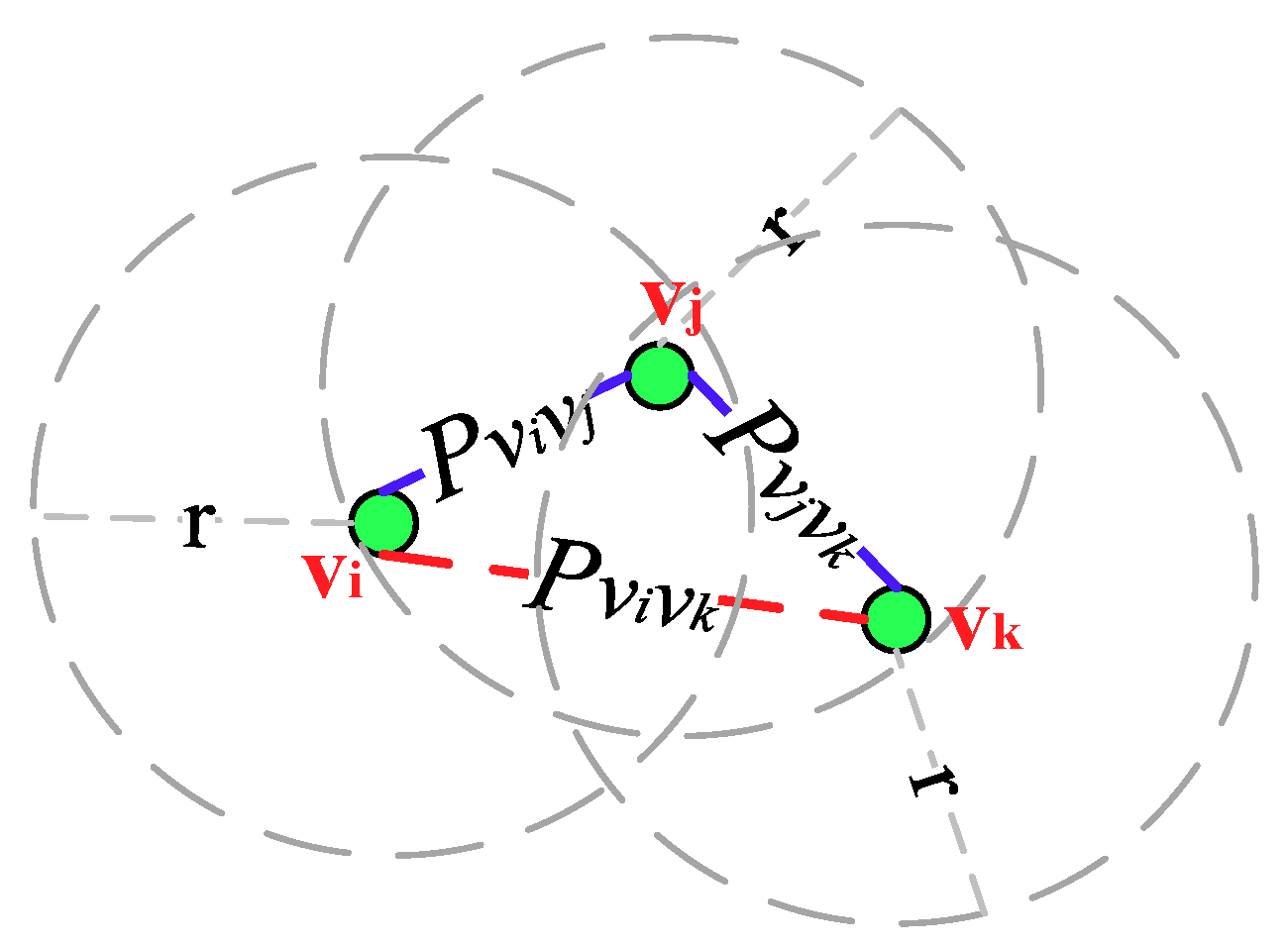
Figure 6 depicts an OCRG with three nodes
vi,
vj and
vk that adopt the asynchronous working–sleeping cycle strategy to save energy. Nodes
vi and
vj are adjacent neighbors while
vj and
vk are adjacent neighbors, and the link connectivity between them are
and
, respectively, hence there exists an opportunistic connection. Since node
vi is not adjacent to
vj, their link connectivity P
vivk is 0.
4.4. The Optimal Path Calculation Based on the Opportunistic Connection Random Graph
Once the OCRG is constructed, it needs to find the optimal path from any node to the mobile sink to realize the reliable sensing data forwarding. In this work, a spanning tree algorithm (Algorithm 2) is designed to calculate the optimal path with the max value of Path Connectivity (PC) (Definition 3) from the mobile sink to each node based on this OCRG. By employing this algorithm, the mobile sink can produce a spanning tree, based on which, each node can get its optimal path to the sink with the corresponding PC of it. Therefore, the mobile sink will broadcast this spanning tree to nodes under the long radio range .
Definition 3. Path Connectivity (PC). In the OCRG, the PC of a path is related to the link connectivity between any two adjacent nodes on this path, which is used to reflect the reliability of this path when delivering data. As for a path (, , k), where node is the source node, node represents the node k hops away from on this path, k is the hops on the path and satisfies 1 ≤ k ≤ N − 1, the PC of this path is defined as: During constructing this spanning tree, all nodes in the OCRG are subdivided into two sets: (i) set K: including the nodes whose optimal paths from the mobile sink to themselves are known, and (ii) set U: including the remaining nodes. In the beginning, set K includes only the mobile sink while set U includes the remaining nodes in the OCRG, and a node in set U will be transferred to set K if the mobile sink finds the optimal path to it.
The algorithm includes two phases, of which the first phase is initialization. In this phase, the mobile sink calculates the PC of the paths from itself to all nodes in set U as follows:
And the nodes on each path can be denoted as follows:
In the second phase, the mobile sink selects a node
with a max value of PC from set U and transfers it to set K, and then updates the PC of the path from
to each node
in set U but directly connected to
as follows:
For each path, once the PC of it is updated, the nodes on it should be updated as follows:
Repeating the work in second phase until set U is empty, a spanning tree with the mobile sink as the root node can be generated.
The algorithm improves the efficiency of finding the optimal path. If the mobile sink calculates and selects the optimal path of each node directly, for each node, it needs to explore all the possible paths between them to determine which one has the maximum PC, which is inefficient and brings high delay. Furthermore, when the network density increases or the data collection scope expands, the number of the paths from a node to the mobile sink increases greatly, which could further decrease its efficiency.
| Algorithm 2. The spanning tree algorithm |
- 1.
Input: an OCRG; - 2.
Output: a spanning tree with the mobile sink as the root node; - 3.
Add into set K; - 4.
Add the remaining nodes in the OCRG into set U; - 5.
for each node in set U do // initialization - 6.
if ( is directly connected to ) - 7.
= ; // is the PC of the path from to - 8.
= {,}; // is used to store the nodes on the path from to - 9.
else - 10.
= 0; - 11.
= ∅; - 12.
end if - 13.
end for - 14.
= 1; // set the PC of the path from to is 1 - 15.
while (set U is not empty) - 16.
Select the node with max from set U; - 17.
Transfer from set U to set K; - 18.
for each neighbor of do // is still in set U - 19.
temp ←×; - 20.
if (temp > ) - 21.
← temp; // update the PC of the path from to - 22.
← + ; // update the nodes on the path from to - 23.
end if - 24.
end for - 25.
end while
|
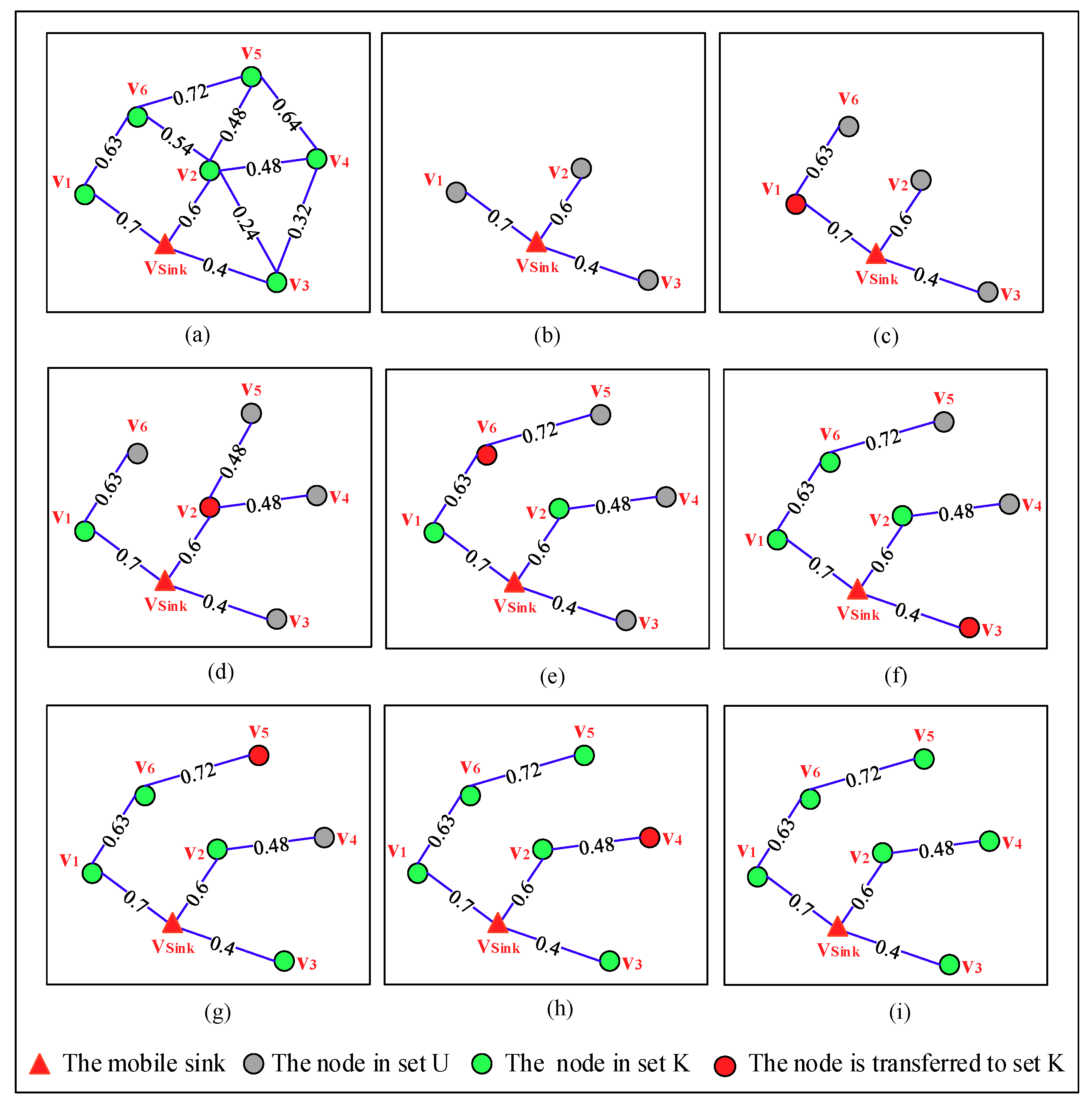
Figure 7 depicts the detailed process of constructing the spanning tree step by step in an OCRG with seven nodes. From
Figure 7a we can see, sets K and U can be denoted as {
} and {
,
,
,
,
,
}, respectively. In the first phase of the algorithm,
calculates the PC of the paths from itself to all nodes in set U and finds the nodes on each path, the results of which are shown in
Table 3 and
Figure 7b, respectively. The PC[
] (
i = 1, 2,…, 6) used in this table indicates the PC of the path from the mobile sink to node
, and the value with bold format is the max value of PC in set U. The second phase of this algorithm includes 6 steps, which can be seen from
Figure 7c–h. In step 1, node
is transferred to set K due to it has the max value of PC among that of all nodes in set U, which can be seen in the table. By checking the OCRG,
learns that only
in set U is directly connected to
, so it updates the PC of the path from itself to
and the nodes on this path. In the next 5 steps, by repeating the work in step 1, a spanning tree is generated which can be seen in
Figure 7i.
When the spanning tree is generated, the mobile sink should broadcast it to the nodes under its long radio range so that they can forward the sensing data to it according to this spanning tree. On receiving the spanning tree, here it is noticing that, only a node that is on it could obtain the optimal path from itself to the mobile sink, and store the path and the PC of the path locally. However, if a node does not find itself on the spanning tree, it will re-send its probe message to the mobile sink according to the energy efficient probe message forwarding mechanism. Moreover, recalling that the mobile sink can choose to re-broadcast the tag message randomly during the current data collection period, the nodes that have not received this tag message will also send their probe messages to the mobile sink.
On receiving these probe messages, the mobile sink could re-construct an OCRG, then re-calculate the optimal path from itself to each node in this OCRG and update the spanning tree accordingly.
In fact, for a node, its optimal path on the spanning tree is the most reliable path for it to forward its sensing data to the mobile sink. However, due to using the asynchronous working–sleeping cycle strategy for nodes, so during data transmission process along this path, any forwarder on the path may be in sleeping status which could lead to the failed link connection, it further causes the failure of data transmission. To solve this problem, a routing protocol that adapts to different nodes operating statuses is proposed to improve the reliability of data transmission and Algorithm 3 gives the detailed routing protocol. In this routing protocol, assuming that the sensing data from node is being forwarded along its optimal path on the spanning tree to the mobile sink. When an intermediate node receives the data, it should forward it to its father node only if is in working status, otherwise, should select other forwarder from its neighbors to continue this data forwarding. This kind of forwarder selection method is described as follows.
For each neighbor of that is on the spanning tree, calculates the link connectivity between them according to Equation (14), by obtaining the value of PC () stored in locally it then can calculate (×) to get the PC of the path --, accordingly, selects the neighbor on path -- with a max value of PC as the forwarder.
| Algorithm 3. The routing protocol |
- 1.
Assuming that the sensing data from node is forwarded along its optimal path on the spanning tree to the mobile sink; - 2.
When an intermediate node receives the sensing data: - 3.
if (its father node is in working status) - 4.
Forward the sensing data to ; - 5.
employs this routing protocol to forward the data; - 6.
else //is in sleeping status - 7.
if ( has neighbors on the spanning tree) - 8.
for each neighbor do - 9.
Calculate according to Equation (14); - 10.
Calculate the PC of the path --; - 11.
end for - 12.
Select the neighbor that on a path with a max value of PC as the forwarder; - 13.
Forward the sensing data to this forwarder; - 14.
The forwarder employs this routing protocol to forward the data; - 15.
else - 16.
Stop forwarding this data; - 17.
end if - 18.
end if
|
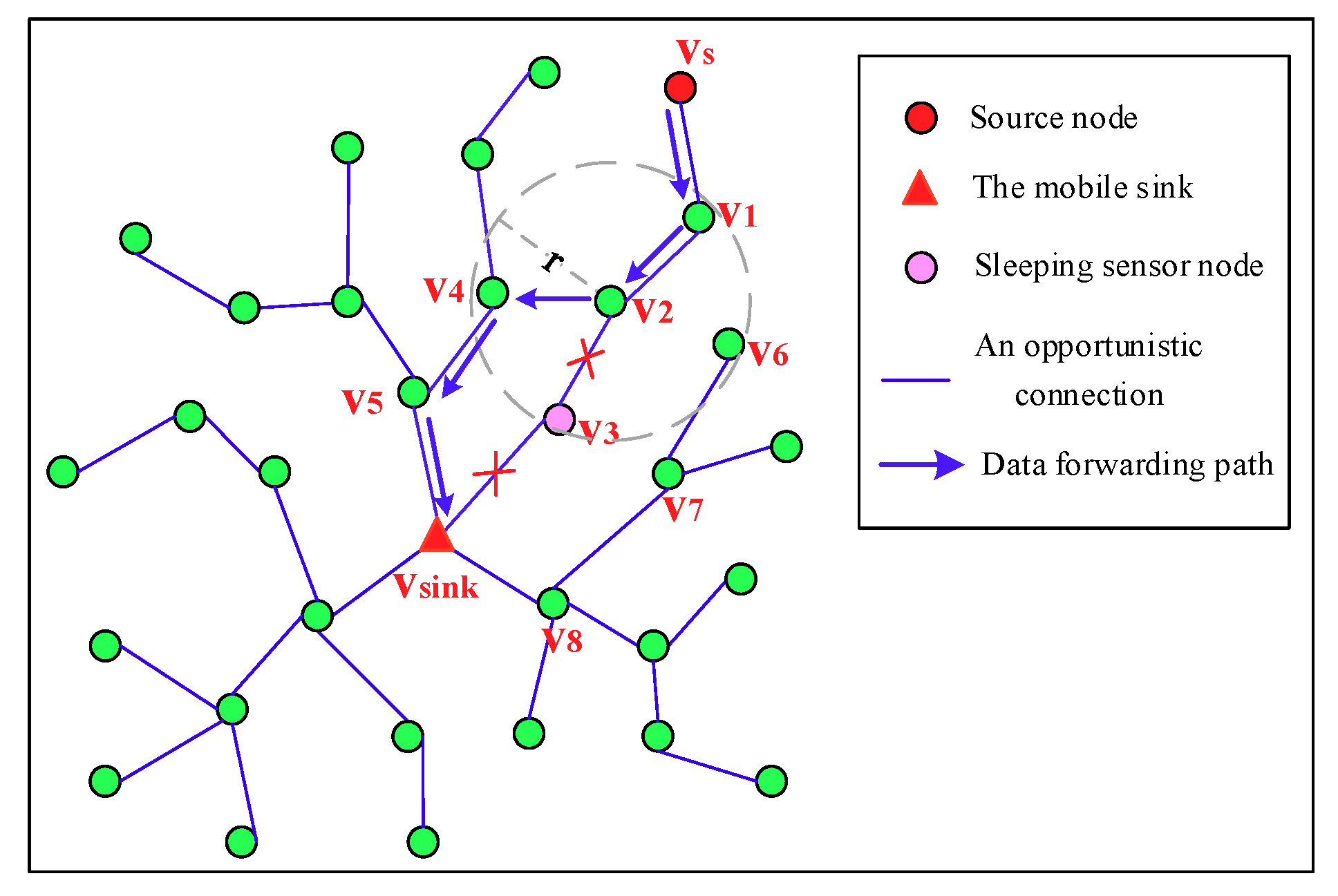
Figure 8 depicts the detailed process of a source node
forwards its sensing data to
. Node
forwards the data to its father node
, and then
forwards it to its father node
. Since the father node
of
is in sleeping status,
needs to find other forwarder. For neighbors
and
of
that are on the spanning tree,
calculates link connectivity
and
, respectively, by obtaining the value of PC stored in
,
locally it then can calculate (
×
) and (
×
), respectively, to get the PC of the path
-
-
- and path
-
-
-
-. Since the PC of the path
-
-
- is greater than that of the path
-
-
-
-, node
is selected as the forwarder, then the sensing data is forwarded to
along the path
-
-.