Consensus-Based Filter for Distributed Sensor Networks with Colored Measurement Noise
Abstract
1. Introduction
2. Background
2.1. Problem Formulation
2.2. Consensus Algorithm
3. Proposed Method
3.1. Augmented State Approach
- (1)
- Prediction of local filter: Compute the predicted augmented state estimate and the corresponding state error covariance
- (2)
- Update of local filter: Calculate the residual and the associated covarianceCalculate the local filter gainUpdate the augmented state and the associated error covariance
- (3)
- Consensus on the original information matrices and information vectors: For a L-step consensus iteration, the consensus on posterior information is carried out in the formwhere is the consensus step, is the consensus weight. A convex combination is adopted by supposing and [8]. The iteration is initialized bywhere , and n is the dimension of the original state.
- (4)
- Reset the local filter:where , and d is the dimension of the measurement of each node.
3.2. Measurement Differencing Approach
- (1)
- Update of local filter:where
- (2)
- Consensus on the information matrices and information vectors: For a L-step consensus iteration, the consensus on posterior information is carried out bywhere is the consensus step, is the consensus weight. A convex combination is adopted by supposing and . The iteration can be initialized by
- (3)
- Prediction of local filter:where
3.3. Discussion
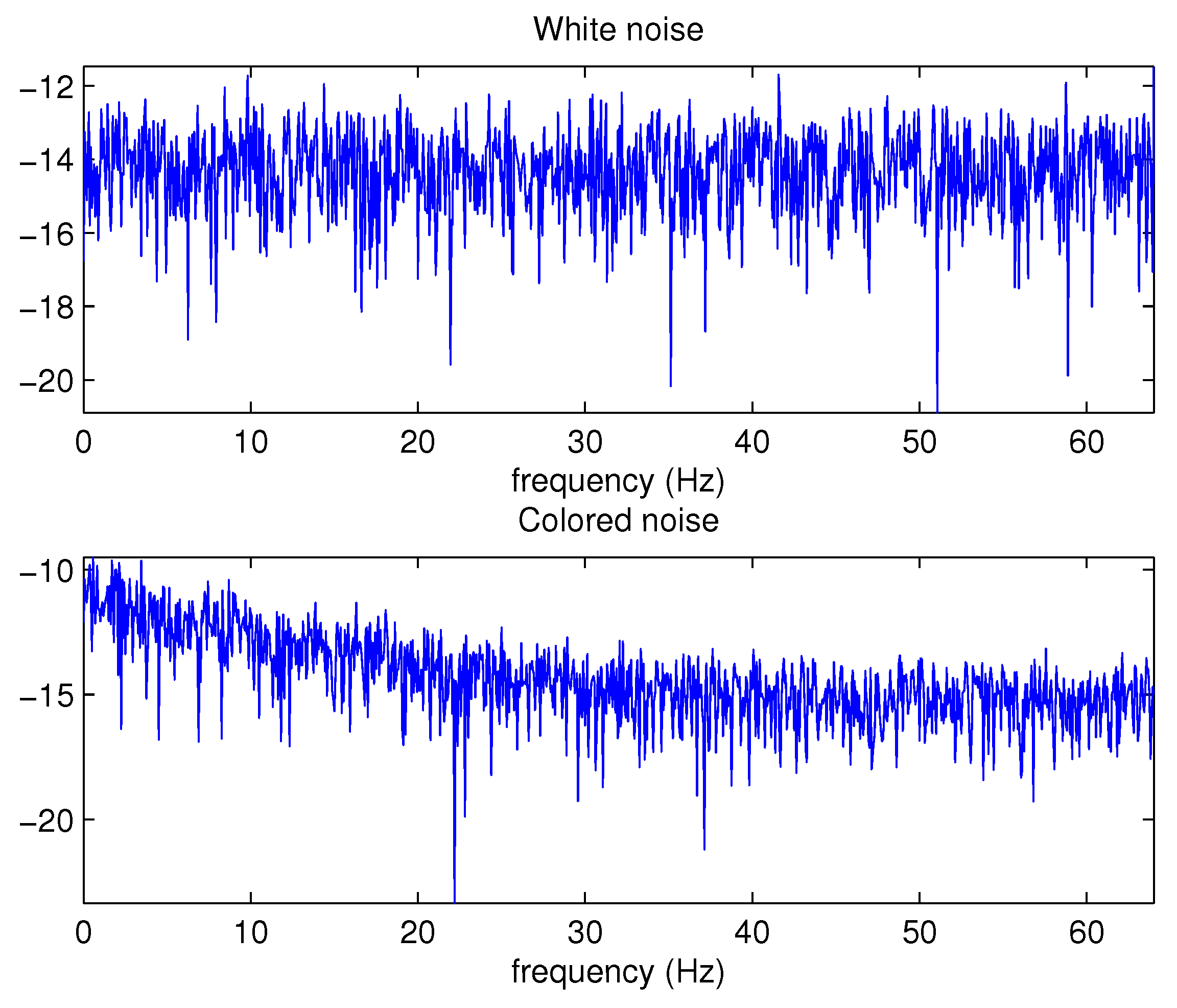
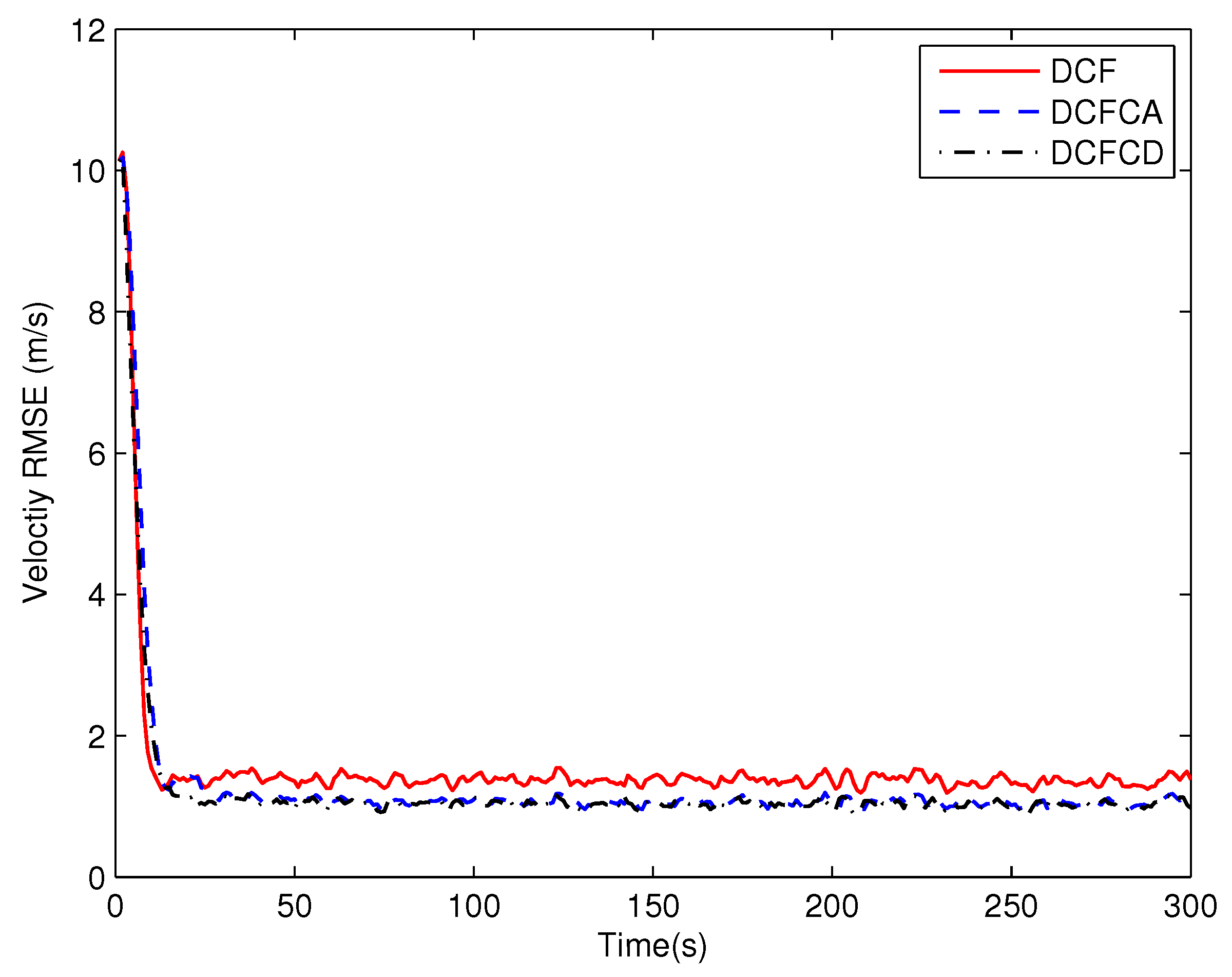
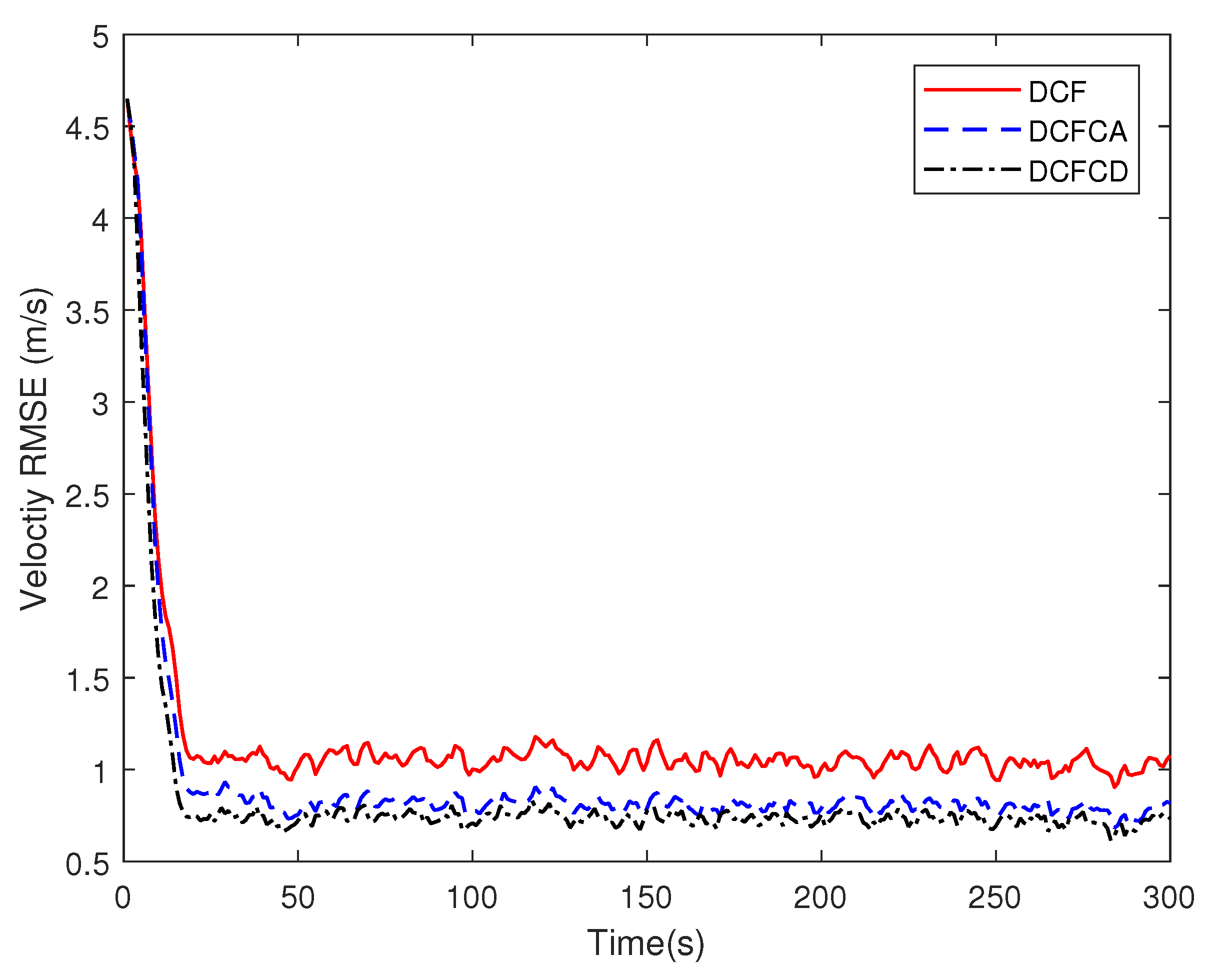
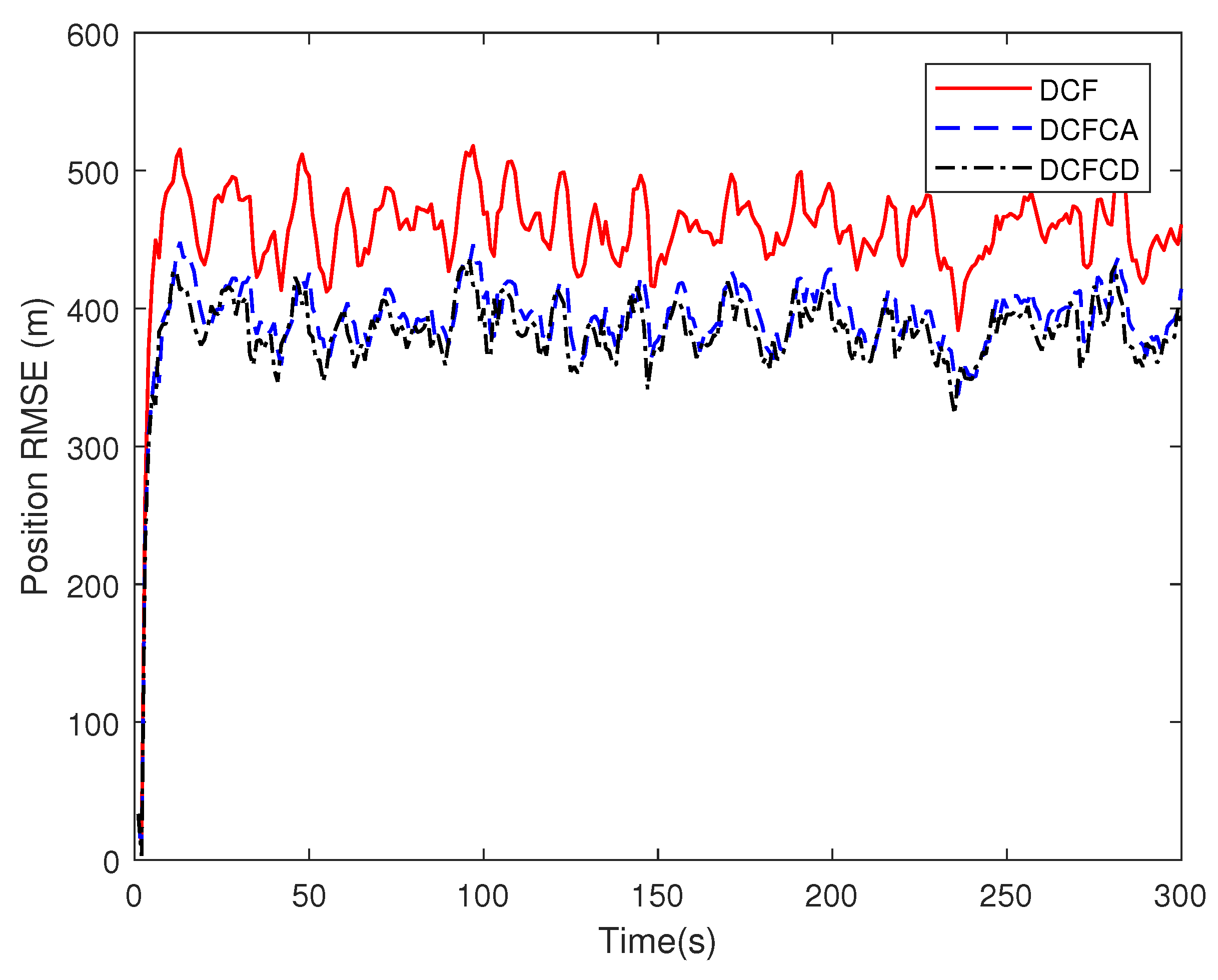
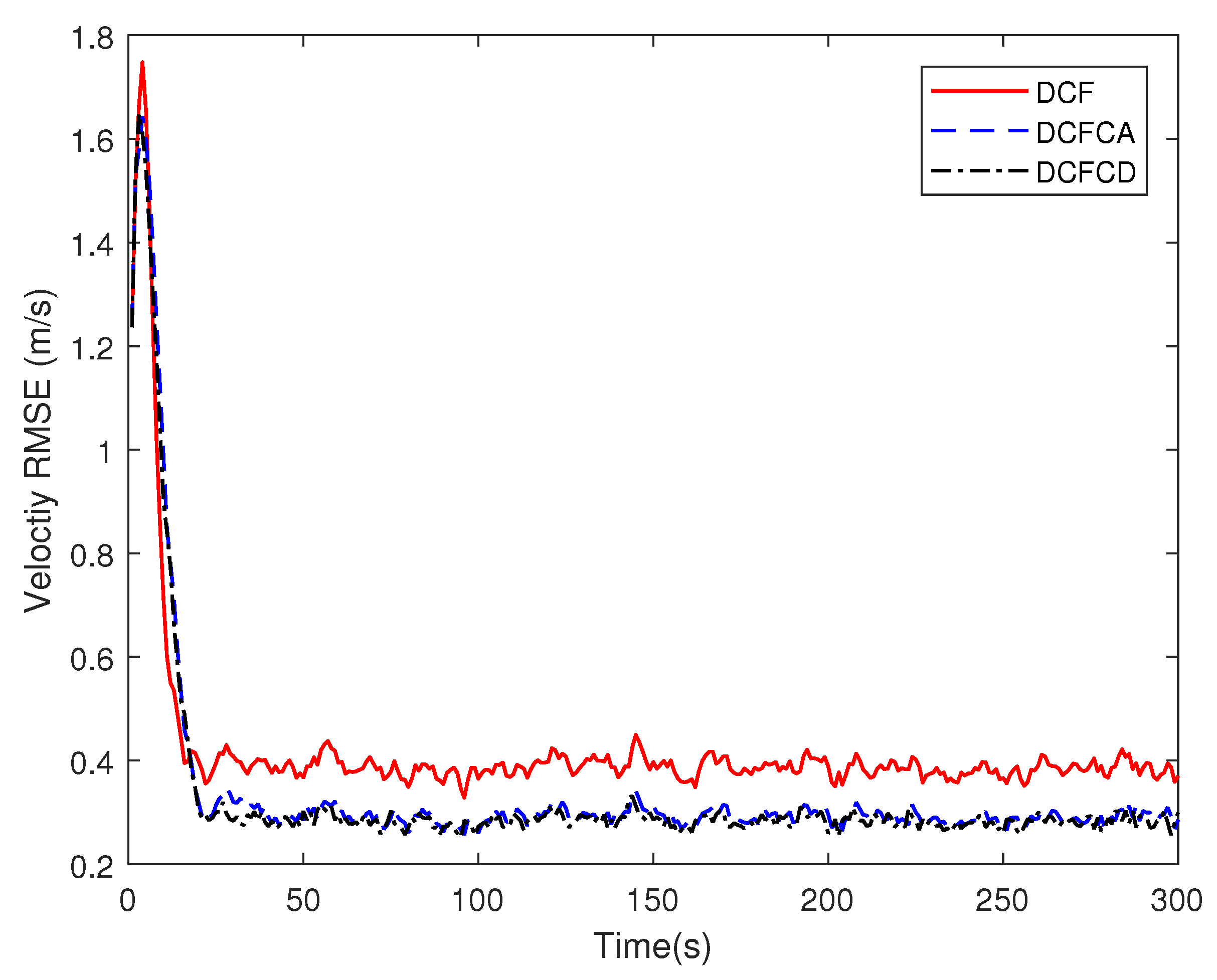
4. Simulations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Battistelli, G.; Chisci, L.; Mugnai, G.; Farina, A.; Graziano, A. Consensus-Based Linear and Nonlinear Filtering. IEEE Trans. Autom. Control 2015, 60, 1410–1415. [Google Scholar] [CrossRef]
- Farina, M.; Betti, G.; Giulioni, L.; Scattolini, R. An Approach to Distributed Predictive Control for Tracking–Theory and Applications. IEEE Trans. Control Syst. Technol. 2014, 22, 1558–1566. [Google Scholar]
- Keshavarz-Mohammadiyan, A.; Khaloozadeh, H. Consensus-based distributed unscented target tracking in wireless sensor networks with state-dependent noise. Signal Process. 2018, 144, 283–295. [Google Scholar] [CrossRef]
- Farina, M.; Carli, R. Partition-Based Distributed Kalman Filter With Plug and Play Features. IEEE Trans. Control Netw. Syst. 2018, 5, 560–570. [Google Scholar] [CrossRef]
- Cao, M.L.; Meng, Q.H.; Jing, Y.Q.; Wang, J.Y.; Zeng, M. Distributed Sequential Location Estimation of a Gas Source via Convex Combination in WSNs. IEEE Trans. Instrum. Meas. 2016, 65, 1484–1494. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Fax, J.A.; Murray, R.M. Consensus and Cooperation in Networked Multi-Agent Systems. Proc. IEEE 2007, 95, 215–233. [Google Scholar] [CrossRef]
- Das, S.; Moura, J.M.F. Distributed Kalman Filtering With Dynamic Observations Consensus. IEEE Trans. Signal Process. 2015, 63, 4458–4473. [Google Scholar] [CrossRef]
- Battistelli, G.; Chisci, L. Stability of consensus extended Kalman filter for distributed state estimation. Automatica 2016, 68, 169–178. [Google Scholar] [CrossRef]
- Das, S.; Moura, J.M.F. Consensus+InnovationsDistributed Kalman Filter With Optimized Gains. IEEE Trans. Signal Process. 2017, 65, 467–481. [Google Scholar] [CrossRef]
- He, X.; Xue, W.; Fang, H. Consistent distributed state estimation with global observability over sensor network. Automatica 2018, 92, 162–172. [Google Scholar] [CrossRef]
- Dimakis, A.G.; Kar, S.; Moura, J.M.; Rabbat, M.G.; Scaglione, A. Gossip algorithms for distributed signal processing. Proc. IEEE 2010, 98, 1847–1864. [Google Scholar] [CrossRef]
- Franceschelli, M.; Giua, A.; Seatzu, C. Fast discrete consensus based on gossip for makespan minimization in networked systems. Automatica 2015, 56, 60–69. [Google Scholar] [CrossRef]
- Falsone, A.; Margellos, K.; Garatti, S.; Prandini, M. Finite time distributed averaging over gossip-constrained ring networks. IEEE Trans. Control Netw. Syst. 2017, 5, 879–887. [Google Scholar] [CrossRef]
- Cattivelli, F.S.; Sayed, A.H. Diffusion LMS strategies for distributed estimation. IEEE Trans. Signal Process. 2010, 58, 1035–1048. [Google Scholar] [CrossRef]
- Chen, F.; Li, X.; Duan, S.; Wang, L.; Wu, J. Diffusion generalized maximum correntropy criterion algorithm for distributed estimation over multitask network. Digit. Signal Process. 2018, 81, 16–25. [Google Scholar] [CrossRef]
- Al-Sayed, S.; Plata-Chaves, J.; Muma, M.; Moonen, M.; Zoubir, A.M. Node-specific diffusion LMS-based distributed detection over adaptive networks. IEEE Trans. Signal Process. 2018, 66, 682–697. [Google Scholar] [CrossRef]
- Olfati-Saber, R. Kalman-Consensus Filter: Optimality, stability, and performance. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control, Shanghai, China, 15–18 December 2009; pp. 7036–7042. [Google Scholar]
- Olfati-Saber, R. Distributed Kalman Filter with Embedded Consensus Filters. In Proceedings of the 44th IEEE Conference on Decision and Control, Seville, Spain, 15 December 2005; pp. 8179–8184. [Google Scholar]
- Battistelli, G.; Chisci, L. Kullback–Leibler average, consensus on probability densities, and distributed state estimation with guaranteed stability. Automatica 2014, 50, 707–718. [Google Scholar] [CrossRef]
- Liu, G.; Tian, G. Square-Root Sigma-Point Information Consensus Filters for Distributed Nonlinear Estimation. Sensors 2017, 17, 800. [Google Scholar] [CrossRef] [PubMed]
- Ji, H.; Lewis, F.L.; Hou, Z.; Mikulski, D. Distributed information-weighted Kalman consensus filter for sensor networks. Automatica 2017, 77, 18–30. [Google Scholar] [CrossRef]
- Jenabzadeh, A.; Safarinejadian, B.; Mohammadnia, F. Distributed consensus filter for a class of continuous-time nonlinear stochastic systems in sensor networks. Asian J. Control 2017, 19, 1284–1294. [Google Scholar] [CrossRef]
- Shen, K.; Jing, Z.; Dong, P. A Consensus Nonlinear Filter With Measurement Uncertainty in Distributed Sensor Networks. IEEE Signal Process. Lett. 2017, 24, 1631–1635. [Google Scholar] [CrossRef]
- Dong, P.; Jing, Z.; Shen, K.; Li, M. A Distributed Consensus Filter for Sensor Networks with Heavy-tailed Measurement Noise. Sci. China Inf. Sci. 2018, 61, 119201. [Google Scholar] [CrossRef]
- Shen, K.; Jing, Z.; Dong, P. Simultaneous Target Tracking and Sensor Location Refinement in Distributed Sensor Networks. Signal Process. 2018, 153, 123–131. [Google Scholar] [CrossRef]
- Dong, P.; Jing, Z.; Leung, H.; Shen, K.; Li, M. Robust Consensus Nonlinear Information Filter for Distributed Sensor Networks with Measurement Outliers. IEEE Trans. Cybern. 2018. [Google Scholar] [CrossRef] [PubMed]
- Petovello, M.G.; O’Keefe, K.; Lachapelle, G.; Cannon, M.E. Consideration of time-correlated errors in a Kalman filter applicable to GNSS. J. Geod. 2009, 83, 51–56. [Google Scholar] [CrossRef]
- Le Chevalier, F. Principles of Radar and Sonar Signal Processing; Artech House: Norwood, MA, USA, 2002. [Google Scholar]
- Matei, I.; Baras, J.S. Consensus-based linear distributed filtering. Automatica 2012, 48, 1776–1782. [Google Scholar] [CrossRef]
- Bryson, A.; Johansen, D. Linear filtering for time-varying systems using measurements containing colored noise. IEEE Trans. Autom. Control 1965, 10, 4–10. [Google Scholar] [CrossRef]
- Lee, K.; Johnson, E.N. State estimation using Gaussian process regression for colored noise systems. In Proceedings of the 2017 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2017. [Google Scholar]
- Gibson, J.D.; Koo, B.; Gray, S.D. Filtering of colored noise for speech enhancement and coding. IEEE Trans. Signal Process. 1991, 39, 1732–1742. [Google Scholar] [CrossRef]
- Bryson, A., Jr.; Henrikson, L. Estimation using sampled data containing sequentially correlated noise. J. Spacecr. Rocket. 1968, 5, 662–665. [Google Scholar] [CrossRef]
- Bryson, A.; Ho, Y.C. Applied Optimal Control: Optimization, Estimation, and Control, Revised ed.; Taylor & Francis: Levittown, PA, USA, 1975. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Wang, X.; Liang, Y.; Pan, Q.; Zhao, C.; Yang, F. Nonlinear Gaussian smoothers with colored measurement noise. IEEE Trans. Autom. Control 2015, 60, 870–876. [Google Scholar] [CrossRef]
- Liu, W. Optimal filtering for discrete-time linear systems with time-correlated multiplicative measurement noises. IEEE Trans. Autom. Control 2016, 61, 1972–1978. [Google Scholar] [CrossRef]
- Liu, W. State estimation for discrete-time Markov jump linear systems with time-correlated measurement noise. Automatica 2017, 76, 266–276. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, Y.; Li, J.Y.; Li, Y. Robust state estimation for discrete time systems with colored noises and communication constraints. J. Frankl. Inst. 2018, 355, 5790–5810. [Google Scholar] [CrossRef]




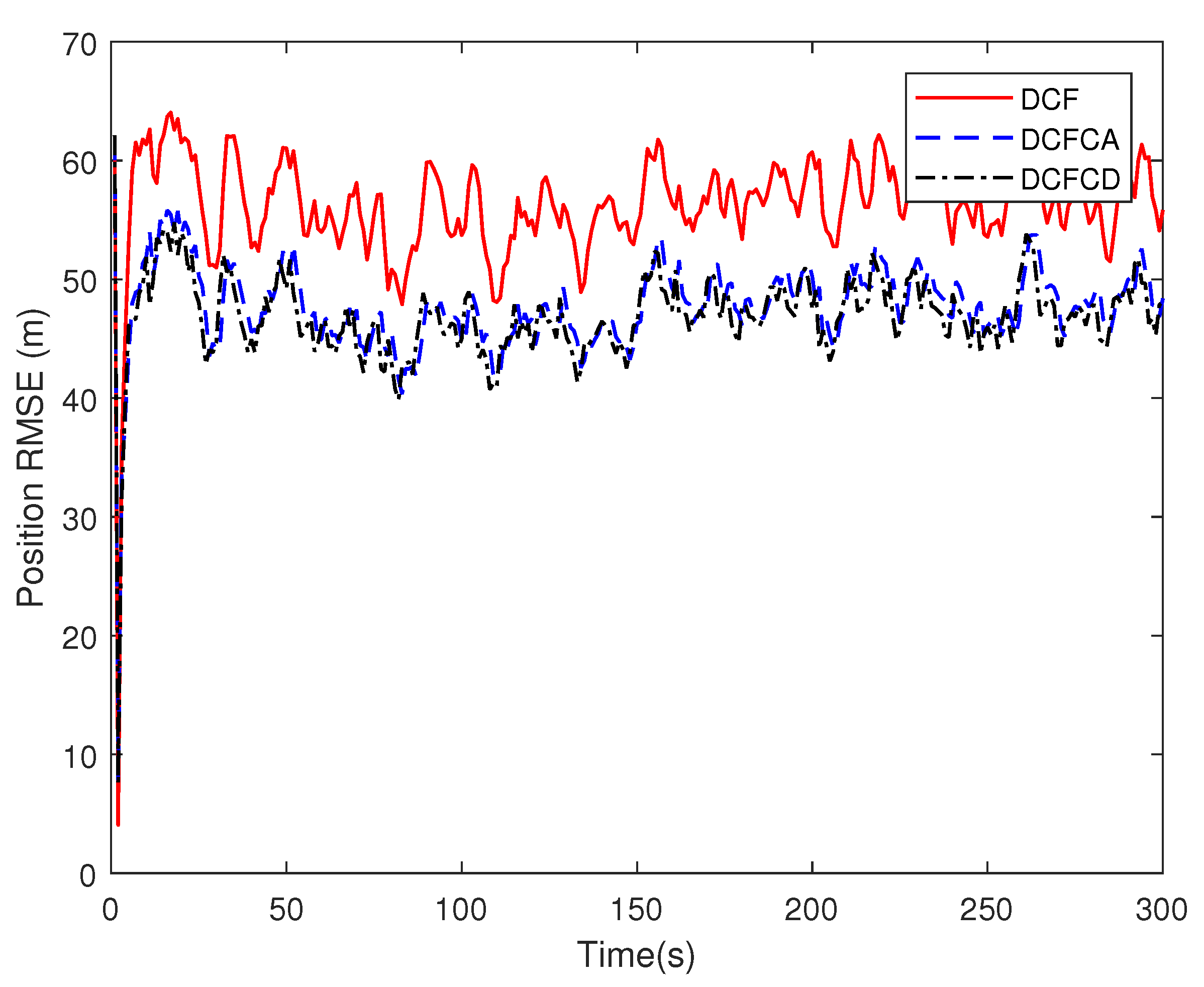
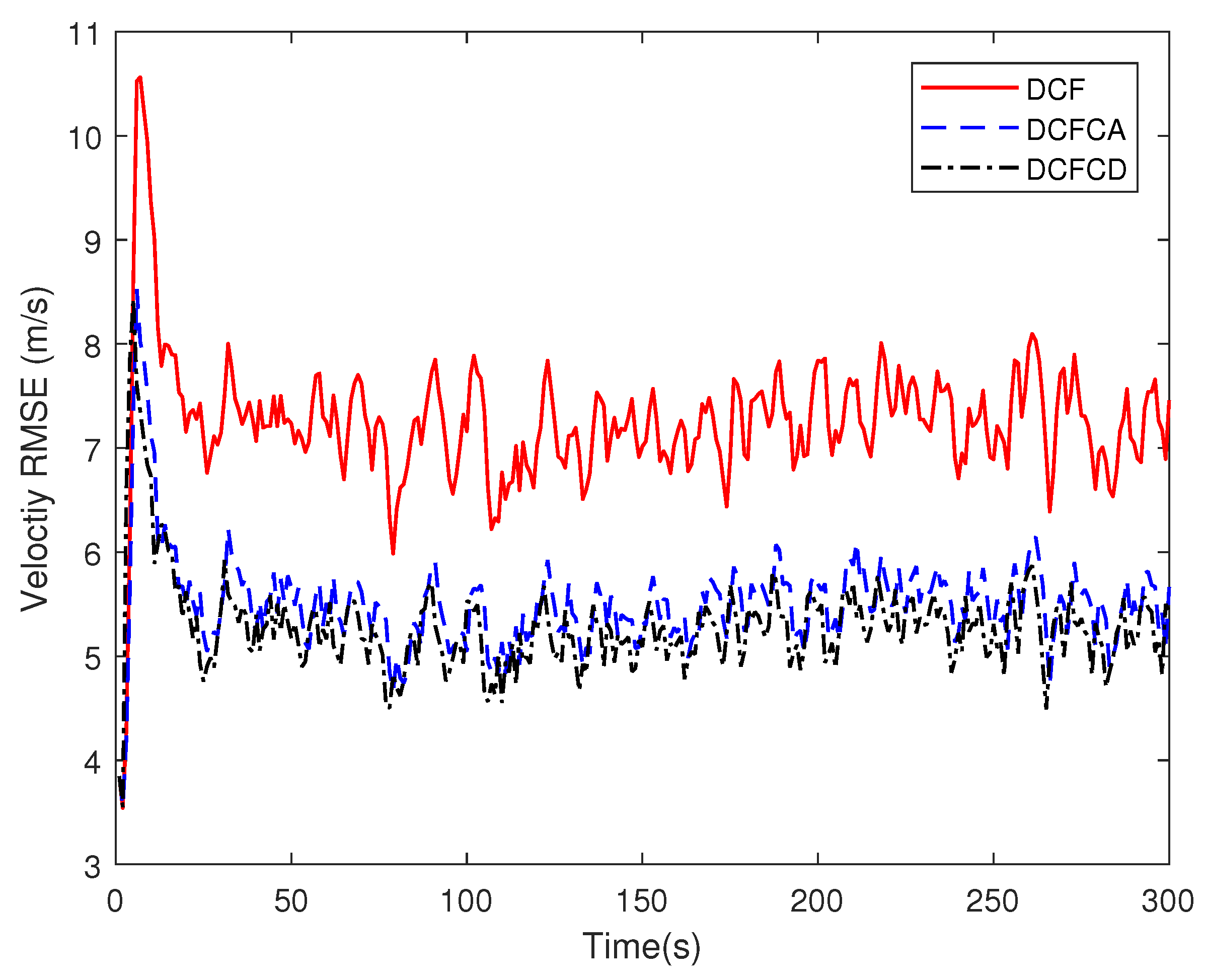

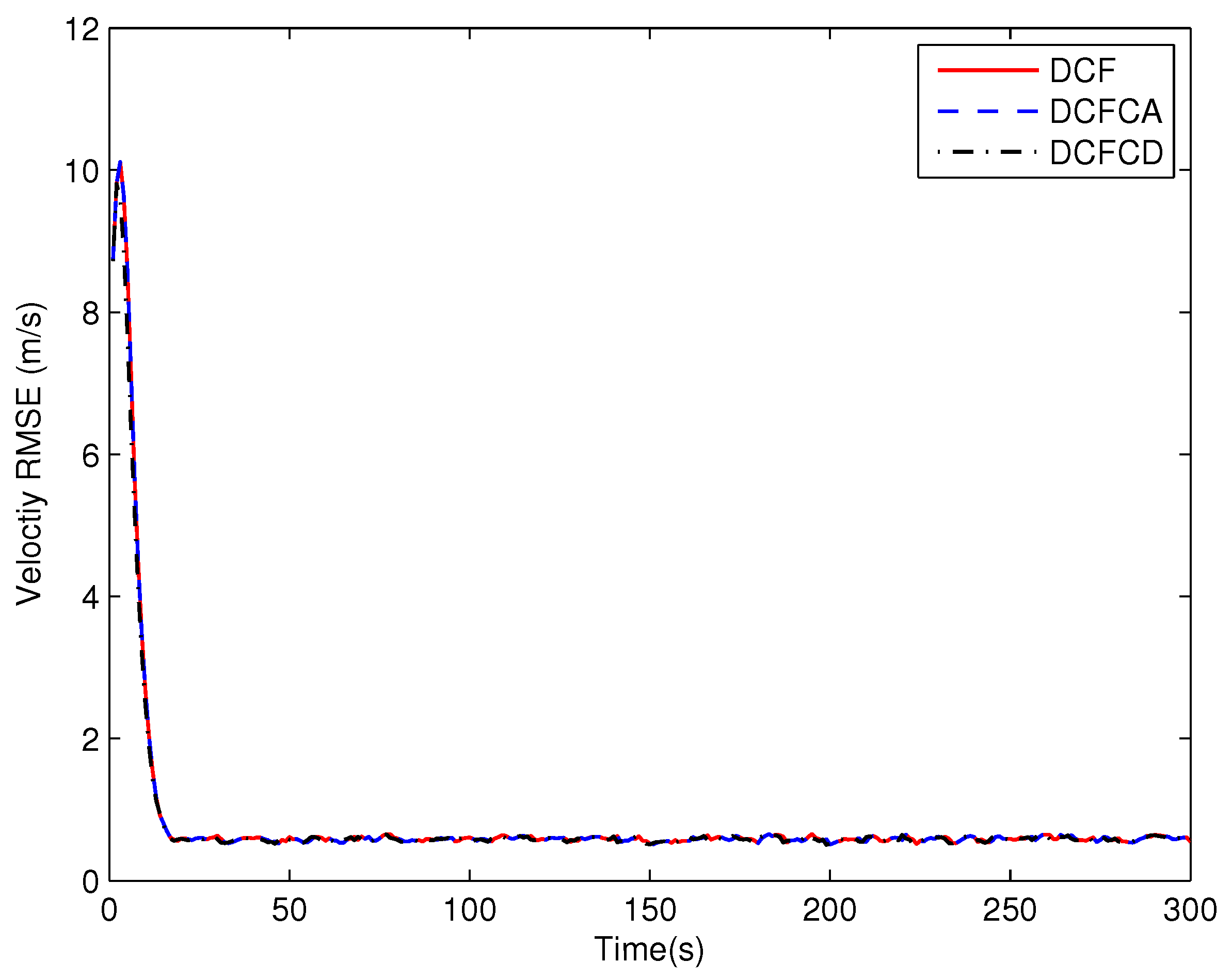

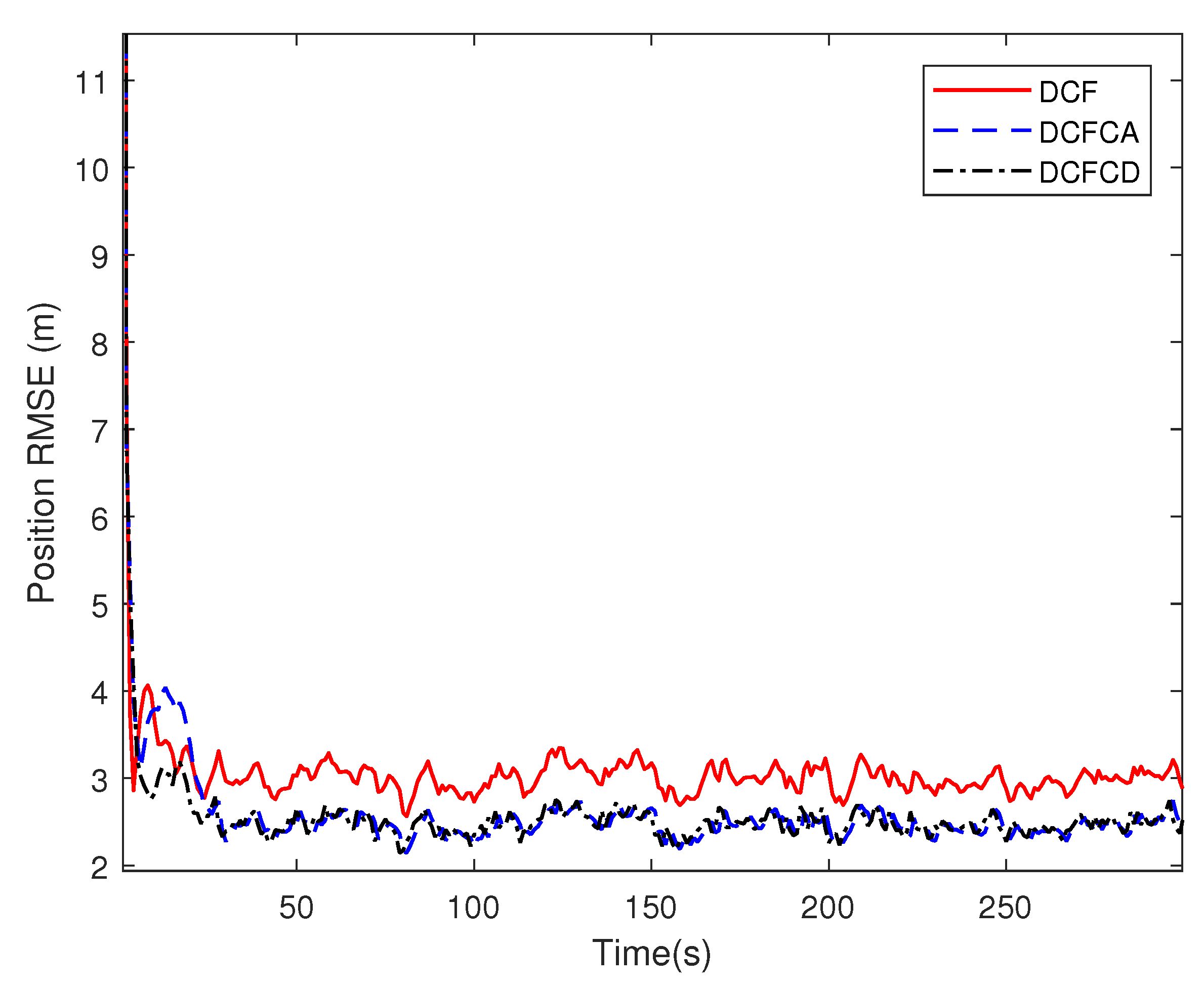
| Methods | |||||
|---|---|---|---|---|---|
| DCF | 4.9628 | 5.4981 | 6.8682 | 9.2026 | 10.6130 |
| DCFCA | 4.9628 | 5.2320 | 6.4136 | 8.1365 | 9.4174 |
| DCFCD | 4.4384 | 4.8552 | 5.9054 | 7.6690 | 8.9543 |
| Methods | |||||
|---|---|---|---|---|---|
| DCF | 0.8141 | 0.7640 | 1.0856 | 1.2654 | 1.4003 |
| DCFCA | 0.8141 | 0.7090 | 0.9712 | 1.0109 | 1.0312 |
| DCFCD | 0.7947 | 0.6905 | 0.9108 | 0.9288 | 0.9262 |
| Methods | |||||
|---|---|---|---|---|---|
| DCF | 2.3499 | 4.5342 | 6.1405 | 7.9913 | 9.1410 |
| DCFCA | 2.1226 | 4.1622 | 5.5639 | 7.1183 | 7.9679 |
| DCFCD | 1.9234 | 3.8094 | 5.1714 | 6.7969 | 7.7378 |
| Methods | |||||
|---|---|---|---|---|---|
| DCF | 0.6127 | 0.8994 | 1.0441 | 1.0877 | 1.0977 |
| DCFCA | 0.5070 | 0.7686 | 0.8670 | 0.8854 | 0.8924 |
| DCFCD | 0.5029 | 0.7163 | 0.8075 | 0.8335 | 0.8512 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Dong, P.; Jing, Z.; Cheng, J. Consensus-Based Filter for Distributed Sensor Networks with Colored Measurement Noise. Sensors 2018, 18, 3678. https://doi.org/10.3390/s18113678
Wang J, Dong P, Jing Z, Cheng J. Consensus-Based Filter for Distributed Sensor Networks with Colored Measurement Noise. Sensors. 2018; 18(11):3678. https://doi.org/10.3390/s18113678
Chicago/Turabian StyleWang, Jinran, Peng Dong, Zhongliang Jing, and Jin Cheng. 2018. "Consensus-Based Filter for Distributed Sensor Networks with Colored Measurement Noise" Sensors 18, no. 11: 3678. https://doi.org/10.3390/s18113678
APA StyleWang, J., Dong, P., Jing, Z., & Cheng, J. (2018). Consensus-Based Filter for Distributed Sensor Networks with Colored Measurement Noise. Sensors, 18(11), 3678. https://doi.org/10.3390/s18113678





