Time Sequential Single-Cell Patterning with High Efficiency and High Density
Abstract
1. Introduction
2. Design and Theoretical Modeling
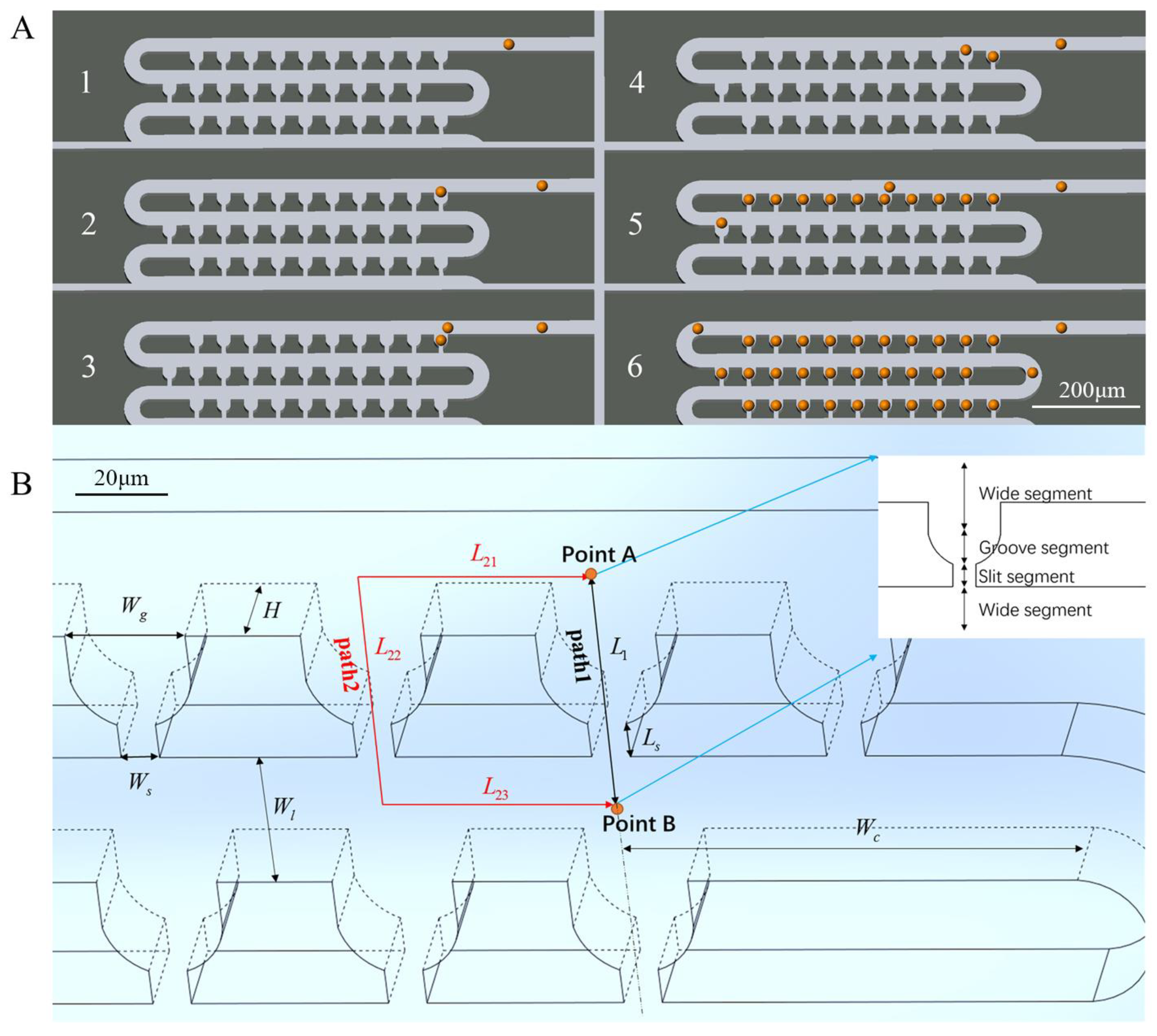
2.1. Structural Design
2.2. Theoretical Modeling
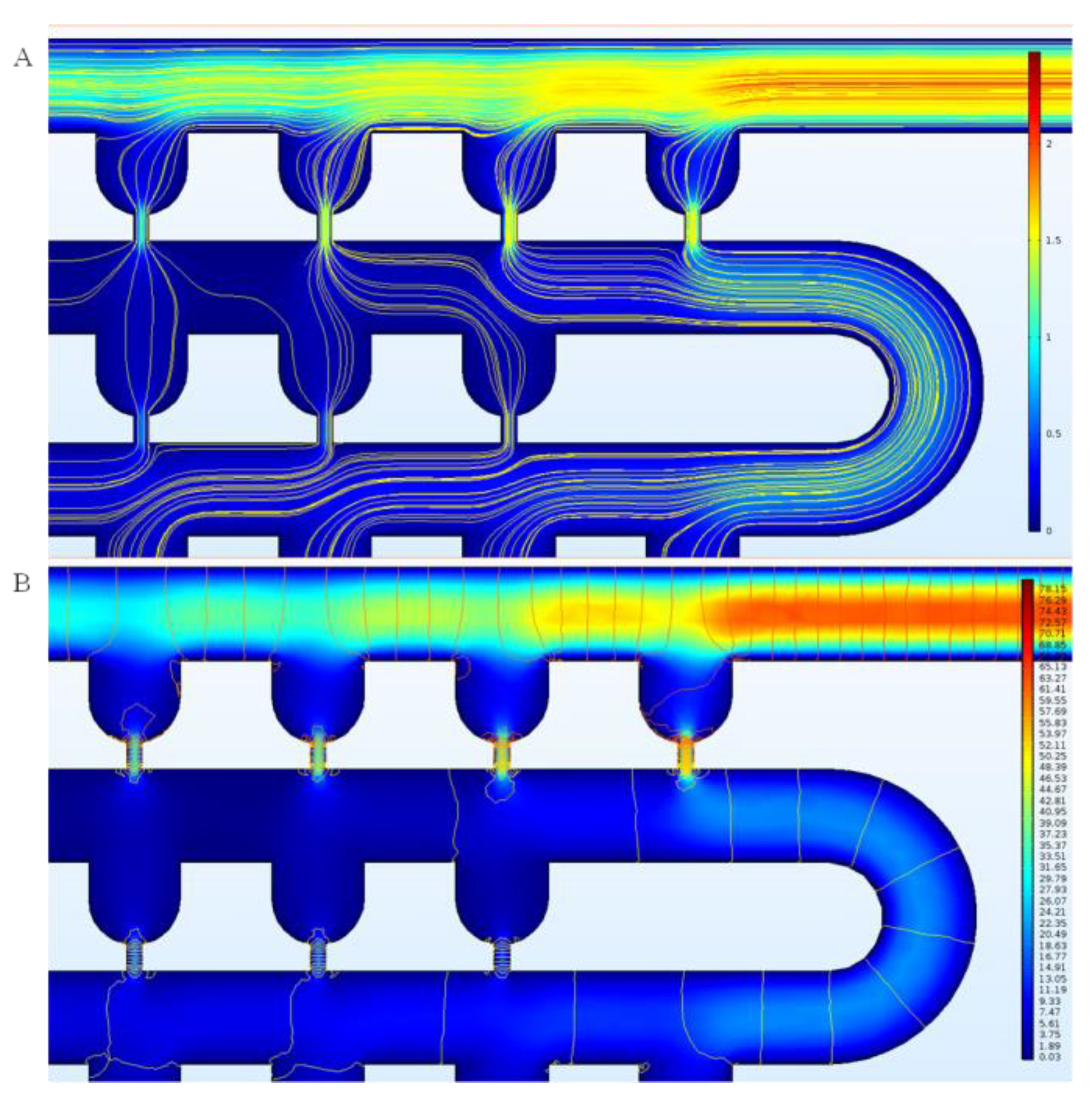
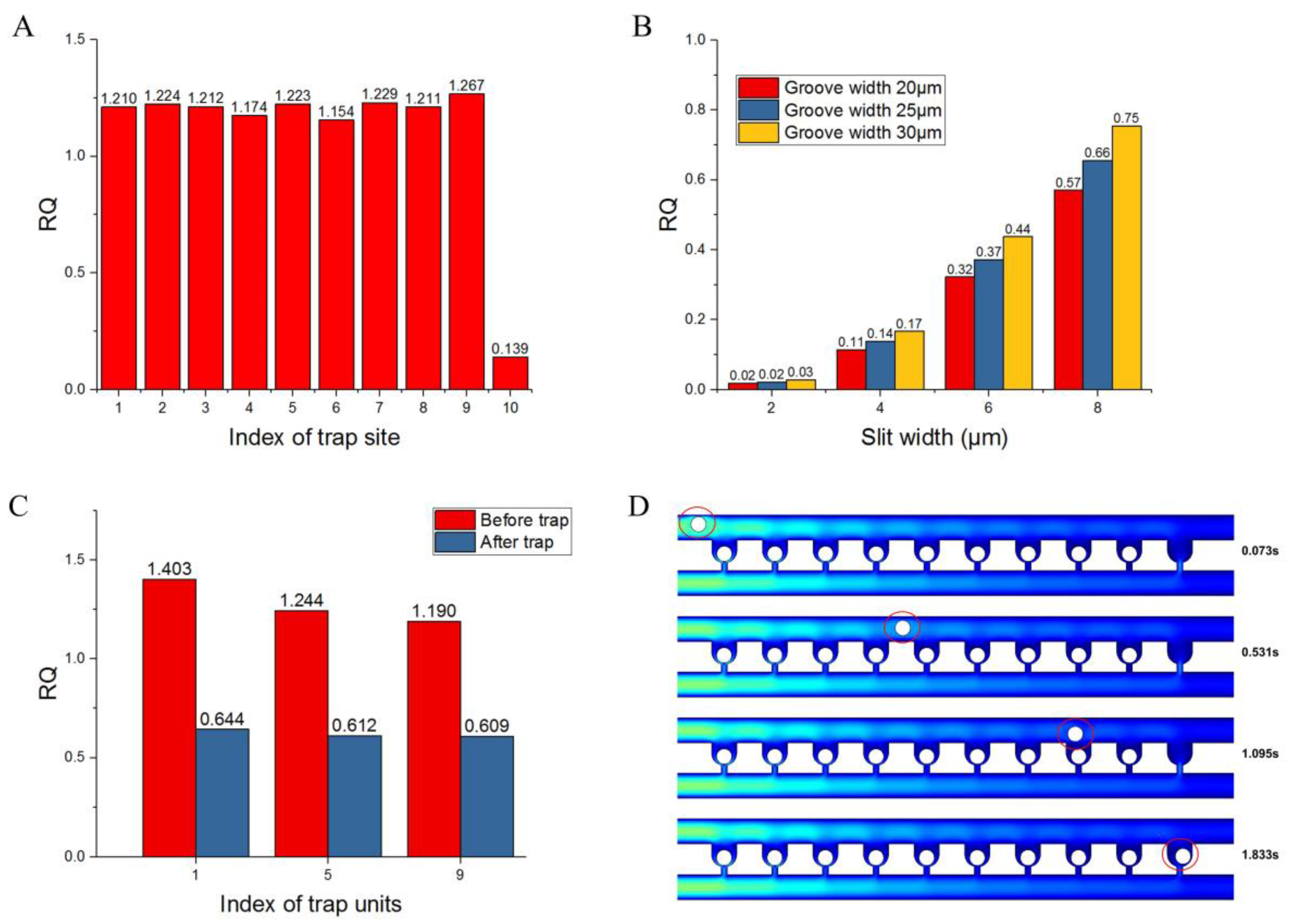
2.3. Simulation Analysis
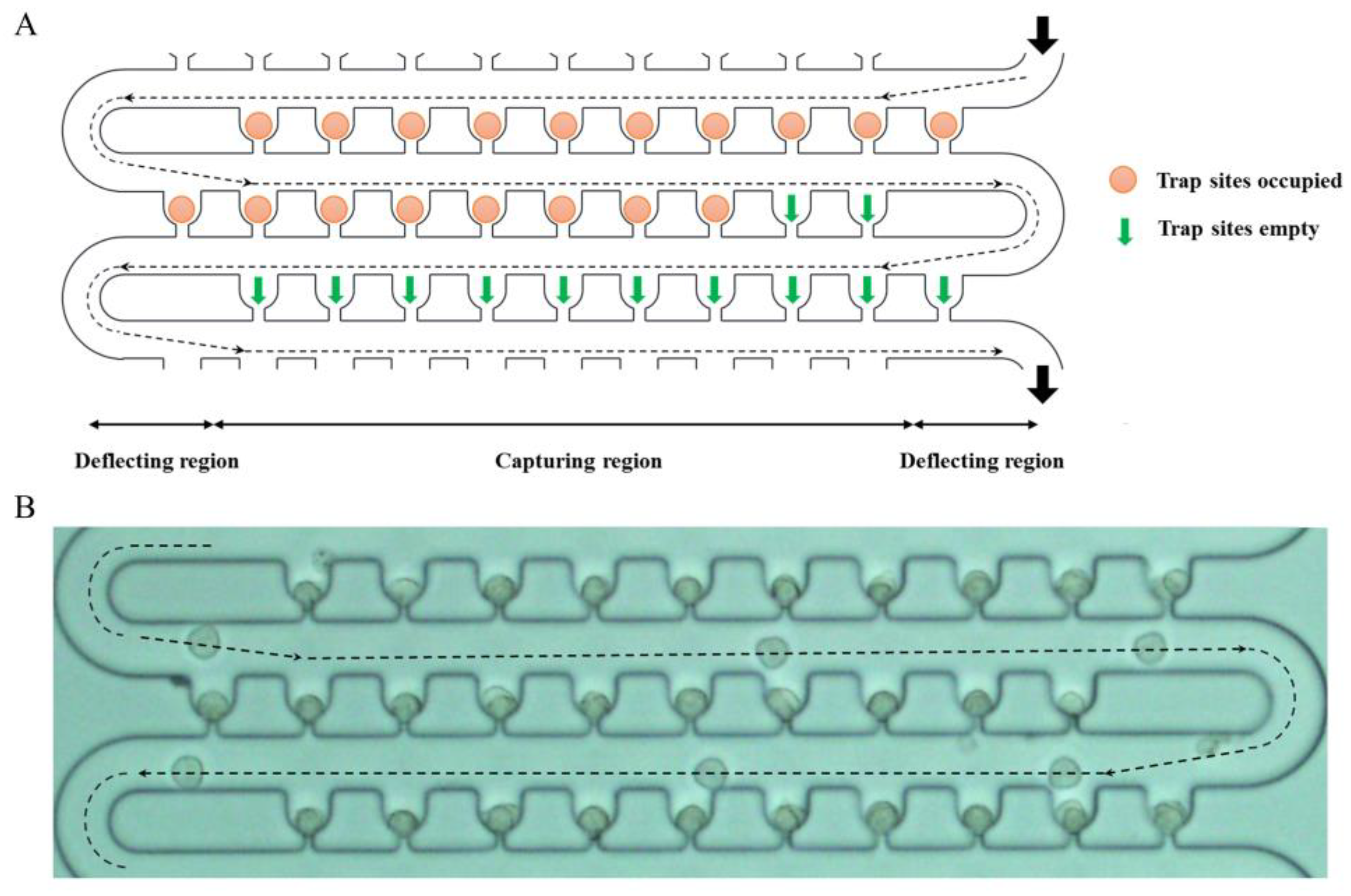
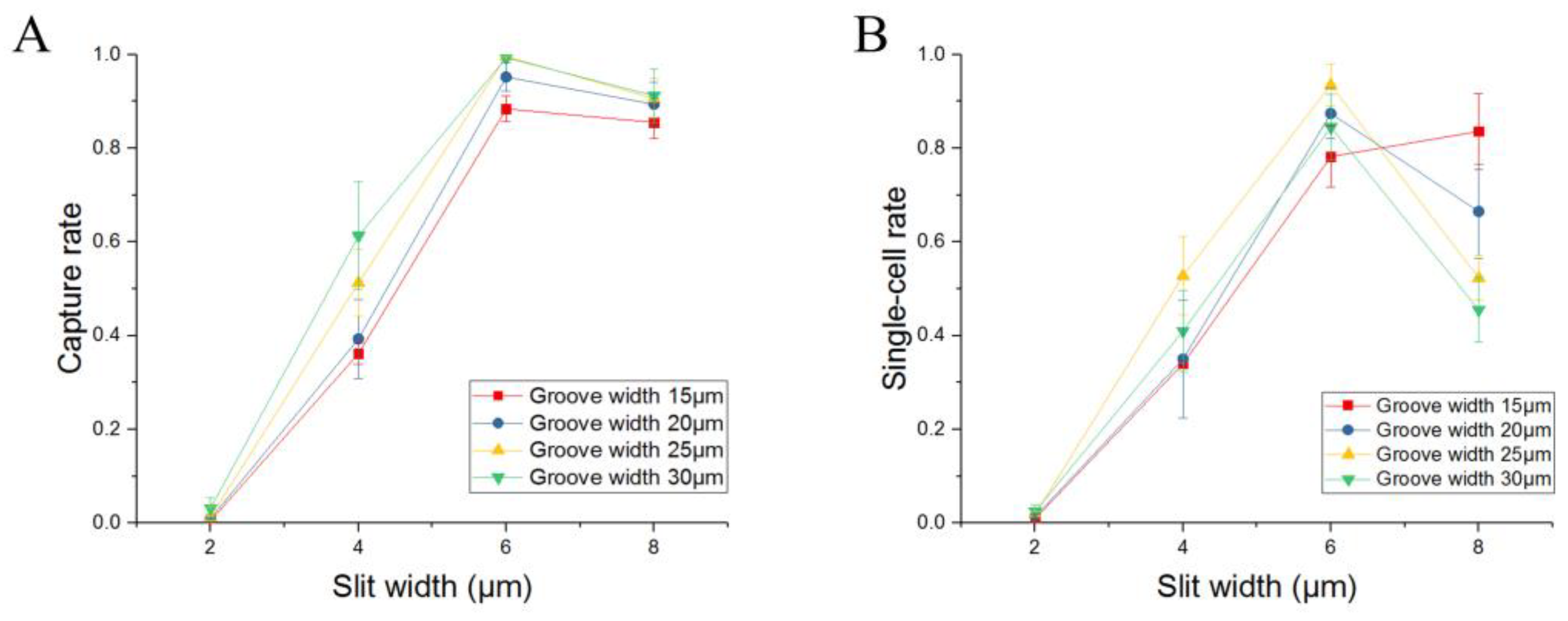
3. Experiment and Analysis
3.1. Fabrication of the Device
3.2. Cell Culture and Staining
3.3. Microfluidic System Operation
3.4. Single-Cell Trapping
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Amir, E.D.; Davis, K.L.; Tadmor, M.D.; Simonds, E.F.; Levine, J.H.; Bendall, S.C.; Shenfeld, D.K.; Krishnaswamy, S.; Nolan, G.P.; Pe’er, D. viSNE enables visualization of high dimensional single-cell data and reveals phenotypic heterogeneity of leukemia. Nat. Biotechnol. 2013, 31, 545–552. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhang, W.; Jia, Y.; Yu, Q.; Grau, G.E.; Peng, L.; Ran, Y.; Yang, Z.; Deng, H.; Lou, J. Single-cell clones of liver cancer stem cells have the potential of differentiating into different types of tumor cells. Cell Death Dis. 2013, 4, e857. [Google Scholar] [CrossRef] [PubMed]
- Ginsberg, S.D.; Che, S.; Counts, S.E.; Mufson, E.J. Single cell gene expression profiling in Alzheimer’s disease. NeuroRx 2006, 3, 302–318. [Google Scholar] [CrossRef] [PubMed]
- Ren, D.; Xia, Y.; Wang, B.; You, Z. Multiplexed Analysis for Anti-Epidermal Growth Factor Receptor Tumor Cell Growth Inhibition Based on Quantum Dot Probes. Anal. Chem. 2016, 88, 4318–4327. [Google Scholar] [CrossRef] [PubMed]
- Yamamura, S.; Yamada, E.; Kimura, F.; Miyajima, K.; Shigeto, H. Separation and Analysis of Adherent and Non-Adherent Cancer Cells Using a Single-Cell Microarray Chip. Sensors 2017, 17, 2410. [Google Scholar] [CrossRef] [PubMed]
- Ren, D.H.; Cui, M.Y.; Xia, Y.Q.; You, Z. Micropatterning and Its Applications in Biomedical Research. Prog. Biochem. Biophys. 2012, 39, 931–944. [Google Scholar] [CrossRef]
- Nagrath, S.; Sequist, L.V.; Maheswaran, S.; Bell, D.W.; Irimia, D.; Ulkus, L.; Smith, M.R.; Kwak, E.L.; Digumarthy, S.; Muzikansky, A.; et al. Isolation of rare circulating tumour cells in cancer patients by microchip technology. Nature 2007, 450, 1235–1239. [Google Scholar] [CrossRef] [PubMed]
- Ren, D.H.; Xia, Y.Q.; You, Z. Multiplexed living cells stained with quantum dot bioprobes for multiplexed detection of single-cell array. J. Biomed. Opt. 2013, 18, 96005. [Google Scholar] [CrossRef] [PubMed]
- Taff, B.M.; Voldman, J. A scalable addressable positive-dielectrophoretic cell-sorting array. Anal. Chem. 2005, 77, 7976–7983. [Google Scholar] [CrossRef] [PubMed]
- Voldman, J. Electrical forces for microscale cell manipulation. Annu. Rev. Biomed. Eng. 2006, 8, 425–454. [Google Scholar] [CrossRef] [PubMed]
- Kauffmann, P.; Ith, A.; O’Brien, D.; Gaude, V.; Boue, F.; Combe, S.; Bruckert, F.; Schaack, B.; Dempsey, N.M.; Haguet, V.; et al. Diamagnetically trapped arrays of living cells above micromagnets. Lab Chip 2011, 11, 3153–3161. [Google Scholar] [CrossRef] [PubMed]
- Che, X.; Boldrey, J.; Zhong, X.; Unnikandam-Veettil, S.; Schneider, I.; Jiles, D.; Que, L. On-Chip Studies of Magnetic Stimulation Effect on Single Neural Cell Viability and Proliferation on Glass and Nanoporous Surfaces. ACS Appl. Mater. Interfaces 2018, 10, 28269–28278. [Google Scholar] [CrossRef] [PubMed]
- Jeffries, G.D.M.; Edgar, J.S.; Zhao, Y.Q.; Shelby, J.P.; Fong, C.; Chiu, D.T. Using polarization-shaped optical vortex traps for single-cell nanosurgery. Nano Lett. 2007, 7, 415–420. [Google Scholar] [CrossRef] [PubMed]
- Collins, D.J.; Morahan, B.; Garcia-Bustos, J.; Doerig, C.; Plebanski, M.; Neild, A. Two-dimensional single-cell patterning with one cell per well driven by surface acoustic waves. Nat. Commun. 2015, 6, 8686. [Google Scholar] [CrossRef] [PubMed]
- Banaeiyan, A.A.; Ahmadpour, D.; Adiels, C.B.; Goksor, M. Hydrodynamic Cell Trapping for High Throughput Single-Cell Applications. Micromachines 2013, 4, 414–430. [Google Scholar] [CrossRef]
- Davey, H.M.; Kell, D.B. Flow cytometry and cell sorting of heterogeneous microbial populations: The importance of single-cell analyses. Microbiol. Rev. 1996, 60, 641–696. [Google Scholar] [PubMed]
- Ren, D.; Xia, Y.Q.; Wang, J.; You, Z. Micropatterning of single cell arrays using the PEG-Silane and Biotin-(Strept) Avidin System with photolithography and chemical vapor deposition. Sens. Actuators B-Chem. 2013, 188, 340–346. [Google Scholar] [CrossRef]
- Lindstrom, S.; Andersson-Svahn, H. Overview of single-cell analyses: Microdevices and applications. Lab Chip 2010, 10, 3363–3372. [Google Scholar] [CrossRef] [PubMed]
- Bithi, S.S.; Vanapalli, S.A. Behavior of a train of droplets in a fluidic network with hydrodynamic traps. Biomicrofluidics 2010, 4, 044110. [Google Scholar] [CrossRef] [PubMed]
- Rettig, J.R.; Folch, A. Large-scale single-cell trapping and imaging using microwell arrays. Anal. Chem. 2005, 77, 5628–5634. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Chou, C.K.; Xia, X.F.; Hung, M.C.; Qin, L.D. Block-Cell-Printing for live single-cell printing. Proc. Natl. Acad. Sci. USA 2014, 111, 2948–2953. [Google Scholar] [CrossRef] [PubMed]
- Delincé, M.J.; Bureau, J.B.; López-Jiménez, A.T.; Cosson, P.; Soldati, T.; McKinney, J.D. A microfluidic cell-trapping device for single-cell tracking of host–microbe interactions. Lab Chip 2016, 16, 3276–3285. [Google Scholar] [CrossRef] [PubMed]
- Lindstrom, S.; Andersson-Svahn, H. Miniaturization of biological assays—Overview on microwell devices for single-cell analyses. Biochim. Biophys. Acta-Gen. Subj. 2011, 1810, 308–316. [Google Scholar] [CrossRef] [PubMed]
- Jang, M.; Yang, S.; Kim, P. Microdroplet-based cell culture models and their application. BioChip J. 2016, 10, 310–317. [Google Scholar] [CrossRef]
- Kobel, S.; Valero, A.; Latt, J.; Renaud, P.; Lutolf, M. Optimization of microfluidic single cell trapping for long-term on-chip culture. Lab Chip 2010, 10, 857–863. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.; Pan, Q.; Lee, L.P. Single-cell level co-culture platform for intercellular communication. Integr. Biol. 2012, 4, 374–380. [Google Scholar] [CrossRef] [PubMed]
- Tan, W.H.; Takeuchi, S. A trap-and-release integrated microfluidic system for dynamic microarray applications. Proc. Natl. Acad. Sci. USA 2007, 104, 1146–1151. [Google Scholar] [CrossRef] [PubMed]
- Lawrenz, A.; Nason, F.; Cooper-White, J.J. Geometrical effects in microfluidic-based microarrays for rapid, efficient single-cell capture of mammalian stem cells and plant cells. Biomicrofluidics 2012, 6, 433–441. [Google Scholar] [CrossRef] [PubMed]
- Nuhn, J.A.; Gong, S.; Che, X.; Que, L.; Schneider, I.C. Microtissue size and cell-cell communication modulate cell migration in arrayed 3D collagen gels. Biomed. Microdevices 2018, 20, 62. [Google Scholar] [CrossRef] [PubMed]
- Frimat, J.P.; Becker, M.; Chiang, Y.Y.; Marggraf, U.; Janasek, D.; Hengstler, J.G.; Franzke, J.; West, J. A microfluidic array with cellular valving for single cell co-culture. Lab Chip 2011, 11, 231–237. [Google Scholar] [CrossRef] [PubMed]
- Che, X.; Nuhn, J.; Schneider, I.; Que, L. High throughput studies of cell migration in 3D microtissues fabricated by a droplet microfluidic chip. Micromachines 2016, 7, 84. [Google Scholar] [CrossRef]
- Mi, L.; Huang, L.; Li, J.X.; Xu, G.Q.; Wu, Q.; Wang, W.H. A fluidic circuit based, high-efficiency and large-scale single cell trap. Lab Chip 2016, 16, 4507–4511. [Google Scholar] [CrossRef] [PubMed]
- Judy, J.; Maynes, D.; Webb, B.W. Characterization of frictional pressure drop for liquid flows through microchannels. Int. J. Heat Mass Transf. 2002, 45, 3477–3489. [Google Scholar] [CrossRef]
- Liu, D.; Garimella, S.V. Investigation of liquid flow in microchannels. J. Thermophys. Heat Transf. 2004, 18, 65–72. [Google Scholar] [CrossRef]
- Jin, D.; Deng, B.; Li, J.X.; Cai, W.; Tu, L.; Chen, J.; Wu, Q.; Wang, W.H. A microfluidic device enabling high-efficiency single cell trapping. Biomicrofluidics 2015, 9, 20173–20178. [Google Scholar] [CrossRef] [PubMed]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Ren, D.; Ling, X.; Liang, W.; Li, J.; You, Z.; Yalikun, Y.; Tanaka, Y. Time Sequential Single-Cell Patterning with High Efficiency and High Density. Sensors 2018, 18, 3672. https://doi.org/10.3390/s18113672
Liu Y, Ren D, Ling X, Liang W, Li J, You Z, Yalikun Y, Tanaka Y. Time Sequential Single-Cell Patterning with High Efficiency and High Density. Sensors. 2018; 18(11):3672. https://doi.org/10.3390/s18113672
Chicago/Turabian StyleLiu, Yang, Dahai Ren, Xixin Ling, Weibin Liang, Jing Li, Zheng You, Yaxiaer Yalikun, and Yo Tanaka. 2018. "Time Sequential Single-Cell Patterning with High Efficiency and High Density" Sensors 18, no. 11: 3672. https://doi.org/10.3390/s18113672
APA StyleLiu, Y., Ren, D., Ling, X., Liang, W., Li, J., You, Z., Yalikun, Y., & Tanaka, Y. (2018). Time Sequential Single-Cell Patterning with High Efficiency and High Density. Sensors, 18(11), 3672. https://doi.org/10.3390/s18113672






