Delay Analysis for End-to-End Synchronous Communication in Monitoring Systems
Abstract
:1. Introduction
- (1)
- A class of typical communication model for the monitoring system is investigated in this paper. The transmission network in the smart grid monitoring system is modeled as a transmission service node, such that network calculus theory can be applied. In this sense, the analysis methods proposed in this paper can be used under most scenarios of monitoring systems in the field of smart grid.
- (2)
- It is notable that due to the synchronous property of the smart grid applications, the original network calculus theory cannot be directly applied in the delay analysis discussed in this paper. Based on the network calculus theory, an upper bound for the end-to-end delay in the synchronous communication system is derived. The simulations demonstrate the feasibility of the proposed method. With the development of the smart grid systems, there will be more applications based on the monitoring systems, and the theoretical results obtained in this paper can be utilized to improve the reliability and efficiency of the smart grid systems.
- (3)
- In this paper, three theorems are proposed as our main results. In Theorem 1, the upper bound for the transmission delay in a transmission service node with strict service curve is derived. The data transmission delay in different time periods are discussed in detail. In Theorem 2, the formula for upper bound of system’s delay with multiple times of data exchange is derived. In Theorem 3, a general upper bound for transmission delay in the considered system is proposed.
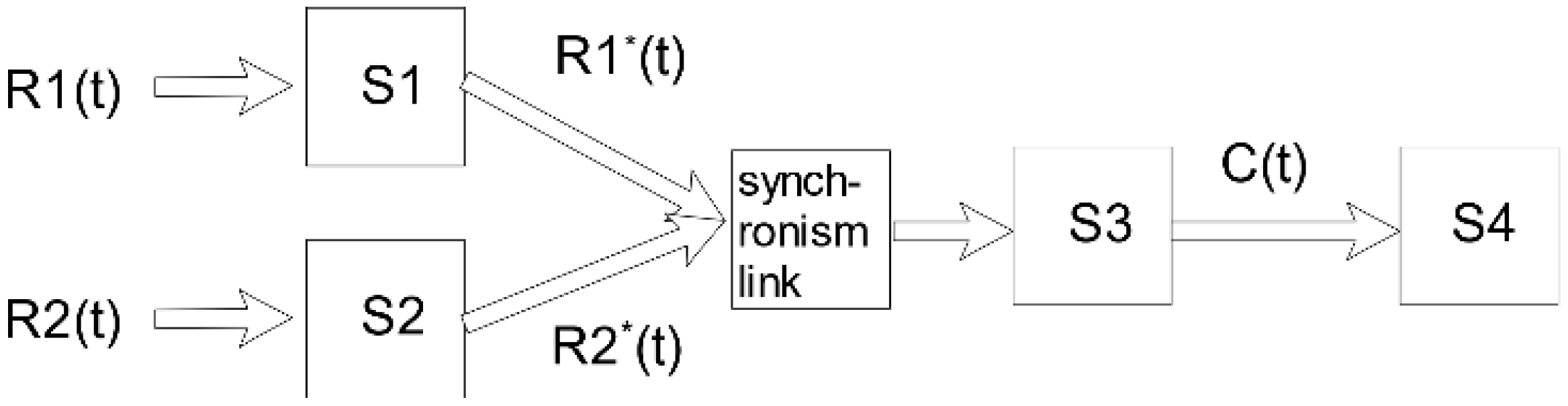
2. Typical Models for the Synchronous Communication Systems
3. Calculation of Equivalent Delay of Monitoring System
3.1. Delay Theorem of Suspension Service System
3.2. Synchronization System Delay Analysis
3.3. Synchronization System Delay Upper Bound Theorem
3.4. The Method of Calculation of the Upper Bound Equivalent Synchronization System Delay
4. Monitoring System Delay Experimental Tests
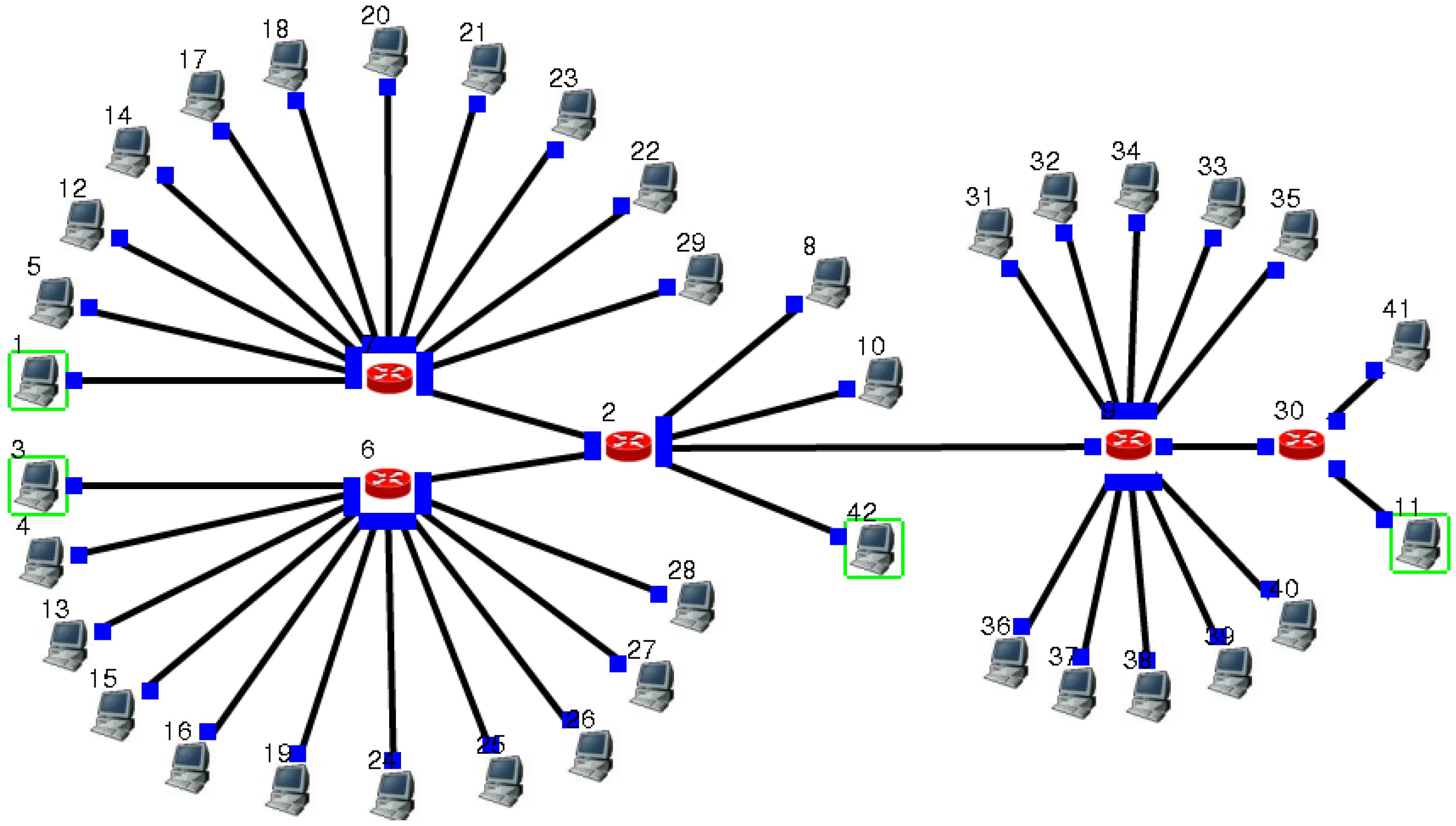
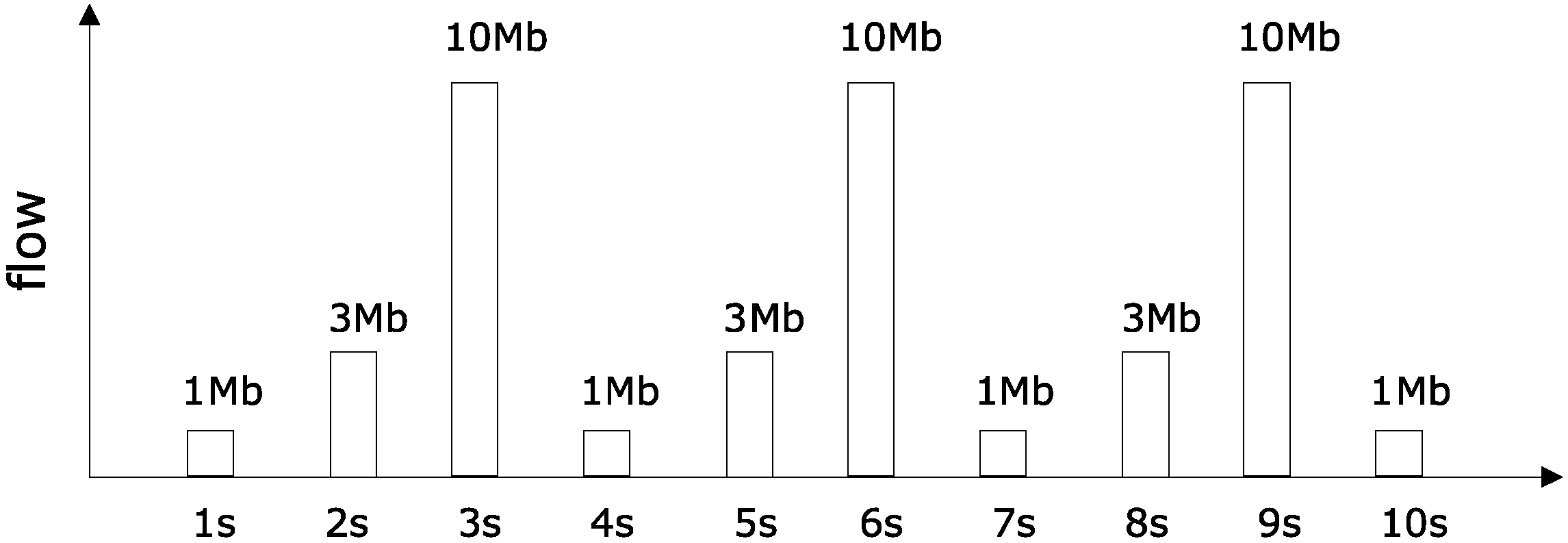
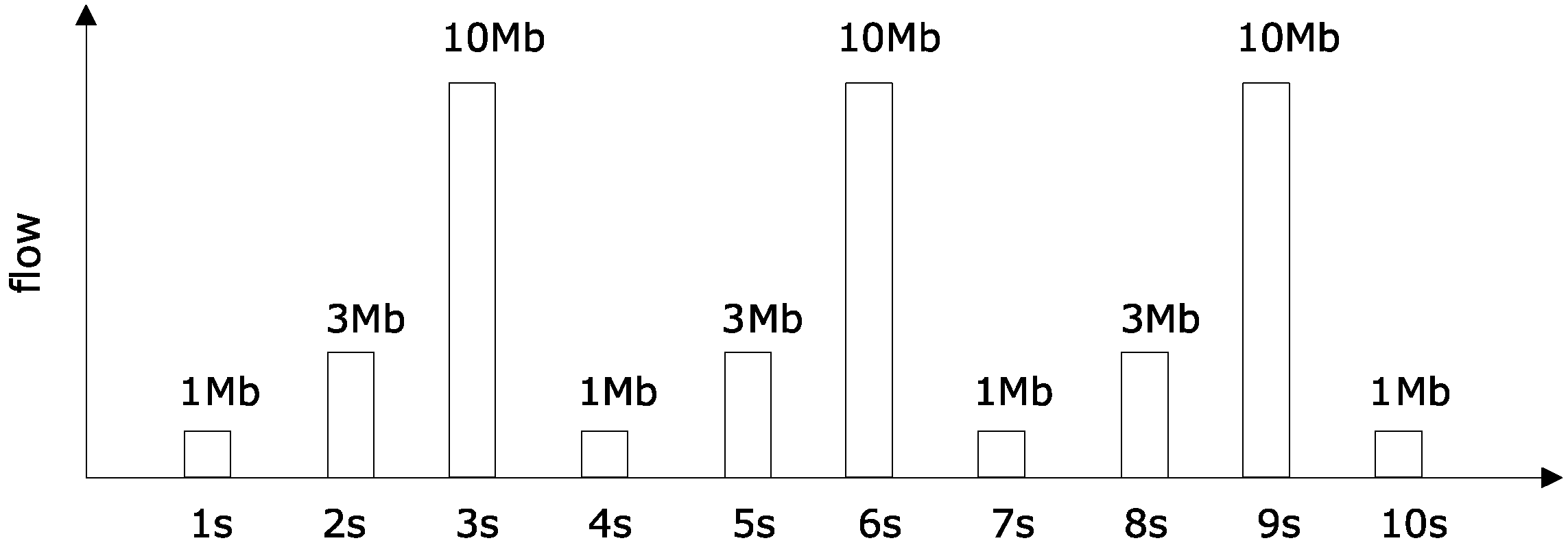
4.1. Network Topology Simulation and Experimental Design
| Algorithm 1: |
| 1. Node 1 and 3 send packets in size of 100 kb at intervals of one second to node 42, denoting arrived curves as and . |
| 2. Send node 42 packets of data to node 11 after synchronization. |
| 3. No. 5, 12, 14, 17, 18, 20, 21, 23, 22, 29 nodes send competing data packets to node 8, to constitute competing flow , which reaches curve . |
| 4. No. 4, 13, 15, 16, 19, 24, 25, 26, 27, 28 nodes send competing data packets to node 8, to constitute competing flow , which reaches curve . |
| 5. No. 31, 32, 33, 34, 35, 36, 37, 38, 39, 40 nodes send competing data packets to node 8, to constitute competing flow , which reaches curve . |
| 6. All the links take bandwidth of 10 Mb. For all routers, the same configuration is used. |
4.2. Theoretical Analysis of Delay Bound for Monitoring System
4.2.1. First, the Computation Service Curve and the Scaling Function of Node 42 of the Synchronous Link Are Given
4.2.2. When There Are no Competing flows , and
4.2.3. When Adding Competing Flows of , and
4.2.4. Time Delay Increasing due to Forwarding
4.2.5. Arrival Flow Curve
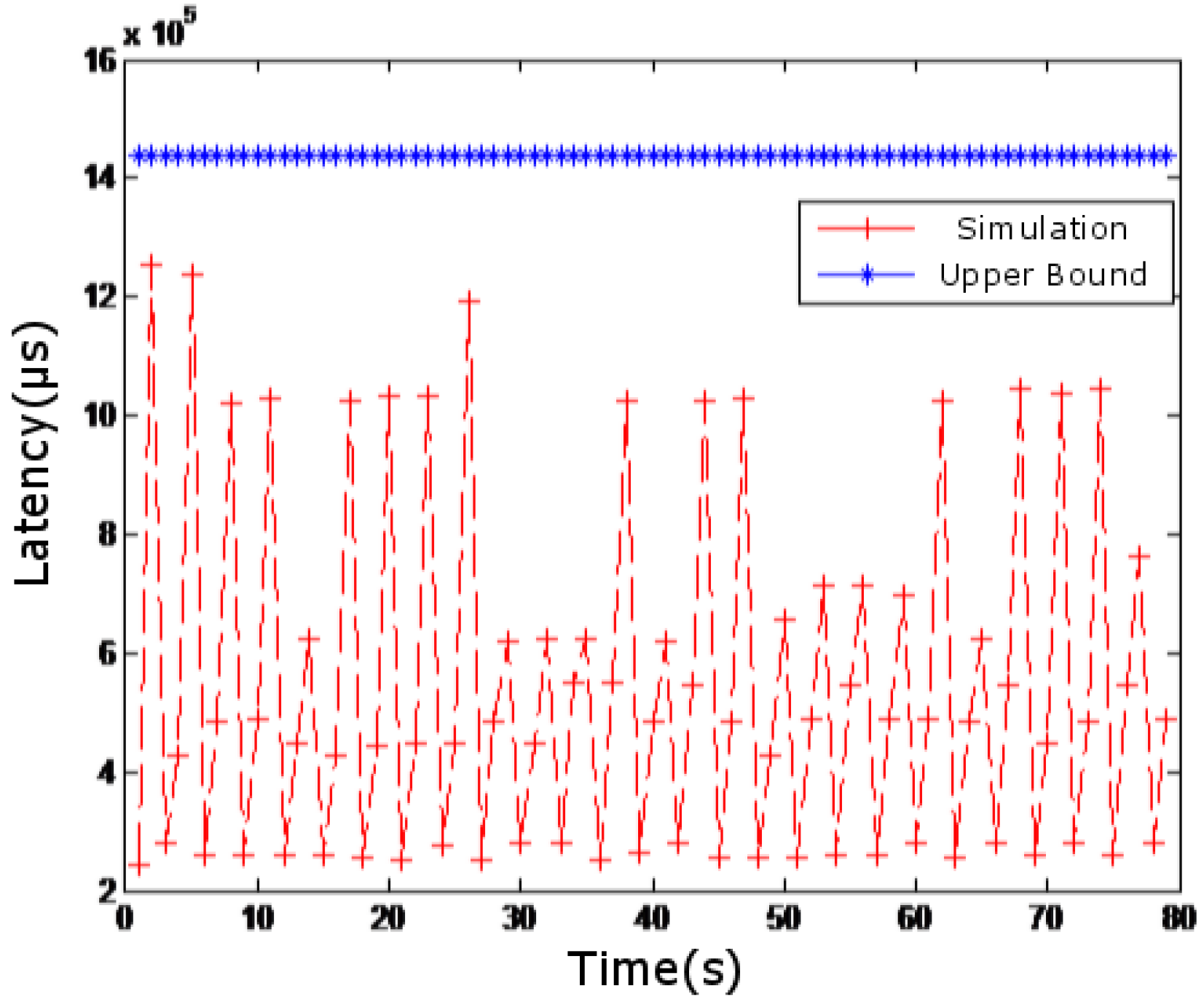
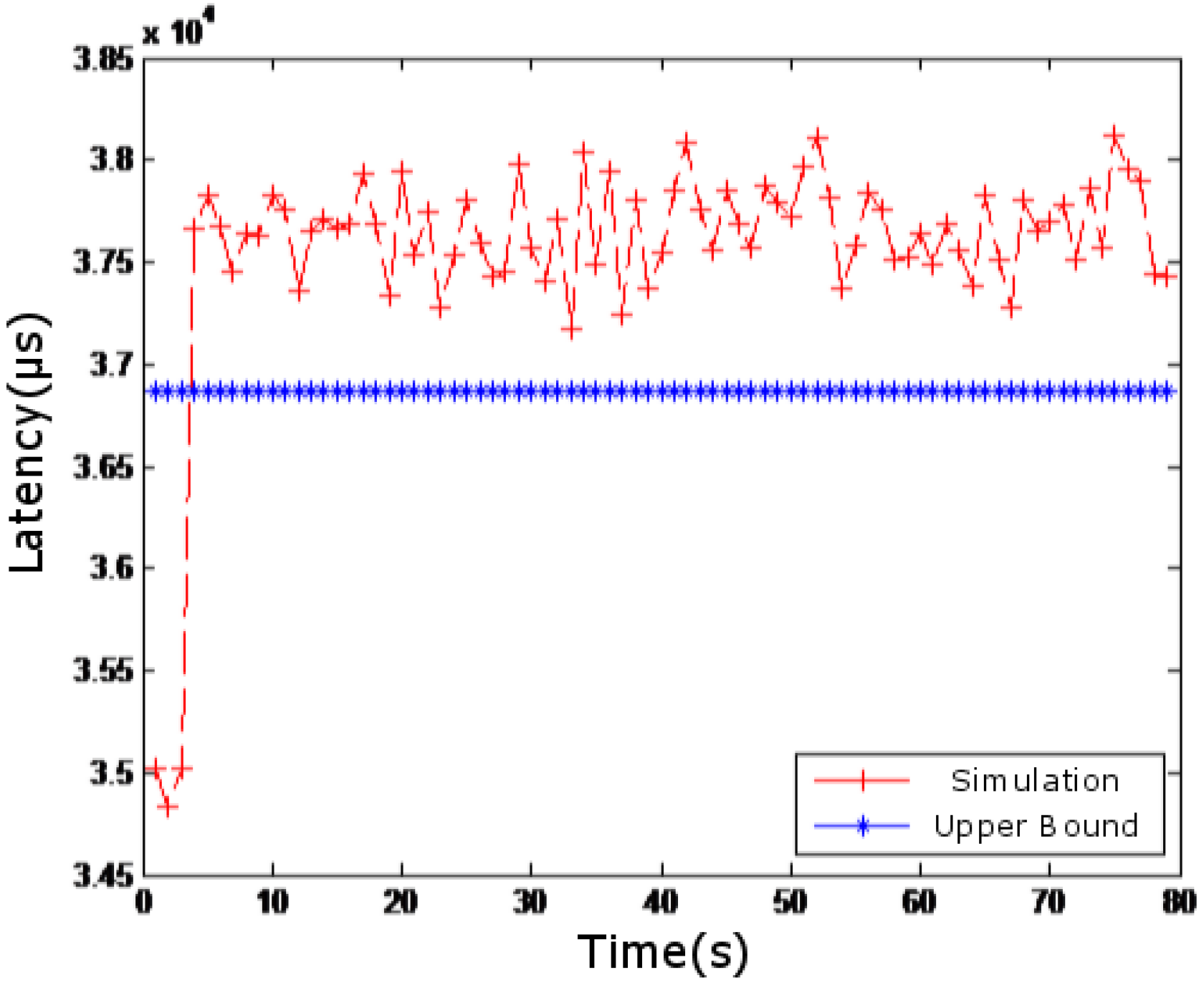
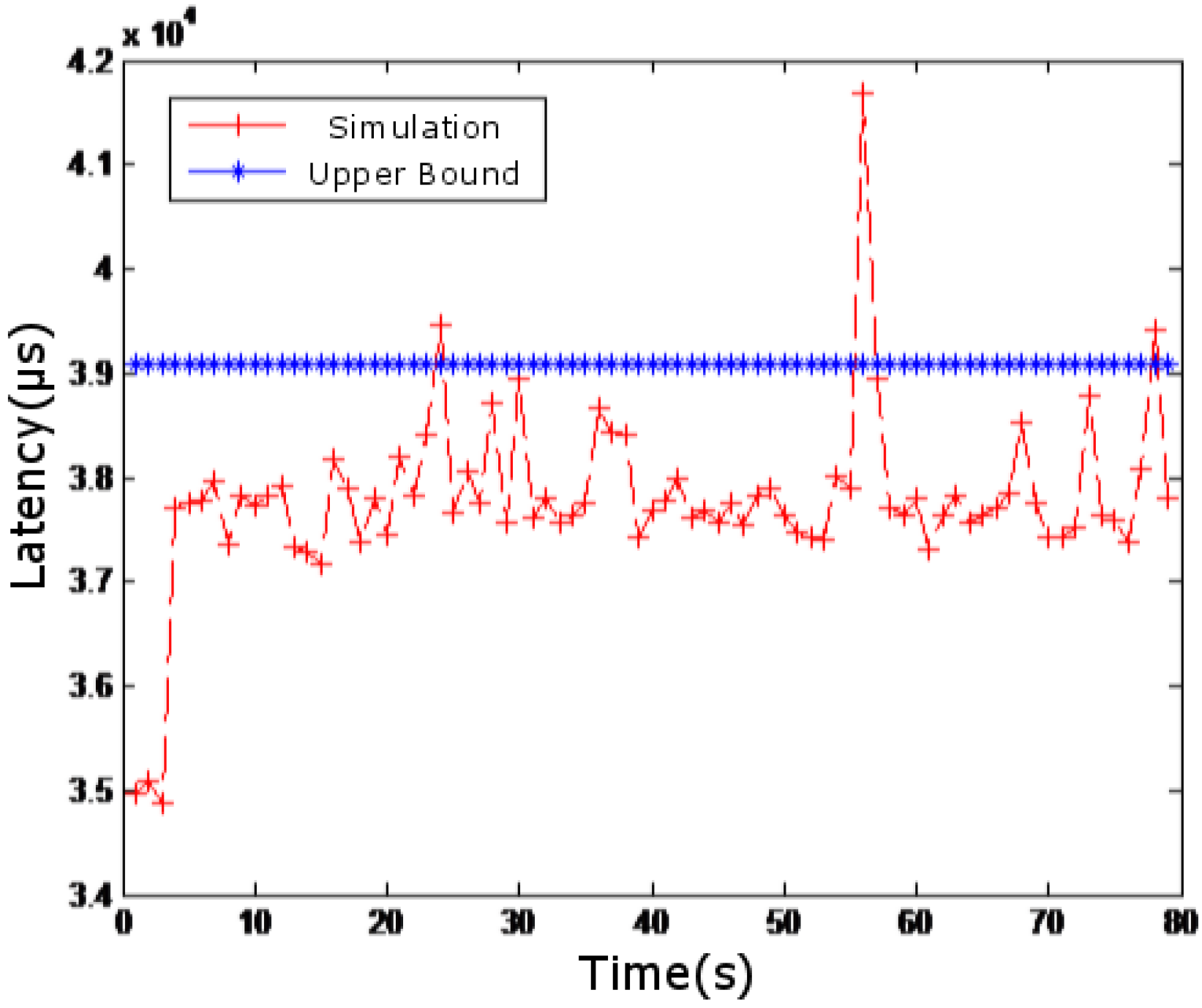
4.3. Simulation Results of Monitoring System Delay
5. Summary
Author Contributions
Funding
Conflicts of Interest
Appendix A.
Appendix A.1. Proof of Theorem 1
Appendix A.2. Discussions for the Value of in
- i
- If , data of with time scale arrives at the synchronization link after the data with the previous time scale is processed. It means that at time , ’s backlog would not increase. According to Theorem 1,
- ii
- If , according to the rules that first come first served, for , data will not be processed until time . Since data of arrives first, data of with time scale has arrived at time . would have to wait until before processing the data. The system delay can be expressed by the equivalent delay of , and we have
Appendix A.3. Proof of Theorem 2
Appendix A.4. Proof of Theorem 3
References
- Lasseter, R.H.; Paigi, P. Microgrid: A conceptual solution. In Proceedings of the IEEE 35th Annual Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; pp. 4285–4290. [Google Scholar]
- Cecati, C.; Mokryani, G.; Piccolo, A.; Siano, P. An overview on the smart grid concept. In Proceedings of the 36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 3322–3327. [Google Scholar]
- Hua, H.; Hao, C.; Qin, Y.; Cao, J. A class of control strategies for energy Internet considering system robustness and operation cost optimization. Energies 2018, 11, 1593. [Google Scholar] [CrossRef]
- Hua, H.; Cao, J.; Yang, G.; Ren, G. Voltage control for uncertain stochastic nonlinear system with application to energy Internet: Nonfragile robust H∞ approach. J. Math. Anal. Appl. 2018, 463, 93–110. [Google Scholar] [CrossRef]
- Galli, S.; Scaglione, A.; Wang, Z. For the grid and through the grid: The role of power line communications in the smart grid. Proc. IEEE 2011, 99, 998–1027. [Google Scholar] [CrossRef]
- Ancillotti, E.; Bruno, R.; Conti, M. The role of communication systems in smart grids: Architectures, technical solutions and research challenges. Comput. Commun. 2013, 36, 1665–1697. [Google Scholar] [CrossRef]
- Cao, J.; Wan, Y.; Hua, H.; Yang, G. Performance modelling for data monitoring services in smart grid. Unpublished work. 2018. [Google Scholar]
- Musleh, A.S.; Muyeen, S.M.; Al-Durra, A.; Kamwa, I.; Masoum, M.A.; Islam, S. Time-Delay Analysis of Wide-Area Voltage Control Considering Smart Grid Contingences in a Real-Time Environment. IEEE Trans. Ind. Inform. 2018, 14, 1242–1252. [Google Scholar] [CrossRef]
- He, D.; Chan, S.; Guizani, M. Cyber security analysis and protection of wireless sensor networks for smart grid monitoring. IEEE Wirel. Commun. 2017, 24, 98–103. [Google Scholar] [CrossRef]
- Cao, Y.; Lu, H.; Shi, X.; Duan, P. Evaluation model of the cloud systems based on queuing petri net. In Proceedings of the International Conference on Algorithms and Architectures for Parallel Processing, Zhangjiajie, China, 18–20 November 2015; pp. 413–423. [Google Scholar]
- Pramanik, S.; Datta, R.; Chatterjee, P. Self-similarity of data traffic in a Delay Tolerant Network. In Proceedings of the Wireless Days 2017, Porto, Portugal, 29–31 March 2017; pp. 39–42. [Google Scholar]
- Cruz, R.L. A calculus for network delay. I. Network elements in isolation. IEEE Trans. Inf. Theory 1991, 37, 114–131. [Google Scholar] [CrossRef]
- Ren, S.; Feng, Q.; Wang, Y.; Dou, W. A Service Curve of Hierarchical Token Bucket Queue Discipline on Soft-Ware Defined Networks Based on Deterministic Network Calculus: An Analysis and Simulation. J. Adv. Comput. Netw. 2017, 5, 8–12. [Google Scholar] [CrossRef]
- Le Boudec, J.Y.; Thiran, P. Network Calculus: A Theory of Deterministic Queuing Systems for the Internet, 1st ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2001; pp. 3–81. ISBN 978-3-540-45318-5. [Google Scholar]
- Fan, Z.; Kulkarni, P.; Gormus, S.; Efthymiou, C.; Kalogridis, G.; Sooriyabandara, M.; Chin, W.H. Smart grid communications: Overview of research challenges, solutions, and standardization activities. IEEE Commun. Surv. Tutor. 2013, 15, 21–38. [Google Scholar] [CrossRef]
- Bayram, I.S.; Shakir, M.Z.; Abdallah, M.; Qaraqe, K. A survey on energy trading in smart grid. In Proceedings of the 2014 IEEE Global Conference on Signal and Information Processing, Atlanta, GA, USA, 3–5 December 2014; pp. 258–262. [Google Scholar]
- Ciucu, F.; Schmitt, J. Perspectives on network calculus: No free lunch, but still good value. ACM SIGCOMM Comput. Commun. Rev. 2012, 42, 311–322. [Google Scholar] [CrossRef]
- Wang, K.; Low, S.; Lin, C. How stochastic network calculus concepts help green the power grid. In Proceedings of the 2011 IEEE International Conference on Smart Grid Communications, Brussels, Belgium, 17–20 October 2011; pp. 55–60. [Google Scholar]
- Wang, K.; Ciucu, F.; Lin, C.; Low, S.H. A stochastic power network calculus for integrating renewable energy sources into the power grid. IEEE J. Sel. Areas Commun. 2012, 30, 1037–1048. [Google Scholar] [CrossRef]
- Kounev, V.; Tipper, D. Advanced metering and demand response communication performance in Zigbee based HANs. In Proceedings of the 2013 IEEE Conference on Computer Communications Workshops, Turin, Italy, 14–19 April 2013; pp. 3405–3410. [Google Scholar]
- Huang, C.; Li, F.; Ding, T.; Jiang, Y.; Guo, J.; Liu, Y. A bounded model of the communication delay for system integrity protection schemes. IEEE Trans. Power Deliv. 2016, 31, 1921–1933. [Google Scholar] [CrossRef]
- Cruz, R.L. A calculus for network delay. II. Network analysis. IEEE Trans. Inf. Theory 1991, 37, 132–141. [Google Scholar] [CrossRef]
- BC-Ethernet Traces of LAN and WAN Traffic. Available online: http://ita.ee.lbl.gov/html/contrib/BC.html (accessed on 23 October 2018).
- Rifkin, J. The Third Industrial Revolution: How Lateral Power Is Transforming Energy, the Economy, and the World; Palgrave Macmillan: New York, NY, USA, 2013; pp. 31–46. [Google Scholar]
- Cao, J.; Hua, H.; Ren, G. Energy use and the Internet. In The SAGE Encyclopedia of the Internet; SAGE Publications: Thousand Oaks, CA, USA, 2018; pp. 344–350. [Google Scholar]
- Hua, H.; Qin, Y.; Cao, J. Coordinated frequency control for multiple microgrids in energy Internet: A stochastic H∞ approach. In Proceedings of the 2018 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Singapore, 22–25 May 2018; pp. 810–815. [Google Scholar] [CrossRef]
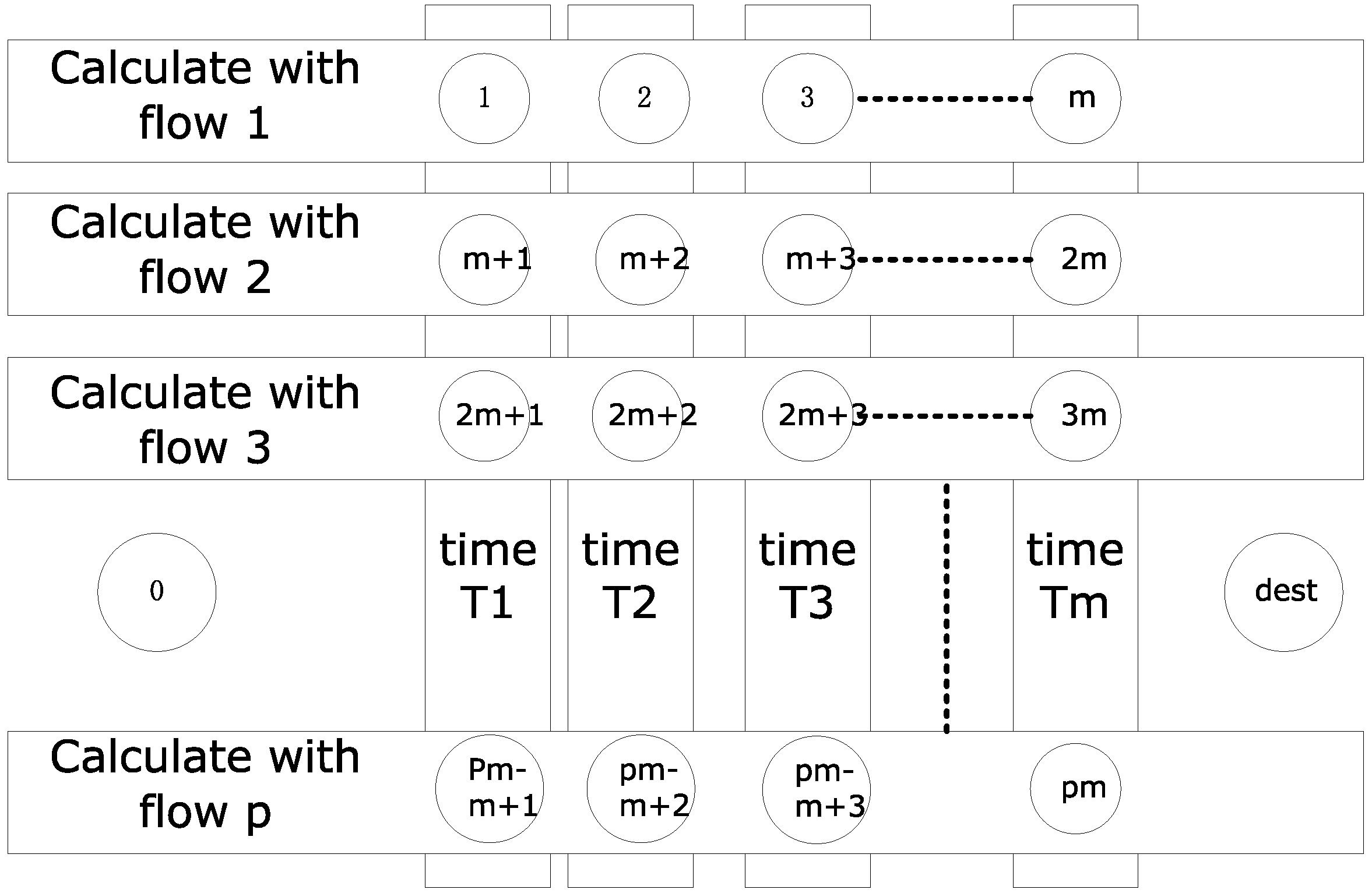

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Wan, Y.; Hua, H.; Qin, Y. Delay Analysis for End-to-End Synchronous Communication in Monitoring Systems. Sensors 2018, 18, 3615. https://doi.org/10.3390/s18113615
Cao J, Wan Y, Hua H, Qin Y. Delay Analysis for End-to-End Synchronous Communication in Monitoring Systems. Sensors. 2018; 18(11):3615. https://doi.org/10.3390/s18113615
Chicago/Turabian StyleCao, Junwei, Yuxin Wan, Haochen Hua, and Yuchao Qin. 2018. "Delay Analysis for End-to-End Synchronous Communication in Monitoring Systems" Sensors 18, no. 11: 3615. https://doi.org/10.3390/s18113615
APA StyleCao, J., Wan, Y., Hua, H., & Qin, Y. (2018). Delay Analysis for End-to-End Synchronous Communication in Monitoring Systems. Sensors, 18(11), 3615. https://doi.org/10.3390/s18113615