A Non-Linear Model of an All-Elastomer, in-Plane, Capacitive, Tactile Sensor Under the Application of Normal Forces
Abstract
1. Introduction
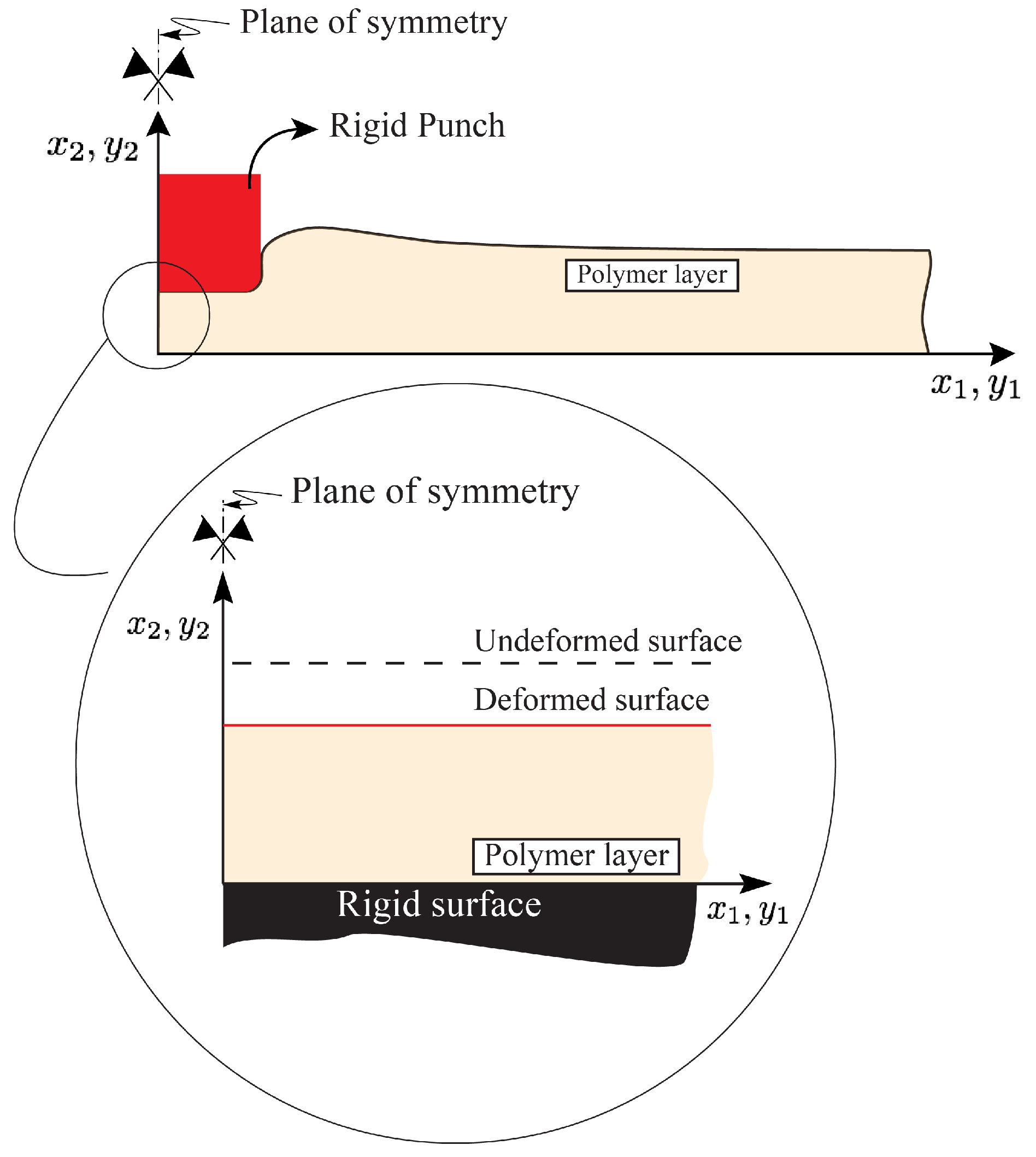
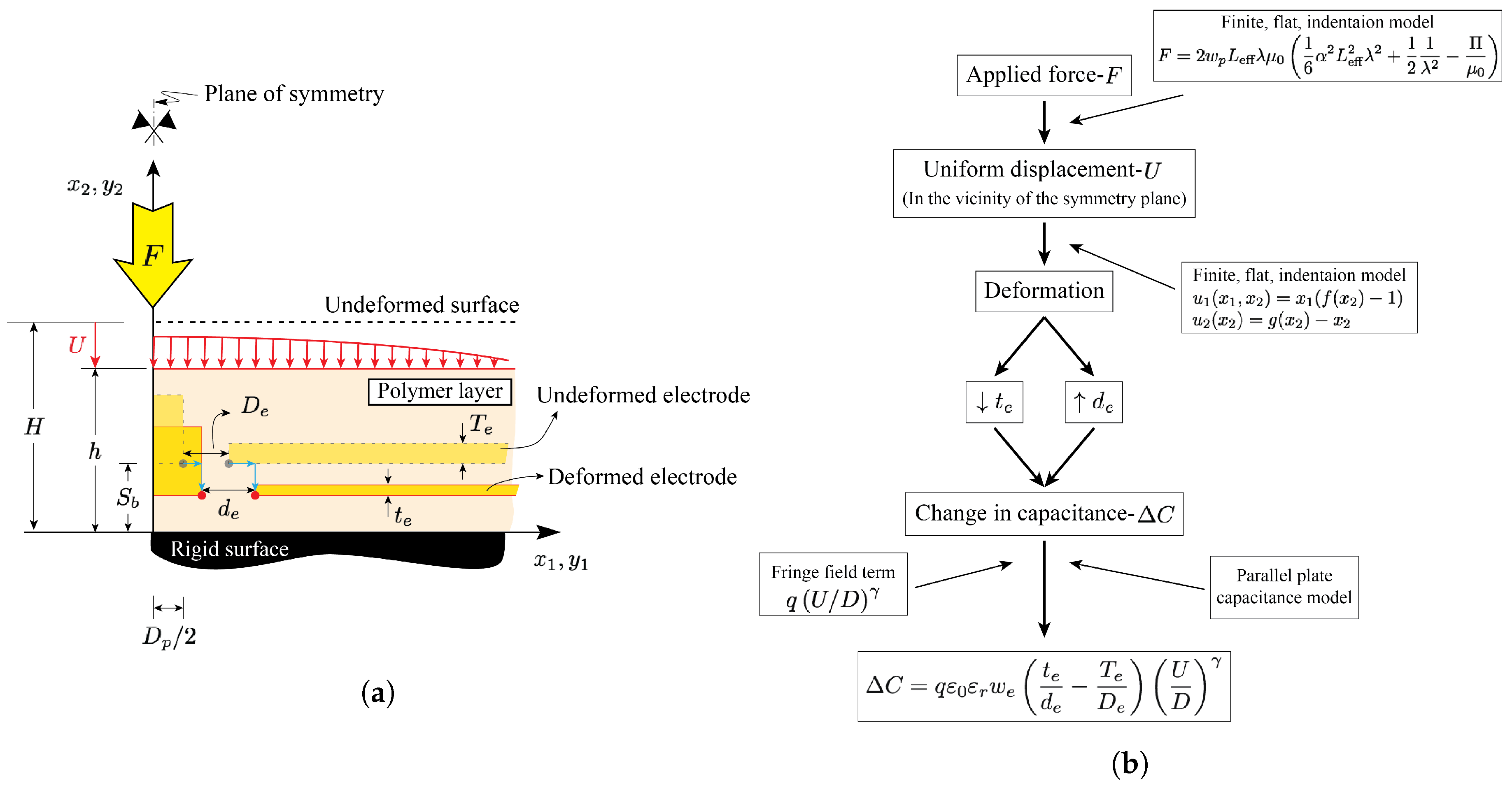
2. Summary of the Finite Flat Punch Indentation Model
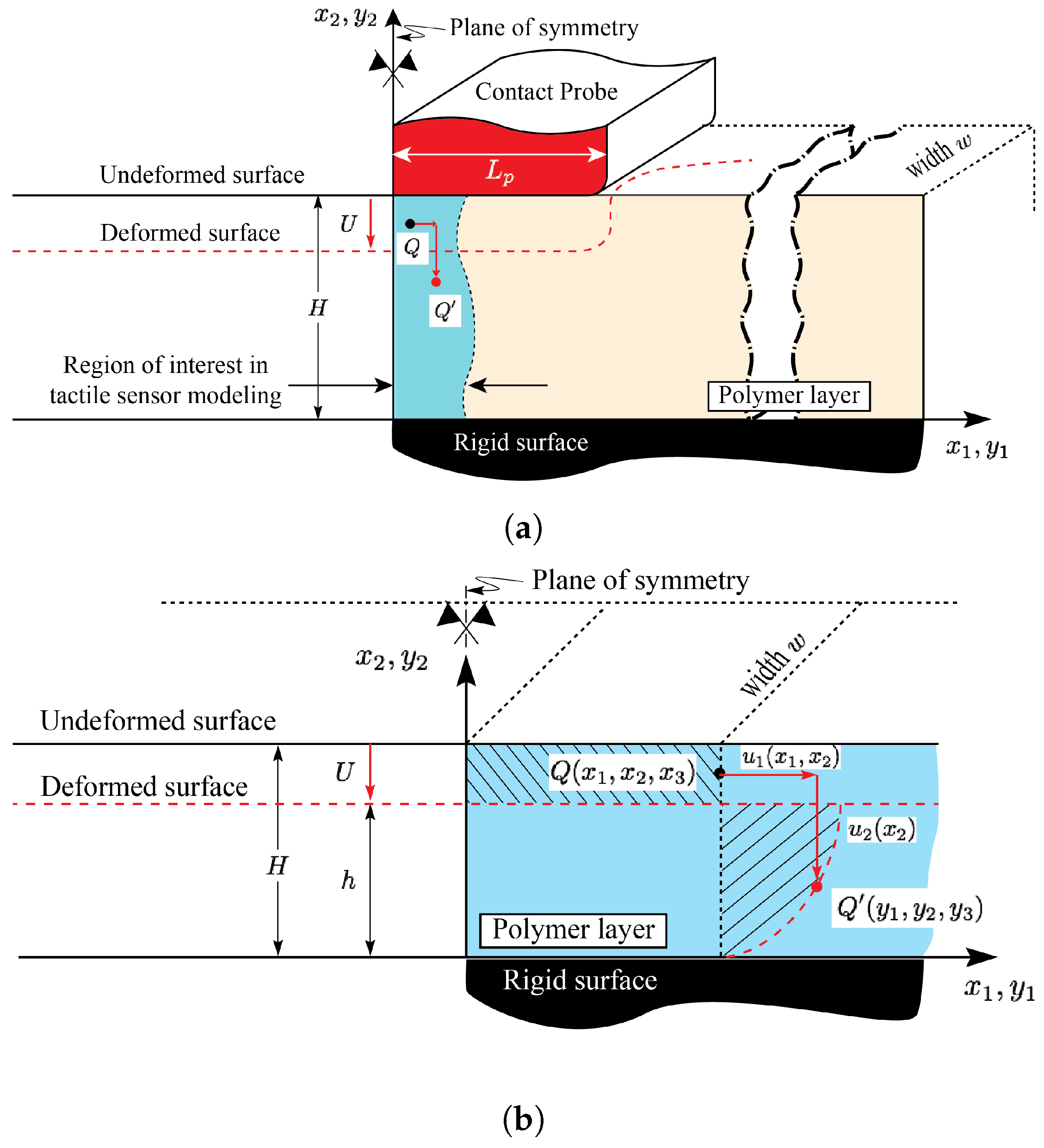
2.1. Layer Kinematics
2.2. Stress Analysis
2.3. Contact Force Calculation
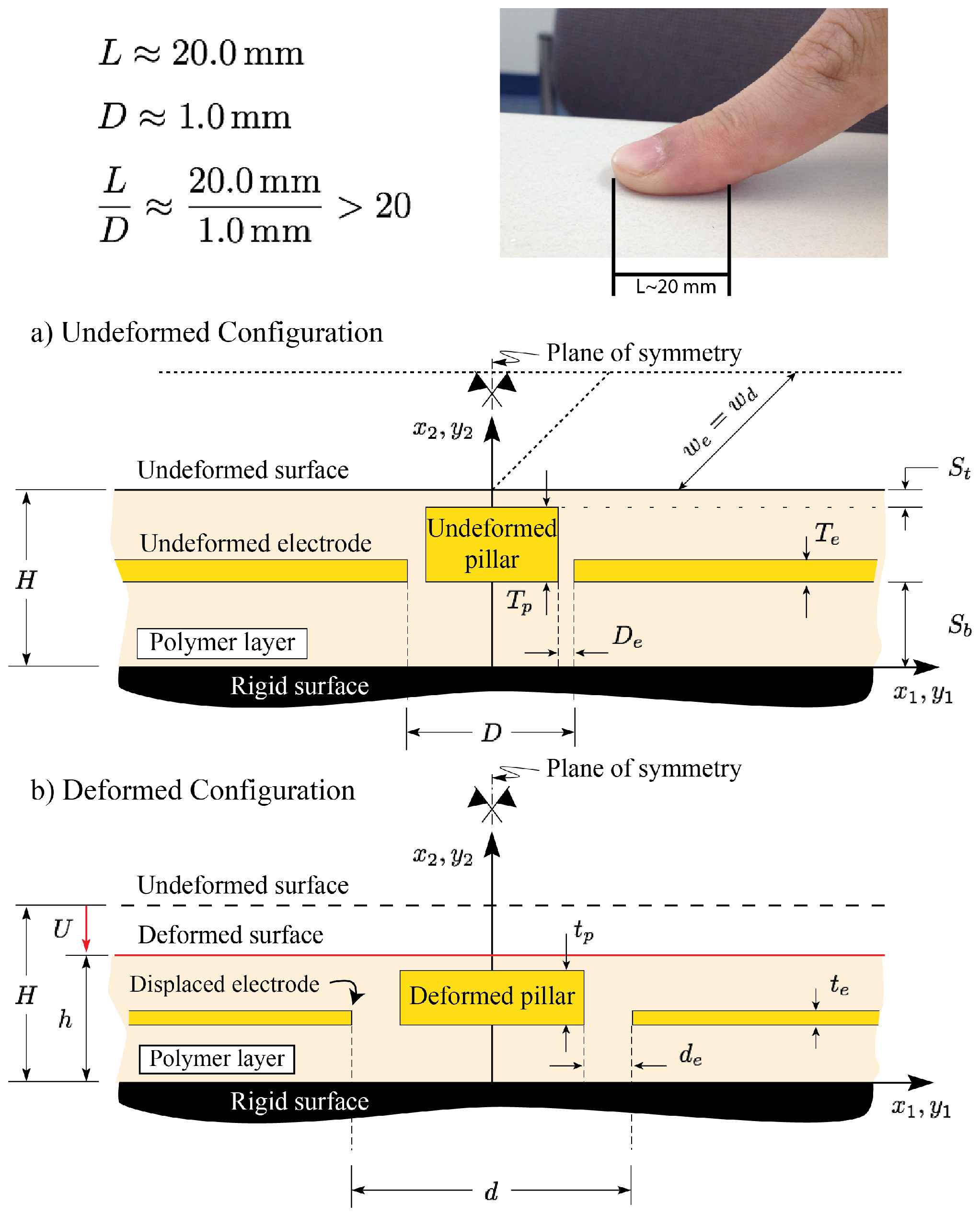
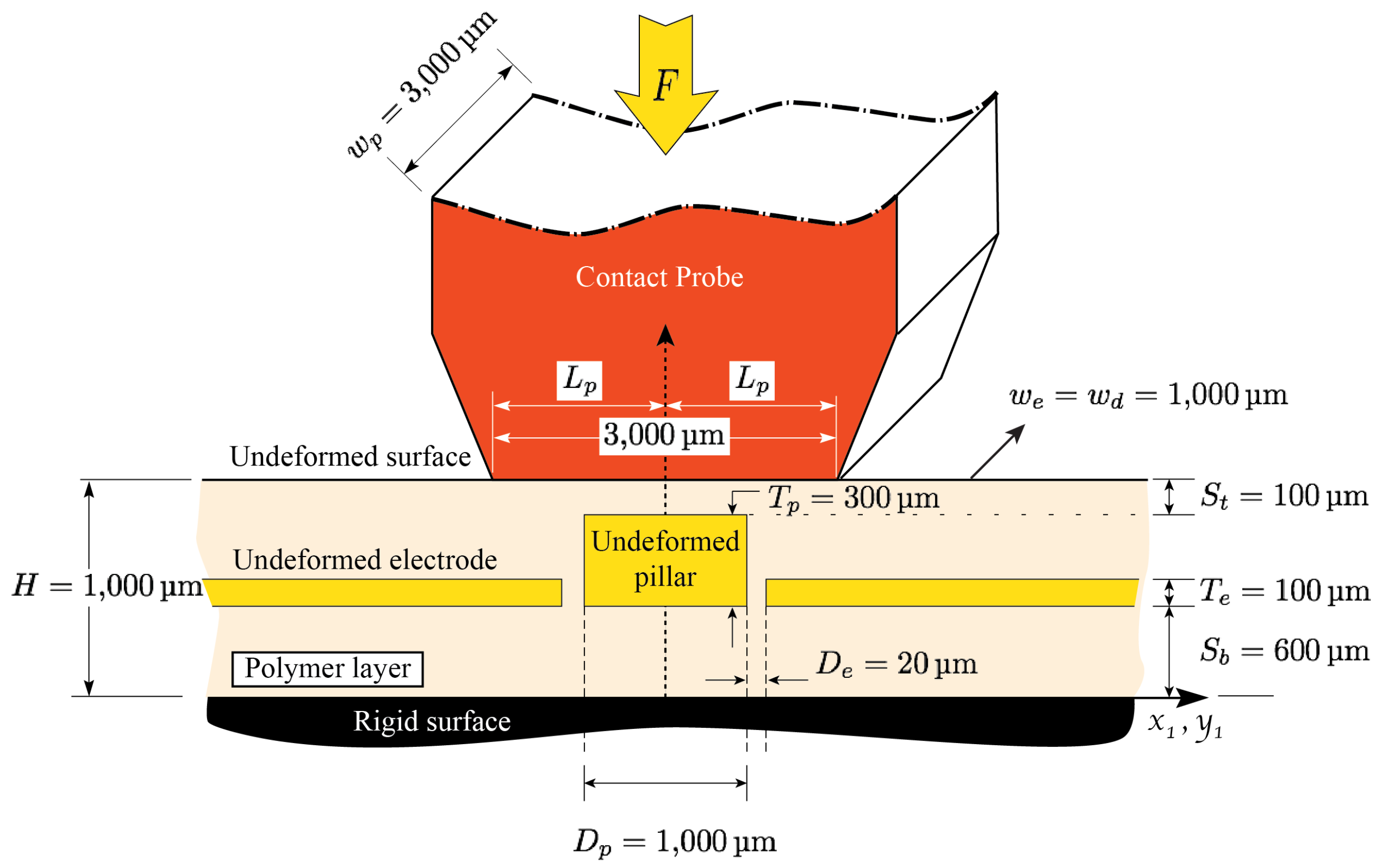
3. Tactile Unit-Sensor Model Development
3.1. Dimensions of Fabricated Sensors
3.2. Experimental Results
3.3. Tactile Unit-Sensor Capacitance Estimates
4. Identification of Constitutive Parameters From the Force-Deformation Curves
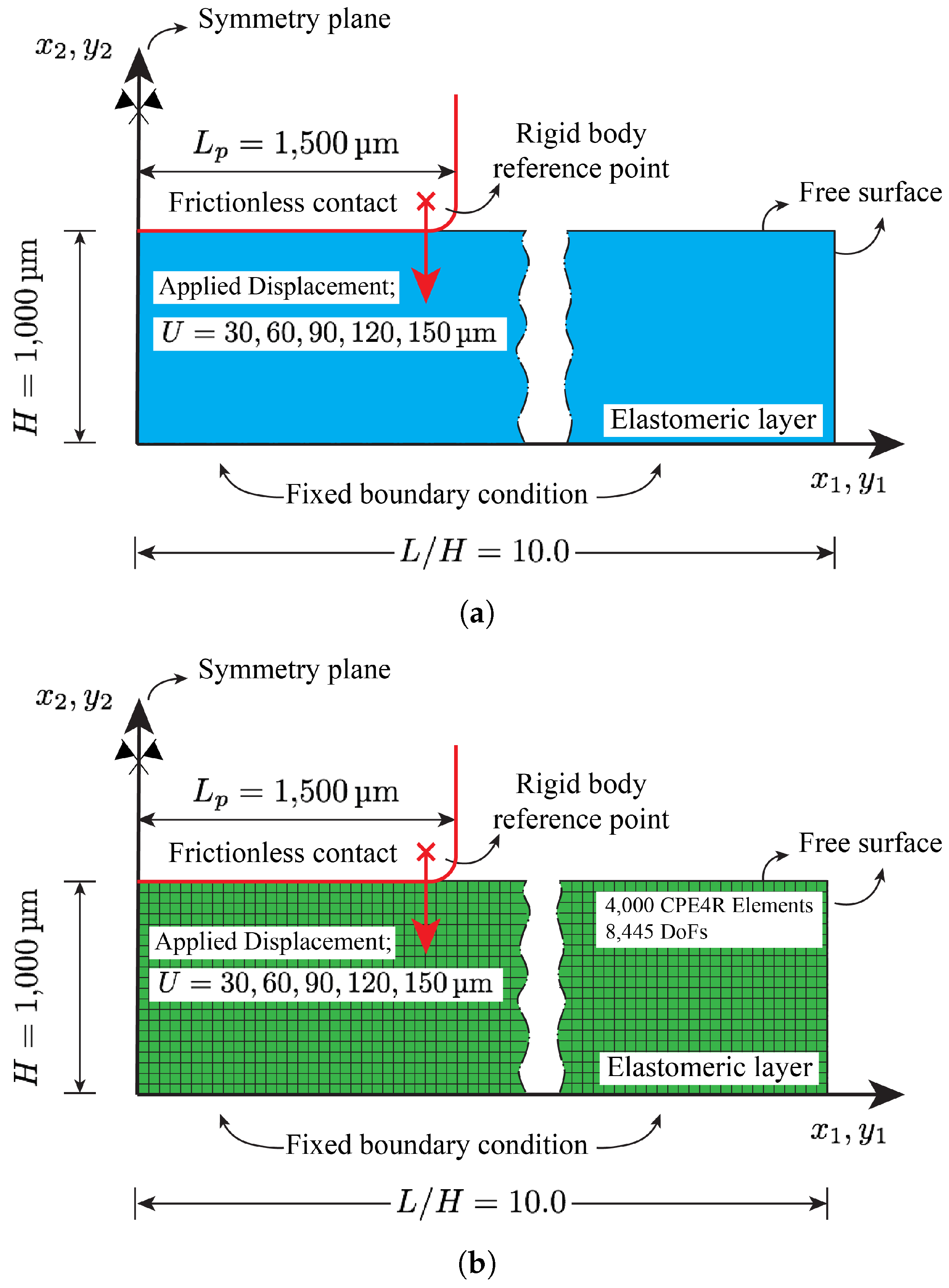
4.1. Finite Element Modeling
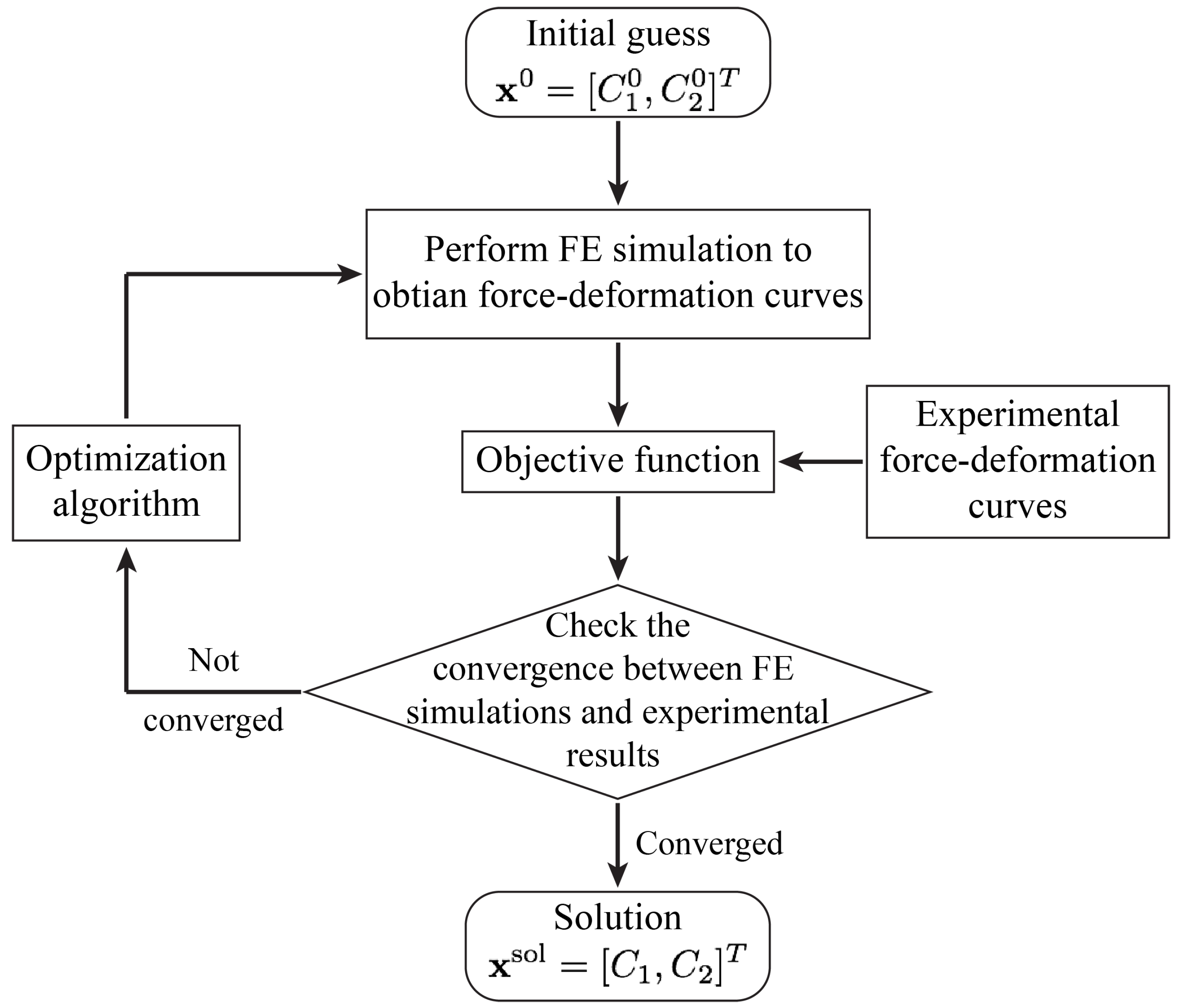
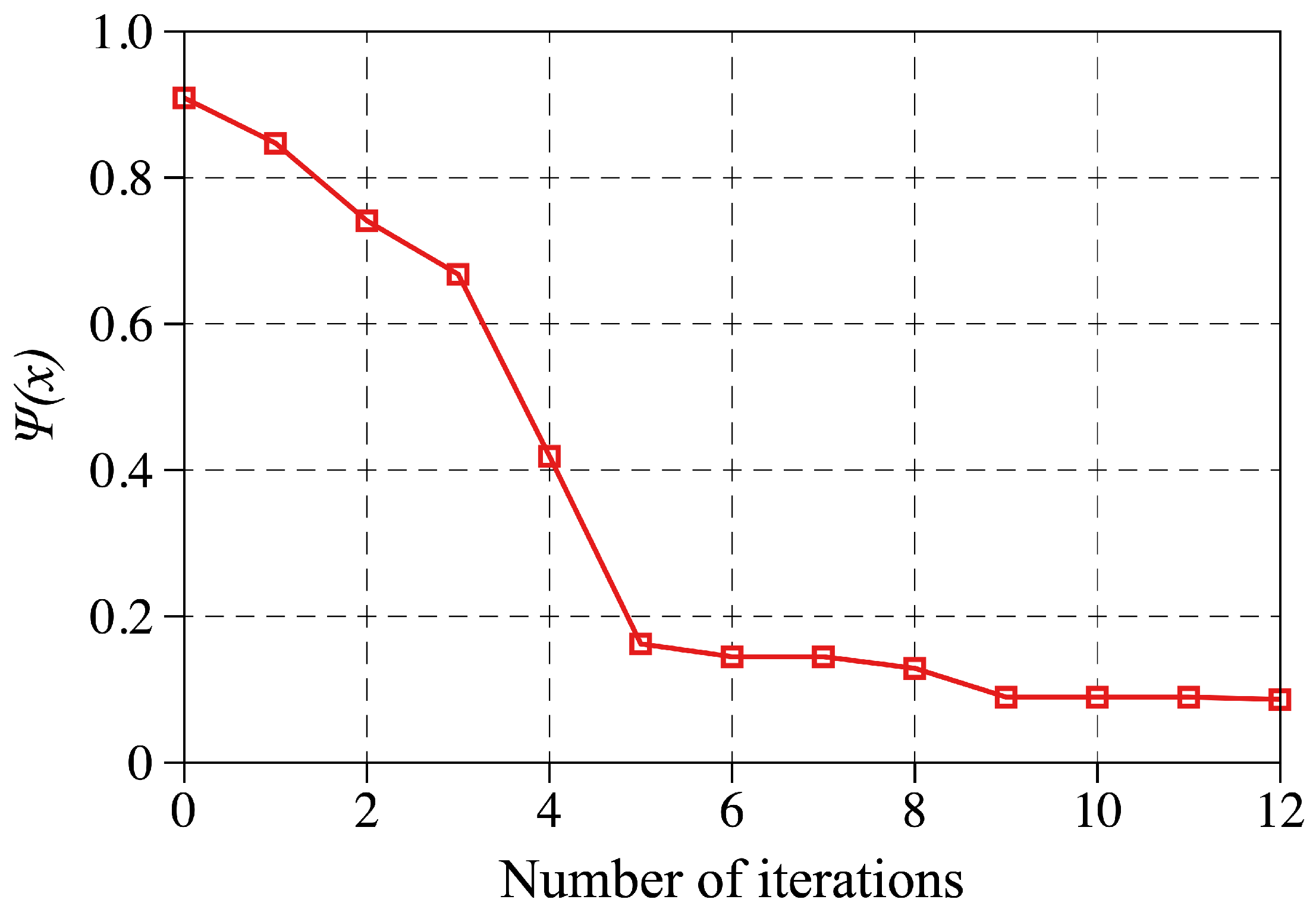
4.2. Inverse Analysis
5. Results and Discussion
5.1. The Sensor-Probe Contact Force
5.2. The Change in Capacitance-Applied Force Curves
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zou, L.; Ge, C.; Wang, Z.J.; Cretu, E.; Li, X. Novel Tactile Sensor Technology and Smart Tactile Sensing Systems: A Review. Sensors 2017, 17, 2653. [Google Scholar] [CrossRef] [PubMed]
- Chi, C.; Sun, X.; Xue, N.; Li, T.; Liu, C. Recent Progress in Technologies for Tactile Sensors. Sensors 2018, 18, 948. [Google Scholar] [CrossRef] [PubMed]
- Yogeswaran, N.; Dang, W.; Navaraj, W.; Shakthivel, D.; Khan, S.; Polat, E.; Gupta, S.; Heidari, H.; Kaboli, M.; Lorenzelli, L.; et al. New materials and advances in making electronic skin for interactive robots. Adv. Robot. 2015, 29, 1359–1373. [Google Scholar] [CrossRef]
- Watanabe, K.; Sohgawa, M.; Kanashima, T.; Okuyama, M.; Norna, H. Identification of various kinds of papers using multi-axial tactile sensor with micro-cantilevers. In Proceedings of the 2013 World Haptics Conference (WHC), Daejeon, Korea, 14–18 April 2013. [Google Scholar]
- Xu, D.; Loeb, G.E.; Fishel, J.A. Tactile identification of objects using Bayesian exploration. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013. [Google Scholar]
- Friedl, K.E.; Voelker, A.R.; Peer, A.; Eliasmith, C. Human-Inspired Neurorobotic System for Classifying Surface Textures by Touch. IEEE Robot. Autom. Lett. 2016, 1, 516–523. [Google Scholar]
- Kaboli, M.; Cheng, G. Robust Tactile Descriptors for Discriminating Objects From Textural Properties via Artificial Robotic Skin. IEEE Trans. Robot. 2018, 34, 985–1003. [Google Scholar] [CrossRef]
- Kaboli, M.; Yao, K.; Feng, D.; Cheng, G. Tactile-based active object discrimination and target object search in an unknown workspace. Auton. Robot. 2018, 1–30. [Google Scholar] [CrossRef]
- Dahiya, R.; Metta, G.; Valle, M.; Sandini, G. Tactile Sensing—From Humans to Humanoids. IEEE Trans. Robot. 2010, 26, 1–20. [Google Scholar]
- Ji, Z.; Zhu, H.; Liu, H.; Liu, N.; Chen, T.; Yang, Z.; Sun, L. The Design and Characterization of a Flexible Tactile Sensing Array for Robot Skin. Sensors 2016, 16, 2001. [Google Scholar] [CrossRef]
- Dai, C.; Lu, P.; Wu, C.; Chang, C. Fabrication of Wireless Micro Pressure Sensor Using the CMOS Process. Sensors 2009, 9, 8748–8760. [Google Scholar] [CrossRef] [PubMed]
- Jindal, S.K.; Mahajan, A.; Raghuwanshi, S.K. Reliable before-fabrication forecasting of normal and touch mode MEMS capacitive pressure sensor: modeling and simulation. J. Micro/Nanolithogr. MEMS MOEMS 2017, 16, 1. [Google Scholar] [CrossRef]
- Parthasarathy, E.S.M. Modeling and analysis of MEMS capacitive differential pressure sensor structure for altimeter application. Microsyst. Technol. 2017, 23, 1343–1349. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Lin, C.L.; Lai, Y.T.; Yang, Y.J. A polymer-based capacitive sensing array for normal and shear force measurement. Sensors 2010, 10, 10211–10225. [Google Scholar] [CrossRef] [PubMed]
- Liu, C. Recent Developments in Polymer MEMS. Adv. Mater. 2007, 19, 3783–3790. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, Y.; Nomani, M.W.; Wen, X.; Hsia, T.Y.; Koley, G. A highly sensitive pressure sensor using a Au-patterned polydimethylsiloxane membrane for biosensing applications. J. Micromech. Microeng. 2013, 23, 025022. [Google Scholar] [CrossRef]
- Kilaru, R.; Celik-Butler, Z.; Butler, D.P.; Gonenli, I.E. NiCr MEMS Tactile Sensors Embedded in Polyimide Toward Smart Skin. J. Microelectromech. Syst. 2013, 22, 349–355. [Google Scholar] [CrossRef]
- Pyo, S.; Lee, J.I.; Kim, M.O.; Chung, T.; Oh, Y.; Lim, S.C.; Park, J.; Kim, J. Development of a flexible three-axis tactile sensor based on screen-printed carbon nanotube-polymer composite. J. Micromech. Microeng. 2014, 24, 075012. [Google Scholar] [CrossRef]
- Maita, F.; Maiolo, L.; Minotti, A.; Pecora, A.; Ricci, D.; Metta, G.; Scandurra, G.; Giusi, G.; Ciofi, C.; Fortunato, G. Ultraflexible Tactile Piezoelectric Sensor Based on Low-Temperature Polycrystalline Silicon Thin-Film Transistor Technology. IEEE Sens. J. 2015, 15, 3819–3826. [Google Scholar] [CrossRef]
- Park, Y.L.; Chen, B.R.; Wood, R.J. Design and Fabrication of Soft Artificial Skin Using Embedded Microchannels and Liquid Conductors. IEEE Sens. J. 2012, 12, 2711–2718. [Google Scholar] [CrossRef]
- Kim, K.; Lee, K.R.; Kim, W.H.; Park, K.B.; Kim, T.H.; Kim, J.S.; Pak, J.J. Polymer-based flexible tactile sensor up to 32*32 arrays integrated with interconnection terminals. Sens. Actuators A Phys. 2009, 156, 284–291. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Tsao, C.M.; Lai, Y.Z.; Yang, Y.J. The development of a highly twistable tactile sensing array with stretchable helical electrodes. Sens. Actuators A Phys. 2011, 166, 226–233. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Huang, X.H.; Ma, C.W.; Yang, Y.J. A flexible capacitive tactile sensing array with floating electrodes. J. Micromech. Microeng. 2009, 19, 115001. [Google Scholar] [CrossRef]
- Seminara, L.; Pinna, L.; Valle, M.; Basirico, L.; Loi, A.; Cosseddu, P.; Bonfiglio, A.; Ascia, A.; Biso, M.; Ansaldo, A.; et al. Piezoelectric Polymer Transducer Arrays for Flexible Tactile Sensors. IEEE Sens. J. 2013, 13, 4022–4029. [Google Scholar] [CrossRef]
- Kim, M.S.; Ahn, H.R.; Lee, S.; Kim, C.; Kim, Y.J. A dome-shaped piezoelectric tactile sensor arrays fabricated by an air inflation technique. Sens. Actuators A Phys. 2014, 212, 151–158. [Google Scholar] [CrossRef]
- Du, W.Y. Resistive, Capacitive, Inductive, and Magnetic Sensor Technologies (Series in Sensors); CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Maiolino, P.; Galantini, F.; Mastrogiovanni, F.; Gallone, G.; Cannata, G.; Carpi, F. Soft dielectrics for capacitive sensing in robot skins: Performance of different elastomer types. Sens. Actuators A Phys. 2015, 226, 37–47. [Google Scholar] [CrossRef]
- Jang, H.; Yoon, H.; Ko, Y.; Choi, J.; Lee, S.; Jeon, I.; Kim, J.; Kim, H. Enhanced performance in capacitive force sensors using carbon nanotube/polydimethylsiloxane nanocomposites with high dielectric properties. Nanoscale 2016, 8, 5667–5675. [Google Scholar] [CrossRef] [PubMed]
- Charalambides, A.; Bergbreiter, S. All-elastomer in-plane MEMS capacitive tactile sensor for normal force detection. In Proceedings of the 2013 IEEE Sensors, Baltimore, MD, USA, 4–6 November 2013; pp. 1–4. [Google Scholar]
- Charalambides, A.; Cheng, J.; Li, T.; Bergbreiter, S. 3-axis all elastomer MEMS tactile sensor. In Proceedings of the 2015 28th IEEE International Conference Micro Electro Mechanical Systems (MEMS), Estoril, Portugal, 18–22 January 2015; pp. 726–729. [Google Scholar]
- Kalayeh, K.M.; Charalambides, A.; Bergbreiter, S.; Charalambides, P.G. Development and Experimental Validation of a Non-Linear, All-Elastomer In-Plane Capacitive Pressure Sensor Model. IEEE Sens. J. 2017, 17, 274–285. [Google Scholar] [CrossRef]
- Phillips, J.; Johnson, K. Tactile spatial resolution. III. A continuum mechanics model of skin predicting mechanoreceptor responses to bars, edges, and gratings. J. Neurophysiol. 1981, 46, 1204–1225. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Fearing, R.S.; Hollerbach, J.M. Basic solid mechanics for tactile sensing. Int. J. Robot. Res. 1985, 4, 40–54. [Google Scholar] [CrossRef]
- Maier-Schneider, D.; Maibach, J.; Obermeier, E. A new analytical solution for the load-deflection of square membranes. J. Microelectromech. Syst. 1995, 4, 238–241. [Google Scholar] [CrossRef]
- Wang, Q.; Ko, W.H. Modeling of touch mode capacitive sensors and diaphragms. Sens. Actuators A Phys. 1999, 75, 230–241. [Google Scholar] [CrossRef]
- Liang, G.; Deqing, M.; Yancheng, W.; Zichen, C. Modeling and Analysis of a Flexible Capacitive Tactile Sensor Array for Normal Force Measurement. IEEE Sens. J. 2014, 14, 4095–4103. [Google Scholar] [CrossRef]
- Liang, G.; Wang, Y.; Mei, D.; Xi, K.; Chen, Z. A modified analytical model to study the sensing performance of a flexible capacitive tactile sensor array. J. Micromech. Microeng. 2015, 25, 035017. [Google Scholar] [CrossRef]
- Liang, G.; Wang, Y.; Mei, D.; Xi, K.; Chen, Z. An analytical model for studying the structural effects and optimization of a capacitive tactile sensor array. J. Micromech. Microeng. 2016, 26, 045007. [Google Scholar] [CrossRef]
- Vásárhelyi, G.; Fodor, B.; Roska, T. Tactile sensing-processing: Interface-cover geometry and the inverse-elastic problem. Sens. Actuators A Phys. 2007, 140, 8–18. [Google Scholar] [CrossRef]
- Liu, W.; Gu, C.; Zeng, R.; Yu, P.; Fu, X. A Novel Inverse Solution of Contact Force Based on a Sparse Tactile Sensor Array. Sensors 2018, 18, 351. [Google Scholar] [CrossRef]
- Muhammad, H.; Oddo, C.; Beccai, L.; Recchiuto, C.; Anthony, C.; Adams, M.; Carrozza, M.; Hukins, D.; Ward, M. Development of a bioinspired MEMS based capacitive tactile sensor for a robotic finger. Sens. Actuators A Phys. 2011, 165, 221–229. [Google Scholar] [CrossRef]
- Tiwana, M.I.; Shashank, A.; Redmond, S.J.; Lovell, N.H. Characterization of a capacitive tactile shear sensor for application in robotic and upper limb prostheses. Sens. Actuators A Phys. 2011, 165, 164–172. [Google Scholar] [CrossRef]
- Jamali, N.; Sammut, C. Majority Voting: Material Classification by Tactile Sensing Using Surface Texture. IEEE Trans. Robot. 2011, 27, 508–521. [Google Scholar] [CrossRef]
- Decherchi, S.; Gastaldo, P.; Dahiya, R.S.; Valle, M.; Zunino, R. Tactile-Data Classification of Contact Materials Using Computational Intelligence. IEEE Trans. Robot. 2011, 27, 635–639. [Google Scholar] [CrossRef]
- Fishel, J.; Loeb, G. Bayesian exploration for intelligent identification of textures. Front Neurorobot. 2012, 6, 4. [Google Scholar] [CrossRef] [PubMed]
- Yaser, S.A.M.; Magdon-Ismail, M.; Lin, H. Learning from Data: A Short Course. 2012. Available online: AMLBook.com (accessed on 22 October 2018).
- Charalambides, A.; Bergbreiter, S. A novel all-elastomer MEMS tactile sensor for high dynamic range shear and normal force sensing. J. Micromech. Microeng. 2015, 25, 095009. [Google Scholar] [CrossRef]
- Kalayeh, K.M.; Charalambides, P.G. Large deformation mechanics of a soft elastomeric layer under compressive loading for a MEMS tactile sensor application. Int. J. Non-Linear Mech. 2015, 76, 120–134. [Google Scholar] [CrossRef]
- Kalayeh, K.M.; Charalambides, P.G. Large deformation mechanics of a soft elastomeric layer compressed by a finite flat rigid punch for tactile sensor applications. Int. J. Non-Linear Mech. 2018, 106, 115–129. [Google Scholar] [CrossRef]
- MATLAB. Version 9.1.0 (R2016b); The MathWorks Inc.: Natick, MA, USA, 2016. [Google Scholar]
- Gamonpilas, C.; Charalambides, M.; Williams, J.; Dooling, P.; Gibbon, S. Predicting the mechanical behaviour of starch gels through inverse analysis of indentation data. Appl. Rheol. 2010, 20, 33283. [Google Scholar]
- Fellay, L.S.; Fasce, L.A.; Czerner, M.; Pardo, E.; Frontini, P.M. On the Feasibility of Identifying First Order Ogden Constitutive Parameters of Gelatin Gels from Flat Punch Indentation Tests. Soft Mater. 2015, 13, 188–200. [Google Scholar] [CrossRef]
- Feng, Y.; Lee, C.; Sun, L.; Ji, S.; Zhao, X. Characterizing white matter tissue in large strain via asymmetric indentation and inverse finite element modeling. J. Mech. Behav. Biomed. Mater. 2017, 65, 490–501. [Google Scholar] [CrossRef] [PubMed]
- Habbit Karlsson, S.I. Abaqus Documentation; Dassault Systèmes: Vélizy-Villacoublay, France, 2013. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder–Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
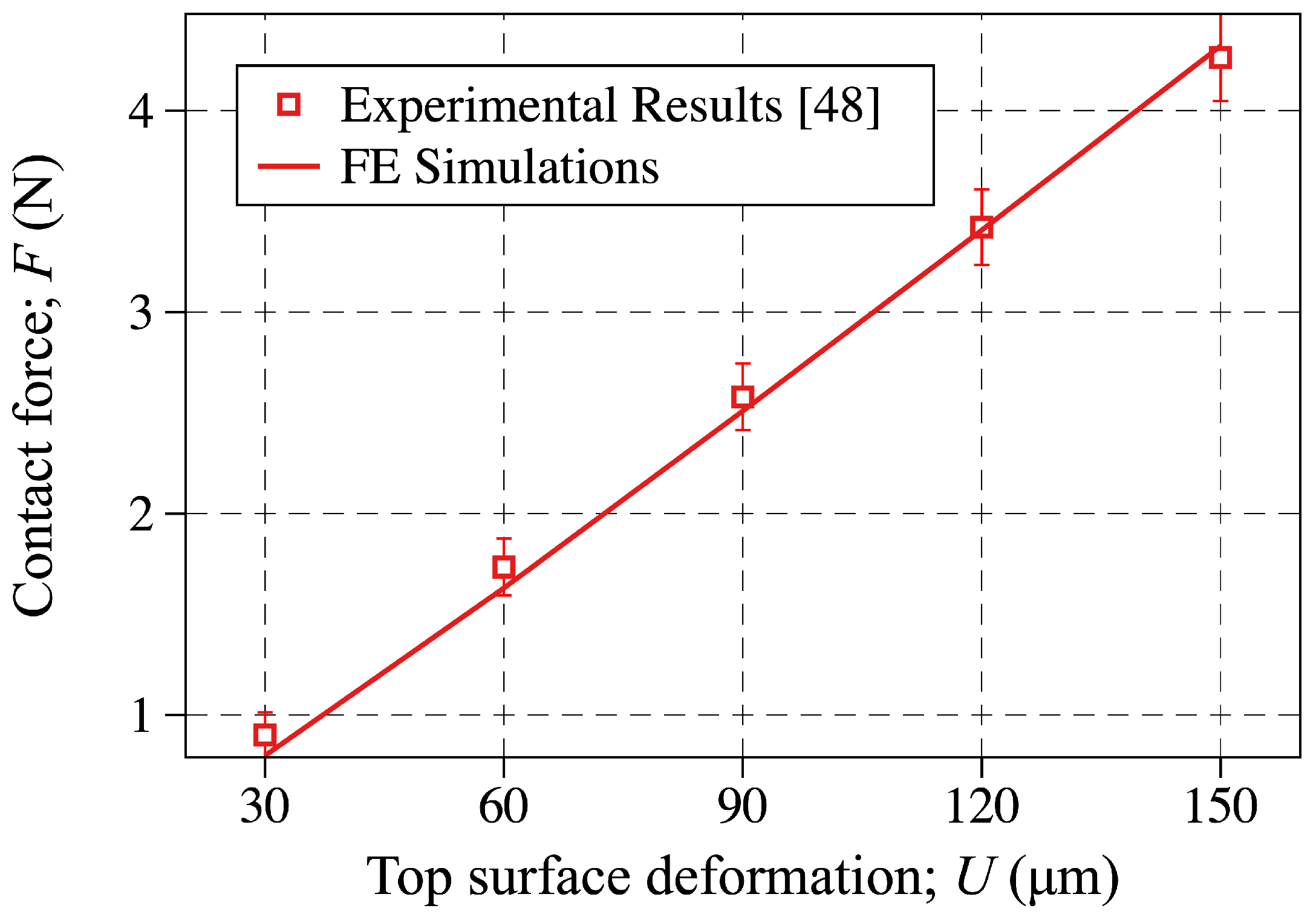
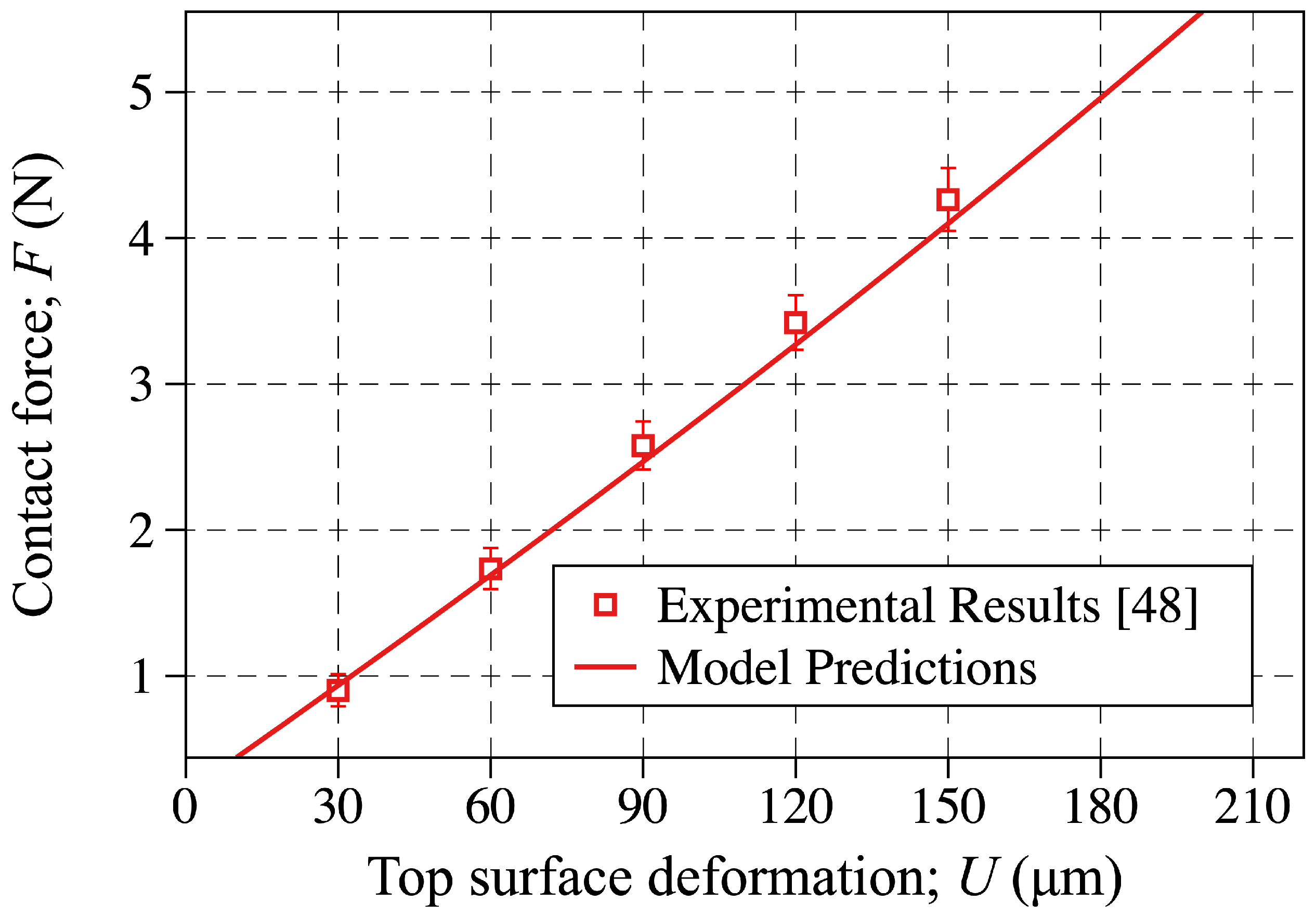
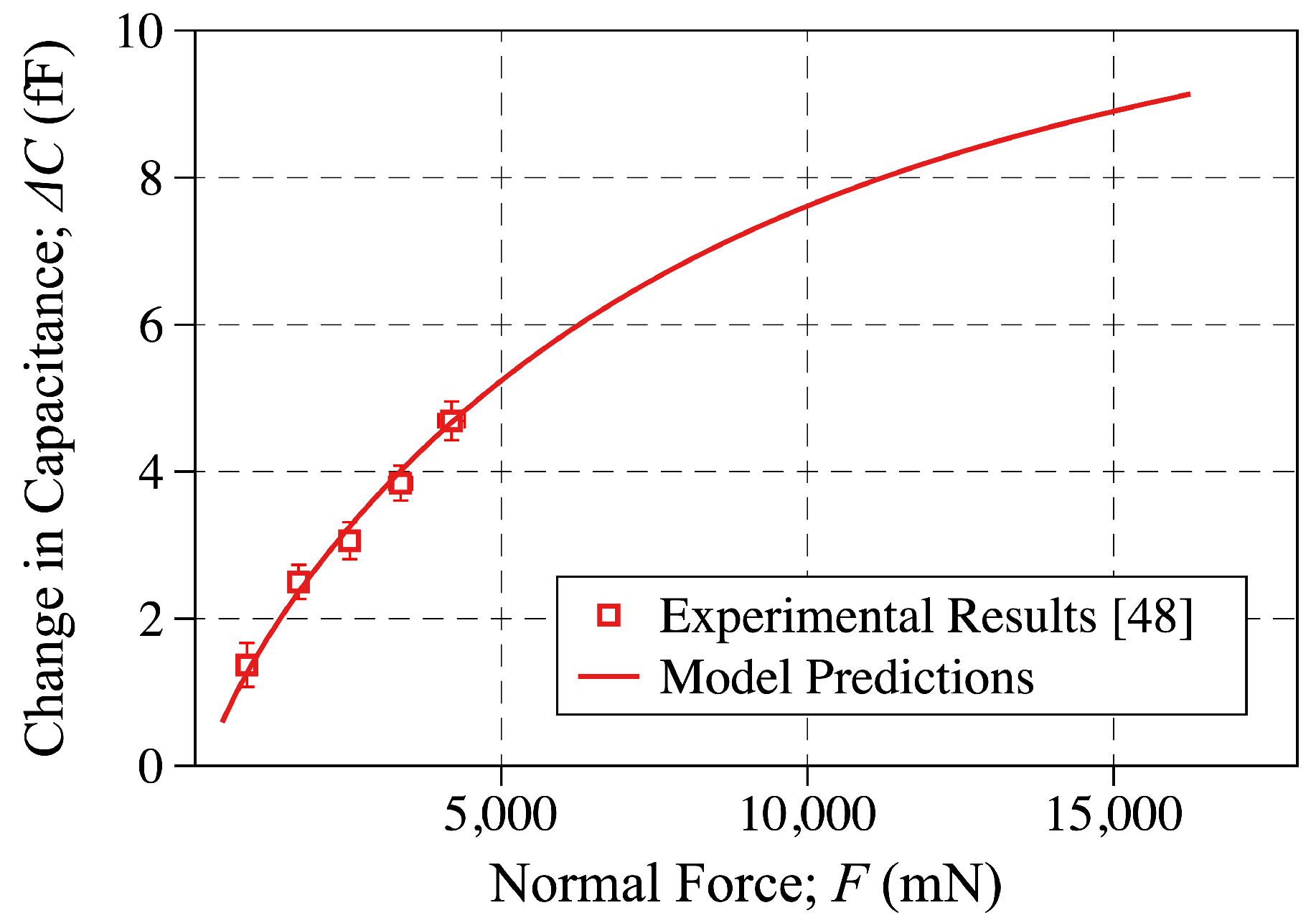
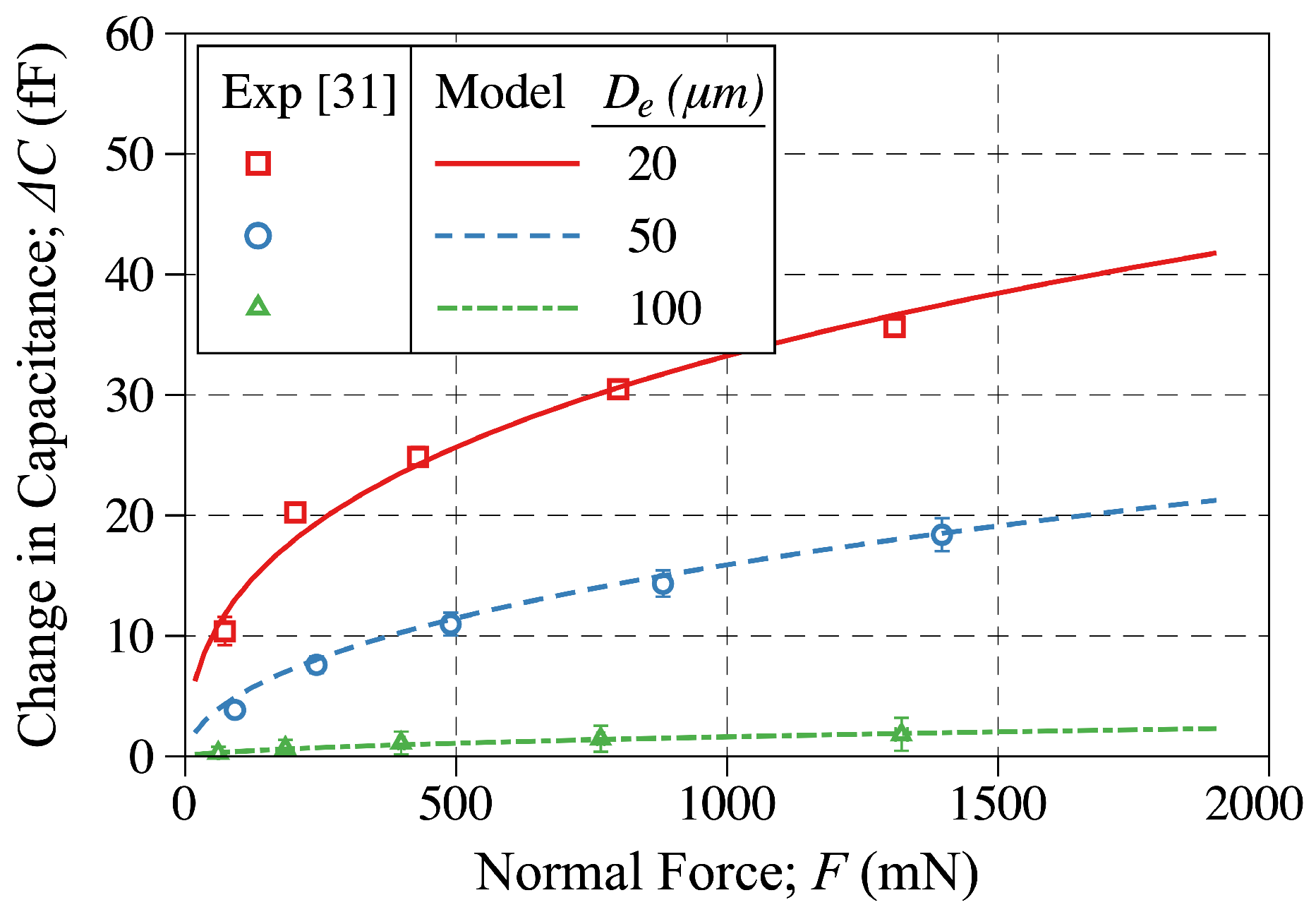

| U (m) | F (N) | (fF) |
|---|---|---|
| 30 | 0.9021 | 1.3710 |
| 60 | 1.7351 | 2.5004 |
| 90 | 1.5792 | 3.0618 |
| 120 | 3.4213 | 3.8438 |
| 150 | 4.2637 | 4.6920 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
M. Kalayeh, K.; G. Charalambides, P. A Non-Linear Model of an All-Elastomer, in-Plane, Capacitive, Tactile Sensor Under the Application of Normal Forces. Sensors 2018, 18, 3614. https://doi.org/10.3390/s18113614
M. Kalayeh K, G. Charalambides P. A Non-Linear Model of an All-Elastomer, in-Plane, Capacitive, Tactile Sensor Under the Application of Normal Forces. Sensors. 2018; 18(11):3614. https://doi.org/10.3390/s18113614
Chicago/Turabian StyleM. Kalayeh, Kourosh, and Panos G. Charalambides. 2018. "A Non-Linear Model of an All-Elastomer, in-Plane, Capacitive, Tactile Sensor Under the Application of Normal Forces" Sensors 18, no. 11: 3614. https://doi.org/10.3390/s18113614
APA StyleM. Kalayeh, K., & G. Charalambides, P. (2018). A Non-Linear Model of an All-Elastomer, in-Plane, Capacitive, Tactile Sensor Under the Application of Normal Forces. Sensors, 18(11), 3614. https://doi.org/10.3390/s18113614





