Development, Dynamic Modeling, and Multi-Modal Control of a Therapeutic Exoskeleton for Upper Limb Rehabilitation Training
Abstract
1. Introduction
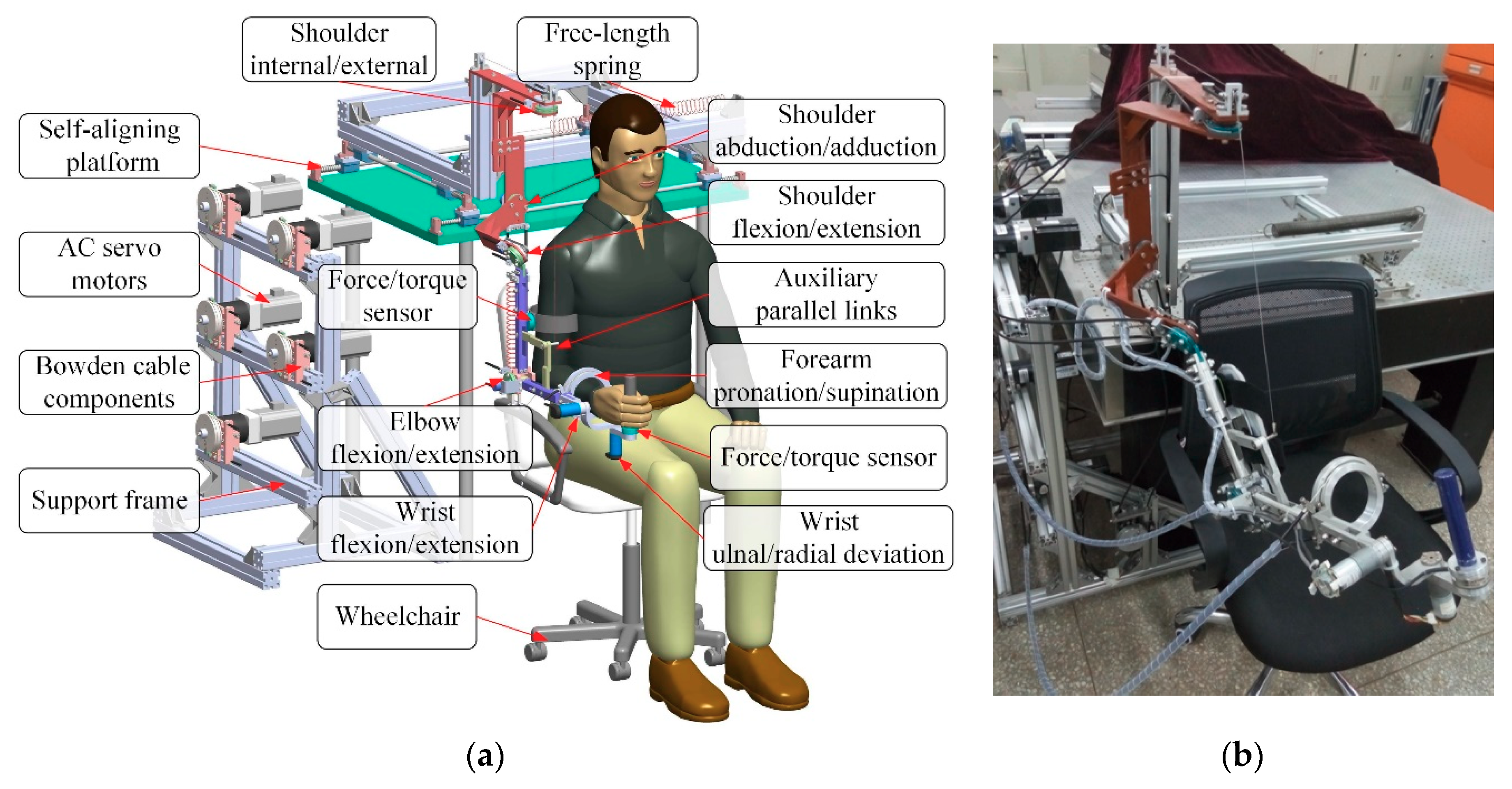
2. System Description
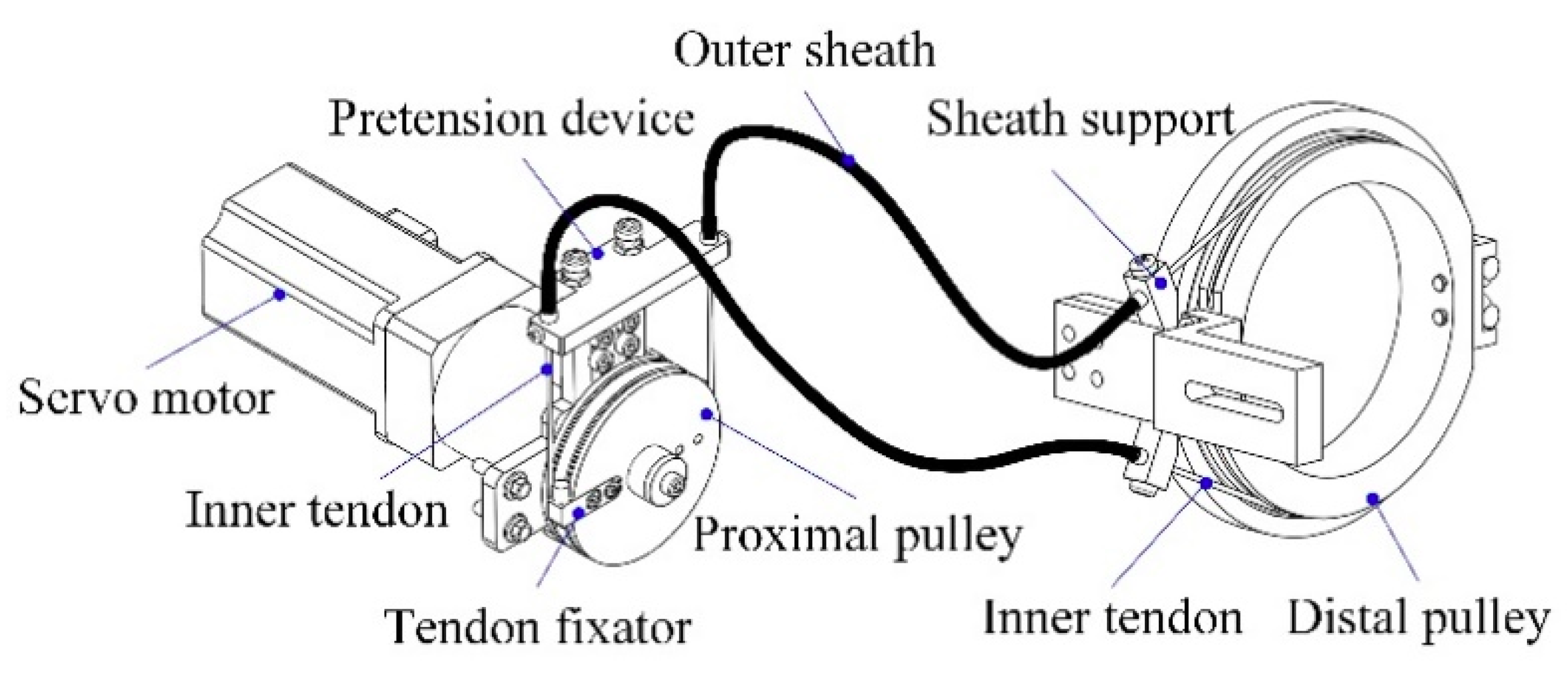
2.1. Exoskeleton Robot Design
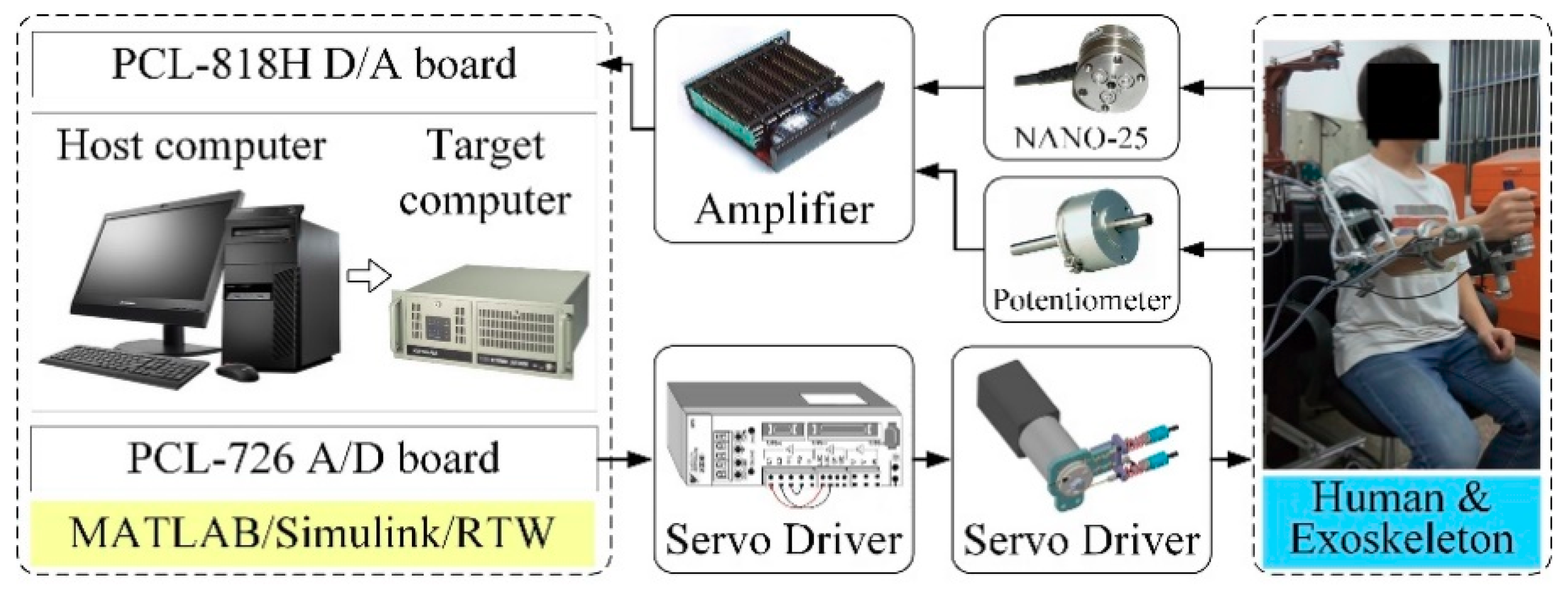
2.2. Electrical Control System
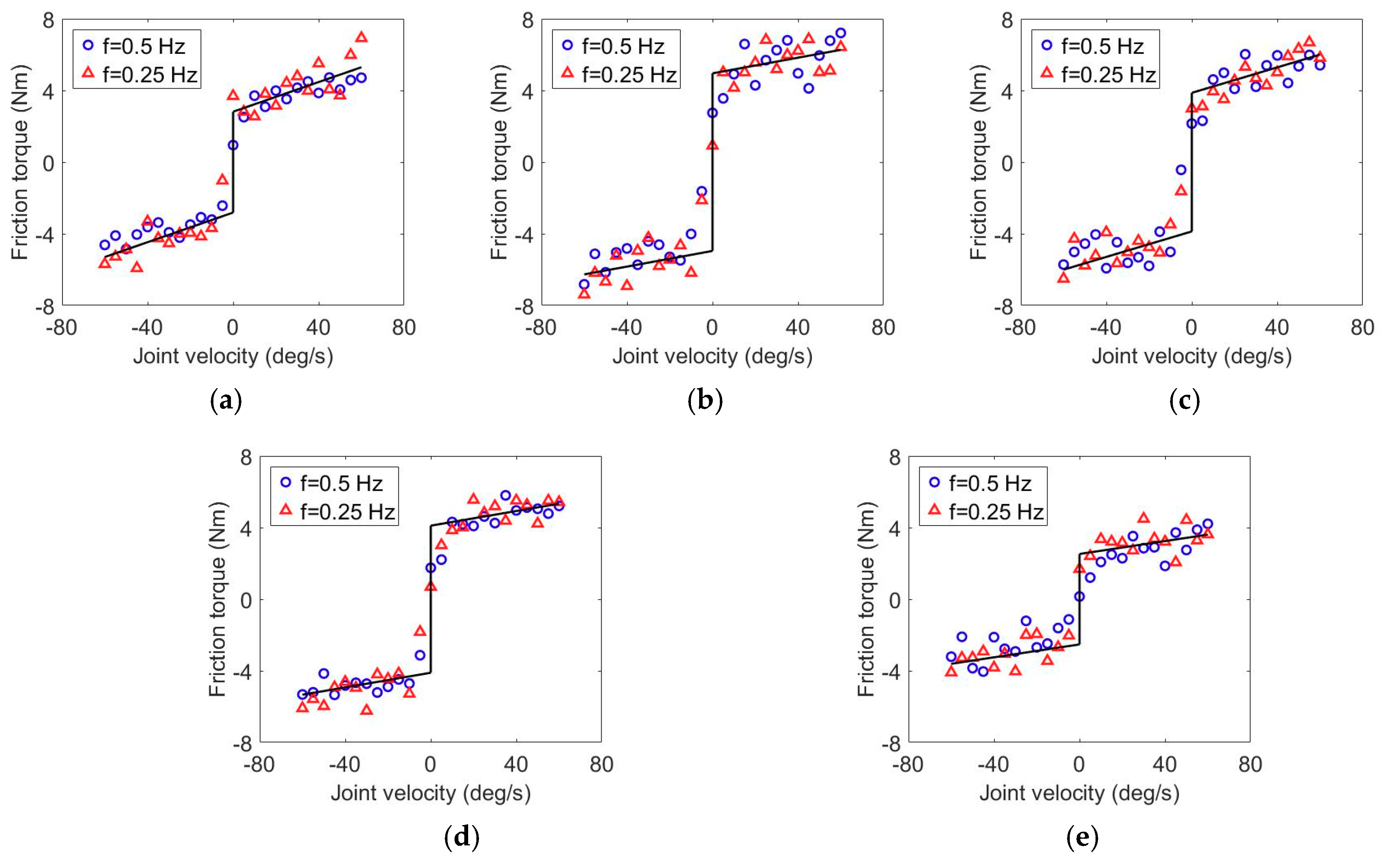
3. Dynamics Modeling and Calibration
- Step (a):
- The servomotor of the targeted identification joint was set to run in torque control mode and track a sinusoidal trajectory with fixed frequency, while other motors were set to run in braking mode and remain in fixed position.
- Step (b):
- The angular displacement, velocity, acceleration, and driving torque of the targeted identification joint were measured and calculated respectively. The friction torque was computed according to Equation (7).
- Step (c):
- The trajectory tracking experiment was repeated and recorded with different frequency.
- Step (d):
- Based on the relation between angular velocity and friction torque, terms bi and τe,i can be identified by employing the least squares fitting method to the experimental data.
- Step (e):
- The targeted identification joint was changed, and the steps from (a) to (d) were repeated to acquire the entire friction model parameters.
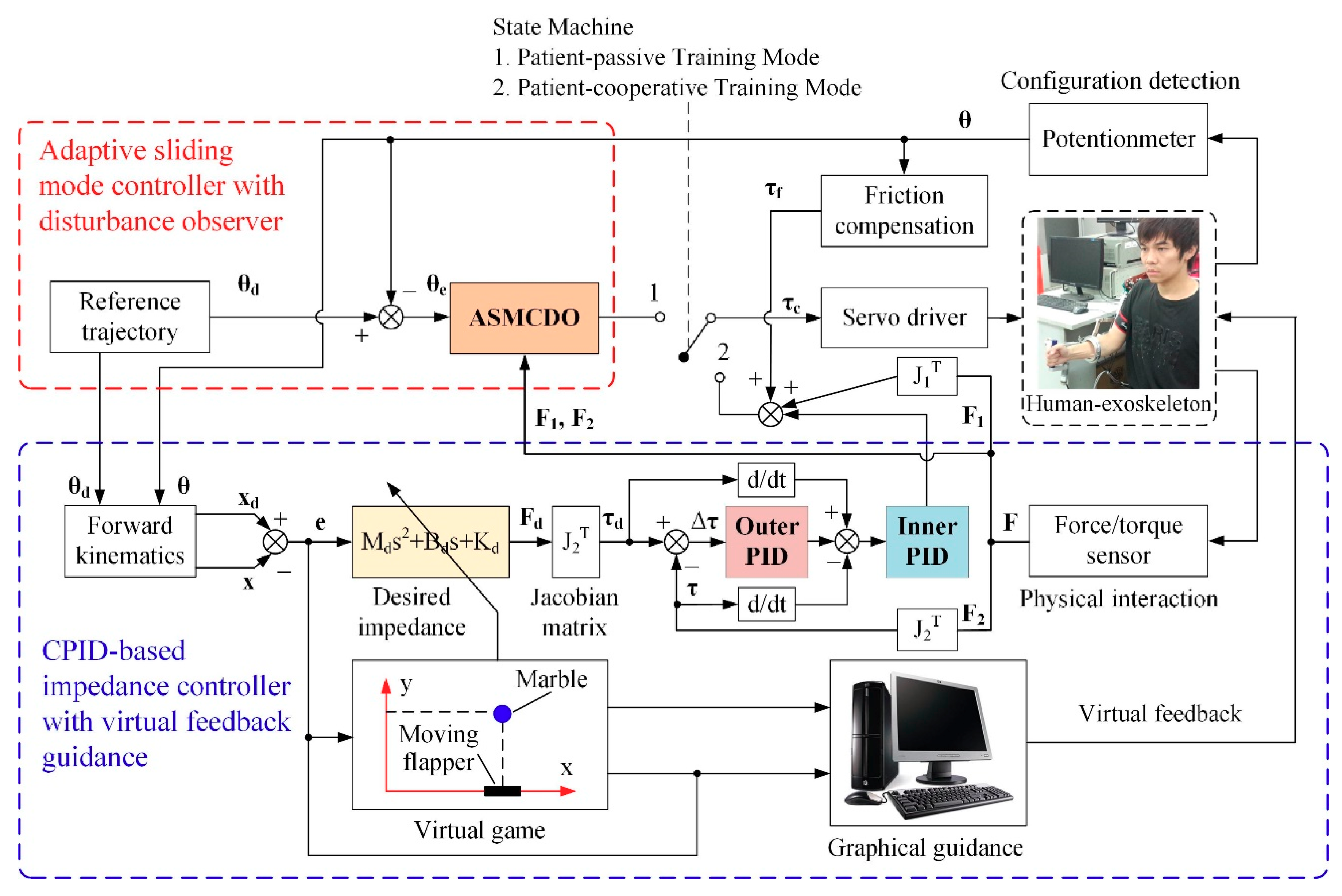
4. Development of Multi-Modular Control Strategy
4.1. Adaptive Sliding Mode Control with Disturbance Observer
4.2. CPID-Based Impedance Control
5. Experiments and Discussion
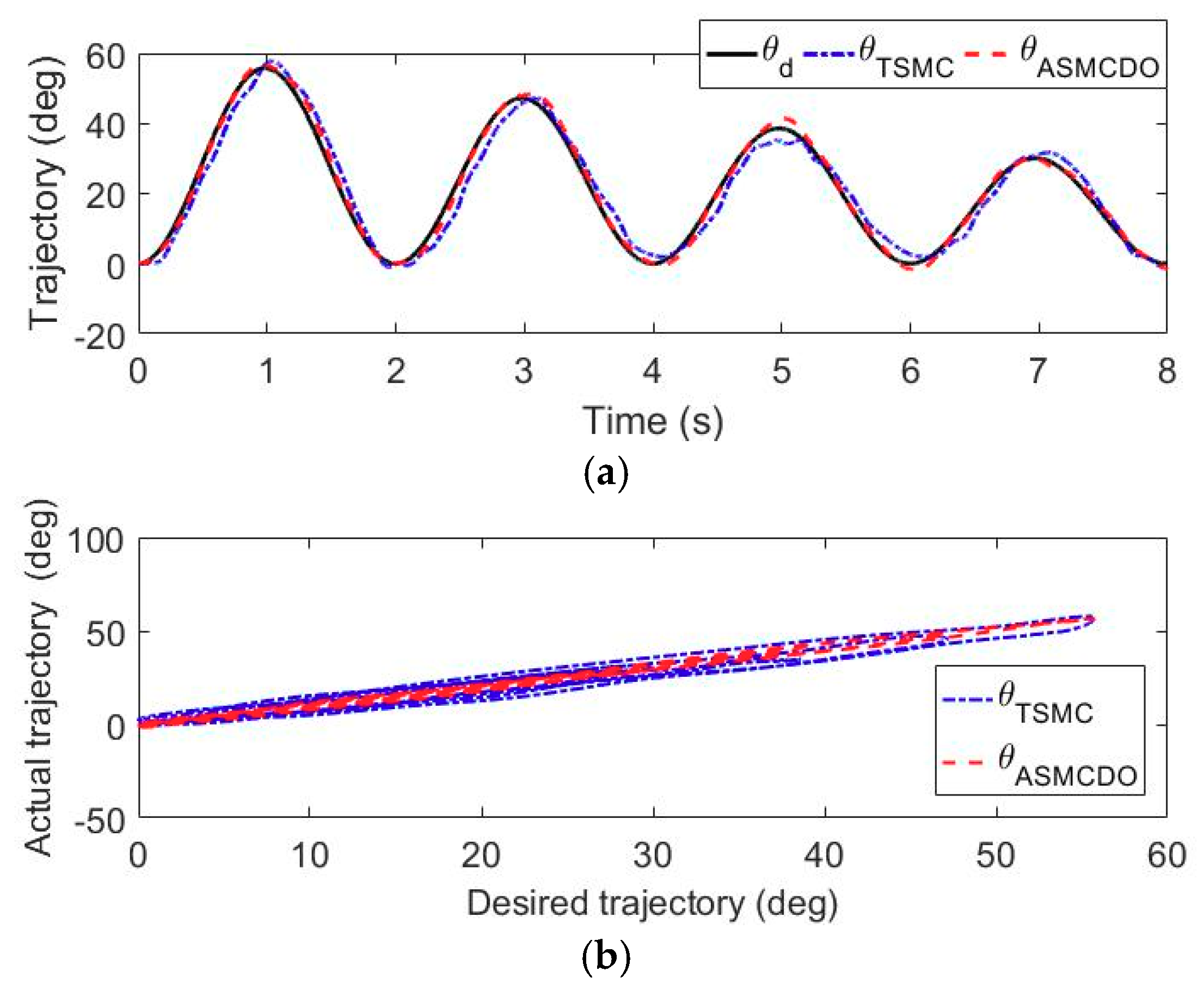
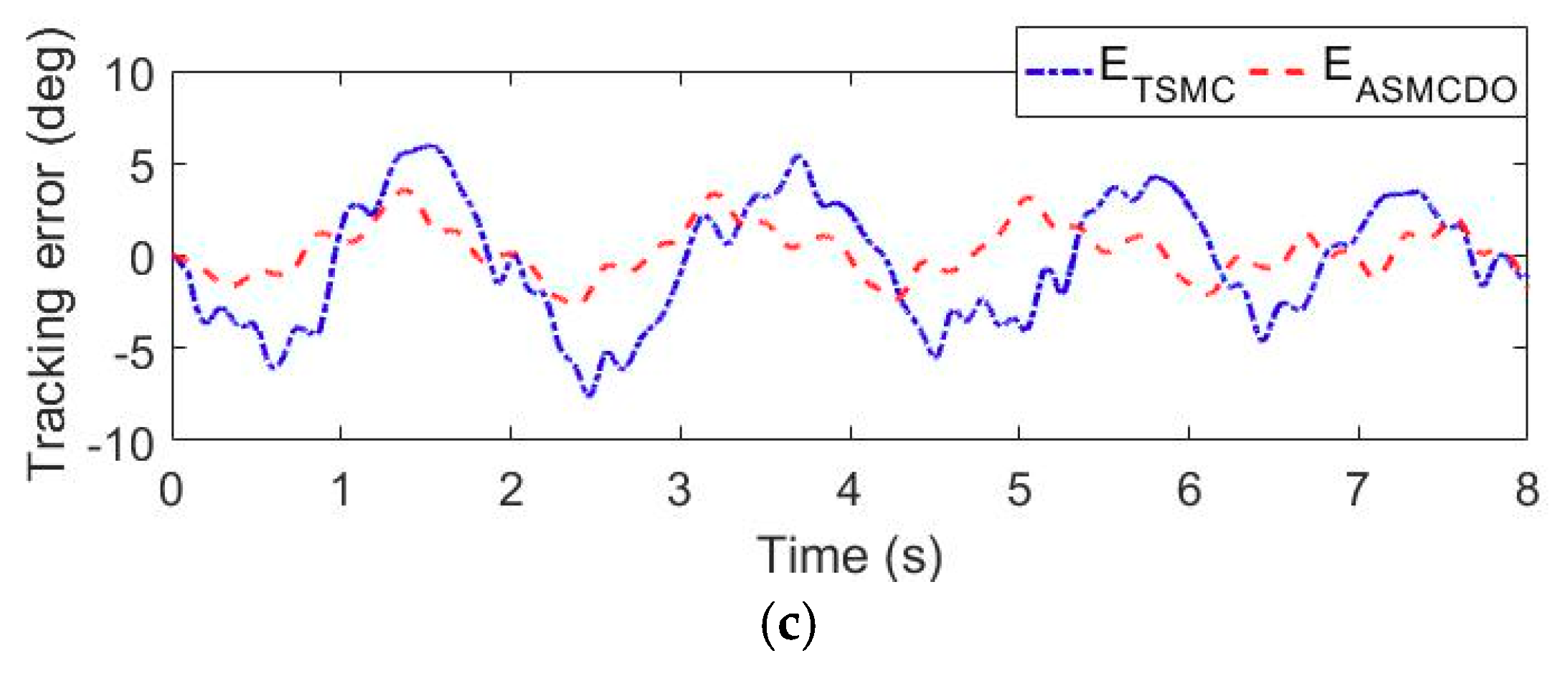
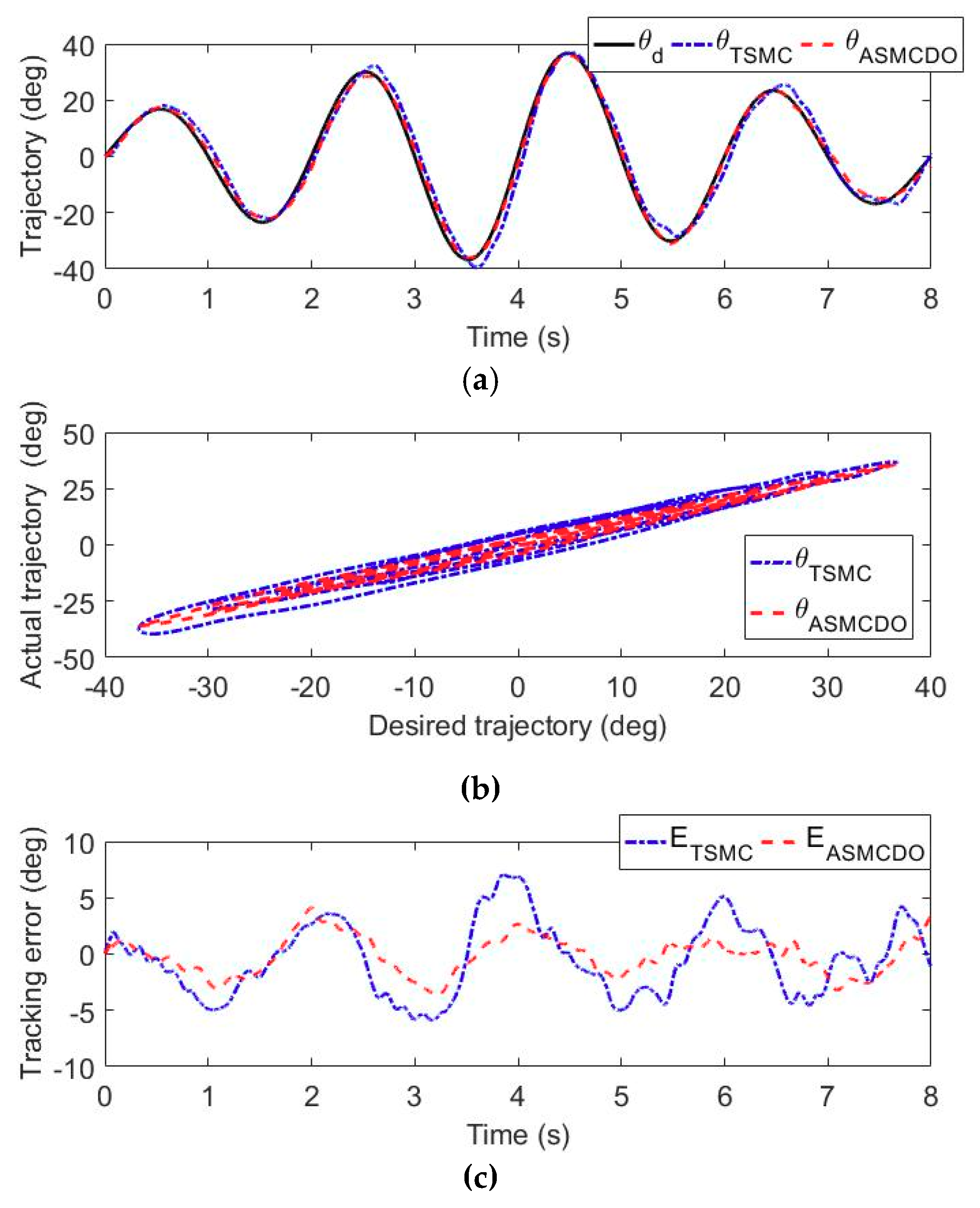
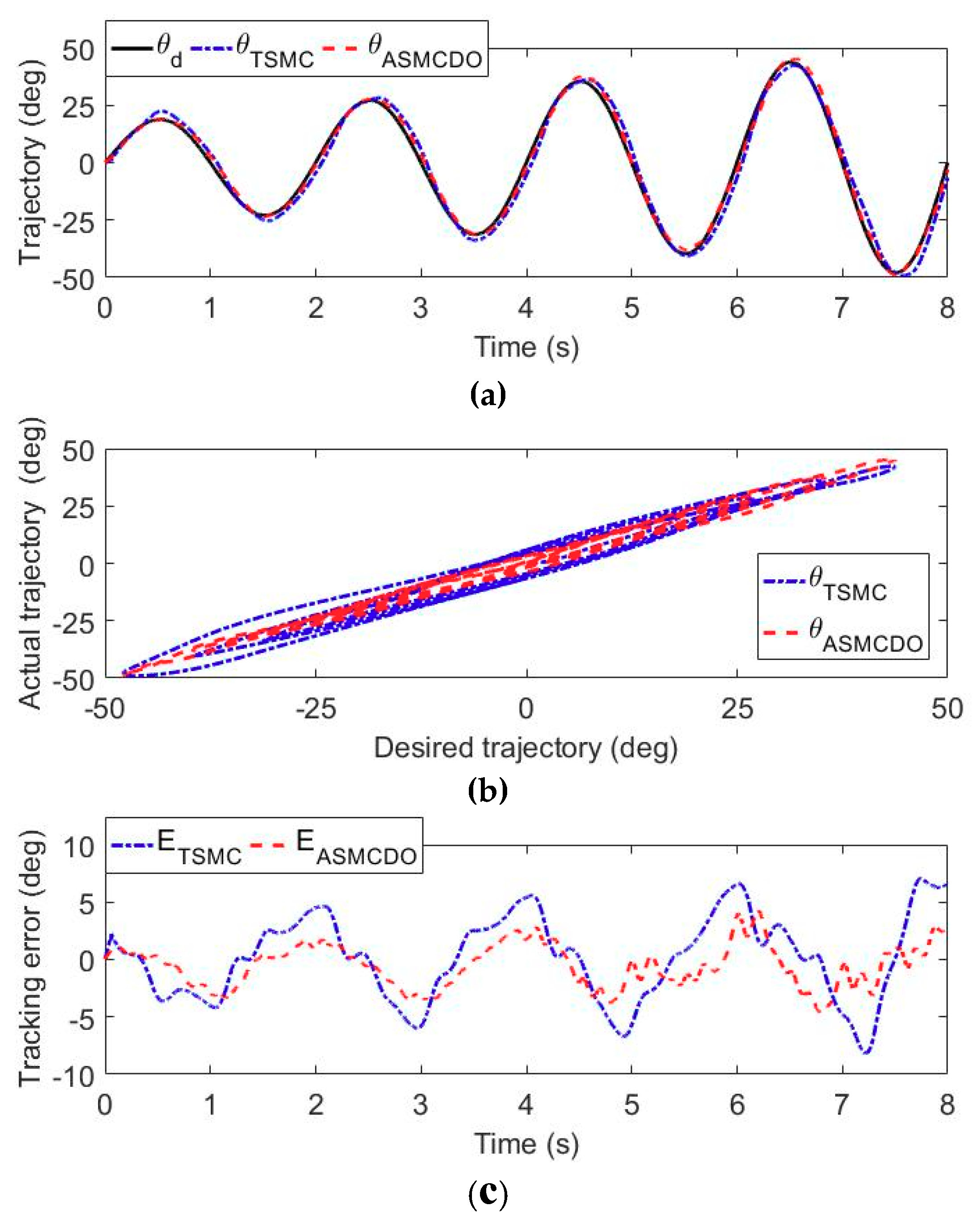
5.1. Trajectory Tracking Experiments
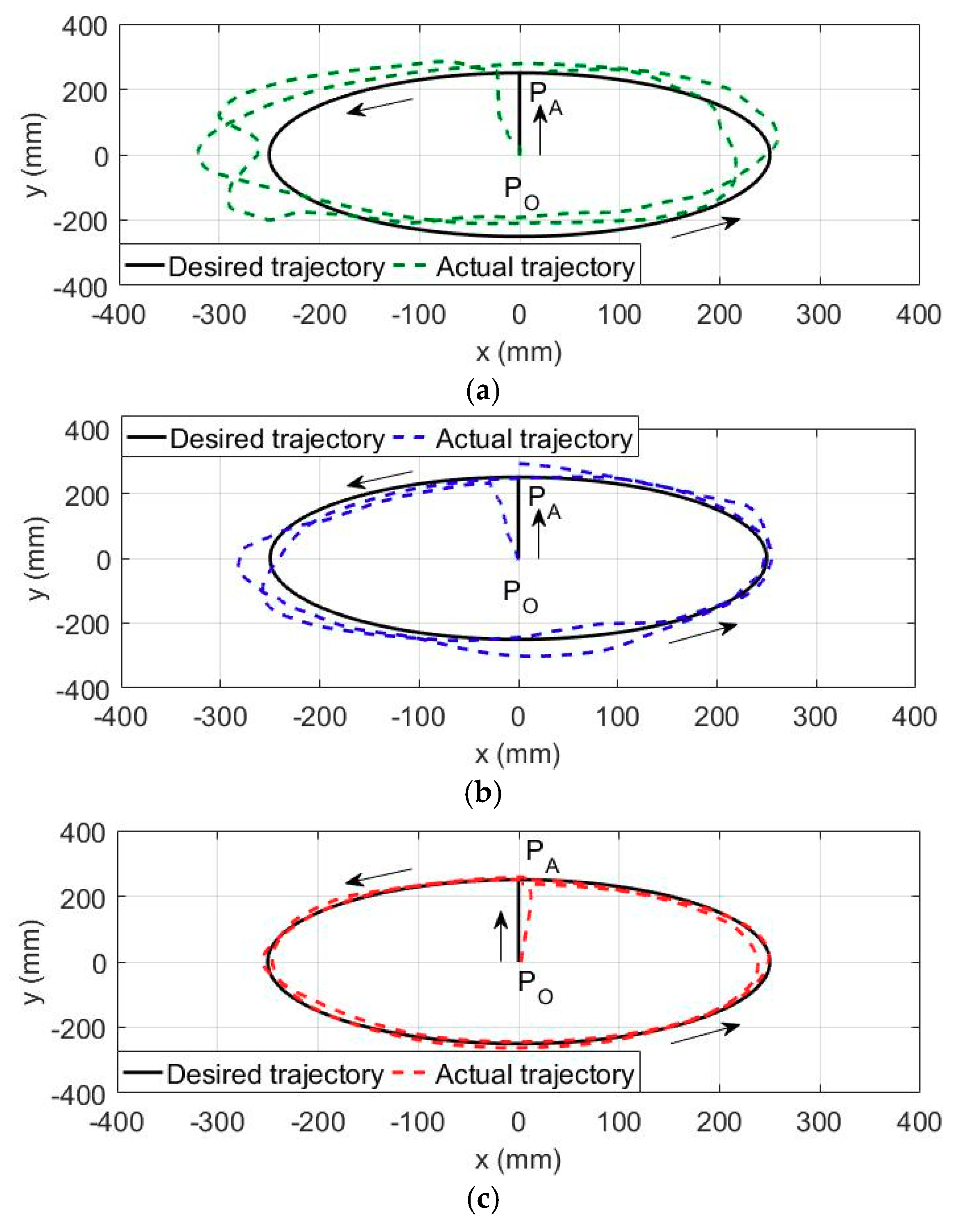
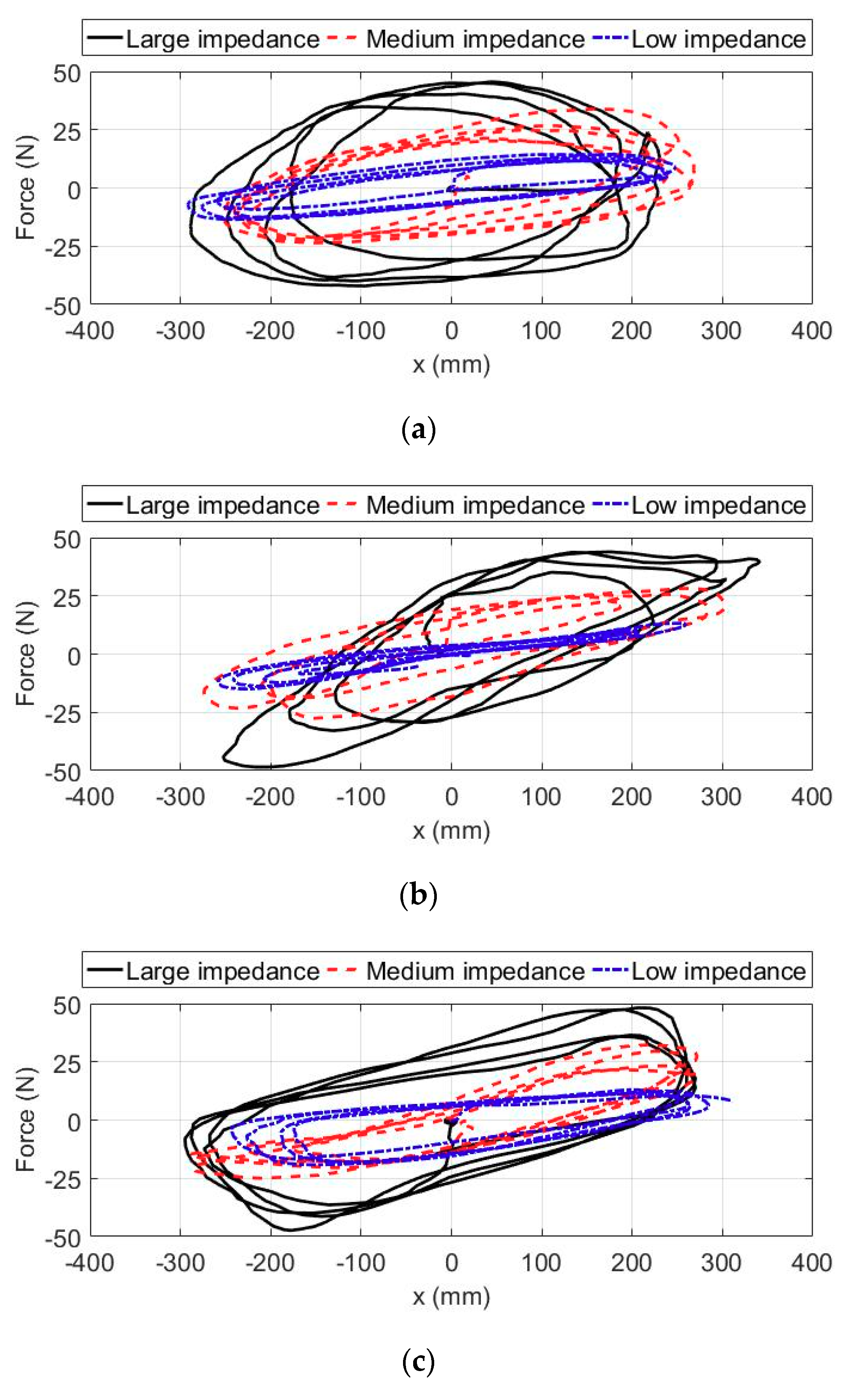
5.2. Trajectory Tracking Experiments with Impedance Adjustment
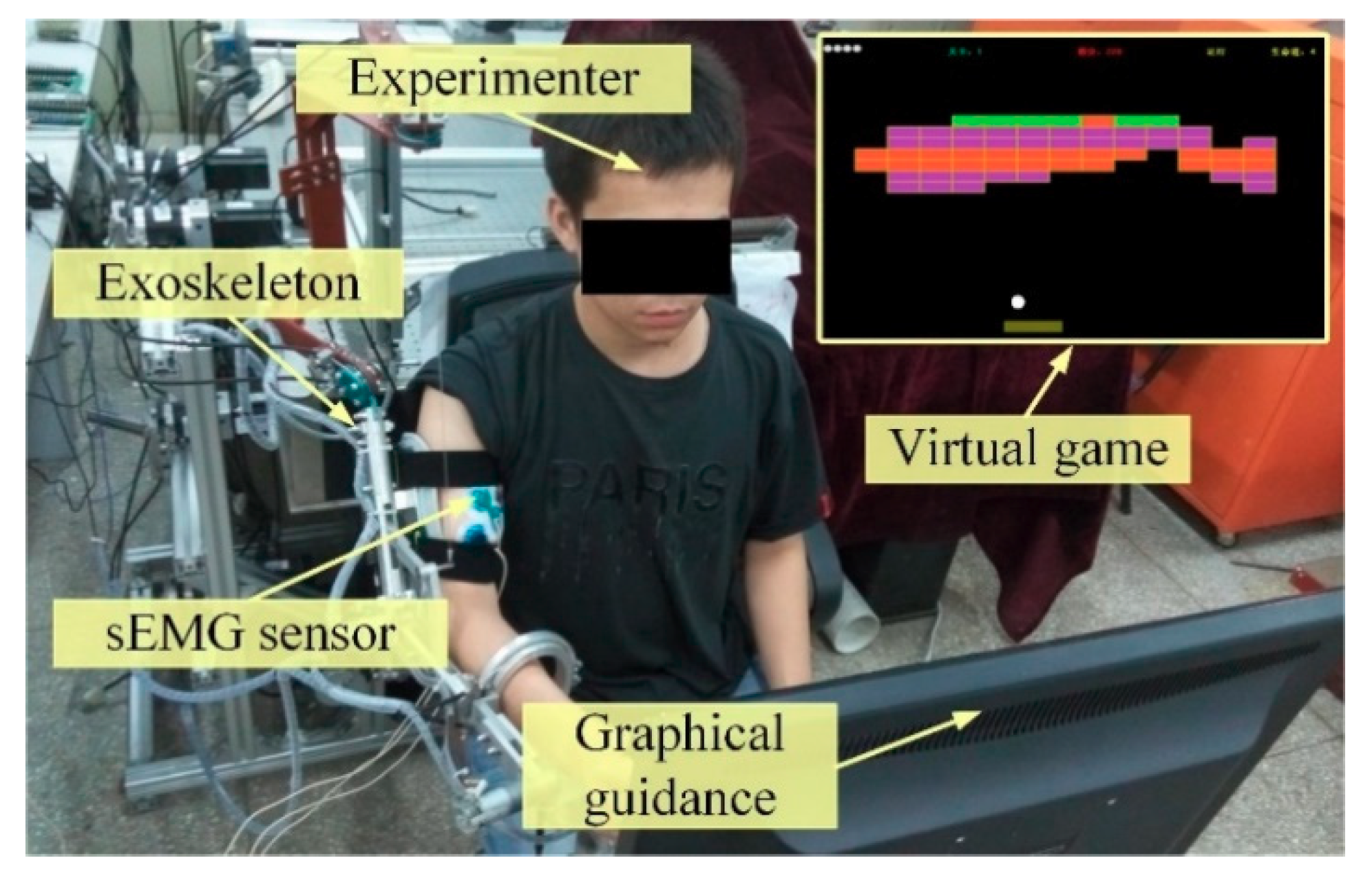
5.3. Intention-Based Training Experiments
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jackson, N.; Haxton, E.; Morrison, K.; Markey, E.; Andreoli, L.J.; Maloney, T.; Omelchenko, N.; Aroose, A.; Stevens, L.B. Reflections on 50 years of neuroscience nursing: the growth of stroke nursing. J. Neurosci. Nurs. 2018, 50, 188–192. [Google Scholar] [CrossRef] [PubMed]
- Ai, Q.; Zhu, C.; Zuo, J.; Meng, W.; Liu, Q.; Xie, S.Q.; Yang, M. Disturbance-estimated adaptive backstepping sliding mode control of a pneumatic muscles-driven ankle rehabilitation robot. Sensors 2018, 18, 66. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Deng, J.; Zha, F.; Qiu, S.; Wang, X.; Chen, F. Towards online estimation of human joint muscular torque with a lower limb exoskeleton robot. Appl. Sci. 2018, 8, 1610. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Chen, B.; Wu, H. Patient-active control of a powered exoskeleton targeting upper limb rehabilitation training. Front. Neurol. 2018, 9, 817. [Google Scholar] [CrossRef]
- Miller, C.L.; Torres, R.R.; Arno, H.A.; Julius, P. A wrist and finger force sensor module for use during movements of the upper limb in chronic hemiparetic stroke. IEEE Trans. Biomed. Eng. 2009, 56, 2312–2317. [Google Scholar] [CrossRef] [PubMed]
- Pedro, A.; Mata, V.; Díaz-Rodríguez, M.; Angel, V.; Alvaro, P. Design and kinematic analysis of a novel 3UPS/RPU parallel kinematic mechanism with 2T2R motion for knee diagnosis and rehabilitation tasks. J. Mech. Robot. 2017, 9. [Google Scholar] [CrossRef]
- Kang, X.K.; Chin, P.J.H.; Che, F.Y. Portable and reconfigurable wrist robot improves hand function for post-stroke subjects. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1864–1873. [Google Scholar]
- Ho, P.H.A.; Nguyen, N.S.; Cao, V.K. Adaptive neural compliant force-position control of serial PAM robot. J. Intell. Robot. Syst. 2018, 89, 351–369. [Google Scholar]
- Liu, Y.; Li, C.; Ji, L.; Bi, S.; Zhang, X.; Huo, J.F.; Ji, R. Development and implementation of an end-effector upper limb rehabilitation robot for hemiplegic patients with line and circle tracking training. J. Healthc. Eng. 2017, 2017, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.-K.; Washabaugh, E.P.; Gwozdziowski, A.; Remy, C.D.; Krishnan, C. A semi-passive planar manipulandum for upper-extremity rehabilitation. Ann. Biomed. Eng. 2018, 46, 1047–1065. [Google Scholar] [CrossRef] [PubMed]
- Cerasa, A.; Pignolo, L.; Gramigna, V.; Serra, S.; Olivadese, G.; Rocca, F.; Perrotta, P.; Dolce, G.; Quattrone, A.; Tonin, P. Exoskeleton-robot assisted therapy in stroke patients: a lesion mapping study. Front. Neuroinform. 2018, 12, 44. [Google Scholar] [CrossRef] [PubMed]
- Washabaugh, E.; Guo, J.; Chang, C.K.; Remy, D.; Krishnan, C. A portable passive rehabilitation robot for upper-extremity functional resistance training. IEEE Trans. Biomed. Eng. 2018. [Google Scholar] [CrossRef] [PubMed]
- Bertomeu-Motos, A.; Blanco, A.; Badesa, F.J.; Barios, J.A.; Zollo, L.; Garcia-Aracil, N. Human arm joints reconstruction algorithm in rehabilitation therapies assisted by end-effector robotic devices. J Neuroeng. Rehabil. 2018, 15, 10. [Google Scholar] [CrossRef] [PubMed]
- Keller, U.; van Hedel, H.; Klamroth-Marganska, V.; Riener, R. ChARMin: the first actuated exoskeleton robot for pediatric arm rehabilitation. IEEE/ASME Trans. Mechatron. 2016, 21, 2201–2213. [Google Scholar] [CrossRef]
- Simon, C.; Shaoping, B. Kinematic analysis and design of a novel shoulder exoskeleton using a double parallelogram linkage. J. Mech. Robot. 2018, 10, 041008. [Google Scholar]
- Crea, S.; Nann, M.; Trigili, E.; Cordella, F.; Baldoni, A.; Badesa, F. Feasibility and safety of shared EEG/EOG and vision-guided autonomous whole-arm exoskeleton control to perform activities of daily living. Sci. Rep. 2018, 8, 10823. [Google Scholar] [CrossRef] [PubMed]
- Cui, X.; Chen, W.; Jin, X.; Agrawal, S.K. Design of a 7-DOF cable-driven arm exoskeleton (CAREX-7) and a controller for dexterous motion training or assistance. IEEE-ASME Trans. Mech. 2017, 22, 161–172. [Google Scholar] [CrossRef]
- Huang, J.; Tu, X.; He, J. Design and evaluation of the RUPERT wearable upper extremity exoskeleton robot for clinical and in-home therapies. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 926–935. [Google Scholar] [CrossRef]
- Riani, A.; Madani, T.; Benallegue, A. A daptive integral terminal sliding mode control for upper-limb rehabilitation exoskeleton. Control Eng. Pract. 2018, 75, 108–117. [Google Scholar] [CrossRef]
- Wu, W.; Fong, J.P; Crocher, V.; Lee, P.; Oetomo, D.; Tan, Y.; Ackland, D. Modulation of shoulder muscle and joint function using a powered upper-limb exoskeleton. J. Biomech. 2018, 72, 7–16. [Google Scholar] [CrossRef] [PubMed]
- Ekelem, A.; Goldfarb, M. Supplemental stimulation improves swing phase kinematics during exoskeleton assisted gait of SCI subjects with severe muscle spasticity. Front. Neurosci. 2018, 12, 374. [Google Scholar] [CrossRef] [PubMed]
- Brahim, B.; Saad, M.; Luna, C.O.; Rahman, M.H.; Brahmi, A. Adaptive tracking control of an exoskeleton robot with uncertain dynamics based on estimated time delay control. IEEE-ASME Trans. Mech. 2018, 23, 575–585. [Google Scholar] [CrossRef]
- Yu, W.; Rosen, J. Neural PID control of robot manipulators with application to an upper limb exoskeleton. IEEE Trans. Cybern. 2013, 43, 673–684. [Google Scholar] [PubMed]
- Jiang, X.Z.; Huang, X.H.; Xiong, C.H.; Sun, R.H.; Xiong, Y.L. Position control of a rehabilitation robotic joint based on neuron proportion-integral and feedforward control. J. Comput. Nonlinear Dyn. 2012, 7, 024502. [Google Scholar] [CrossRef]
- Han, S.; Wang, H.; Tian, Y. Model-free based adaptive nonsingular fast terminal sliding mode control with time-delay estimation for a 12 DOF multi-functional lower limb exoskeleton. Adv. Eng. Softw. 2018, 119, 38–47. [Google Scholar] [CrossRef]
- Ziting, C.; Zhijun, L.; Philip, C. Disturbance observer-based fuzzy control of uncertain MIMO mechanical systems with input nonlinearities and its application to robotic exoskeleton. IEEE Trans. Cybern. 2017, 47, 984–994. [Google Scholar]
- Wu, Q.; Wang, X.; Chen, B.; Wu, H. Development of an RBFN-based neural-fuzzy adaptive control strategy for an upper limb rehabilitation exoskeleton. Mechatronics 2018, 53, 85–94. [Google Scholar] [CrossRef]
- Khanh, D.B.; Xiloyannis, M.; Cappello, L.; Chris, W.A.; Shih-Cheng, Y.; Lorenzo, M. Adaptive backlash compensation in upper limb soft wearable exoskeletons. Robot. Autom. Syst. 2017, 92, 173–186. [Google Scholar]
- Pehlivan, A.U.; Losey, D.P.; O’Malley, M.K. Minimal assist-as-needed controller for upper limb robotic rehabilitation. IEEE Trans. Robot. 2016, 32, 113–124. [Google Scholar] [CrossRef]
- Lu, Z.; Chen, X.; Tong, K.Y. Real-time control of an exoskeleton hand robot with myoelectric pattern recognition. Int. J. Neural. Syst. 2017, 5, 1750009. [Google Scholar] [CrossRef] [PubMed]
- Teramae, T.; Noda, T.; Morimoto, J. EMG-Based model predictive control for physical human-robot interaction: application for assist-as-needed control. IEEE Robot. Autom. Lett. 2017, 3, 210–217. [Google Scholar] [CrossRef]
- Pehlivan, A.U.; Sergi, F.; O'Malley, M.K. A Subject-adaptive controller for wrist robotic rehabilitation. IEEE/ASME Trans. Mechatron. 2015, 20, 1338–1350. [Google Scholar] [CrossRef]
- Ayas, M.S.; Altas, I.H. Fuzzy logic based adaptive admittance control of a redundantly actuated ankle rehabilitation robot. Control Eng. Pract. 2017, 59, 44–54. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Chen, B.; Wu, H. Development of a minimal-intervention-based admittance control strategy for upper extremity rehabilitation exoskeleton. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1005–1016. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Chen, L.; Du, F. Transmission model and compensation control of double-tendon-sheath actuation system. IEEE Trans. Ind. Electron. 2015, 62, 1599–1609. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Du, F. Development and analysis of a gravity-balanced exoskeleton for active rehabilitation training of upper limb. Proc. Inst. Mech. Eng. C-J. Mech. 2016, 230, 3777–3790. [Google Scholar] [CrossRef]
- Lee, H.D.; Lee, B.K.; Kim, W.S.; Han, J.S.; Shin, K.S.; Han, C.S. Human robot cooperation control based on a dynamic model of an upper limb exoskeleton for human power amplification. Mechatronics 2014, 24, 168–176. [Google Scholar] [CrossRef]
- Ming-Shaung, J.; Lin, C.; Dong, H.L.; Hwang, I.S.; Chen, S.M. A rehabilitation robot with force-position hybrid fuzzy controller: hybrid fuzzy control of rehabilitation robot. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 349–358. [Google Scholar]
- Wu, Q.; Wang, X.; Chen, B.; Wu, H. Development and hybrid force/position control of a compliant rescue manipulator. Mechatronics 2017, 46, 143–153. [Google Scholar] [CrossRef]
- Su, J.; Chen, W.H.; Li, B. High order disturbance observer design for linear and nonlinear systems. In Proceedings of the 2015 IEEE International Conference on Information and Automation (ICIA), Lijiang, China, 8–10 August 2015; pp. 1893–1898. [Google Scholar]
- Chen, W. Disturbance observer based control for nonlinear systems. IEEE/ASME Trans. Mechatron. 2004, 9, 706–710. [Google Scholar] [CrossRef]
- Oscar, B.; Patxi, A. Position control of the induction motor using an adaptive sliding-mode controller and observers. IEEE Trans. Ind. Electron. 2014, 61, 6556–6565. [Google Scholar]
- He, W.; Dong, Y.; Sun, C. Adaptive neural impedance control of a robotic manipulator with input saturation. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 334–343. [Google Scholar] [CrossRef]
- Wu, Q.; Wang, X.; Du, F. Analytical inverse kinematic resolution of a redundant exoskeleton for upper-limb rehabilitation. Int. J. Hum. Robot. 2016, 13, 1550042. [Google Scholar] [CrossRef]
- Zolotas, A.; Hassan, F.; Smith, T. Optimized Ziegler-Nichols based PID control design for tilt suspensions. J. Eng. Sci. Technol. Rev. 2017, 10, 17–24. [Google Scholar]
- Tang, Y. Terminal sliding mode control for rigid robots. Automatica 1998, 34, 51–56. [Google Scholar] [CrossRef]
| Link i | θi/Home (deg) | Mass (kg) | Link Length (mm) | Inertia (kg·m2·10−3) | ROM (deg) |
|---|---|---|---|---|---|
| 1 | θ1/180 | 1.48 | 300 | 58.1 | 150~240 |
| 2 | θ2/−60 | 0.71 | 185 | 16.6 | −180~−45 |
| 3 | θ3/−90 | 1.25 | 320~380 | 75.9~77.6 | −120~30 |
| 4 | θ4/−90 | 0.79 | 156 | 13.5 | −180~−30 |
| 5 | θ5/0 | 0.31 | 108.5~148.5 | 2.26~2.45 | −85~60 |
| 6 | θ6/90 | 0.09 | 100 | 0.72 | 80~120 |
| 7 | θ7/0 | 0.42 | 95.5 | 1.63 | −30~60 |
| Joint | Coulomb Coefficient (N·m) | Viscous Coefficient (N·m·s/deg) | RMSE (N·m) |
|---|---|---|---|
| Shoulder internal/external | 2.81 | 0.041 | 0.32 |
| Shoulder abduction/adduction | 4.95 | 0.021 | 0.78 |
| Shoulder flexion/extension | 3.86 | 0.035 | 0.62 |
| Elbow flexion/extension | 4.10 | 0.020 | 0.42 |
| Forearm pronation/supination | 2.52 | 0.018 | 0.49 |
| Wrist flexion/extension | 0.21 | 0.002 | - |
| Wrist ulnal/radial deviation | 0.21 | 0.002 | - |
| Subject | Controller | Shoulder Flexion/Extension | Elbow Flexion/Extension | Forearm Pronation/Supination | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAXE (°) | RMSE (°) | MAE (°) | MAXE (°) | RMSE (°) | MAE (°) | MAXE (°) | RMSE (°) | MAE (°) | ||
| S1 | TSMC | 7.61 | 3.37 | 2.88 | 7.09 | 3.30 | 2.81 | 8.17 | 3.63 | 2.99 |
| ASMCDO | 3.56 | 1.42 | 1.16 | 4.11 | 1.72 | 1.43 | 4.60 | 1.96 | 1.61 | |
| S2 | TSMC | 7.82 | 3.41 | 2.95 | 7.57 | 3.83 | 3.01 | 8.23 | 3.69 | 3.23 |
| ASMCDO | 3.65 | 1.56 | 1.33 | 4.35 | 2.10 | 1.69 | 4.72 | 2.07 | 1.72 | |
| S3 | TSMC | 8.05 | 3.92 | 3.02 | 7.63 | 3.79 | 3.22 | 8.61 | 3.87 | 3.36 |
| ASMCDO | 3.74 | 1.59 | 1.37 | 4.58 | 2.23 | 1.81 | 4.83 | 2.23 | 1.79 | |
| Experimental Condition | Impedance Parameters | Subject | MAXE (mm) | RMSE (mm) | MAE (mm) | ||
|---|---|---|---|---|---|---|---|
| Md (N·s2/mm) | Bd (N·s/mm) | Kd (N/mm) | |||||
| Low impedance | diag [0.015, 0.015, 0.015] | diag [0.015, 0.015, 0.015] | diag [0.015, 0.015, 0.015] | S1 | 82.79 | 44.23 | 39.71 |
| S2 | 88.65 | 46.96 | 41.77 | ||||
| S3 | 87.34 | 47.03 | 43.31 | ||||
| Medium impedance | diag [0.035, 0.035, 0.035] | diag [0.035, 0.035, 0.035] | diag [0.035, 0.035, 0.035] | S1 | 51.75 | 29.01 | 25.36 |
| S2 | 49.22 | 28.34 | 23.39 | ||||
| S3 | 53.98 | 31.73 | 27.50 | ||||
| Large impedance | diag [0.065, 0.065, 0.065] | diag [0.065, 0.065, 0.065] | diag [0.065, 0.065, 0.065] | S1 | 16.64 | 10.41 | 9.57 |
| S2 | 17.76 | 12.34 | 10.69 | ||||
| S3 | 18.05 | 14.25 | 11.43 | ||||
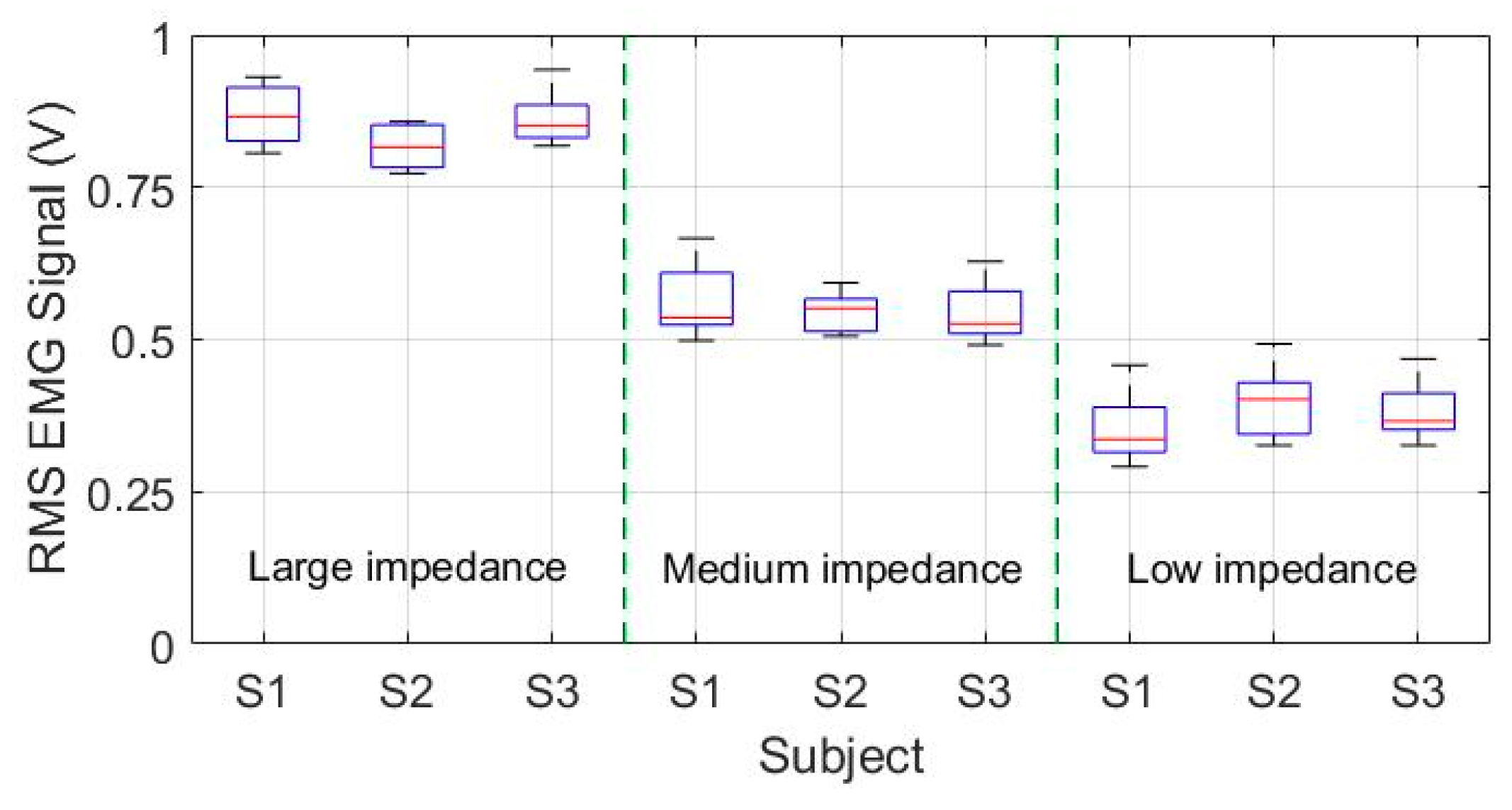
| Experimental Condition | RMS EMG Values of Different Subjects (V) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | |||||||
| Max 1 | Med 2 | Min 3 | Max | Med | Min | Max | Med | Min | |
| Large impedance | 0.931 | 0.856 | 0.803 | 0.859 | 0.815 | 0.773 | 0.943 | 0.849 | 0.818 |
| Medium impedance | 0.663 | 0.535 | 0.498 | 0.593 | 0.551 | 0.506 | 0.628 | 0.525 | 0.493 |
| Low impedance | 0.457 | 0.336 | 0.291 | 0.497 | 0.402 | 0.323 | 0.467 | 0.369 | 0.325 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Wu, H. Development, Dynamic Modeling, and Multi-Modal Control of a Therapeutic Exoskeleton for Upper Limb Rehabilitation Training. Sensors 2018, 18, 3611. https://doi.org/10.3390/s18113611
Wu Q, Wu H. Development, Dynamic Modeling, and Multi-Modal Control of a Therapeutic Exoskeleton for Upper Limb Rehabilitation Training. Sensors. 2018; 18(11):3611. https://doi.org/10.3390/s18113611
Chicago/Turabian StyleWu, Qingcong, and Hongtao Wu. 2018. "Development, Dynamic Modeling, and Multi-Modal Control of a Therapeutic Exoskeleton for Upper Limb Rehabilitation Training" Sensors 18, no. 11: 3611. https://doi.org/10.3390/s18113611
APA StyleWu, Q., & Wu, H. (2018). Development, Dynamic Modeling, and Multi-Modal Control of a Therapeutic Exoskeleton for Upper Limb Rehabilitation Training. Sensors, 18(11), 3611. https://doi.org/10.3390/s18113611





