Terahertz Imaging of Thin Film Layers with Matched Field Processing
Abstract
:1. Introduction
1.1. Matched Field Processing (MFP)
1.2. Applying MFP Techniques to THz Tomography
2. Methodology
2.1. Conventional THz TOF Processing
2.2. Mathematical Model for Terahertz Measurement Data
2.3. Generating THz Replica Spectra
2.4. Sample Covariance Matrix
2.5. Objective Functions
2.5.1. Bartlett Processor
2.5.2. Minimum Variance (MV) Processor
2.6. Ambiguity Surfaces
2.7. Accuracy Limitations
3. Results
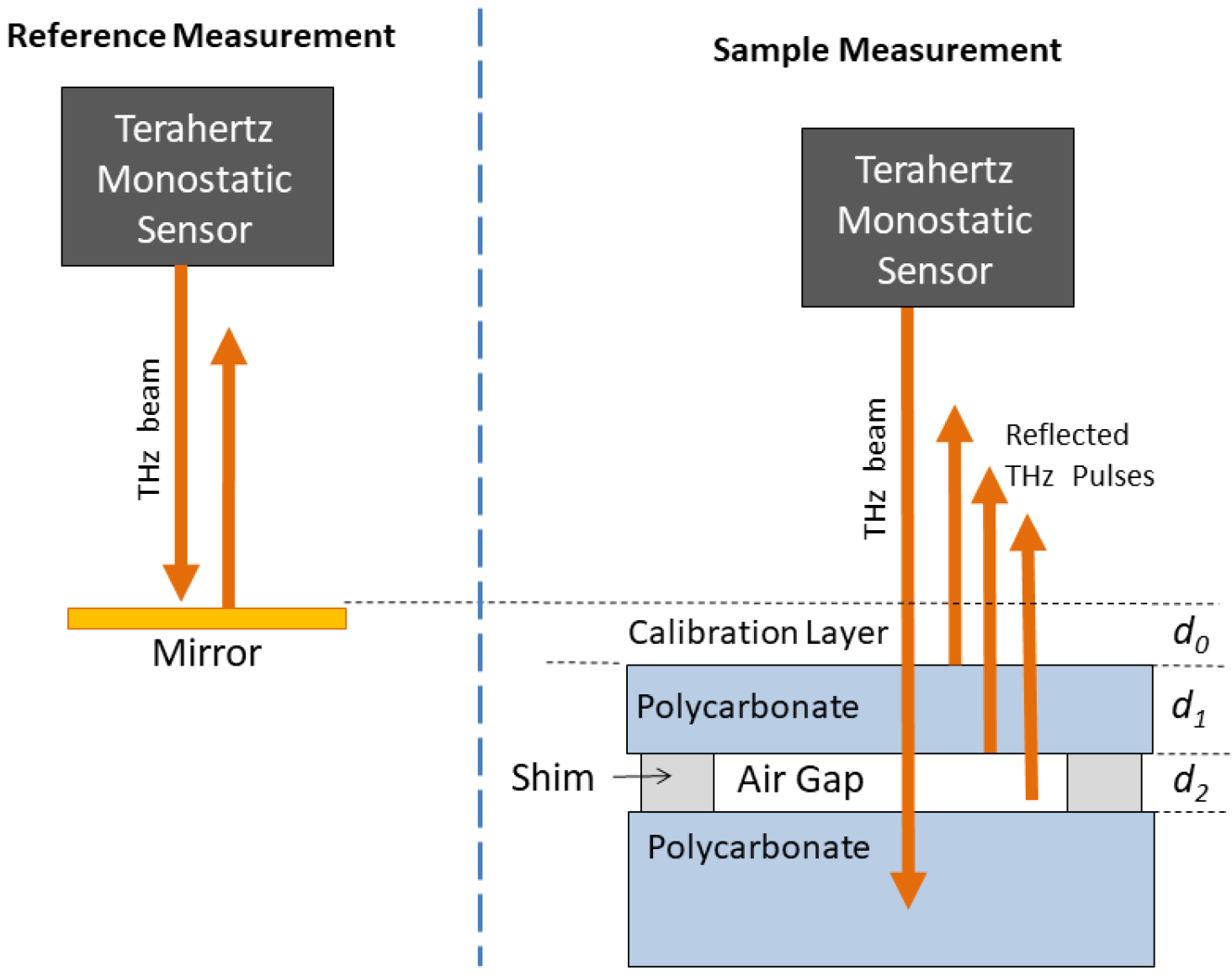
3.1. Terahertz Measurement System
3.2. Layered Media Samples
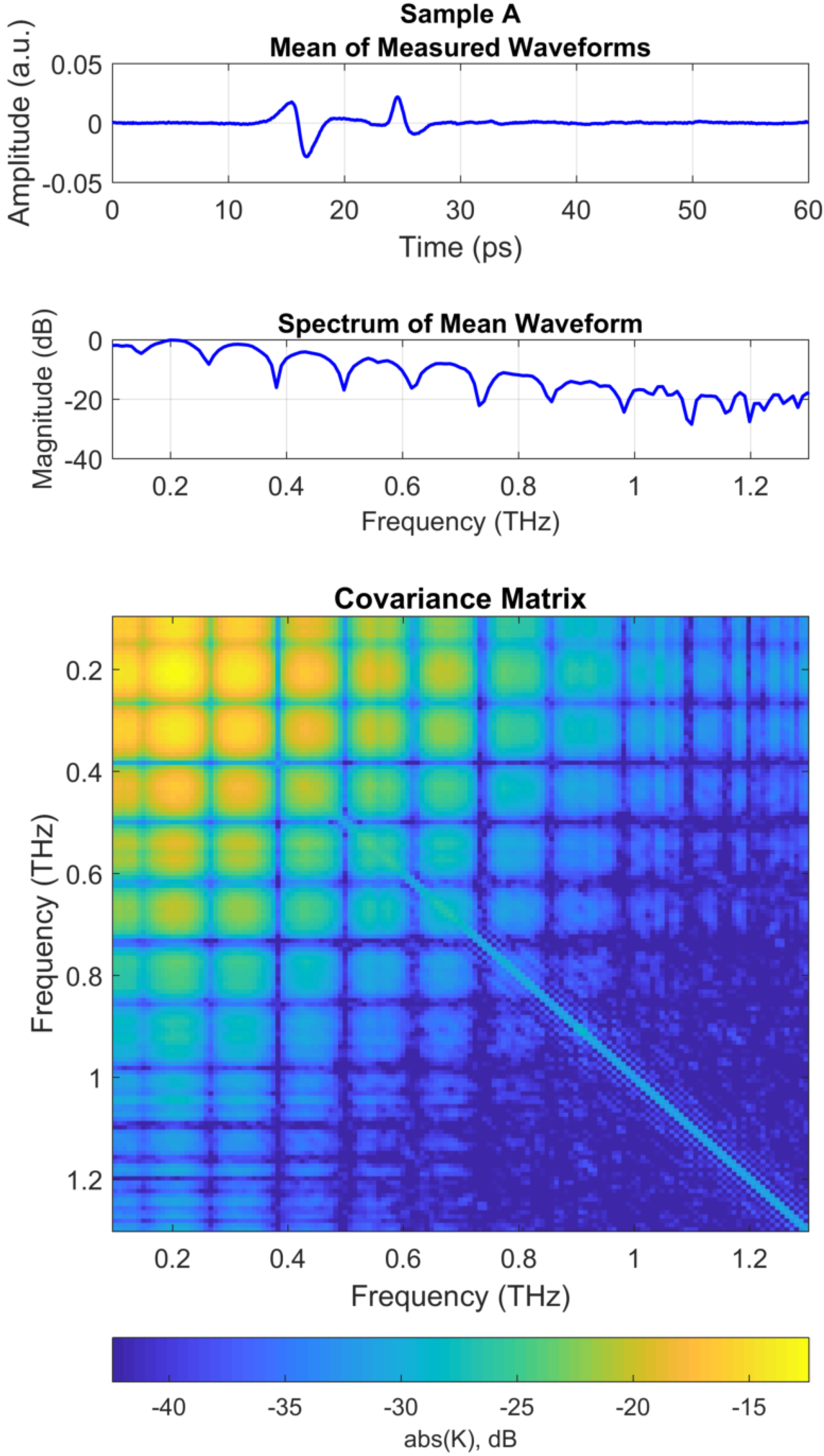
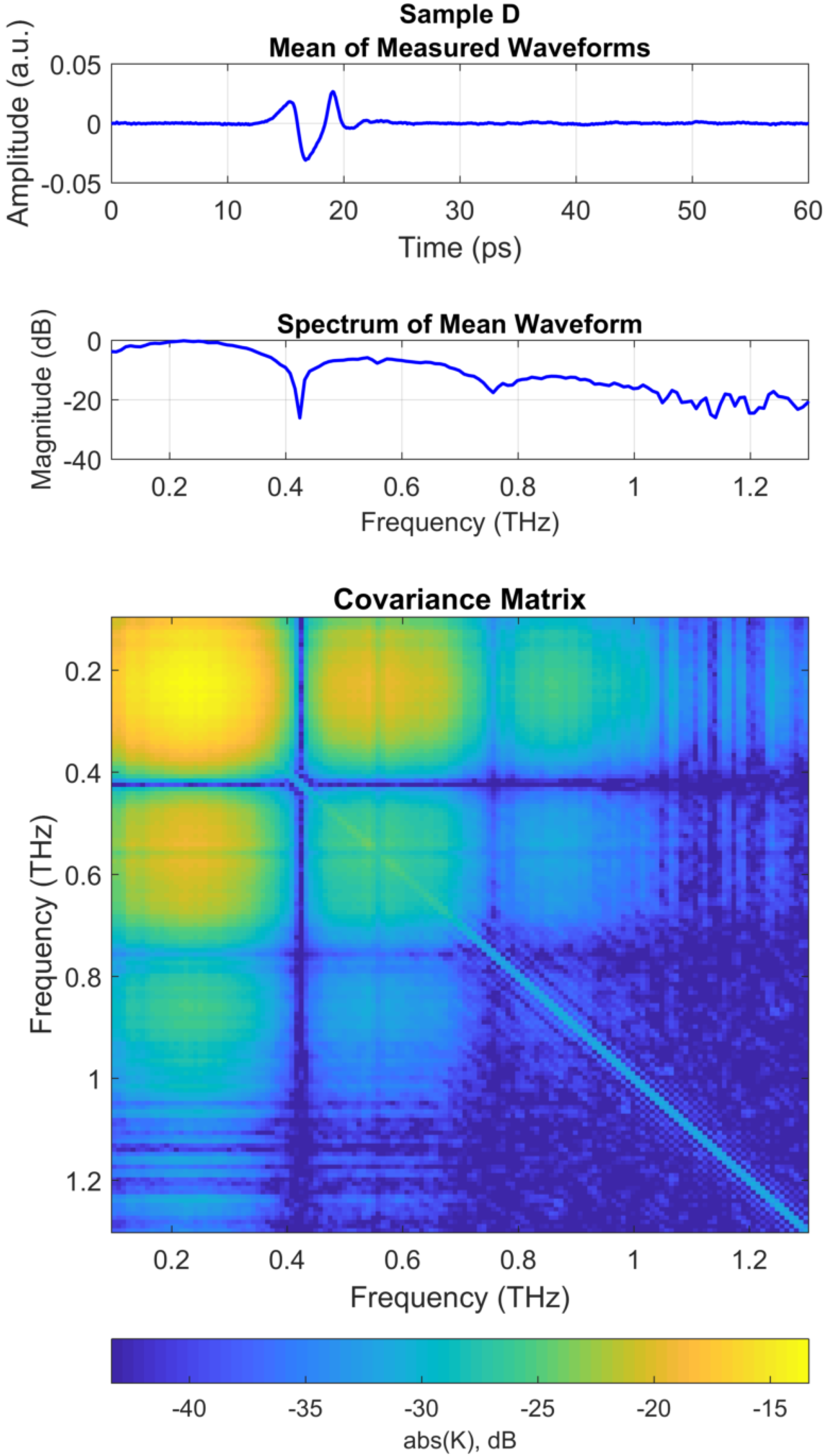
3.3. Measurement Data Processing
3.4. Generating Replica Spectra
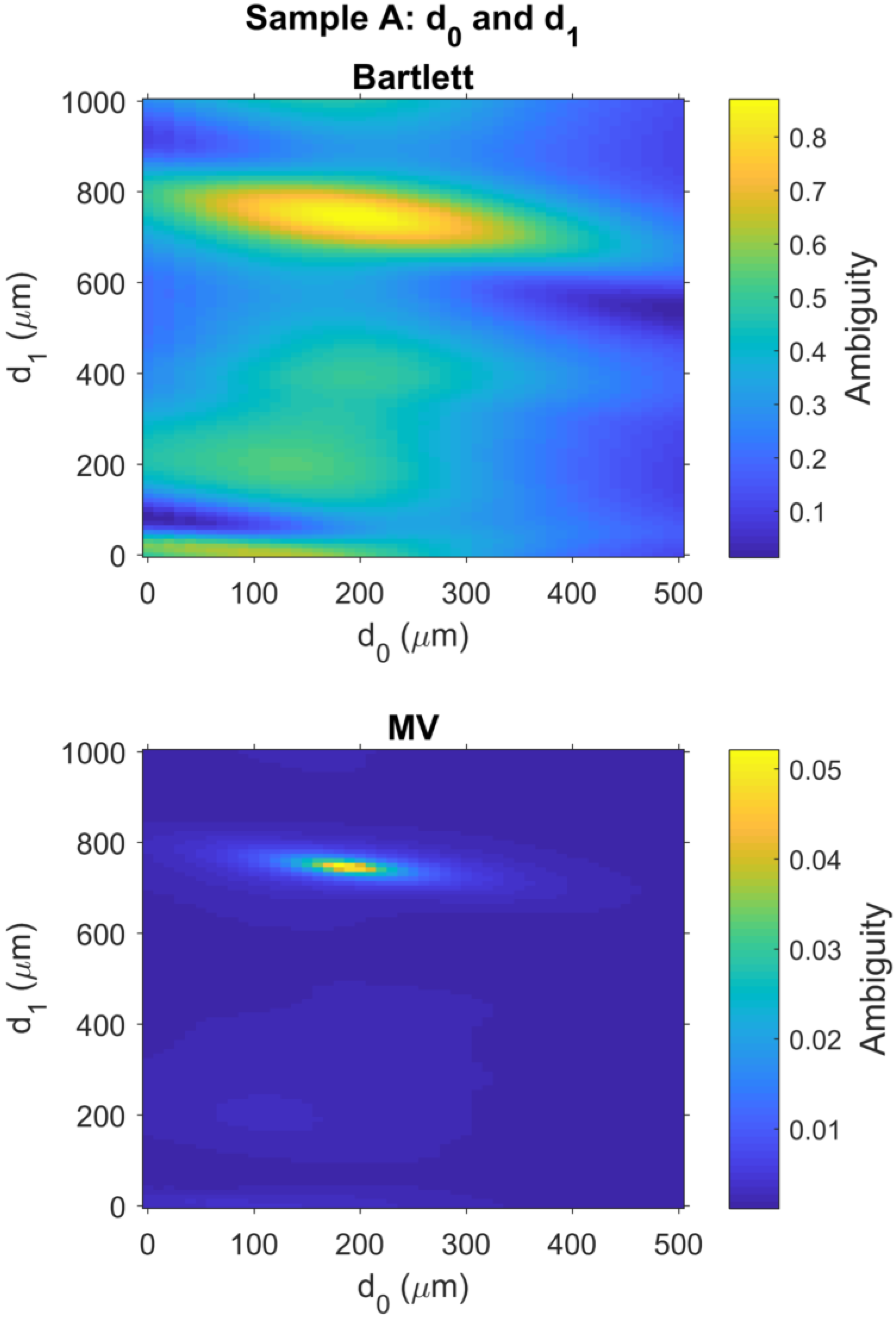
3.5. THz MFP Results for Sample A
3.6. THz MFP Results for Sample D
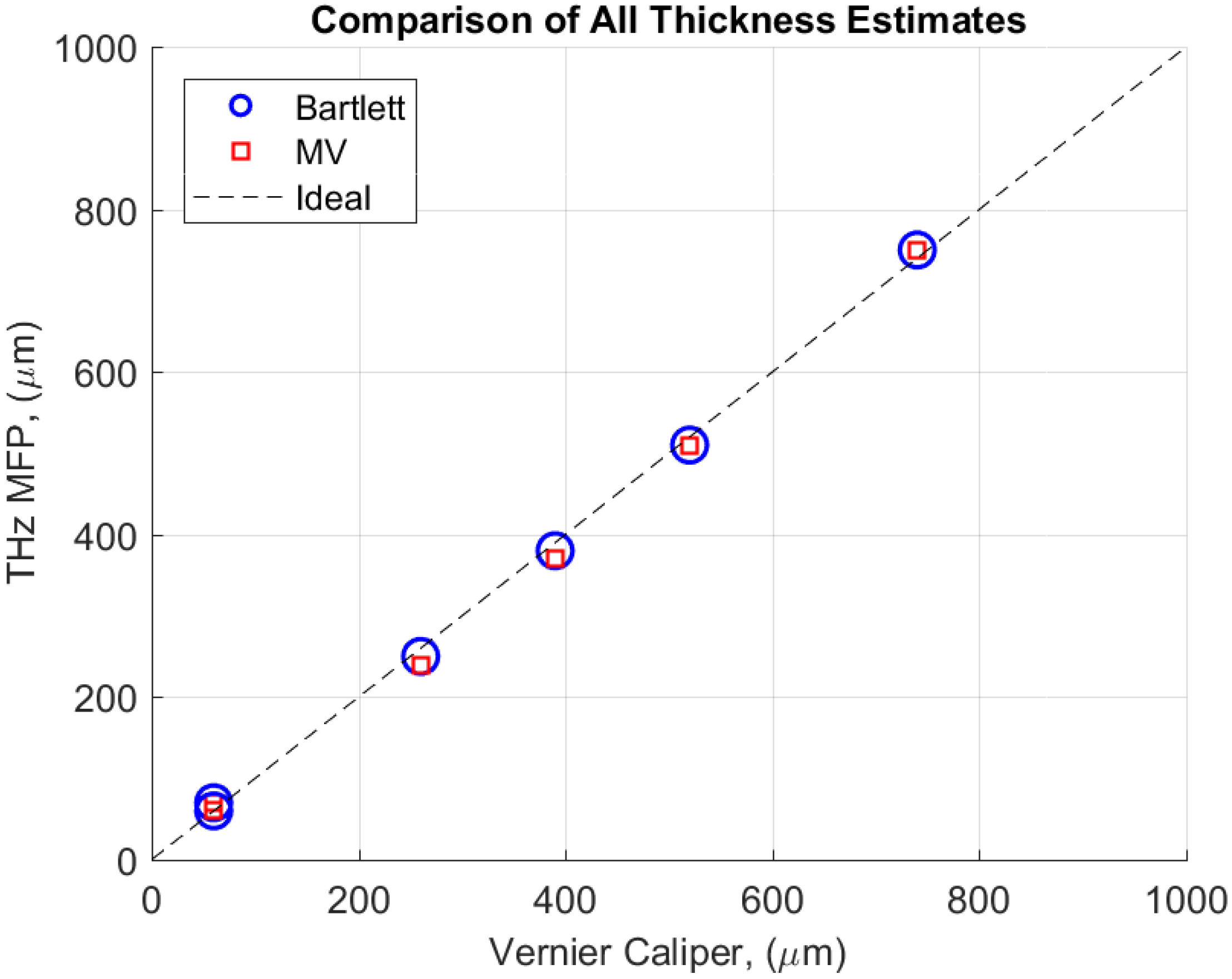
3.7. Error Analysis for All THz MFP Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Propagation within Layered Media
References
- Jansen, C.; Wietzke, S.; Peters, O.; Scheller, M.; Vieweg, N.; Salhi, M.; Krumbholz, N.; Jordens, C.; Hochrein, T.; Koch, M. Terahertz imaging: Applications and perspectives. Appl. Opt. 2010, 49, E48–E57. [Google Scholar] [CrossRef] [PubMed]
- Peiponen, K.E.; Zeitler, A.; Kuwata-Gonokami, M. Terahertz Spectroscopy and Imaging; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Shen, Y.C.; Taday, P.F.; Newnham, D.A.; Kemp, M.C.; Pepper, M. 3D Chemical Mapping Using Terahertz Pulsed Imaging; SPIE: San Jose, CA, USA, 2005; Volume 5727, pp. 24–31. [Google Scholar]
- Zeitler, J.A.; Shen, Y.; Baker, C.; Taday, P.F.; Pepper, M.; Rades, T. Analysis of coating structures and interfaces in solid oral dosage forms by three dimensional terahertz pulsed imaging. J. Pharm. Sci. 2007, 96, 330–340. [Google Scholar] [CrossRef] [PubMed]
- Zeitler, J.A.; Gladden, L.F. In-vitro tomography and non-destructive imaging at depth of pharmaceutical solid dosage forms. Eur. J. Pharm. Biopharm. 2009, 71, 2–22. [Google Scholar] [CrossRef] [PubMed]
- TeraView Limited. Using 3-Dimensional Terahertz Pulsed Imaging to Analyse Automotive Coatings; Technical Report; TeraView Limited: Cambridge, UK, 2013. [Google Scholar]
- Teraview. TeraCota-Terahertz Coating Thickness Analysis. Available online: http://www.teraview.com/products/TeraCota/index.html (accessed on 16 October 2018).
- Ellrich, F.; Klier, J.; Weber, S.; Jonuscheit, J.; von Freymann, G. Terahertz time-domain technology for thickness determination of industrial relevant multi-layer coatings. In Proceedings of the 2016 41st International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Copenhagen, Denmark, 25–30 September 2016. [Google Scholar]
- Zimdars, D.; Duling, I.; Fichter, G.; White, J. Production Process Monitoring of Multilayered Materials Using Timedomain Terahertz Gauges. AIP Conf. Proc. 2010, 29, 564–571. [Google Scholar] [CrossRef]
- Zimdars, D.; Fichter, G.; Megdanoff, C.; Murdock, M.; Duling, I.; White, J.; Williamson, S.L. Portable video rate time domain terahertz line imager for security and aerospace non destructive examination. In Proceedings of the Terahertz Physics, Devices, and Systems IV: Advanced Applications in Industry and Defense, Orlando, FL, USA, 26 April 2010; Volume 7671. [Google Scholar] [CrossRef]
- Palka, N.; Krimi, S.; Ospald, F.; Beigang, R.; Miedzinska, D. Transfer matrix method for precise determination of thicknesses in a 150-ply polyethylene composite material. In Proceedings of the 2015 40th International Conference on Infrared, Millimeter, and Terahertz Waves (IRMMW-THz), Hong Kong, China, 23–28 August 2015; pp. 1–2. [Google Scholar]
- Schecklman, S.; Kniffin, G.; Zurk, L. Terahertz Non-destructive Evaluation of Layered Media with the Maximum Likelihood Estimator. In Proceedings of the 2014 International Symposium on Optomechatronic Technologies, Seattle, WA, USA, 5–7 November 2014; pp. 81–85. [Google Scholar]
- O’Hara, J.; Withayachumnankul, W.; Al-Naib, I. A Review on Thin-film Sensing with Terahertz Waves. J. Infrared Millim. Terahertz Waves 2012, 33, 245–291. [Google Scholar] [CrossRef]
- Zimdars, D.; White, J.; Fichter, G.; Chernovsky, A.; Williamson, S.L. Quantitative Measurement of Laminar Material Properties and Structure Using Time Domain Reflection Imaging; SPIE: Orlando, FL, USA, 2008; Volume 6949. [Google Scholar] [CrossRef]
- Su, K.; Shen, Y.C.; Zeitler, J. Terahertz Sensor for Non-Contact Thickness and Quality Measurement of Automobile Paints of Varying Complexity. IEEE Trans. Terahertz Sci. Technol. 2014, 4, 432–439. [Google Scholar] [CrossRef]
- van Mechelen, J.L.M.; Kuzmenko, A.B.; Merbold, H. Stratified dispersive model for material characterization using terahertz time-domain spectroscopy. Opt. Lett. 2014, 39, 3853–3856. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Jha, A.; Akhtar, M. A contactless thickness measurement of multilayer structure using terahertz time domain spectroscopy. In Proceedings of the 2015 IEEE Conference on Antenna Measurements & Applications (CAMA), Chiang Mai, Thailand, 30 November–2 December 2015; pp. 1–4. [Google Scholar]
- Krimi, S.; Klier, J.; Jonuscheit, J.; von Freymann, G.; Urbansky, R.; Beigang, R. Highly accurate thickness measurement of multi-layered automotive paints using terahertz technology. Appl. Phys. Lett. 2016, 109, 021105. [Google Scholar] [CrossRef]
- Krimi, S.; Klier, J.; Jonuscheit, J.; von Freymann, G.; Urbansky, R.; Beigang, R. Self-calibrating approach for terahertz thickness measurements of ceramic coatings. In Proceedings of the 2016 41st International Conference on Infrared, Millimeter, and Terahertz waves (IRMMW-THz), Copenhagen, Denmark, 25–30 September 2016; pp. 1–2. [Google Scholar]
- Baggeroer, A.; Kuperman, W.; Mikhalevsky, P. An overview of matched field methods in ocean acoustics. IEEE J. Ocean. Eng. 1993, 18, 401–424. [Google Scholar] [CrossRef]
- Tolstoy, A. Matched Field Processing for Underwater Acoustics; World Scientific Publishing Company: Singapore, 1993. [Google Scholar]
- Jensen, F.B.; Kuperman, W.A.; Porter, M.B.; Schmidt, H. Computational Ocean Acoustics (Modern Acoustics and Signal Processing), 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Tolstoy, A.; Diachok, O.; Frazer, L.N. Acoustic tomography via matched field processing. J. Acoust. Soc. Am. 1991, 89, 1119–1127. [Google Scholar] [CrossRef]
- Bucker, H. Use of calculated sound fields and matched-field detection to locate sound sources in shallow water. J. Acoust. Soc. Am. 1976, 59, 368–373. [Google Scholar] [CrossRef]
- Gingras, D.; Gerstoft, P.; Gerr, N. Electromagnetic matched-field processing: Basic concepts and tropospheric simulations. IEEE Trans. Antennas Propag. 1997, 45, 1536–1545. [Google Scholar] [CrossRef]
- Michalopoulou, Z.H.; Porter, M. Matched-field processing for broad-band source localization. IEEE J. Ocean. Eng. 1996, 21, 384–392. [Google Scholar] [CrossRef]
- Michalopoulou, Z.H. Robust multi-tonal matched-field inversion: A coherent approach. J. Acoust. Soc. Am. 1998, 104, 163–170. [Google Scholar] [CrossRef]
- Siderius, M.; Gerstoft, P.; Nielsen, P. Broadband Geoacoustic Inversion From Sparse Data Using Genetic Algorithms. J. Comput. Acoust. 1998, 6, 117–134. [Google Scholar] [CrossRef]
- Dosso, S.E.; Wilmut, M.J. Maximum-likelihood and other processors for incoherent and coherent matched-field localization. J. Acoust. Soc. Am. 2012, 132, 2273–2285. [Google Scholar] [CrossRef] [PubMed]
- Zurk, L.; Henry, S.; Schecklman, S. Terahertz spectral imaging using correlation processing. In Proceedings of the 2012 37th International Conference on Infrared, Millimeter, and Terahertz Waves, Wollongong, NSW, Australia, 23–28 September 2012; pp. 1–2. [Google Scholar]
- Henry, S.C.; Zurk, L.M.; Schecklman, S.; Duncan, D.D. Three-dimensional broadband terahertz synthetic aperture imaging. Opt. Eng. 2012, 51, 091603. [Google Scholar] [CrossRef]
- Henry, S.; Zurk, L.; Schecklman, S. Terahertz Spectral Imaging Using Correlation Processing. IEEE Trans. Terahertz Sci. Technol. 2013, 3, 486–493. [Google Scholar] [CrossRef]
- Kniffin, G.; Zurk, L.M. Parabolic Equation Methods for Terahertz 3-D Synthetic Aperture Imaging. IEEE Trans. Terahertz Sci. Technol. 2016, 6, 784–792. [Google Scholar] [CrossRef]
- Hecht, E. Optics, 4th ed.; Addison-Wesley: Boston, MA, USA, 2001. [Google Scholar]
- Kay, S. Fundamentals of Statistical Signal Processing: Vol. 1 Estimation Theory; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1993. [Google Scholar]
- Van Trees, H.L. Detection, Estimation, and Modulation Theory, Optimum Array Processing; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Mickan, S.; Zhang, X.C. T-ray sensing and imaging. Int. J. High Speed Electron. Syst. 2003, 13, 601–676. [Google Scholar] [CrossRef]
- Jin, Y.S.; Kim, G.J.; Jeon, S.G. Terahertz dielectric properties of polymers. J. Korean Phys. Soc. 2006, 49, 513–517. [Google Scholar]
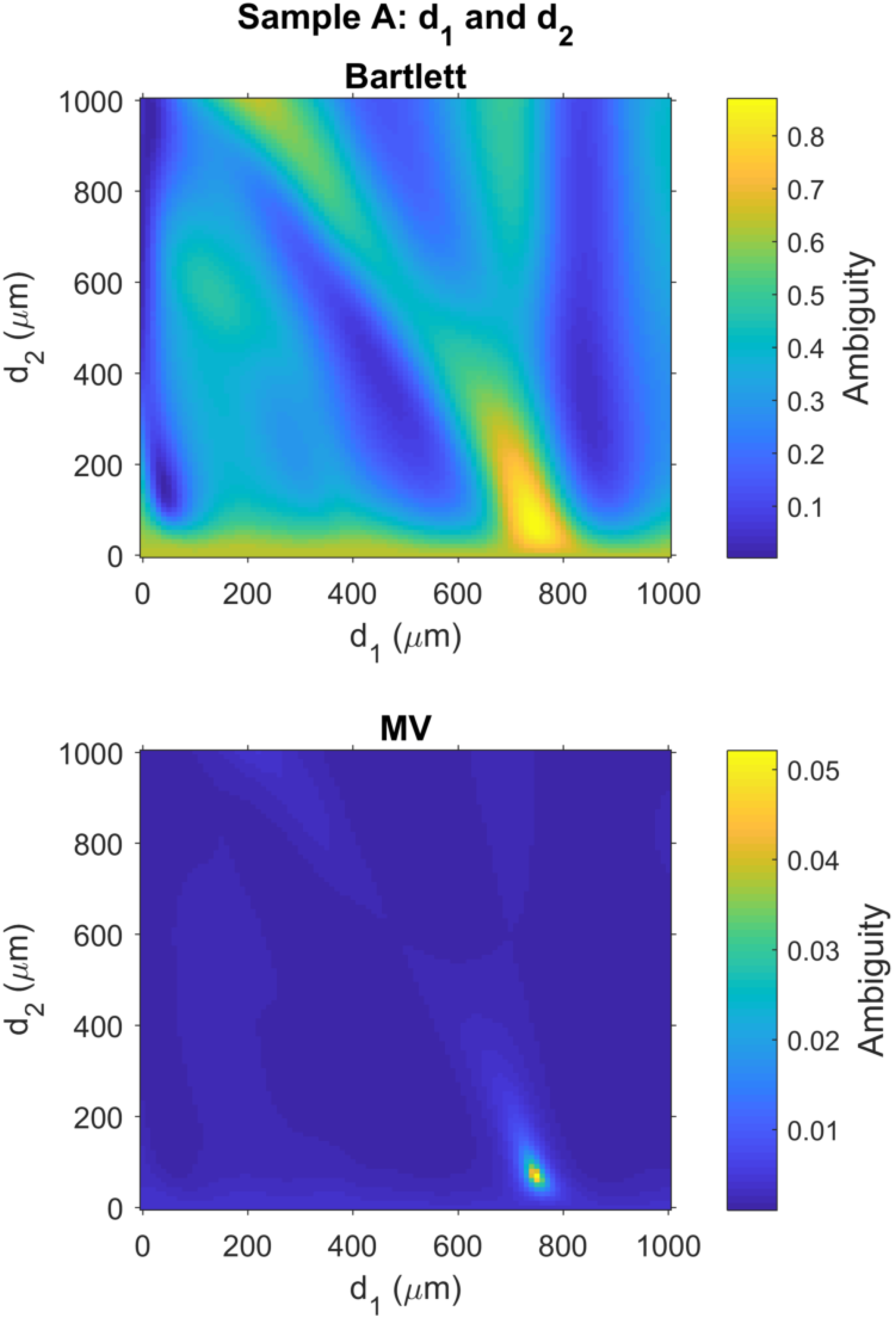

| Sample | Manuf. Spec. (mils) | Vernier Cal. (m) |
|---|---|---|
| A | 30 mil | 740 |
| B | 20 mil | 520 |
| C | 15 mil | 390 |
| D | 10 mil | 260 |
| Sample | Layer | Vernier Cal. | THz MFP Bartlett | THz MFP: MV |
|---|---|---|---|---|
| ID | ID | (m) | (m) | (m) |
| A | 740 | 750 | 750 | |
| A | 60 | 70 | 70 | |
| B | 520 | 510 | 510 | |
| B | 60 | 70 | 70 | |
| C | 390 | 380 | 370 | |
| C | 60 | 60 | 70 | |
| D | 260 | 250 | 240 | |
| D | 60 | 60 | 60 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schecklman, S.; Zurk, L.M. Terahertz Imaging of Thin Film Layers with Matched Field Processing. Sensors 2018, 18, 3547. https://doi.org/10.3390/s18103547
Schecklman S, Zurk LM. Terahertz Imaging of Thin Film Layers with Matched Field Processing. Sensors. 2018; 18(10):3547. https://doi.org/10.3390/s18103547
Chicago/Turabian StyleSchecklman, Scott, and Lisa M. Zurk. 2018. "Terahertz Imaging of Thin Film Layers with Matched Field Processing" Sensors 18, no. 10: 3547. https://doi.org/10.3390/s18103547
APA StyleSchecklman, S., & Zurk, L. M. (2018). Terahertz Imaging of Thin Film Layers with Matched Field Processing. Sensors, 18(10), 3547. https://doi.org/10.3390/s18103547




