A Tactile Sensor Decoupling Process
Abstract
1. Introduction
2. The Model of Tactile Sensors
2.1. Tactile Sensor
2.2. The Numerical Model of Tactile Sensor
3. Improved Homotopy Method
3.1. Homotopy Method
3.2. Imbeded Time-Varying Variable
3.3. Diagram of the Improved Homotopy Method
4. Zero Path Tracking Operators
5. Tracking Stepsize and Accuracy
5.1. Stepsize of the Tracking
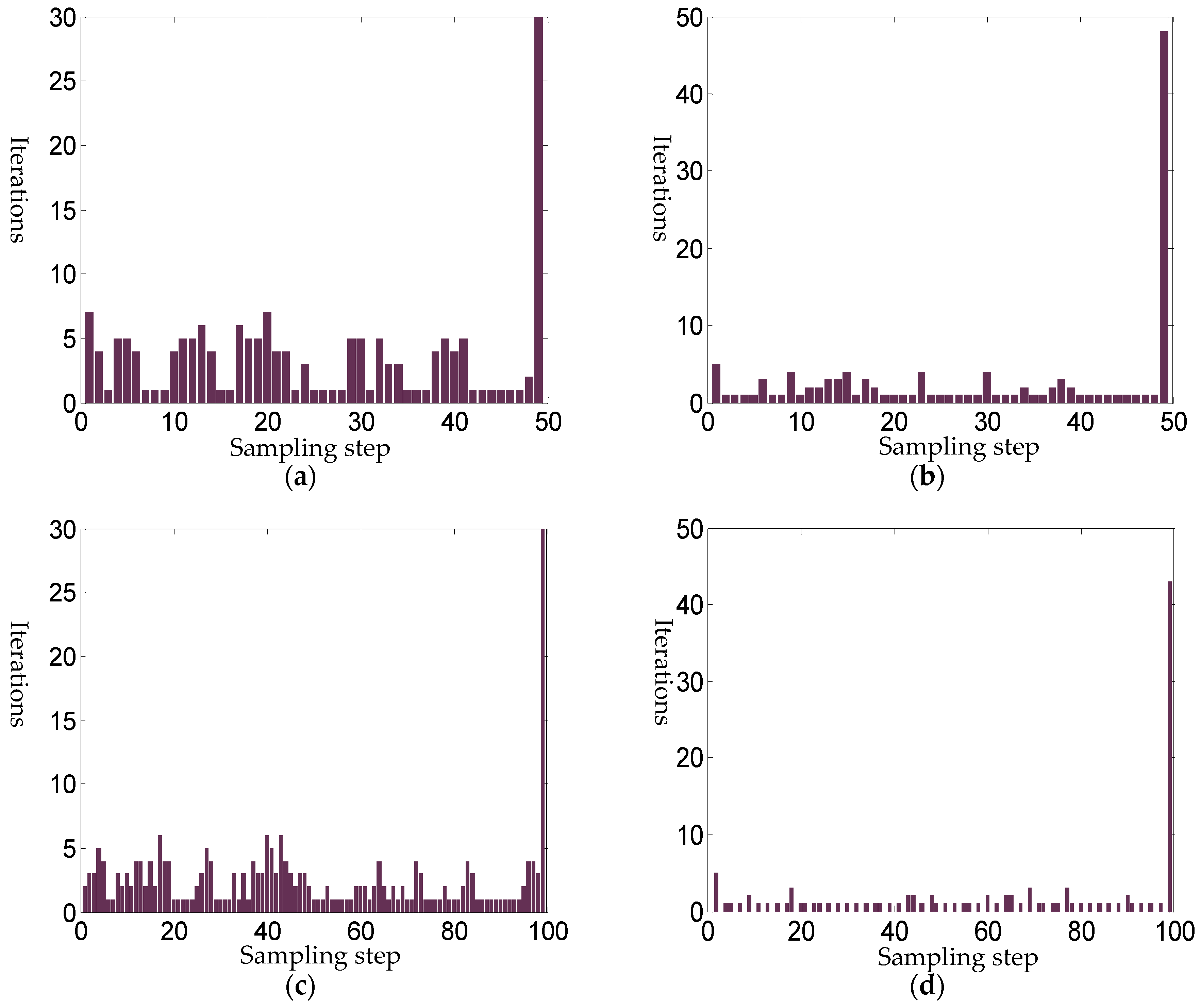
5.2. Accuracy of the Tracking
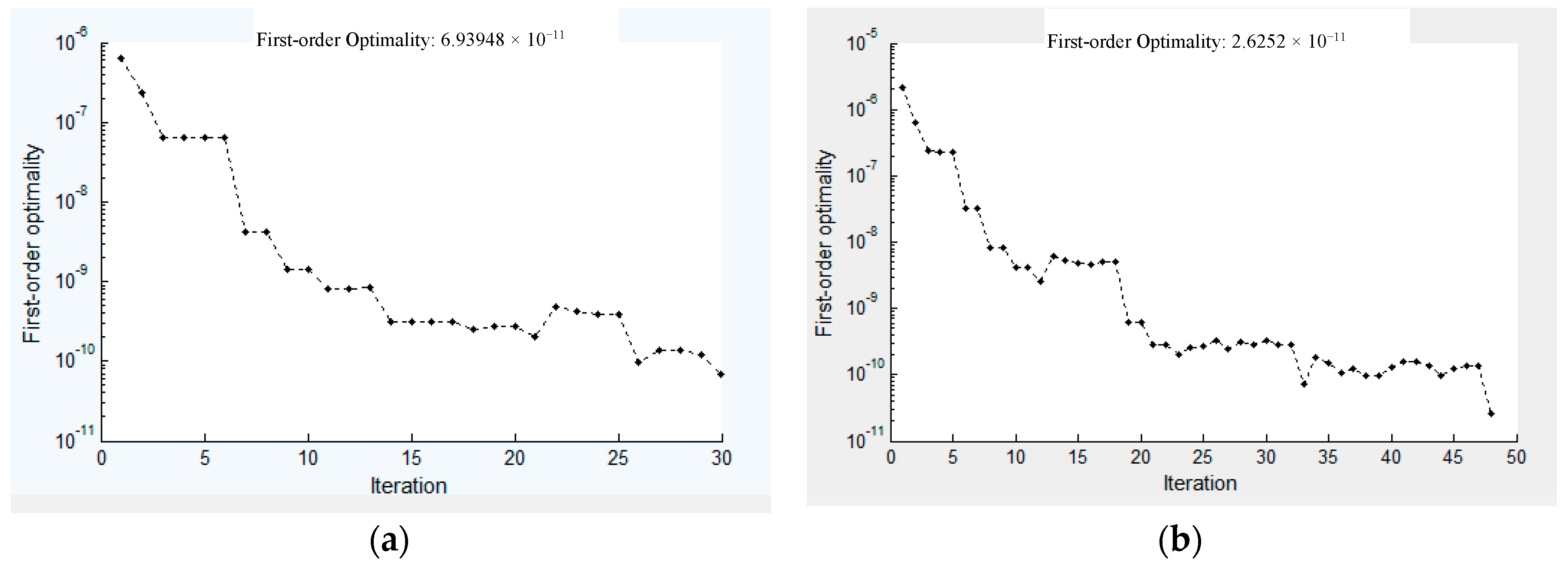
5.3. Accuracy of the Solution
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, Y.; Liu, P.; Zhang, Y.; Qiu, H.; Ge, Y. Piezoresistive characteristic of conductive rubber for flexible tactile sensor. J. Wuhan Univ. Technol. Mater. Sci. Ed. 2011, 26, 443–448. [Google Scholar] [CrossRef]
- Kim, H.K.; Lee, S.; Yun, K.S. Capacitive tactile sensor array for touch screen application. Sens. Actuators A Phys. 2011, 165, 2–7. [Google Scholar] [CrossRef]
- Sumer, B.; Aksak, B.; Sahin, K.; Chuengsatiansup, K.; Sitti, M. Piezoelectric polymer fiber arrays for tactile sensing applications. Sens. Lett. 2011, 9, 457–463. [Google Scholar] [CrossRef]
- Chu, Z.; Sarro, P.M.; Middelhoek, S. Silicon three-axial tactile sensor. Sens. Actuators A Phys. 1996, 54, 505–510. [Google Scholar] [CrossRef]
- Strohmayr, M.W.; Saal, H.P.; Potdar, A.H.; Van Der Smagt, P. The DLR touch sensor I: A flexible tactile sensor for robotic hands based on a crossed-wire approach. In Proceedings of the 23rd IEEE/RSJ 2010 International Conference on Intelligent Robots and Systems (IROS 2010), Taipei, Taiwan, 18–22 October 2010; pp. 897–903. [Google Scholar]
- Lipomi, D.J.; Vosgueritchian, M.; Tee, B.C.; Hellstrom, S.L.; Lee, J.A.; Fox, C.H.; Bao, Z. Skin-like pressure and strain sensors based on transparent elastic films of carbon nanotubes. Nat. Nanotechnol. 2011, 6, 788–792. [Google Scholar] [CrossRef] [PubMed]
- Koc, I.M.; Akca, E. Design of a piezoelectric based tactile sensor with bio-inspired micro/nano-pillars. Tribol. Int. 2013, 59, 321–331. [Google Scholar]
- Oballe-Peinado, Ó.; Hidalgo-López, J.A.; Castellanos-Ramos, J.; Sánchez-Durán, J.A.; Navas-González, R.; Herrán, J.; Vidal-Verdú, F. FPGA-Based Tactile Sensor Suite Electronics for Real-Time Embedded Processing. IEEE Trans. Ind. Electron. 2017, 64, 9657–9665. [Google Scholar] [CrossRef]
- Baglio, S.; Muscato, G.; Savalli, N. Tactile measuring systems for the recognition of unknown surfaces. IEEE Trans. Instrum. Meas. 2002, 51, 522–531. [Google Scholar] [CrossRef]
- Petra, I.; Holding, D.J.; Blow, K.J.; Tam, B.; Ma, X.; Brett, P.N. The design of a flexible digit towards wireless tactile sense feedback. In Proceedings of the 8th International Conference on Control, Automation, Robotics and Vision (ICARCV), Kunming, China, 6–9 December 2004; pp. 468–473. [Google Scholar]
- Schram, G.; Gopisetty, S.M.; Stengel, R.F. A fuzzy logic—Parity space approach to actuator failure detection and identification. In Proceedings of the 36th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 12–15 January 1998; pp. 98–1014. [Google Scholar]
- Ma, J.; Song, A.; Xiao, J. A robust static decoupling algorithm for 3-axis force sensors based on coupling error model and ε-SVR. Sensors 2012, 12, 14537–14555. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Sun, X.; Wang, Y.; Ding, J.; Pan, H.; Song, Q.; Yu, Y.; Shuang, F. Decoupling research of a three-dimensional force tactile sensor based on radical basis function neural network. Sens. Transducers 2013, 159, 289–298. [Google Scholar]
- He, J.H. A coupling method of a homotopy technique and a perturbation technique for non-linear problems. Int. J. Non-Linear Mech. 2000, 35, 37–43. [Google Scholar] [CrossRef]
- Ku, C.Y.; Yeih, W.; Liu, C.S. Solving Non-Linear Algebraic Equations by a Scalar Newton-homotopy Continuation Method. Int. J. Nonlinear Sci. Numer. Simul. 2010, 11, 435–450. [Google Scholar] [CrossRef]
- Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Park, C.H.; Shim, H.-T. What is the homotopy method for a system of nonlinear equations (survey)? J. Appl. Math. Inform. 2005, 17, 689–700. [Google Scholar]
- Xu, F.; Huang, Y.; Yu, Y.; Ding, J.; Hao, C.; Ge, Y. Structural design and simulation research of a novel three-dimensional force tactile sensor. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics, Guilin, China, 19–23 December 2009; pp. 141–146. [Google Scholar]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1994, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Wedderburn, R.W. Quasi-likelihood functions, generalized linear models, and the Gauss—Newton method. Biometrika 1974, 61, 439–447. [Google Scholar] [CrossRef]
- Byrd, R.H.; Gilbert, J.C.; Nocedal, J. A trust region method based on interior point techniques for nonlinear programming. Math. Prog. 2000, 89, 149–185. [Google Scholar] [CrossRef]
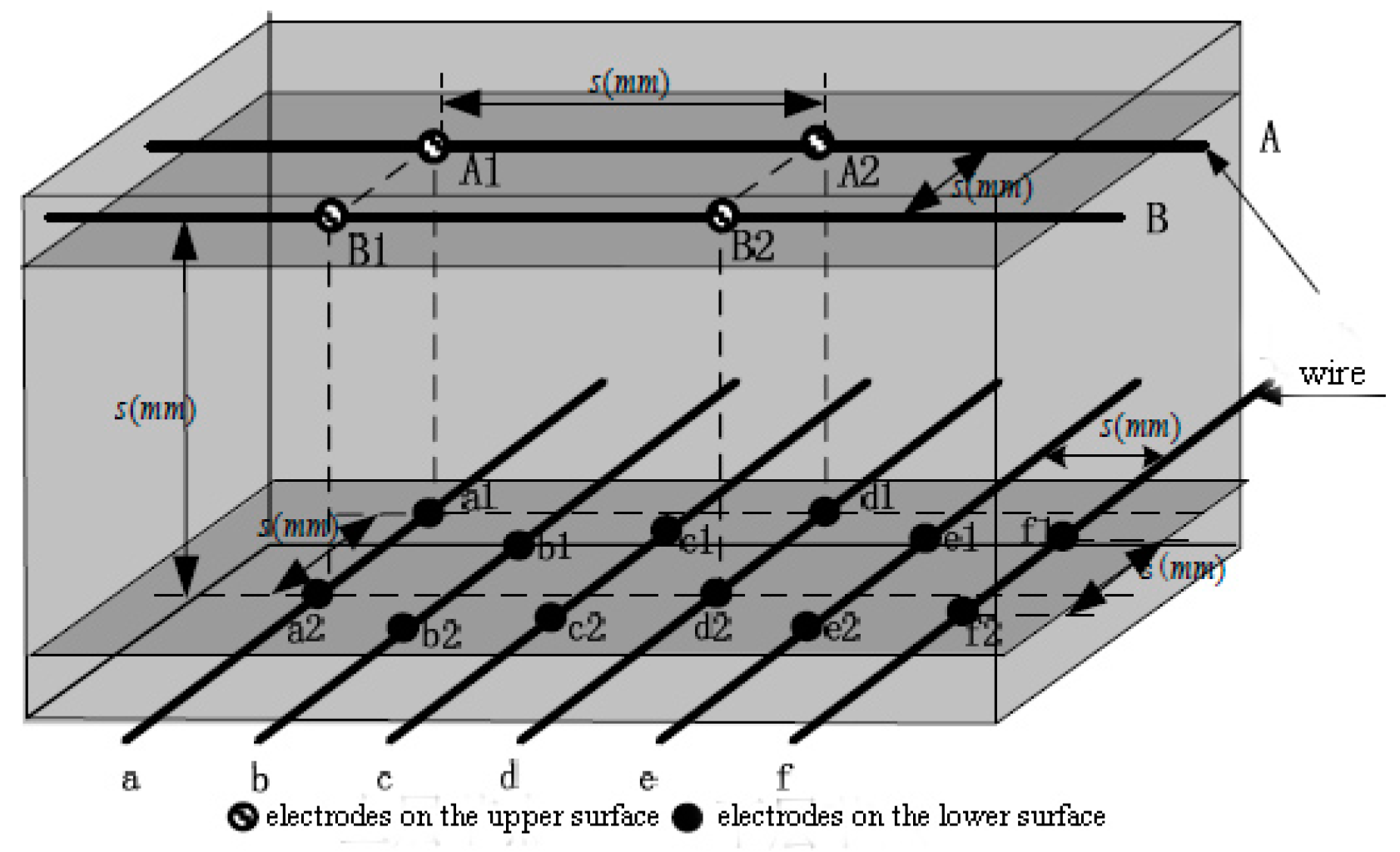
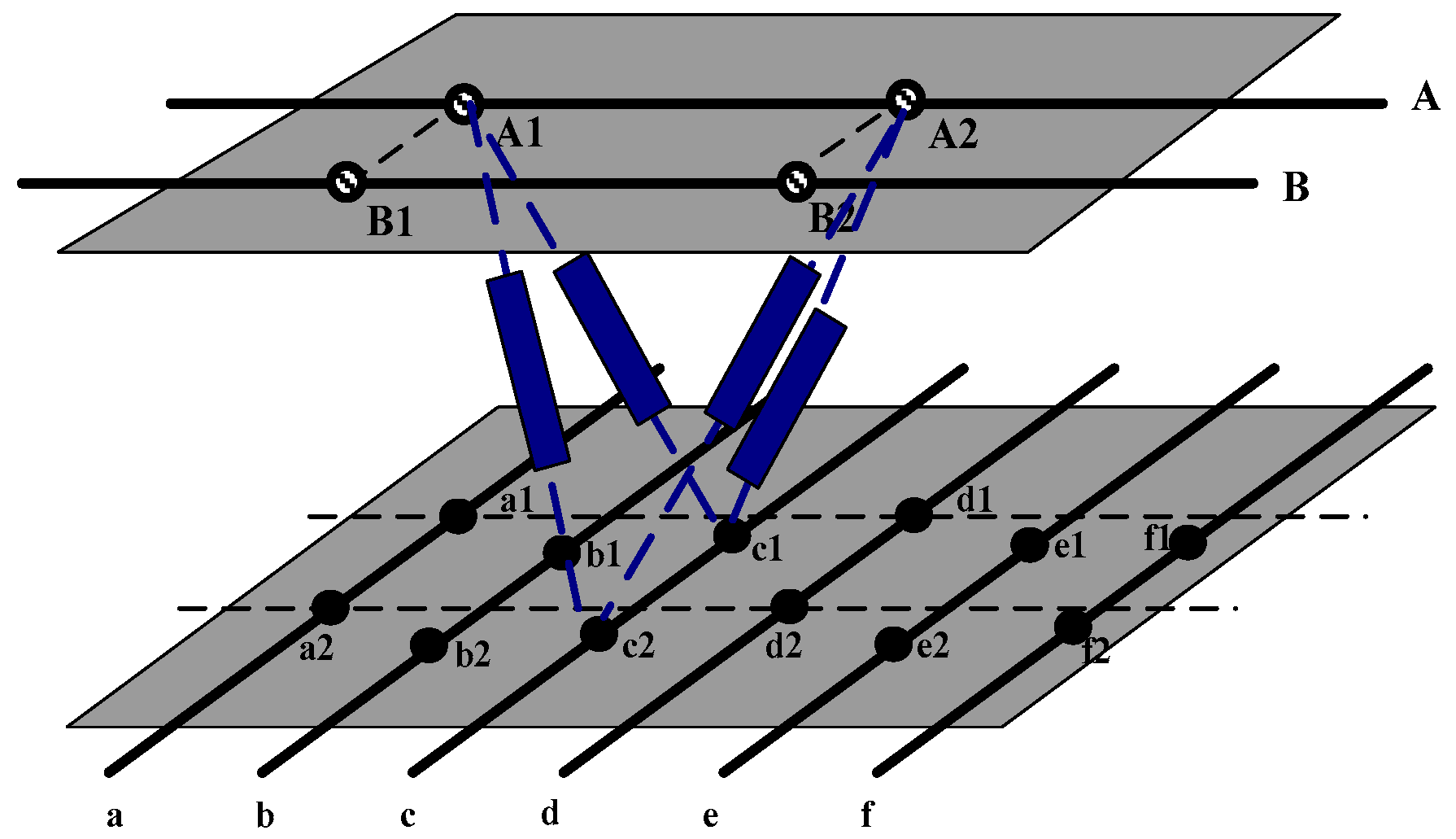
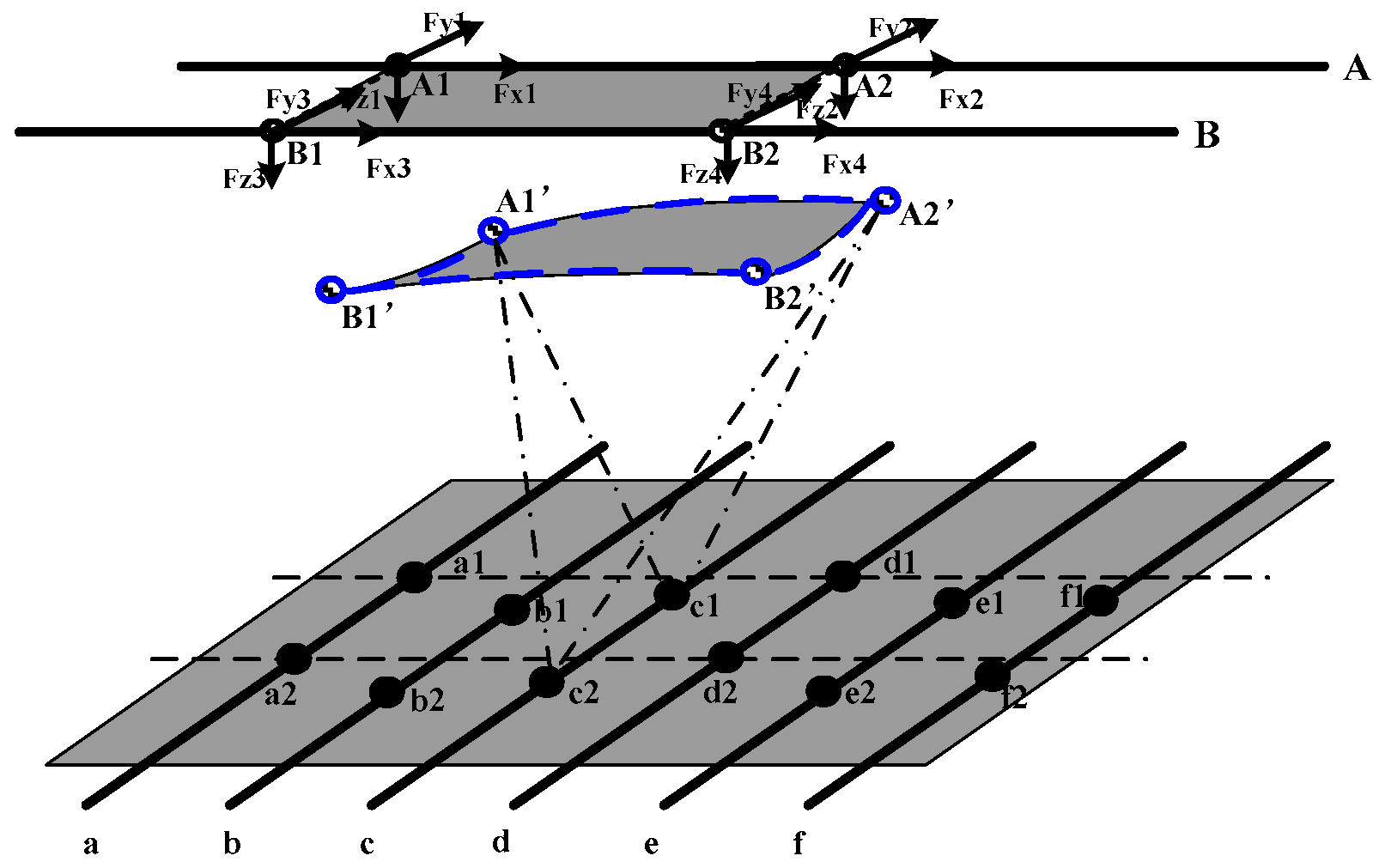
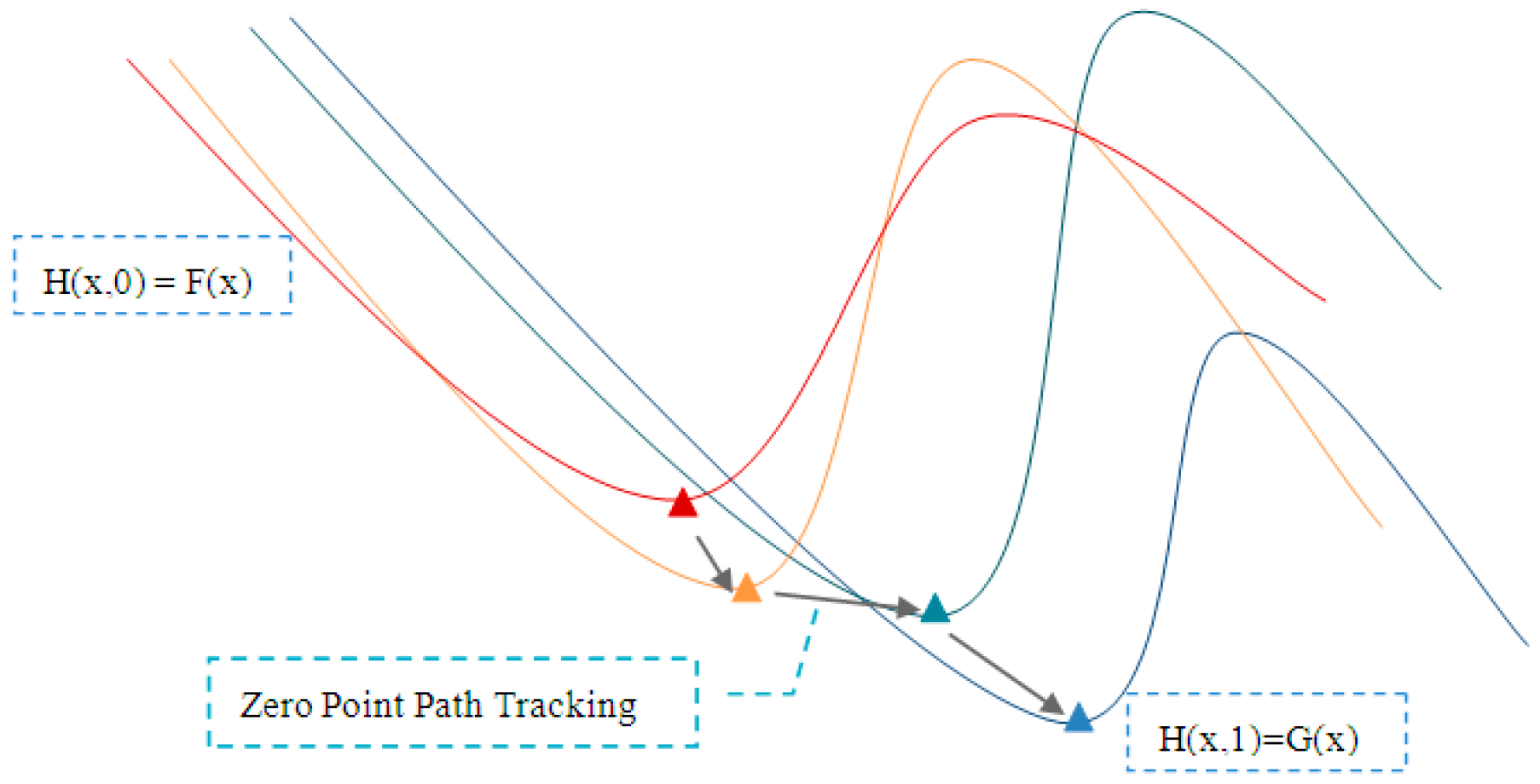
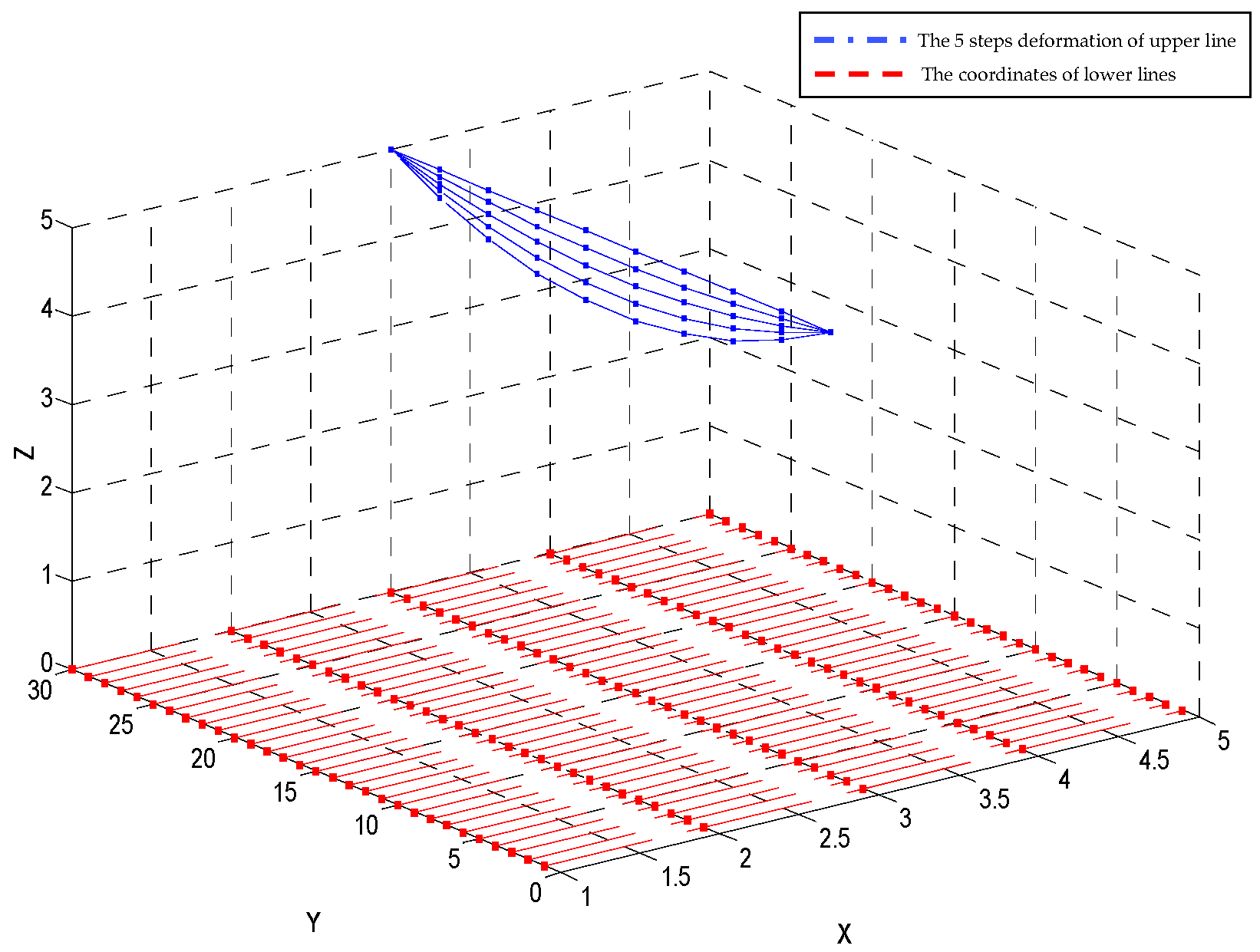
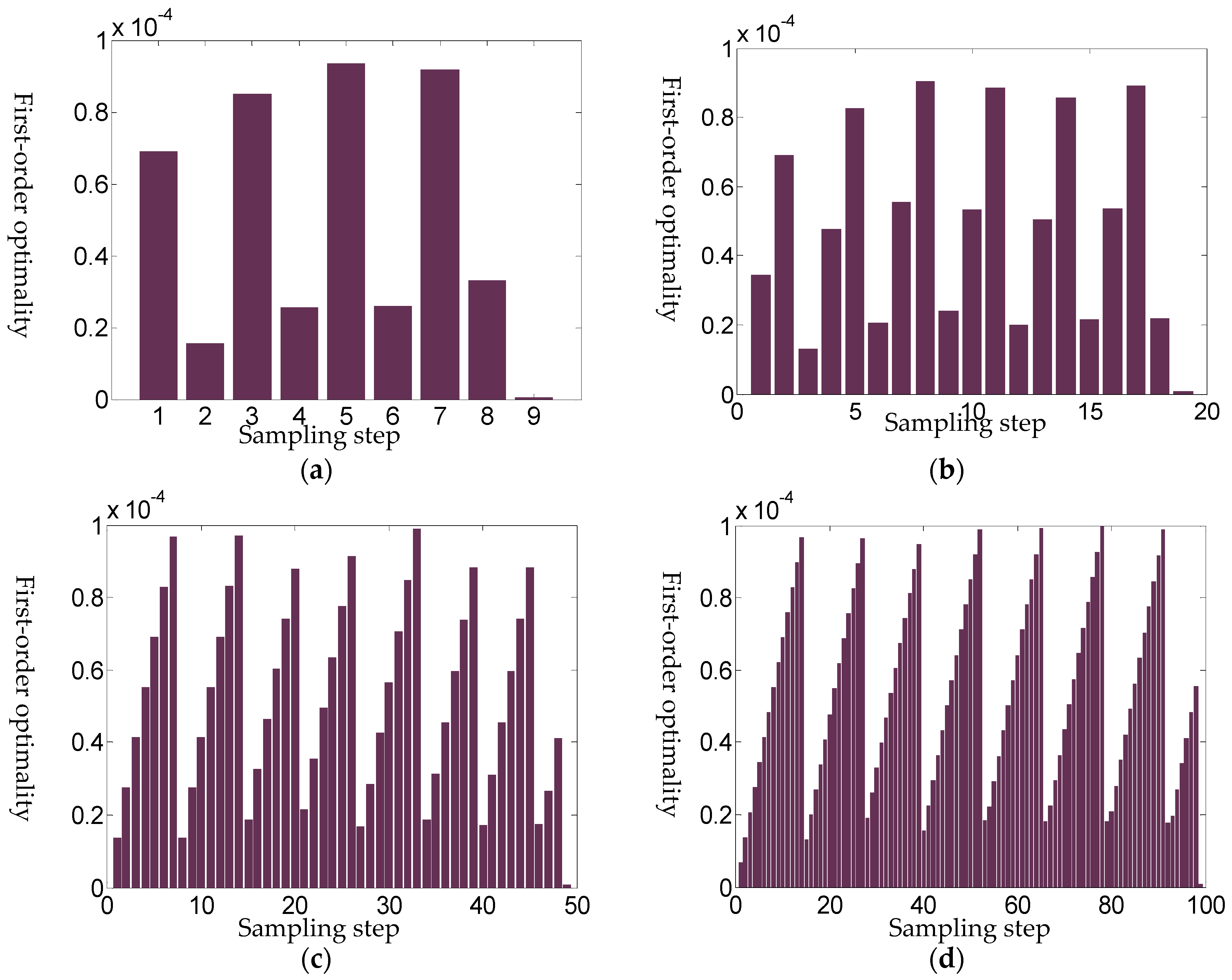
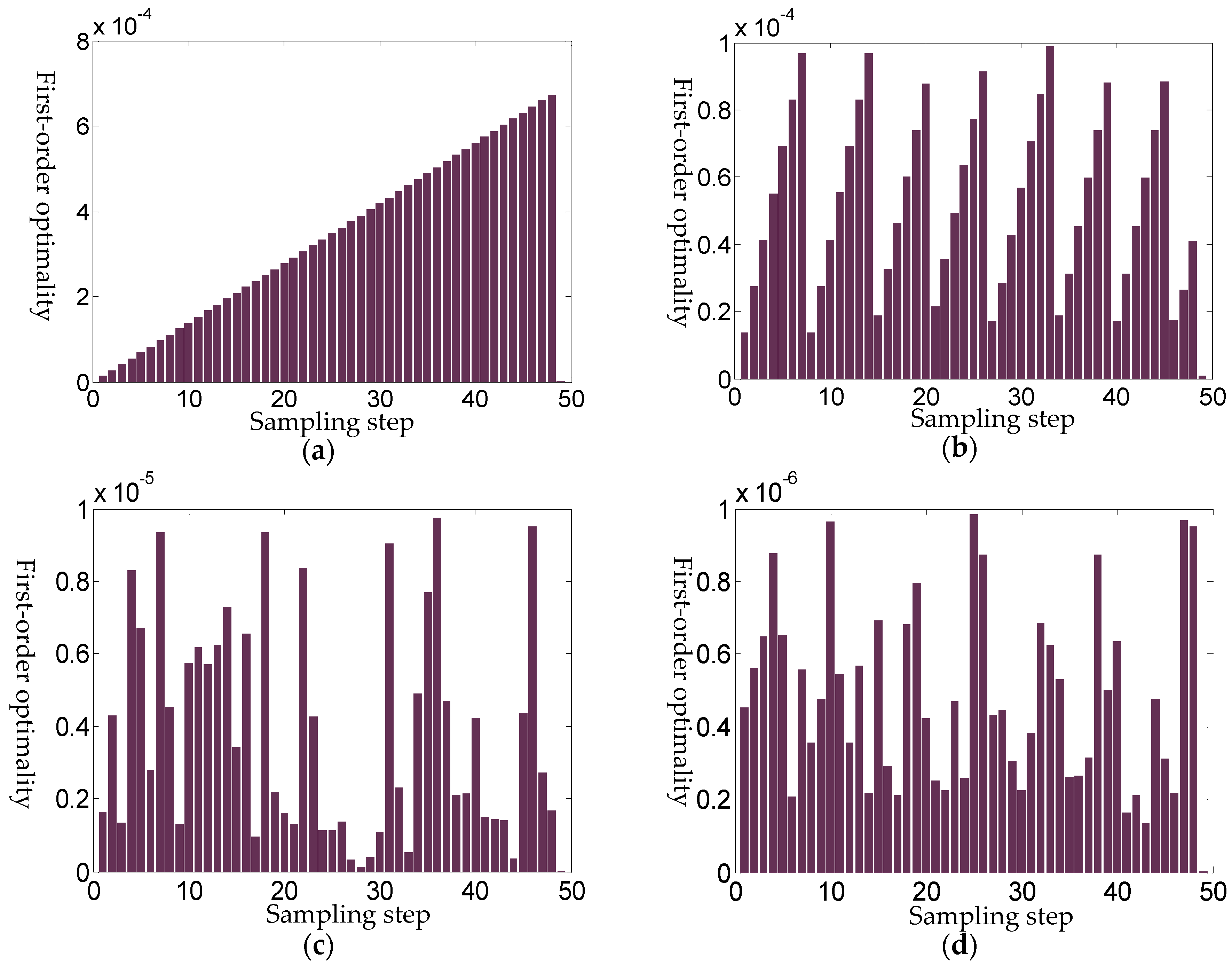
| Step 1. Initialize the sampling frequency of the external circuit, namely determining the steps of the Homotopy tracking path. If there needs N steps in the tracking path, then the sampled resistances should be . The original coordinates of the upper surface electrode is recorded as X(0). |
| Step 2. Put into the Equation (7), and run the kth zero point tracking operator dog-leg step to get the kth zero point . Use the current zero point as the start point of next Homotopy step, and meanwhile put the into the Equation (7) to solve the next zero point. |
| Step 3. Repeat Step 2 until the zero point is obtained, and now use iteration termination conditions of higher precision for the Nth step, which can reach the final solution of the system equations. |
| Operator | LM (Times) | GN (Times) | Dogleg (Times) |
|---|---|---|---|
| 5 steps | 403.00 | 195.00 | 251.50 |
| 10 steps | 403.00 | 102.30 | 220.29 |
| 20 steps | 397.53 | 91.50 | 149.06 |
| 50 steps | 388.48 | 80.50 | 104.90 |
| 100 steps | 280.50 | 62.00 | 82.70 |
| Operator | LM (%) | GN (%) | Dogleg (%) |
|---|---|---|---|
| 5 steps | 0.78 | (Failed) | 6.88 |
| 10 steps | 0.037 | (Failed) | 0.19 |
| 20 steps | 0.025 | 8.64 | 0.18 |
| 50 steps | 0.0042 | 7.56 | 0.16 |
| 100 steps | 0.0026 | 5.89 | 0.14 |
| Steps | Function Calls | Tol_X | Runtime (s) | Accuracy (%) |
|---|---|---|---|---|
| 5 | 251.50 | 5.57 × 10−12 | 1.21 | 6.88 |
| 10 | 220.29 | 4.70 × 10−12 | 2.03 | 0.19 |
| 20 | 149.06 | 1.24 × 10−12 | 4.32 | 0.18 |
| 50 | 104.90 | 1.18 × 10−12 | 9.18 | 0.16 |
| 100 | 82.70 | 1.49 × 10−12 | 20.58 | 0.14 |
| 200 | 67.40 | 1.01 × 10−12 | 48.80 | 0.14 |
| 500 | 64.50 | 0.94 × 10−12 | 72.73 | 0.14 |
| 1000 | 63.40 | 0.91 × 10−12 | 271.58 | 0.14 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Zhuang, X.; Hu, G.; Pan, H.; Shuang, F. A Tactile Sensor Decoupling Process. Sensors 2018, 18, 3515. https://doi.org/10.3390/s18103515
Xu Y, Zhuang X, Hu G, Pan H, Shuang F. A Tactile Sensor Decoupling Process. Sensors. 2018; 18(10):3515. https://doi.org/10.3390/s18103515
Chicago/Turabian StyleXu, Yuyun, Xuekun Zhuang, Guangyu Hu, Hongqing Pan, and Feng Shuang. 2018. "A Tactile Sensor Decoupling Process" Sensors 18, no. 10: 3515. https://doi.org/10.3390/s18103515
APA StyleXu, Y., Zhuang, X., Hu, G., Pan, H., & Shuang, F. (2018). A Tactile Sensor Decoupling Process. Sensors, 18(10), 3515. https://doi.org/10.3390/s18103515





