Photoacoustic Signal Enhancement: Towards Utilization of Low Energy Laser Diodes in Real-Time Photoacoustic Imaging
Abstract
1. Introduction
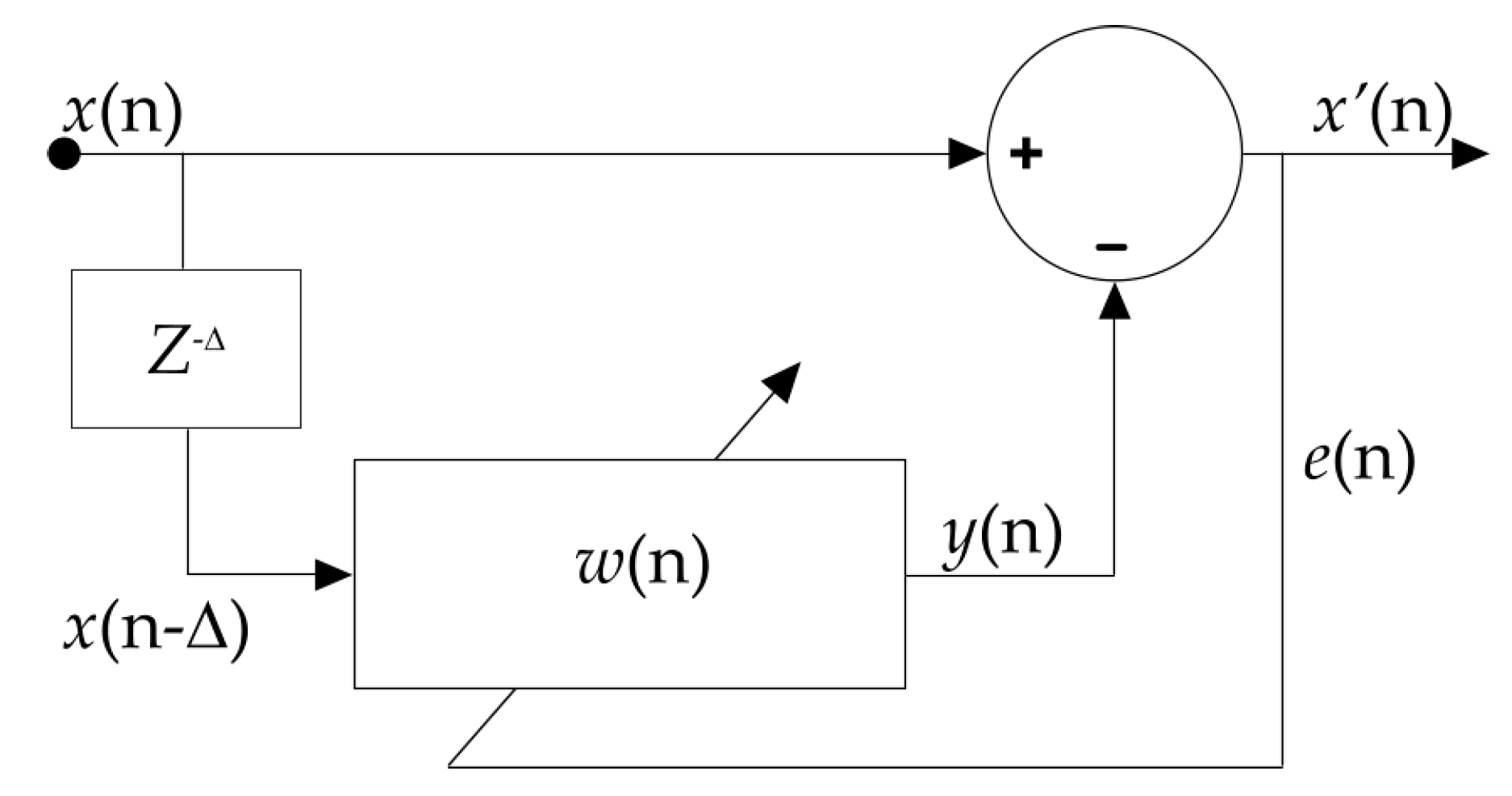
2. Adaptive Denoising Filter Design
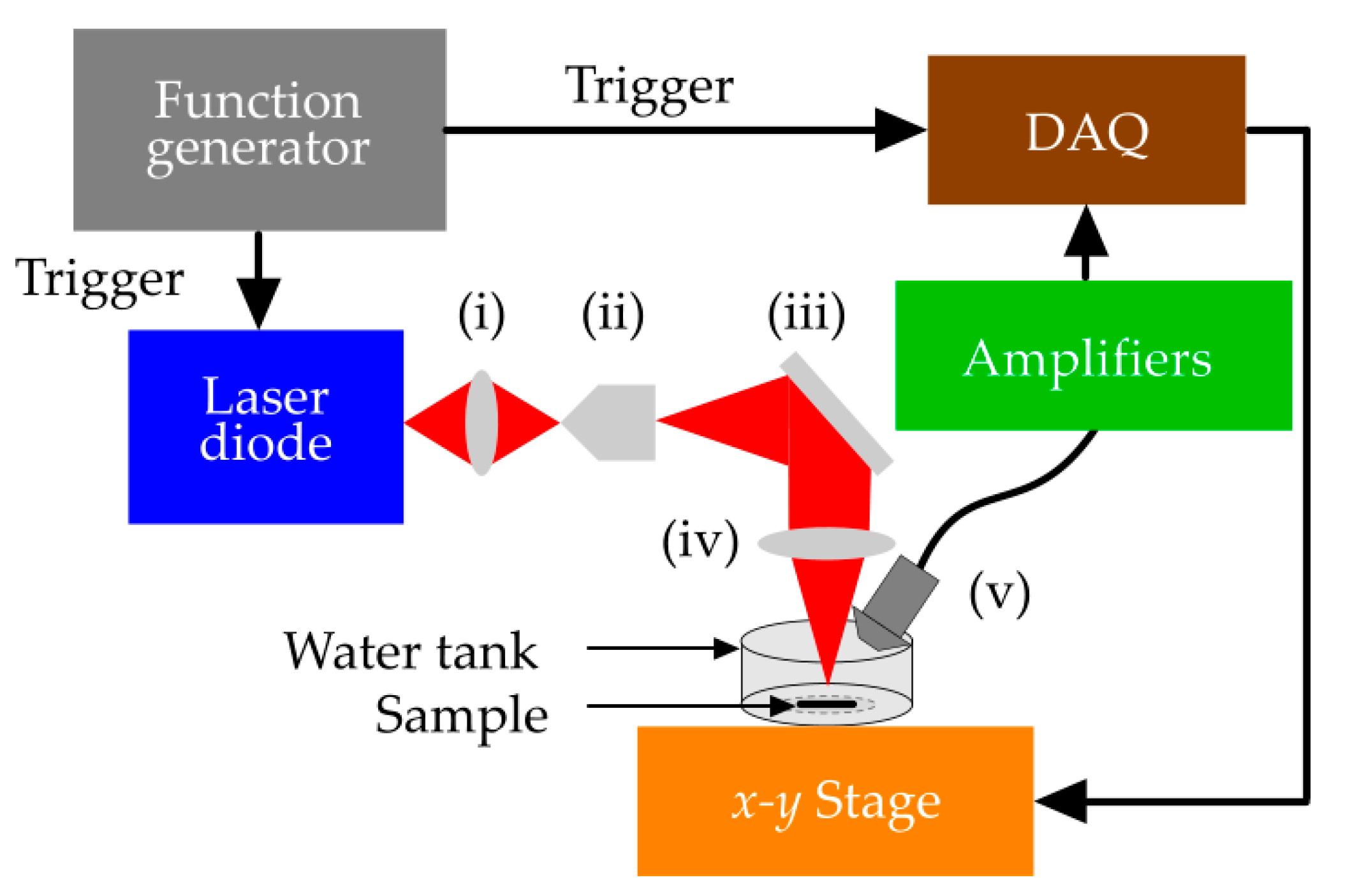
3. Materials and Methods
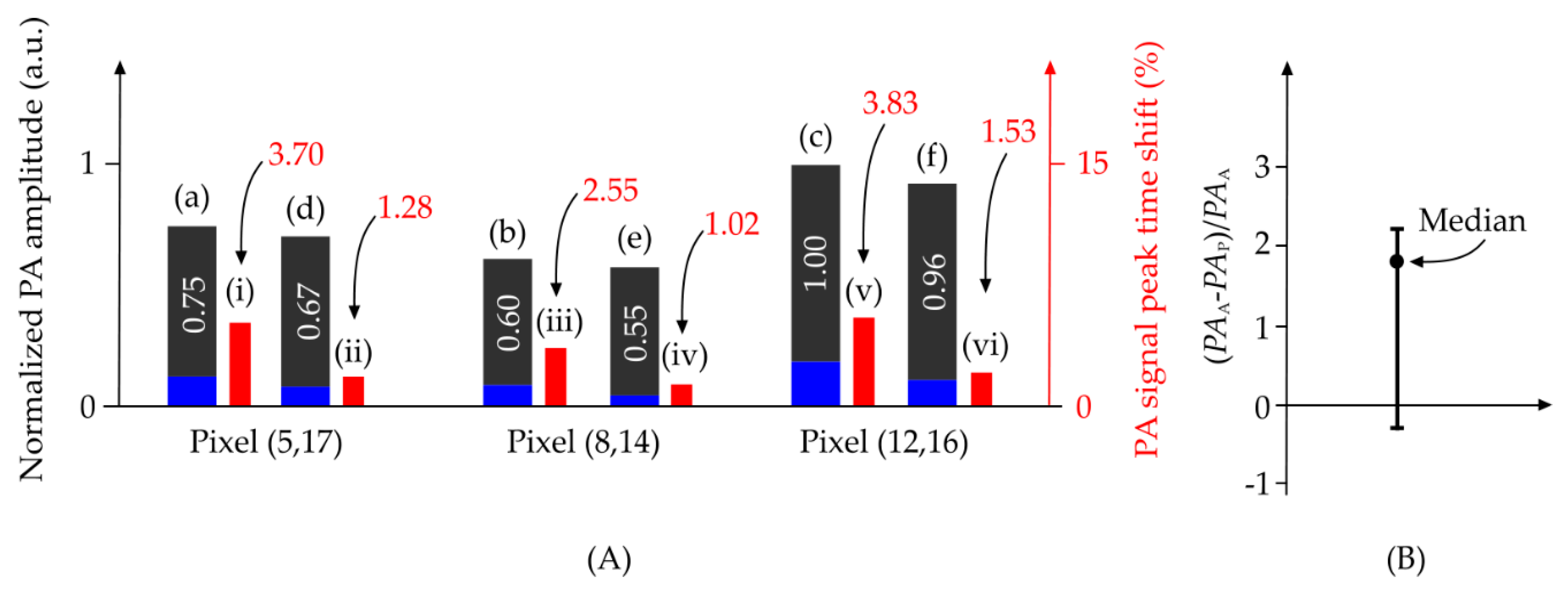
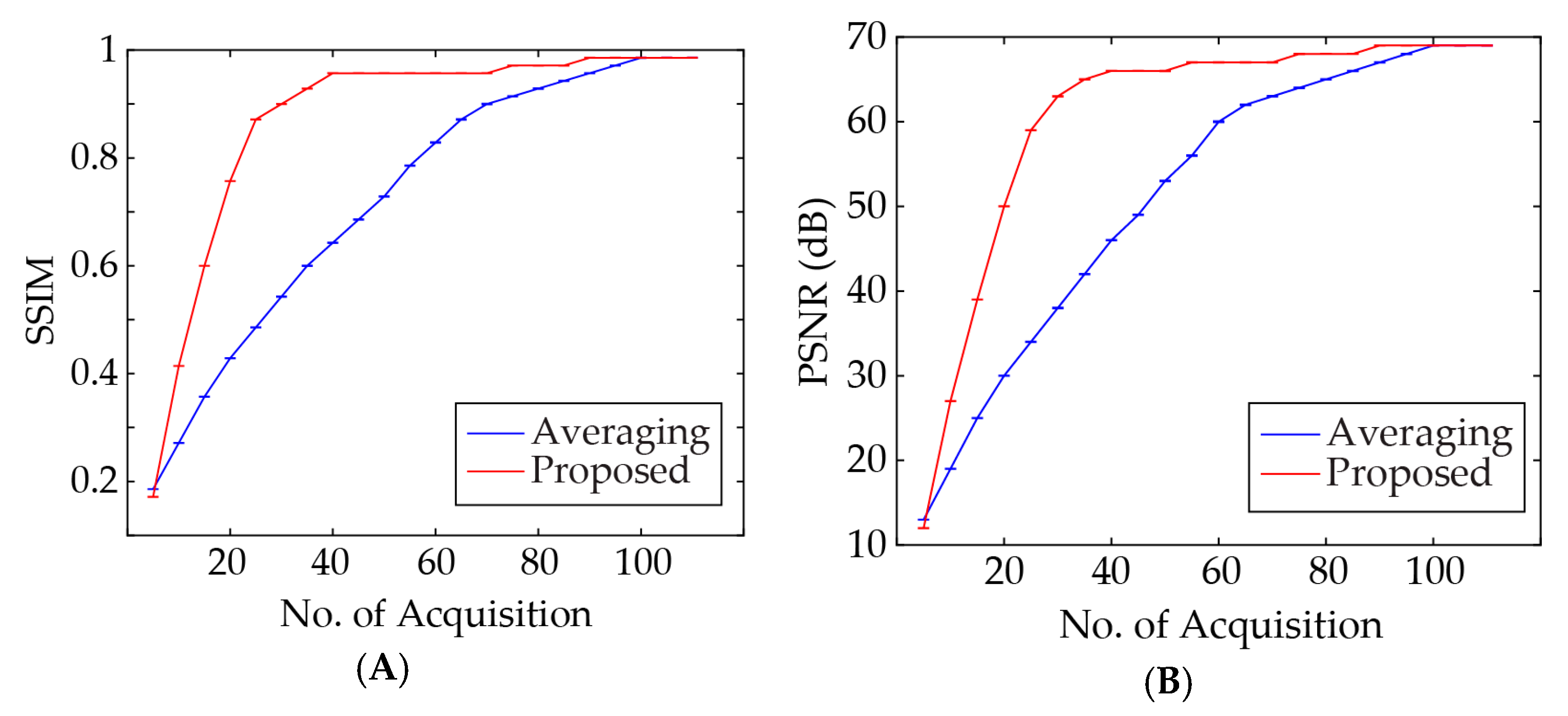
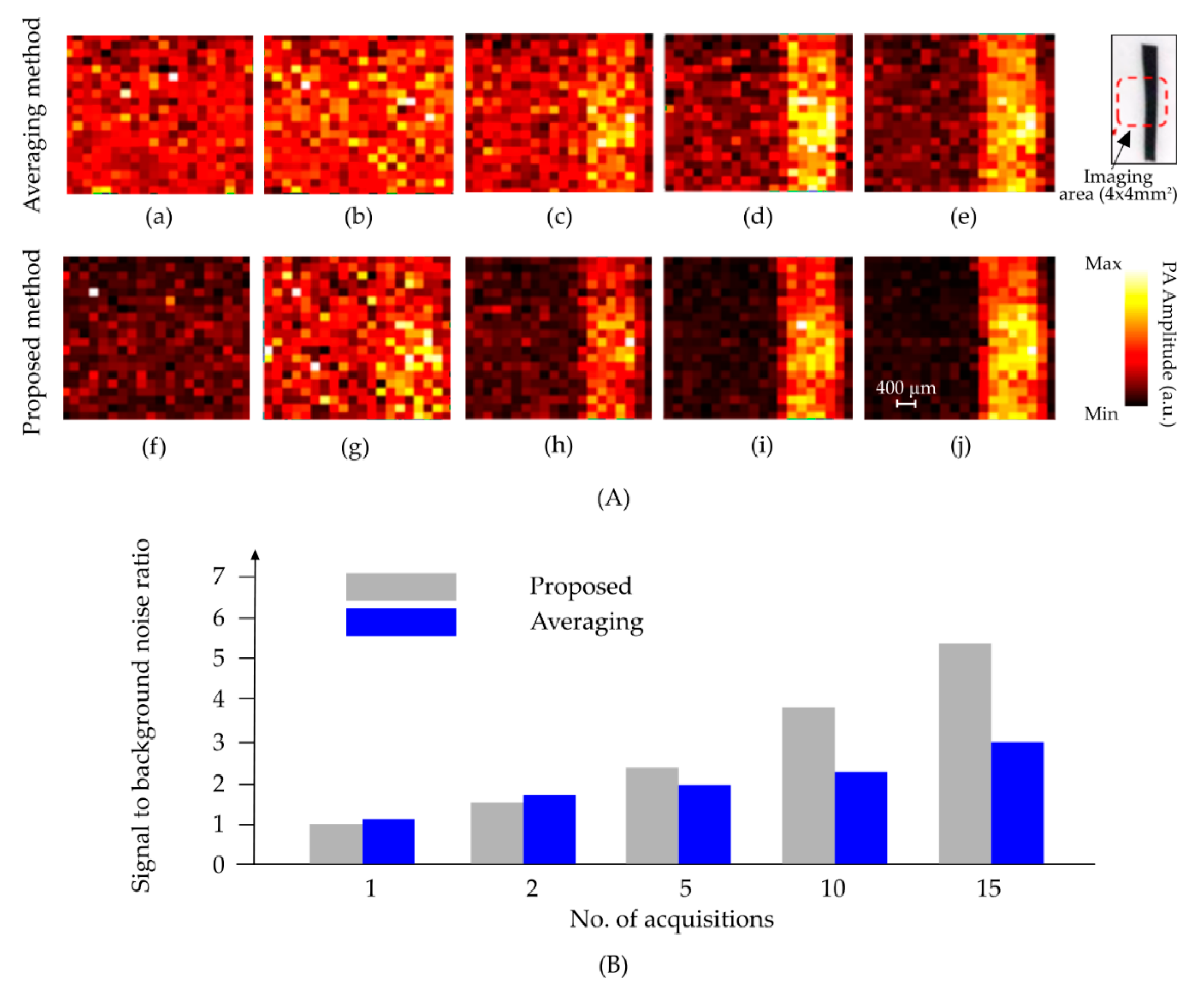
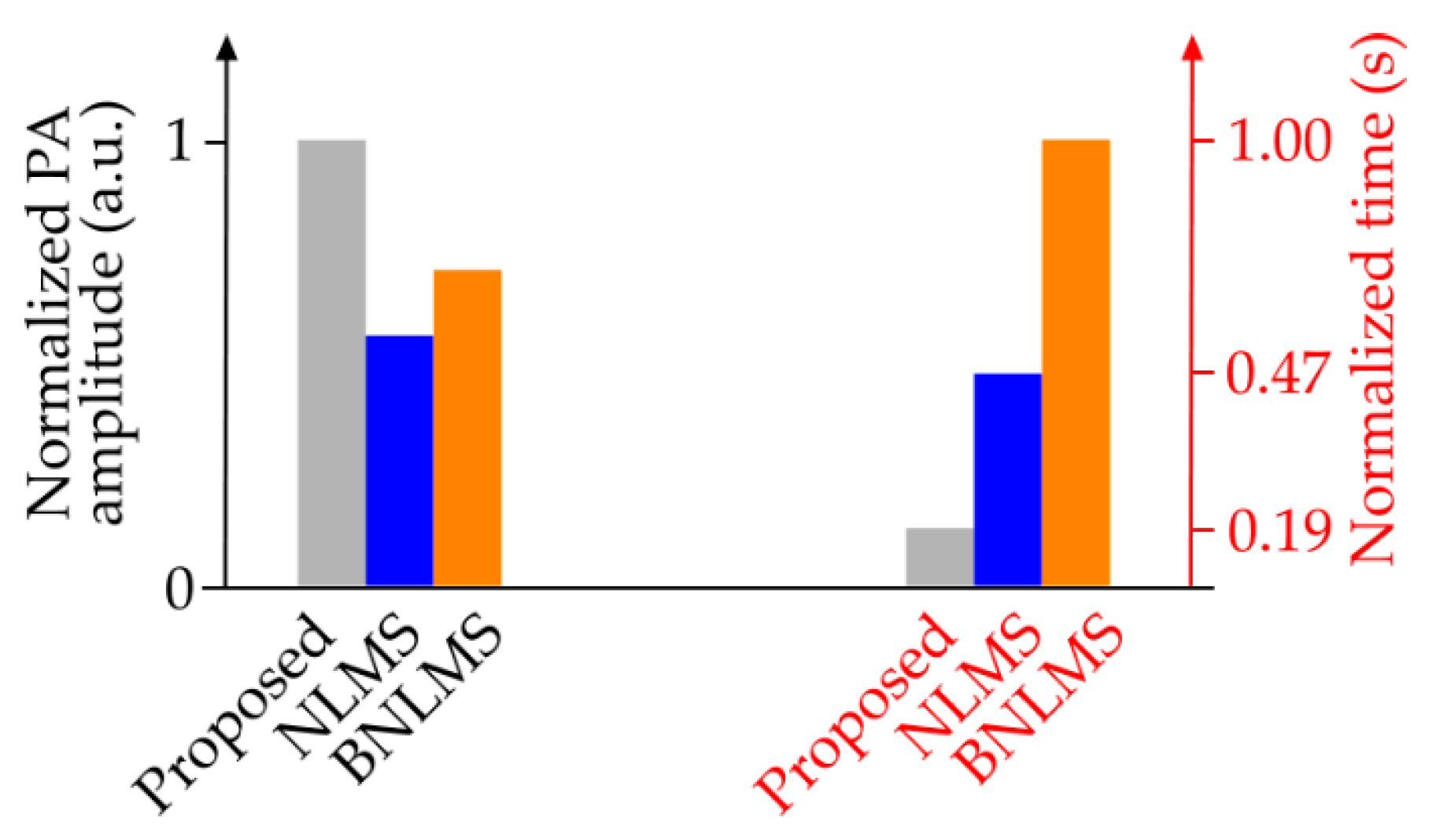
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, L.V. Tutorial on photoacoustic microscopy and computed tomography. IEEE J. Sel. Top. Quantum Electron. 2008, 14, 171–179. [Google Scholar] [CrossRef]
- Yao, J.; Wang, L.V. Photoacoustic microscopy. Laser Photonics Rev. 2013, 7, 758–778. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Hong, H.; Cai, W. Photoacoustic imaging. Cold Spring Harb. Protoc. 2011, 2011, 1015–1025. [Google Scholar] [CrossRef] [PubMed]
- Zhong, H.; Duan, T.; Lan, H.; Zhou, M.; Gao, F. Review of low-cost photoacoustic sensing and imaging based on laser diode and light-emitting diode. Sensors 2018, 18, 2264. [Google Scholar] [CrossRef] [PubMed]
- Hariri, A.; Fatima, A.; Mohammadian, N.; Mahmoodkalayeh, S.; Ansari, M.A.; Bely, N.; Avanaki, M.R. Development of low-cost photoacoustic imaging systems using very low-energy pulsed laser diodes. J. Biomed. Opt. 2017, 22, 075001. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi-Nejad, A.-R.; Mahmoudzadeh, M.; Hassanpour, M.S.; Wallois, F.; Muzik, O.; Papadelis, C.; Hansen, A.; Soltanian-Zadeh, H.; Gelovani, J.; Nasiriavanaki, M. Neonatal brain resting-state functional connectivity imaging modalities. Photoacoustics 2018, 10, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Nasiriavanaki, M.; Xia, J.; Wan, H.; Bauer, A.Q.; Culver, J.P.; Wang, L.V. High-resolution photoacoustic tomography of resting-state functional connectivity in the mouse brain. Proc. Natl. Acad. Sci. USA 2014, 111, 21–26. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.D.; Shin, J.G.; Hyun, H.; Yu, B.-A.; Eom, T.J. Label-free photoacoustic microscopy for in-vivo tendon imaging using a fiber-based pulse laser. Sci. Rep. 2018, 8, 4805. [Google Scholar] [CrossRef] [PubMed]
- Mozaffarzadeh, M.; Mahloojifar, A.; Orooji, M.; Kratkiewicz, K.; Adabi, S.; Nasiriavanaki, M. Linear-array photoacoustic imaging using minimum variance-based delay multiply and sum adaptive beamforming algorithm. J. Biomed. Opt. 2018, 23, 026002. [Google Scholar] [CrossRef] [PubMed]
- Telenkov, S.; Mandelis, A. Signal-to-noise analysis of biomedical photoacoustic measurements in time and frequency domains. Rev. Sci. Instrum. 2010, 81, 124901. [Google Scholar] [CrossRef] [PubMed]
- Winkler, A.M.; Maslov, K.I.; Wang, L.V. Noise-equivalent sensitivity of photoacoustics. J. Biomed. Opt. 2013, 18, 097003. [Google Scholar] [CrossRef] [PubMed]
- Mahmoodkalayeh, S.; Jooya, H.Z.; Hariri, A.; Zhou, Y.; Xu, Q.; Ansari, M.A.; Avanaki, M.R. Low temperature-mediated enhancement of photoacoustic imaging depth. Sci. Rep. 2018, 8, 4873. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Wang, L.V. Sensitivity of photoacoustic microscopy. Photoacoustics 2014, 2, 87–101. [Google Scholar] [CrossRef] [PubMed]
- Erfanzadeh, M.; Kumavor, P.D.; Zhu, Q. Laser scanning laser diode photoacoustic microscopy system. Photoacoustics 2018, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Hariri, A.; Lemaster, J.; Wang, J.; Jeevarathinam, A.S.; Chao, D.L.; Jokerst, J.V. The characterization of an economic and portable led-based photoacoustic imaging system to facilitate molecular imaging. Photoacoustics 2018, 9, 10–20. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Xu, G.; Yuan, J.; Jo, J.; Gandikota, G.; Demirci, H.; Agano, T.; Sato, N.; Shigeta, Y.; Wang, X. Light emitting diodes based photoacoustic imaging and potential clinical applications. Sci. Rep. 2018, 8, 9885. [Google Scholar] [CrossRef] [PubMed]
- Omidi, P.; Zafar, M.; Mozaffarzadeh, M.; Hariri, A.; Haung, X.; Orooji, M.; Nasiriavanaki, M. A novel dictionary-based image reconstruction for photoacoustic computed tomography. Appl. Sci. 2018, 8, 1570. [Google Scholar] [CrossRef]
- Li, J.; Yu, B.; Zhao, W.; Chen, W. A review of signal enhancement and noise reduction techniques for tunable diode laser absorption spectroscopy. Appl. Spectrosc. Rev. 2014, 49, 666–691. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences; The Royal Society: London, UK, 2004; pp. 1597–1611. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Burke, E.K.; Gendreau, M.; Hyde, M.; Kendall, G.; Ochoa, G.; Özcan, E.; Qu, R. Hyper-heuristics: A survey of the state of the art. J. Oper. Res. Soc. 2013, 64, 1695–1724. [Google Scholar] [CrossRef]
- Smith, C.B.; Agaian, S.; Akopian, D. A wavelet-denoising approach using polynomial threshold operators. IEEE Signal Process. Lett. 2008, 15, 906–909. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Z.; Tan, C.; Si, L.; Zhang, L.; Liu, X. Adaptive wavelet threshold denoising method for machinery sound based on improved fruit fly optimization algorithm. Appl. Sci. 2016, 6, 199. [Google Scholar] [CrossRef]
- Sindelar, C.V.; Grigorieff, N. An adaptation of the wiener filter suitable for analyzing images of isolated single particles. J. Struct. Boil. 2011, 176, 60–74. [Google Scholar] [CrossRef] [PubMed]
- Widrow, B.; Glover, J.R.; McCool, J.M.; Kaunitz, J.; Williams, C.S.; Hearn, R.H.; Zeidler, J.R.; Dong, J.E.; Goodlin, R.C. Adaptive noise cancelling: Principles and applications. Proc. IEEE 1975, 63, 1692–1716. [Google Scholar] [CrossRef]
- Redler, G.; Epel, B.; Halpern, H.J. Principal component analysis enhances snr for dynamic electron paramagnetic resonance oxygen imaging of cycling hypoxia in vivo. Magn. Reson. Med. 2014, 71, 440–450. [Google Scholar] [CrossRef] [PubMed]
- Pan, D.; Pramanik, M.; Senpan, A.; Ghosh, S.; Wickline, S.A.; Wang, L.V.; Lanza, G.M. Near infrared photoacoustic detection of sentinel lymph nodes with gold nanobeacons. Biomaterials 2010, 31, 4088–4093. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Bustamante, G.; Peterson, R.; Ye, J.Y. An adaptive filtered back-projection for photoacoustic image reconstruction. Med. Phys. 2015, 42, 2169–2178. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Yao, J.; Wang, L.V. Photoacoustic tomography: Principles and advances. Electromagn. Waves 2014, 147, 1. [Google Scholar] [CrossRef]
- Yu, Z.; Li, H.; Lai, P. Wavefront shaping and its application to enhance photoacoustic imaging. Appl. Sci. 2017, 7, 1320. [Google Scholar]
- Zeng, L.; Piao, Z.; Huang, S.; Jia, W.; Chen, Z. Label-free optical-resolution photoacoustic microscopy of superficial microvasculature using a compact visible laser diode excitation. Opt. Express 2015, 23, 31026–31033. [Google Scholar] [CrossRef] [PubMed]
- Avanaki, M.R.; Cernat, R.; Tadrous, P.J.; Tatla, T.; Podoleanu, A.G.; Hojjatoleslami, S.A. Spatial compounding algorithm for speckle reduction of dynamic focus oct images. IEEE Photonics Technol. Lett. 2013, 25, 1439–1442. [Google Scholar] [CrossRef]
- Kellnberger, S. Photoacoustic Imaging in Time Domain and Frequency Domain. Available online: https://mediatum.ub.tum.de/doc/1113396/1113396.pdf (accessed on 10 October 2018).
- American National Standard Institute. American National Standard for Safe Use of Lasers; Laser Institute of America: Orlando, FL, USA, 2007. [Google Scholar]
- Foster, F.S.; Pavlin, C.J.; Harasiewicz, K.A.; Christopher, D.A.; Turnbull, D.H. Advances in ultrasound biomicroscopy. Ultrasound Med. Boil. 2000, 26, 1–27. [Google Scholar] [CrossRef]
| No. of Signal Acquisitions | Method | PSNR | SSIM |
|---|---|---|---|
| 1 | Averaging | 15.83 | 0.22054 |
| Proposed | 15.67 | 0.13695 | |
| 2 | Averaging | 19.58 | 0.33235 |
| Proposed | 22.39 | 0.37588 | |
| 5 | Averaging | 24.73 | 0.53189 |
| Proposed | 32.08 | 0.73874 | |
| 10 | Averaging | 28.85 | 067040 |
| Proposed | 38.68 | 0.93019 | |
| 15 | Averaging | 31.54 | 0.75843 |
| Proposed | 40.10 | 0.93797 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manwar, R.; Hosseinzadeh, M.; Hariri, A.; Kratkiewicz, K.; Noei, S.; N. Avanaki, M.R. Photoacoustic Signal Enhancement: Towards Utilization of Low Energy Laser Diodes in Real-Time Photoacoustic Imaging. Sensors 2018, 18, 3498. https://doi.org/10.3390/s18103498
Manwar R, Hosseinzadeh M, Hariri A, Kratkiewicz K, Noei S, N. Avanaki MR. Photoacoustic Signal Enhancement: Towards Utilization of Low Energy Laser Diodes in Real-Time Photoacoustic Imaging. Sensors. 2018; 18(10):3498. https://doi.org/10.3390/s18103498
Chicago/Turabian StyleManwar, Rayyan, Matin Hosseinzadeh, Ali Hariri, Karl Kratkiewicz, Shahryar Noei, and Mohammad R. N. Avanaki. 2018. "Photoacoustic Signal Enhancement: Towards Utilization of Low Energy Laser Diodes in Real-Time Photoacoustic Imaging" Sensors 18, no. 10: 3498. https://doi.org/10.3390/s18103498
APA StyleManwar, R., Hosseinzadeh, M., Hariri, A., Kratkiewicz, K., Noei, S., & N. Avanaki, M. R. (2018). Photoacoustic Signal Enhancement: Towards Utilization of Low Energy Laser Diodes in Real-Time Photoacoustic Imaging. Sensors, 18(10), 3498. https://doi.org/10.3390/s18103498





