A LN/Si-Based SAW Pressure Sensor
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fabrication Process
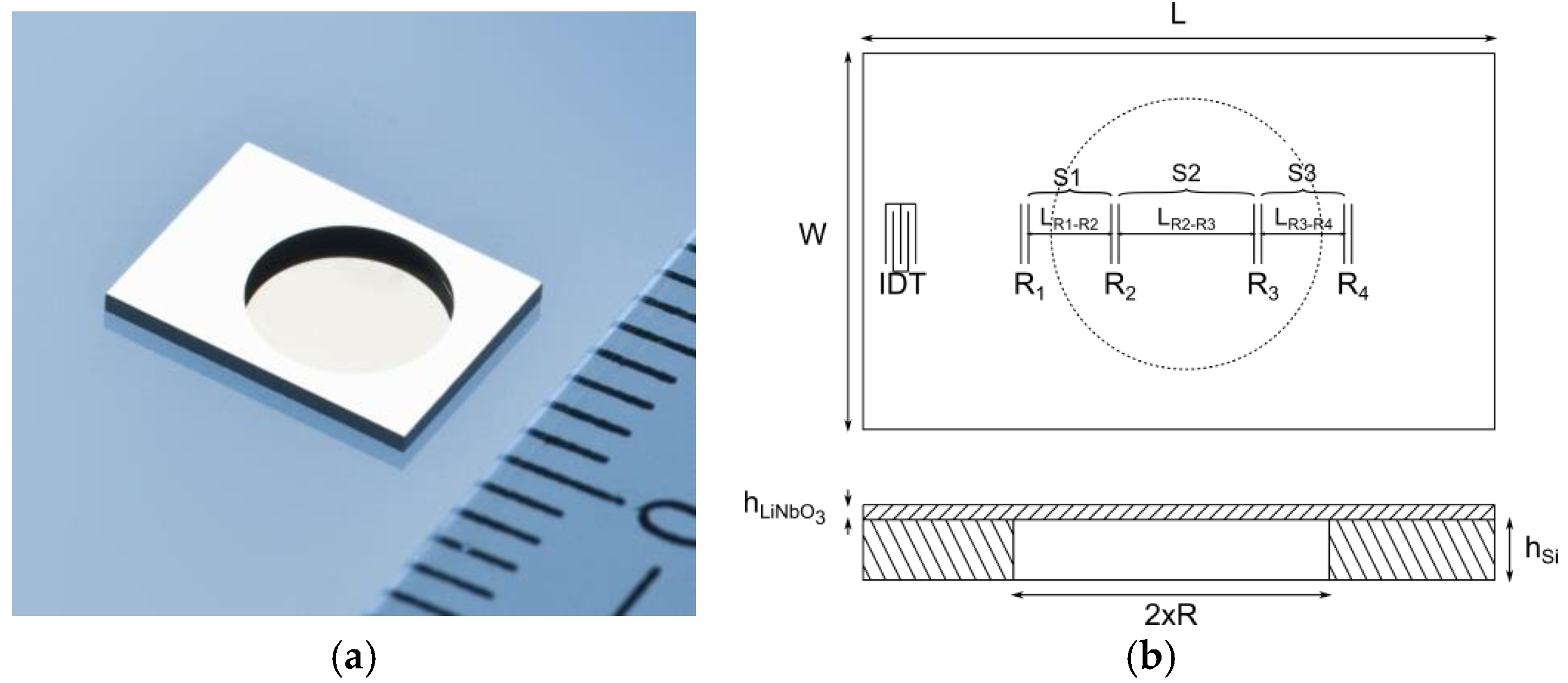
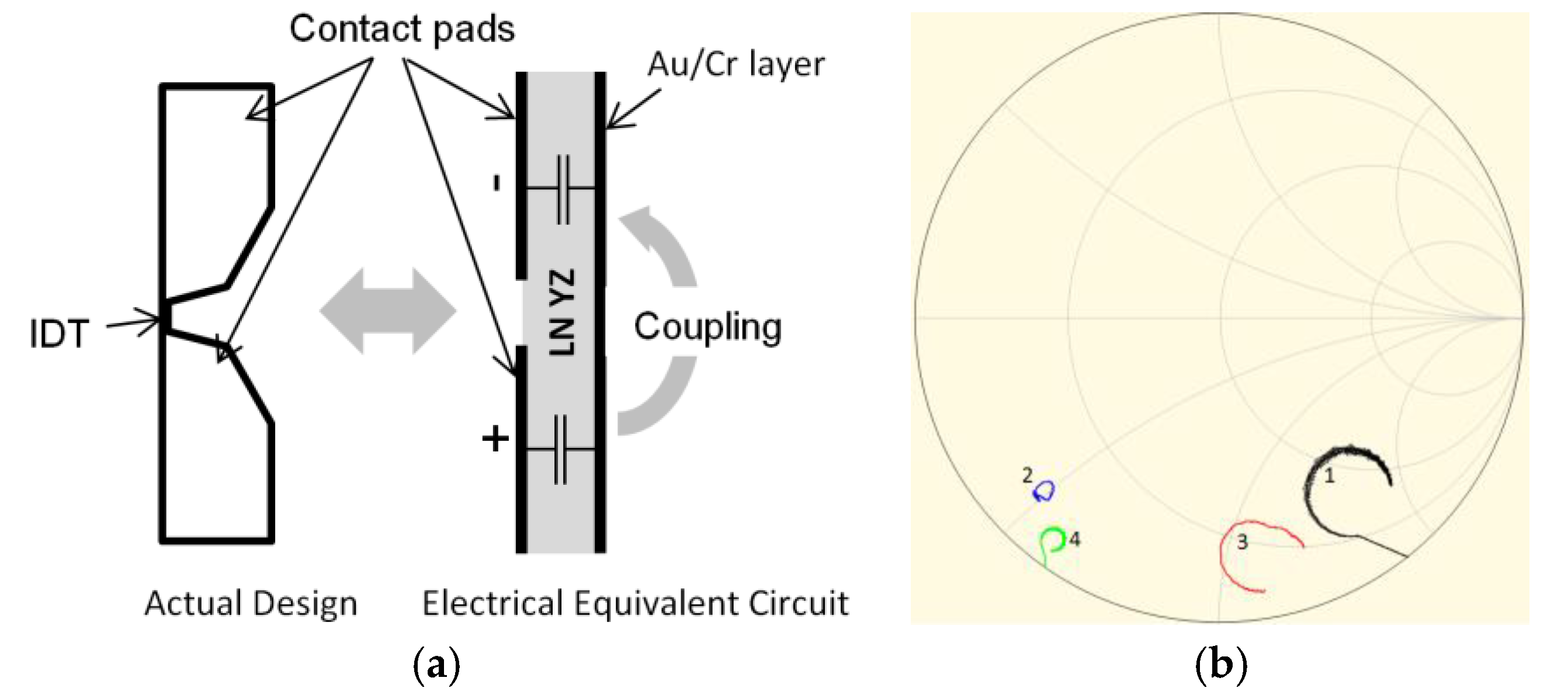
2.2. Sensor Design
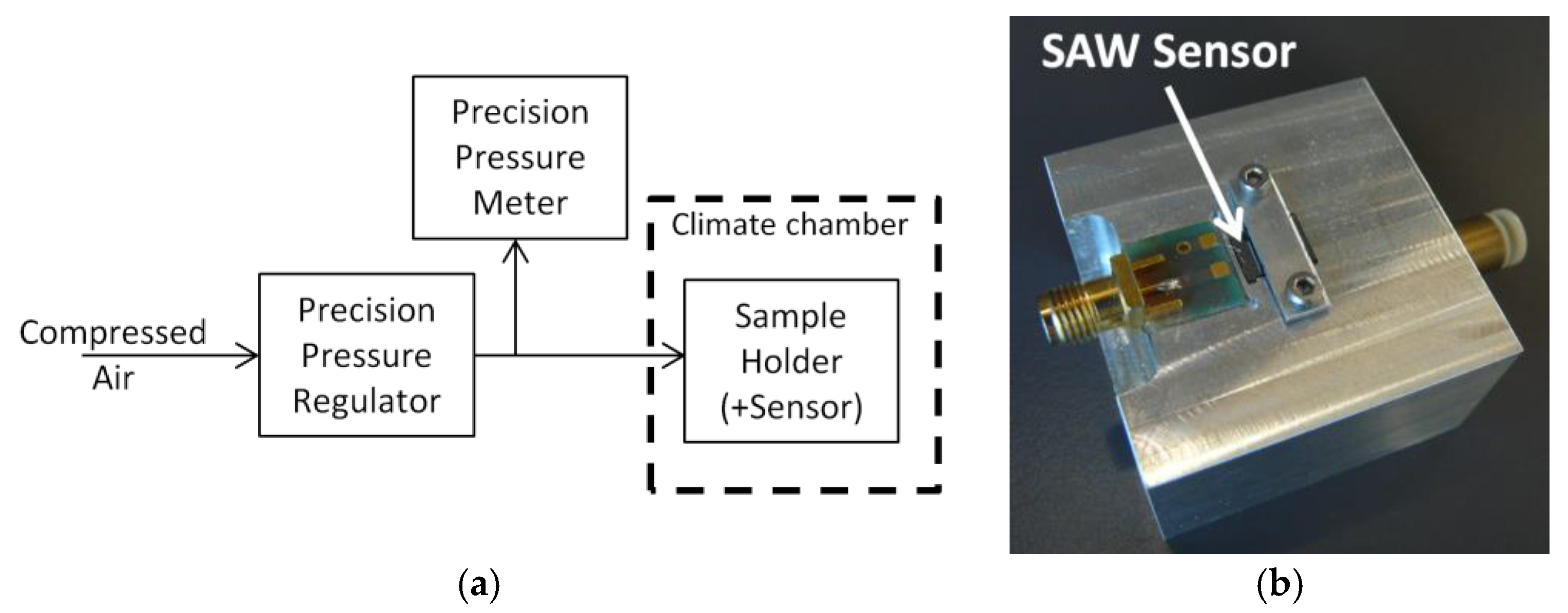
2.3. Characterization Set-Up and Procedure
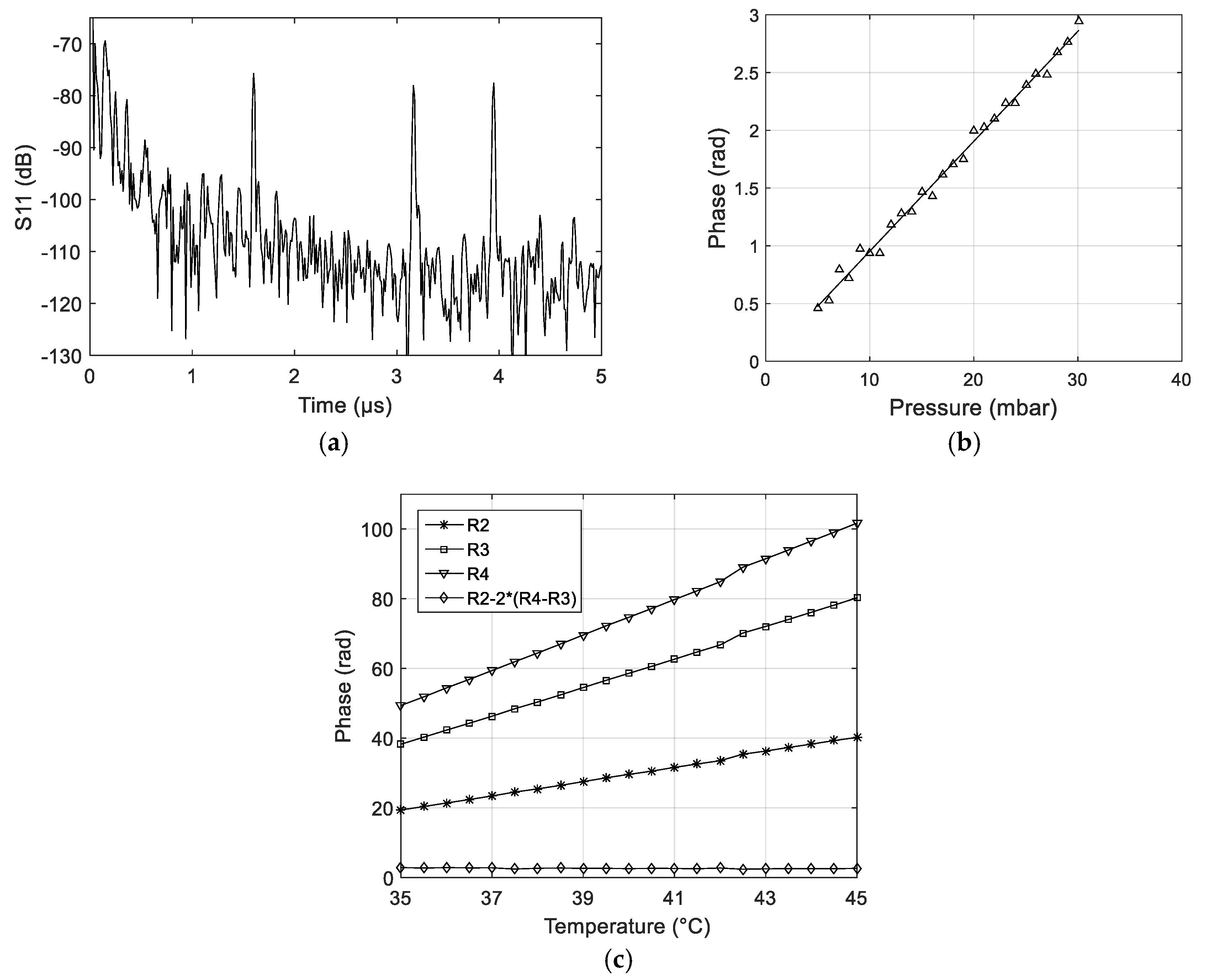
3. Results
4. Discussion
4.1. Residual Temperature Sensitivity
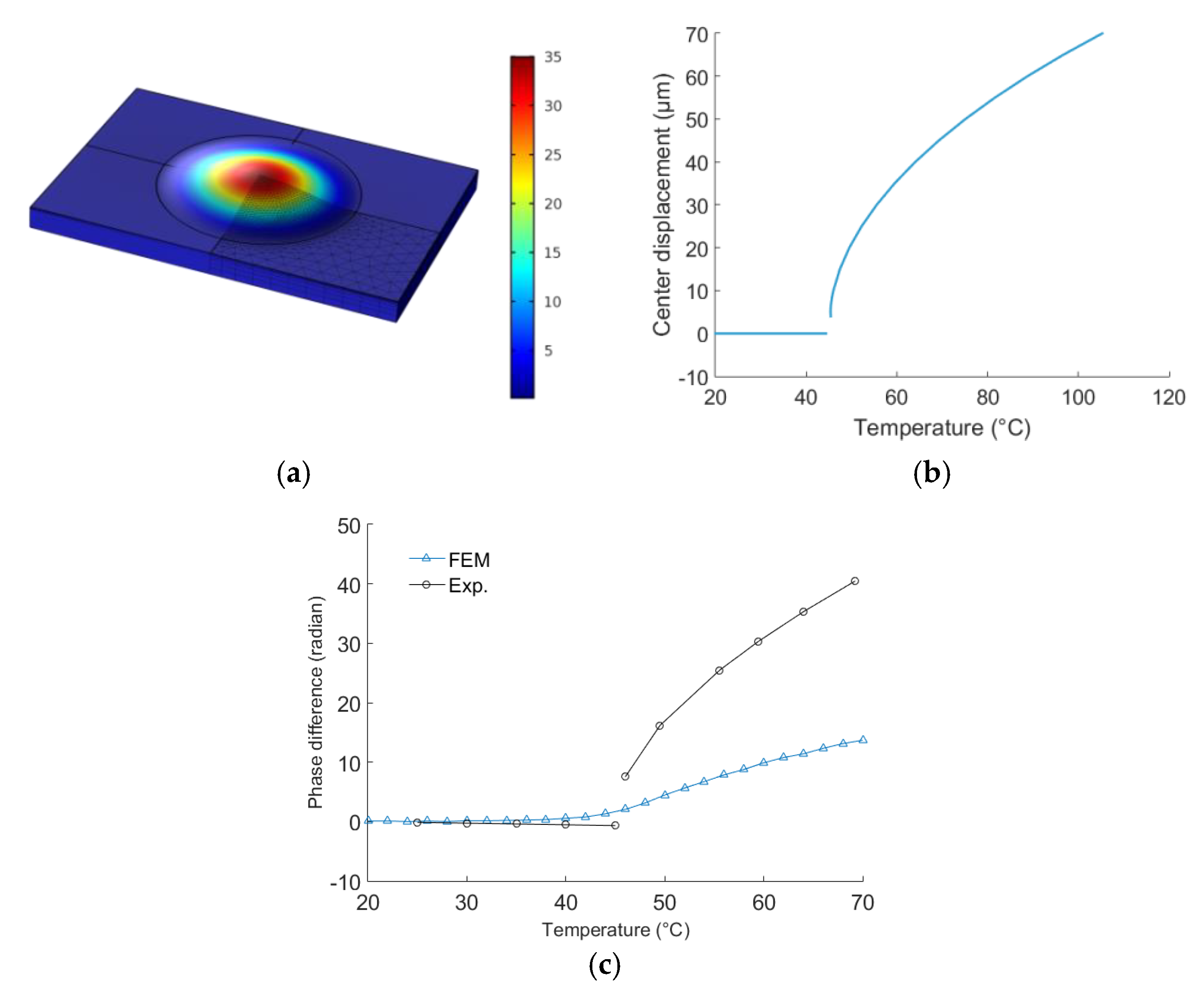
4.2. Membrane Buckling
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Springer, A.; Weigel, R.; Pohl, A.; Seifert, F. Wireless identification and sensing using surface acoustic wave devices. Mechatronics 1999, 9, 745–756. [Google Scholar] [CrossRef]
- Pohl, A. A review of wireless SAW sensors. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2000, 47, 317–332. [Google Scholar] [CrossRef] [PubMed]
- Buff, W. SAW sensors for direct and remote measurement. In Proceedings of the 2002 IEEE Ultrasonics Symposium, Munich, Germany, 8–11 October 2002; Volume 1, pp. 435–443. [Google Scholar]
- Kalinin, V. Wireless physical SAW sensors for automotive applications. In Proceedings of the 2011 IEEE International Ultrasonics Symposium, Orlando, FL, USA; 2011; pp. 212–221. [Google Scholar] [CrossRef]
- Reindl, L.M. Wireless Passive Sensors: Basic principles and performances. In Proceedings of the 2008 IEEE SENSORS, Lecce, Italy, 24–28 October 2008; pp. 1607–1610. [Google Scholar]
- Pereira da Cunha, M.; Maskay, A.; Lad, R.J.; Coyle, T.; Harkay, G. Langasite 2.45 GHz ISM band SAW resonator for harsh environment wireless applications. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016; pp. 1–4. [Google Scholar]
- Fisher, B.H.; Malocha, D.C. Cryogenic Liquid Sensing Using SAW Devices. In Proceedings of the 2007 IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum, Geneva, Switzerland, 29 May–1 June 2007; pp. 505–510. [Google Scholar]
- Greve, D.W.; Chin, T.L.; Zheng, P.; Ohodnicki, P.; Baltrus, J.; Oppenheim, I.J. Surface Acoustic Wave Devices for Harsh Environment Wireless Sensing. Sensors 2013, 13, 6910–6935. [Google Scholar] [CrossRef] [PubMed]
- Nicolay, P.; Chambon, H.; Bruckner, G. SAW RFID sensors and devices for industrial applications, a short review. In Proceedings of the 7th International Symposium on Aircraft Materials (ACMA2018), Compiègne, France, 24–26 April 2018. [Google Scholar]
- Collin, G.; Chami, A.; Luxey, C.; Le Thuc, P.; Staraj, R. Human implanted spiral antenna for a 2. In 45 GHz wireless temperature and pressure SAW sensor system. In Proceedings of the 2008 IEEE Antennas and Propagation Society International Symposium, San Diego, CA, USA, 5–11 July 2008; pp. 1–4. [Google Scholar]
- Tourette, S.; Chommeloux, L.; Le Guen, J.-F.; Friedt, J.-M.; Ménage, P.; Collin, G.; Staraj, R.; Hermelin, D.; Ballandras, S.; Luxey, C.; et al. Implantable SAW sensor for telemetry of temperature and blood pressure: The ANR-TECSAN CIMPA project. IRBM 2010, 31, 101–106. [Google Scholar] [CrossRef]
- Liang, B.; Fang, L.; Tu, C.L.; Zhou, C.C.; Wang, X.J.; Wang, Q.; Wang, P.; Ye, X.S. A novel implantable SAW sensor for blood pressure monitoring. In Proceedings of the 2011 16th International Solid-State Sensors, Actuators and Microsystems Conference, Beijing, China, 5–9 June 2011; pp. 2184–2187. [Google Scholar]
- Murphy, O.H.; Bahmanyar, M.R.; Borghi, A.; McLeod, C.N.; Navaratnarajah, M.; Yacoub, M.H.; Toumazou, C. Continuous in vivo blood pressure measurements using a fully implantable wireless SAW sensor. Biomed. Microdevices 2013. [Google Scholar] [CrossRef] [PubMed]
- Bruckner, G.; Schicker, J.; Schobernig, N.; Stojanov, V.; Schlumpf, P. Design Study of a Wireless Pressure Sensor for Medical Application. In Proceedings of the AMA Conferences 2013, Nürnberg, Gemany, 14–16 May 2013; pp. 192–197. [Google Scholar] [CrossRef]
- Grousset, S.; Augendre, E.; Benaissa, L.; Signamarcheix, T.; Baron, T.; Courjon, E.; Ballandras, S. SAW Pressure Sensor Based on Single-Crystal Quartz Layer Transferred on Silicon. In Proceedings of the 2013 Joint UFFC, EFTF and PFM Symposium, Prague, Czech Republic, 21–25 July 2013; pp. 980–983. [Google Scholar]
- Beckley, J.; Kalinin, V.; Lee, M.; Voliansky, K. Non-contact torque sensors based on SAW resonators. In Proceedings of the 2002 IEEE International Frequency Control Symposium and PDA Exhibition (Cat. No.02CH37234), New Orleans, LA, USA, 31 May 2002; pp. 202–213. [Google Scholar]
- Reindl, L.; Scholl, G.; Ostertag, T.; Scherr, H.; Wolff, U.; Schmidt, F. Theory and application of passive SAW radio transponders as sensors. Trans. Ultrason. Ferroelectr. Freq. Control 1998, 45, 1281–1292. [Google Scholar] [CrossRef] [PubMed]
- Devkota, J.; Ohodnicki, P.R.; Greve, D.W. SAW Sensors for Chemical Vapors and Gases. Sensors 2017, 17, 801. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Lee, K.; Woo, I.; Park, I.; Yang, S. Optimal design on SAW sensor for wireless pressure measurement based on reflective delay line. Sens. Actuators A Phys. 2007, 139, 2–6. [Google Scholar] [CrossRef]
- Menzel, S.; Pekarcikova, M.; Hofmann, M.; Gemming, T.; Wetzig, K. Material transport in Al-metallizations of power-loaded SAW structures. Appl. Surface Sci. 2005, 252, 215–217. [Google Scholar] [CrossRef]
- Scherr, H.; Scholl, G.; Seifert, F.; Weigel, R. Quartz pressure sensor based on SAW reflective delay line. In Proceedings of the 1996 IEEE Ultrasonics Symposium, San Antonio, TX, USA, 3–6 November 1996; Volume 1, pp. 347–350. [Google Scholar]
- Fachberger, R.; Bruckner, G.; Hauser, R.; Reindl, L. Wireless SAW based high-temperature measurement systems. In Proceedings of the 2006 IEEE International Frequency Control Symposium and Exposition, Miami, FL, USA, 5–7 June 2006; pp. 358–367. [Google Scholar]
- Binder, A.; Fachberger, R.; Lenzhofer, M. Phase stability comparison of SAW sensor evaluation with various CW type radars. In Proceedings of the Eurosensors XXIV, Linz, Austria, 5–8 September 2010. [Google Scholar]
- Chambon, H.; Nicolay, P.; Bruckner, G.; Benjeddou, A. Analysis of the sensitivity to pressure and temperature of a membrane based SAW sensor. Int. J. Smart Nano Mater. 2017, 8, 95–109. [Google Scholar] [CrossRef]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicolay, P.; Chambon, H.; Bruckner, G.; Gruber, C.; Ballandras, S.; Courjon, E.; Stadler, M. A LN/Si-Based SAW Pressure Sensor. Sensors 2018, 18, 3482. https://doi.org/10.3390/s18103482
Nicolay P, Chambon H, Bruckner G, Gruber C, Ballandras S, Courjon E, Stadler M. A LN/Si-Based SAW Pressure Sensor. Sensors. 2018; 18(10):3482. https://doi.org/10.3390/s18103482
Chicago/Turabian StyleNicolay, Pascal, Hugo Chambon, Gudrun Bruckner, Christian Gruber, Sylvain Ballandras, Emilie Courjon, and Matthias Stadler. 2018. "A LN/Si-Based SAW Pressure Sensor" Sensors 18, no. 10: 3482. https://doi.org/10.3390/s18103482
APA StyleNicolay, P., Chambon, H., Bruckner, G., Gruber, C., Ballandras, S., Courjon, E., & Stadler, M. (2018). A LN/Si-Based SAW Pressure Sensor. Sensors, 18(10), 3482. https://doi.org/10.3390/s18103482





