Adaptive Single Photon Compressed Imaging Based on Constructing a Smart Threshold Matrix
Abstract
1. Introduction
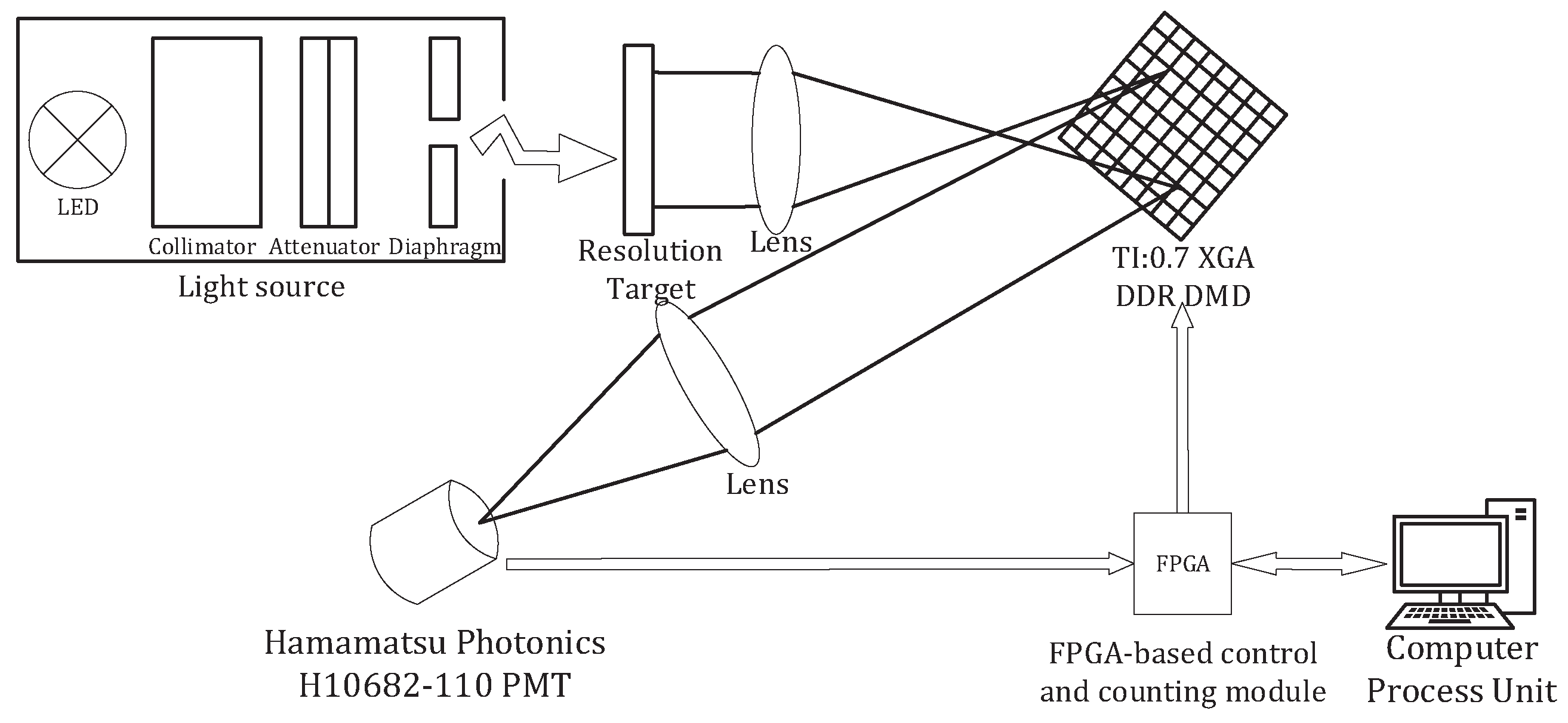
2. Principle and Realization of Single-Photon Compressed Imaging
3. The Construction of an Adaptive Measurement Matrix
4. Experimental Results and Discussion
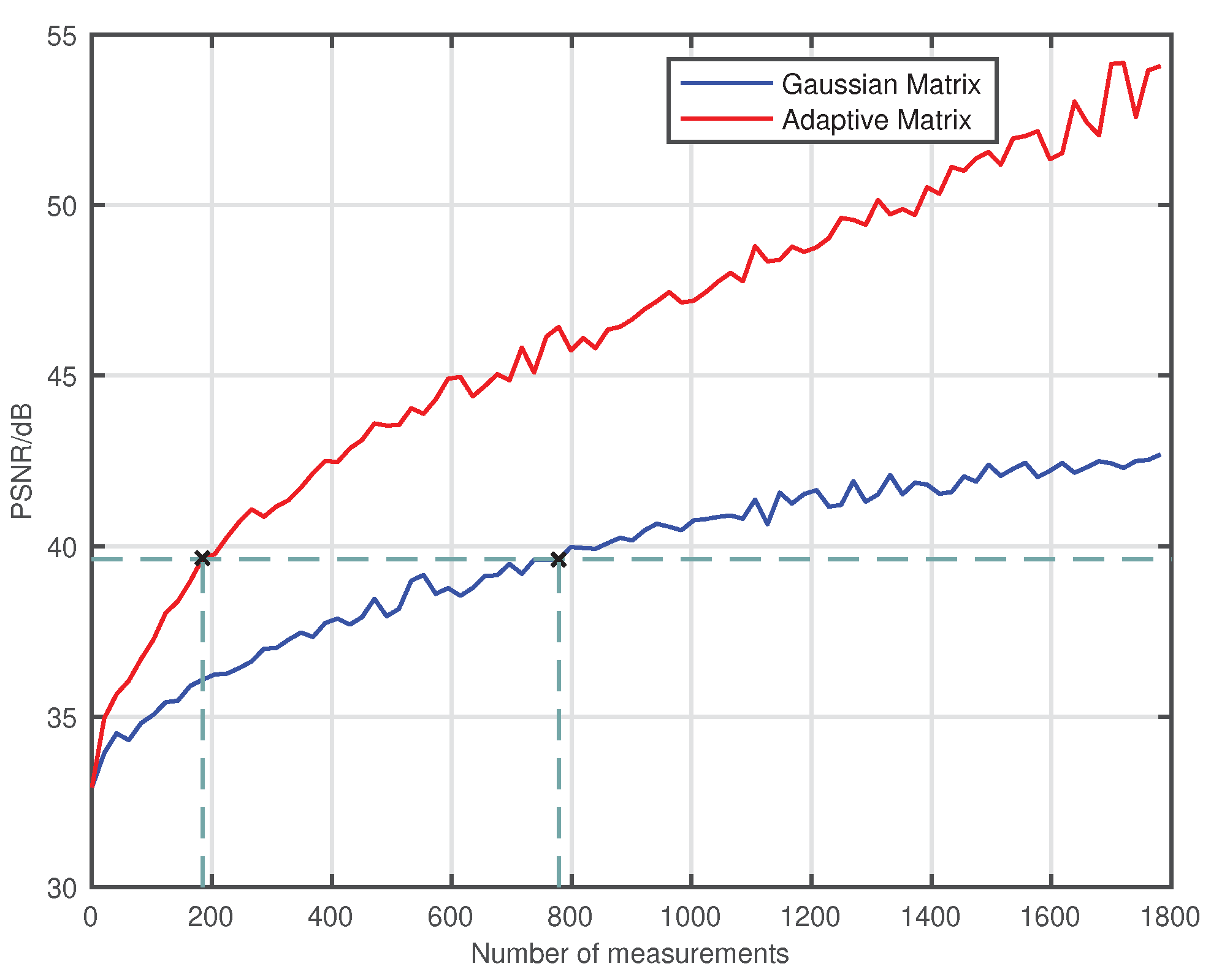
4.1. Effect of Measurement Times on Imaging Quality
4.2. Effect of Reconstruction Algorithm on Imaging Quality
4.3. Anti-Noise Ability of Adaptive Measurement Matrix
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Studer, V.; Bobin, J.; Chahid, M.; Mousavi, H.S.; Candes, E.; Dahan, M. Compressive fluorescence microscopy for biological and hyperspectral imaging. Proc. Natl. Acad. Sci. USA 2012, 109, 10136–10137. [Google Scholar] [CrossRef] [PubMed]
- Becker, W.; Bergmann, A.; Hink, M.A.; König, K.; Benndorf, K.; Biskup, C. Fluorescence lifetime imaging by time-correlated single-photon counting. Microsc. Res. Tech. 2004, 63, 58–66. [Google Scholar] [CrossRef] [PubMed]
- Pourmorteza, A.; Symons, R.; Sandfort, V.; Mallek, M.; Fuld, M.K.; Henderson, G.; Jones, E.C.; Malayeri, A.A.; Folio, L.R.; Bluemke, D.A. Abdominal Imaging with Contrast-enhanced Photon-counting CT: First Human Experience. Radiology 2016, 279, 239–245. [Google Scholar] [CrossRef] [PubMed]
- Taguchi, K.; Iwanczyk, J.S. Vision 20/20: Single photon counting x-ray detectors in medical imaging. Med. Phys. 2013, 40, 100901. [Google Scholar] [CrossRef] [PubMed]
- Michel, J.; Liu, J.; Kimerling, L.C. High-performance Ge-on-Si photodetectors. Nat. Photonics 2010, 4, 527–534. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Namekata, N.; Sasamori, S.; Inoue, S. 800 MHz single-photon detection at 1550-nm using an InGaAs/InP avalanche photodiode operated with a sine wave gating. Opt. Express 2006, 14, 10043–10049. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Sima, B.; Cheng, Y.; Chen, W.; Chen, Q. Photon counting imaging based on GM-APD. Opt. Precis. Eng. 2012, 20, 1831–1837. [Google Scholar] [CrossRef]
- Roth, J.M.; Murphy, T.E.; Xu, C. Ultrasensitive and high-dynamic-range two-photon absorption in a GaAs photomultiplier tube. Opt. Lett. 2002, 27, 2076. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.K.; Liu, X.F.; Yao, X.R.; Wang, C.; Zhai, G.J.; Zhao, Q. Single-photon compressive imaging with some performance benefits over raster scanning. Phys. Lett. A 2014, 378, 3406–3411. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Averbuch, A.; Dekel, S.; Deutsch, S. Adaptive compressed image sensing using dictionaries. SIAM J. Imaging Sci. 2012, 5, 57–89. [Google Scholar] [CrossRef]
- Aβmann, M.; Bayer, M. Compressive adaptive computational ghost imaging. Sci. Rep. 2013, 3, 1545. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Hou, J.M.; Ning, H.E.; Ke, L.V. Image Fast Reconstruction Method Based on Compressive Sensing. Comput. Eng. 2011, 37, 215–216. [Google Scholar] [CrossRef]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic decomposition by basis pursuit. SIAM Rev. 2001, 43, 129–159. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Needell, D.; Vershynin, R. Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit. Found. Comput. Math. 2009, 9, 317–334. [Google Scholar] [CrossRef]
- Blumensath, T.; Davies, M.E. Iterative hard thresholding for compressed sensing. Appl. Comput. Harmonic Anal. 2009, 27, 265–274. [Google Scholar] [CrossRef]
- Thomas, B.; Davies, M.E. Normalized Iterative Hard Thresholding: Guaranteed Stability and Performance. IEEE J. Sel. Top. Signal Process. 2010, 4, 298–309. [Google Scholar] [CrossRef]
- Blumensath, T. Accelerated iterative hard thresholding. Signal Process. 2012, 92, 752–756. [Google Scholar] [CrossRef]
- Li, C.; Yin, W.; Jiang, H.; Zhang, Y. An efficient augmented Lagrangian method with applications to total variation minimization. Comput. Optim. Appl. 2013, 56, 507–530. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, S.; Xiong, R.; Ma, S.; Zhao, D. Improved total variation based image compressive sensing recovery by nonlocal regularization. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS2013), Beijing, China, 19–23 May 2013; pp. 2836–2839. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Near-Optimal Signal Recovery From Random Projections: Universal Encoding Strategies? IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Candès, E.J. Compressive Sampling. In Proceedings of the International Congress of Mathematiciansm, Madrid, Spain, 22–30 August 2006; pp. 1433–1452. [Google Scholar] [CrossRef]
- Chen, T.; Li, Z.-W.; Wang, J.L.; Wang, B.; Guo, S. Imaging system of single pixel camera based on compressed sensing. Opt. Precis. Eng. 2012, 20, 2523–2530. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Decoding by linear programming. IIEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2010, 59, 1207–1223. [Google Scholar] [CrossRef]
- Li, S.-T.; Wei, D. A Survey on Compressive Sensing. Acta Autom. Sin. 2009, 35, 1369–1377. [Google Scholar] [CrossRef]
- Liu, X.F.; Yao, X.R.; Wang, C.; Guo, X.Y.; Zhai, G.J. Quantum limit of photon-counting imaging based on compressed sensing. Opt. Express 2017, 25, 3286–3296. [Google Scholar] [CrossRef] [PubMed]










© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shangguan, W.; Yan, Q.; Wang, H.; Yuan, C.; Li, B.; Wang, Y. Adaptive Single Photon Compressed Imaging Based on Constructing a Smart Threshold Matrix. Sensors 2018, 18, 3449. https://doi.org/10.3390/s18103449
Shangguan W, Yan Q, Wang H, Yuan C, Li B, Wang Y. Adaptive Single Photon Compressed Imaging Based on Constructing a Smart Threshold Matrix. Sensors. 2018; 18(10):3449. https://doi.org/10.3390/s18103449
Chicago/Turabian StyleShangguan, Wentao, Qiurong Yan, Hui Wang, Chenglong Yuan, Bing Li, and Yuhao Wang. 2018. "Adaptive Single Photon Compressed Imaging Based on Constructing a Smart Threshold Matrix" Sensors 18, no. 10: 3449. https://doi.org/10.3390/s18103449
APA StyleShangguan, W., Yan, Q., Wang, H., Yuan, C., Li, B., & Wang, Y. (2018). Adaptive Single Photon Compressed Imaging Based on Constructing a Smart Threshold Matrix. Sensors, 18(10), 3449. https://doi.org/10.3390/s18103449




