Using the Pulse Contour Method to Measure the Changes in Stroke Volume during a Passive Leg Raising Test
Abstract
1. Introduction
2. Methods
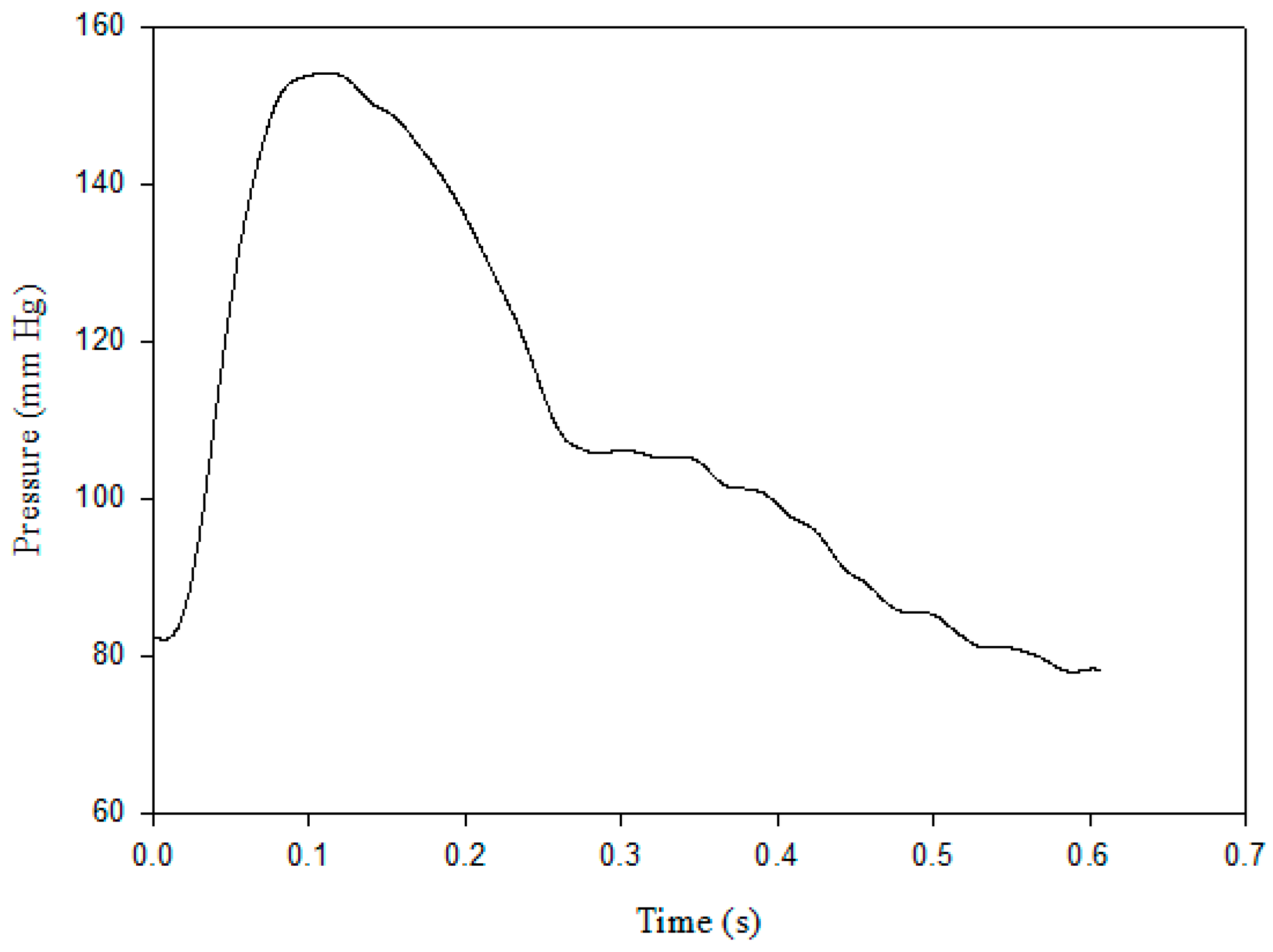
2.1. Pulse Contour Measurement
2.2. Compliance of Brachial Artery
2.3. Resistance of Peripheral Artery
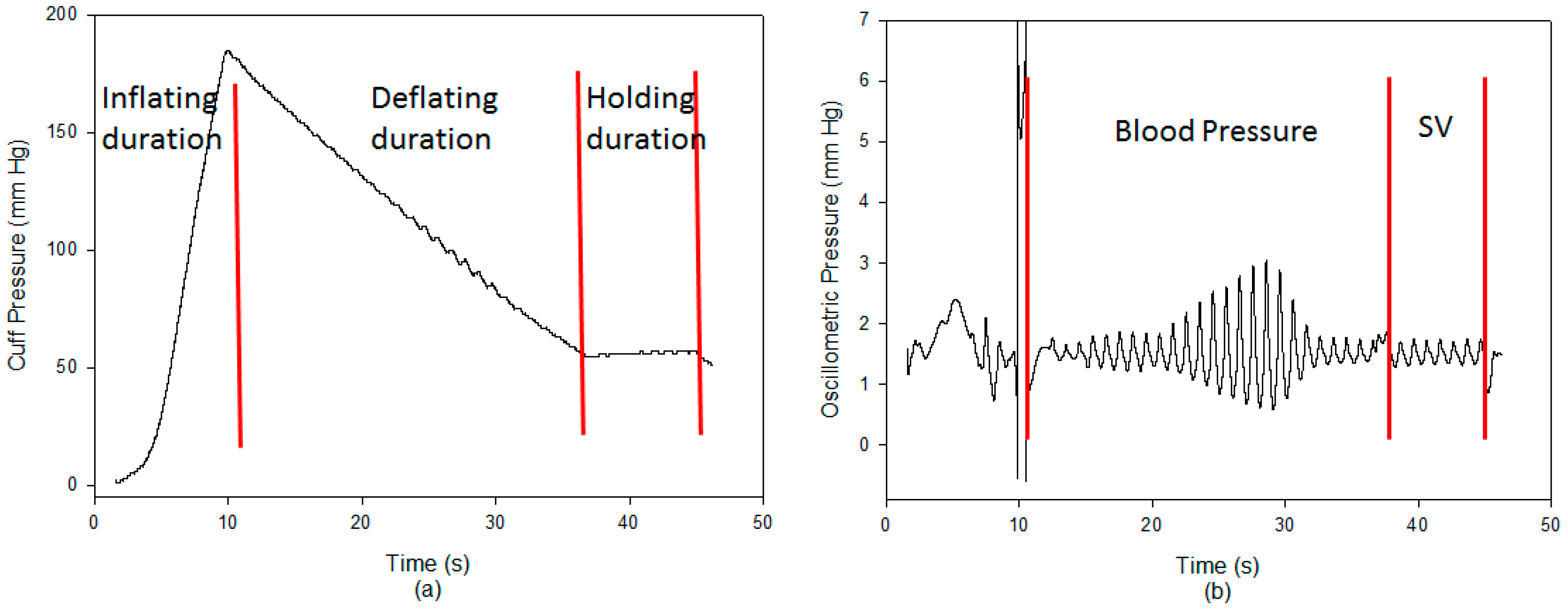
2.4. Stroke Volume Measurement
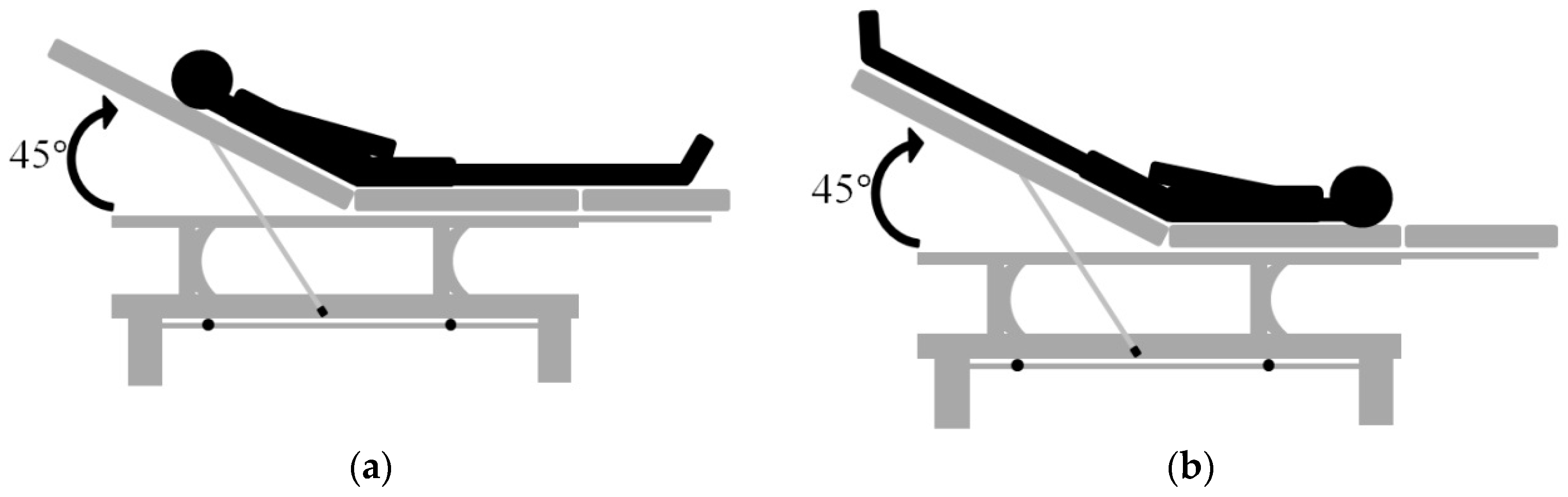
2.5. Experimental Protocol
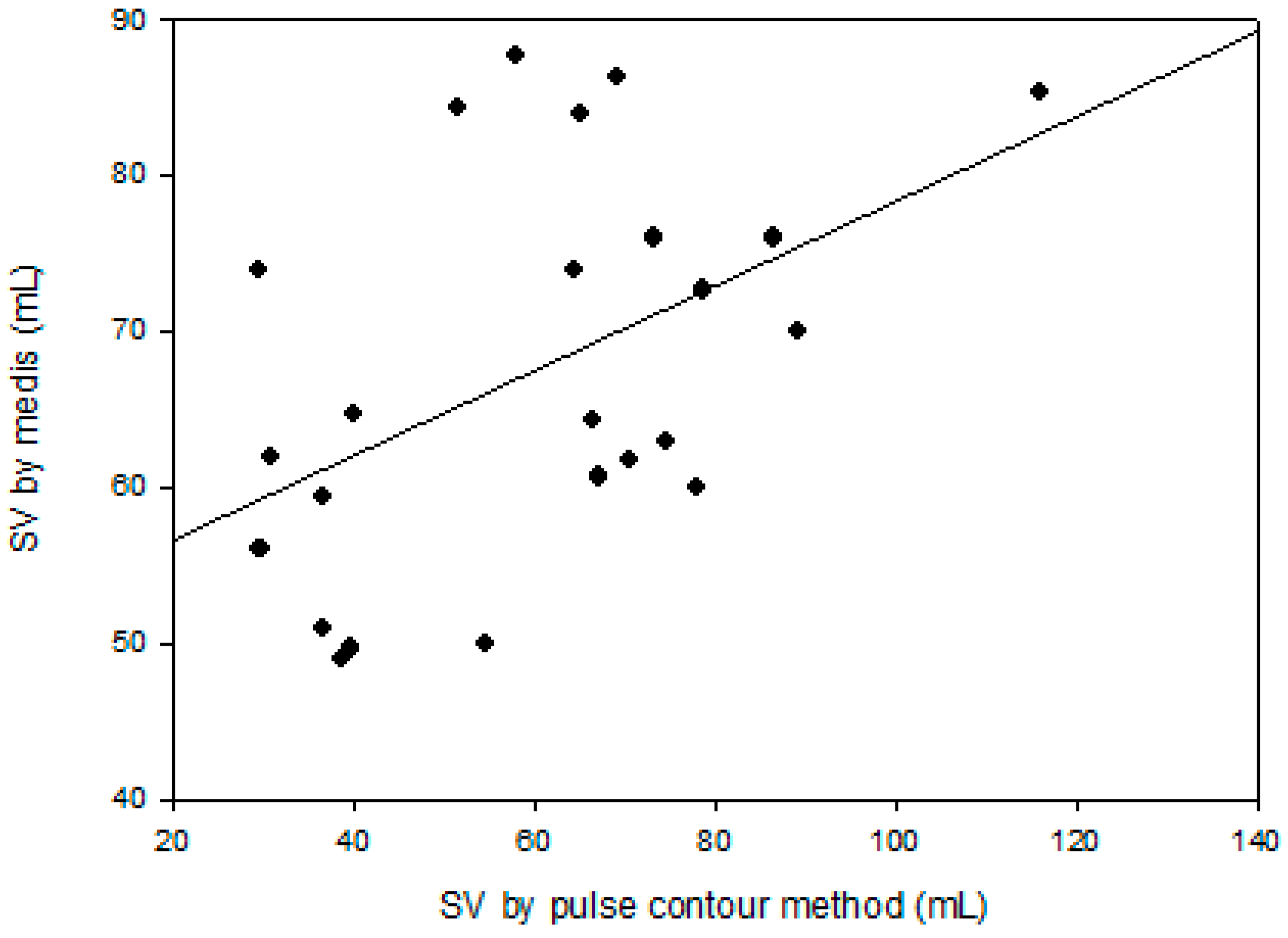
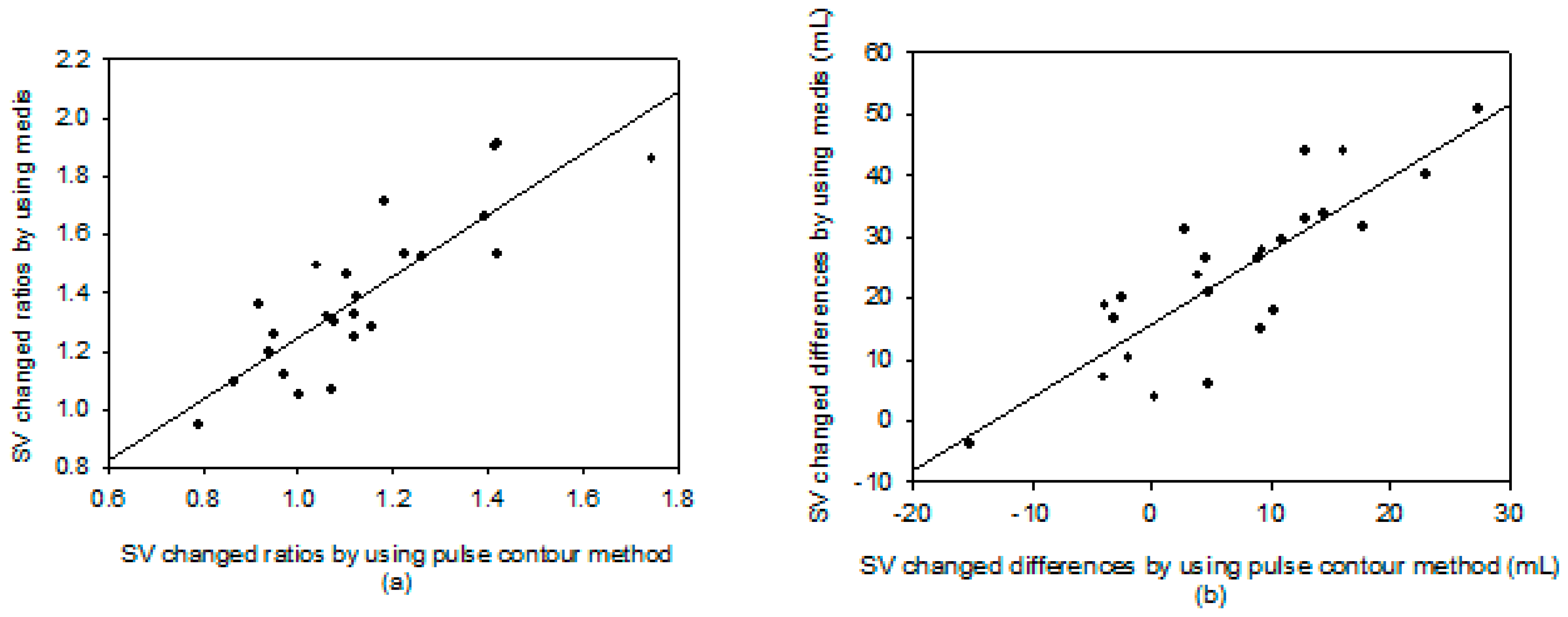
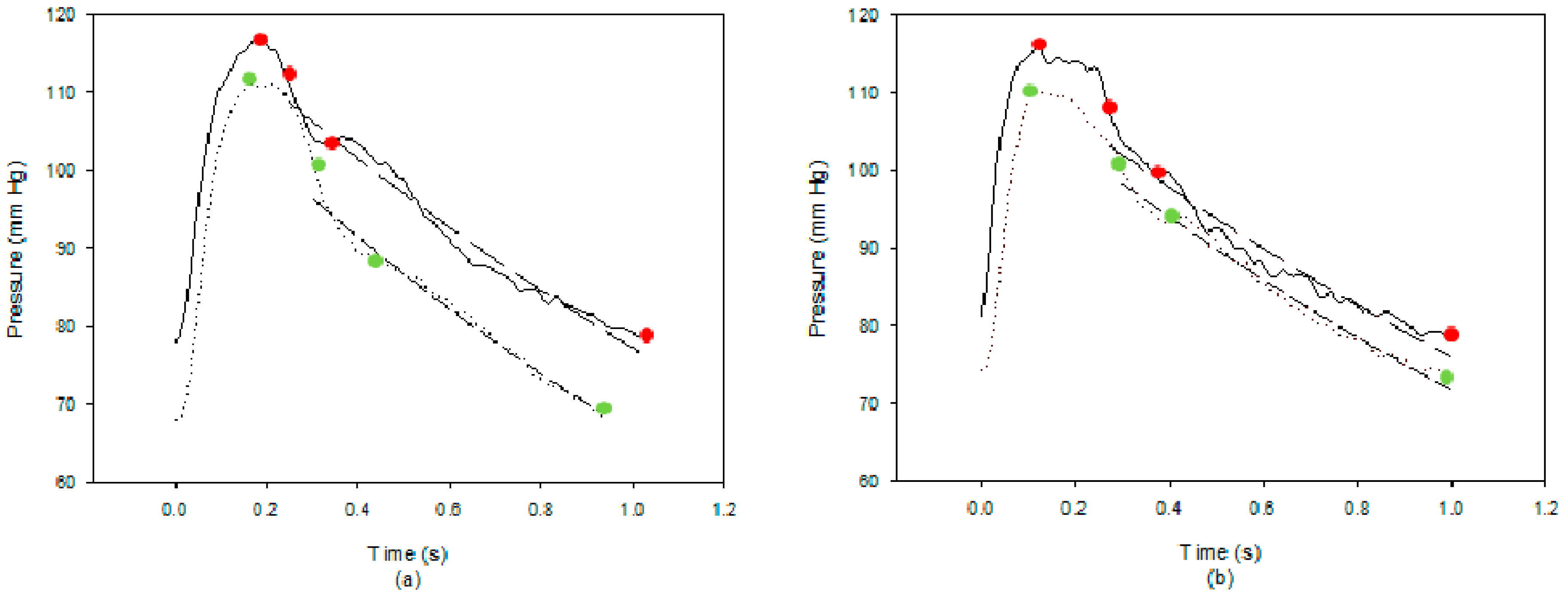
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Phillips, R.A.; Smith, B.E.; Madigan, V.M. Stroke volume monitoring: Novel continuous wave Doppler parameters, algorithms and advanced noninvasive hemodynamic concepts. Curr. Anesthesiol. Rep. 2017, 7, 387–398. [Google Scholar] [CrossRef] [PubMed]
- Braun, F.; ProencËa, M.; Adler, A.; Riedel, T.; Thiran, J.-P.; Solà, J. Accuracy and reliability of noninvasive stroke volume monitoring via ECG-gated 3D electrical impedance tomography in healthy volunteers. PLoS ONE 2018, 13, e0191870. [Google Scholar] [CrossRef] [PubMed]
- Kern, J.W.; Shoemaker, W.C. Meta-analysis of hemodynamic optimization in high-risk patients. Crit. Care Med. 2002, 30, 1686–1692. [Google Scholar] [CrossRef] [PubMed]
- Drzewiecki, G.; Hood, R.; Apple, H. Theory of the oscillometric maximum and the systolic and diastolic detection ratios. Ann. Biomed. Eng. 1994, 22, 88–96. [Google Scholar] [CrossRef] [PubMed]
- Schiller, N.; Acquatella, H.; Ports, Y.; Drew, D.; Goerke, J.; Ringertz, H.; Silverman, N.H.; Brundage, B.; Botvinick, E.H.; Boswell, R.; et al. Left ventricular volume from paired bioplane two-dimensional echocardiography. Circulation 1979, 60, 547–555. [Google Scholar] [CrossRef] [PubMed]
- Kubicek, W.G.; Karngis, J.N.; Patterson, R.P.; Wrrsoe, D.A.; Mattson, R.H. Development and evaluation of an impedance cardiac output system. Aerosp. Med. 1966, 37, 1208–1212. [Google Scholar] [PubMed]
- Joosten, A.; Desebbe, O.; Suehiro, K.; Murphy, L.S.L.; Essiet, M.; Alexander, B.; Fischer, M.-O.; Barvais, L.; Van Obbergh, L.; Maucort-Boulch, D.; et al. Accuracy and precision of non-Invasive cardiac output monitoring devices in perioperative medicine: A systematic review and meta-analysis. Br. J. Anaesth. 2017, 118, 298–310. [Google Scholar] [CrossRef] [PubMed]
- Monnet, X.; Teboul, J.L. Passive leg raising. Intensive Care Med. 2008, 34, 659–663. [Google Scholar] [CrossRef] [PubMed]
- Rocha, P.; Lemaigre, D.; Leroy, M.; Desfonds, P.; De Zuttere, D.; Liot, F. Nitroglycerin induced decrease of carbon monoxide diffusion capacity in acute myocardial infarction reversed by elevating legs. Crit. Care Med. 1987, 15, 131–133. [Google Scholar] [CrossRef] [PubMed]
- Michard, F.; Teboul, J.L. Predicting fluid responsiveness in ICU patients: A critical analysis of the evidence. Chest 2002, 121, 2000–2008. [Google Scholar] [CrossRef] [PubMed]
- Wesseling, K.H.; Jansen, J.C.; Settels, J.J.; Schreuder, J.J. Computation of artic flow from pressure in humans using a nonlinear three-element model. J. Appl. Physiol. 1993, 74, 2566–2573. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.-H.; Lin, T.-H.; Cheng, D.-C.; Wang, J.-J. Assessment of stroke volume from brachial Blood pressure using arterial characteristics. IEEE Trans. Biomed. Eng. 2015, 62, 2151–2157. [Google Scholar] [CrossRef] [PubMed]
- Romano, S.M.; Pistolesi, M. Assessment of cardiac output from systemic arterial pressure in human. Crit. Care Med. 2002, 30, 1834–1841. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Gao, Z.; Xiong, H.; Ghista, D.; Ren, L.; Zhang, H.; Wu, W.; Huang, W.; Hau, W.K. Three-dimensional hemodynamics analysis of the circle of Willis in the patient-specific nonintegral arterial structures. Biomech. Model. Mechanobiol. 2016, 15, 1439–1456. [Google Scholar] [CrossRef] [PubMed]
- Podbregar, M.; Kosir, M.; Stajar, D.; Zdovc, J.; Plaskan, S. Evaluation of continuous monitoring of stroke volume and cardiac output in patient supported by an intra-aortic balloon pump. Minerva Anestesiol. 2013, 79, 713–715. [Google Scholar]
- Reisner, A.T.; Xu, D.; Ryan, K.L.; Convertino, V.A.; Rickards, C.A.; Mukkamala, R. Monitoring non-invasive cardiac output and stroke volume during experimental human hypovolaemia and resuscitation. Br. J. Anaesth. 2011, 106, 23–30. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Lin, F.-Q.; Fu, S.-K.; Chen, G.-Q.; Yang, X.-H.; Zhu, C.-Y.; Zhang, L.-J.; Li, Q. Stroke volume variation for prediction of fluid responsiveness in patients undergoing gastrointestinal surgery. Int. J. Med. Sci. 2013, 10, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Harms, M.; Wesseling, K.H.; Pott, F.; Jenstrup, M.; Van Goudoever, J.; Secher, N.; Van Lieshout, J. Continuous stroke volume monitoring by modelling flow from non-invasive measurement of arterial pressure in humans under orthostatic stress. Clin. Sci. 1999, 97, 291–301. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Li, Y.; Sun, Y.; Yang, J.; Xiong, H.; Zhang, H.; Liu, X.; Wu, W.; Liang, D.; Li, S. Motion tracking of the carotid artery wall from ultrasound image sequences: A nonlinear state-space approach. IEEE Trans. Med. Imaging 2018, 37, 273–283. [Google Scholar] [CrossRef] [PubMed]
- Cotter, G.; Moshkovitz, Y.; Kaluski, E.; Cohen, A.; Miller, H.; Goor, D.; Vered, Z. Accurate, Noninvasive continuous monitoring of cardiac output by whole-body electrical bioimpedance. Chest 2004, 125, 1431–1440. [Google Scholar] [CrossRef] [PubMed]
- Sageman, W.S.; Riffenburgh, R.H.; Spiess, B.D. Equivalence of bioimpedance and thermodilution in measuring cardiac index after cardiac surgery. J. Cardiothorac. Vasc. Anesth. 2002, 16, 8–14. [Google Scholar] [CrossRef] [PubMed]
- Monnet, X.; Rienzo, M.; Osman, D.; Anguel, N.; Richard, C.; Pinsky, M.R.; Teboul, J.L. Passive leg raising predicts fluid responsiveness in the critically ill. Crit. Care Med. 2006, 34, 1402–1407. [Google Scholar] [PubMed]
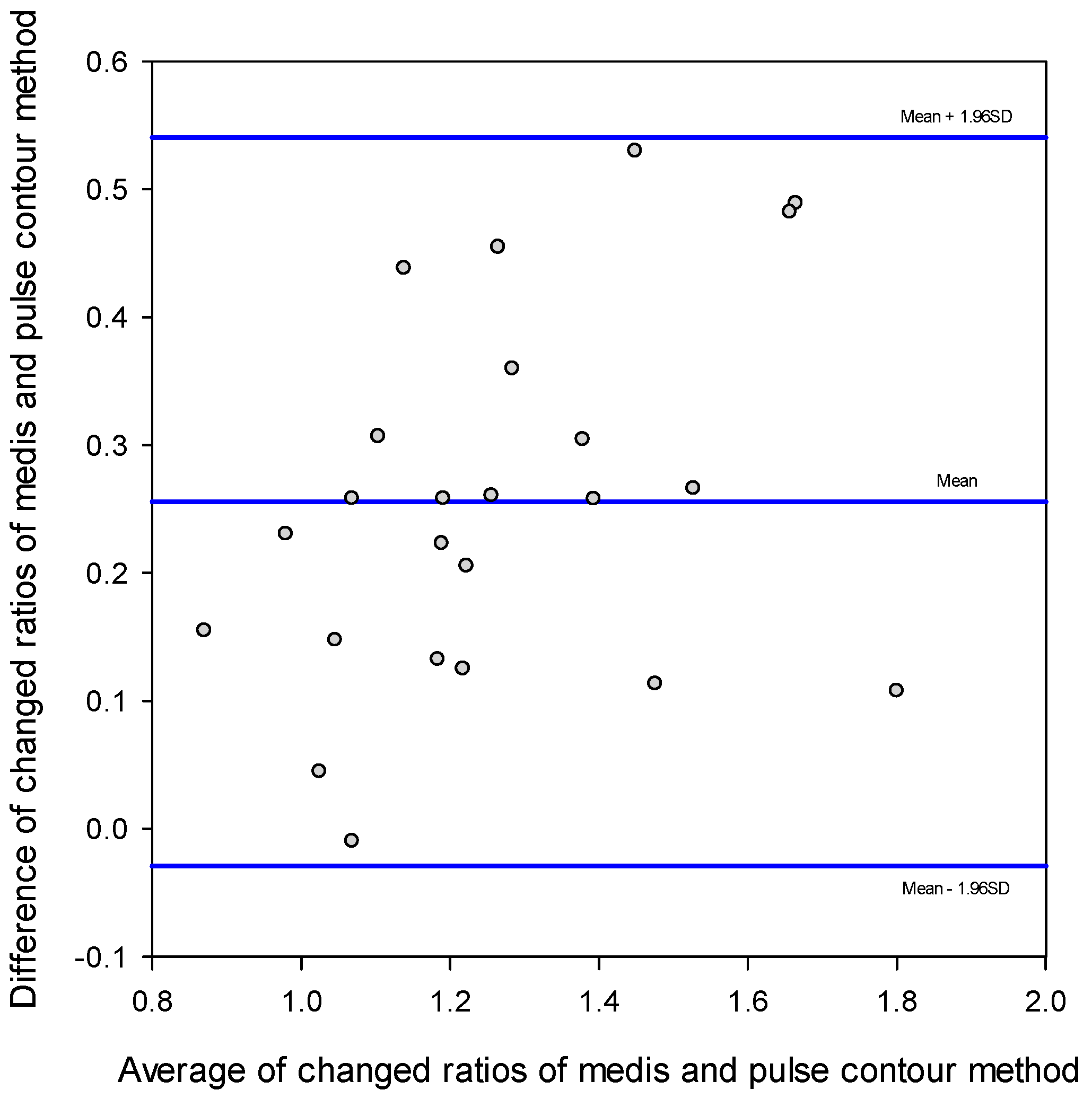
| i-BP 130 | Medis | |||
|---|---|---|---|---|
| Before | Under | Before | Under | |
| Sys (mm Hg) | 117.0 ± 17.1 | 115.9 ± 16.1 | ||
| Dia (mm Hg) | 80.0 ± 11.7 | 74.9 ± 10.0 ** | ||
| PP (mm Hg) | 37.0 ± 6.7 | 41.0 ± 8.8 * | ||
| SV (mL) | 60.3 ± 22.1 | 67.1 ± 22.1 * | 67.5 ± 12.4 | 91.2 ± 11.4 * |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, C.-H.; Liu, S.-H.; Tan, T.-H.; Lo, C.-H. Using the Pulse Contour Method to Measure the Changes in Stroke Volume during a Passive Leg Raising Test. Sensors 2018, 18, 3420. https://doi.org/10.3390/s18103420
Su C-H, Liu S-H, Tan T-H, Lo C-H. Using the Pulse Contour Method to Measure the Changes in Stroke Volume during a Passive Leg Raising Test. Sensors. 2018; 18(10):3420. https://doi.org/10.3390/s18103420
Chicago/Turabian StyleSu, Chun-Hung, Shing-Hong Liu, Tan-Hsu Tan, and Chien-Hsien Lo. 2018. "Using the Pulse Contour Method to Measure the Changes in Stroke Volume during a Passive Leg Raising Test" Sensors 18, no. 10: 3420. https://doi.org/10.3390/s18103420
APA StyleSu, C.-H., Liu, S.-H., Tan, T.-H., & Lo, C.-H. (2018). Using the Pulse Contour Method to Measure the Changes in Stroke Volume during a Passive Leg Raising Test. Sensors, 18(10), 3420. https://doi.org/10.3390/s18103420







