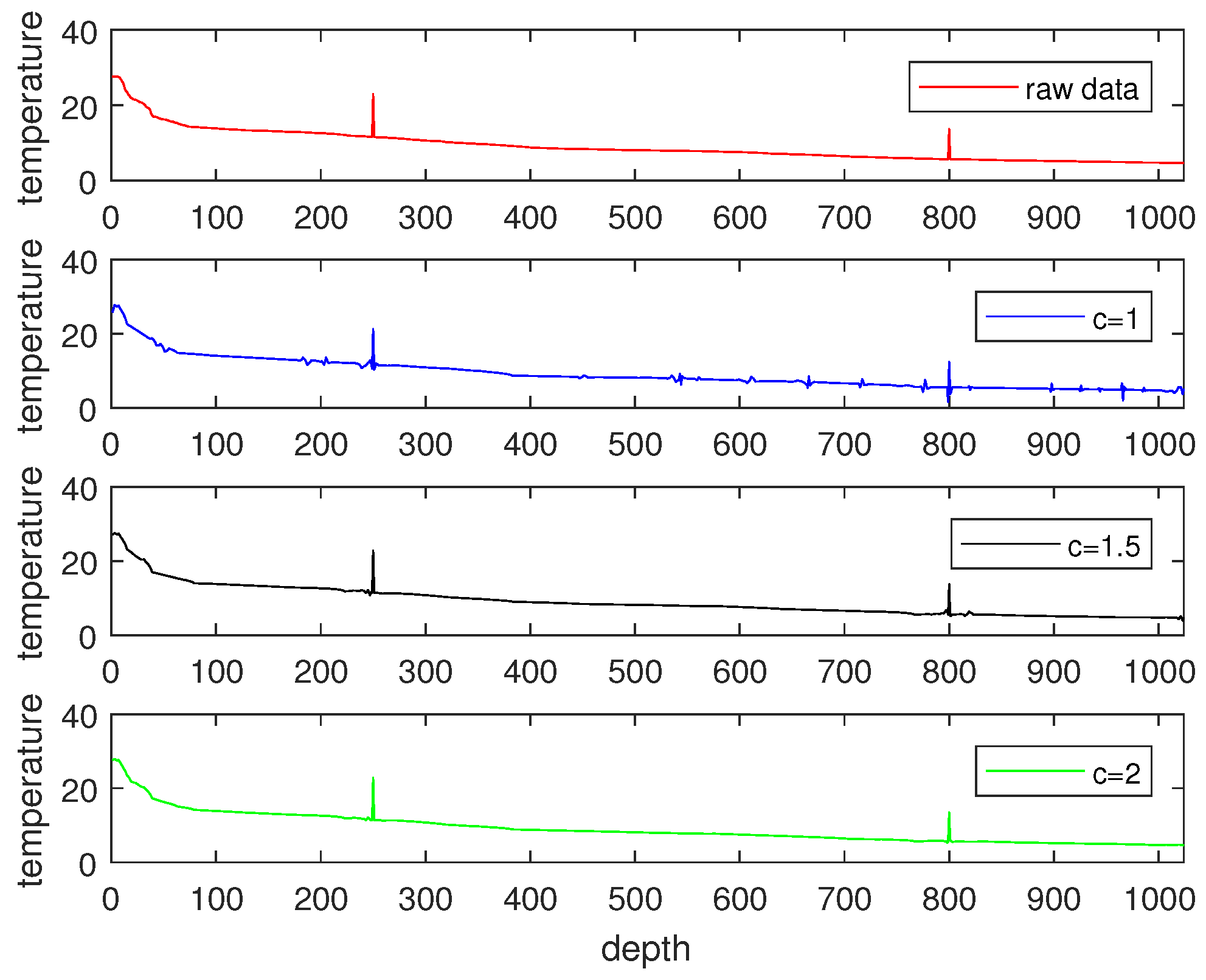
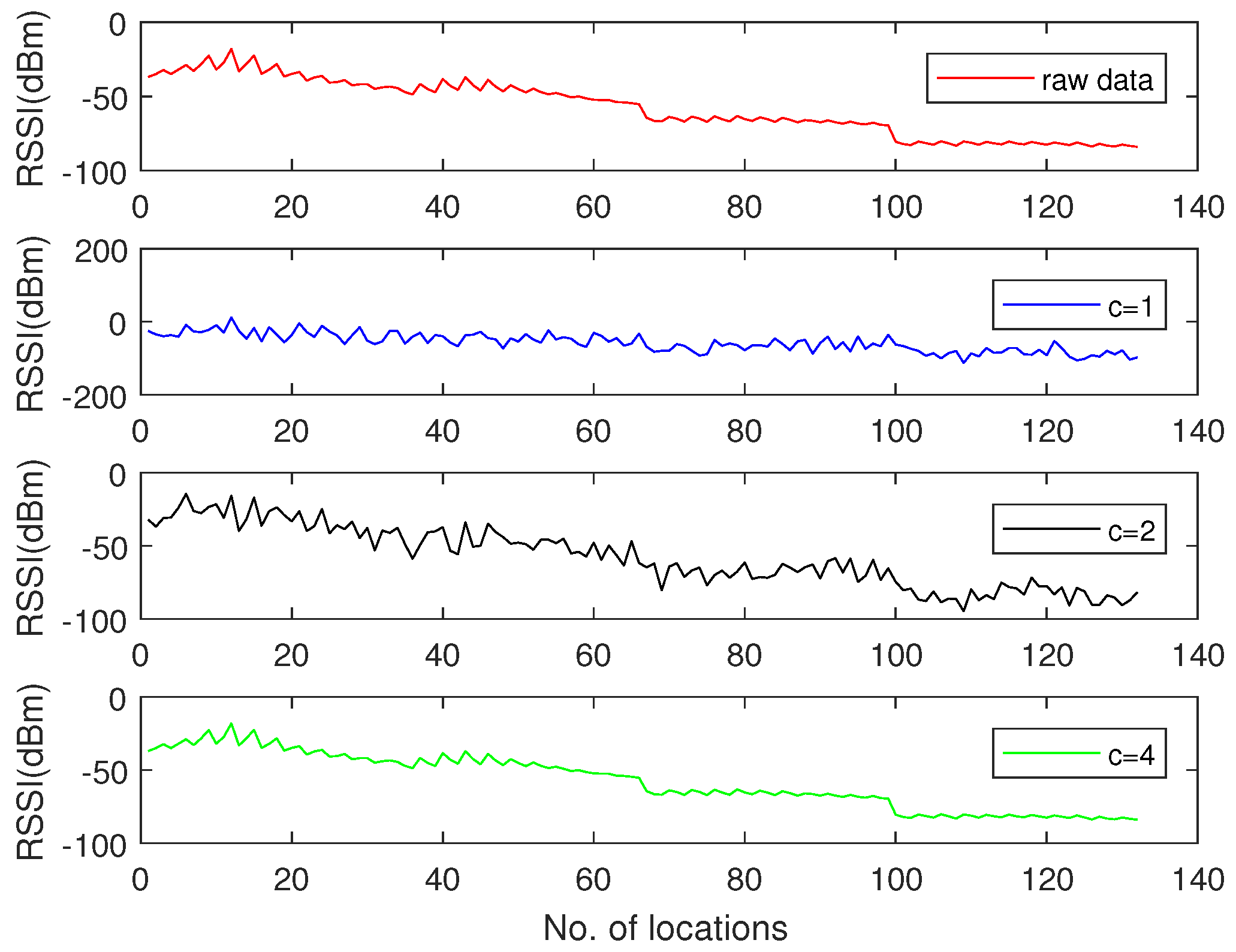
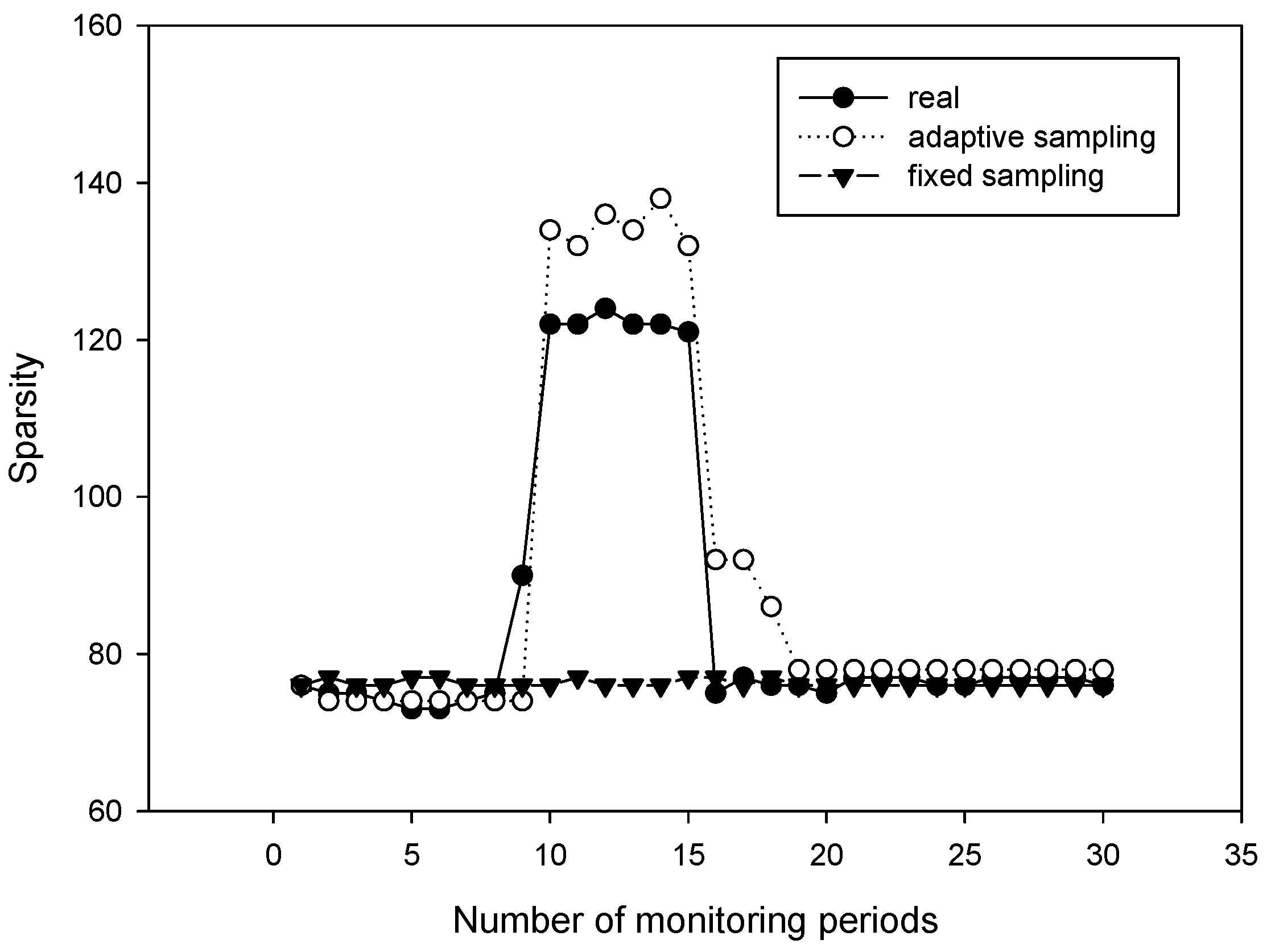
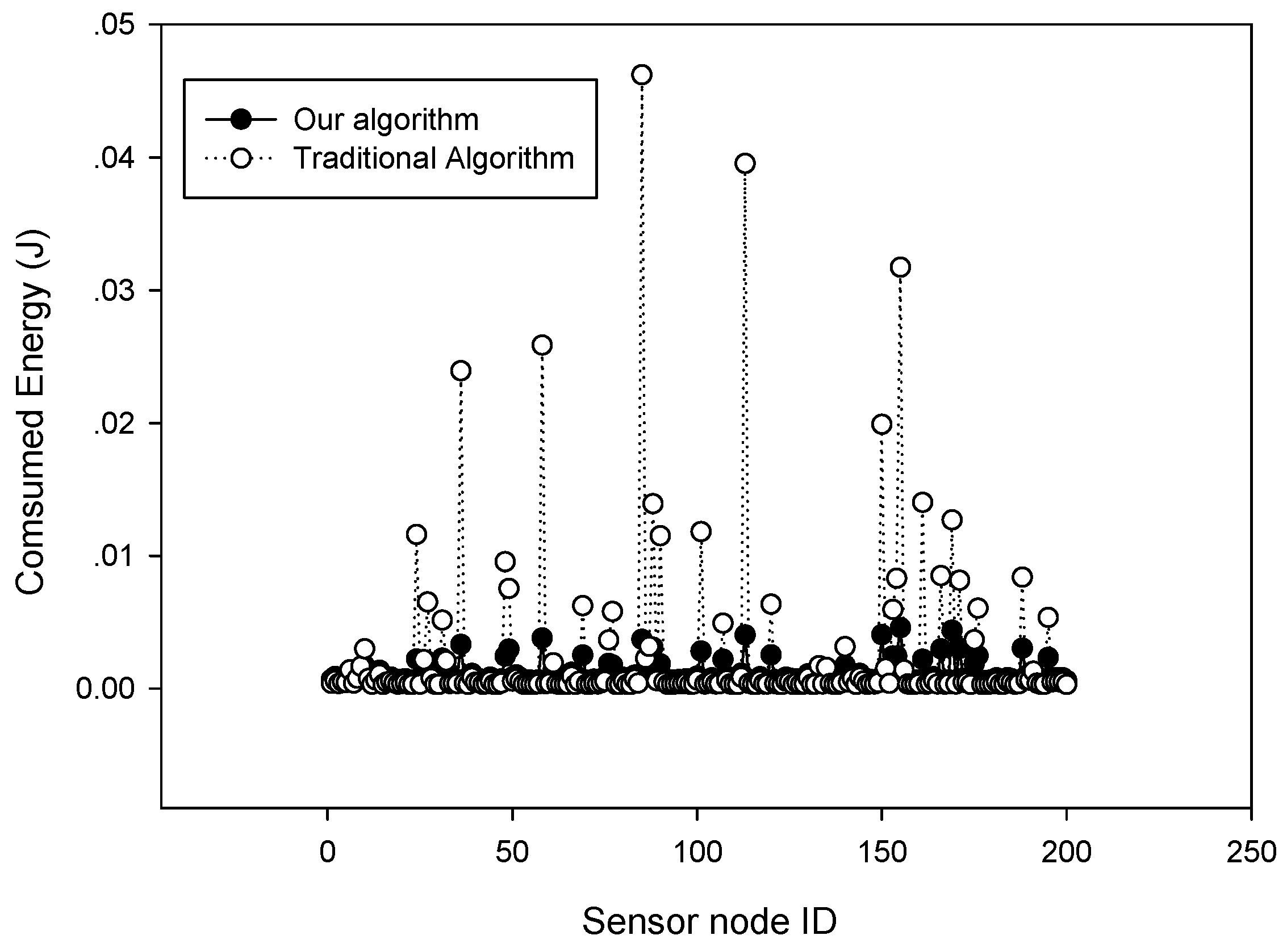
1. Introduction
Wireless Sensor Networks (WSNs), which are capable of sensing, computing, and wireless communication, can be applied to a wide range of applications, such as scientific observation, emergence detection, climate detection, ecosystem surveillance, and physical hazard prevention [
1]. In many of these applications, sensor nodes are powered by battery and deployed in an unattended hostile environment with high density. Once deployed, these nodes should send their sensing results to the sink node periodically. Due to the constraints of application environments, it is crucial to prolong the network lifetime of WSN. According to the energy consumption model presented in [
2], the energy consumed in a sensor node is exponentially increased with the communication distance. As a result, sensor nodes usually follow the routine to the sink node via multihop transmission, thus saving energy. Besides that, multihop communication is essential for large-scale WSNs for cases where the transmission range of sensor nodes is much smaller than the size of the target area.
Since all the sensor nodes forward their data to only one sink node, the routing tree in WSNs usually exhibits a many-to-one structure, which is often called
convergecast [
3,
4]. The main drawback of the
convergecast structure is the energy hole problem, chiefly because the sensor nodes close to the sink node have to relay more packets and tend to run out of energy sooner. As a result, the entire network is subject to premature death because it is separated by the energy hole. In order to avoid uneven energy depletion and to extend the network’s lifetime, several advanced hardware and software solutions have been recently proposed. As for the design of hardware, wireless energy charging technologies are applied to harvest energy from ambient sources [
5,
6]. However, recharging is impossible or not worth it in many applications [
7]. As for the design of software, data gathering solutions have been proposed to reduce the traffic load. Since the physical phenomena collected by sensor nodes often possesses strong temporal and spatial correlations, it is inefficient to deliver raw data to the sink node. Many solutions have incorporated data correlations into data gathering, such as distributed source coding [
8] and the distributed compression algorithm [
9]. However, conventional data compression techniques, which are usually associated with the design of routing, require heavy computation and communication loads on sensor nodes [
10]. Source coding techniques are also incompatible with WSNs, since they work with the assumption that the statistical structure of the underlaying data distribution should be known prior [
11].
The emerging technology of compressive sensing (CS) opens up a new perspective for data gathering in WSNs. The basic idea of CS is that if the signal is sparse or compressible at a certain level , it can be reconstructed from a small number of linear measurements lower than the Shannon–Nyquist limit [
12]. The application of CS for data gathering in multi-hop WSNs has drawn much attention recently. [
13] investigated how to apply CS theory for data gathering. They also designed a simple but efficient measurement matrix that satisfies the restricted isometry property (RIP). CS based techniques can substantially reduce the amount of data transmission and balance the traffic load throughout the entire network with a very low level of complexity. In order to further reduce the energy consumption and improve the energy efficiency, a novel measurement matrix generation incorporating a transmission design was proposed in [
14]. In [
15], the CS principle was used as a compression and forwarding scheme to minimize the transmission data. In Ref. [
16], CS based data aggregation combined with routing was designed to reduce the entire energy consumption. In Ref. [
17], a CS method of cluster-based WSNs was designed, and centralized and distributed clustering methods were proposed to reduce the number of transmissions. Considering the spatial correlations between sensor nodes, the compressive sleeping strategy was designed in Refs. [
18,
19] for high density WSNs, where only a subset of sensor nodes were active and all the other sensor nodes were turned off to save the energy and extend the network’s lifetime. By utilizing the spatial correlations of the data in densely deployed WSNs, a distributed compressive sensing scheme for data gathering was proposed in Ref. [
20], where the belief propagation algorithm was employed for signal recovery. In Ref. [
21], the spatial interpolation method was proposed to transform a predetermined sparsifying measurement matrix for WSNs with only local communications, avoiding the complete position knowledge of the entire network being obtained. In Ref. [
22], the CS based signal and data acquisition for WSNs as well as the Internet of Things (IoT) was proposed, and a cluster-sparse reconstruction algorithm was proposed for in-network compression to achieve accurate signal recovery and energy efficiency. By exploiting a similar sparsity structure of acoustic signals from nodes in the same array, a collaborative reconstruction method was proposed for data gathering in wireless sensor array networks [
23].
Even though various applications of CS for data gathering have been extensively studied, they all assume that the sparsity of the signal is static or changing sufficiently slowly over time. However, such an assumption is too restrictive for many monitoring applications, where the sparsity of the signal changes rapidly with time or conditions. For example, for an anti-fire forest monitoring WSN, due to the fact that the number of measurements is linearly related to the underlying signal sparsity level, the signal sparsity with and without fire is apparently different. When the sparsity of the signal is changed, ignoring the rapid change of signal sparsity will result in performance degradation in signal recovery. Therefore, it becomes important to design an adaptive compressive sensing in accordance with the variation of the signal sparsity.
After gathering the data with compressive sensing, another challenge is how to design a signal recovery algorithm with fast reconstruction and reliable accuracy. Recently, the signal recovery algorithm applied in WSNs was classified into two categories: (1) the basis pursuit (BP) which was proposed to find the
minimization using linear programming, and (2) the iterative greedy pursuit, for example, the orthogonal matching pursuit (OMP), the stagewise OMP (StOMP) [
24] and the compressive sampling matching pursuit (CoSaMP) [
25]. Among them, BP requires the least number of measurements; however, its high computational complexity prevents it from being used for large scale applications. OMP and StOMP adopt a bottom-up approach in signal recovery, and their complexity levels are much lower than that of BP. However, they require more measurements and have a lack of recovery guarantee. CoSaMP adopts a top-down approach and can offer an acceptable recovery performance, similar to that of the BP method, but with a much lower recovery complexity. However, all these algorithms discussed above assume that the sparsity of the signal is known prior. These algorithms cannot be directly applied to the construction of a signal with unknown sparsity. For blind signal recovery with unknown sparsity, the most commonly applied algorithm is the sparsity adaptive matching pursuit (SAMP) [
26], where the sparsity of signal and the true support of the signal is estimated stage by stage with the “divide and conquer” method. SAMP can also be viewed as a generalization of existing algorithms, such as OMP or CoSaMP. However, the design of an appropriate step variation to guarantee fast convergence and accuracy is still an open problem.
Different from aforementioned works, the aim of this work was to design an adaptive compressive sensing framework for periodical monitoring of WSNs. As we know, the most related work to this research is the intelligent compressive sensing scheme proposed in Refs. [
27,
28]. The main difference between our work and their works is the sparsity determination. In Ref. [
27], sparsity was obtained with local correlations, and the signal was recovered by successive reconstruction applied at the sink node. In Ref. [
28], the compressive sampling was applied in a single-hop IoT system, and a learning phase was designed at the central smart object to select the sparsity level. However, in our work, compressive sampling is applied in multi-hop wireless sensor networks, and the variation in the sparsity is determined by very few re-sampling iterations . Additionally, we present an improved SAMP to recover signal with unknown sparsity. The main contributions of this paper are summarized as follows:
We propose an adaptive compressive sensing framework for periodical monitoring of WSNs, where a reconstruction error estimation module is designed to check whether the current sampling rate is still sufficient for signal reconstruction, and a sparsity determination module is designed to estimate the sparsity and calculate the required sampling rate at the next monitoring period.
We propose an efficient sparsity variation determination algorithm, which can determine the current sparsity as well as the new sampling rate by only re-sampling a few measurements to save the energy cost and guarantee the recovery performance.
We propose an improved SAMP algorithm to recover the signal with unknown sparsity, where both the linear and non-linear step size variation are designed to guarantee fast convergence and reliable accuracy.
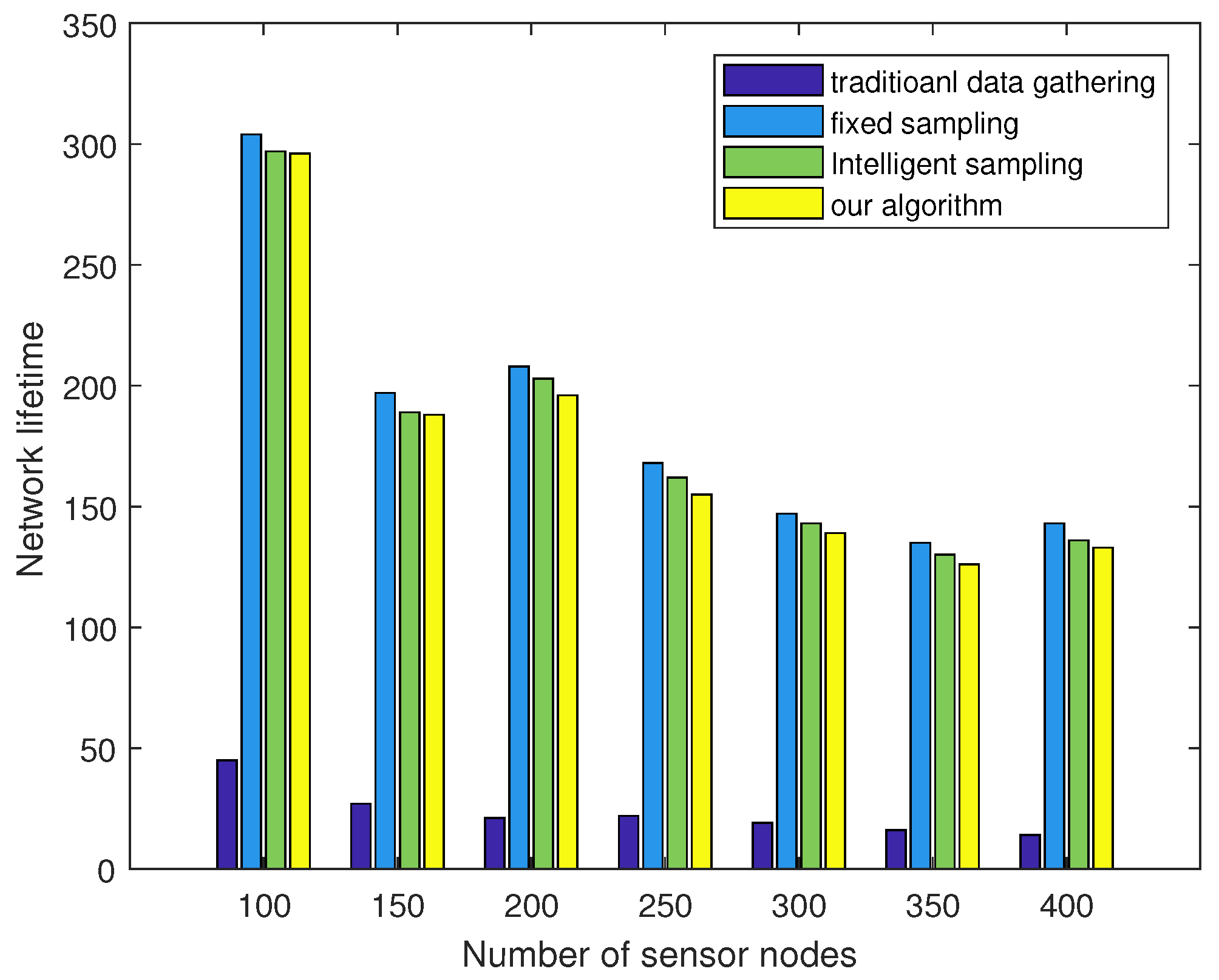
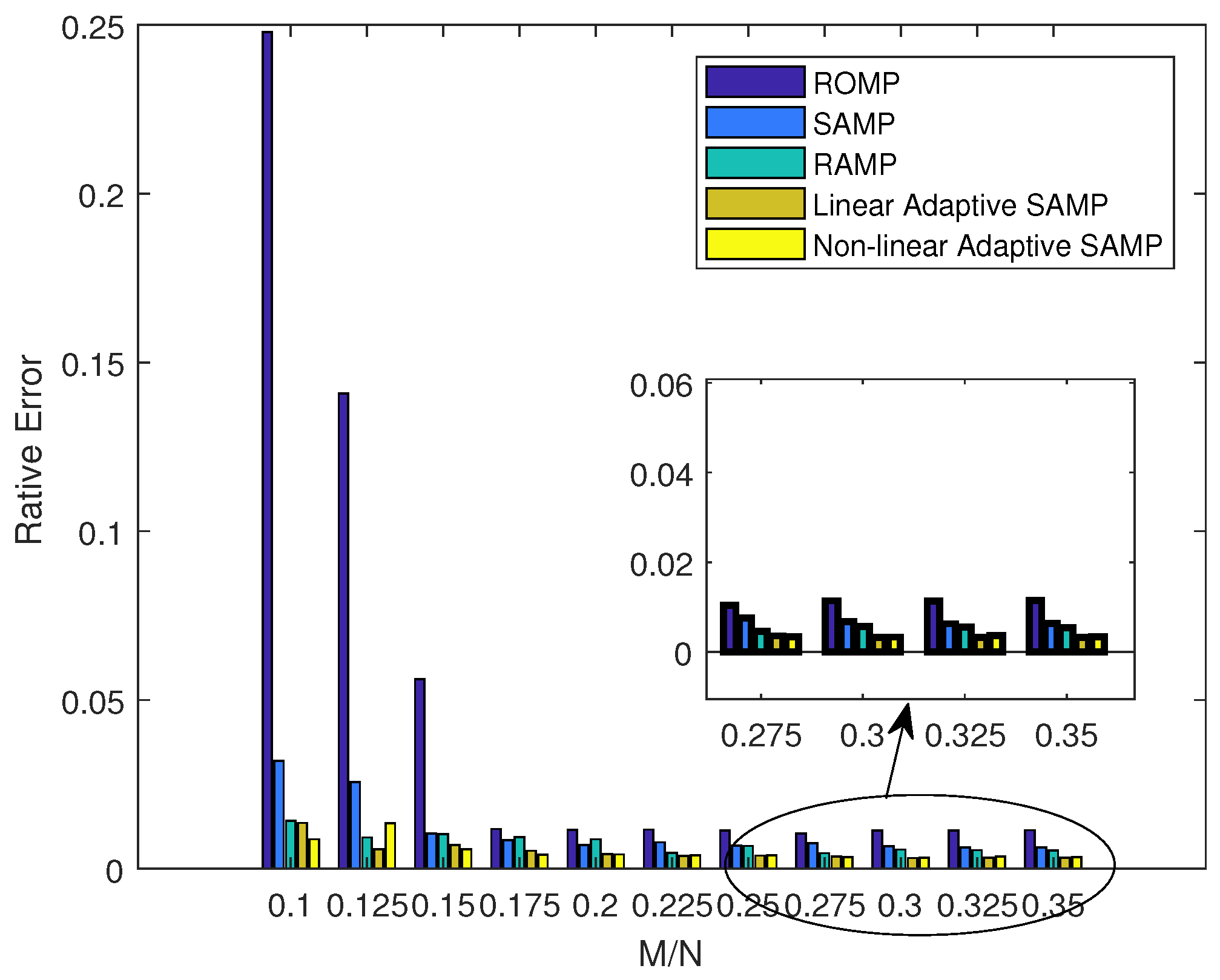
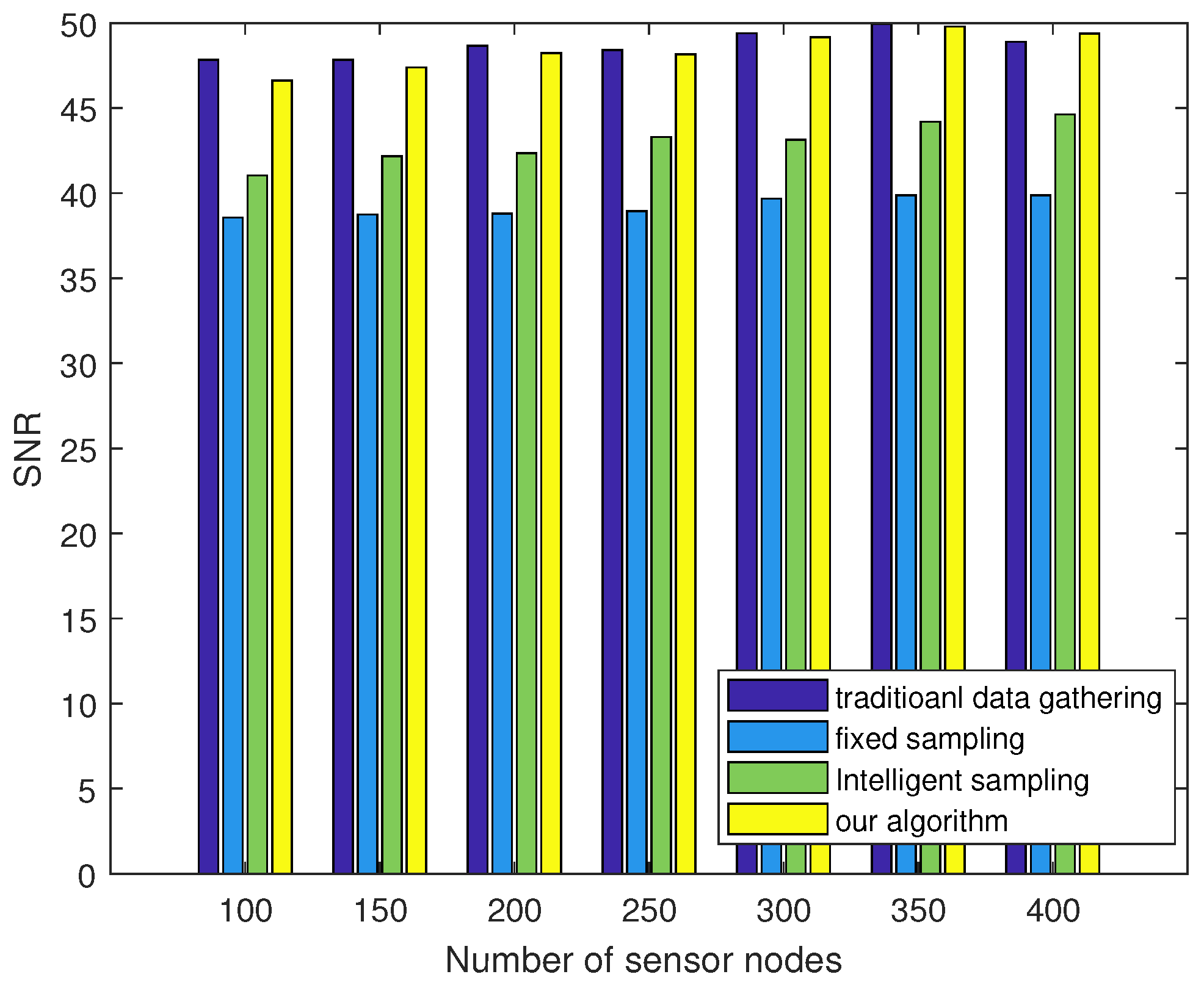
We evaluate the proposed algorithms with extensive simulations and study the impacts of multiple environmental factors, including the number of sensors and the different sampling rates. The simulation results show that our proposed algorithm could achieve substantial improvements compared with existing algorithms in terms of sparsity matching and signal recovery.
The remainder of this paper is organized as follows. Section II presents the mathematical details for the CS and data gathering. We propose our adaptive signal sampling method with unknown sparsity in Section III. The signal recovery algorithm is presented in Section IV. Section V presents the numerical results, and Section VI concludes the paper.
2. Data Gathering Based on Compressive Sensing
We consider a monitoring WSN consisting of N sensor nodes and a sink node, where the set of sensor nodes is denoted as , and the only sink node is denoted as S. We denote the monitoring period as P. Sensor nodes are distributed in the target area to sense the physical conditions and report the sensory reading to the sink node in each period ().
It is assumed that the sensed data for sensor node
i (
) in time period
p is
, and the signal of all the sensor nodes in time period
p can be represented by an
N-dimensional vector,
. It is said that
is a
k-sparse signal in domain
if
can be represented by a
k-sparse vector,
, in domain
, and is given by
where
(
) is the orthonormal basis, and
represents the transform coefficients with only
k non-zero values.
The compressive sensing theory states that an
N-dimensional signal with
k-sparsity can be represented by
M linearly projected measurements. Let
(
) be the measurement matrix,
can be given as
According to Ref. [
29], the exact recovery of
can be achieved through solving the following combinatorial optimization problem:
This is an NP-hard problem, and it is hard to obtain the optimal solution. However, it is equivalent to the following
optimization problem if the incoherence property between
and
or the restricted isometry property (RIP) [
30] of matrix
satisfies
The above 1-minimization problem is more tractable and can be solved with linear programming (LP) techniques [
31]. We can further obtain the recovered signal,
, with the known orthonormal basis,
.
With the above discussion, it is clear that applying CS to WSNs relies greatly on two important issues: First, how to choose or find an efficient orthonormal basis to represent the original signal. Generally, sensor readings are spatially smooth and sparse in the frequency domain; thus, we can use the wavelet transform or the discrete cosine transform can be applied to add sparsity to the original signal [
14]. However, for signals with abnormal reading or transmission errors, it is hard to add sparsity in the frequency domain. To cope with this, sparse representation based on overcomplete dictionaries has been proposed [
32]. With an overcomplete dictionary that contains prototype signal-atoms, signals are described by sparse linear combinations of these atoms. Various dictionary learning methods have been proposed in the literature. For example, the original (synthesis) K-SVD is one such method which allows the construction of an overcomplete dictionary that is suitable for sparse synthesis by learning the dictionary from the data itself [
32]. After find a sparsity method, another problem in designing compressive sensing is how to design a measurement matrix (
) such that a good RIP is attained. It has been shown that a random matrix with Gaussian variables complying to
has a good RIP [
33]. Algorithm 1 illustrates the process of compressed sampling with sampling rate
M in detail. In this algorithm, each time a sensor (
i) in period
p has a value
to transmit to the sink node, it first calculates a new value (
) by multiplying value
with a Gaussian variable,
(
). Then, this new value (
) is aggregated and transmitted along the path to the parent node (
j). In this way, the transmitted data of sensor node
j is the summation of
and the value from all its children (
), where
is the set of children of sensor node
i. Finally, the sink node receives the value as
. This process is repeated until
M linearly projected measurements are obtained, as shown in
Figure 1. Similarly to Refs. [
14,
17,
34], we assume the measurement coefficient
is generated using a pseudorandom number generator seeded with the identifier of node
i, which means that the measurement matrix can be easily constructed locally at the node itself.
| Algorithm 1: Compressive sampling with sampling rate M |
![Sensors 18 03369 i001]() |
According to the CS theory in Ref. [
33], when the number of measurements (
M) satisfies
with a constant (
c), the original signal with
k-sparsity can be recovered with high probability. Due to the fact that the sparsity of a signal usually satisfies
, it is clear that the amount of data transmission in CS-based data gathering is much smaller than that in these traditional methods; thus, reducing the communication costs and achieving energy efficiency during data gathering.
3. Adaptive Sampling for Signals with Dynamic Sparsity
From the description of the CS based data gathering, it can be known that for a signal with
k-sparsity, the optimal sampling rate should be at least
to guarantee the recovery accuracy and to save communication energy. However, for a signal with unknown sparsity, it is very challenging to select the optimal sampling rate to match the sparsity. In this section, we therefore propose an adaptive sampling mechanism for signals with variable sparsity. In our approach, we assume that the sparsity of the signal in period
p, denoted as
, remains fixed during the entire period, as shown in
Figure 2. However, at the starting time of the next period, its sparsity is re-examined, and the new sampling rate is determined corresponding to its new sparsity.
It should be noted that at the starting time of period , it is hard to decide whether the previous sampling () still matches the sparsity of the signal at period . A straightforward solution is to conduct raw data gathering with all active sensor nodes. This approach, however, results in the decrease of the network’s lifetime and is inefficient for networks with larger numbers of sensor nodes. Therefore, in order to determine the minimum sampling rate required to recover a signal with unknown sparsity, a compressive sampling method based on sequential observations is proposed.
is denoted as the recovered signal with sampling rate
M. When noiseless measurements are taken using the random Gaussian ensemble, we have the following lemma [
35].
Lemma 1. For a Gaussian measurement ensemble, if , then we can conclude that with a probability of 1.
According to Lemma 1, the recovered signals with
M samples and
samples are first compared. If the samples match, we declare that these signals are correctly recovered. In a practical setting, most of the coefficients after orthogonal transformations are relatively small, rather than being exactly zero, which means only approximate sparseness is obtained. Thus, the recovery error between the original signal and the recovery with
M sequential samples is given by [
35]
where
is the angle between vectors
and
, and has the following approximation
The recovery error can be further approximated as
In our paper, the recovery error between and is applied to determine the variation of the sparsity, and an adaptive sampling approach is proposed for the periodical monitoring of sensor networks.
In Algorithm 2, the process of the adaptive sampling is illustrated in detail. In this algorithm,
is denoted as the sampling rate at period
p. Initially, raw data gathering is applied, to obtain accurate sparsity of the entire signal. After that, at the starting time of period
p, the sampled data obtained at period
, denoted as
, is recovered as
. Meanwhile, a data re-sampling operation is executed to get re-sampled data (
) with a fixed number of sampling points as
. After re-sampling,
and
are further combined as
and recovered as
at the sink node. Therefore, the performances of
and
are compared to decide whether the gap between them is larger than the predefined threshold (
). If it is detected that the recovery gap is smaller than
, it is concluded that the sparsity is the same as that in period
, and the sampling rate in period
p is set as
. If it is detected that the recovery gap is larger than
, the novel sparsity is calculated. Due to fact that re-sampling with a fixed sampling rate (
) may be unable to recover the original signal, extra sampling with sampling rate
is executed, where
, and
is a scale coefficient related to the recovery gap. From the expression of
, it is known that the larger the gap is, the more re-sampling iterations needed to obtain its new sparsity level. After that, the sampling rate for period
p is determined and broadcast to all the sensor nodes. Similar to Refs. [
14,
17], it is assumed that the signal recovery and sparsity estimation are conducted at the sink node, and only the determined sparsity is sent back to each sensor node, thus reducing the energy consumption of each sensor node. It should be noted that our algorithm adopts the same data gathering procedure (shown in Algorithm 1) as that of traditional compressive based methods. The only difference lies in the degree to which the sampling rate corresponds with the signal variation, which means that the data transmission delay is almost the same. Compared with raw data gathering, the time consumed in compressive data transmission is much longer, which is mainly because compressive based data gathering needs to occur on the same date
M times. However, it should be noted that compressive based data gathering obtains balanced energy consumption among all sensor nodes, and has a much longer network lifetime than raw data gathering. For clarity,
Figure 3 illustrates the detailed process of how to decide the sparsity at period
p.
| Algorithm 2: Adaptive compressive sampling |
![Sensors 18 03369 i002]() |
4. Signal Recovery with Unknown Sparsity
In sequential-based data gathering, signal recovery requires the use of non-linear algorithms to find the sparsest signal from the measurements. One challenging question in CS research is the design of a fast reconstruction algorithm with reliable accuracy and (nearly) optimal theoretical performance. The existing signal recovery algorithms always require the signal sparsity first. For signals with unknown sparsity, the sparsity adaptive matching pursuit (SAMP) has already been widely used to recover many blind signals with unknown sparsity.
In contrast to other state-of-the-art greedy algorithms, SAMP takes advantage of both the “bottom-up” approach and the “top-down” approach, where the “bottom-up” method is applied to estimate the sparsity of the signal, step-by-step, and the “top-down” method is applied to identify the true support of the signal by backtracking strategy.
Figure 4 shows the conceptual diagram of SAMP, and it can be observed that the sizes of the candidate set (
) and finalist (
) are adaptive. However, the recovery accuracy and speed of SAMP highly relies on the step size (
s). In order to avoid overestimation, the safest choice is to set
s as 1 for an unknown
k, but many more iterations are needed for convergence. How to provide a recovery accuracy with fast convergence speed has become a major challenge.
In this paper, we propose an adaptive step decision that corresponds with the number of iterations. The step size at iteration
t is denoted as
, which is given by
where
is the weight factor employed to regulate the trade-off between the speed and accuracy, and
is the fixed step difference between any two adjacent iterations.
In our paper, two step variation approaches are proposed: the linear decrement weight factor and the non-linear decrement weight factor. For the linear weight factor decrement approach, the weight factor is given by
where
and
are the maximum and minimum weight factors, and
is the maximum number of iterations. For the non-linear weight factor decrement approach, the weight factor is given by
where the parameter
is applied to control the convergence speed, and
decreases with an increase in
. In constrast to the linear weight factor decrement, the decrease in the step size is much smaller than that with the linear method, reducing the possibility of getting the local optimal solution.
Algorithm 3 presents the detailed pseudo code of the proposed recovery algorithm with an adaptive step. Here, represents the transpose of matrix , represents the Moore–Penrose inverse of matrix , s represents the step size of the finalist, and the function returns s elements corresponding to the largest absolute value of vector . Additionally, for a set , is the sub-matrix of with indices (). At the s-th iteration, , , , and denote the shortlist, the candidate list, the finalist, and the observation residual. In this paper, the maximum iteration time () is set as the stopping rule, and the recovering threshold () is applied as the halting condition.
| Algorithm 3: Adaptive compressive sampling |
![Sensors 18 03369 i003]() |