Research on a Mixed Gas Recognition and Concentration Detection Algorithm Based on a Metal Oxide Semiconductor Olfactory System Sensor Array
Abstract
1. Introduction
- (1)
- This paper proposes a KPCA-KNN gas identification method aiming at the low identification rate of binary mixed gas in the existing machine olfactory system. The method uses KPCA to extract the nonlinear characteristics of a binary mixed gas with different concentration ratios, composes the mixed gas feature set, and then uses a KNN classifier to identify the gases.
- (2)
- To improve binary mixture gas detection accuracy, this paper proposes to use MVRVM’s multi-input multi-output feature, with the MOS gas sensor array’s response signal as the input and the two target gas concentrations as the output, to achieve binary mixed gas concentration detection.
- (3)
- The accuracy of the proposed method is verified by qualitative analysis and quantitative detection of CO and CH4 mixed gases. The experimental results show that the proposed method has better resolution accuracy for binary mixed signals than other methods do.
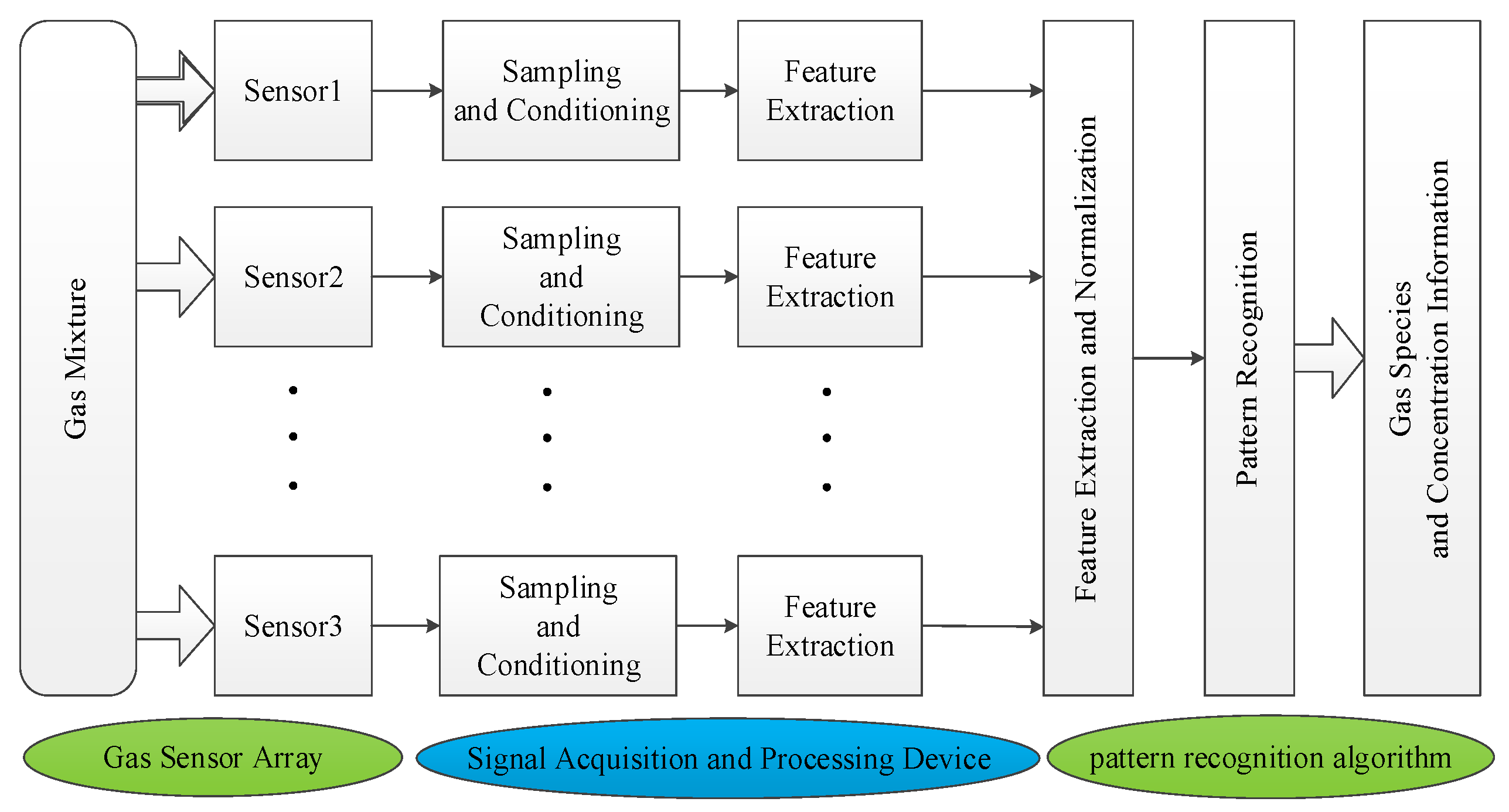
2. Mixed Gas Qualitative Identification
2.1. KPCA Feature Extraction
2.2. KNN Proximity Algorithm
3. Mixture Gas Concentration Estimation
4. Hybrid Gas Detection Method
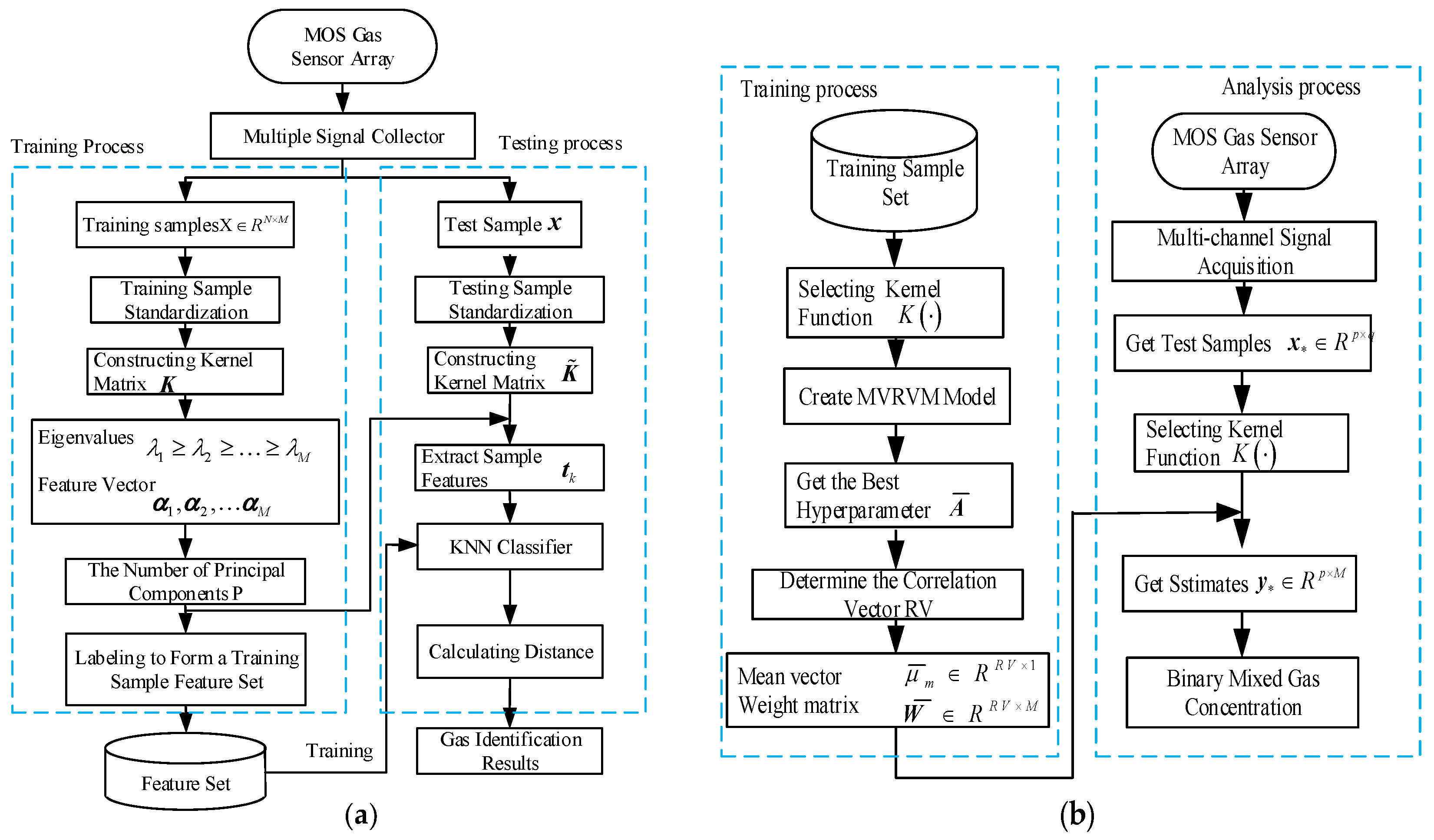
- Step 1:
- Use the MOS gas sensor array to collect the response signals of mixed gas samples of different compositions. To remove the influence of the baseline, subject the collected data to a baseline reduction process.
- Step 2:
- By constructing a kernel matrix from the training sample set, use KPCA to extract the features of all training samples and forms a training sample feature set.
- Step 3:
- Use the feature vector of the training sample set obtained by KPCA to obtain the characteristics of the test sample.
- Step 4:
- Identify the characteristics of the test sample using the KNN algorithm, select the K points with the smallest distance, and count the number of occurrences of the category to which the K-point belongs the most. The category corresponding to the most frequent point is the category of the measured point.
- Step 1:
- Collect the response signals of the mixed gas samples with different concentrations through the MOS gas sensor array. To remove the influence brought by the baseline, subtract the baseline data from the collected data signals.
- Step 2:
- For the training sample set, select the kernel function K, establish the relevant MVRVM model, obtain the optimal hyperparameter, and determine the number of related vectors to obtain the mean vector and the weight matrix.
- Step 3:
- Calculate the estimated gas concentration by calculating the mean value vector and the weight matrix.
5. Experiment
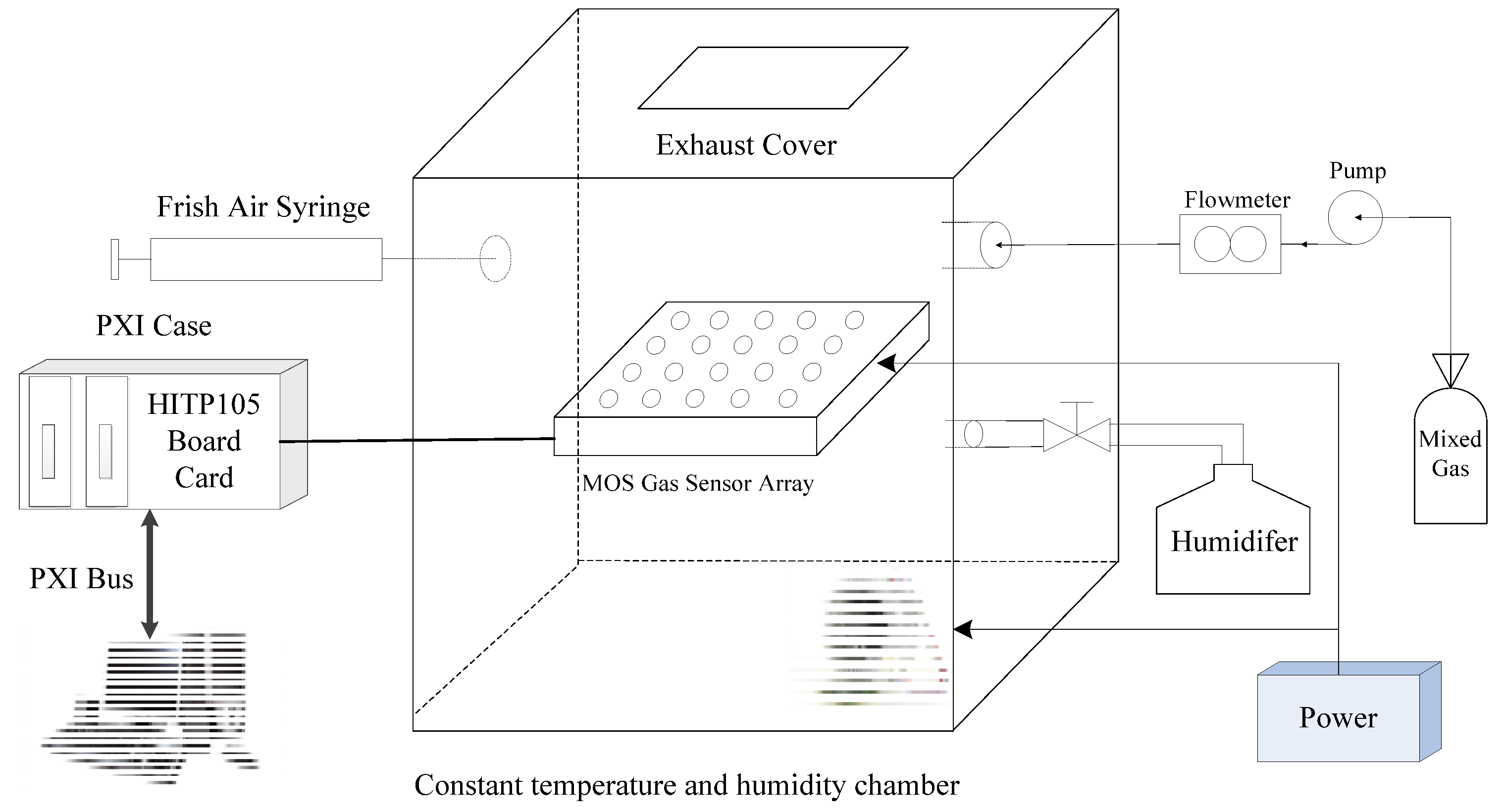
5.1. Experimental Sample Acquisition
5.2. Experimental Sample Composition
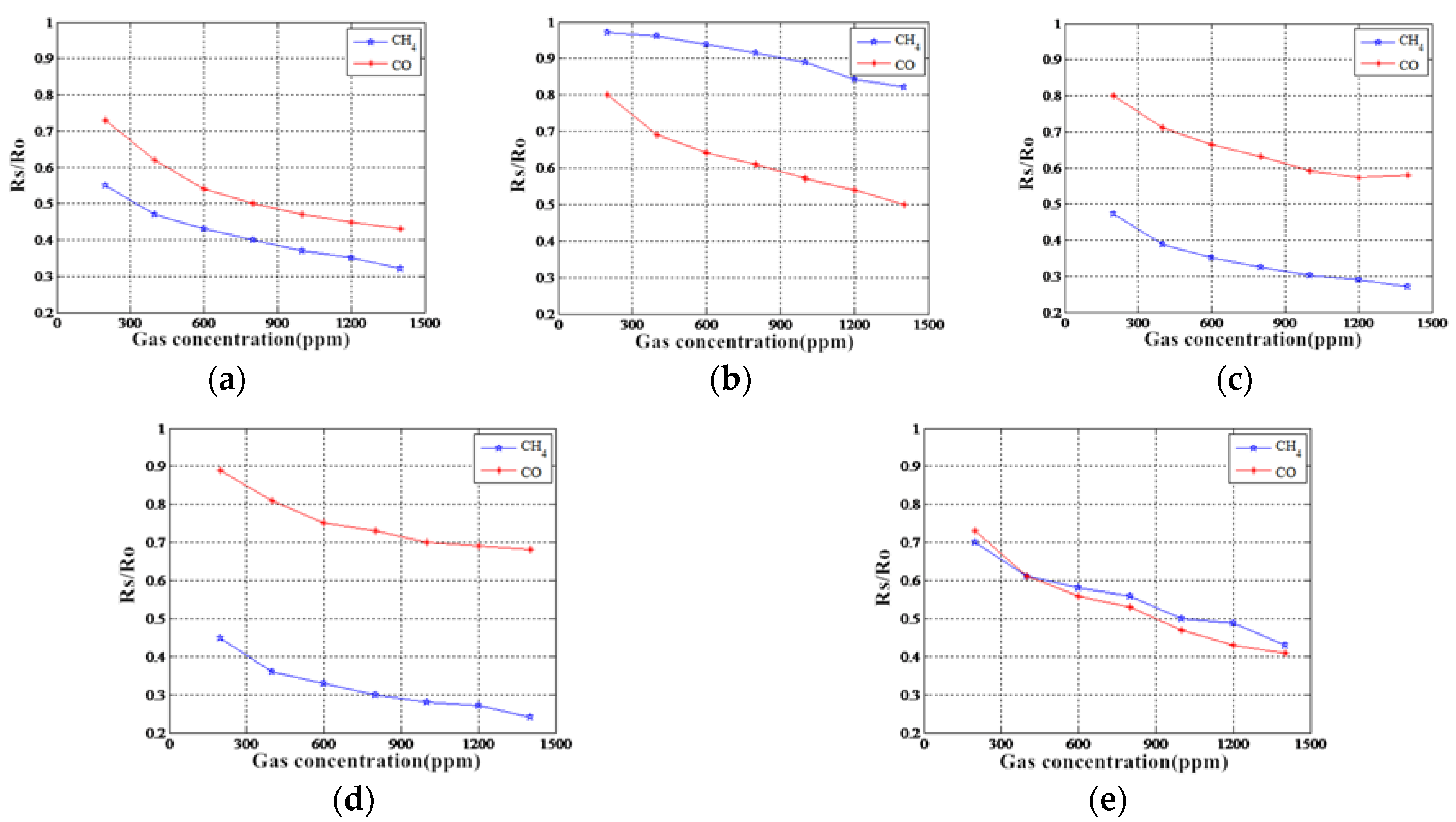
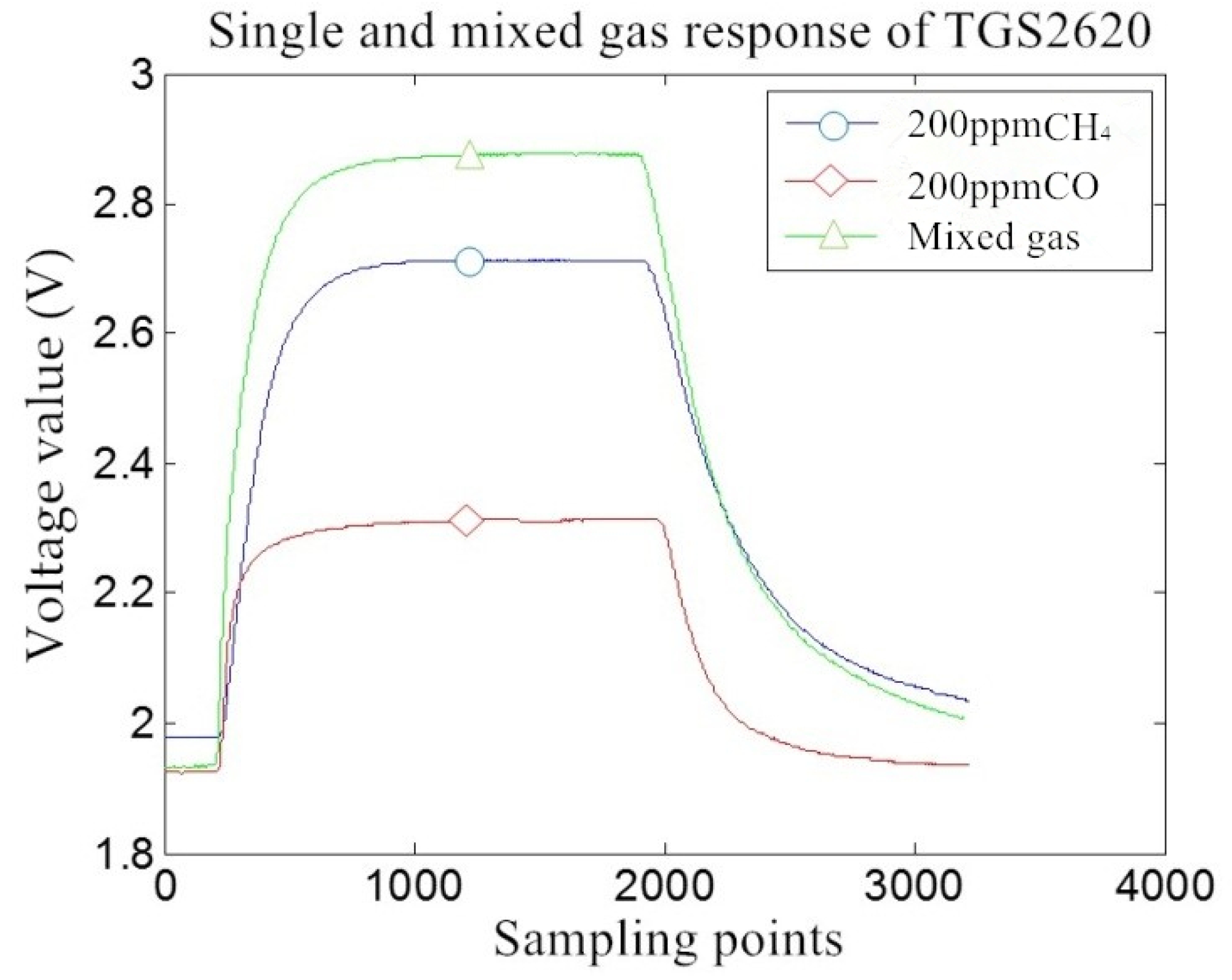
5.3. MOS Gas Sensor Sensitivity Analysis
6. Binary Gas Detection
7. Conclusions
- (1)
- KPCA was verified as a feature extraction method for processing nonlinear signals. Compared with PCA and ICA, KPCA exhibits a good signal feature extraction capability. Using the KNN classification algorithm to construct a gas identification model, the recognition accuracy rate exceeds 98%.
- (2)
- This study also examined the detection of mixed gas concentrations and proposed an MVRVM algorithm that is different from the ANN and requires many training cycles. The average relative error of gas concentration monitoring is within 6%, and the detection time is short, which is more suitable than other methods for real-time detection of mixed gas.
- (3)
- The method for qualitative identification and quantitative detection of the binary mixed gas proposed in this paper was verified via experiments, and the accuracy of detection and the detection of a mixed gas by the machine olfactory system was improved. It is worth expanding the application of the system to the identification and detection of multiple gas mixtures.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gammoudi, I.; Nedil, M.; Aissa, B.; Djaiz, A. Gas Sensor Based on RFID Tag Antenna for Harsh Environment. In Proceedings of the IEEE International Symposium on Antennas & Propagation, Fajardo, Puerto Rico, 26 June–1 July 2016; pp. 1271–1272. [Google Scholar]
- Bhattacharyya, R.; Amin, E.; Ehrenberg, I.; Sarma, S. Towards low-cost, wireless blood anomaly sensing: An RFID-based anemia detection sensor. In Proceedings of the IEEE International Conference on RFID, San Diego, CA, USA, 15–17 April 2015; pp. 189–196. [Google Scholar]
- Li, W.; Liu, H.; Xie, D.; He, Z.; Pi, X. Lung Cancer Screening Based on Type-Different Sensor Arrays. Sci. Rep. 2017, 7, 1969. [Google Scholar] [CrossRef] [PubMed]
- Haridas, D.; Chowdhuri, A.; Sreenivas, K.; Gupta, V. Fabrication of SnO2 Thin Film Based Electronic Nose for Industrial Environment. In Proceedings of the IEEE Sensors Applications Symposium, Limerick, Ireland, 23–25 March 2010; pp. 173–189. [Google Scholar]
- Zhang, Q.; Li, H.; Tang, Z. Knowledge-Based Genetic Algorithms Data Fusion and Its Application in Mine Mixed-Gas Detection. J. Softw. 2012, 7, 1334–1338. [Google Scholar]
- Korotcenkov, G.; Cho, B.K. Instability of metal oxide-based conductometric gas sensors and approaches to stability improvement (short survey). Sens. Actuators B Chem. 2011, 156, 527–538. [Google Scholar] [CrossRef]
- Baldwin, E.A.; Bai, J.; Plotto, A.; Dea, S. Electronic noses and tongues applications for the food and pharmaceutical industries. Sensors 2011, 11, 4744–4766. [Google Scholar] [CrossRef] [PubMed]
- Keller, A.; Gerkin, R.C.; Guan, Y.F.; Dhurandhar, A.; Turu, G.; Szalai, B.; Mainland, J.D.; Ihara, Y.; Yu, C.W.; Wolfinger, R.; et al. Predicting human olfactory perception from chemical features of odor molecules. Science 2017, 355, 820–826. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Zhai, D.; Wang, W. Failure Mode Analysis and Dynamic Response of a Coal Mine Refuge Chamber with a Gas Explosion. Appl. Sci. 2016, 6, 145. [Google Scholar] [CrossRef]
- Santonico, M.; Pennazza, G.; Parente, F.R.; Grasso, S.; Zompanti, A.; Stornelli, V.; Ferri, G.; Bizzarri, M.; Amico, A.D. A Gas Sensor Device for Oxygen and Carbon Dioxide Detection. Proceedings 2017, 1, 447. [Google Scholar] [CrossRef]
- Ayari, T.; Bishop, C.; Jordan, M.B.; Sundaram, S.; Li, X.; Alam, S.; ElGmili, Y.; Patriarche, G.; Voss, P.L.; Salvestrini, J.P.; et al. Gas sensors boosted by two-dimensional h-BN enabled transfer on thin substrate foils: Towards wearable and portable applications. Sci. Rep. 2017, 7, 15212. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Cheng, S.; Liu, H.; Hu, S.; Zhang, D.; Ning, H. A Survey on Gas Sensing Technology. Sensors 2012, 12, 9635–9665. [Google Scholar] [CrossRef] [PubMed]
- Castell, N.; Dauge, F.R.; Schneider, P.; Vogt, M.; Lerner, U.; Fishbain, B.; Broday, D.; Bartonova, A. Can commercial low-cost sensor platforms contribute to air quality monitoring and exposure estimates? Environ. Int. 2017, 99, 293–302. [Google Scholar] [CrossRef] [PubMed]
- Arshak, K.; Moore, E.; Lyons, G.M.; Harris, J.; Clifford, S. A review of gas sensors employed in electronic nose applications. Sens. Rev. 2004, 24, 181–198. [Google Scholar] [CrossRef]
- Waitz, T.; Becker, B.; Wagner, T.; Sauerwald, T.; Kohl, C.D.; Tiemann, M. Ordered Nanoporous SnO2 Gas Sensors with High Thermal Stability. Sens. Actuators B 2010, 150, 788–793. [Google Scholar] [CrossRef]
- Comini, E. Metal oxide nanowire chemical sensors: Innovation and quality of life. Mater. Today 2016, 19, 559–567. [Google Scholar] [CrossRef]
- Golovanov, V.; Liu, C.C.; Kiv, A.; Fuks, D.; Ivanovskaya, M. Microfabricated One-electrode In2O3 and Fe2O3- In2O3 Composite Sensors. Comput. Model. New Technol. 2009, 13, 68–73. [Google Scholar]
- Han, N.; Tian, Y.; Wu, X. Improving Humidity Selectivity in Formaldehyde Gas Sensing by a Two-Sensor Array Made of Ga-Doped ZnO. Sens. Actuators B 2009, 138, 228–235. [Google Scholar] [CrossRef]
- Fernandez, L.; Guney, S.; Gutierrez-Galvez, A.; Marco, S. Calibration Transfer in Temperature Modulated Gas Sensor. Sens. Actuators B Chem. 2016, 231, 276–284. [Google Scholar] [CrossRef]
- Sankaran, S.; Khot, L.R.; Panigrahi, S. Biology and applications of olfactory sensing system: A review. Sens. Actuators B Chem. 2012, 171–172, 1–17. [Google Scholar] [CrossRef]
- Gutierrez-Osuna, R. Pattern analysis for machine olfaction: A review. IEEE Sens. J. 2002, 2, 189–202. [Google Scholar] [CrossRef]
- Marco, S.; Gutierrez-Galvez, A. Signal and Data Processing for Machine Olfaction and Chemical Sensing: A Review. IEEE Sens. J. 2012, 12, 3189–3214. [Google Scholar] [CrossRef]
- Presmanes, L.; Thimont, Y.; Younsi, I.E.; Chapelle, A.; Blanc, F.; Talhi, C.; Bonninque, C.; Barnabé, A.; Menini, P.; Tailhades, P. Integration of P-CuO Thin Sputtered Layers onto Microsensor Platforms for Gas Sensing. Sensors 2017, 17, 1409. [Google Scholar] [CrossRef] [PubMed]
- Eusebio, L.; Capelli, L.; Sironi, S. Electronic Nose Testing Procedure for the Definition of Minimum Performance Requirements for Environmental Odor Monitoring. Sensors 2016, 16, 1548–1564. [Google Scholar] [CrossRef] [PubMed]
- Far, A.B.; Flitti, F.; Guo, B.; Bermak, A. A Bio-Inspired Pattern Recognition System for Tin-Oxide Gas Sensor Applications. IEEE Sens. J. 2009, 9, 713–722. [Google Scholar] [CrossRef]
- Shi, Z.B.; Yu, T.; Zhao, Q.; Li, Y.; Lan, Y.B. Comparison of Algorithms for an Electronic Nose in Identifying Liquors. J. Bionic Eng. 2008, 5, 253–257. [Google Scholar] [CrossRef]
- Zhang, L.; Tian, F.C.; Dang, L.J.; Li, G.R.; Peng, X.W.; Yin, X.; Liu, S.Q. A Novel Background Interferences Method in Electronic Nose Using Pattern Recognition. Sens. Actuators A Phys. 2013, 201, 254–263. [Google Scholar] [CrossRef]
- Zhang, L.; Tian, F.C.; Pei, G.S. A Novel Sensor Selection Using Pattern Recongnition in Electronic Nose. Measurement 2014, 54, 31–39. [Google Scholar] [CrossRef]
- Shinmyo, N.; Iwata, T.; Hashizume, K.; Kuroki, K.; Sawada, K. Development of potentiometric miniature gas sensor arrays feasible for small olfactory chips and gas recognition from their response patterns. In Proceedings of the 2017 IEEE Sensors, Glasgow, UK, 29 October–1 November 2017. [Google Scholar]
- Zou, X.; Zhao, J.; Wu, S.; Huang, X. Vinegar Classification Based on Feature Extraction and Selection from Tin Oxide Gas Sensor Array Data. Sensors 2003, 3, 127–142. [Google Scholar]
- Wang, Y.; Xing, J.G.; Qian, S. Selectivity Enhancement in Electronic Nose Based on an Optimized DQN. Sensors 2017, 17, 2356. [Google Scholar] [CrossRef] [PubMed]
- Hyvärinen, A. Fast and Robust Fixed-Point Algorithms for Independent Component Analysis. IEEE Trans. Neural Netw. 1999, 10, 626–634. [Google Scholar] [CrossRef] [PubMed]
- Bell, A.J.; Sejnowski, T.J. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995, 7, 1129–1159. [Google Scholar] [CrossRef] [PubMed]
- Meksiarun, P.; Ishigaki, M.; Huck-Pezzei, V.A.; Huck, C.W.; Wonqravee, K.; Sato, H.; Ozaki, Y. Comparison of Multivariate Analysis Methods for Extracting the Paraffin Component from the Paraffin-Embedded Cancer Tissue Spectra for Raman Imaging. Sci. Rep. 2017, 7, 44890. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Tian, F.C. Performance Study of Multilayer Perceptrons in a Low-Cost Electronic Nose. IEEE Trans. Instrum. Meas. 2014, 63, 1670–1679. [Google Scholar] [CrossRef]
- Wen, T.L.; Yan, J.; Huang, D.Y.; Lu, K.; Deng, C.J.; Zeng, T.Y.; Yu, S.; He, Z.Y. Feature Extraction of Electronic Nose Signals Using QPSO-Based Multiple KFDA Signal Processing. Sensors 2018, 18, 388. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.H.; Meng, Q.H.; Qi, P.F.; Zhou, Y.; Ma, S.G. Boosting-Based One-Class SVM for Recognizing True-Fake Chinese Liquors Using Electronic Noses. In Proceedings of the Intelligent Control and Automation 12th World Congress, Guilin, China, 12–15 June 2016; pp. 1208–1413. [Google Scholar]
- Dang, L.; Tian, F.; Zhang, L.; Kadri, C.; Yin, X.; Peng, X.W.; Liu, S.Q. A novel classifier ensemble for recognition of multiple indoor air contaminants by an electronic nose. Sens. Actuators A Phys. 2014, 207, 67–74. [Google Scholar] [CrossRef]
- Peterson, J.D.P.; Aujla, A.; Grant, K.H.; Brundle, A.G.; Thompson, M.R.; Hey, J.V.; Leigh, R.J. Practical Use of Metal Oxide Semiconductor Gas Sensors for Measuring Nitrogen Dioxide and Ozone in Urban Environments. Sensors 2017, 17, 1653. [Google Scholar] [CrossRef] [PubMed]
- Pardo, M.; Sberveglieri, G. Classification of electronic nose data with support vector machines. Sens. Actuators B 2005, 107, 730–737. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, X.; Yang, J.; Xu, Y. A gas concentration estimation method based on multivariate relevance vector machine using MOS gas sensor arrays. In Proceedings of the 2017 IEEE International Instrumentation and Measurement Technology Conference, Turin, Italy, 22–25 July 2017; pp. 1–5. [Google Scholar]
- Jia, P.F.; Tian, F.H.; He, Q.H.; Fan, S.; Liu, J.L.; Yang, S.X. Feature extraction of wound infection data for electronic nose based on a novel weighted KPCA. Sens. Actuators B Chem. 2014, 201, 555–566. [Google Scholar] [CrossRef]
- Sarma, M.S.; Srinivas, Y.; Abhiram, M.; Ullala, L.; Prasanthi, M.S.; Rao, J.R. Insider Threat detection with Face Recognition and KNN User Classification. In Proceedings of the 2017 IEEE International Conference on Cloud Computing in Emerging Markets International Conference, Bangalore, India, 1–3 November 2017; pp. 39–44. [Google Scholar]
- Thayanantheana, A.; Navaratnama, R.; Stengerb, B.; Torr, P.H.S.; Roberto, C. Multivariate Relevance Vector Machines for Tracking. In Proceedings of the 9th European Conference on Computer Vision, Graz, Austria, 7–13 May 2006; pp. 124–138. [Google Scholar]
- Liu, Z.W.; Guo, W.; Tang, Z.C.; Chen, Y.Q. Multi-Sensor Data Fusion Using a Relevance Vector Machine Based on an Ant Colony for Gearbox Fault Detection. Sensors 2015, 15, 21857–21875. [Google Scholar] [CrossRef] [PubMed]
- Andriyas, T.; Andriysa, S. Use of Multivariate Relevance Vector Machines in forecasting multiple geomagnetic indices. J. Atmos. Sol. Terr. Phys. 2017, 153, 21–32. [Google Scholar] [CrossRef]
- Thayanantheana, A.; Navaratnama, R.; Stengerb, B.; Torr, P.H.; Cipolla, R. Pose estimation and tracking using multivariate regression. Pattern Recognit. Lett. 2008, 29, 1302–1310. [Google Scholar] [CrossRef]
- Hosseini-Golgoo, H.M.; Ebrahimpour, N. Comparison of different feature reduction methods in the improvement of gas diagnosis of a temperature modulated resistive gas sensor. Mater. Sci. Eng. 2016, 108, 012001. [Google Scholar] [CrossRef]
| CH4 (ppm) | CO (ppm) | |||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 200 | 400 | 600 | 800 | 1000 | 1200 | 1400 | |
| 0 | TS | ES | TS | ES | TS | ES | TS | |
| 200 | TS | ES | TS | ES | TS | ES | TS | |
| 400 | ES | TS | ES | TS | ES | TS | ES | |
| 600 | TS | ES | TS | ES | TS | ES | TS | |
| 800 | ES | TS | ES | TS | ES | TS | ES | |
| 1000 | TS | ES | TS | ES | TS | ES | TS | |
| 1200 | ES | TS | ES | TS | ES | TS | ES | |
| 1400 | TS | |||||||
| Principal Component | Eigenvalues | Contribution Rate | Cumulative Contribution Rate |
|---|---|---|---|
| PC1 | 0.1072 | 11.96% | 11.96% |
| PC2 | 0.0932 | 10.40% | 22.36% |
| PC3 | 0.0739 | 8.25% | 30.61% |
| PC4 | 0.0565 | 6.30% | 36.91% |
| PC5 | 0.0524 | 5.85% | 42.76% |
| PC6 | 0.0432 | 4.82% | 47.58% |
| PC7 | 0.0373 | 4.17% | 51.75% |
| … | … | … | … |
| PC32 | 0.0055 | 0.60% | 90.31% |
| … | … | … | … |
| PC43 | 0.0027 | 0.29% | 95.11% |
| Category | Sample | Detection Sample Recognition Rate | ||
|---|---|---|---|---|
| PCA | ICA | KPCA | ||
| CO | 150 | 86.70% | 100% | 93.30% |
| CH4 | 150 | 100% | 53.30% | 100% |
| Mixed Gas | 900 | 92.20% | 86.70% | 98.80% |
| Average | ----- | 92.5% | 84.17% | 98.33% |
| Gas Category | Single Gas | Mixed Gas | ||
|---|---|---|---|---|
| Gas Composition | CO | CH4 | CO | CH4 |
| Optimal Kernel Parameters | 0.76 | 0.25 | 0.67 | |
| Average Relative Error | 2.36% | 2.01% | 9.01% | 8.79% |
| Performance | Method | ||
|---|---|---|---|
| MVRVM | Single RVM | LS-SVR | |
| Average Relative Error of CO (%) | |||
| Average Relative Error of CH4 (%) | |||
| Average Detection Time (ms) | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Zhao, X.; Chen, Y.; Zhao, W. Research on a Mixed Gas Recognition and Concentration Detection Algorithm Based on a Metal Oxide Semiconductor Olfactory System Sensor Array. Sensors 2018, 18, 3264. https://doi.org/10.3390/s18103264
Xu Y, Zhao X, Chen Y, Zhao W. Research on a Mixed Gas Recognition and Concentration Detection Algorithm Based on a Metal Oxide Semiconductor Olfactory System Sensor Array. Sensors. 2018; 18(10):3264. https://doi.org/10.3390/s18103264
Chicago/Turabian StyleXu, Yonghui, Xi Zhao, Yinsheng Chen, and Wenjie Zhao. 2018. "Research on a Mixed Gas Recognition and Concentration Detection Algorithm Based on a Metal Oxide Semiconductor Olfactory System Sensor Array" Sensors 18, no. 10: 3264. https://doi.org/10.3390/s18103264
APA StyleXu, Y., Zhao, X., Chen, Y., & Zhao, W. (2018). Research on a Mixed Gas Recognition and Concentration Detection Algorithm Based on a Metal Oxide Semiconductor Olfactory System Sensor Array. Sensors, 18(10), 3264. https://doi.org/10.3390/s18103264





