Methodology for Simulating 5G and GNSS High-Accuracy Positioning
Abstract
:1. Introduction
2. Scenario Definition
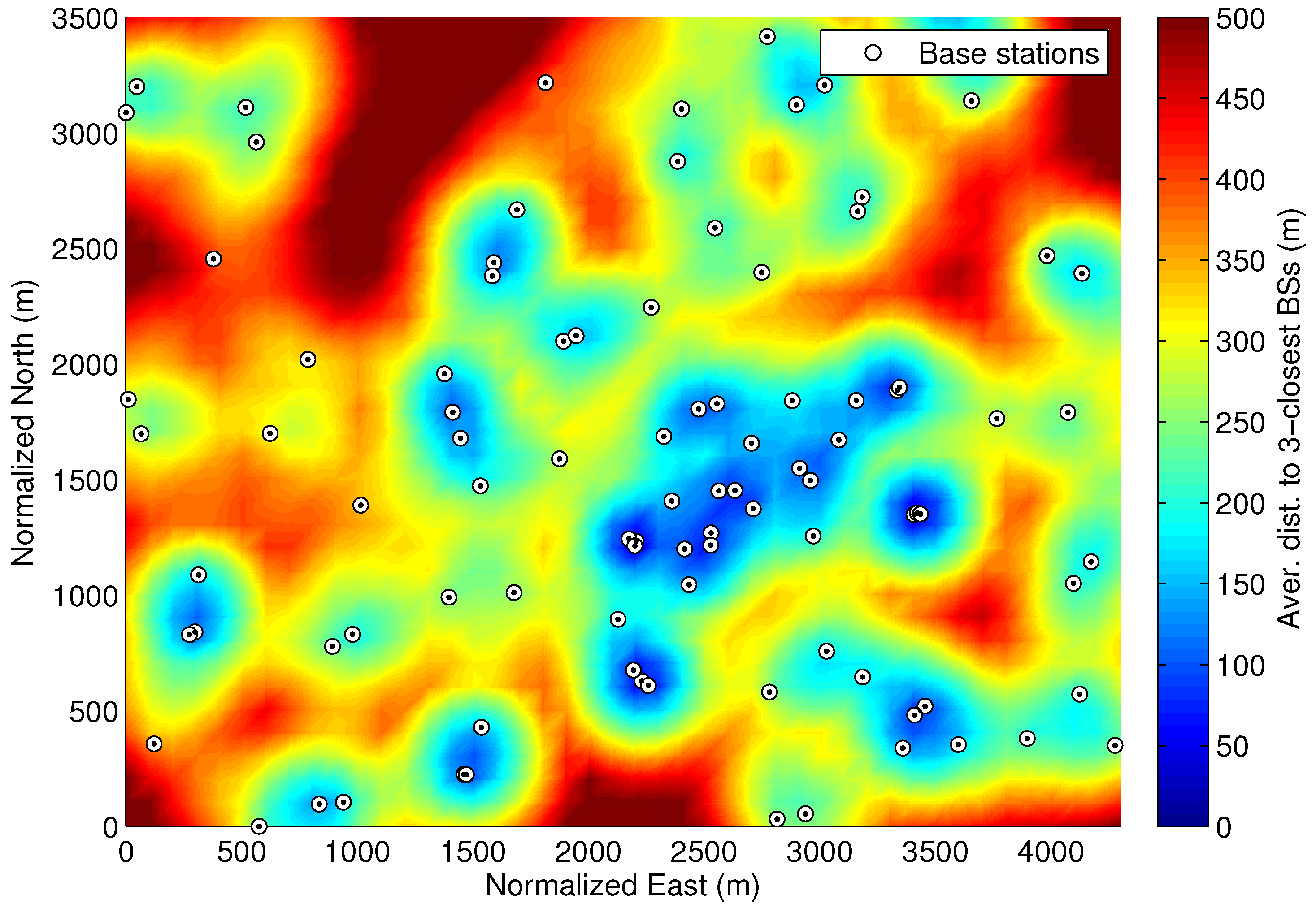
2.1. Network of Cellular Transmitters
- 5G cmWave networks: The 5G cmWave networks operate at frequency bands between 450 MHz and 6 GHz [15]. Due to the limited available spectrum, there is a reduced system bandwidth of up to 100 MHz, which can be improved with carrier aggregation. Thanks to the favorable propagation conditions at sub-6 GHz frequencies, rural macro cells achieve a large coverage area. According to [16], the inter-site distance (ISD) between rural macro BSs is defined to 1732 m or 5000 m. In urban areas, the ISD of the macro cells is reduced to 500 m, and hotspots are covered with small cells or micro sites of ISD equal to 200 m [16].
- 5G mmWave networks: The 5G mmWave networks are defined for the frequency range (FR) from 24.25 GHz to 52.6 GHz, where large system bandwidths between 50 and 400 MHz can be allocated [15]. These networks are deployed over small cells, which may be co-located with micro cmWave sites or dedicated mmWave sites, in order to cope with very high communications demands over specific urban areas. The high attenuation losses at mmWave frequencies can be overcome thanks to massive antenna arrays [17] and innovative array signal processing [18].
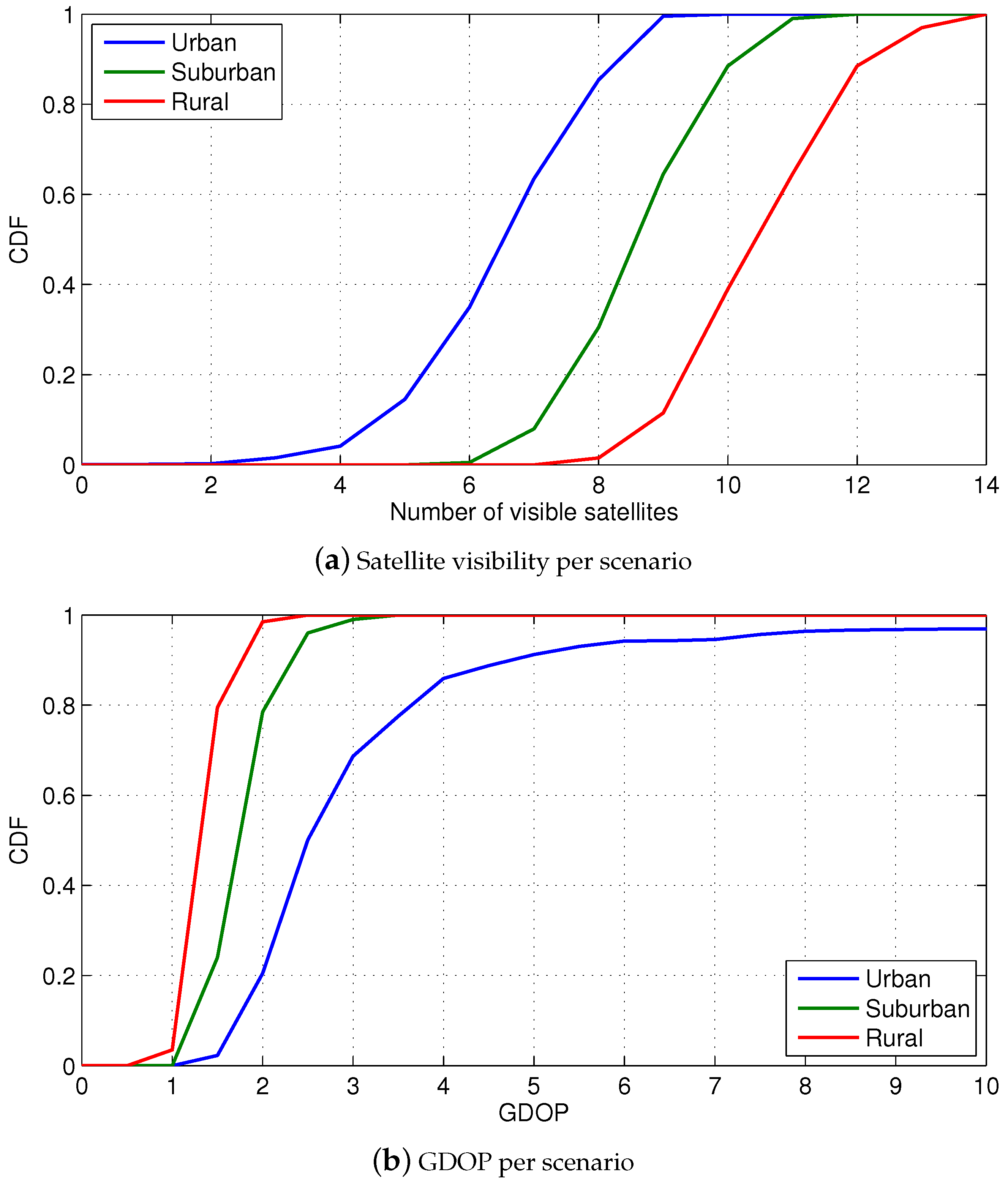
2.2. GNSS Satellite Visibility
3. Characterization of the Observables
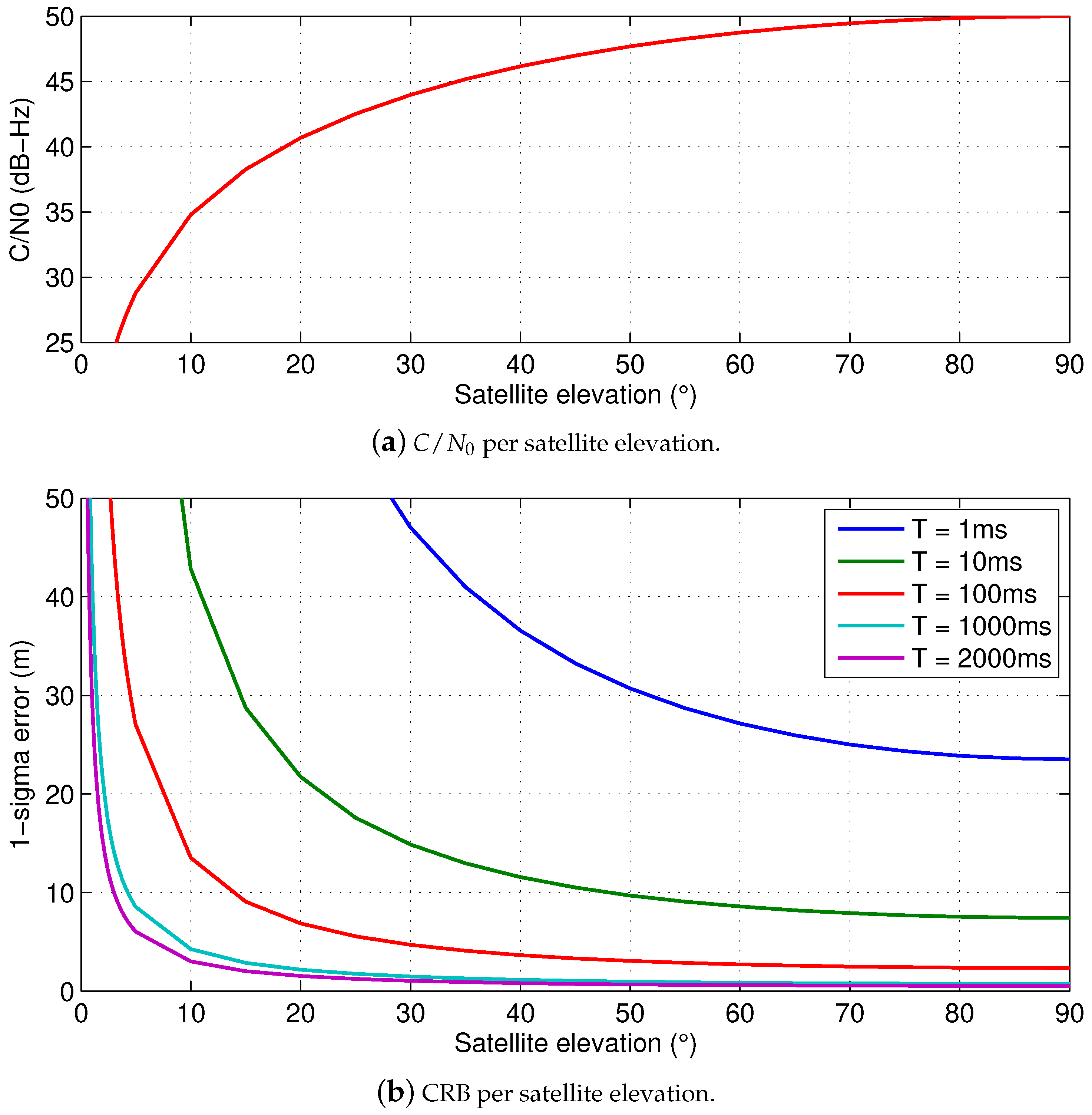
3.1. GNSS
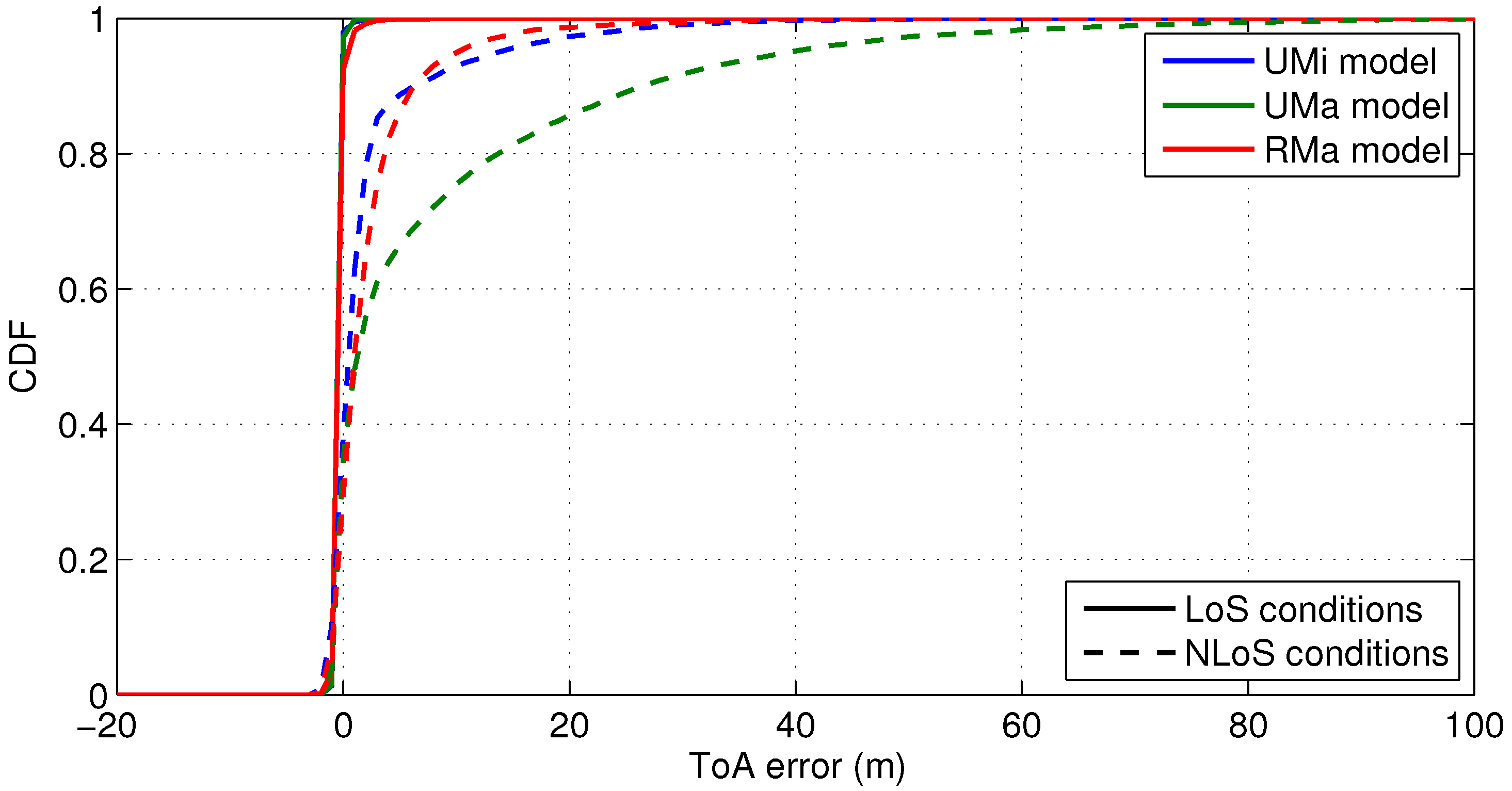
3.2. cmWave
3.3. mmWave
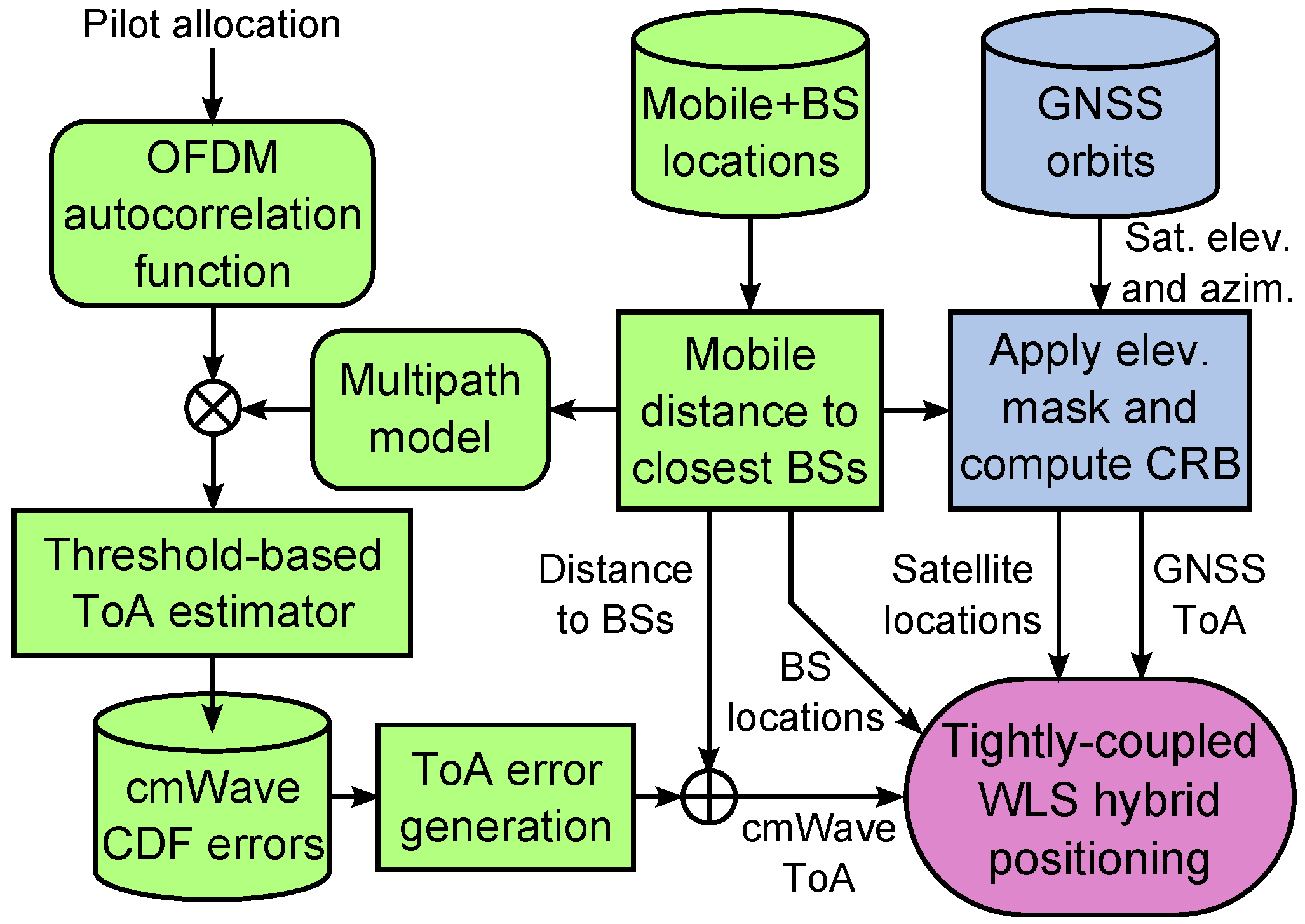
4. Position Solution
4.1. Tightly Coupled GNSS and cmWave Cellular Positioning
4.2. Stand-Alone mmWave Positioning
5. Performance Results
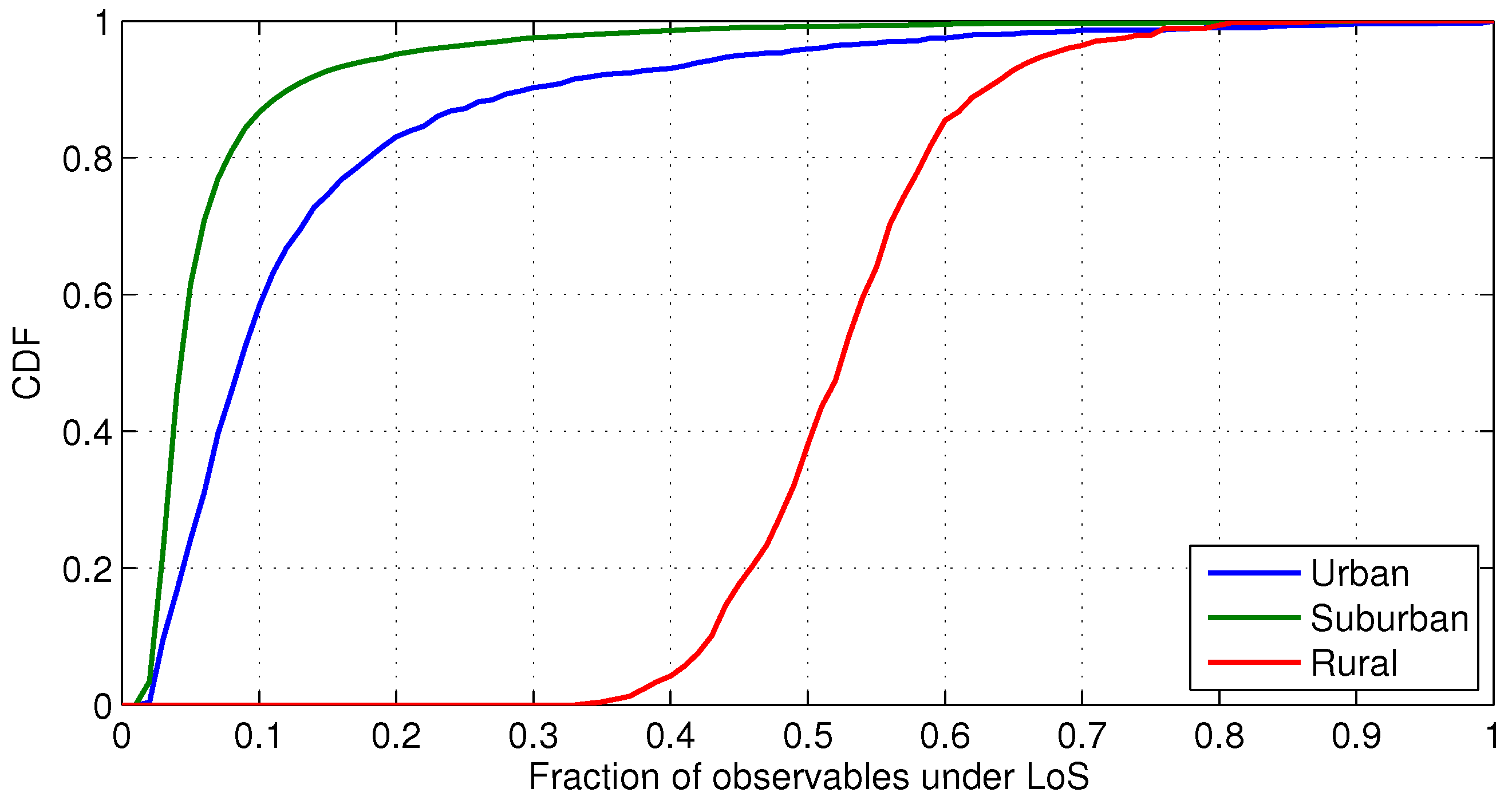
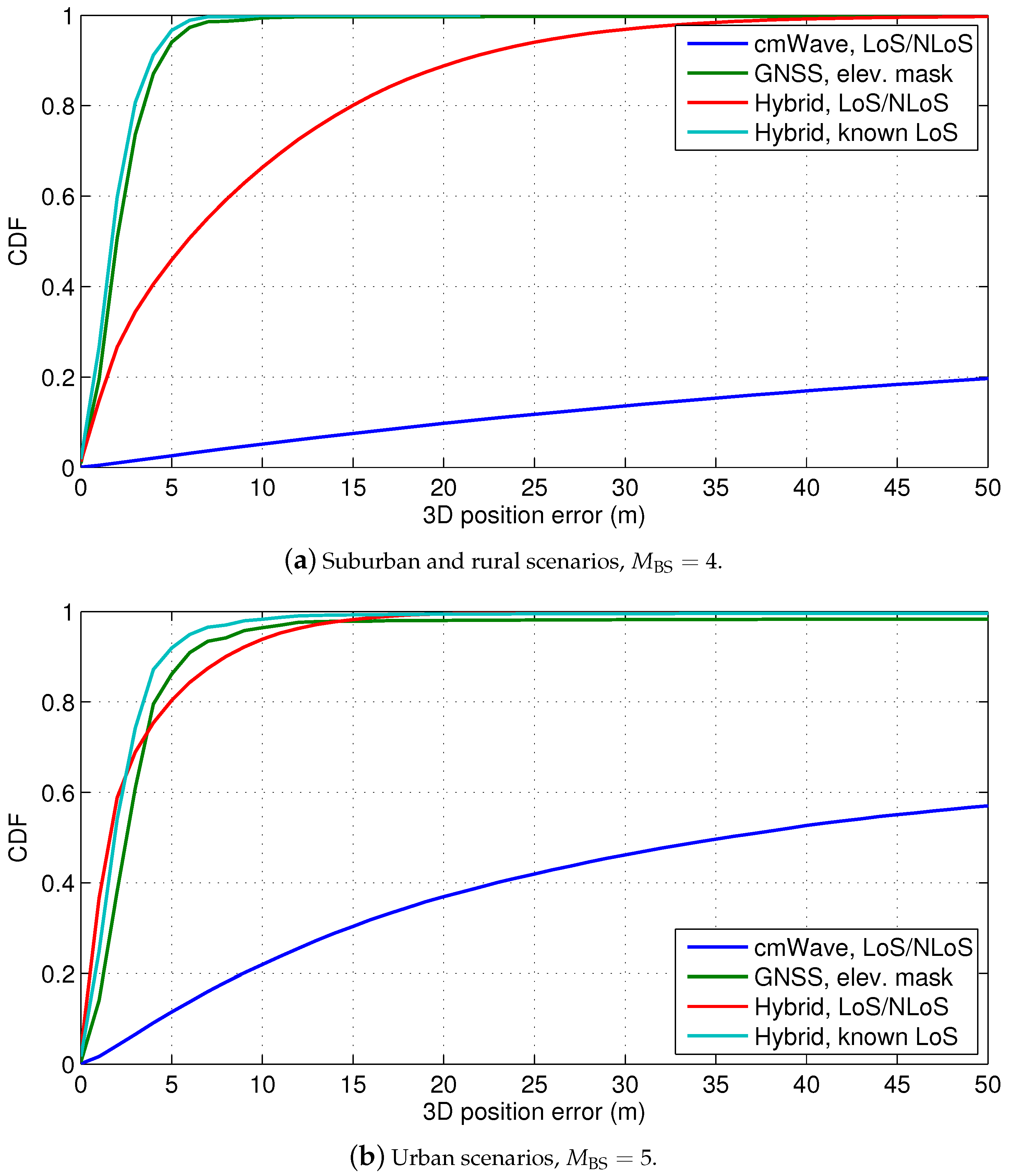
5.1. Suburban and Rural Scenarios
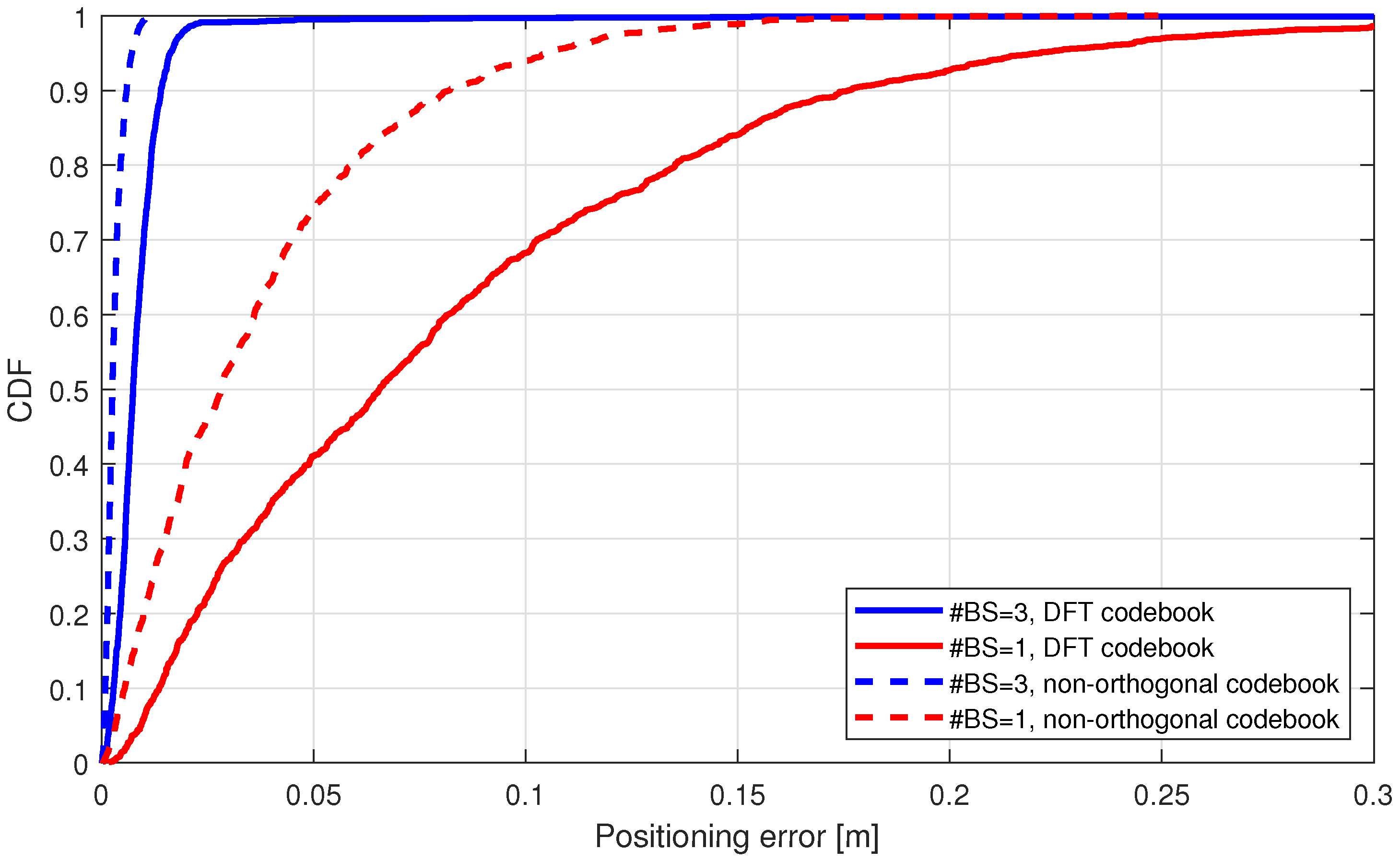
5.2. Urban Scenarios with cmWave Deployments
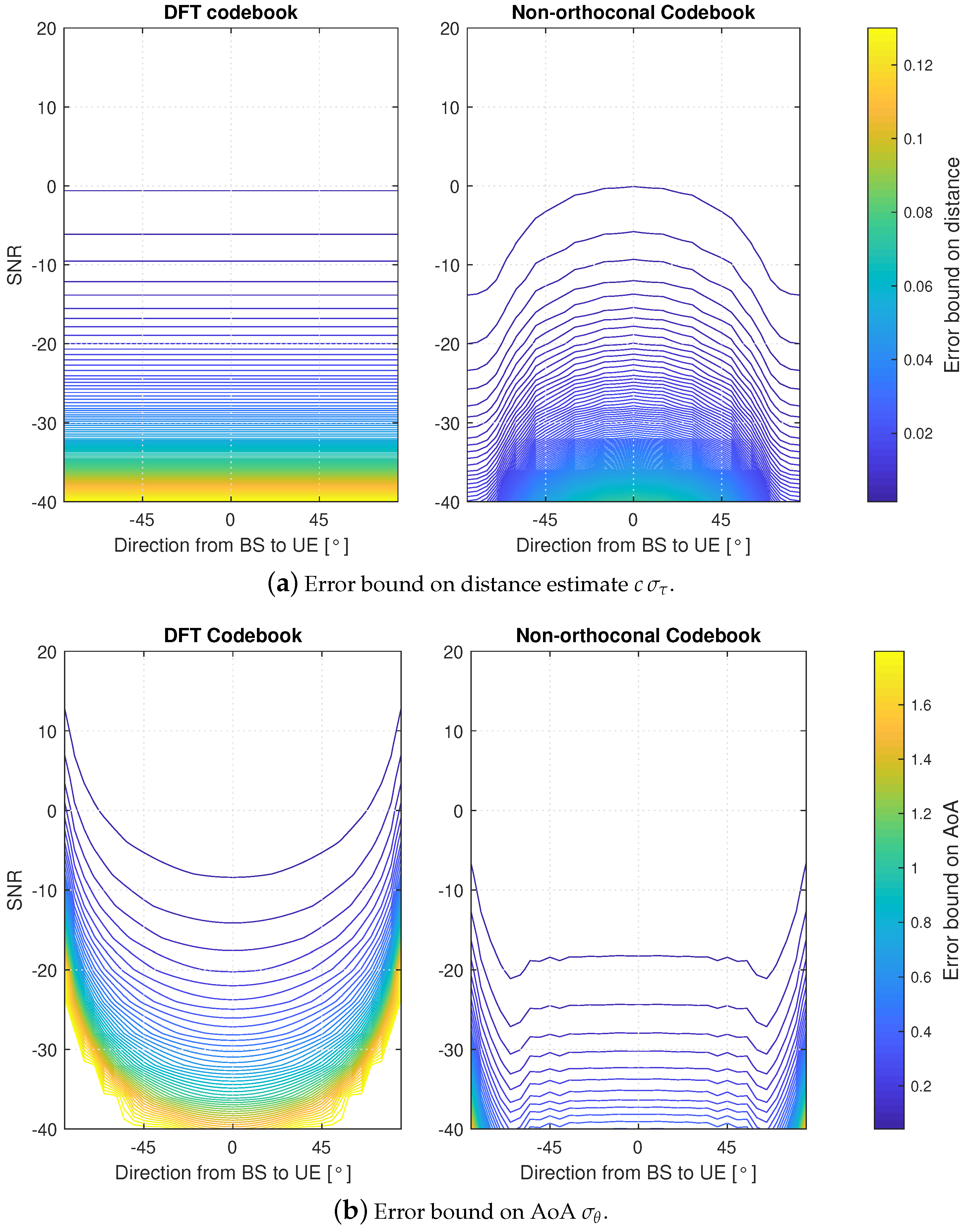
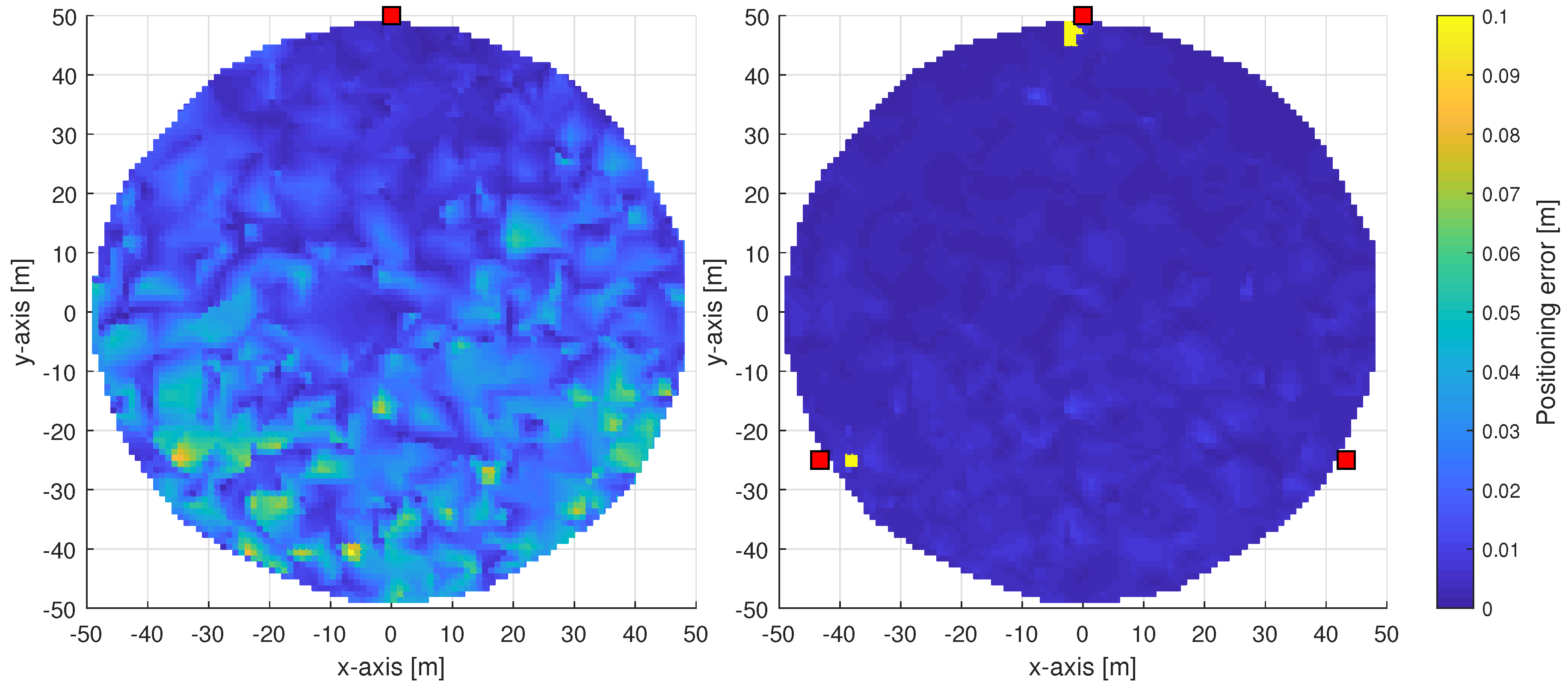
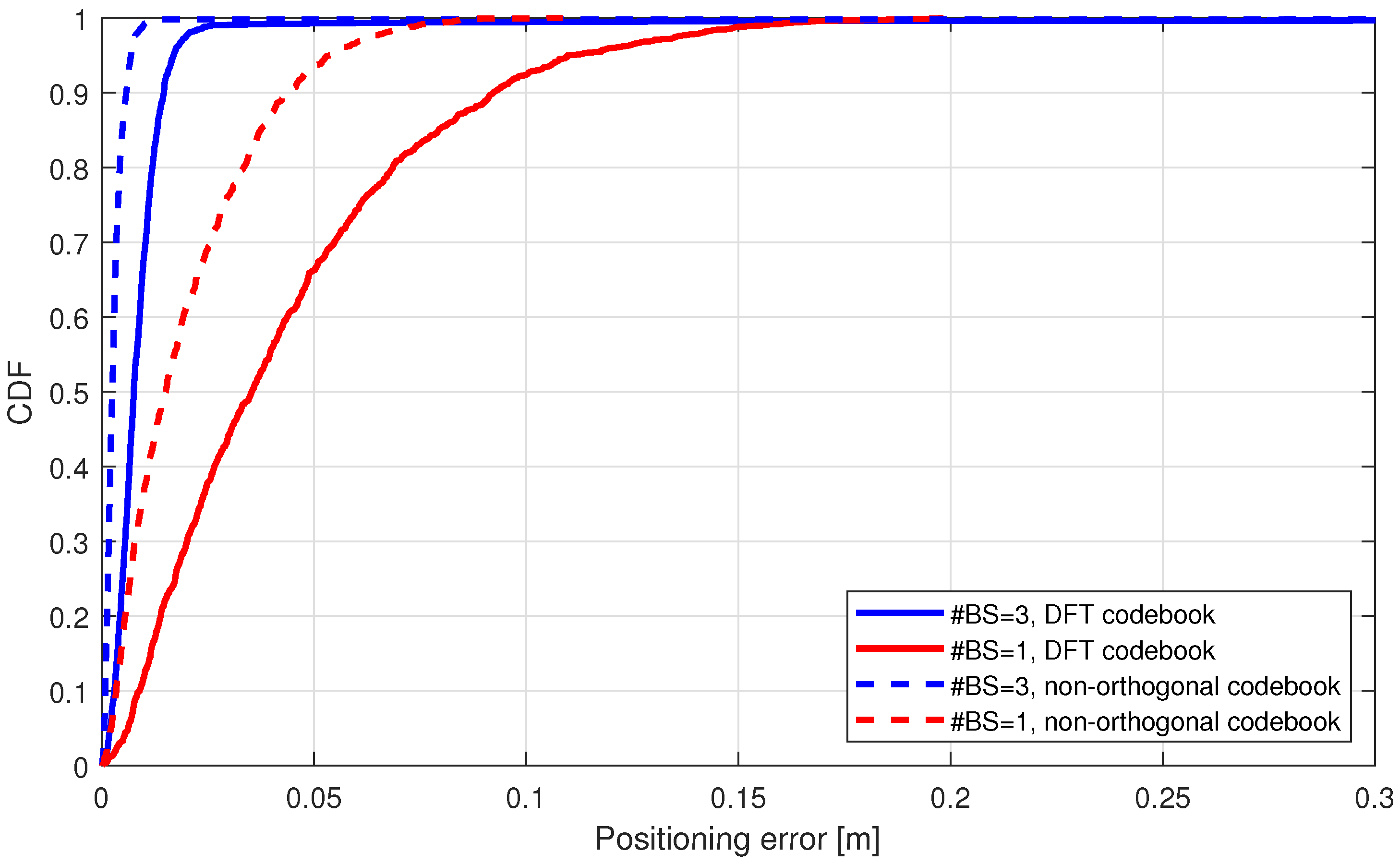
5.3. Urban Scenarios with mmWave Deployments
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. CRLB on mmWave Channel Parameters
References
- 3GPP TR 22.872. Study on Positioning Use Cases; Stage 1; 3GPP: Sophia Antipolis, France, 2018. [Google Scholar]
- 5G-PPP. 5G Automotive Vision; White Paper; 5G-PPP: Heidelberg, Germany, 2015. [Google Scholar]
- del Peral-Rosado, J.A.; Raulefs, R.; López-Salcedo, J.A.; Seco-Granados, G. Survey of cellular mobile radio localization methods: From 1G to 5G. IEEE Commun. Surv. Tutor. 2018, 20, 1124–1148. [Google Scholar] [CrossRef]
- Botteron, C.; Firouzi, E.; Farine, P.A. Performance analysis of mobile station location using hybrid GNSS and cellular network measurements. In Proceedings of the GNSS 17th International Technical Meeting of the Satellite Division, Tampa, FL, USA, 21–24 September 2004; Volume 17, pp. 2458–2467. [Google Scholar]
- De Angelis, G.; Baruffa, G.; Cacopardi, S. GNSS/cellular hybrid positioning system for mobile users in urban scenarios. IEEE Trans. Intell. Transp. Syst. 2013, 14, 313–321. [Google Scholar] [CrossRef]
- Mensing, C.; Sand, S.; Dammann, A. Hybrid data fusion and tracking for positioning with GNSS and 3GPP-LTE. Int. J. Navig. Obs. 2010, 2010, 812945. [Google Scholar] [CrossRef]
- Medbo, J.; Siomina, I.; Kangas, A.; Furuskog, J. Propagation channel impact on LTE positioning accuracy: A study based on real measurements of observed time difference of arrival. In Proceedings of the IEEE 20th International Symposium on Personal, Indoor and Mobile Radio Communications, Tokyo, Japan, 13–16 September 2009. [Google Scholar] [CrossRef]
- Wymeersch, H.; Seco-Granados, G.; Destino, G.; Dardari, D.; Tufvesson, F. 5G mmWave positioning for vehicular networks. IEEE Wirel. Commun. 2017, 24, 80–86. [Google Scholar] [CrossRef]
- 3GPP TSG RAN Meeting #80, RP-180897. New SID: Study on NR Positioning Support; 3GPP: Sophia Antipolis, France, 2018. [Google Scholar]
- Mueck, M.; Strinati, E.C.; Kim, I.G.; Clemente, A.; Dore, J.B.; Domenico, A.D.; Kim, T.; Choi, T.; Chung, H.K.; Destino, G.; et al. 5G CHAMPION—Rolling out 5G in 2018. In Proceedings of the 2016 IEEE Globecom Workshops (GC Wkshps), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- 3GPP TR 37.857. Study on Indoor Positioning Enhancements for UTRA and LTE; 3GPP: Sophia Antipolis, France, 2015. [Google Scholar]
- 3GPP TR 38.855. Study on NR Positioning Support; 3GPP: Sophia Antipolis, France, 2018. [Google Scholar]
- ETSI TS 103 246-3. Satellite Earth Stations and Systems (SES); GNSS Based Location Systems; Part 3: Performance Requirements; European Telecommunications Standards Institute: Sophia Antipolis, France, 2015. [Google Scholar]
- 3GPP TS 36.171. Requirements for Support of Assisted Global Navigation Satellite System (A-GNSS); 3GPP: Sophia Antipolis, France, 2017. [Google Scholar]
- 3GPP TR 38.104. Base Station (BS) Radio Transmission and Reception; 3GPP: Sophia Antipolis, France, 2018. [Google Scholar]
- 3GPP TR 38.901. Study on Channel Model for Frequencies from 0.5 to 100 GHz; 3GPP: Sophia Antipolis, France, 2017. [Google Scholar]
- Zhang, J.A.; Huang, X.; Dyadyuk, V.; Guo, Y.J. Massive hybrid antenna array for millimeter-wave cellular communications. IEEE Wirel. Commun. 2015, 22, 79–87. [Google Scholar] [CrossRef]
- Heath, R.W.; González-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A.M. An overview of signal processing techniques for millimeter wave MIMO systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Antenna Bureau, Radiocommunications Agency of The Netherlands. Available online: http://www.antenneregister.nl/register (accessed on 21 June 2018).
- Sand, S.; Dammann, A.; Mensing, C. Chapter 6: Scenarios and models. In Positioning in Wireless Communications Systems, 1st ed.; John Wiley & Sons, Ltd.: Hooboken, NJ, USA, 2014; pp. 119–133. [Google Scholar]
- del Peral-Rosado, J.A.; Estatuet-Castillo, R.; Míguez-Sanchez, J.; Navarro-Gallardo, M.; García-Molina, J.A.; López-Salcedo, J.A.; Seco-Granados, G.; Zanier, F.; Crisci, M. Performance analysis of hybrid GNSS and LTE localization in urban scenarios. In Proceedings of the 2016 8th ESA Workshop on Satellite Navigation Technologies and European Workshop on GNSS Signals and Signal Processing (NAVITEC), Noordwijk, The Netherlands, 14–16 December 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Kaplan, E.; Hegarty, C. Understanding GPS: Principles and Applications; Artech House: Norwood, MA, USA, 2005. [Google Scholar]
- López-Salcedo, J.A.; Parro-Jiménez, J.M.; Seco-Granados, G. Multipath detection metrics and attenuation analysis using a GPS snapshot receiver in harsh environments. In Proceedings of the 2009 3rd European Conference on Antennas and Propagation, Berlin, Germany, 23–27 March 2009; pp. 3692–3696. [Google Scholar]
- Egea-Roca, D.; Seco-Granados, G.; López-Salcedo, J.A.; Moriana, C.; Paśnikowski, M.J.; Domínguez, E.; Aguado, E.; Lowe, D.; Naberezhnykh, D.; Dovis, F.; et al. Signal-level integrity and metrics based on the application of quickest detection theory to multipath detection. In Proceedings of the the 28th International Technical Meeting of the ION Satellite Division, Tampa, FL, USA, 14–18 September 2015; pp. 2926–2938. [Google Scholar]
- Obst, M.; Bauer, S.; Wanielik, G. Urban multipath detection and mitigation with dynamic 3D maps for reliable land vehicle localization. In Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 685–691. [Google Scholar] [CrossRef]
- Strode, P.R.R.; Groves, P.D. GNSS multipath detection using three-frequency signal-to-noise measurements. GPS Solut. 2016, 20, 399–412. [Google Scholar] [CrossRef]
- Gaglione, S.; Innac, A.; Carbone, S.P.; Troisi, S.; Angrisano, A. Robust estimation methods applied to GPS in harsh environments. In Proceedings of the 2017 European Navigation Conference (ENC), Lausanne, Switzerland, 9–12 May 2017; pp. 14–25. [Google Scholar] [CrossRef]
- Kyösti, P.; Meinilä, J.; Hentilä, L.; Zhao, X.; Jämsä, T.; Schneider, C.; Narandzić, M.; Milojević, M.; Hong, A.; Ylitalo, J. IST-WINNER II Project Deliverable D1.1.2. WINNER II Channel Models; Technical Report; FP6-IST WINNER II Project, European Commission: Brussels, Belgium, 2007. [Google Scholar]
- 3GPP TR 36.873. Study on 3D Channel Model for LTE; 3GPP: Sophia Antipolis, France, 2015. [Google Scholar]
- Shahmansoori, A.; Garcia, G.E.; Destino, G.; Seco-Granados, G.; Wymeersch, H. Position and orientation estimation through millimeter-wave MIMO in 5G systems. IEEE Trans. Wirel. Commun. 2018, 17, 1822–1835. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Sun, S.; Mayzus, R.; Zhao, H.; Azar, Y.; Wang, K.; Wong, G.N.; Schulz, J.K.; Samimi, M.; Gutierrez, F. Millimeter wave mobile communications for 5G cellular: It will work! IEEE Access 2013, 1, 335–349. [Google Scholar] [CrossRef]
- Rydén, H.; Razavi, S.M.; Gunnarsson, F.; Olofsson, I. Cellular network positioning performance improvements by richer device reporting. In Proceedings of the 2018 IEEE 87th Vehicular Technology Conference (VTC Spring), Porto, Portugal, 3–6 June 2018. [Google Scholar]
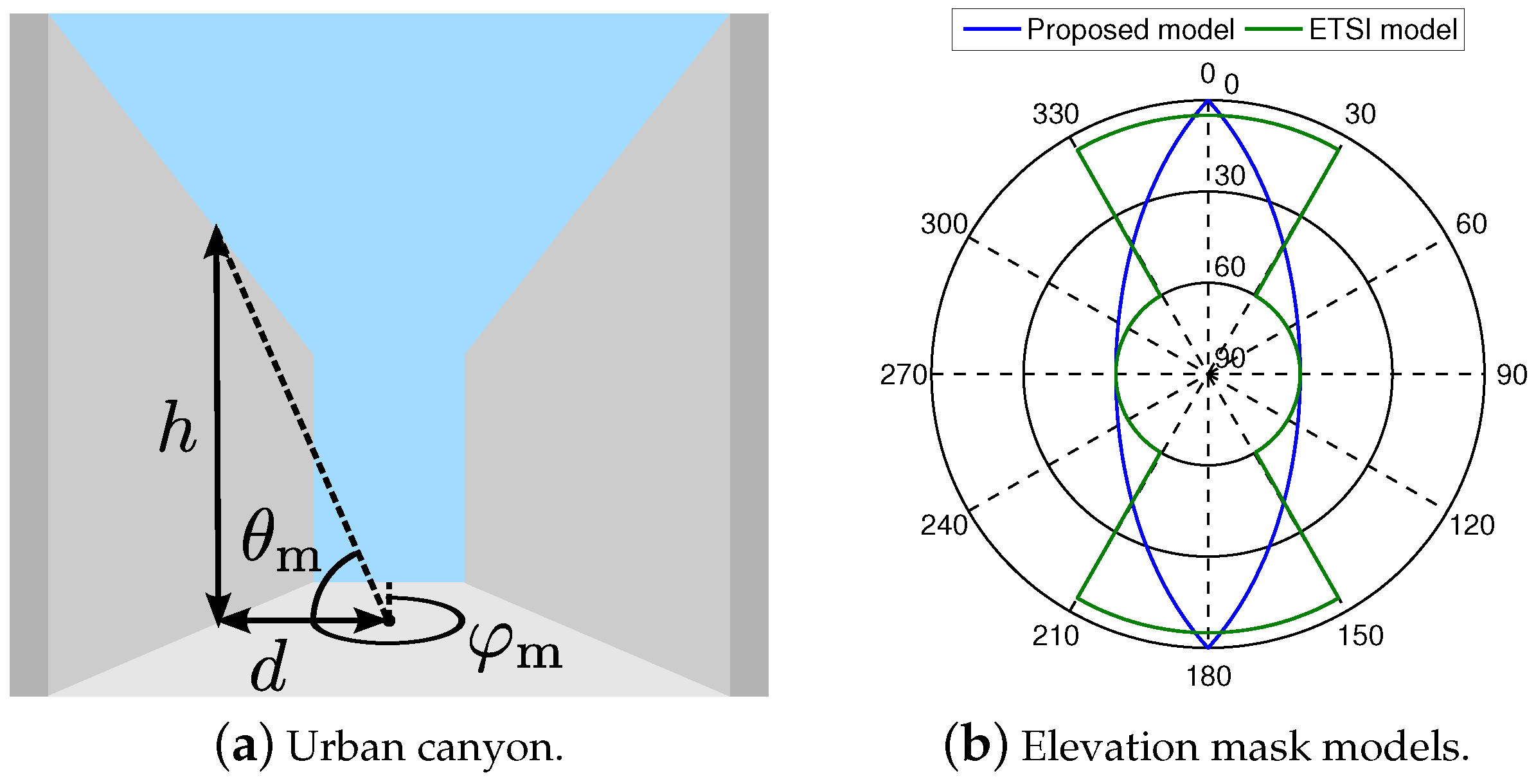
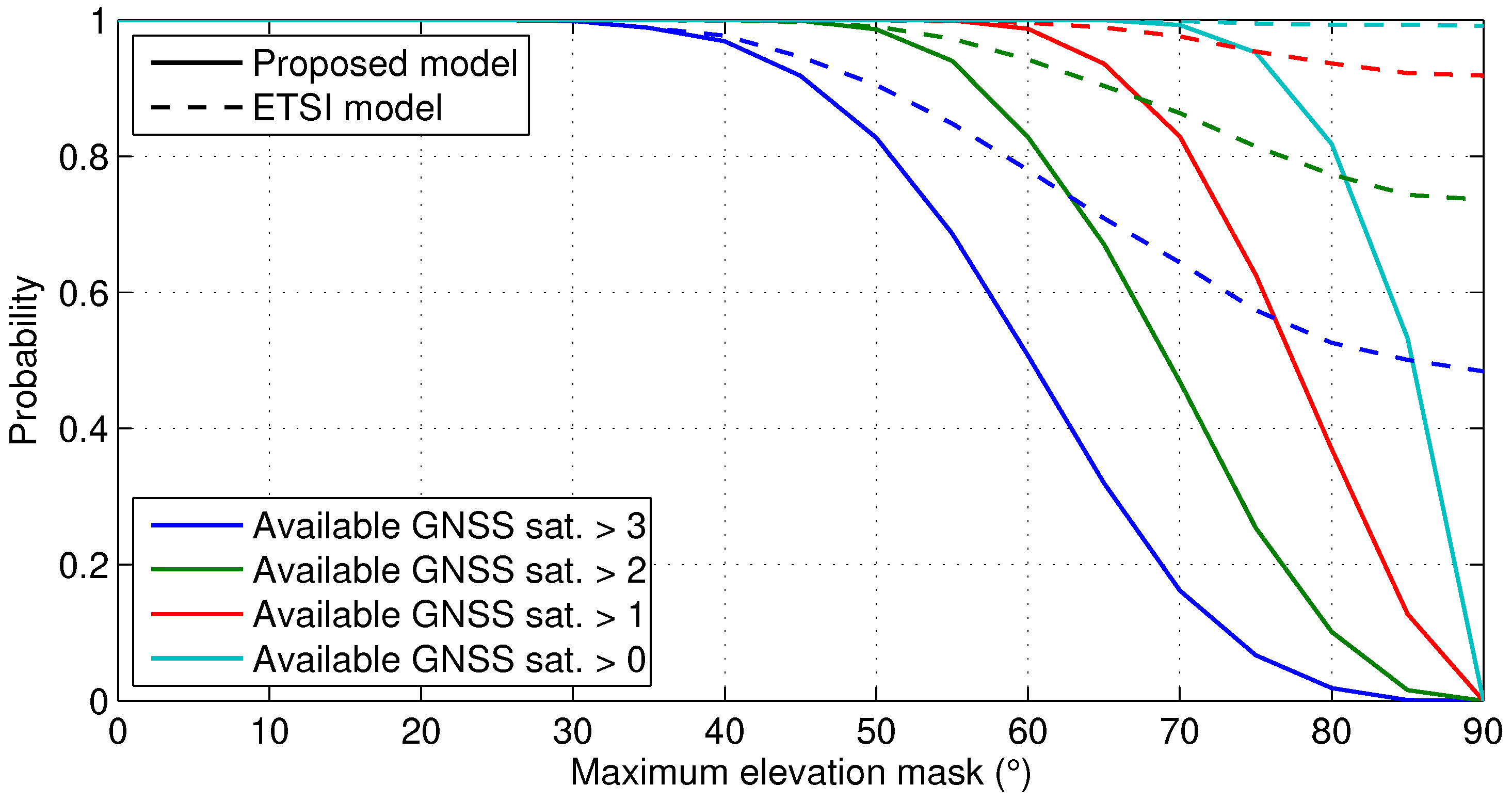

| Model | Elevation Mask Definition | Description | Application Scenario |
|---|---|---|---|
| ETSI [13] | Constant for a range of azimuths | Simple and partially accurate | Predefined urban canyon |
| Sand et al. [20] | Dependent on street width, building height, receiver location and azimuth | Flexible and accurate | Receiver at any location of any symmetrical street |
| Proposed [21] | Dependent on street width, building height and azimuth | Generic and accurate | Receiver at the center of any symmetrical street |
| Scenario | Average Distance to 3 Closest BSs (m) | Channel Model | Max. Elevation Mask (°) |
|---|---|---|---|
| Rural | RMa | 5 | |
| Suburban | UMa | 15 | |
| Urban | UMi | 30 | |
| Urban | UMi | 50 | |
| Urban | UMi | 70 |
| Scenario | ||||||
|---|---|---|---|---|---|---|
| Urban | 100.8 | >10 | 60.5 | >10 | 20.4 | 4.4 |
| Suburban | 100.8 | >10 | 100.4 | >10 | 59.3 | 4.9 |
| Rural | 100.5 | >10 | 59.6 | >10 | 27.0 | 9.9 |
| Scenario | GNSS (with Corrections) | Hybrid (LoS/NLoS) | Hybrid (Known LoS) | |||
|---|---|---|---|---|---|---|
| Urban, 5 BSs | 8.5 | 7.2 | 10.8 | 1.6 | 6.0 | 4.7 |
| Suburban, 4 BSs | 4.9 | 2.5 | 26.9 | 1.5 | 4.7 | 2.4 |
| Rural, 4 BSs | 4.8 | 1.9 | 5.5 | 1.4 | 3.3 | 1.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Del Peral-Rosado, J.A.; Saloranta, J.; Destino, G.; López-Salcedo, J.A.; Seco-Granados, G. Methodology for Simulating 5G and GNSS High-Accuracy Positioning. Sensors 2018, 18, 3220. https://doi.org/10.3390/s18103220
Del Peral-Rosado JA, Saloranta J, Destino G, López-Salcedo JA, Seco-Granados G. Methodology for Simulating 5G and GNSS High-Accuracy Positioning. Sensors. 2018; 18(10):3220. https://doi.org/10.3390/s18103220
Chicago/Turabian StyleDel Peral-Rosado, José A., Jani Saloranta, Giuseppe Destino, José A. López-Salcedo, and Gonzalo Seco-Granados. 2018. "Methodology for Simulating 5G and GNSS High-Accuracy Positioning" Sensors 18, no. 10: 3220. https://doi.org/10.3390/s18103220
APA StyleDel Peral-Rosado, J. A., Saloranta, J., Destino, G., López-Salcedo, J. A., & Seco-Granados, G. (2018). Methodology for Simulating 5G and GNSS High-Accuracy Positioning. Sensors, 18(10), 3220. https://doi.org/10.3390/s18103220





