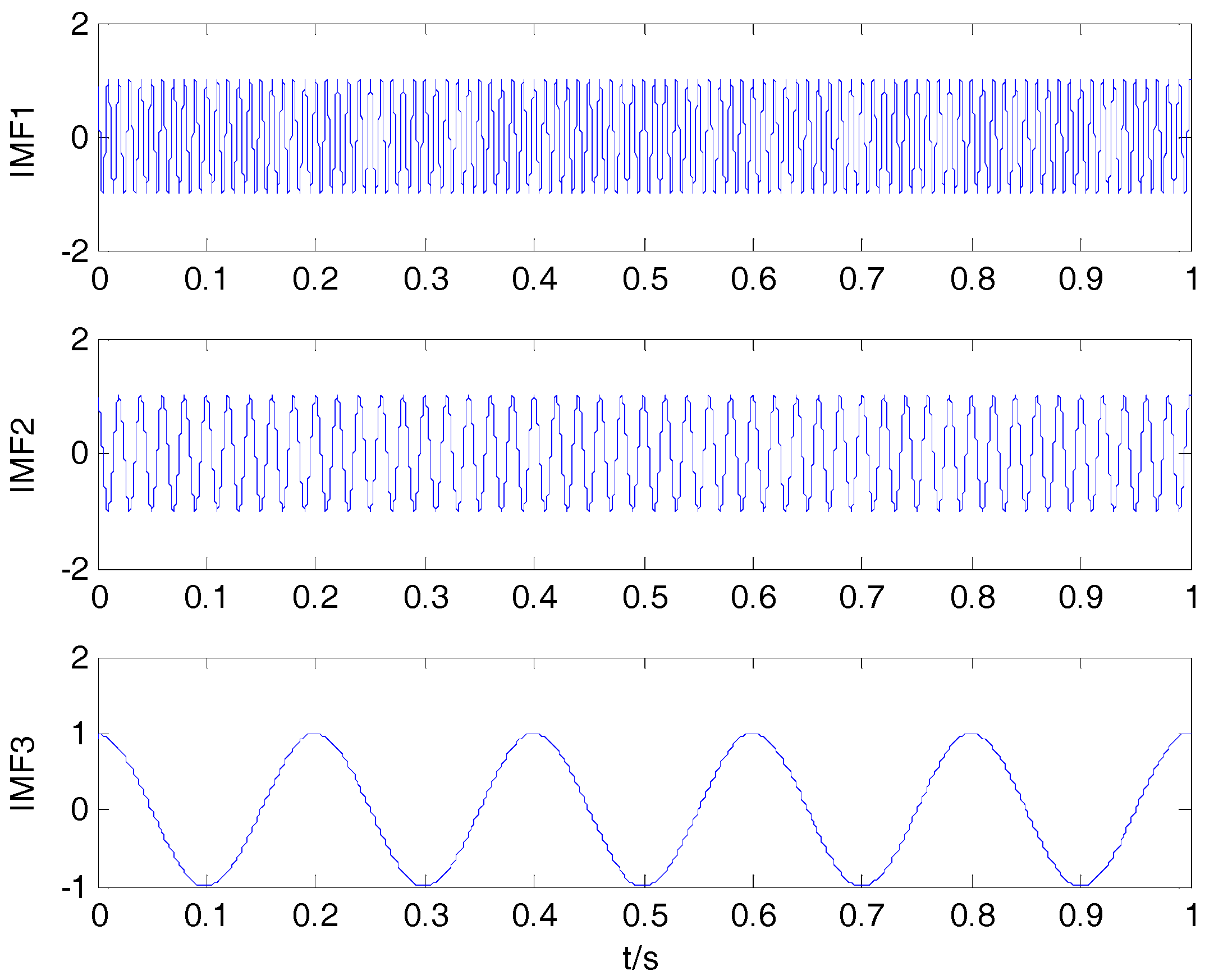
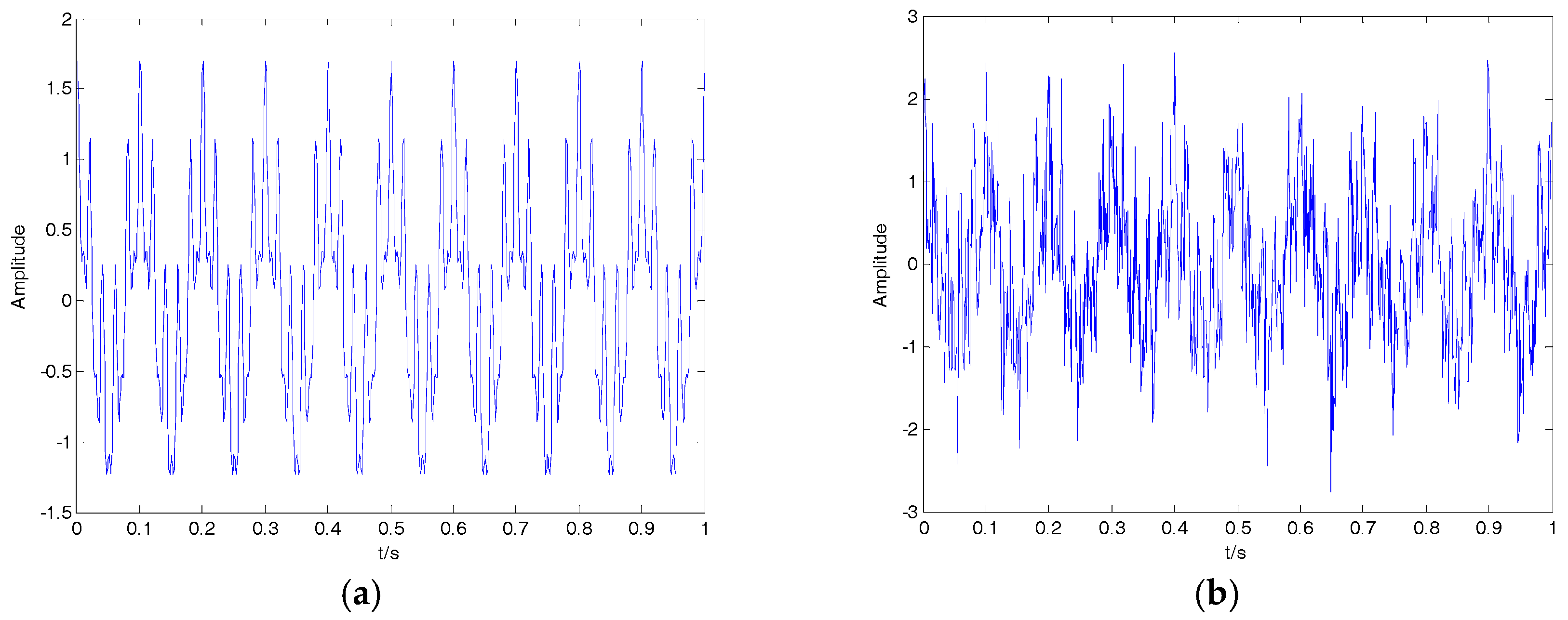
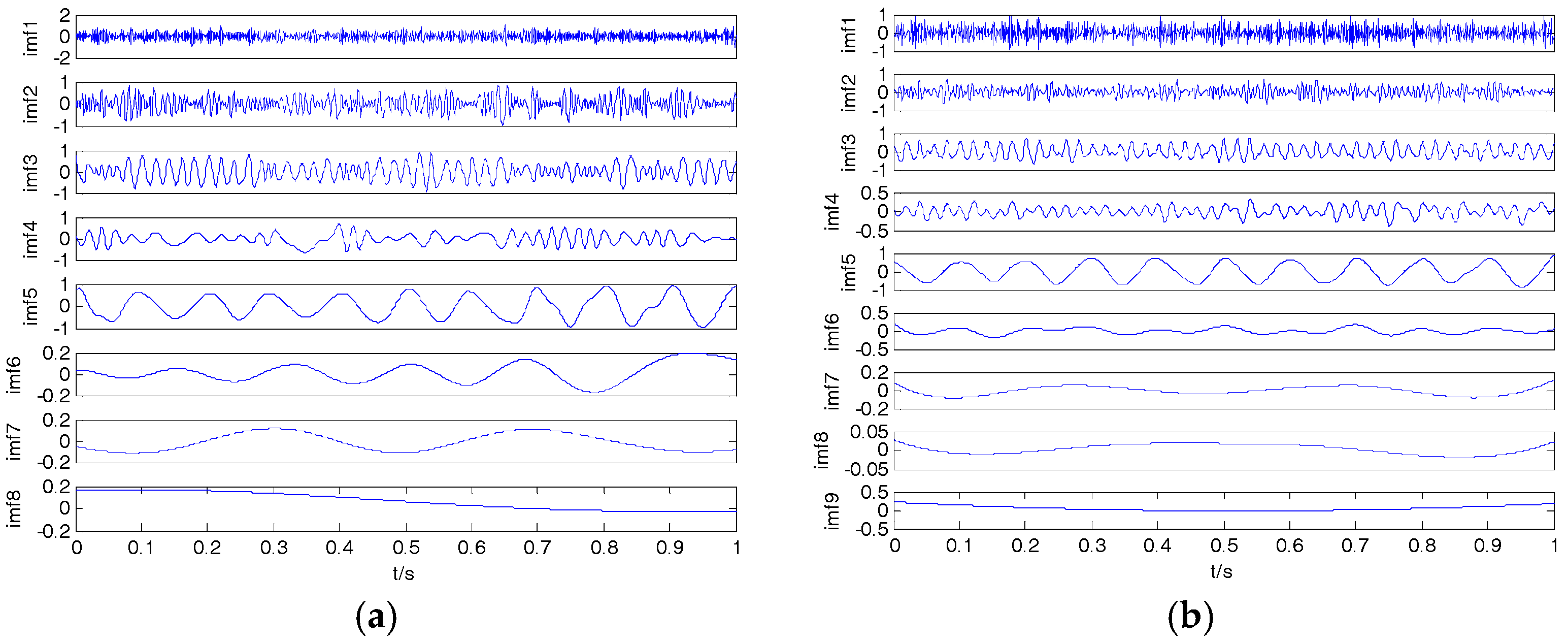
1. Introduction
In the practical measuring process, measured signals are often mixed with noise and useless signal components which come from the surrounding complex environment and the measurement equipment itself. The time domain waveforms of the polluted signals are often different from those of original signals, and it is not easy to identify the original signal from the polluted signal. In the frequency domain, the bandwidth of the clear signal and the noisy signal also partially or even completely overlap. In this case, traditional spectrum analysis techniques and linear filtering algorithms cannot effectively eliminate noise. Therefore, the question of how to eliminate noise from the polluted signal must be solved in the signal processing field [
1,
2].
There is a kind of common denoising algorithm, the basic ideas of which is to extract components of signal obtained by one signal decomposition algorithm, identify and remove noise components by screening criteria, then reconstruct the useful components. For this kind of denoising algorithm, the focus is on selecting signal decomposition algorithm and noise-screening criteria. For instance, the wavelet denoising algorithm [
3,
4] has been widely used in various fields, and a good effect is gained. However, using different types of wavelet functions and different numbers of decomposition have a great influence on denoising [
5].
A kind of self-adaptive signal processing algorithm is empirical mode decomposition (EMD) [
6,
7], originally proposed by Huang et al. This is an absolutely data-driven and adaptive algorithm that depends on local characteristics of data in the time domain. EMD can decompose complex signal into intrinsic mode functions (IMFs), with each IMF indicating one oscillation mode of the complex signal. However, EMD faces problems of mode-mixing and end effects and also lacks mathematical demonstration. Ensemble EMD (EEMD) [
8], as an algorithm that improves on EMD, can reduce the phenomena of modes overlap to some extent. A growing number of researchers are focusing on developing EMD and improved EMD algorithms, and these algorithms are widely employed in various fields, especially in mechanical fault diagnosis [
9,
10,
11], medical science [
12], meteorology [
13], oceanography [
14,
15,
16,
17,
18] and so on. Many denoising algorithms using EMD and improved EMD algorithms have been proposed. For example, high-frequency IMFs are regarded as noise IMFs; the rest of the IMFs are reconstructed for denoising [
19]. Nevertheless, this denoising algorithm cannot completely eliminate noise components, and the reconstructed signal lacks some detailed information. Many denoising algorithms have been proposed to solve the problems of this denoising algorithm by the threshold for IMFs [
20,
21].
As a kind of non-recursive and self-adaptive signal-processing algorithm, variational mode decomposition (VMD) [
22,
23,
24], originally put forward by Dragomiretskiy et al., can effectively decompose a multi-component signal into several bandwidth-limited IMFs. Every IMF has a corresponding central frequency updated in real-time. Compared with EMD and the improved EMD algorithms, VMD has not only a solid theoretical foundation, but also good robustness to noise. In the field of fault diagnosis, a new diagnosis algorithm based on VMD denoising is proposed in [
25], which uses the IMFs obtained by VMD to reconstruct the IMFs according to the correlation coefficients (CCs) between IMFs and the original signal in order to realize denoising, and then extracts the bearing fault characteristics by means of a morphological difference filter to demodulate the signals after denoising, with simulated signal and experimental results showing the validity of the algorithm. In research [
26], a new denoising algorithm based on the non-convex framework has been proposed. By comparing with wavelet denoising and 1-order total variation denoising algorithms, the validity is verified by analyzing the simulation signals and the vibration signals. In research [
27], an adaptive denoising algorithm for a chaotic signal has been proposed by using independent component analysis (ICA) and EMD. In research [
28], an adaptive denoising algorithm using a probability density function and VMD has been proposed, and a small mean-error square and a high signal-to-noise ratio prove the effectiveness of the denoising algorithm. These denoising algorithms also demonstrate the feasibility of EMD and VMD in signal denoising.
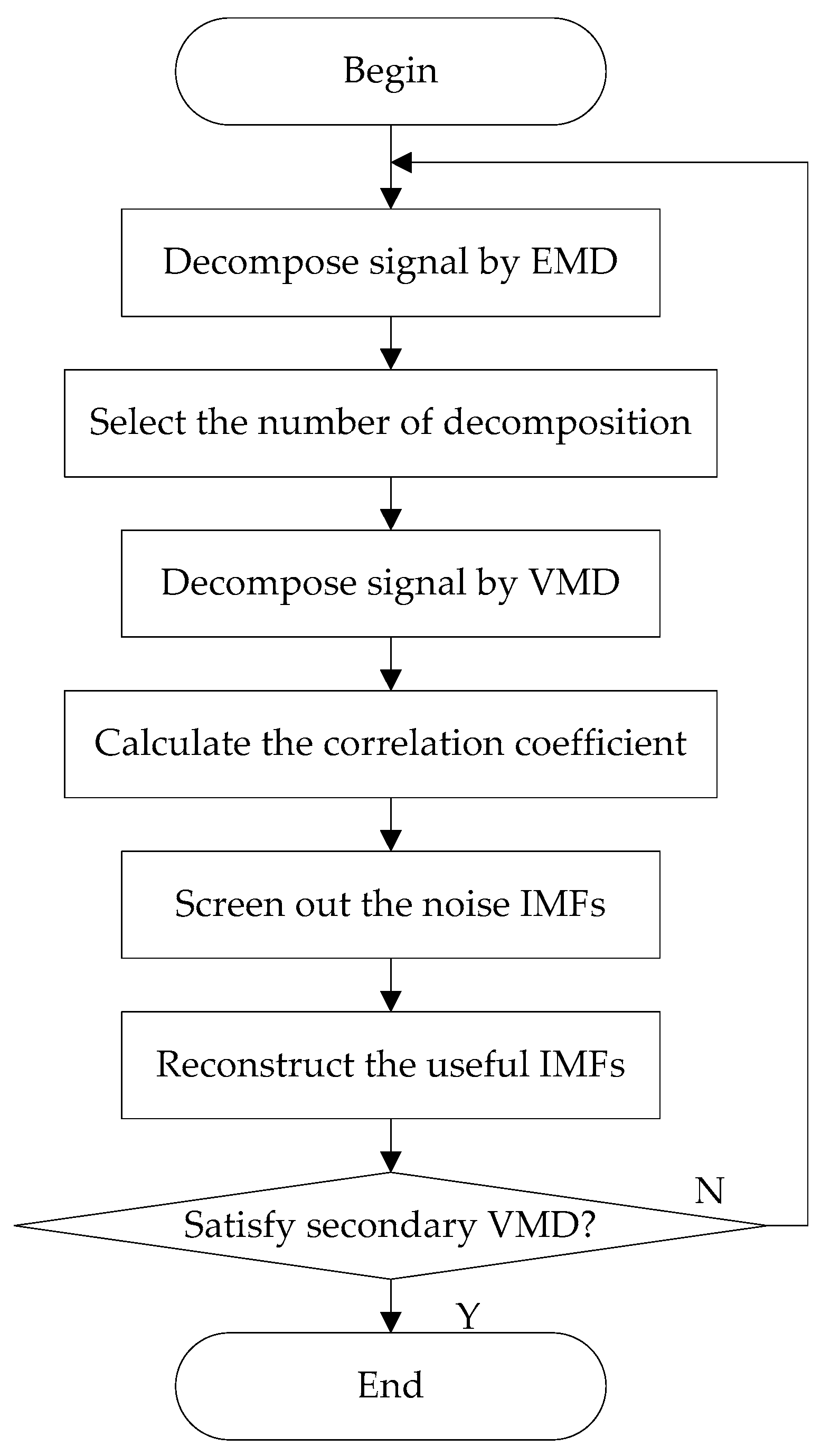
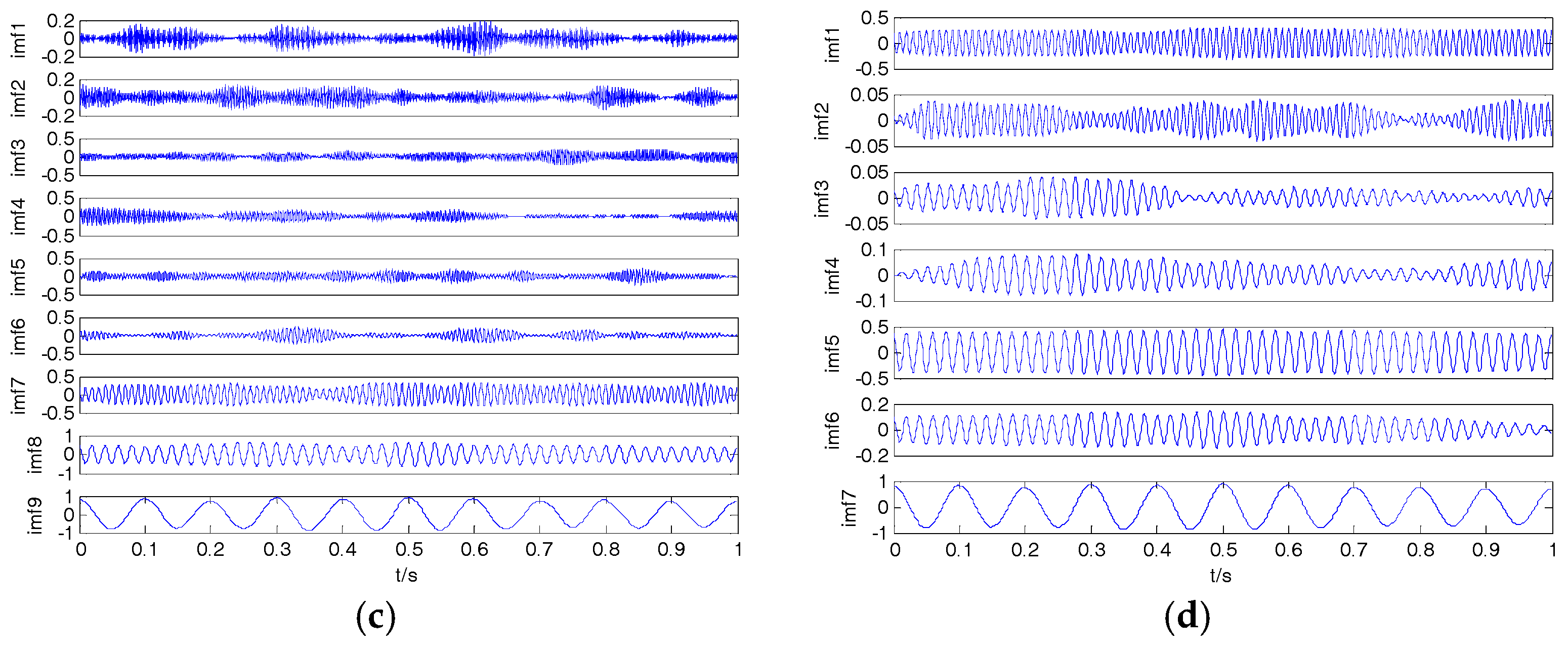
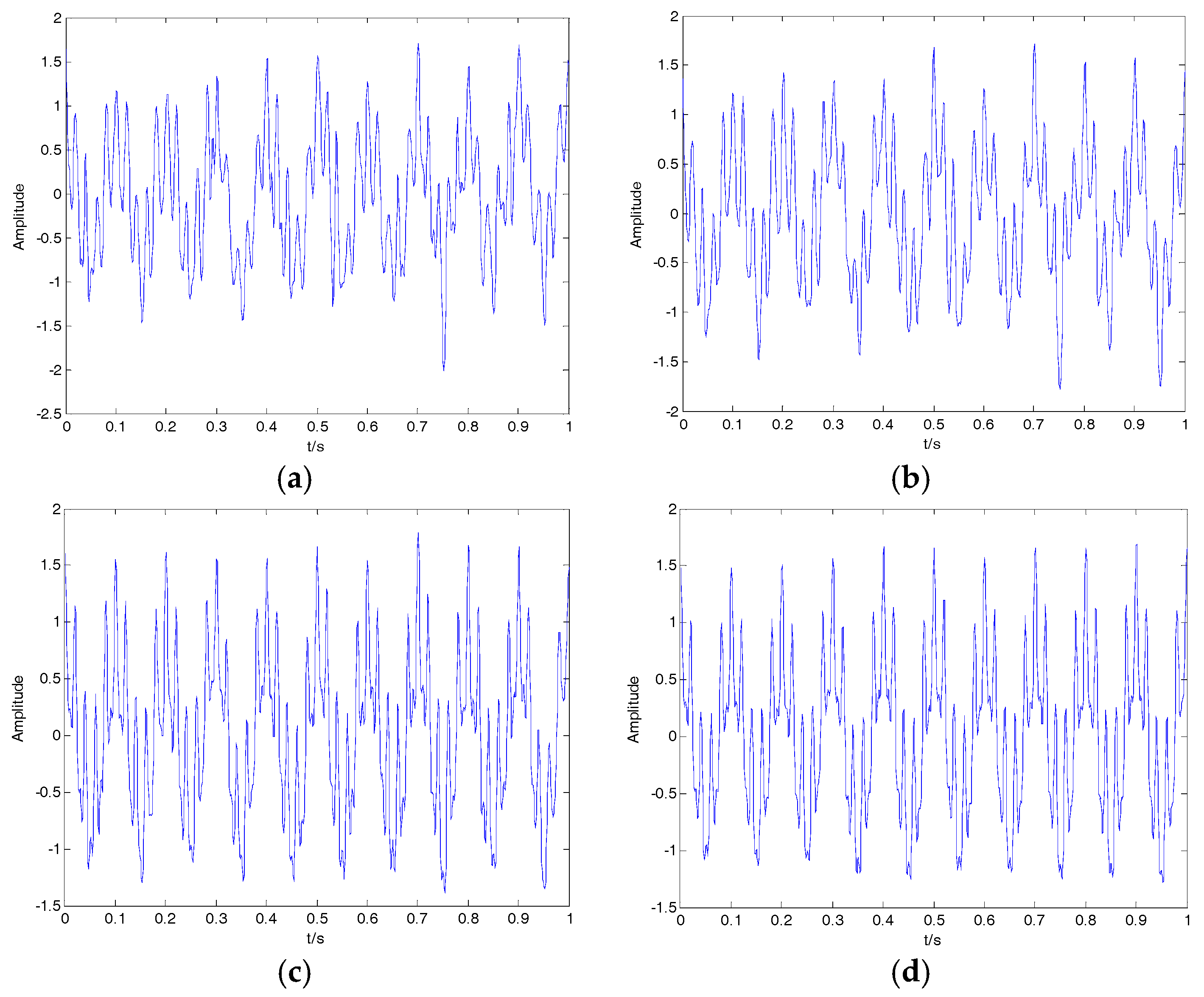
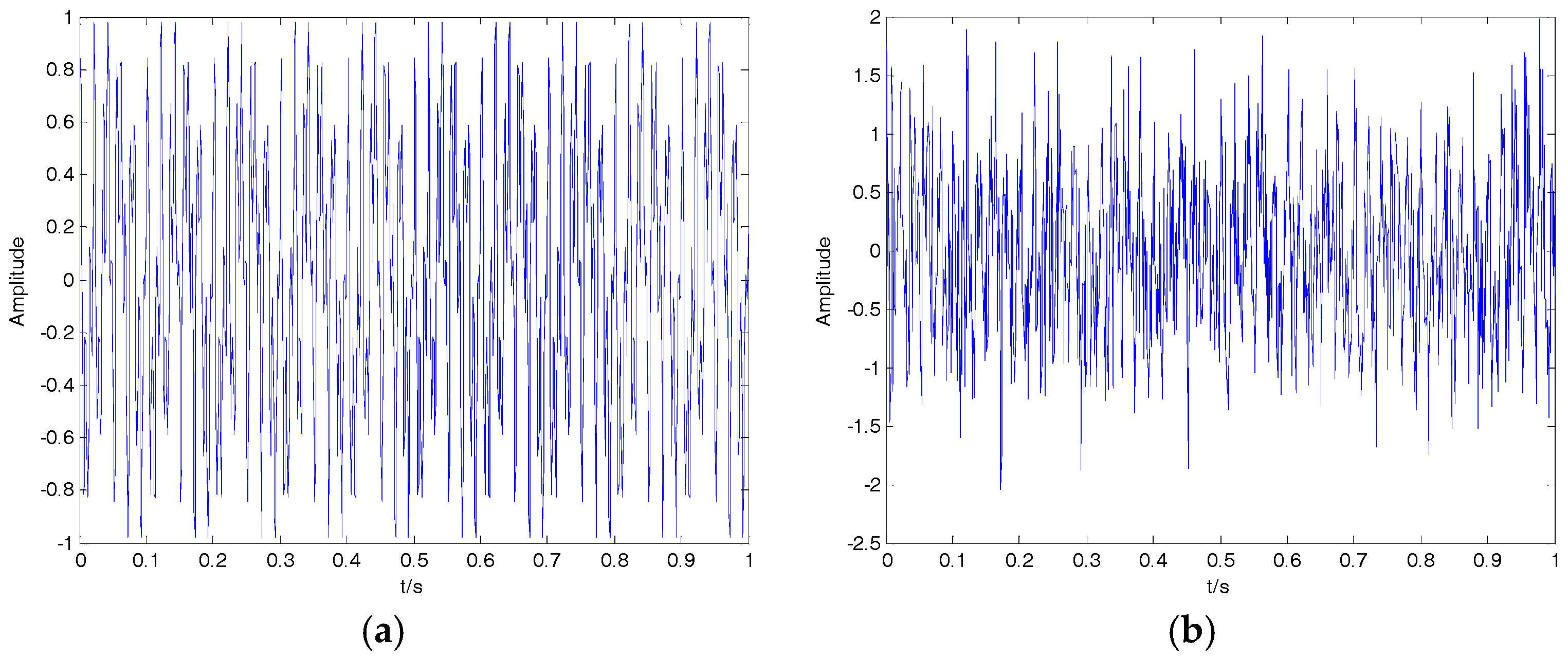
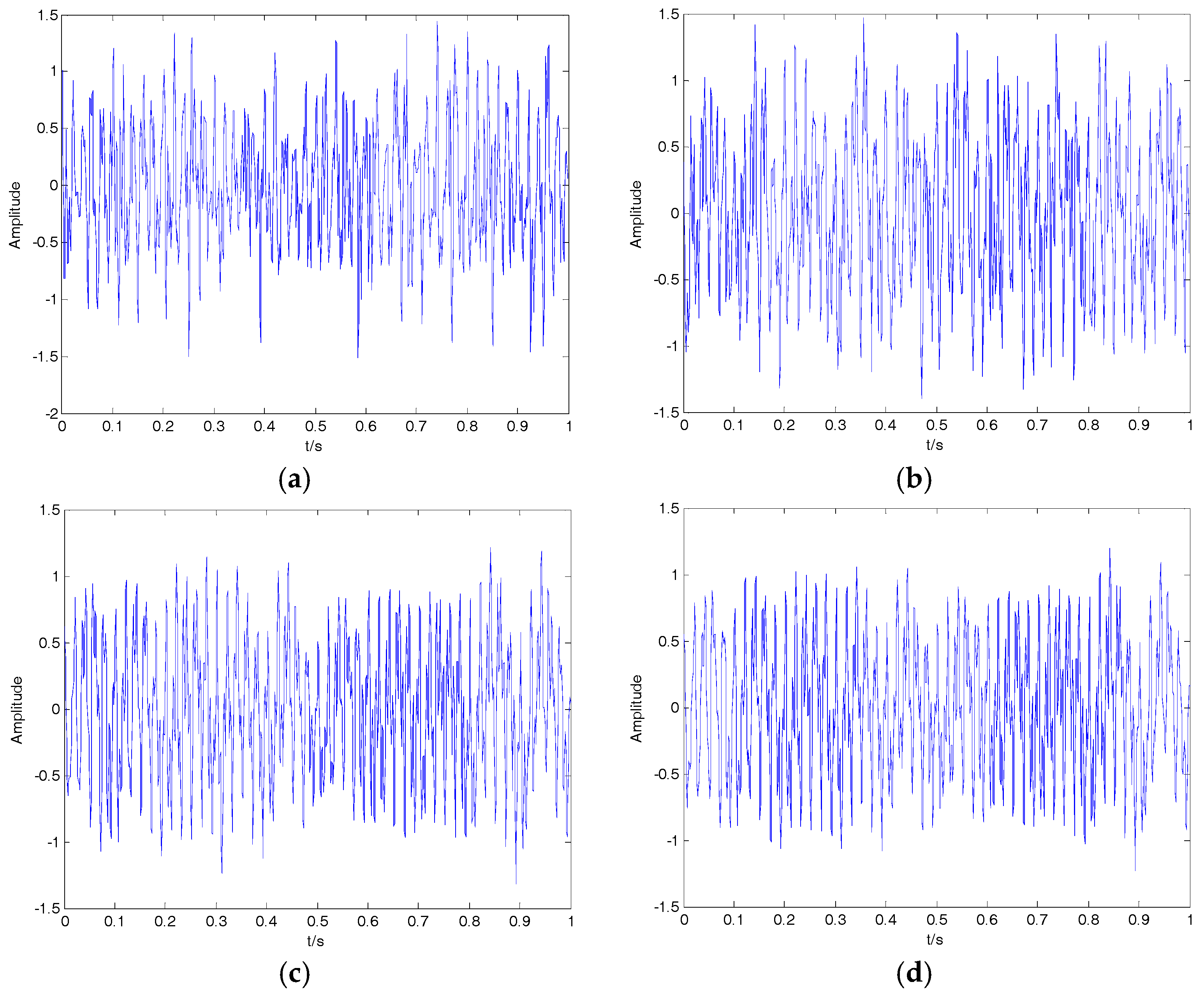
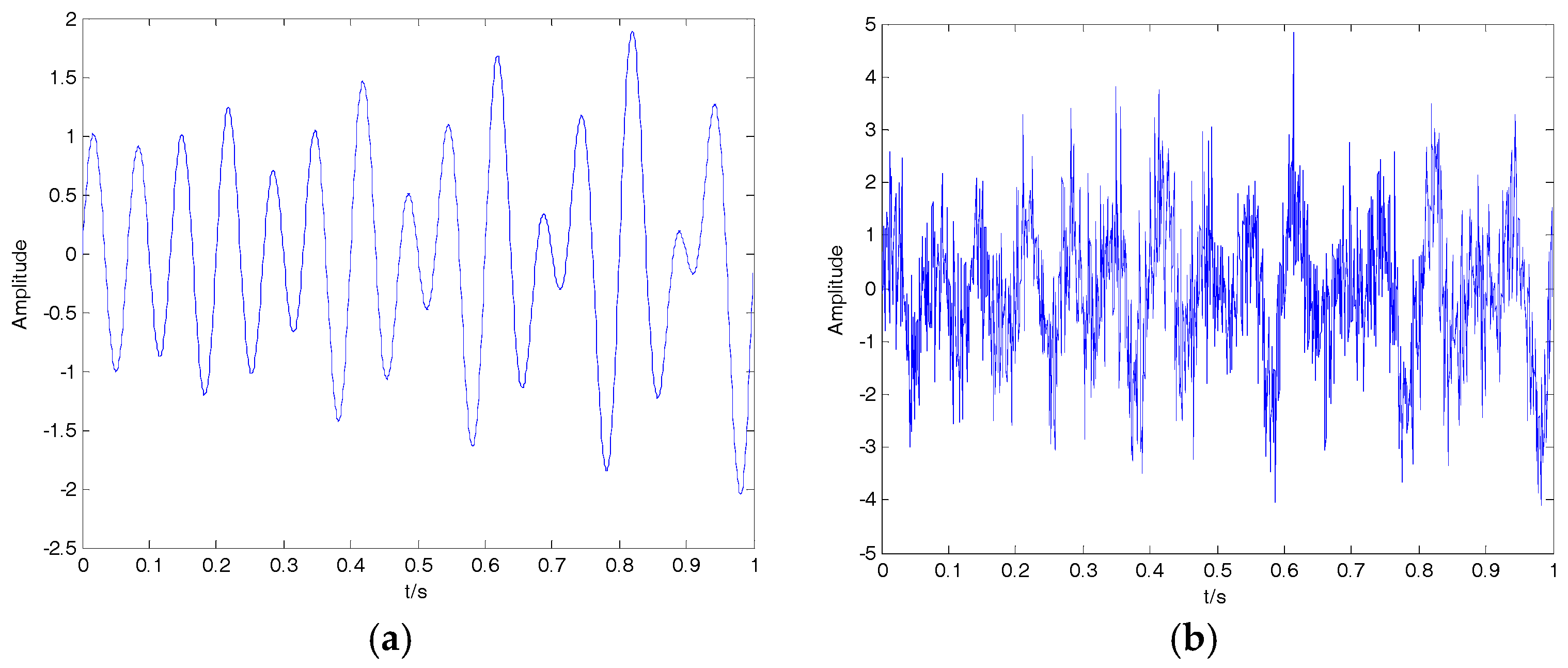
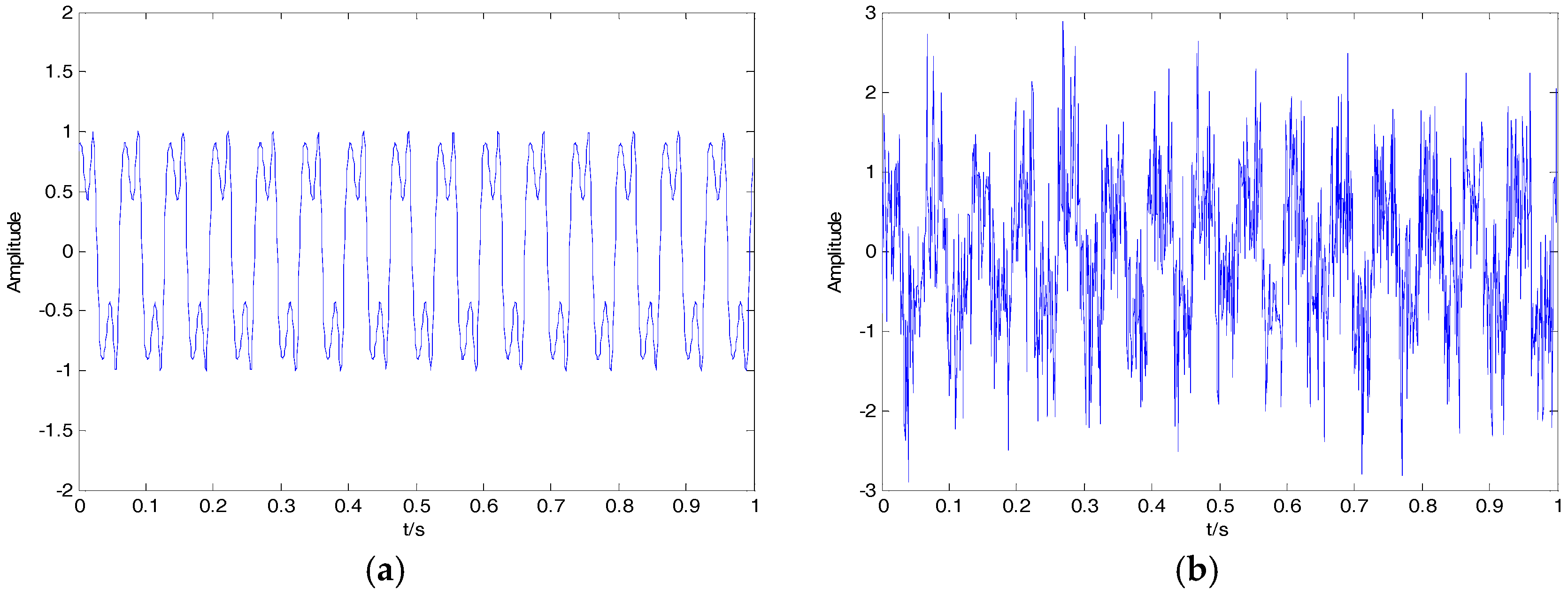
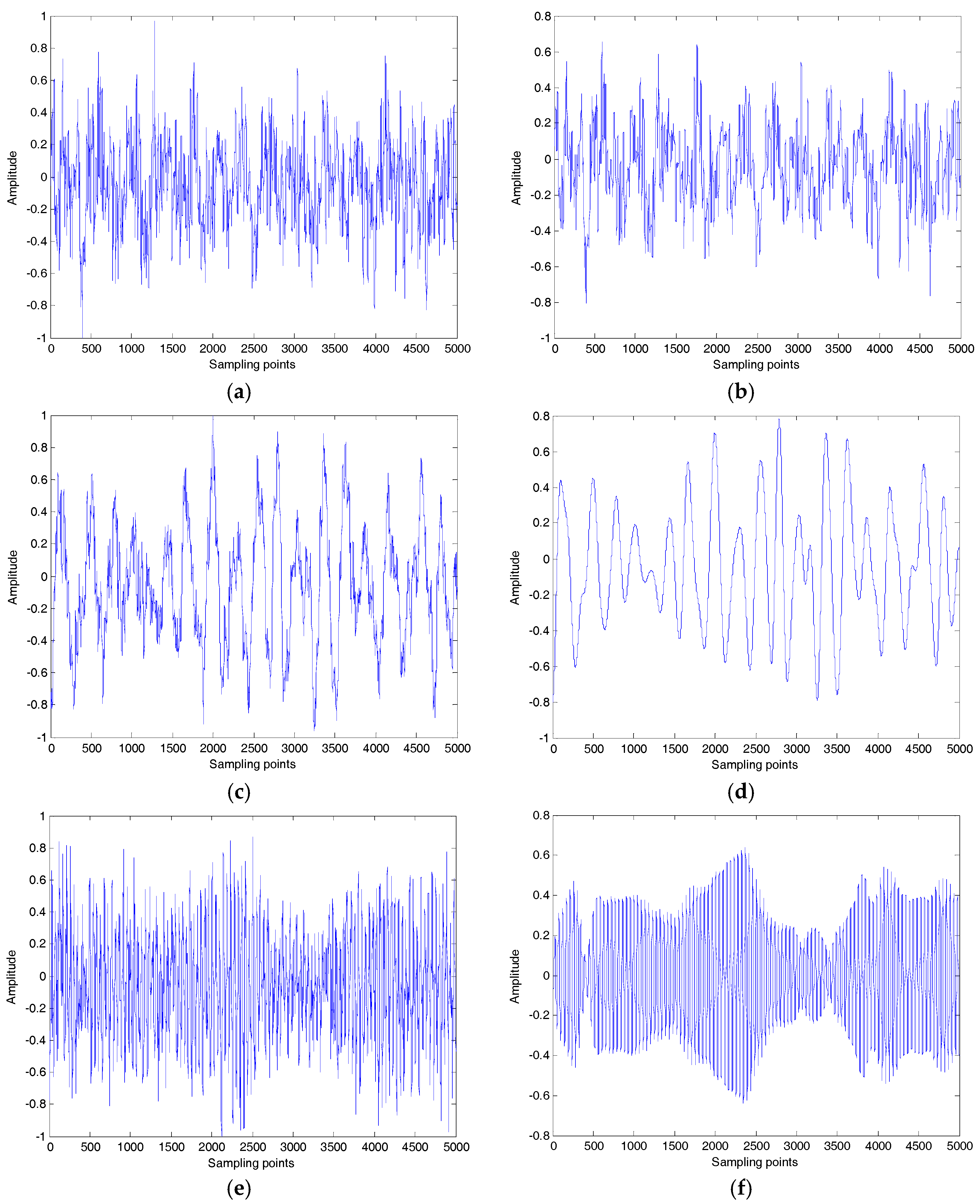
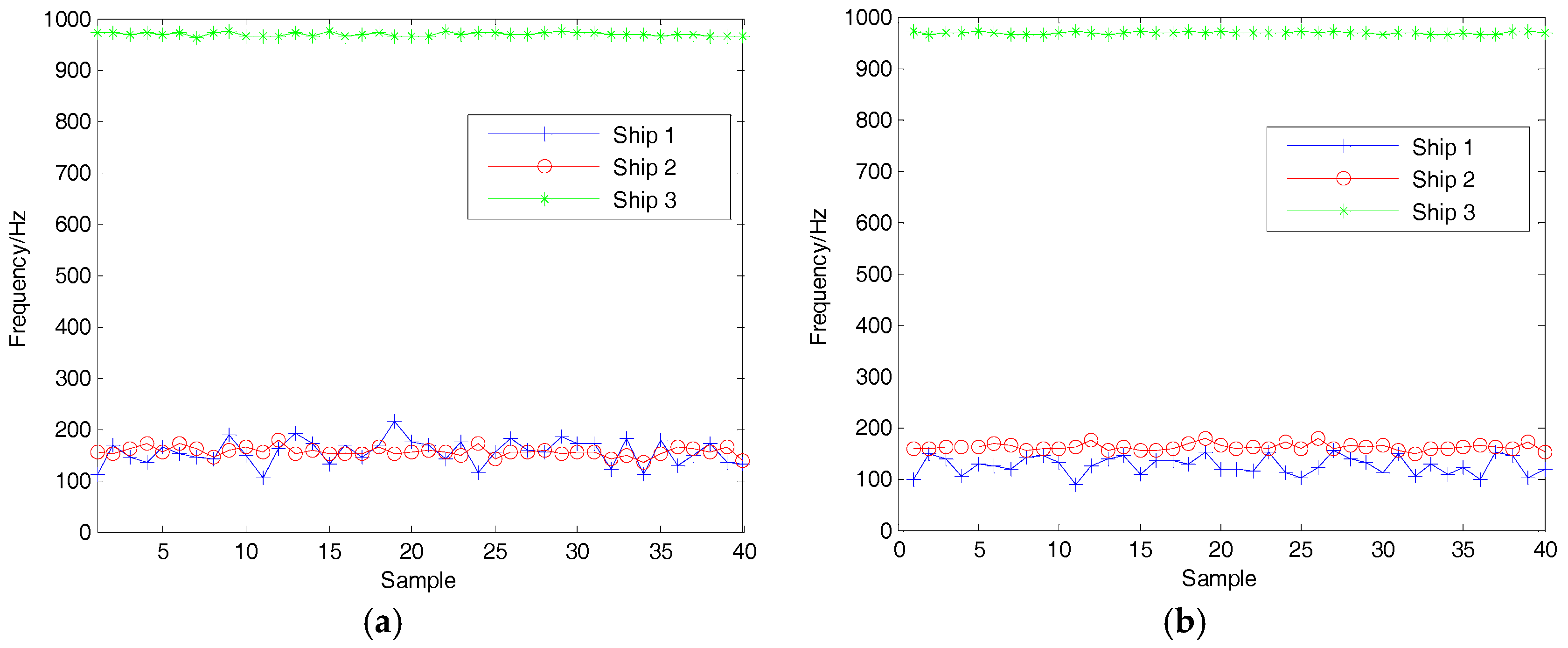
In this article, we proposed a new denoising algorithm for ship-radiated noise (SN) signals. We used VMD and CC to decompose the original signals into IMFs and identify noise IMFs, respectively; the decomposition number by VMD is equal to the number by EMD. According to the threshold of the CC, noise IMFs and useful IMFs can be distinguished effectively. Then, the first denoising can be realized by reconstructing useful IMFs. Secondary denoising can be accomplished by repeating the above steps of decomposition, mode-identification and reconstruction. The final result of denoising is determined according to the CC between IMFs and the original signal. Simulation results indicate that the proposed denoising algorithm based on the secondary VMD (2VMD) and CC is better than existing denoising ones. The proposed 2VMD denoising algorithm is used to feature extraction and classification for SN signals, which can effectively improve the recognition rate of different kinds of ships.
The outline of the article is as follows.
Section 2 provides the background to VMD, CC and the evaluation criterion; a review of the proposed 2VMD denoising algorithm is presented in
Section 3; in
Section 4 and
Section 5, the proposed 2VMD denoising algorithm is used to simulation data and SN signals respectively; finally, the last section is the conclusions.