Implementation of a Virtual Microphone Array to Obtain High Resolution Acoustic Images
Abstract
1. Introduction
2. Material and Methods
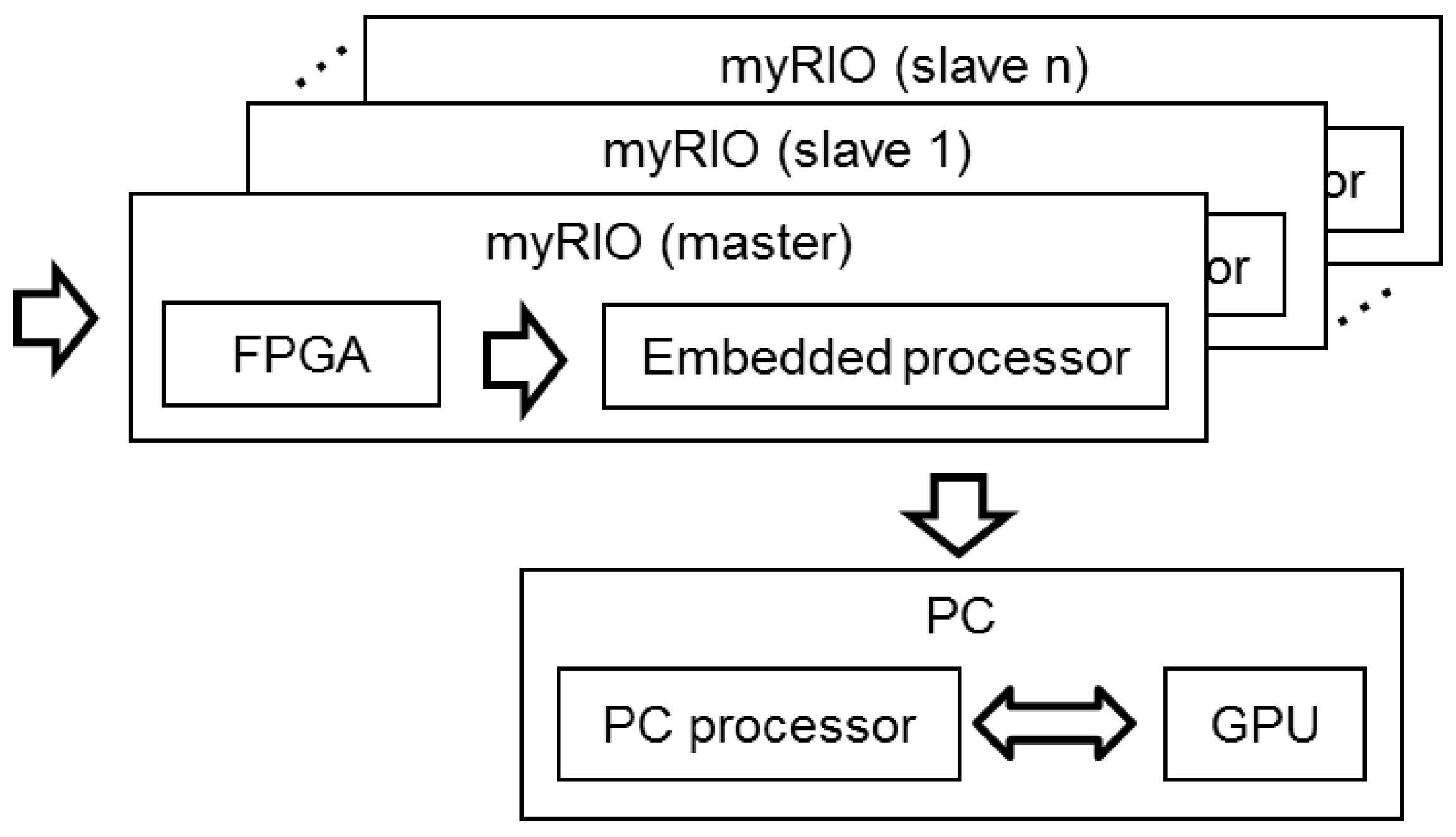
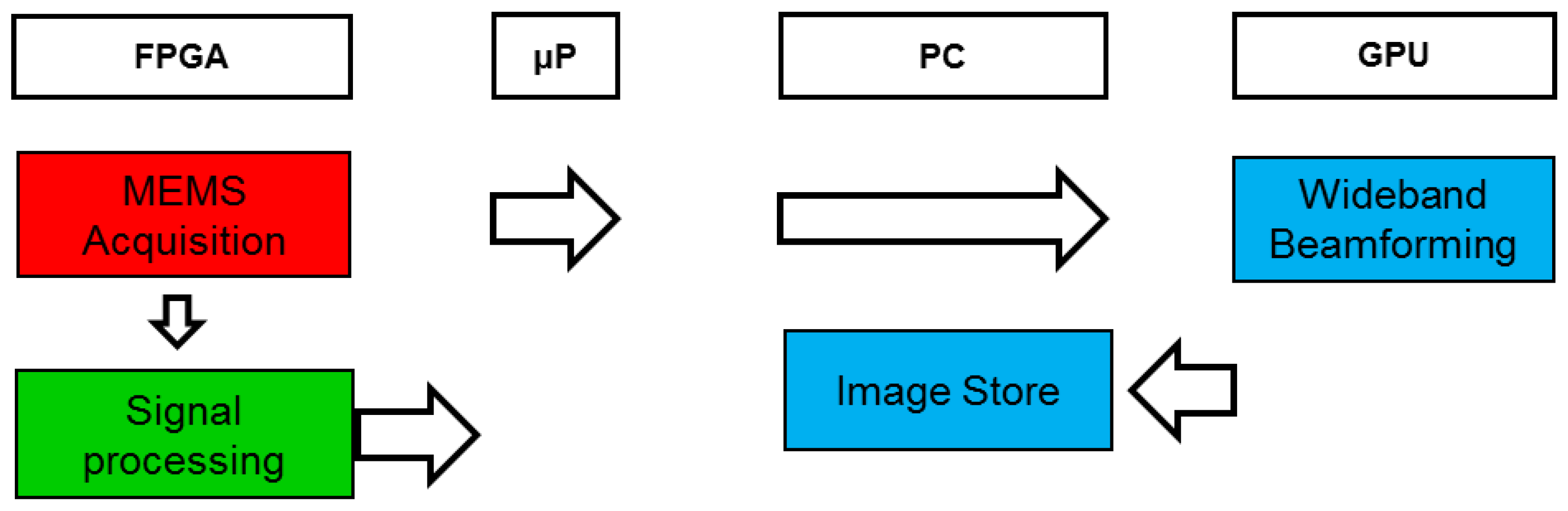
2.1. Processing and Acquisition System
- In the acquisition block, each MEMS microphone with a PDM interface performs signal acquisition.
- In the signal processing block, two routines are implemented: deinterlacing and decimate and filtering, obtaining 64 independent signals (one of each MEMS of the array).
- Finally, in the image generation block, based on wideband beamforming, a set of N × N steering directions are defined, and the beamformer output are assessed for each of these steering directions. The images generated are then displayed and stored in the system.
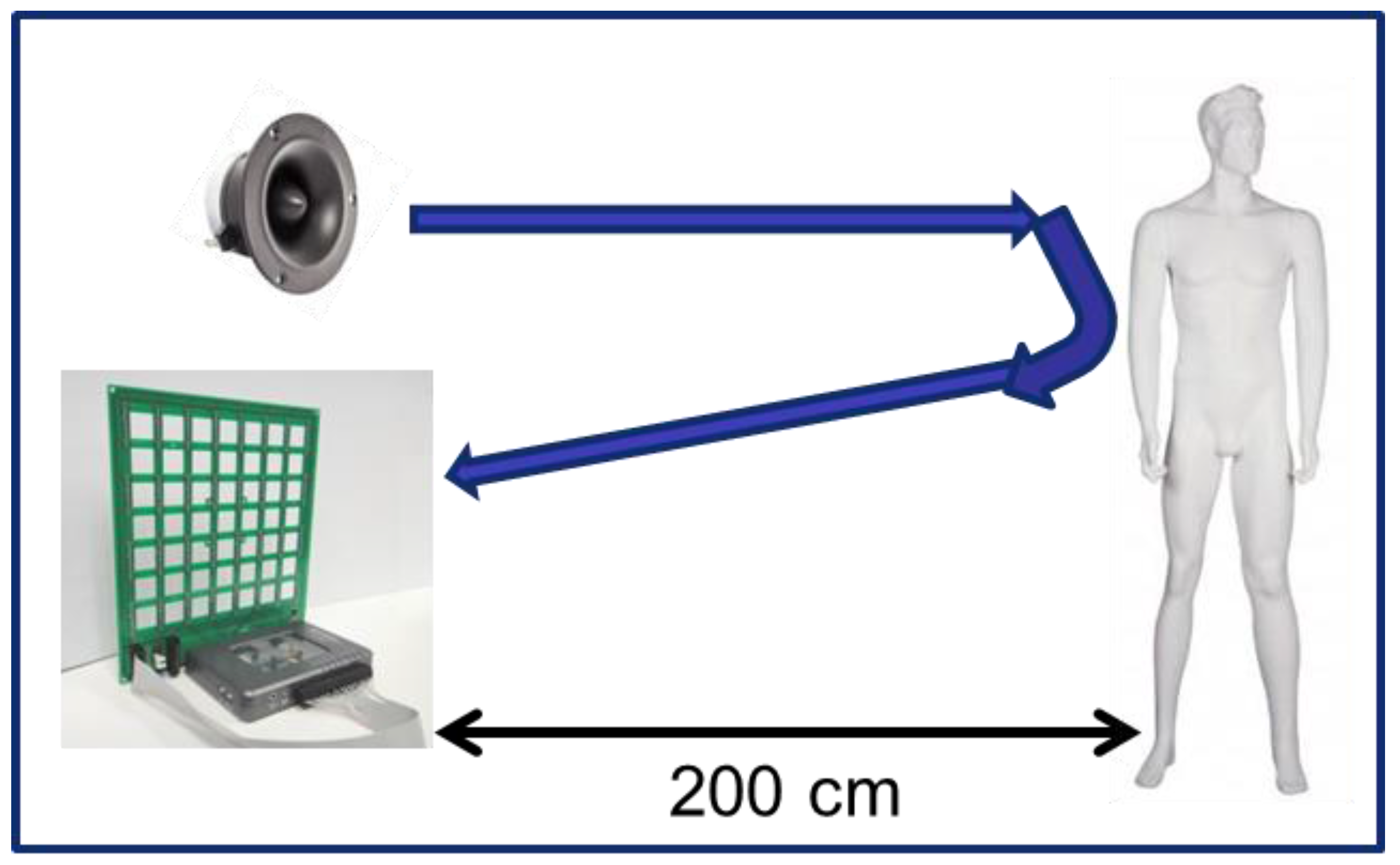
2.2. Positioning System
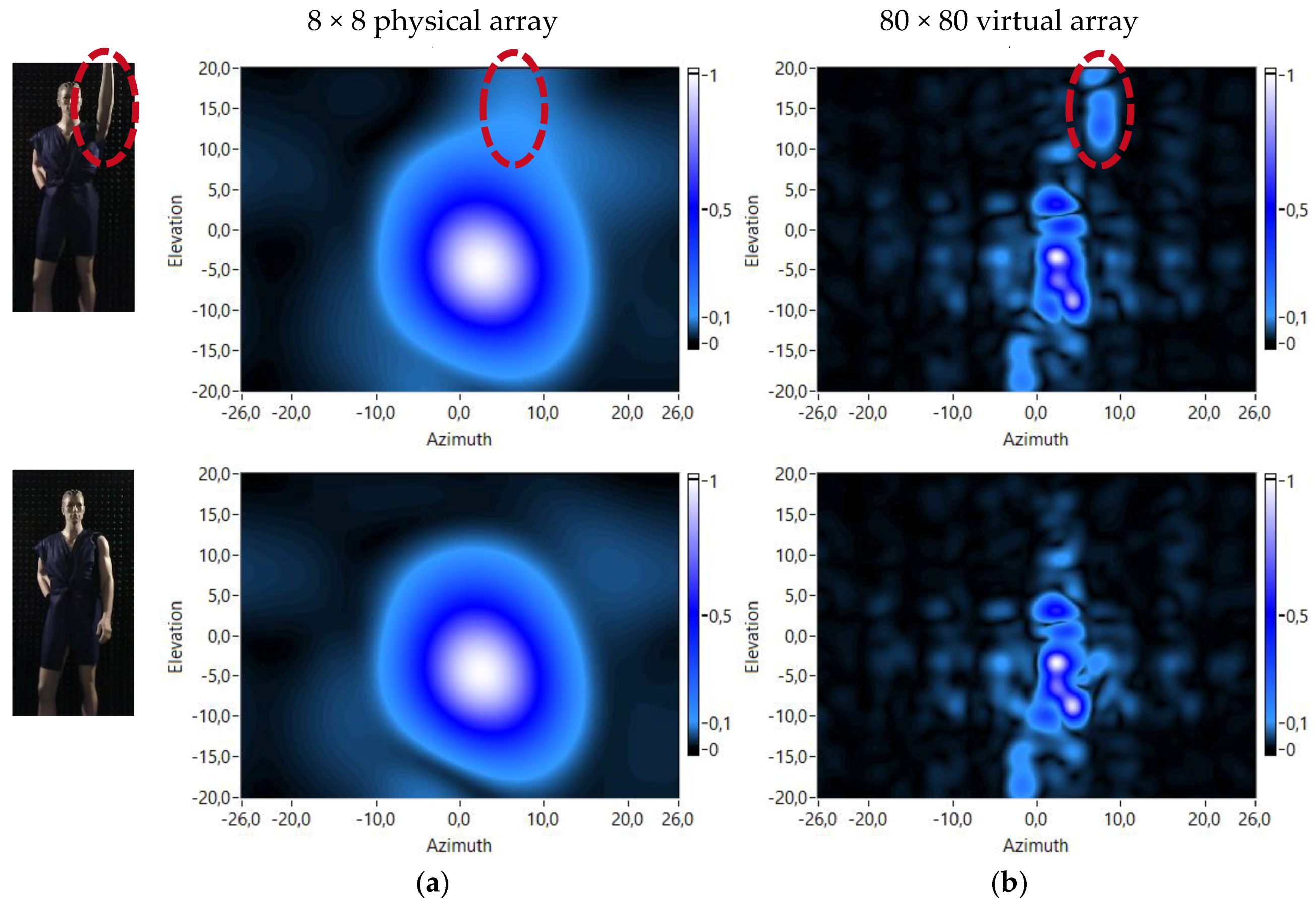
2.3. Virtual Array Principle
- Even steps: 1.25 cm, which is the half sensor spacing of the 8 × 8 array.
- Odd steps: 10 cm, which is the spatial aperture of the 8 × 8 array.
3. Results and Discussion
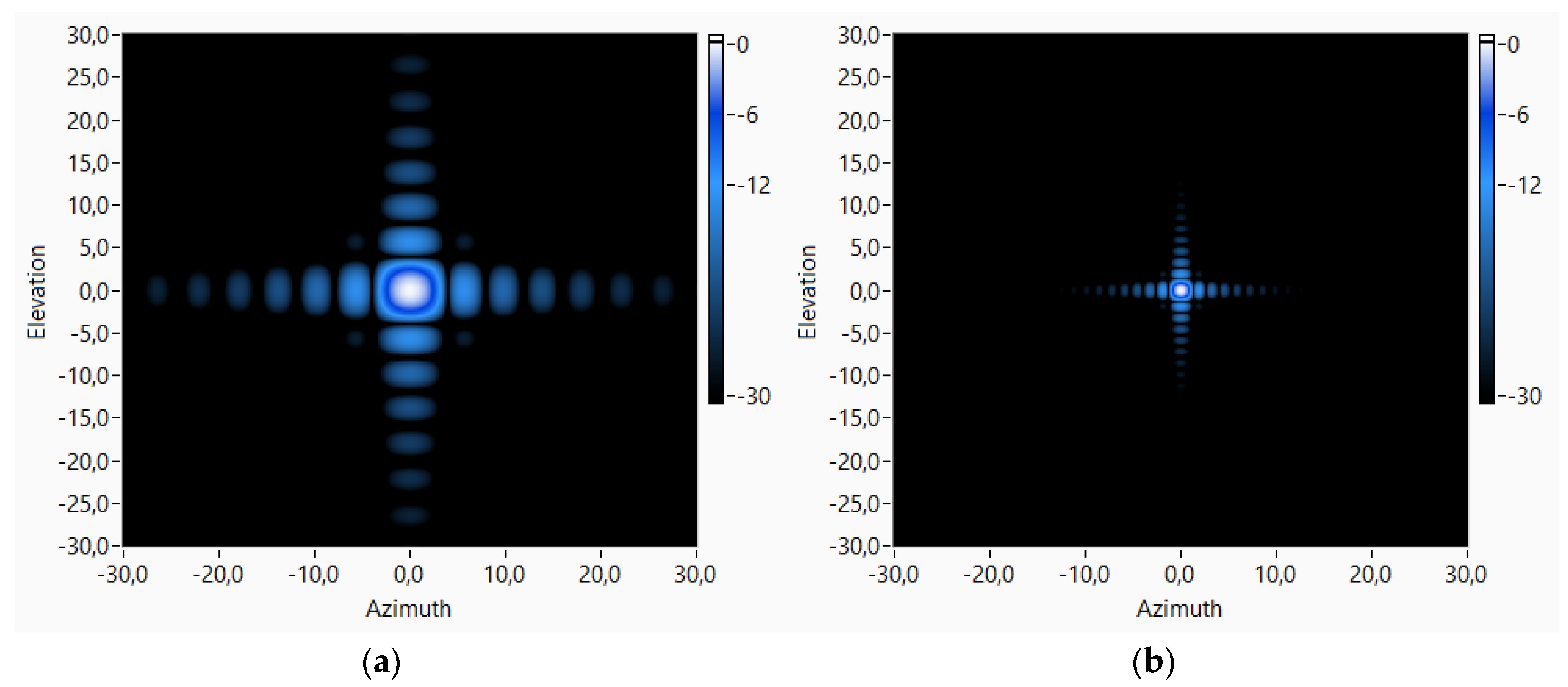
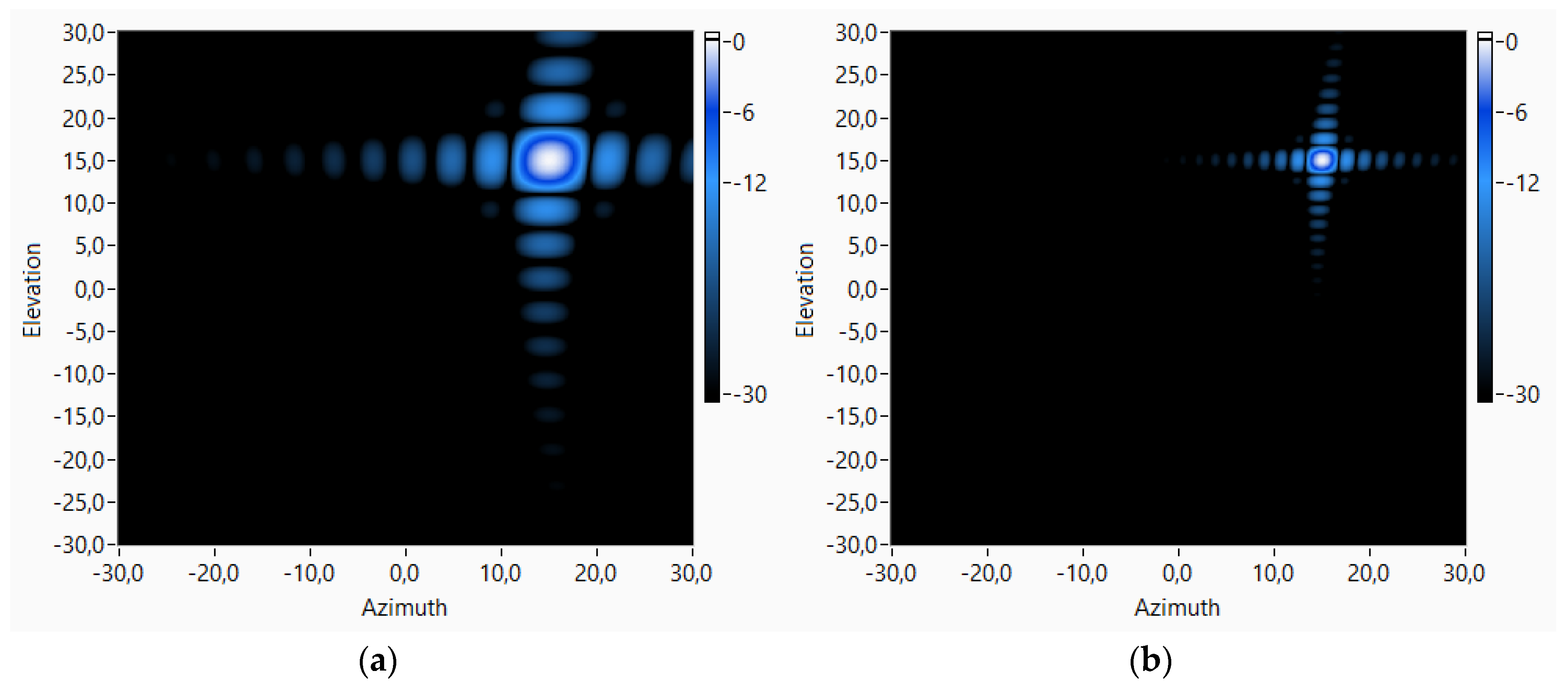
3.1. Virtual Array Performance
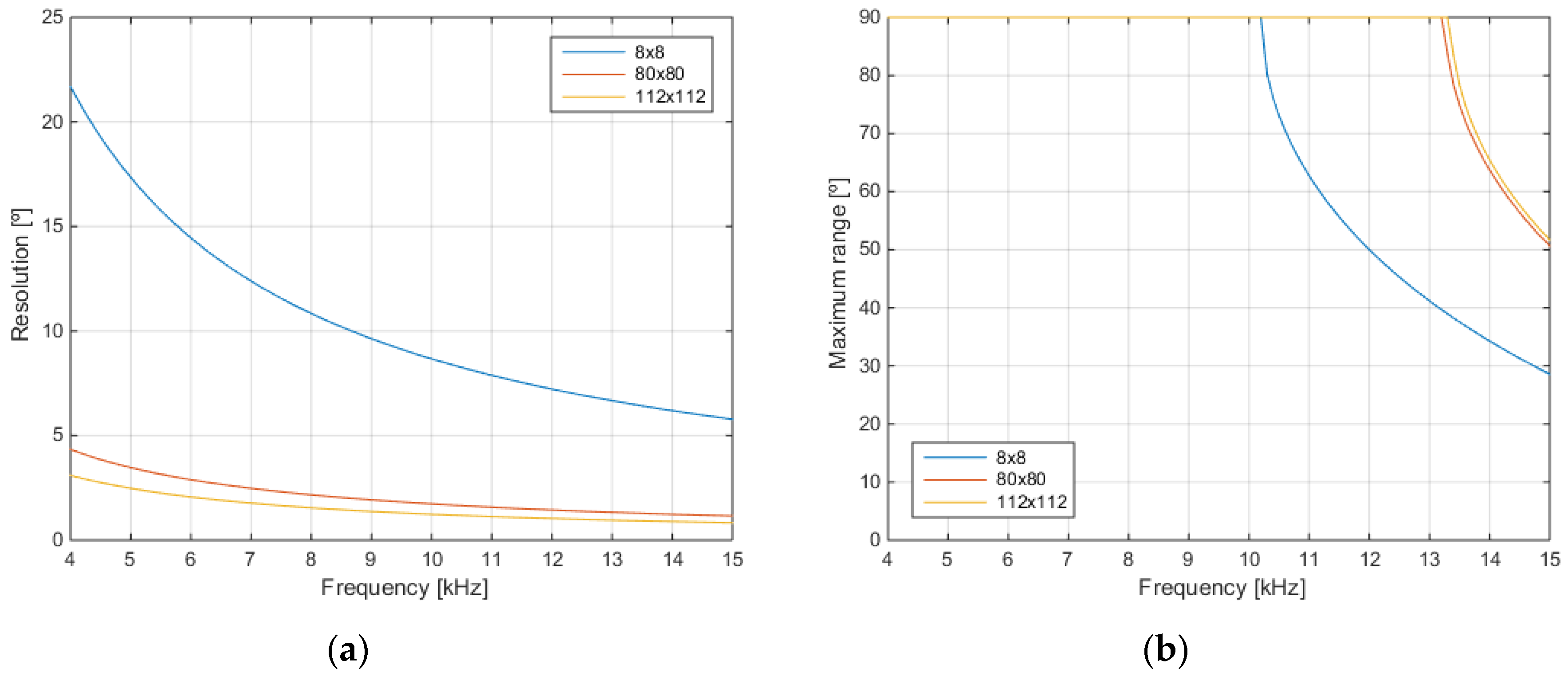
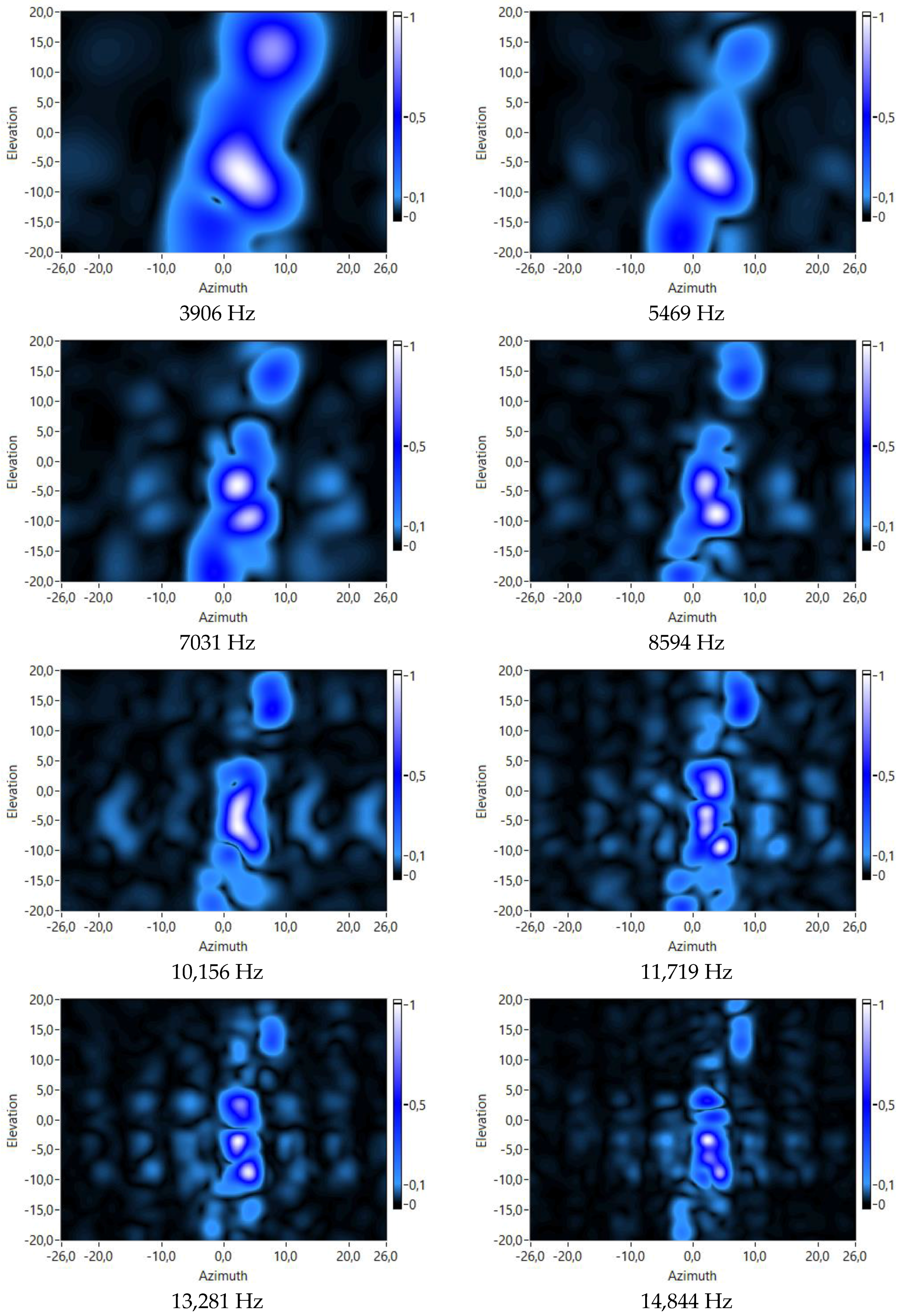
3.2. Analysis of Frequency and Range Dimensions
3.2.1. Frequency Analysis
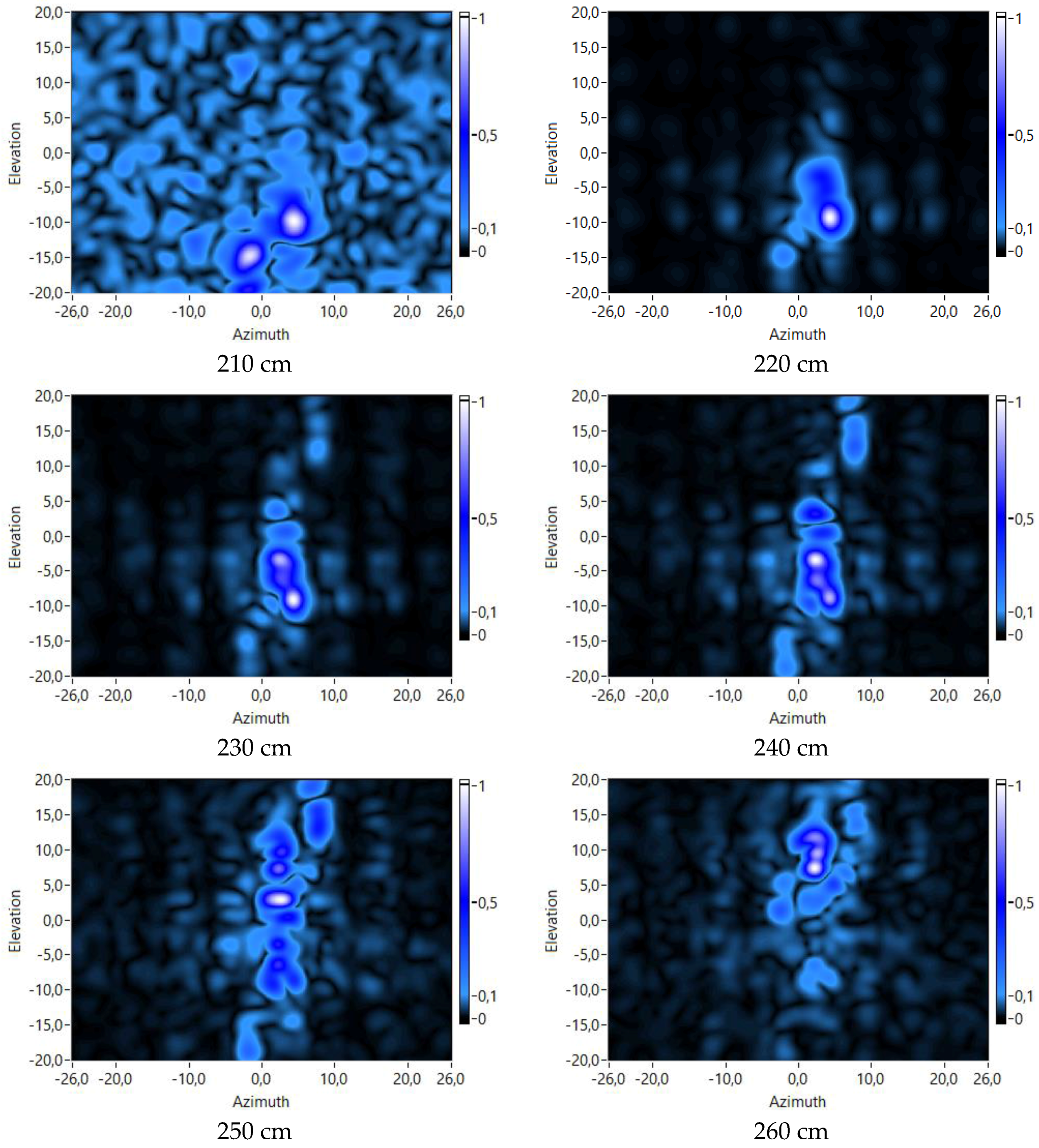
3.2.2. Range Analysis
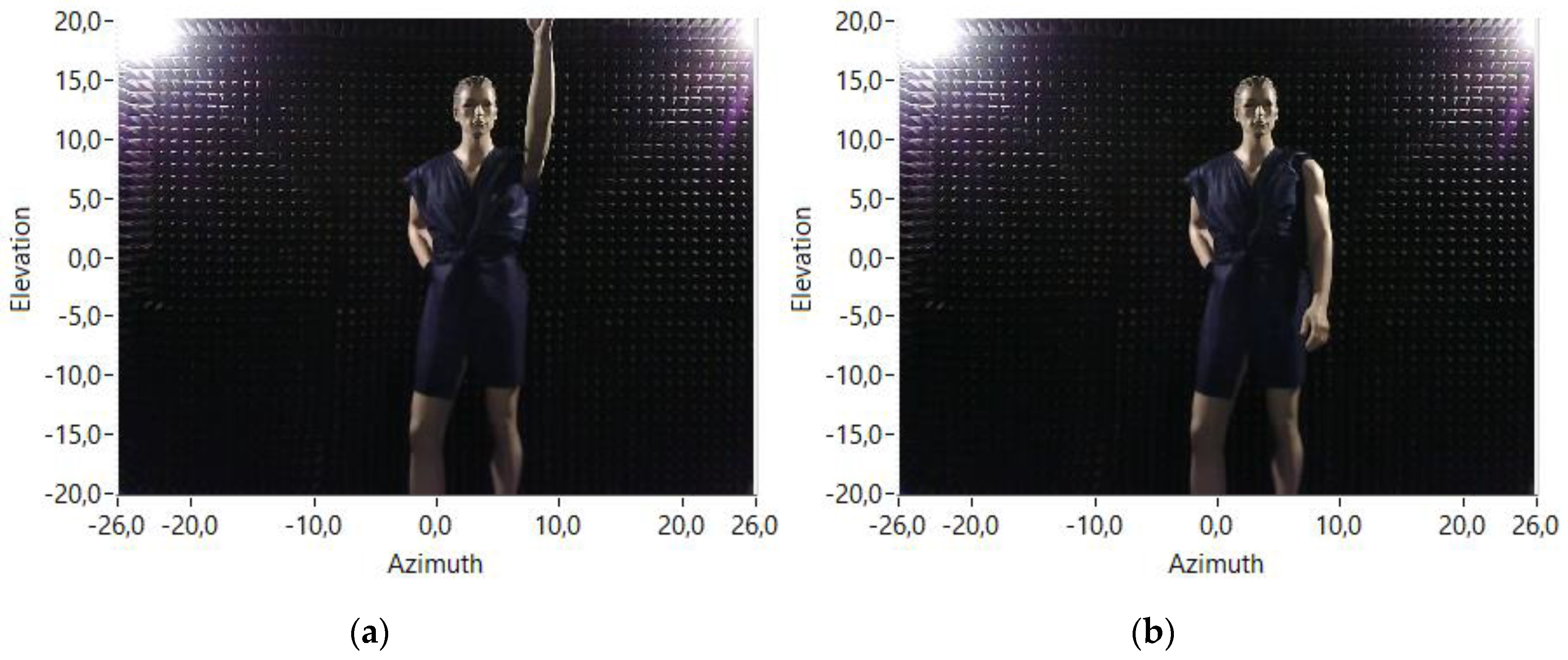
- The legs of the mannequin are a bit closer to the array than its torso. It can be observed that, at low ranges (210–220 cm), the corresponding acoustic images show maxima at lower values of the elevation dimension, which correspond with the position of the legs. At higher values (230–240 cm), the maximum values are at higher elevation values, which correspond with the position of the torso.
- The head of the mannequin is the part of the body that is farther from the array. It can be observed that at higher ranges (250–260 cm), the maxima are shown at high elevation values, which correspond with the position of the head.
- It can also be observed that the head is even farther from the array than the arm that is raised.
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Van Trees, H. Optimum Array Processing: Part IV of Detection, Estimation and Modulation Theory; John Wiley & Sons: New York, NY, USA, 2002; ISBN 9780471093909. [Google Scholar]
- Brandstein, M.; Ward, D. Microphone Arrays; Springer: New York, NY, USA, 2001; ISBN 9783540419532. [Google Scholar]
- Van Veen, B.D.; Buckley, K.M. Beamforming: A Versatile Approach to Spatial Filtering. IEEE ASSP Mag. 1988, 5, 4–24. [Google Scholar] [CrossRef]
- Del Val, L.; Jiménez, M.; Izquierdo, A.; Villacorta, J. Optimisation of sensor positions in random linear arrays based on statistical relations between geometry and performance. Appl. Acoust. 2012, 73, 78–82. [Google Scholar] [CrossRef]
- Izquierdo-Fuente, A.; Villacorta-Calvo, J.; Raboso-Mateos, M.; Martines-Arribas, A.; Rodriguez-Merino, D.; del Val-Puente, L. A human classification system for a video-acoustic detection platform. In Proceedings of the International Carnahan Conference on Security Technology, Albuquerque, NM, USA, 11–14 October 2004; pp. 145–152. [Google Scholar] [CrossRef]
- Izquierdo-Fuente, A.; del Val, L.; Jiménez, M.I.; Villacorta, J.J. Performance evaluation of a biometric system based on acoustic images. Sensors 2011, 11, 9499–9519. [Google Scholar] [CrossRef] [PubMed]
- Villacorta-Calvo, J.J.; Jiménez, M.I.; Del Val, L.; Izquierdo, A. Configurable Sensor Network Applied to Ambient Assisted Living. Sensors 2011, 11, 10724–10737. [Google Scholar] [CrossRef] [PubMed]
- Del Val, L.; Izquierdo-Fuente, A.; Villacorta, J.J.; Raboso, M. Acoustic Biometric System Based on Preprocessing Techniques and Support Vector Machines. Sensors 2015, 15, 14241–14260. [Google Scholar] [CrossRef] [PubMed]
- Beeby, S.; Ensell, G.; Kraft, K.; White, N. MEMS Mechanical Sensors; Artech House Publishers: Norwood, MA, USA, 2004; ISBN 9781580535366. [Google Scholar]
- Scheeper, P.R.; van der Donk, A.G.H.; Olthuis, W.; Bergveld, P. A review of silicon microphones. Sens. Actuators A Phys. 1994, 44, 1–11. [Google Scholar] [CrossRef]
- Izquierdo, A.; Villacorta, J.J.; Del Val Puente, L.; Suárez, L. Design and Evaluation of a Scalable and Reconfigurable Multi-Platform System for Acoustic Imaging. Sensors 2016, 16, 1671. [Google Scholar] [CrossRef] [PubMed]
- Acoustic System of Array Processing Based on High-Dimensional MEMS Sensors for Biometry and Analysis of Noise and Vibration. Available online: http://sine.ni.com/cs/app/doc/p/id/cs-16913 (accessed on 5 October 2017).
- Siong Gan, W. Acoustic Imaging: Techniques and Applications for Engineers; John Wiley & Sons: New York, NY, USA, 2012; ISBN 9780470661604. [Google Scholar]
- Tiete, J.; Domínguez, F.; da Silva, B.; Segers, L.; Steenhaut, K.; Touhafi, A. SoundCompass: A Distributed MEMS Microphone Array-Based Sensor for Sound Source Localization. Sensors 2014, 14, 1918–1949. [Google Scholar] [CrossRef] [PubMed]
- Hafizovic, I.; Nilsen, C.-I.C.; Kjølerbakken, M.; Jahr, V. Design and implementation of a MEMS microphone array system for real-time speech acquisition. Appl. Acoust. 2012, 73, 132–143. [Google Scholar] [CrossRef]
- White, R.; de Jong, R.; Holup, G.; Gallman, J.; Moeller, M. MEMS Microphone Array on a Chip for Turbulent Boundary Layer Measurements. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar] [CrossRef]
- Groschup, R.; Grosse, C.U. MEMS Microphone Array Sensor for Aid-Coupled Impact Echo. Sensors 2015, 15, 14932–14945. [Google Scholar] [CrossRef] [PubMed]
- Vanwynsberghe, C.; Marchiano, R.; Ollivier, F.; Challande, P.; Moingeon, H.; Marchal, J. Design and implementation of a multi-octave-band audio camera for real time diagnosis. Appl. Acoust. 2015, 89, 281–287. [Google Scholar] [CrossRef]
- Sorama: Sound Solutions. Available online: https://www.sorama.eu/Solution/measurements (accessed on 9 September 2017).
- Del Val, L.; Izquierdo, A.; Villacorta, J.J.; Suárez, L. Using a Planar Array of MEMS Microphones to Obtain Acoustic Images of a Fan Matrix. J. Sens. 2014, 2014, 3209142. [Google Scholar] [CrossRef]
- Ravetta, P.; Muract, J.; Burdisso, R. Feasibility study of microphone phased array based machinery health monitoring. Mec. Comput. 2007, 26, 23–37. [Google Scholar]
- LOUD: Large acOUstic Data Array Project. Available online: http://groups.csail.mit.edu/cag/mic-array/ (accessed on 12 December 2017).
- Kendra, J.R. Motion-Extended Array Synthesis—Part I: Theory and Method. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2028–2044. [Google Scholar] [CrossRef]
- Fernández, D.; Holland, K.R.; Escribano, D.G.; de Bree, H.-E. An Introduction to Virtual Phased Arrays for Beamforming Applications. Arch. Acoust. 2014, 39, 81–88. [Google Scholar] [CrossRef]
- Herold, G.; Sarradj, E. Microphone array method for the characterization of rotating sound sources in axial fans. Noise Control Eng. J. 2015, 63, 546–551. [Google Scholar] [CrossRef]
- Havránek, Z. Using Acoustic Holography for Vibration Analysis. Ph.D. Thesis, Faculty of Electrical Engineering and Communication, Brno University of Technology, Brno, Czech Republic, October 2009. [Google Scholar]
- Kwon, H.S.; Kim, Y.H. Moving frame technique for planar acoustic holography. J. Acoust. Soc. Am. 1998, 103, 1734–1741. [Google Scholar] [CrossRef]
- Bös, J.; Kurtze, L. Design and application of a low-cost microphone array for nearfield acoustical holography. In Proceedings of the Joint Congress CFA/DAGA’04, Strasbourg, France, 22–25 March 2004. [Google Scholar]
- Kingsley, S.; Quegan, S. Understanding Radar Systems; McGraw-Hill: New York, NY, USA, 1992; ISBN 0077074262. [Google Scholar]


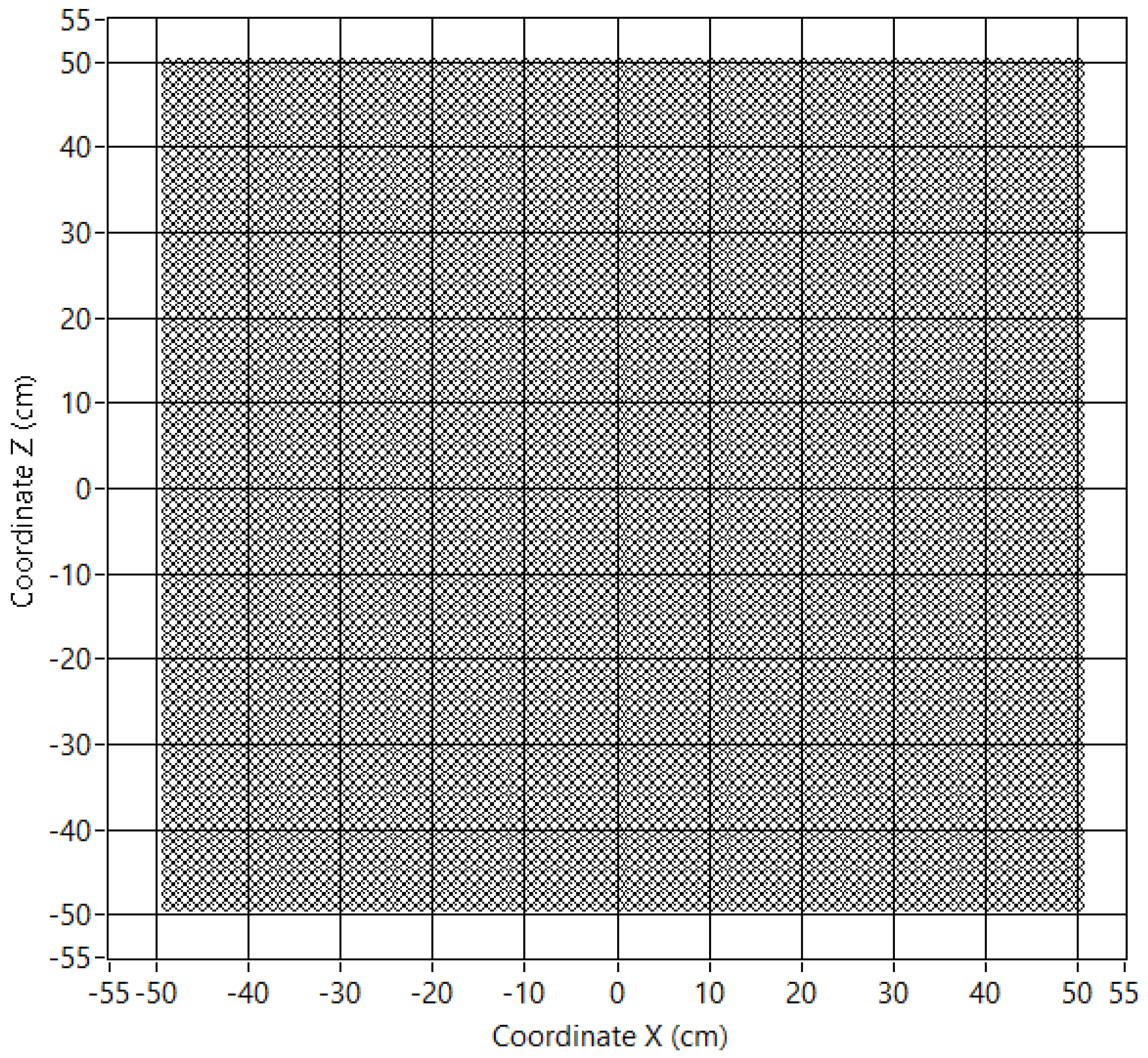
| Sensor Positions | Number of Sensors | Area | Dimensions |
|---|---|---|---|
| 80 × 80 | 6400 | 1 m2 | 1 m × 1 m |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Izquierdo, A.; Villacorta, J.J.; Del Val, L.; Suárez, L.; Suárez, D. Implementation of a Virtual Microphone Array to Obtain High Resolution Acoustic Images. Sensors 2018, 18, 25. https://doi.org/10.3390/s18010025
Izquierdo A, Villacorta JJ, Del Val L, Suárez L, Suárez D. Implementation of a Virtual Microphone Array to Obtain High Resolution Acoustic Images. Sensors. 2018; 18(1):25. https://doi.org/10.3390/s18010025
Chicago/Turabian StyleIzquierdo, Alberto, Juan J. Villacorta, Lara Del Val, Luis Suárez, and David Suárez. 2018. "Implementation of a Virtual Microphone Array to Obtain High Resolution Acoustic Images" Sensors 18, no. 1: 25. https://doi.org/10.3390/s18010025
APA StyleIzquierdo, A., Villacorta, J. J., Del Val, L., Suárez, L., & Suárez, D. (2018). Implementation of a Virtual Microphone Array to Obtain High Resolution Acoustic Images. Sensors, 18(1), 25. https://doi.org/10.3390/s18010025






