Fault Diagnosis of Induction Machines in a Transient Regime Using Current Sensors with an Optimized Slepian Window
Abstract
1. Introduction
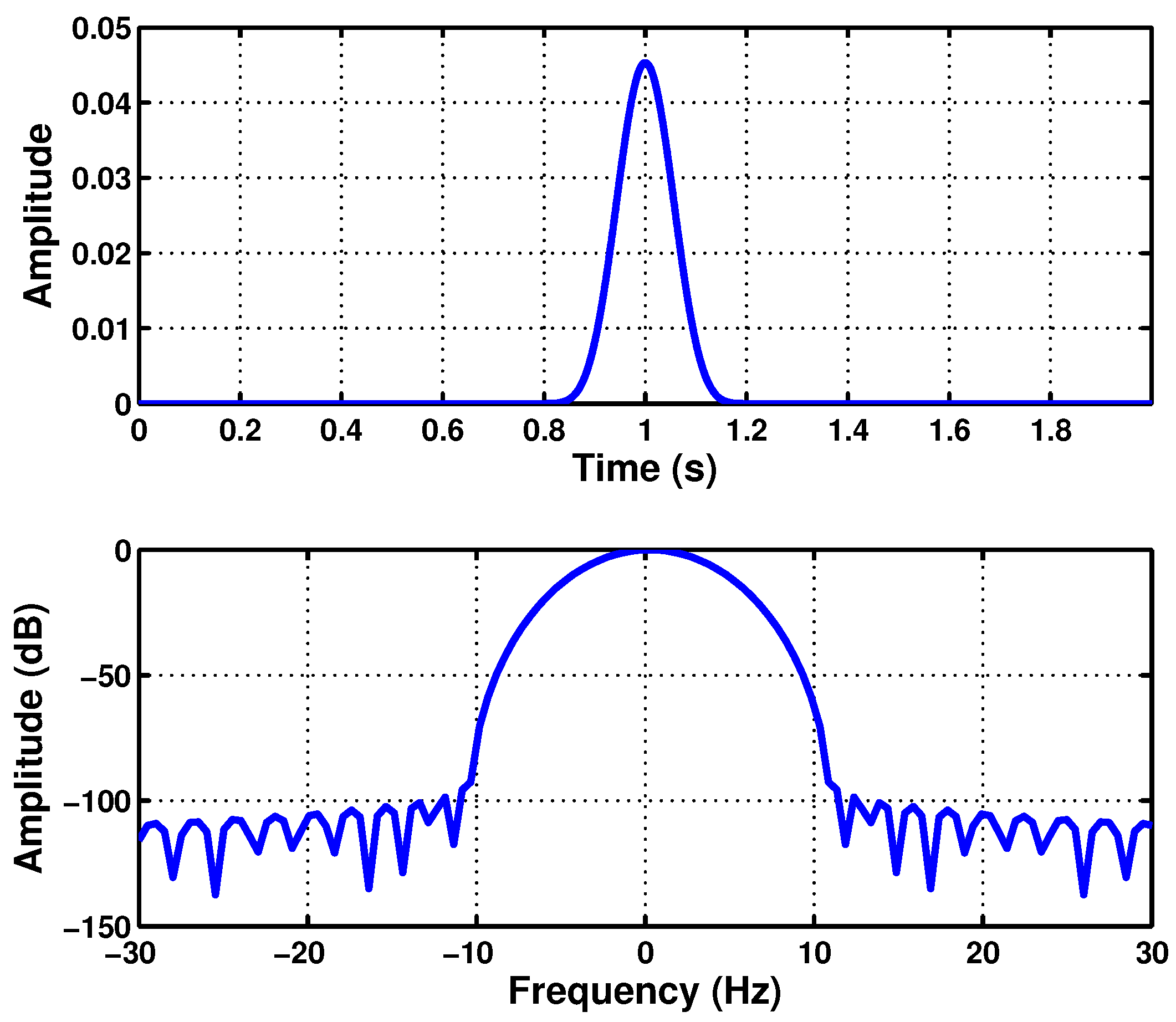
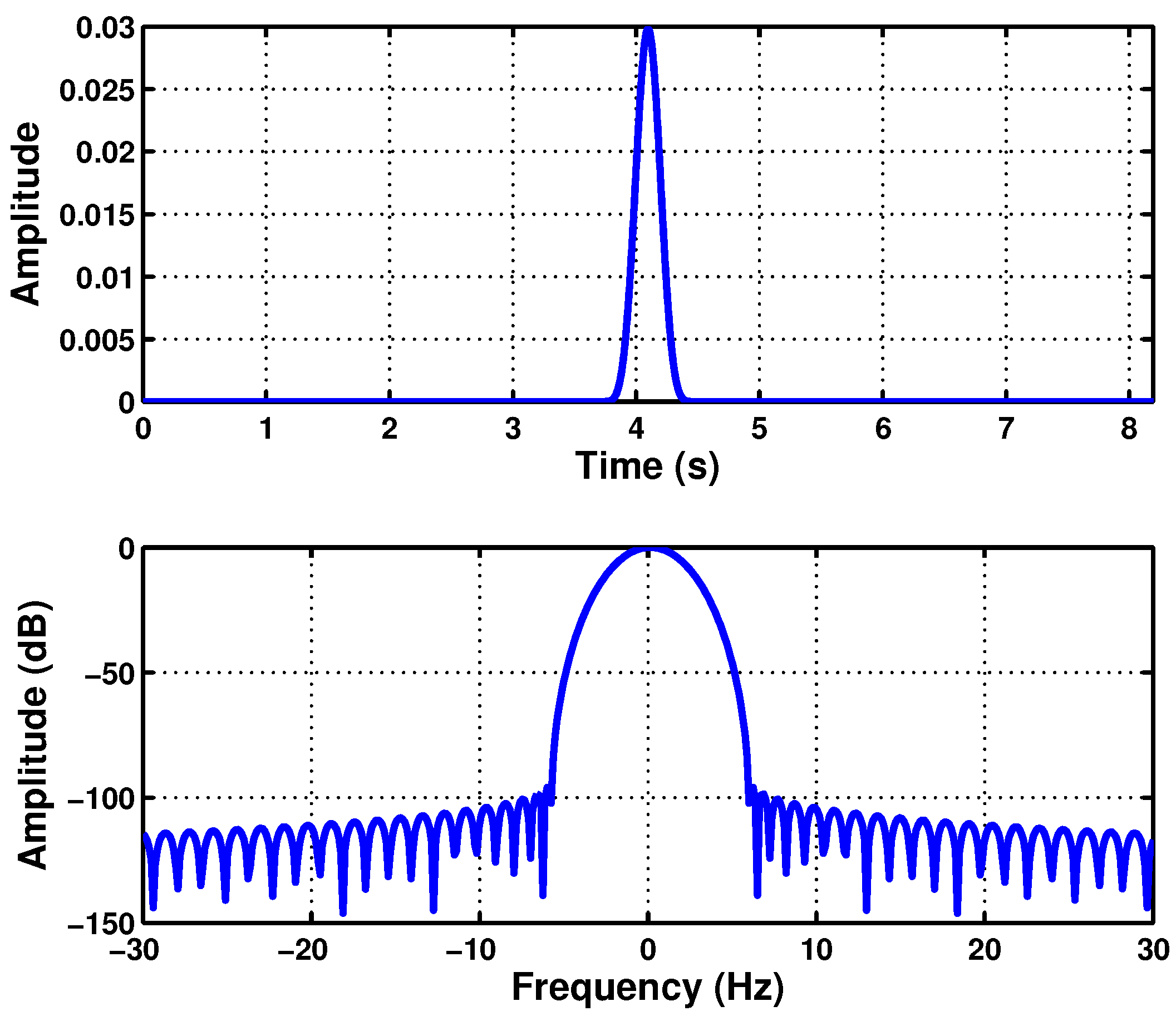
- The Slepians are the band-limited functions that are the most concentrated in a fixed time interval in the -norm [59]. Therefore, they can be considered as the optimal window for TF analysis of non-stationary currents [60], because they can highlight the energy content of the current signal in the joint time-frequency domain with the highest possible resolution among all the almost time- and band-limited windows, including the truncated Gaussian window.
- Alternatively, the Slepians can be considered as the time-limited functions that are the most concentrated in a fixed frequency interval in the -norm. That is, for a given bandwidth, they are the shortest possible windows that can be used for generating the current spectrograms, which allows the reduction of the time needed to build such spectrograms.
2. The Slepian Functions for Fault Diagnosis of Rotating Electrical Machines in the Transient Regime
2.1. Theoretical Introduction to the Slepian Functions
2.2. Energy of the Slepian Windows in a Time Interval
2.3. Energy of the Slepian Windows in a Frequency Interval
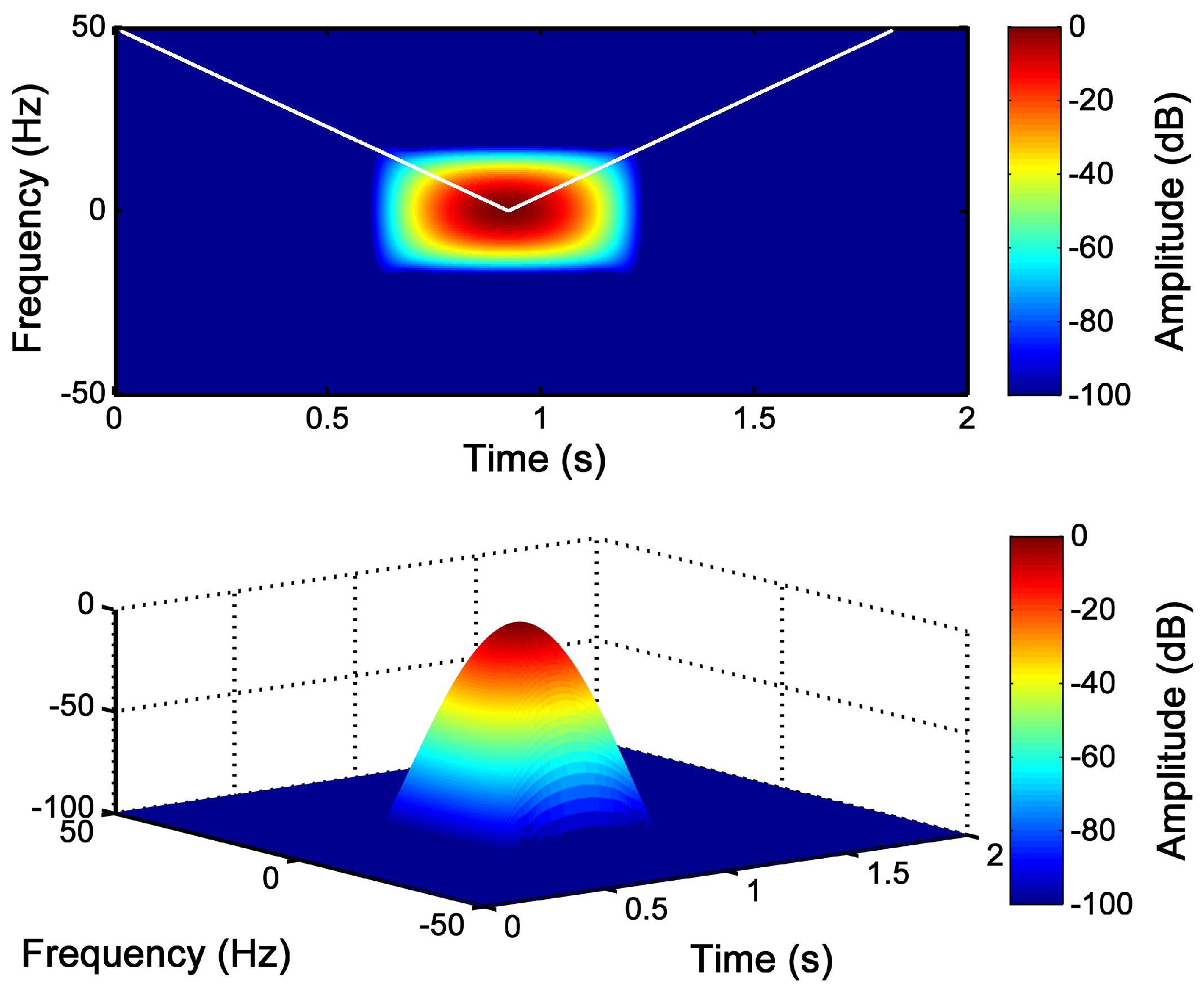
2.4. Energy of the Slepian Windows in the Joint TF Domain
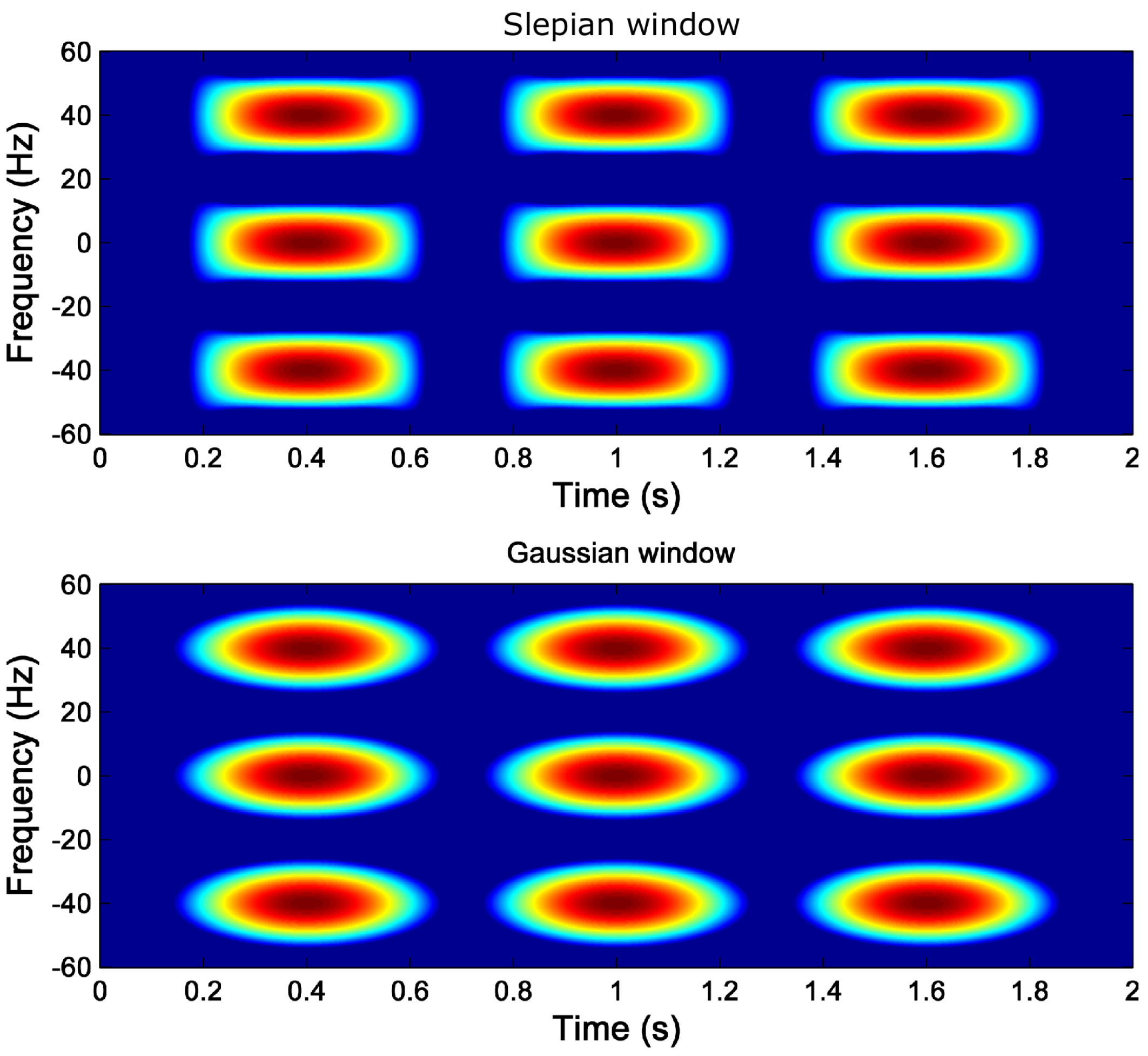
2.5. Comparison between the Slepian Window and the Gaussian Window
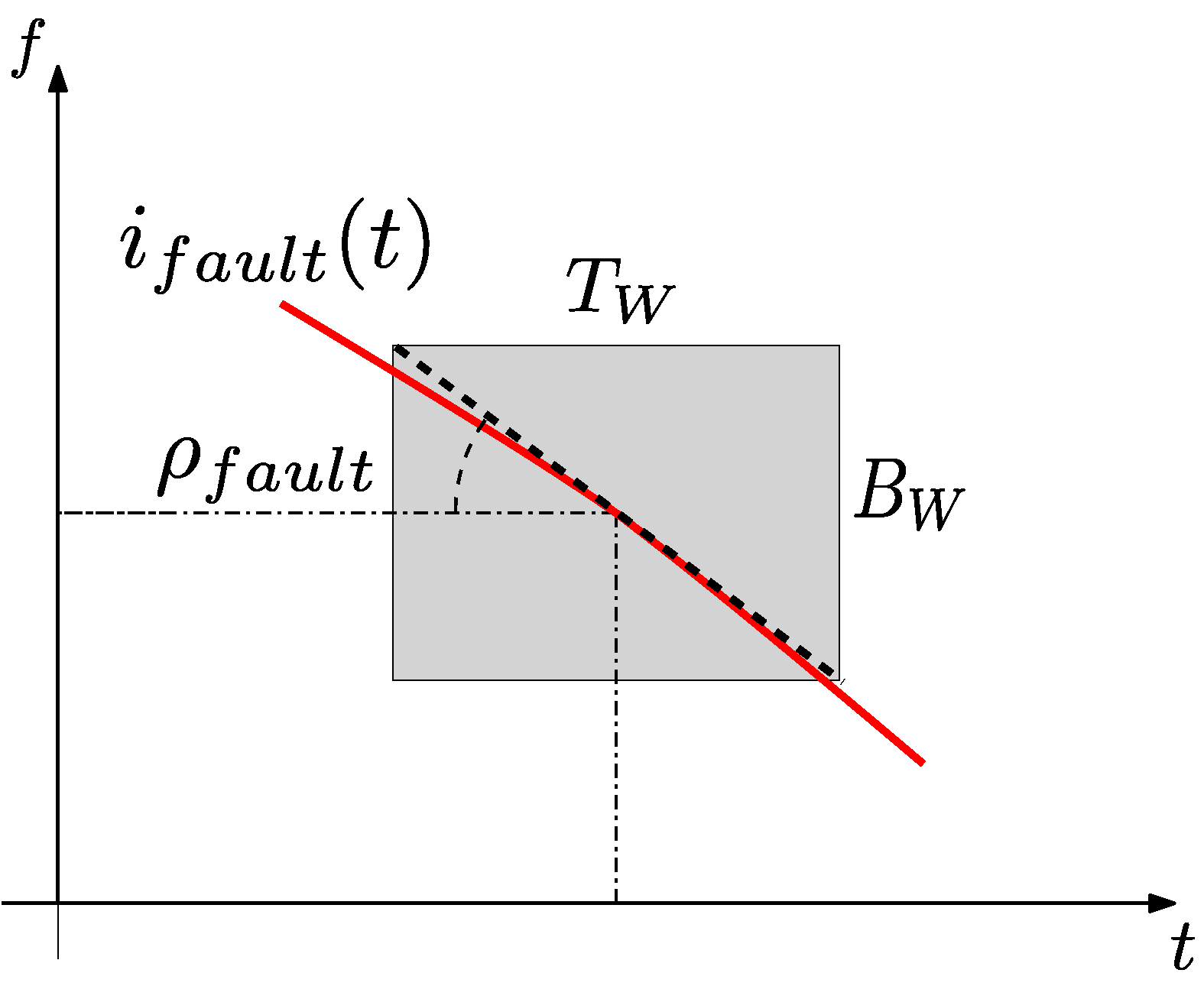
2.6. Proposed Method for the Choice of the Parameters of the Slepian Window
3. STFT of the Start-Up Current of a Simulated IM Using the Slepian Window
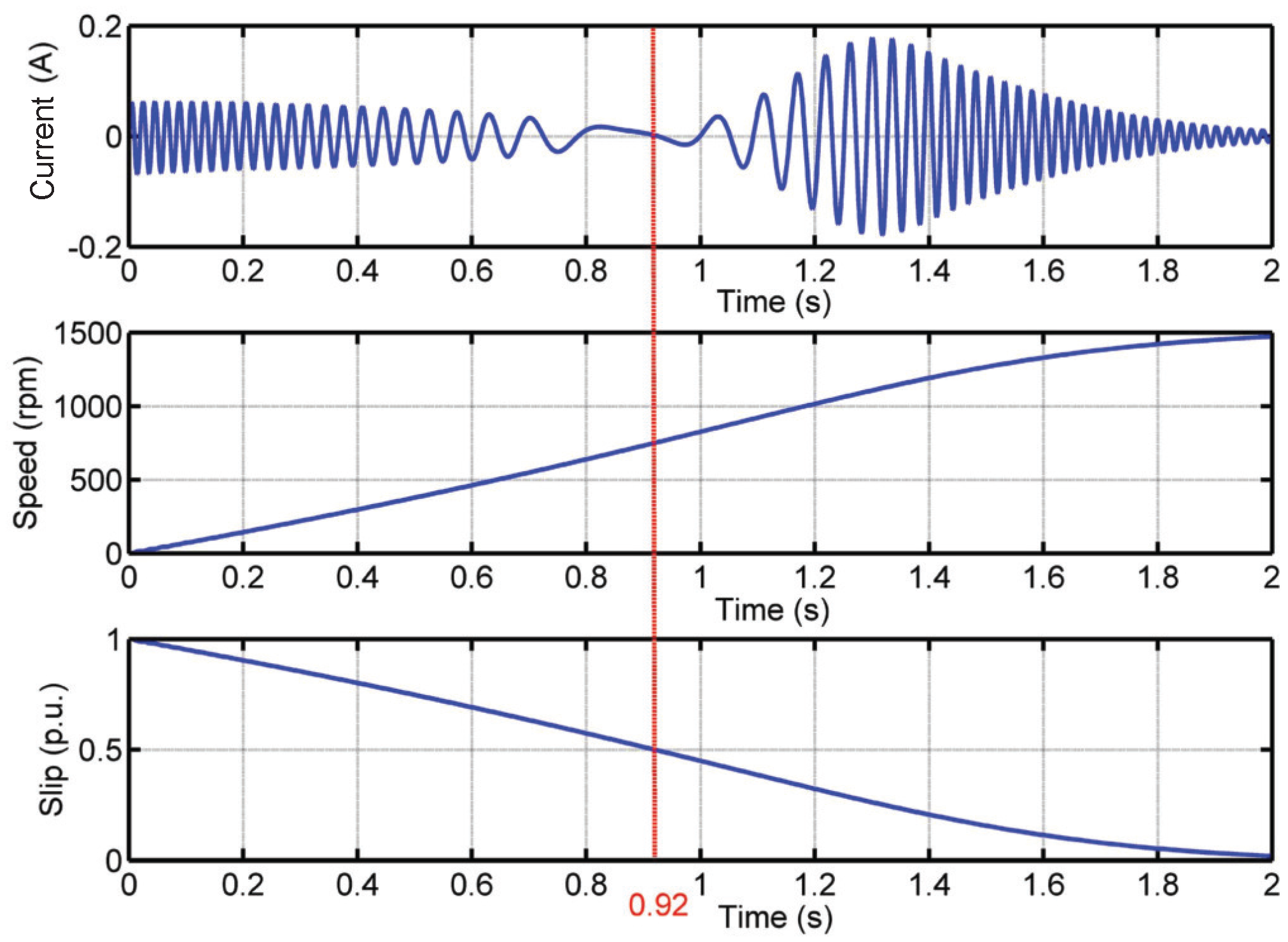
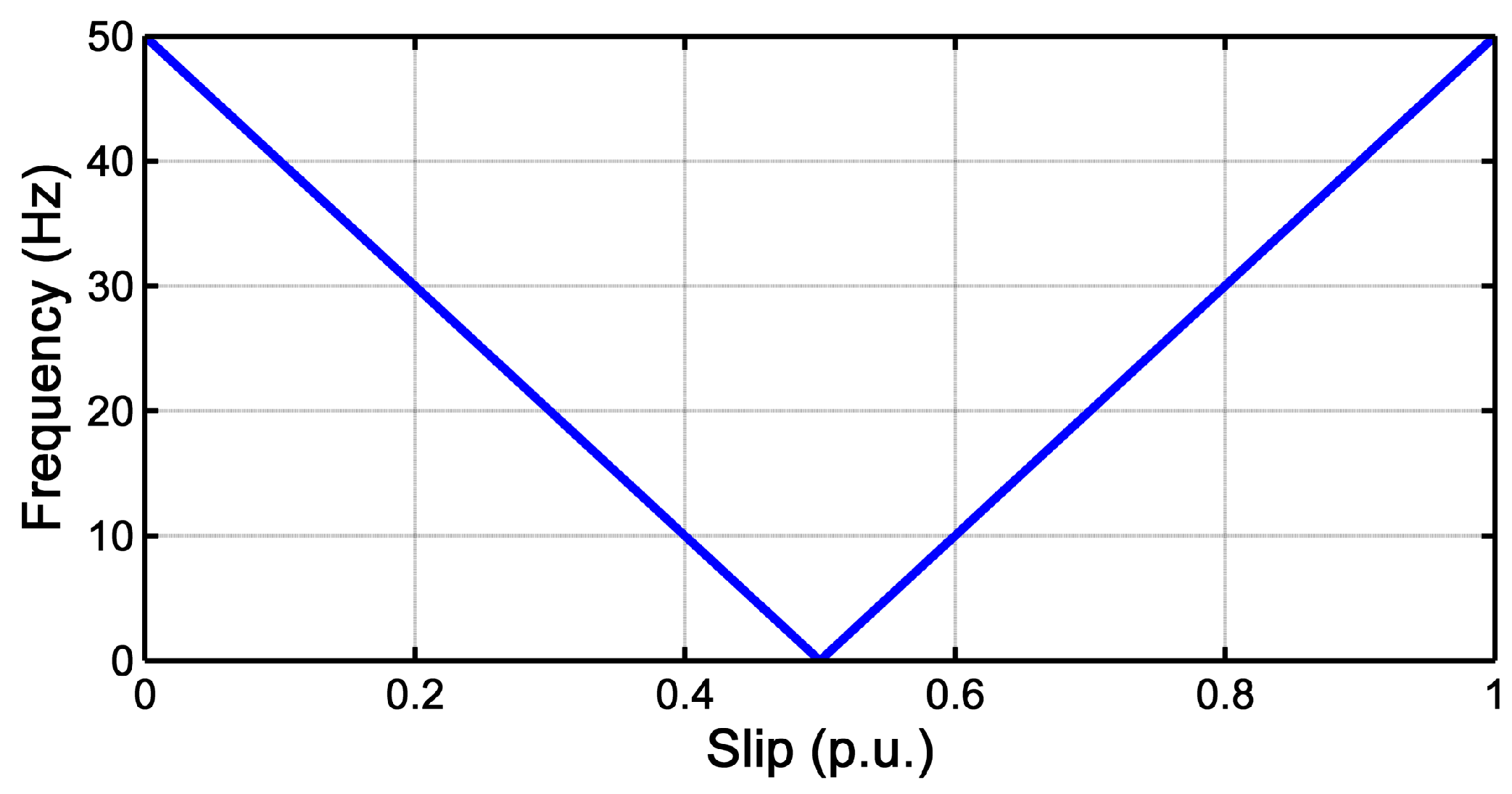
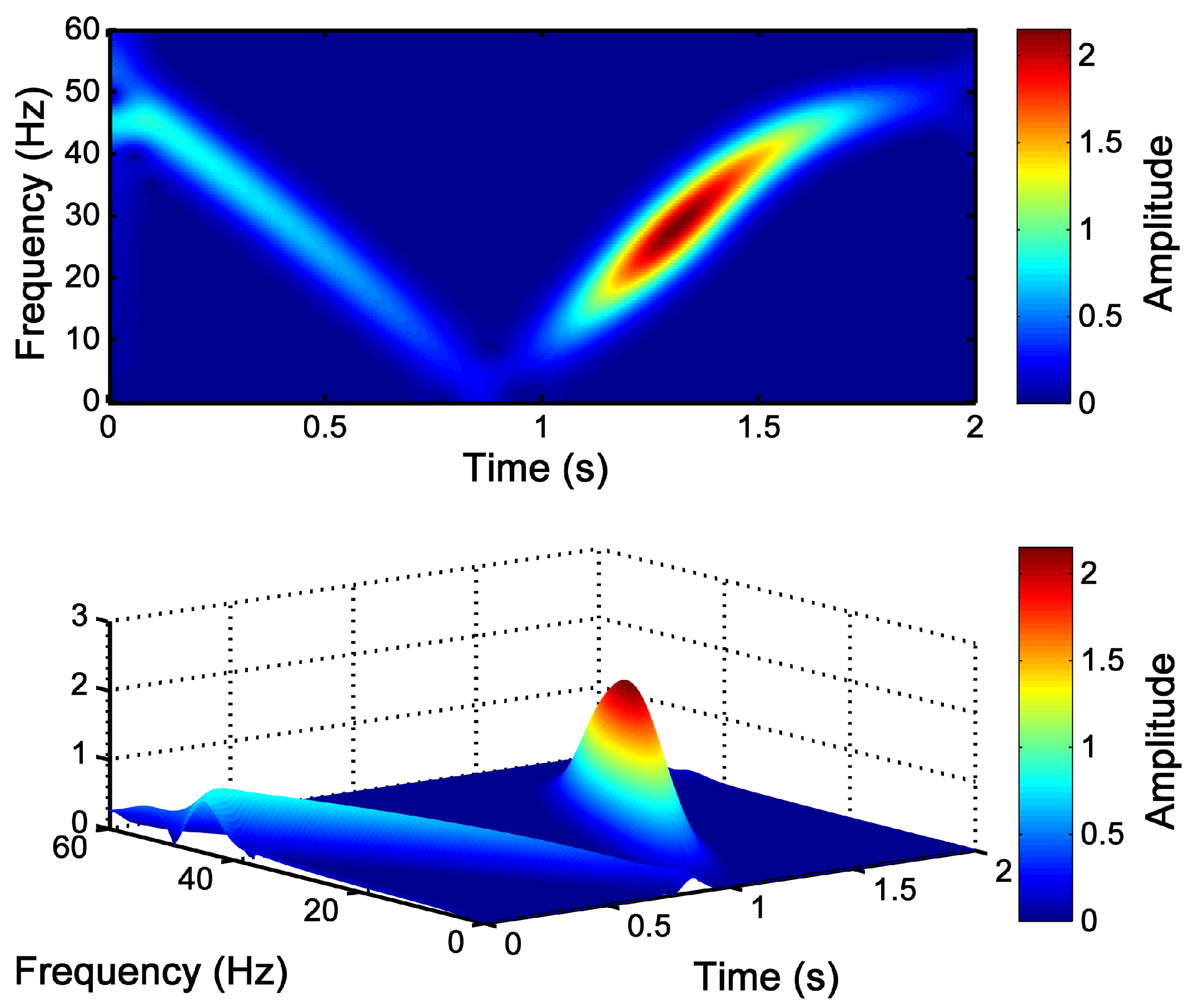
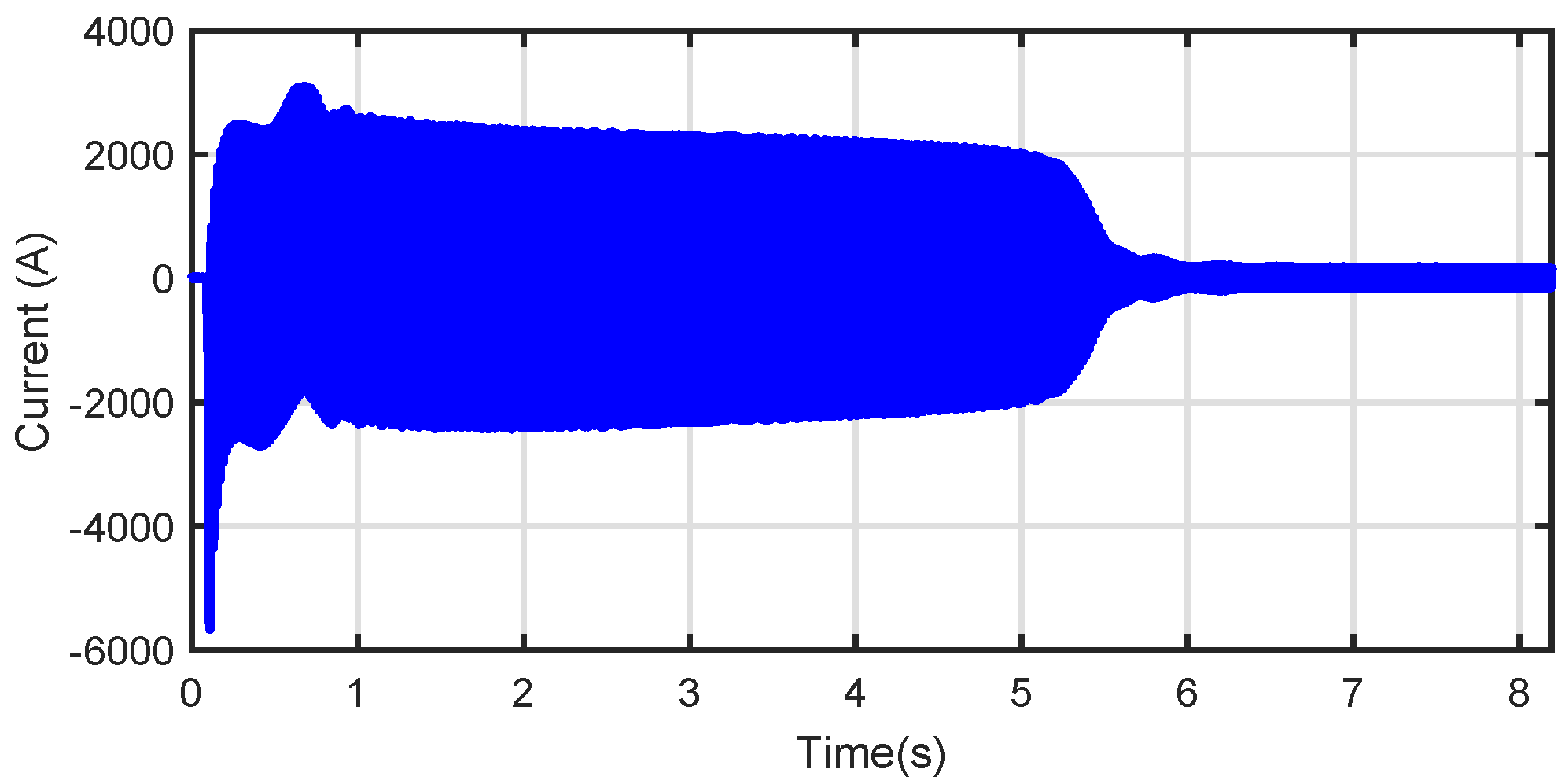
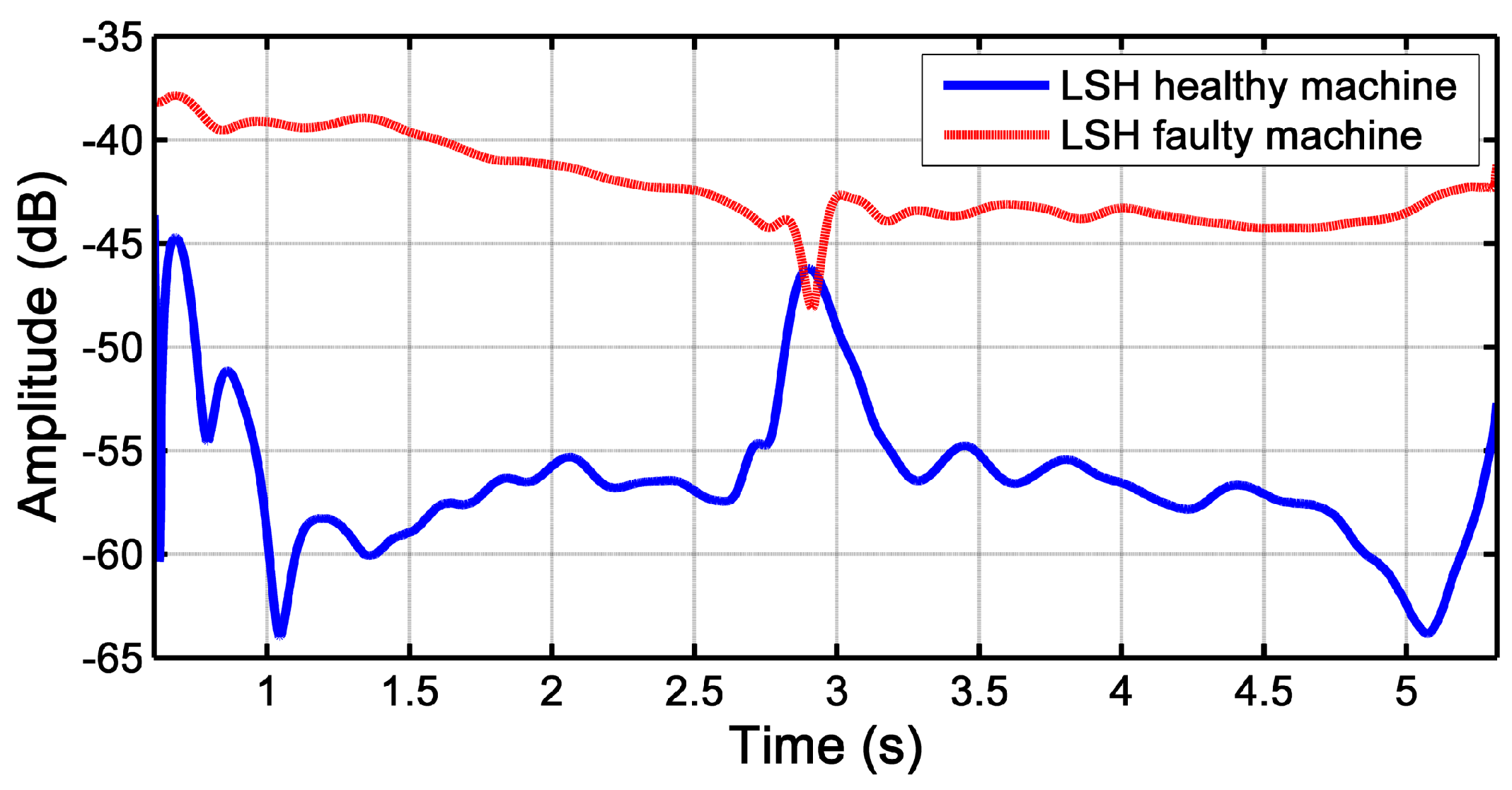
3.1. Evolution of the LSH during the Start-Up Transient of an IM
3.2. Choice of the Parameters of the Slepian Window
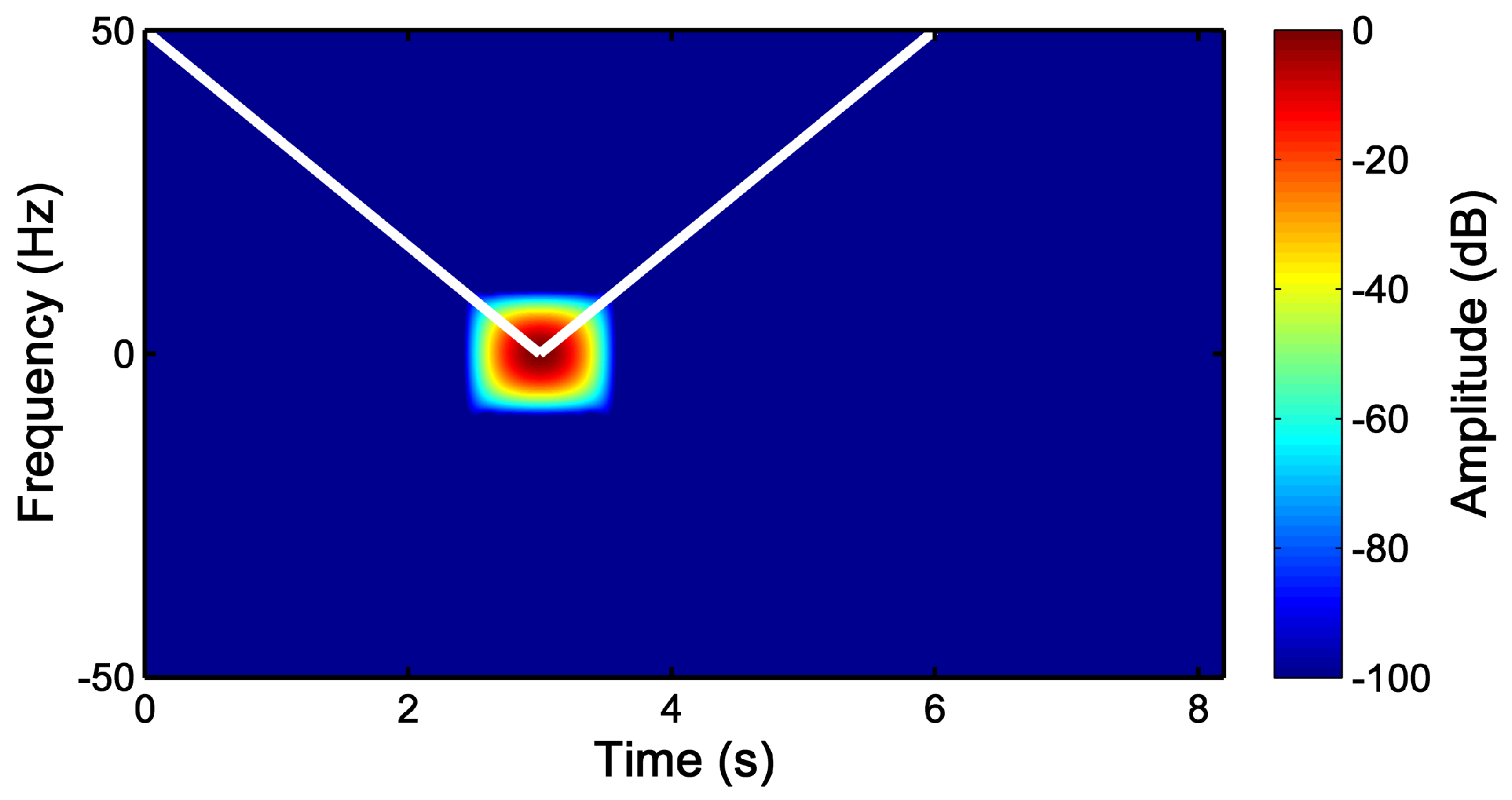
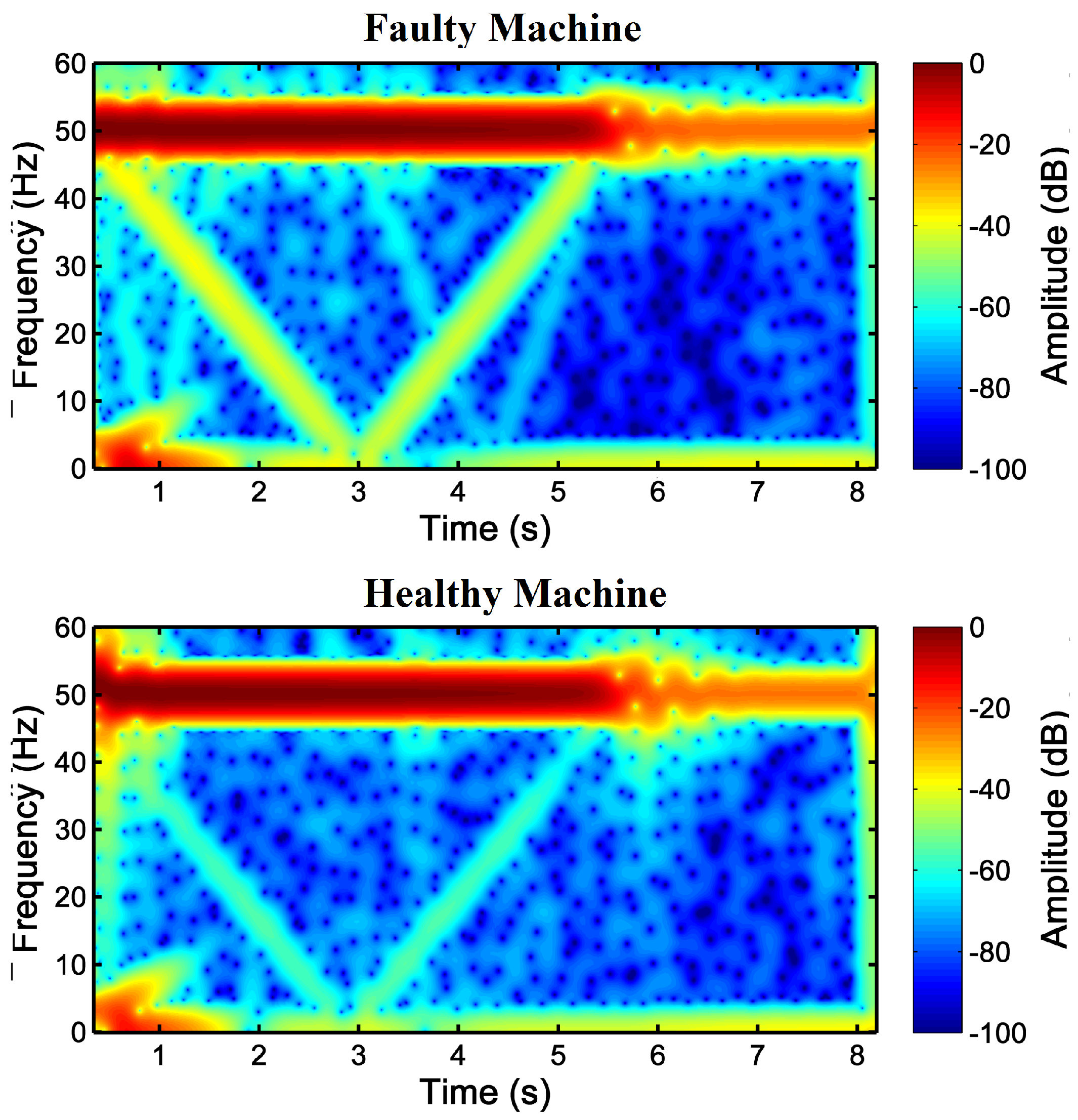
3.3. Detection of the LSH Fault Component with the Slepian Window
4. Experimental Validation on a High-Power, High-Voltage IM
4.1. Choice of the Parameters of the Slepian Window for the Tested IM
4.2. Application of the Slepian Window to the Fault Diagnosis of the Tested IM
5. Cost-Effective IM Fault Diagnosis Using the Truncated Slepian Window
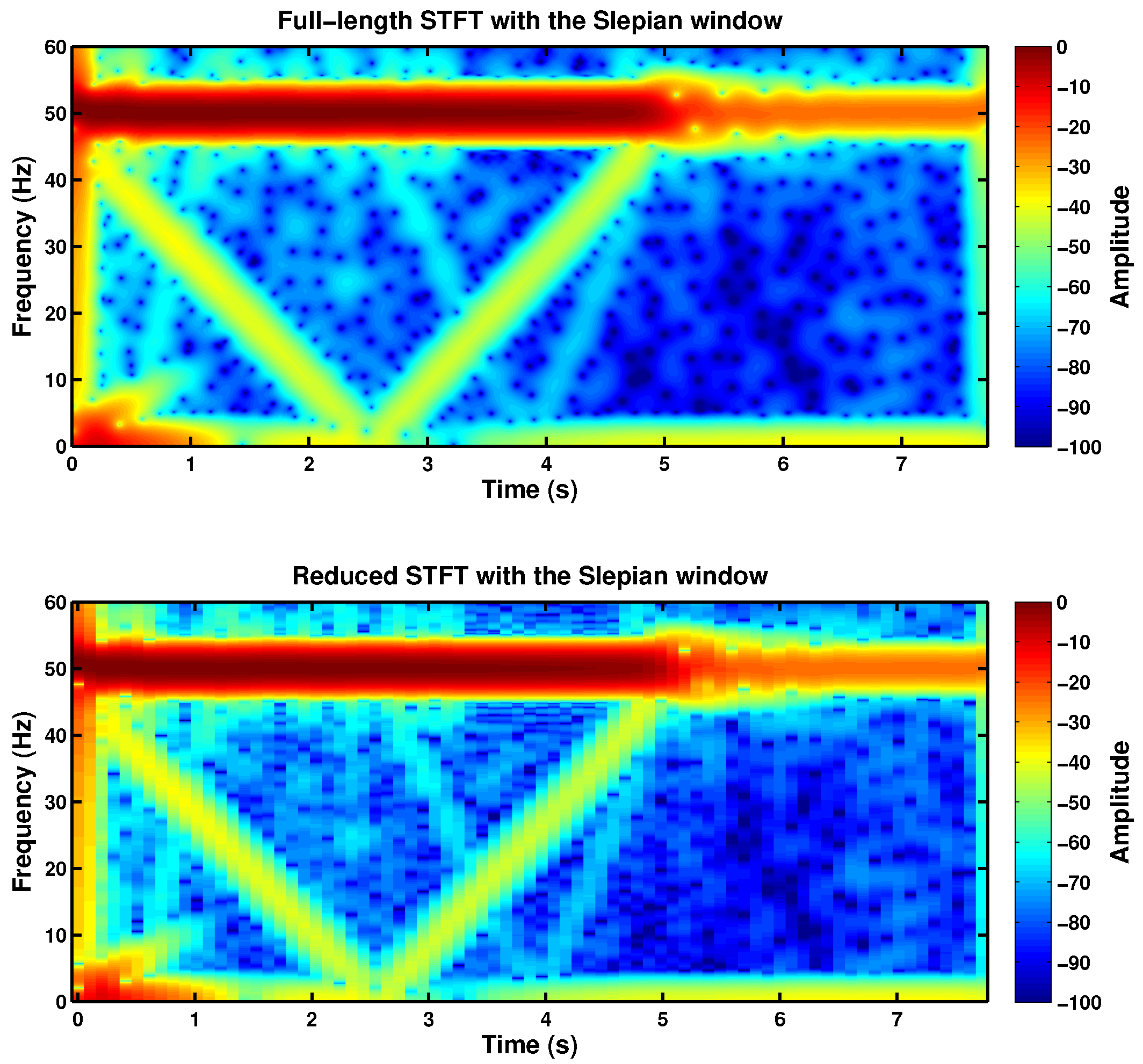
- Reducing the length of the FFT to the time duration of the Slepian window in Equation (35), much smaller than the length of the current signal ; that is, using a truncated Slepian window with a length equal to , instead of the length of the current signal. This is equivalent to setting in Equation (37).
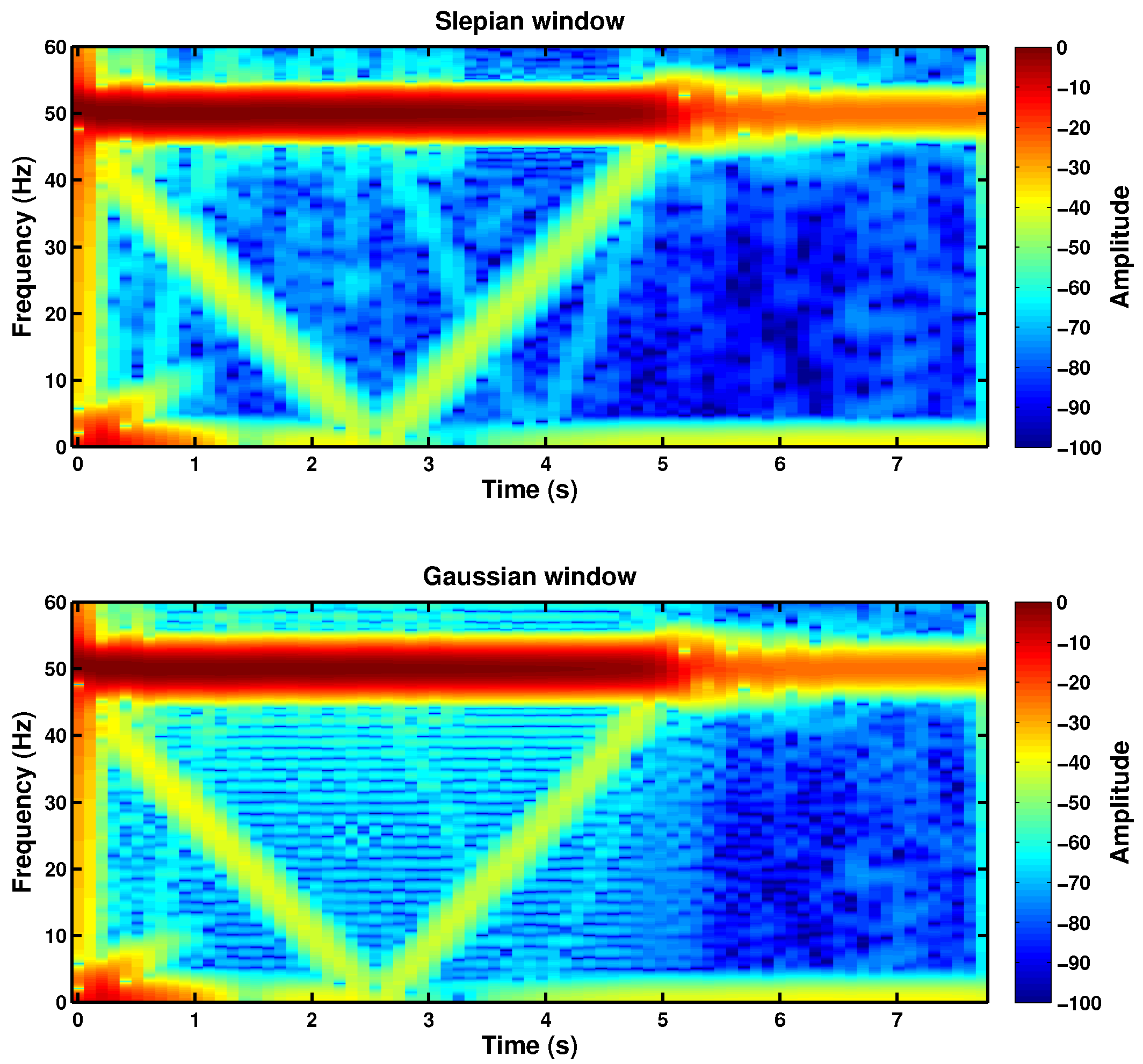
5.1. Comparison between the Spectrograms Generated with the Truncated Gaussian Window and with the Truncated Slepian Window
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A Simulated IM
Appendix B Industrial IM
Appendix C Computer Features
References
- Merizalde, Y.; Hernández-Callejo, L.; Duque-Perez, O. State of the art and trends in the monitoring, detection and diagnosis of failures in electric induction motors. Energies 2017, 10, 1056. [Google Scholar] [CrossRef]
- Doolan Fernandes, J.; Carvalho Souza, F.E.; Cipriano Maniçoba, G.G.; Salazar, A.O.; de Paiva, J.A. Wireless monitoring of induction machine rotor physical variables. Sensors 2017, 17, 2660. [Google Scholar] [CrossRef] [PubMed]
- Kande, M.; Isaksson, A.J.; Thottappillil, R.; Taylor, N. Rotating electrical machine condition monitoring automatio—A review. Machines 2017, 5, 24. [Google Scholar] [CrossRef]
- Bichurin, M.; Petrov, R.; Leontiev, V.; Semenov, G.; Sokolov, O. Magnetoelectric current sensors. Sensors 2017, 17, 1271. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.; Luo, Y.P.; Zhang, C.F.; He, J.; Huang, Y.S. Current sensor fault reconstruction for PMSM drives. Sensors 2016, 16, 178. [Google Scholar] [CrossRef] [PubMed]
- Medina-García, J.; Sánchez-Rodríguez, T.; Galán, J.A.G.; Delgado, A.; Gómez-Bravo, F.; Jiménez, R. A wireless sensor system for real-time monitoring and fault detection of motor arrays. Sensors 2017, 17, 469. [Google Scholar] [CrossRef] [PubMed]
- Cablea, G.; Granjon, P.; Bérenguer, C. Three-phase electrical signals analysis for mechanical faults monitoring in rotating machine systems. Mech. Syst. Signal Process. 2017, 92, 278–292. [Google Scholar] [CrossRef]
- El Bouchikhi, E.H.; Choqueuse, V.; Benbouzid, M. Induction machine faults detection using stator current parametric spectral estimation. Mech. Syst. Signal Process. 2015, 52, 447–464. [Google Scholar] [CrossRef]
- Ghorbanian, V.; Faiz, J. A survey on time and frequency characteristics of induction motors with broken rotor bars in line-start and inverter-fed modes. Mech. Syst. Signal Process. 2015, 54, 427–456. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, L.; Wang, Q.; An, G.; Guo, M.; Lian, H. Application to induction motor faults diagnosis of the amplitude recovery method combined with FFT. Mech. Syst. Signal Process. 2010, 24, 2961–2971. [Google Scholar] [CrossRef]
- Khater, F.M.; Abu El-Sebah, M.I.; Osama, M.; Sakkoury, K.S. Proposed fault diagnostics of a broken rotor bar induction motor fed from PWM inverter. J. Electr. Syst. Inf. Technol. 2016, 3, 387–397. [Google Scholar] [CrossRef]
- Shi, P.; Chen, Z.; Vagapov, Y.; Zouaoui, Z. A new diagnosis of broken rotor bar fault extent in three phase squirrel cage induction motor. Mech. Syst. Signal Process. 2014, 42, 388–403. [Google Scholar] [CrossRef]
- Mustafa, M.O.; Varagnolo, D.; Nikolakopoulos, G.; Gustafsson, T. Detecting broken rotor bars in induction motors with model-based support vector classifiers. Control Eng. Pract. 2016, 52, 15–23. [Google Scholar] [CrossRef]
- Li, D.Z.; Wang, W.; Ismail, F. A spectrum synch technique for induction motor health condition monitoring. IEEE Trans. Energy Convers. 2015, 30, 1348–1355. [Google Scholar] [CrossRef]
- Ebrahimi, B.M.; Faiz, J.; Lotfi-fard, S.; Pillay, P. Novel indices for broken rotor bars fault diagnosis in induction motors using wavelet transform. Mech. Syst. Signal Process. 2012, 30, 131–145. [Google Scholar] [CrossRef]
- Filippetti, F.; Franceschini, G.; Tassoni, C.; Vas, P. AI techniques in induction machines diagnosis including the speed ripple effect. IEEE Trans. Ind. Appl. 1998, 34, 98–108. [Google Scholar] [CrossRef]
- Verucchi, C.; Bossio, J.; Bossio, G.; Acosta, G. Misalignment detection in induction motors with flexible coupling by means of estimated torque analysis and MCSA. Mech. Syst. Signal Process. 2016, 80, 570–581. [Google Scholar] [CrossRef]
- Pons-Llinares, J.; Antonino-Daviu, J.; Roger-Folch, J.; Moríñigo-Sotelo, D.; Duque-Pérez, O. Mixed eccentricity diagnosis in Inverter-Fed Induction Motors via the Adaptive Slope Transform of transient stator currents. Mech. Syst. Signal Process. 2014, 48, 423–435. [Google Scholar] [CrossRef]
- Yahia, K.; Cardoso, A.; Ghoggal, A.; Zouzou, S. Induction motors airgap-eccentricity detection through the discrete wavelet transform of the apparent power signal under non-stationary operating conditions. ISA Trans. 2014, 53, 603–611. [Google Scholar] [CrossRef] [PubMed]
- Prudhom, A.; Antonino-Daviu, J.; Razik, H.; Climente-Alarcon, V. Time-frequency vibration analysis for the detection of motor damages caused by bearing currents. Mech. Syst. Signal Process. 2017, 84, 747–762. [Google Scholar] [CrossRef]
- Elbouchikhi, E.; Choqueuse, V.; Benbouzid, M. Induction machine bearing faults detection based on a multi-dimensional MUSIC algorithm and maximum likelihood estimation. ISA Trans. 2016, 63, 413–424. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.H.; Ahn, J.H.; Koh, B.H. Fault detection of bearing systems through EEMD and optimization algorithm. Sensors 2017, 17, 2477. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Chen, X.; Wang, S.; Sun, R.; Zhao, Z. Wind turbine diagnosis under variable speed conditions using a single sensor based on the synchrosqueezing transform method. Sensors 2017, 17, 1149. [Google Scholar]
- Delgado-Arredondo, P.A.; Morinigo-Sotelo, D.; Osornio-Rios, R.A.; Avina-Cervantes, J.G.; Rostro-Gonzalez, H.; Romero-Troncoso, R.d.J. Methodology for fault detection in induction motors via sound and vibration signals. Mech. Syst. Signal Process. 2017, 83, 568–589. [Google Scholar] [CrossRef]
- Saidi, L.; Ali, J.B.; Fnaiech, F. Bi-spectrum based-EMD applied to the non-stationary vibration signals for bearing faults diagnosis. ISA Trans. 2014, 53, 1650–1660. [Google Scholar] [CrossRef] [PubMed]
- Keskes, H.; Braham, A. Recursive undecimated wavelet packet transform and DAG SVM for induction motor diagnosis. IEEE Trans. Ind. Inform. 2015, 11, 1059–1066. [Google Scholar] [CrossRef]
- Faiz, J.; Ebrahimi, B.M. Mixed fault diagnosis in three-phase squirrel-cage induction motor using analysis of air-gap magnetic field. Prog. Electromagn. Res. 2006, 64, 239–255. [Google Scholar] [CrossRef]
- Boashash, B.; Khan, N.A.; Ben-Jabeur, T. Time-frequency features for pattern recognition using high-resolution TFDs: A tutorial review. Digit. Signal Process. 2015, 40, 1–30. [Google Scholar] [CrossRef]
- da Costa, C.; Kashiwagi, M.; Mathias, M.H. Rotor failure detection of induction motors by wavelet transform and Fourier transform in non-stationary condition. Case Stud. Mech. Syst. Signal Process. 2015, 1, 15–26. [Google Scholar] [CrossRef]
- Liu, Z.; He, Z.; Guo, W.; Tang, Z. A hybrid fault diagnosis method based on second generation wavelet de-noising and local mean decomposition for rotating machinery. ISA Trans. 2016, 61, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Nagarajaiah, S. Blind identification of damage in time-varying systems using independent component analysis with wavelet transform. Mech. Syst. Signal Process. 2014, 47, 3–20. [Google Scholar] [CrossRef]
- Gritli, Y.; Lee, S.B.; Filippetti, F.; Zarri, L. Advanced diagnosis of outer cage damage in double-squirrel-cage induction motors under time-varying conditions based on wavelet analysis. IEEE Trans. Ind. Appl. 2014, 50, 1791–1800. [Google Scholar] [CrossRef]
- He, W.; Zi, Y.; Chen, B.; Wu, F.; He, Z. Automatic fault feature extraction of mechanical anomaly on induction motor bearing using ensemble super-wavelet transform. Mech. Syst. Signal Process. 2015, 54, 457–480. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Wang, K. Fault diagnosis and prognosis using wavelet packet decomposition, Fourier transform and artificial neural network. J. Intel. Manuf. 2013, 24, 1213–1227. [Google Scholar] [CrossRef]
- Sapena-Bano, A.; Pineda-Sanchez, M.; Puche-Panadero, R.; Martinez-Roman, J.; Matic, D. Fault diagnosis of rotating electrical machines in transient regime using a single stator current’s FFT. IEEE Trans. Instrum. Meas. 2015, 64, 3137–3146. [Google Scholar] [CrossRef]
- Chandra, N.H.; Sekhar, A. Fault detection in rotor bearing systems using time frequency techniques. Mech. Syst. Signal Process. 2016, 72, 105–133. [Google Scholar] [CrossRef]
- Sugumaran, V.; Rao, A.V.; Ramachandran, K. A comprehensive study of fault diagnostics of roller bearings using continuous wavelet transform. Int. J. Manuf. Syst. Design 2015, 1, 27–46. [Google Scholar]
- Pineda-Sanchez, M.; Riera-Guasp, M.; Perez-Cruz, J.; Puche-Panadero, R. Transient motor current signature analysis via modulus of the continuous complex wavelet: A pattern approach. Energy Convers. Manag. 2013, 73, 26–36. [Google Scholar] [CrossRef]
- Xiao, Y.; Hong, Y.; Chen, X.; Chen, W. The application of dual-tree complex wavelet transform (DTCWT) energy entropy in misalignment fault diagnosis of doubly-fed wind turbine (DFWT). Entropy 2017, 19, 587. [Google Scholar] [CrossRef]
- Wang, S.; Cai, G.; Zhu, Z.; Huang, W.; Zhang, X. Transient signal analysis based on Levenberg-Marquardt method for fault feature extraction of rotating machines. Mech. Syst. Signal Process. 2015, 54, 16–40. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, J.; Kim, H.J. Development of enhanced Wigner-Ville distribution function. Mech. Syst. Signal Process. 2001, 15, 367–398. [Google Scholar] [CrossRef]
- Pachori, R.B.; Nishad, A. Cross-terms reduction in the Wigner-Ville distribution using tunable-Q wavelet transform. Signal Process. 2016, 120, 288–304. [Google Scholar] [CrossRef]
- Ren, H.; Ren, A.; Li, Z. A new strategy for the suppression of cross-terms in pseudo Wigner-Ville distribution. Signal Image Video Process. 2016, 10, 139–144. [Google Scholar] [CrossRef]
- Damir, M.; Victor, S.; Zlatan, C. Optimizing the reference signal in the cross Wigner-Ville distribution based instantaneous frequency estimation method. Procedia Eng. 2015, 100, 1657–1664. [Google Scholar] [CrossRef]
- Liu, T.; Yan, S.; Zhang, W. Time-frequency analysis of nonstationary vibration signals for deployable structures by using the constant-Q nonstationary Gabor transform. Mech. Syst. Signal Process. 2016, 75, 228–244. [Google Scholar] [CrossRef]
- Cohen, L. Time-Frequency Analysis: Theory and Applications; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1995. [Google Scholar]
- Hlawatsch, F.; Boudreaux-Bartels, G.F. Linear and quadratic time-frequency signal representations. IEEE Signal Process. Mag. 1992, 9, 21–67. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P.; Lin, Y.T.; McLaughlin, S.; Meignen, S.; Oberlin, T.; Wu, H.T. Time-frequency reassignment and synchrosqueezing: An overview. IEEE Signal Process. Mag. 2013, 30, 32–41. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, J. Analysis and design of modified window shapes for S-transform to improve time-frequency localization. Mech. Syst. Signal Process. 2015, 58, 271–284. [Google Scholar] [CrossRef]
- Loughlin, P.; Cohen, L. The uncertainty principle: Global, local, or both? IEEE Trans. Signal Process. 2004, 52, 1218–1227. [Google Scholar] [CrossRef]
- Riera-Guasp, M.; Pineda-Sanchez, M.; Perez-Cruz, J.; Puche-Panadero, R.; Roger-Folch, J.; Antonino-Daviu, J.A. Diagnosis of induction motor faults via Gabor analysis of the current in transient regime. IEEE Trans. Instrum. Meas. 2012, 61, 1583–1596. [Google Scholar] [CrossRef]
- Schroeder, M.R. Computer Speech: Recognition, Compression, Synthesis; Springer Science & Business Media: New York, NY, USA, 2013; Volume 35. [Google Scholar]
- Jaming, P.; Karoui, A.; Spektor, S. The approximation of almost time- and band-limited functions by their expansion in some orthogonal polynomials bases. J. Approx. Theory 2016, 212, 41–65. [Google Scholar] [CrossRef]
- Karoui, A. Unidimensional and bidimensional prolate spheroidal wave functions and applications. J. Frankl. Inst. 2011, 348, 1668–1694. [Google Scholar] [CrossRef]
- Landa, B.; Shkolnisky, Y. Approximation scheme for essentially bandlimited and space-concentrated functions on a disk. Appl. Comput. Harmonic Anal. 2016, 43, 381–403. [Google Scholar] [CrossRef]
- Slepian, D.; Pollak, H.O. Prolate spheroidal wave functions, Fourier analysis and uncertainty—I. Bell Syst. Tech. J. 1961, 40, 43–63. [Google Scholar] [CrossRef]
- Landau, H.J.; Pollak, H.O. Prolate spheroidal wave functions, Fourier analysis and uncertainty—II. Bell Syst. Tech. J. 1961, 40, 65–84. [Google Scholar] [CrossRef]
- Landau, H.J.; Pollak, H.O. Prolate spheroidal wave functions, Fourier analysis and uncertainty–III: The dimension of the space of essentially time-and band-limited signals. Bell Syst. Tech. J. 1962, 41, 1295–1336. [Google Scholar] [CrossRef]
- Hogan, J.A.; Lakey, J.D. Frame properties of shifts of prolate spheroidal wave functions. Appl. Comput. Harmonic Anal. 2015, 39, 21–32. [Google Scholar] [CrossRef]
- Harris, F. On the use of windows for harmonic analysis with the discrete Fourier transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Lindquist, M.A.; Wager, T.D. Spatial smoothing in fMRI using prolate spheroidal wave functions. Hum. Brain Mapp. 2008, 29, 1276–1287. [Google Scholar] [CrossRef] [PubMed]
- Zemen, T.; Mecklenbrauker, C. Time-variant channel estimation using discrete prolate spheroidal sequences. IEEE Trans. Signal Process. 2005, 53, 3597–3607. [Google Scholar] [CrossRef]
- Bronez, T. Spectral estimation of irregularly sampled multidimensional processes by generalized prolate spheroidal sequences. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1862–1873. [Google Scholar] [CrossRef]
- Du, W.; Liao, G.; Yang, Z. Robust space time processing based on bi-iterative scheme of secondary data selection and PSWF method. Digit. Signal Process. 2016, 52, 64–71. [Google Scholar] [CrossRef]
- Moore, I.C.; Cada, M. Prolate spheroidal wave functions, an introduction to the Slepian series and its properties. Appl. Comput. Harmonic Anal. 2004, 16, 208–230. [Google Scholar] [CrossRef]
- Huibin, L.; Kang, D. Energy based signal parameter estimation method and a comparative study of different frequency estimators. Mech. Syst. Signal Process. 2011, 25, 452–464. [Google Scholar] [CrossRef]
- Slepian, D. Prolate spheroidal wave functions, Fourier analysis, and uncertainty—V: The discrete case. Bell Syst. Tech. J. 1978, 57, 1371–1430. [Google Scholar] [CrossRef]
- Barber, N.; Ursell, F. The response of a resonant system to a gliding tone. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1948, 39, 345–361. [Google Scholar] [CrossRef]
- Li, M.; Staunton, R. Optimum Gabor filter design and local binary patterns for texture segmentation. Pat. Recognit. Lett. 2008, 29, 664–672. [Google Scholar] [CrossRef]
- Zielinski, T.P. Joint time-frequency resolution of signal analysis using Gabor transform. IEEE Trans. Instrum. Meas. 2001, 50, 1436–1444. [Google Scholar] [CrossRef]
- Bessam, B.; Menacer, A.; Boumehraz, M.; Cherif, H. Detection of broken rotor bar faults in induction motor at low load using neural network. ISA Trans. 2016, 64, 241–246. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Tavner, P.J.; Tian, W. Wind turbine condition monitoring based on an improved spline-kernelled Chirplet transform. IEEE Trans. Ind. Electron. 2015, 62, 6565–6574. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, Z.K.; Meng, G.; Zhang, W.M. Spline-kernelled chirplet transform for the analysis of signals with time-varying frequency and its application. IEEE Trans. Ind. Electron. 2012, 59, 1612–1621. [Google Scholar] [CrossRef]
- Chen, S.; Dong, X.; Yang, Y.; Zhang, W.; Peng, Z.; Meng, G. Chirplet path fusion for the analysis of time-varying frequency-modulated signals. IEEE Trans. Ind. Electron. 2017, 64, 1370–1380. [Google Scholar] [CrossRef]
- Karoui, A.; Moumni, T. New efficient methods of computing the prolate spheroidal wave functions and their corresponding eigenvalues. Appl. Comput. Harmonic Anal. 2008, 24, 269–289. [Google Scholar] [CrossRef]
- Rezazadeh Mehrjou, M.; Mariun, N.; Misron, N.; Radzi, M.A.M.; Musa, S. Broken rotor bar detection in LS-PMSM based on startup current analysis using wavelet entropy features. Appl. Sci. 2017, 7, 845. [Google Scholar] [CrossRef]
- Riera-Guasp, M.; Antonino-Daviu, J.; Roger-Folch, J.; Molina Palomares, M. The use of the wavelet approximation signal as a tool for the diagnosis of rotor bar failures. IEEE Trans. Ind. Appl. 2008, 44, 716–726. [Google Scholar] [CrossRef]
- Pons-Llinares, J.; Riera-Guasp, M.; Antonino-Daviu, J.A.; Habetler, T.G. Pursuing optimal electric machines transient diagnosis: The adaptive slope transform. Mech. Syst. Signal Process. 2016, 80, 553–569. [Google Scholar] [CrossRef]
- Fischer, S.; Cristobal, G. Minimum entropy transform using Gabor wavelets for image compression. In Proceedings of the 11th International Conference on Image Analysis and Processing, Palermo, Italy, 26–28 September 2001; pp. 428–433. [Google Scholar]
- Romero-Troncoso, R.; Saucedo-Gallaga, R.; Cabal-Yepez, E.; Garcia-Perez, A.; Osornio-Rios, R.; Alvarez-Salas, R.; Miranda-Vidales, H.; Huber, N. FPGA-based online detection of multiple combined faults in induction motors through information entropy and fuzzy inference. IEEE Trans. Ind. Electron. 2011, 58, 5263–5270. [Google Scholar] [CrossRef]
- Sejdić, E.; Djurović, I.; Jiang, J. Time–frequency feature representation using energy concentration: An overview of recent advances. Digit. Signal Process. 2009, 19, 153–183. [Google Scholar] [CrossRef]
- Wiesmeyr, C.; Holighaus, N.; Søndergaard, P.L. Efficient algorithms for discrete Gabor transforms on a nonseparable lattice. IEEE Trans. Signal Process. 2013, 61, 5131–5142. [Google Scholar] [CrossRef]
- Søndergaard, P.L. Efficient algorithms for the discrete Gabor transform with a long FIR window. J. Fourier Anal. Appl. 2012, 18, 456–470. [Google Scholar] [CrossRef]
- Moreno-Picot, S.; Arevalillo-Herraez, M.; Diaz-Villanueva, W. A linear cost algorithm to compute the discrete Gabor transform. IEEE Trans. Signal Process. 2010, 58, 2667–2674. [Google Scholar] [CrossRef]


| Full-Length TF Analysis | Reduced Length TF Analysis | |
|---|---|---|
| Window duration (s) | ||
| Shift step (s) | ||
| FFT length (samples) | ||
| Number of FFTs |
| s , , and | ||
|---|---|---|
| Full-Length TF Analysis | Reduced Length TF Analysis | |
| Window’s length (s) | ||
| Shift step (s) | ||
| FFT length (samples) | 52,480 | 4434 |
| Number of FFTs | 52,480 | 95 |
| Time needed for computing the spectrogram (s) | ||
| Memory needed for computing the spectrogram (kB) | 186,608 | 59 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burriel-Valencia, J.; Puche-Panadero, R.; Martinez-Roman, J.; Sapena-Bano, A.; Pineda-Sanchez, M. Fault Diagnosis of Induction Machines in a Transient Regime Using Current Sensors with an Optimized Slepian Window. Sensors 2018, 18, 146. https://doi.org/10.3390/s18010146
Burriel-Valencia J, Puche-Panadero R, Martinez-Roman J, Sapena-Bano A, Pineda-Sanchez M. Fault Diagnosis of Induction Machines in a Transient Regime Using Current Sensors with an Optimized Slepian Window. Sensors. 2018; 18(1):146. https://doi.org/10.3390/s18010146
Chicago/Turabian StyleBurriel-Valencia, Jordi, Ruben Puche-Panadero, Javier Martinez-Roman, Angel Sapena-Bano, and Manuel Pineda-Sanchez. 2018. "Fault Diagnosis of Induction Machines in a Transient Regime Using Current Sensors with an Optimized Slepian Window" Sensors 18, no. 1: 146. https://doi.org/10.3390/s18010146
APA StyleBurriel-Valencia, J., Puche-Panadero, R., Martinez-Roman, J., Sapena-Bano, A., & Pineda-Sanchez, M. (2018). Fault Diagnosis of Induction Machines in a Transient Regime Using Current Sensors with an Optimized Slepian Window. Sensors, 18(1), 146. https://doi.org/10.3390/s18010146