A False Alarm Reduction Method for a Gas Sensor Based Electronic Nose
Abstract
:1. Introduction
- (i)
- Misclassification or false negative: odor data of a training class is classified to another trained or irrelevant class, and,
- (ii)
- False classification or false positive: odor data of an irrelevant class classified to a training class.
2. Materials and Methods
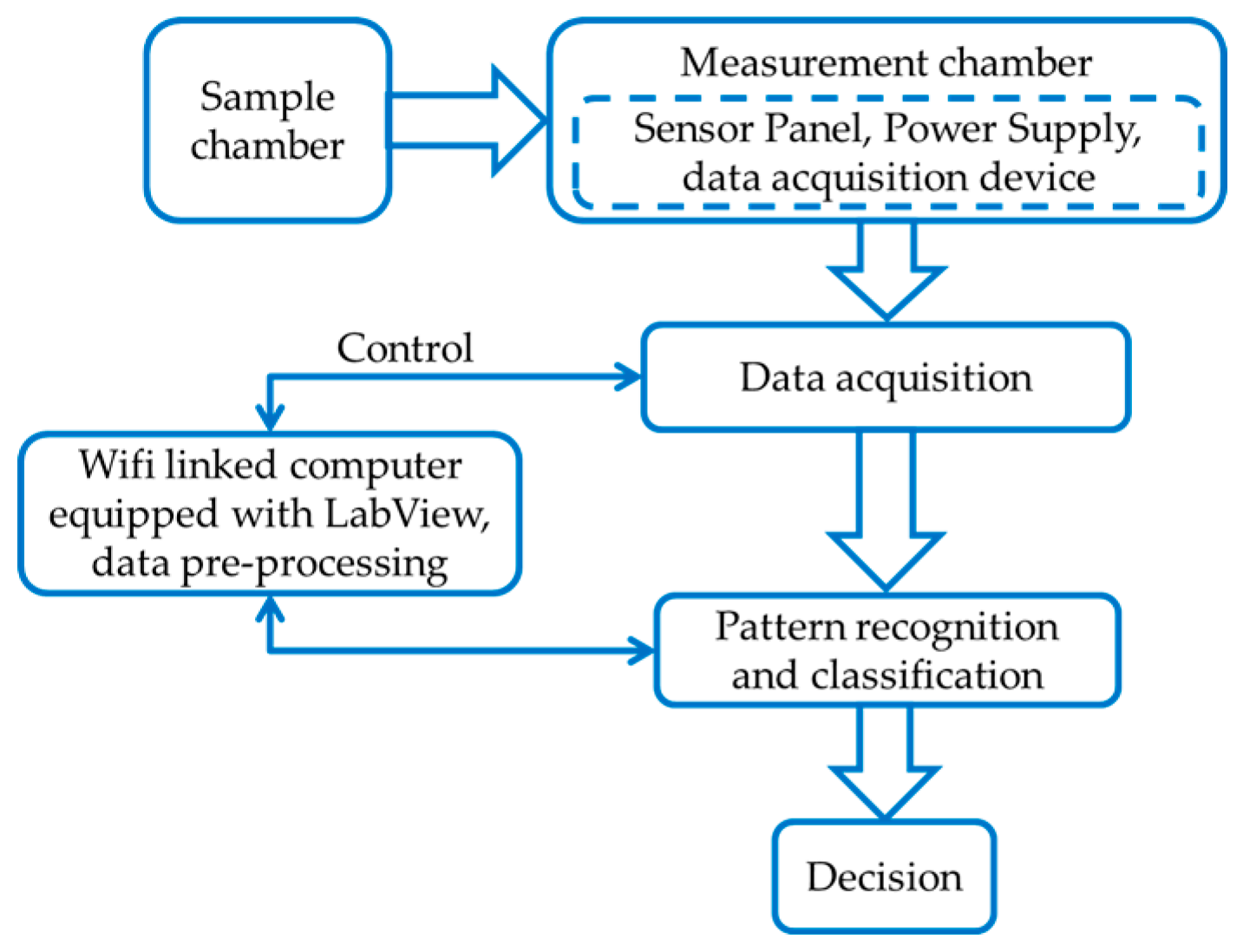
2.1. E-Nose Design Process
2.2. Sample Collection
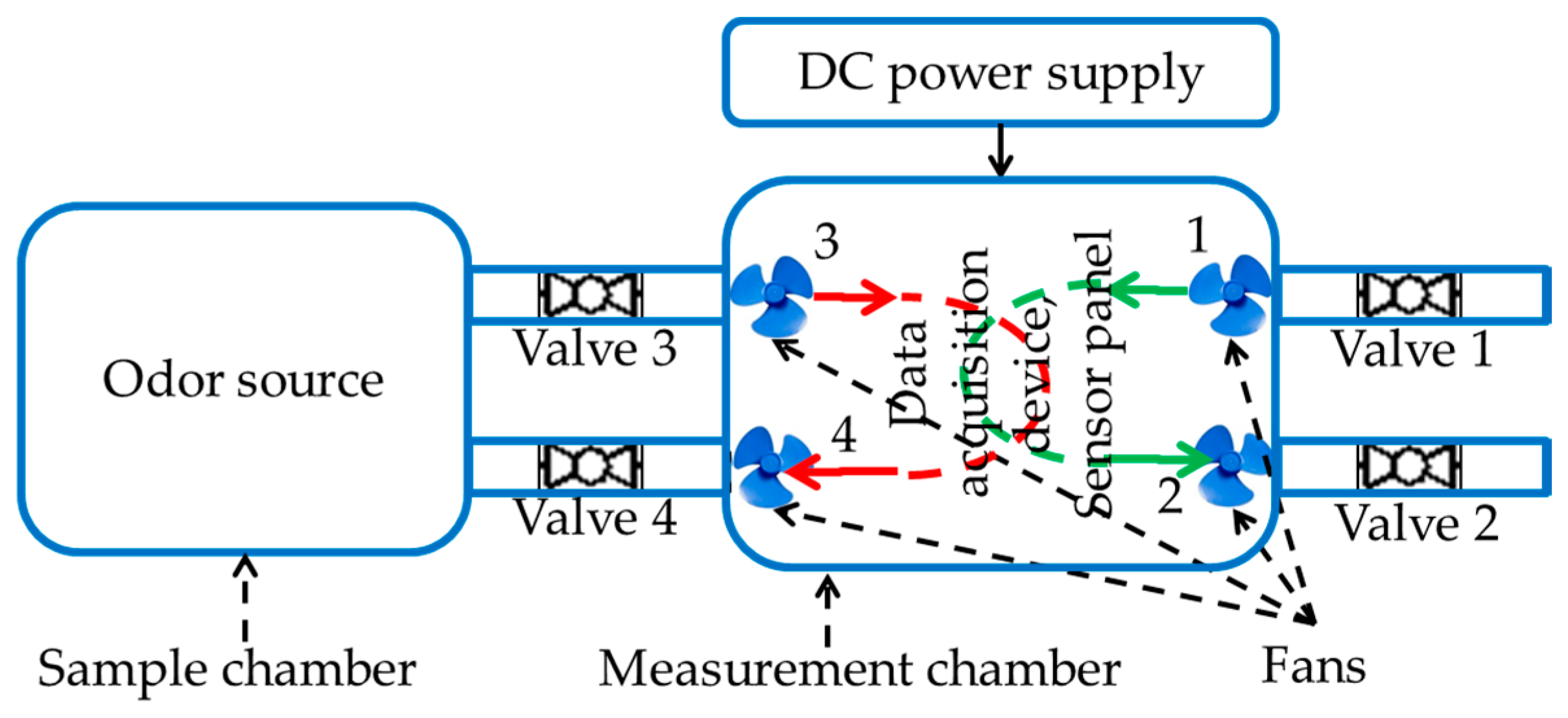
2.3. Sensor Panel
2.4. Experimental Setup
2.5. Data Acquisition
2.6. Pattern Recognition and Classification Algorithms
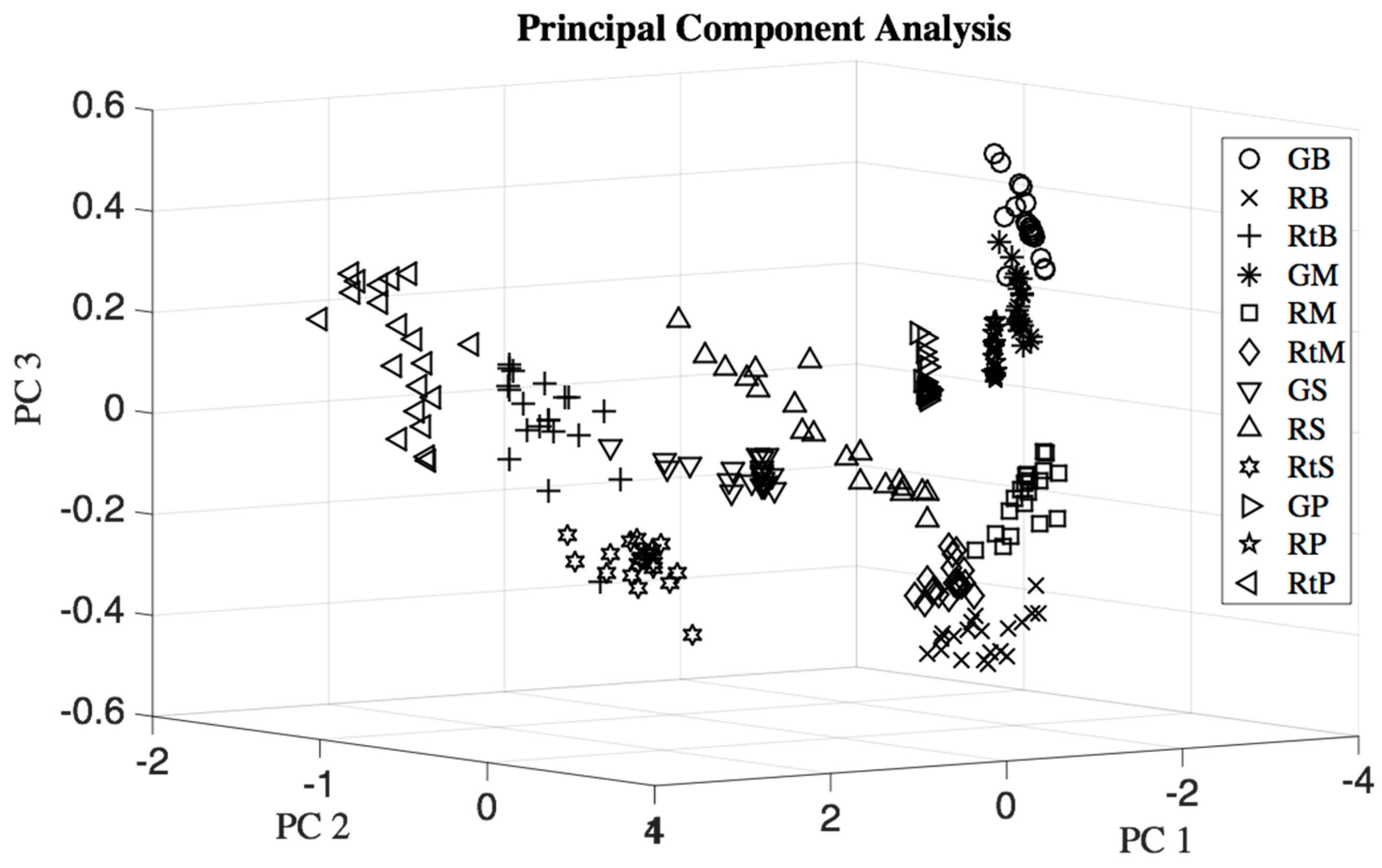
2.6.1. Principal Component Analysis
- Step 1.
- Find the mean vector x = [x1, x2, …, xN], where each element represents the mean of each column of X. N is the number of sensors.
- Step 2.
- Deduct the mean vector x from each row of matrix X.
- Step 3.
- Find the covariance matrix of the mean deducted matrix in Step 2.
- Step 4.
- Find the eigenvalues and eigenvectors of the covariance matrix found in Step 3.
- Step 5.
- Sort the eigenvectors in descending order of eigenvalues.
- Step 6.
- The eigenvector with maximum eigenvalue is PC 1, the eigenvector corresponding to the second largest eigenvalue is PC 2, and so on for the descending eigenvalues.
2.6.2. k-Nearest Neighbor
2.6.3. Support Vector Machine
- Step 1.
- Maximize the Lagrangian [Equation (3)] such that and .where l and g are experiment indices within a class, m and j are class indices, αl,m are Lagrange multipliers, tl,m are class labels (+1 or −1), and x are data vectors.
- Step 2.
- Find the value of αl,m from Equation (3).
- Step 3.
- Put the values of αl,m in Equation (5) to find the weight vector by Equation (4).
- Step 4.
- By the Karush–Kuhn–Tucker condition [38] as shown in Equation 5 below and weights found from Equation (6), bias b is calculated.
- Step 5.
- Classify test data by looking at the sign of the solution to Equation (6) as given below:where, s is support vector index, S is the number of support vectors, b is the bias, and u is the data vector under testing.
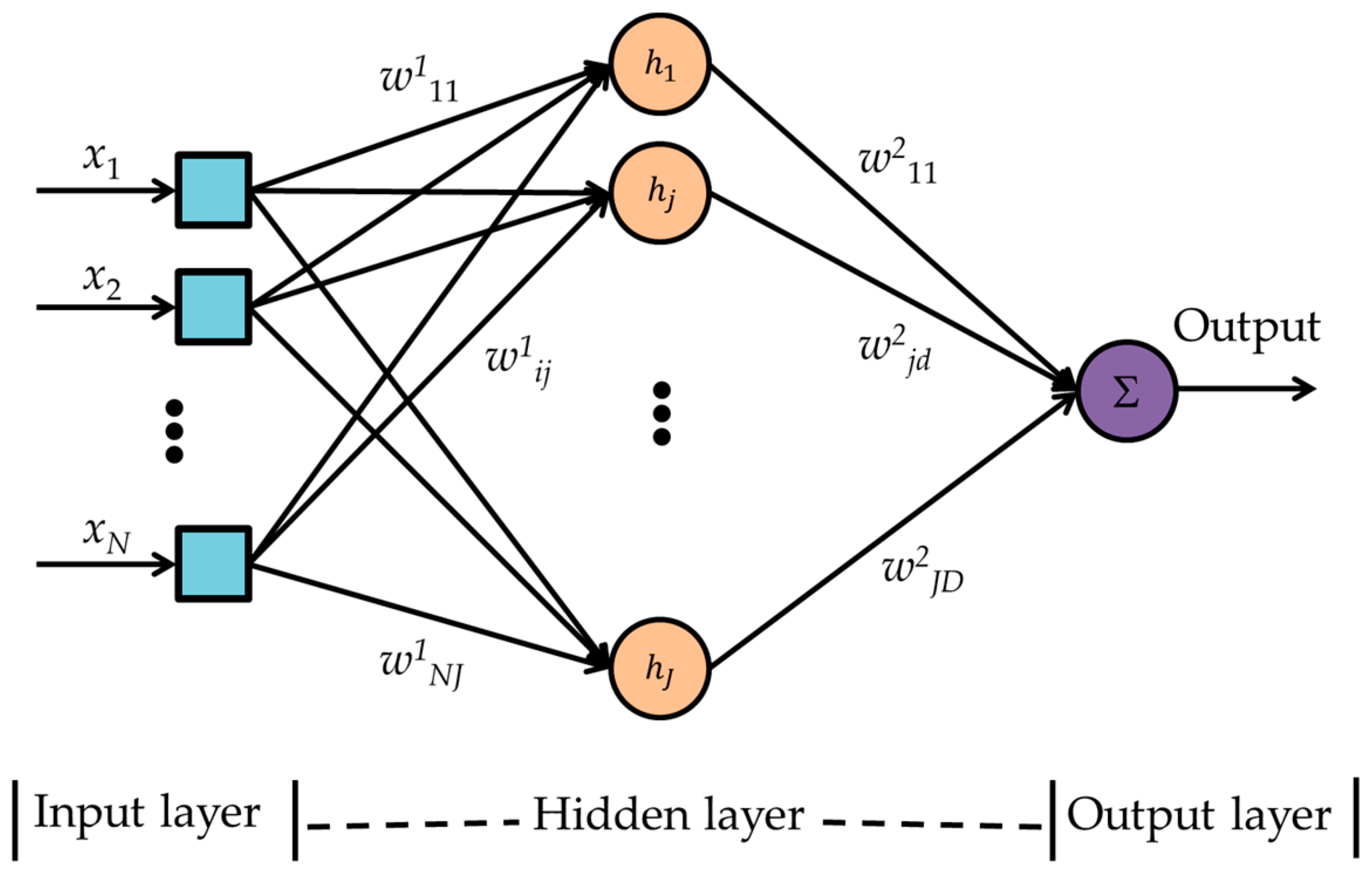
2.6.4. Multilayer Perceptron Neural Network
- Step 1.
- Initialize the weights to small positive and negative random values.
- Step 2.
- Run the network forward with each training data to get the network outputs as given in Equation (7), and calculate the errors as shown in Step 3 to Step 6.where , i is the sensor index, j is the index for the hidden layer neuron, and d is the index of the output layer neuron.
- Step 3.
- Compute the backpropagation error terms for the links to the output neuron as in Equation (8) below:
- Step 4.
- For each hidden node, calculate the backpropagation error term as in Equation (9) below,
- Step 5.
- Update the synaptic weights from a node in Layer 1 to a node (neuron) in Layer 2, as Δw1ij = −ηδ1jxl,m,n, and apply, w1ij = w1ij + Δw1ij. Update the synaptic weights from a node at Layer 2 to a node in Layer 3, as Δw2jd = −ηδ2dyj, and apply, w2jd = w2jd + Δw2jd.
- Step 6.
- Calculate MSE by Equation (10) as follows:where Nts is total number of test samples, and L is multiplied by 0.15, as 15% of the data from each class in matrix X are utilized for validation.
- Step 7.
- Repeat from Step 2 until the error limit or the number of the epoch limit is reached.
- w1ij are weights from node i of layer 1 (input layer) to node j of layer 2 (hidden layer),
- w2jd are weights from node j of layer 2 to node d of layer 3 (output layer),
- hidden layer neurons’ activation functions are sigmoid transfer functions,
- y2j is the output from node j of layer 2,
- y3l,m is the output from the output layer,
- tl,m is the corresponding target,
- η is the learning rate,
2.6.5. Generalized Regression Neural Network
- Step 1.
- Separate all the experimental samples in matrix X into 70% training samples, 15% validation samples, and 15% test samples.
- Step 2.
- Initialize the synaptic weights from the input nodes to the hidden layer neurons to the training samples, and the weights from the hidden layer neurons to the output neuron with the corresponding training targets in vector t.
- Step 3.
- Find the outputs to validation inputs xv,m by Equation (11) as:where v = 1, 2, …, 0.15L, is the validation data index in class m, σ is the spreading factor, and d2l,m = (xv,m –xl,m)T(xv,m − xl,m), [(.)T indicates transpose] is the square Euclidean distance from a training sample xi,m to a validation sample xv,m.
- Step 4.
- Calculate the MSE as:
- Step 5.
- If E > Ethreshold, then adjust σ, and continue to Step 3, otherwise stop.
2.6.6. Radial Basis Function Neural Network
- Step 1.
- Choose a value for ranging randomly from 0 to 1.
- Step 2.
- Choose random weights for the weights from the hidden layer neurons to the output neuron, i.e., w2.
- Step 3.
- Calculate the entries of the Φ matrix, where Φ is defined as below:where, x are N dimensional vectors.
- Step 4.
- Calculate the weight vector, w2 = Φ − 1t.
- Step 5.
- Calculate output, y = w2Φ.
- Step 6.
- Evaluate, mean squared error,
- Step 7.
- If E > Ethreshold, change and continue to step 4 to adjust w2, otherwise exit.
2.6.7. Minimum-Maximum-Mean Hyperspheric Classification Method
- Step 1.
- Compute the maximum, minimum, and mean matrices Q, V, and U from the whole dataset in X, where each row of the matrices Q, V and U corresponds to a class and each column corresponds to a sensor variable.
- Step 2.
- Compare each feature of a test data vector with each feature of the maximum and minimum vectors of all the classes.
- Step 3.
- Assign test data to a class for which the following two criteria satisfy: (i) each feature of the test data vector is less than or equal to the corresponding feature of the maximum vector of the corresponding class, and (ii) each feature of the test data vector is greater than or equal to each element of the minimum vector of the corresponding class. If the test data do not fall within the maximum-minimum range of any of the classes, then label it as “unclassified” or “correctly rejected”, and stop.
- Step 4.
- If any test data are within maximum-minimum limits of multiple classes, then the case of a tie occurs. To break this tie, the test data are assigned to the class whose mean vector (measured by Euclidean distance metric) is the closest to the test data vector. Once the test data are assigned to a class, exit the program.
- Step 5.
- Run the steps from 1 to 4 for the validation dataset and calculate the percentage of error by If the error then exit, otherwise add to the corresponding rows of Q and deduct from mth row of V to expand the hyperspheric classification boundary and continue to Step 1, where, η is the learning rate, and σm is the standard deviation vector of class m.
3. Results
4. Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Persaud, K.; Dodd, G. Analysis of discrimination mechanisms in the mammalian olfactory system using a model nose. Nature 1982, 299, 352–355. [Google Scholar] [CrossRef] [PubMed]
- Berna, A. Metal oxide sensors for electronic noses and their application to food analysis. Sensors 2010, 10, 3882–3910. [Google Scholar] [CrossRef] [PubMed]
- Omatu, S.; Yoshioka, M. Electronic nose for a fire detection system by neural networks. IFAC Proc. Vol. 2009, 42, 209–214. [Google Scholar] [CrossRef]
- Emmanuel, S.; Pisanelli, A.M.; Persaud, K.C. Development of an electronic nose for fire detection. Sens. Actuator B Chem. 2006, 116, 55–61. [Google Scholar] [CrossRef]
- Reimann, P.; Schutze, A. Fire detection in coal mines based on semiconductor gas sensors. Sens. Rev. 2012, 32, 47–58. [Google Scholar] [CrossRef]
- Kwan, C.; Schmera, G.; Smulko, J.M.; Kish, L.B.; Heszler, P.; Granqvist, C.G. Advanced agent identification with fluctuation-enhanced sensing. IEEE Sens. J. 2008, 8, 706–713. [Google Scholar] [CrossRef]
- Gomez, A.H.; Wang, J.; Hu, G.; Pereira, A.G. Discrimination of storage shelf-life for mandarin by electronic nose technique. LWT Food Sci. Technol. 2007, 40, 681–689. [Google Scholar] [CrossRef]
- Gomez, A.H.; Wang, J.; Hu, G.; Pereira, A.G. Monitoring storage shelf life of tomato using electronic nose technique. J. Food Eng. 2008, 85, 625–631. [Google Scholar] [CrossRef]
- Yu, H.; Wang, J. Discrimination of LongJing green-tea grade by electronic nose. Sens. Actuator B Chem. 2007, 122, 134–140. [Google Scholar] [CrossRef]
- Tang, K.T.; Chiu, S.W.; Pan, C.H.; Hsieh, H.Y.; Liang, Y.S.; Liu, S.C. Development of a portable electronic nose system for the detection and classification of fruity odors. Sensors 2010, 10, 9179–9193. [Google Scholar] [CrossRef] [PubMed]
- Guney, S.; Atasoy, A. Multiclass classification of n-butanol concentrations with k-nearest neighbor algorithm and support vector machine in an electronic nose. Sensor Actuat. B Chem. 2012, 166–167, 721–725. [Google Scholar] [CrossRef]
- Shao, X.; Li, H.; Wang, N.; Zhang, Q. Comparison of different classification methods for analyzing electronic nose data to characterize sesame oils and blends. Sensors 2015, 15, 26726–26742. [Google Scholar] [CrossRef] [PubMed]
- Guney, S.; Atasoy, A. Classification of n-butanol concentrations with k-NN algorithm and ANN in electronic nose. In Proceedings of the 2011 International Symposium on Innovations in Intelligent Systems and Applications (INISTA), Istanbul, Turkey, 15–18 June 2011; pp. 138–142. [Google Scholar]
- Khalaf, W.; Pace, C.; Gaudioso, M. Gas detection via machine learning. Int. J. Comput. Electr. Autom. Control Inf. Eng. 2008, 2, 61–65. Available online: http://waset.org/Publication/gas-detection-via-machine-learning/10785 (accessed on 5 August 2016).
- Amari, A.; Barbri, N.E.; Llobet, E.; Bari, N.E.; Correig, X.; Bouchikhi, B. Monitoring the freshness of Moroccan Sardines with a neural-network based electronic nose. Sensors 2006, 6, 1209–1223. [Google Scholar] [CrossRef]
- Sanaeifar, A.; Mohtasebi, S.S.; Varnamkhasti, M.G.; Ahmadi, H.; Lozano, J. Development and application of a new low cost electronic nose for the ripeness monitoring of banana using computational techniques (PCA, LDA, SIMCA, and SVM). Czech J. Food Sci. 2014, 32, 538–548. Available online: http://www.agriculturejournals.cz/publicFiles/138030.pdf (accessed on 30 August 2016).
- Kurup, P.U. An electronic nose for detecting hazardous chemicals and explosives. In Proceedings of the 2008 IEEE Conference on Technologies for Homeland Security, Waltham, MA, USA, 12–13 May 2008; pp. 144–149. [Google Scholar]
- Xiong, Y.; Xiao, X.; Yang, X.; Yan, D.; Zhang, C.; Zou, H.; Lin, H.; Peng, L.; Xiao, X.; Yan, Y. Quality control of Lonicera japonica stored for different months by electronic nose. J. Pharm. Biomed. 2013, 91, 68–72. [Google Scholar] [CrossRef] [PubMed]
- Evans, P.; Persaud, K.C.; McNeish, A.S.; Sneath, R.W.; Hobson, N.; Magan, N. Evaluation of a radial basis function neural network for the determination of wheat quality from electronic nose data. Sens. Actuator B Chem. 2000, 69, 348–358. [Google Scholar] [CrossRef]
- Dutta, R.; Hines, E.L.; Gardner, J.W.; Udrea, D.D.; Boilot, P. Non-destructive egg freshness determination: An electronic nose based approach. Meas. Sci. Technol. 2003, 14, 190–198. [Google Scholar] [CrossRef]
- Dutta, R.; Kashwan, K.R.; Bhuyan, M.; Hines, E.L.; Gardner, J.W. Electronic nose based tea quality standardization. Neural Netw. 2003, 16, 847–853. [Google Scholar] [CrossRef]
- Borah, S.; Hines, E.L.; Leeson, M.S.; Iliescu, D.D.; Bhuyan, M.; Gardner, J.W. Neural network based electronic nose for classification of tea aroma. Sens. Instrum. Food Qual. Saf. 2008, 2, 7–14. [Google Scholar] [CrossRef]
- Anjos, O.; Iglesias, C.; Peres, F.; Martinez, J.; Garcia, A.; Taboada, J. Neural networks applied to discriminate botanical origin of honeys. Food Chem. 2015, 175, 128–136. [Google Scholar] [CrossRef] [PubMed]
- Llobet, E.; Hines, E.L.; Gardner, J.W.; Bartlett, P.N.; Mottram, T.T. Fuzzy ARTMAP based electronic nose data analysis. Sens. Actuator B Chem. 1999, 61, 183–190. [Google Scholar] [CrossRef]
- Cooper, P.W. The hypersphere in pattern recognition. Inform. Control 1962, 5, 324–346. [Google Scholar] [CrossRef]
- Hwang, J.N.; Choi, J.J.; Oh, S.; Marks, R.J. Classification boundaries and gradients of trained multilayer perceptrons. In Proceedings of the 1990 IEEE International Symposium on Circuits and Systems, New Orleans, LA, USA, 1–3 May 1990; pp. 3256–3259. [Google Scholar]
- Tax, D.M.J.; Duin, R.P.W. Support vector domain description. Pattern Recogn. Lett. 1999, 20, 1191–1199. [Google Scholar] [CrossRef]
- Saevels, S.; Lammertyn, J.; Berna, A.Z.; Veraverbeke, E.A.; Di Natale, C.; Nicolai, B.M. An electronic nose and a mass spectrometry-based electronic nose for assessing apple quality during shelf life. Postharvest Biol. Technol. 2004, 31, 9–19. [Google Scholar] [CrossRef]
- Brezmes, J.; Llobet, E.; Vilanova, X.; Saiz, G.; Correig, X. Fruit ripeness monitoring using an electronic nose. Sens. Actuator B Chem. 2000, 69, 223–229. [Google Scholar] [CrossRef]
- Zhang, H.; Chang, M.; Wang, J.; Ye, S. Evaluation of peach quality indices using an electronic nose by MLR, QPST and BP network. Sens. Actuator B Chem. 2008, 134, 332–338. [Google Scholar] [CrossRef]
- Guohua, H.; Yuling, W.; Dandan, Y.; Wenwen, D.; Linshan, Z.; Lvye, W. Study of peach freshness predictive method based on electronic nose. Food Control 2012, 28, 25–32. [Google Scholar] [CrossRef]
- Benedetti, S.; Buratti, S.; Spinardi, A.; Mannino, S.; Mignani, I. Electronic nose as a non-destructive tool to characterise peach cultivars and to monitor their ripening stage during shelf-life. Postharvest Biol. Technol. 2008, 47, 181–188. [Google Scholar] [CrossRef]
- Li, C.; Krewer, G.W.; Ji, P.; Scherm, H.; Kays, S.J. Gas sensor array for blueberry fruit disease detection and classification. Postharvest Biol. Technol. 2010, 55, 144–149. [Google Scholar] [CrossRef]
- Simon, J.E.; Hetzroni, A.; Bordelon, B.; Miles, G.E.; CHARLES, D.J. Electronic sensing of aromatic volatiles for quality sorting of blueberries. J. Food Sci. 1996, 61, 967–970. [Google Scholar] [CrossRef]
- Brezmes, J.; Llobet, E.; Vilanova, X.; Orts, J.; Saiz, G.; Correig, X. Correlation between electronic nose signals and fruit quality indicators on shelf-life measurements with pinklady apples. Sens. Actuator B Chem. 2001, 80, 41–50. [Google Scholar] [CrossRef]
- Huerta, R.; Mosqueiro, T.; Fonollosa, J.; Rulkov, N.F.; Rodriguez-Lujan, I. Online decorrelation of humidity and temperature in chemical sensors for continuous monitoring. Chemom. Intell. Lab. Syst. 2016, 157, 169–176. [Google Scholar] [CrossRef]
- Peris, M.; Escuder-Gilabert, L. A 21st century technique for food control: Electronic noses. Anal. Chim. Acta 2009, 638, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, H.W.; Tucker, A.W. Nonlinear Programming. In Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 31 July–12 August 1950; University of California Press: Berkeley, CA, USA, 1951; pp. 481–492. [Google Scholar]



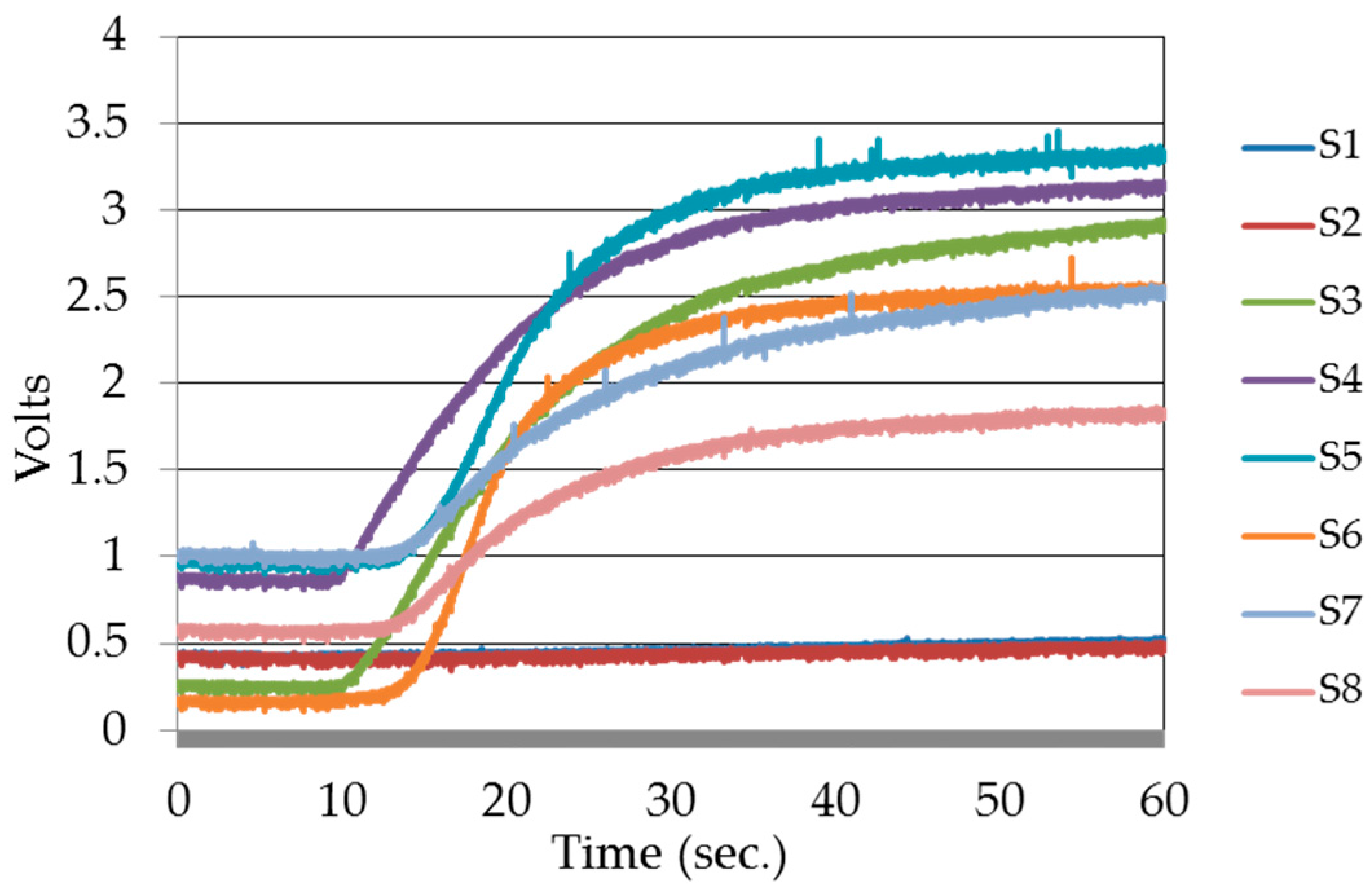

| Sensor Model | Sensor Label | Gases and VOCs | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CH2 | C2H2 | C3H8 | C4H10 | H2 | H2S | CO | C6H6 | NH3 | (CH3)2CO | C6H14 | Trimethyl Amine and Methyl Mercaptan | ||
| TGS 2612 | S1 | √ | √ | √ | √ | ||||||||
| TGS 821 | S2 | √ | √ | √ | √ | ||||||||
| TGS 822 | S3 | √ | √ | √ | √ | √ | √ | √ | |||||
| TGS 813 | S4 | √ | √ | √ | √ | √ | √ | ||||||
| TGS 2602 | S5 | √ | √ | √ | √ | ||||||||
| TGS 2603 | S6 | √ | √ | √ | √ | ||||||||
| TGS 2620 | S7 | √ | √ | √ | √ | √ | |||||||
| TGS 2610 | S8 | √ | √ | √ | √ | √ | |||||||
| Algorithm | Big O Complexity | Train Time (s) | Test Time (s) |
|---|---|---|---|
| k-NN | O(LM(N + k)) | 0.2175 | 0.2175 |
| SVM | O(NL2M2) to O(NL3M3) | 0.7452 | 0.0461 |
| GRNN | O(IGRNN) | 0.3922 | 0.0946 |
| RBFNN | O(IRBFNN) to O(I2RBFNN) | 0.9922 | 0.0230 |
| MLPNN | O(I2MLPNN) | 0.8652 | 0.0153 |
| MMM | O(M) to O(M + Ities(N + k)) | 0.1874 | 0.0047 |
| Algorithm | False Negative (Misclassification Error) | True Positive (Correct Classification) | ||
|---|---|---|---|---|
| Number of Test Samples Misclassified/Total Number of Test Samples | Percent | Number of Test Samples Correctly Classified/Total Number of Test Samples | Percent | |
| k-NN | 1/54 1 | 1.8519 | 53/54 | 98.1481 |
| SVM | 1/54 | 1.8519 | 53/54 | 98.1481 |
| GRNN | 0.5/27 1 | 1.8519 | 26.5/27 | 98.1481 |
| RBFNN | 6.5/27 | 24.0740 | 20.5/27 | 75.9260 |
| MLPNN | 8/27 | 29.6296 | 19/27 | 70.3704 |
| MMM | 0.5/27 | 1.8519 | 26.5/27 | 98.1481 |
| Dataset | k-NN | SVM | MLPNN | RBFNN | GRNN | MMM |
|---|---|---|---|---|---|---|
| Training | 0.9827 | 0.9889 | 0.9349 | 0.9503 | 0.9889 | 0.9867 |
| Validation | 0.9801 | 0.9872 | 0.9217 | 0.9314 | 0.9805 | 0.9872 |
| Test | 0.9819 | 0.9825 | 0.9258 | 0.9361 | 0.9815 | 0.9803 |
| Classification Method | Misclassification Of Irrelevant Data | True Negative (Irrelevant Data Classified to No Trained or Irrelevant Classes i.e., Correctly Rejected) | ||||
|---|---|---|---|---|---|---|
| False Positive (Irrelevant Data Classified to Trained Classes) | Irrelevant Data Classified to Unknown Classes | |||||
| Number of Samples | Percent | Number of Samples | Percent | Number of Samples | Percent | |
| k-NN | 60 | 100 | 0 | 0 | 0 | 0 |
| SVM | 60 | 100 | 0 | 0 | 0 | 0 |
| GRNN | 0 | 0 | 0 | 0 | 60 | 100 |
| RBFNN | 9 | 15 | 51 | 85 | 0 | 0 |
| MLPNN | 21 | 35 | 39 | 65 | 0 | 0 |
| MMM | 0 | 0 | 0 | 0 | 60 | 100 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, M.M.; Charoenlarpnopparut, C.; Suksompong, P.; Toochinda, P.; Taparugssanagorn, A. A False Alarm Reduction Method for a Gas Sensor Based Electronic Nose. Sensors 2017, 17, 2089. https://doi.org/10.3390/s17092089
Rahman MM, Charoenlarpnopparut C, Suksompong P, Toochinda P, Taparugssanagorn A. A False Alarm Reduction Method for a Gas Sensor Based Electronic Nose. Sensors. 2017; 17(9):2089. https://doi.org/10.3390/s17092089
Chicago/Turabian StyleRahman, Mohammad Mizanur, Chalie Charoenlarpnopparut, Prapun Suksompong, Pisanu Toochinda, and Attaphongse Taparugssanagorn. 2017. "A False Alarm Reduction Method for a Gas Sensor Based Electronic Nose" Sensors 17, no. 9: 2089. https://doi.org/10.3390/s17092089
APA StyleRahman, M. M., Charoenlarpnopparut, C., Suksompong, P., Toochinda, P., & Taparugssanagorn, A. (2017). A False Alarm Reduction Method for a Gas Sensor Based Electronic Nose. Sensors, 17(9), 2089. https://doi.org/10.3390/s17092089





