Video Synchronization With Bit-Rate Signals and Correntropy Function
Abstract
:1. Introduction
1.1. Clock Synchronization
1.2. Video Synchronization
2. Background Theory
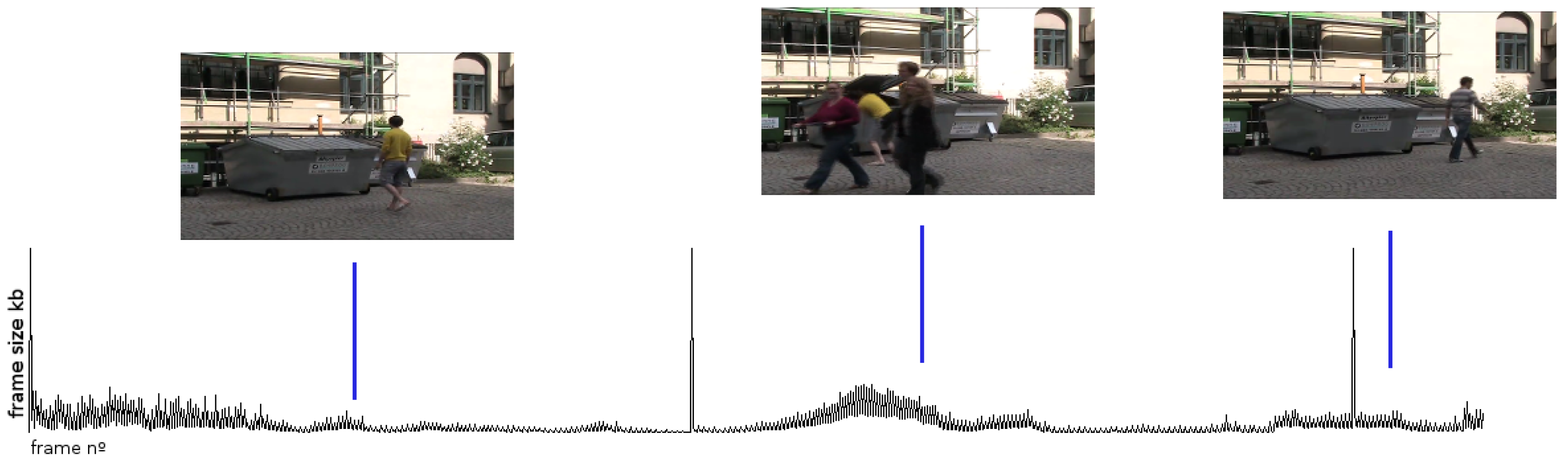
2.1. The Use of VBR Signals
Influence of Encoding Parameters
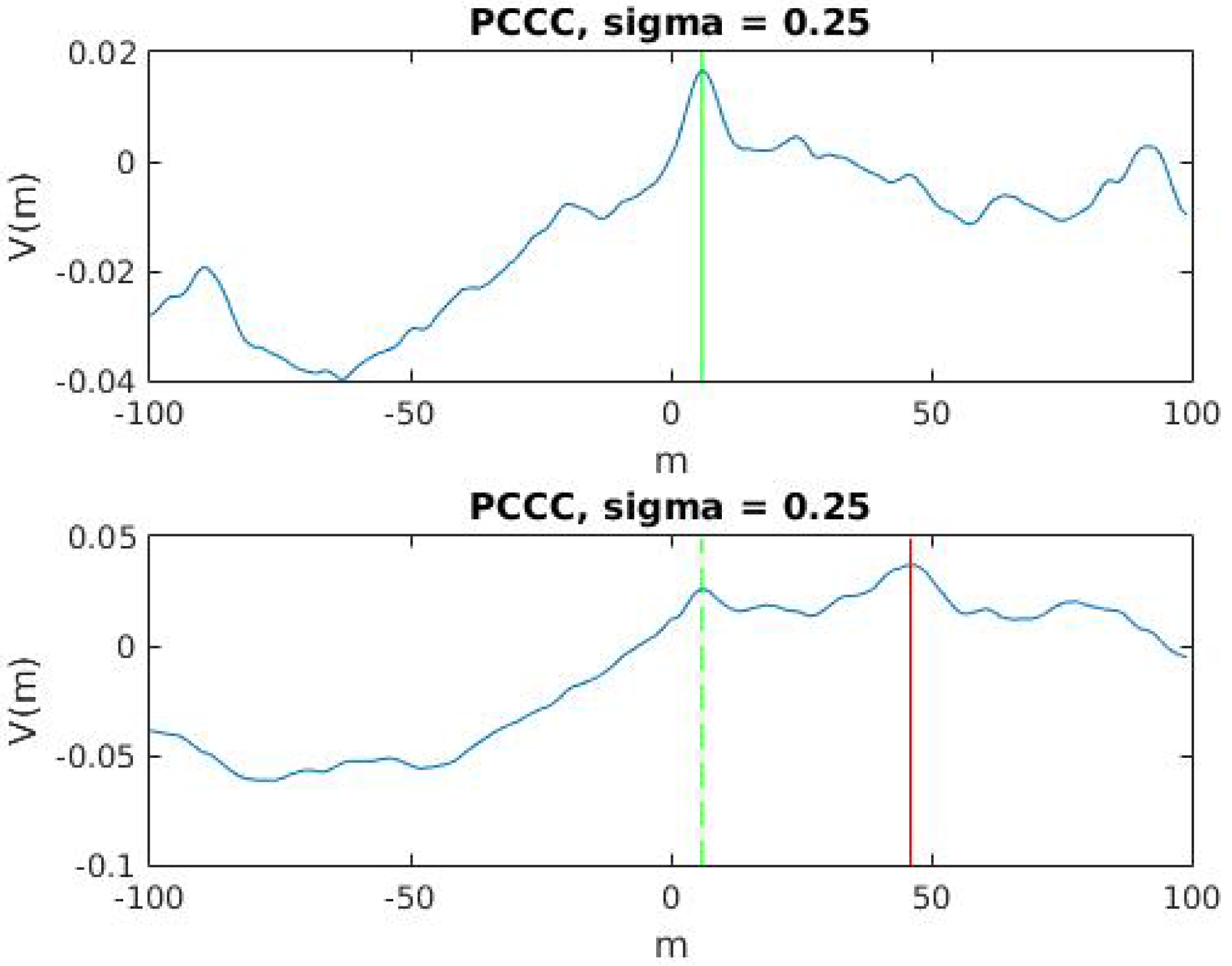
2.2. Correntropy Time-Lag Analysis
3. Proposed Method
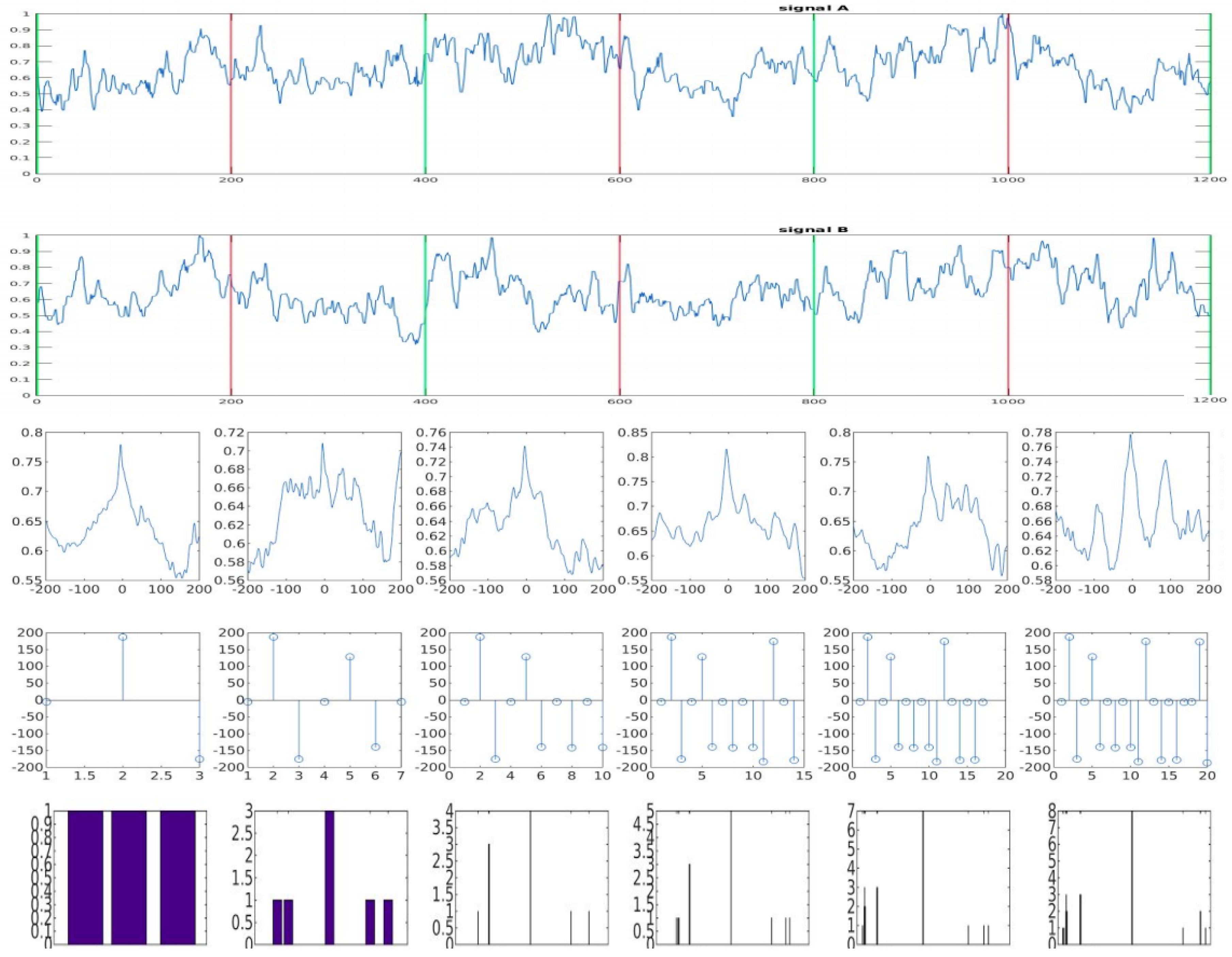
3.1. Classification Algorithm
| Algorithm 1 Classification Algorithm |
|
3.1.1. Window Size N and Overlap Ratio
3.1.2. Inlier Range
3.1.3. Confidence Level and Number of Candidates
4. Experimental Results
4.1. Window Size Ratio Heuristic
4.2. Experiment with Overlap Ratio
4.3. Experiment with Inlier Range
4.4. Experiment with Confidence Level and Number of Candidates
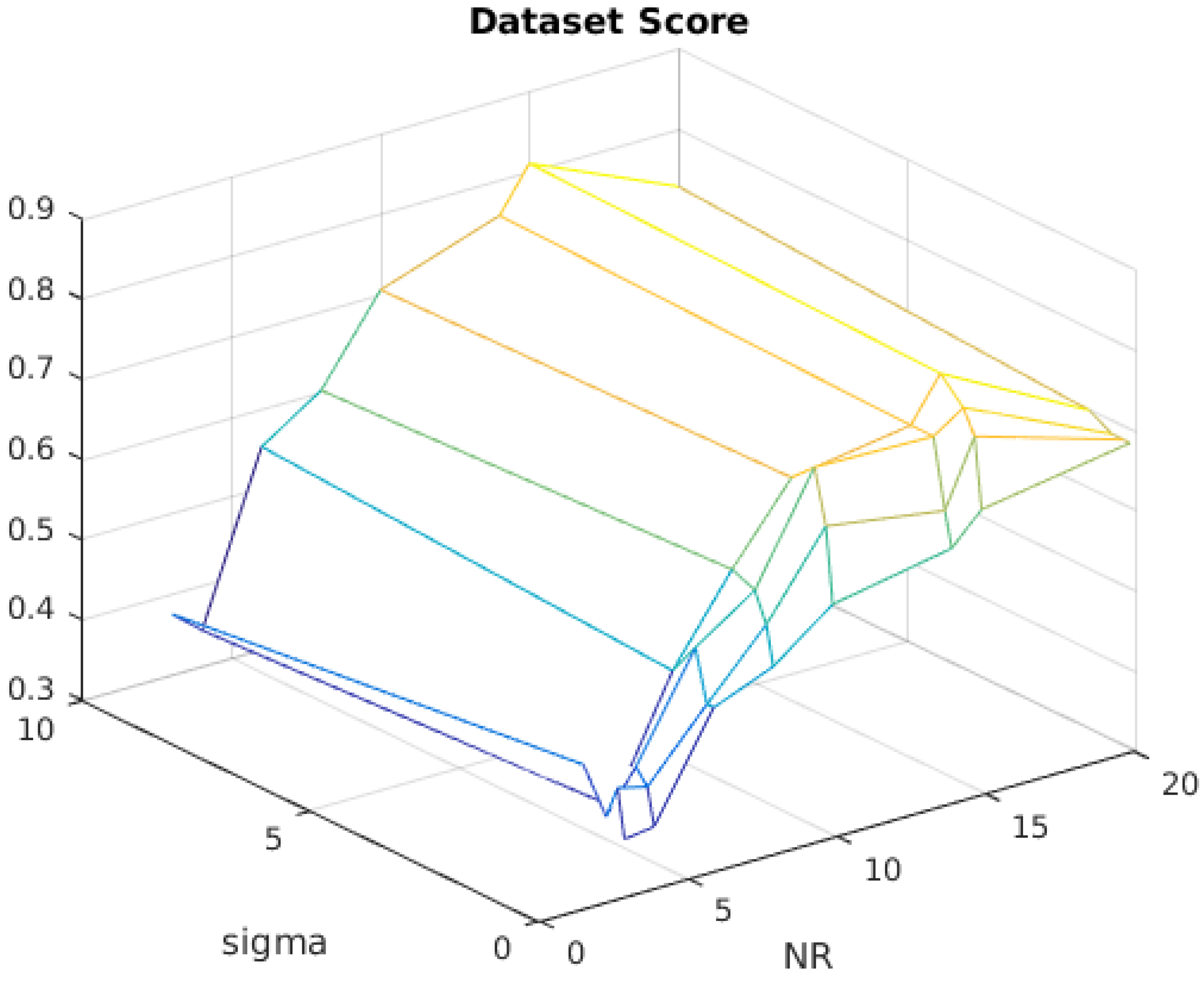
4.5. Overall Dataset Score
4.6. Detailed Comparison with State-of-the-Art Method [25]
5. Conclusions
Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Criminisi, A.; Reid, I.; Zisserman, A. Single view metrology. Int. J. Comput. Vision 2000, 40, 123–148. [Google Scholar] [CrossRef]
- Nicolaou, C. An architecture for real-time multimedia communication systems. IEEE J. Sel. Areas Commun. 1990, 8, 391–400. [Google Scholar] [CrossRef]
- Rai, P.; Tiwari, K.; Guha, P.; Mukerjee, A. Cost-effective multiple camera vision system using FireWire cameras and software synchronization. In Proceedings of the 10th International Conference on High Performance Computing (HiPC 2003), Hyderabad, India, 17–20 December 2003; pp. 17–20. [Google Scholar]
- Litos, G.; Zabulis, X.; Triantafyllidis, G. Synchronous image scquisition based on network synchronization. In Proceedings of the Conference on Computer Vision and Pattern Recognition Workshop, New York, NY, USA, 17–22 June 2006; p. 167. [Google Scholar]
- Sivrikaya, F.; Yener, B. Time synchronization in sensor networks: A survey. IEEE Netw. 2004, 18, 45–50. [Google Scholar] [CrossRef]
- Ganeriwal, S.; Kumar, R.; Srivastava, M.B. Timing-sync protocol for sensor networks. In Proceedings of the First ACM Conference on Embedded Networked Sensor System, Los Angeles, CA, USA, 5–7 November 2003; pp. 138–149. [Google Scholar]
- Maroti, M.; Maroti, M.; Kusy, B.; Kusy, B.; Simon, G.; Simon, G.; Ledeczi, A.; Ledeczi, A. The Flooding Time Synchronization Protocol; ACM Press: New York, NY, USA, 2004; pp. 39–49. [Google Scholar]
- Babaoglu, O.; Binci, T.; Montresor, A.; Jelasity, M. Firefly-inspired heartbeat synchronization in overlay networks. In Proceedings of the First IEEE International Conference on Self-Adaptive and Self-Organizing Systems (SASO), Cambridge, MA, USA, 9–11 July 2007; pp. 539–550. [Google Scholar]
- Hao, C.; Song, P.; Yang, C.; Liu, X. Testing a firefly-inspired dynchronization slgorithm in a complex wireless sensor network. Sensors 2017, 17, 544. [Google Scholar] [CrossRef] [PubMed]
- Arellano-Delgado, A.; Cruz-Hernández, C.; López Gutiérrez, R.M.; Posadas-Castillo, C. Outer synchronization of simple firefly discrete models in coupled networks. Math. Probl. Eng. 2015, 2015, 895379. [Google Scholar]
- Suedomi, Y.; Tamukoh, H.; Tanaka, M.; Matsuzaka, K.; Morie, T. Parameterized digital hardware design of pulse-coupled phase oscillator model toward spike-based computing. In Proceedings of the Neural Information Processing: 20th International Conference, ICONIP 2013, Daegu, Korea, 3–7 November 2013; Lee, M., Hirose, A., Hou, Z.G., Kil, R.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 17–24. [Google Scholar]
- Wang, J.; Xu, C.; Feng, J.; Chen, M.Z.Q.; Wang, X.; Zhao, Y. Synchronization in moving pulse-coupled oscillator networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 2544–2554. [Google Scholar] [CrossRef]
- Mangharam, R.; Rowe, A.; Rajkumar, R. FireFly: A cross-layer platform for real-time embedded wireless networks. Real Time Syst. 2007, 37, 183–231. [Google Scholar] [CrossRef]
- Hou, L.; Kagami, S.; Hashimoto, K. Article frame synchronization of high-speed vision sensors with respect to temporally encoded illumination in highly dynamic environments. Sensors 2013, 13, 4102–4121. [Google Scholar] [CrossRef] [PubMed]
- Tuytelaars, T.; Gool, L.V. Synchronizing video sequences. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Washington, DC, USA, 27 June–2 July 2004; Volume 1, pp. I-762–I-768. [Google Scholar]
- Tresadern, P.A.; Reid, I. Synchronizing image sequences of non-rigid objects. In Proceedings of the British Machine Vision Conference (BMVA), Norwich, UK, 9–11 September 2003; pp. 64.1–64.10. [Google Scholar]
- Caspi, Y.; Simakov, D.; Irani, M. Feature-based sequence-to-sequence matching. Int. J. Comput. Vision 2006, 68, 53–64. [Google Scholar] [CrossRef]
- Stein, G.P. Tracking from multiple view points: Self-calibration of space and time. In Proceedings of the 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (Cat. No PR00149), Fort Collins, CO, USA, 23–25 June 1999; Volume 1, p. 527. [Google Scholar]
- Whitehead, A.; Laganiere, R.; Bose, P. Temporal synchronization of video sequences in theory and in practice. In Proceedings of the Seventh IEEE Workshops on Application of Computer Vision, Breckenridge, CO, USA, 5–7 January 2005; Volume 2, pp. 132–137. [Google Scholar]
- Laptev, I. On space-time interest points. Int. J. Comput. Vision 2005, 64, 107–123. [Google Scholar] [CrossRef]
- Yan, J.; Pollefeys, M. Video synchronization via space-time interest point distribution. In Proceedings of the Advanced Concepts for Intelligent Vision Systems, Brussels, Belgium, 31 August–3 September 2004. [Google Scholar]
- Ushizaki, M.; Okatani, T.; Deguchi, K. Video synchronization based on co-occurrence of appearance changes in video sequences. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR 2006), Hong Kong, China, 20–24 August 2006; Volume 3, pp. 71–74. [Google Scholar]
- Duan, L.; Chandrasekhar, V.; Wang, S.; Lou, Y.; Lin, J.; Bai, Y.; Huang, T.; Kot, A.C.; Gao, W. Compact Descriptors for Video Analysis: The Emerging MPEG Standard. arXiv, 2017; arXiv:1704.08141. [Google Scholar]
- Schroth, G.; Schweiger, F.; Eichhorn, M.; Steinbach, E.; Fahrmair, M.; Kellerer, W. Video synchronization using bit rate profiles. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 1549–1552. [Google Scholar]
- Al-Nuaimi, A.; Cizmeci, B.; Schweiger, F.; Katz, R.; Taifour, S.; Steinbach, E.; Fahrmair, M. ConCor+: Robust and confident video synchronization using consensus-based Cross-correlation. In Proceedings of the 2012 IEEE 14th International Workshop on Multimedia Signal Processing (MMSP), Banff, AB, Canada, 17–19 September 2012; pp. 83–88. [Google Scholar]
- Principe, J.C. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives (Information Science and Statistics); Springer: New York, NY, USA, 2010. [Google Scholar]
- Schweiger, F. Spatio-Temporal Analysis of Multiview Video. Ph.D. Thesis, Technical University Munich, Munich, Germany, 2013. [Google Scholar]
- Yu, L.; Qiu, T.S.; Song, A.M. A Time delay estimation algorithm based on the weighted correntropy spectral density. Circuits Syst. Signal Process. 2016, 36, 1115–1128. [Google Scholar] [CrossRef]
- Linhares, L.L.S.; Fontes, A.I.R.; Martins, A.M.; Araújo, F.M.U.; Silveira, L.F.Q. Fuzzy wavelet neural network using a correntropy criterion for nonlinear dystem identification. Math. Probl. Eng. 2015, 2015, 678965. [Google Scholar]
- Ainara, G.; Karlen, W.; Ansermino, J.M.; Dumont, G.A. Estimating respiratory and heart rates from the correntropy spectral density of the photoplethysmogram. PLoS ONE 2014, 9, e86427. [Google Scholar]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Chapman & Hall: London, UK, 1986. [Google Scholar]

| N.R. | 3 | 4 | 6 | 8 | 10 | 14 | 15 | 20 |
| No. of Combinations | 117 | 110 | 94 | 83 | 75 | 70 | 69 | 63 |
| O.R. | N.R. = 4 | N.R. = 10 | N.R. = 15 |
|---|---|---|---|
| 1 | 31% | 56% | 62% |
| 2 | 34% | 68% | 72% |
| 3 | 43% | 68% | 75% |
| 4 | 44% | 74% | 81% |
| 5 | 42% | 72% | 79% |
| 6 | 45% | 77% | 79% |
| 7 | 45% | 73% | 79% |
| Inlier Range | Min | Avg | Max |
|---|---|---|---|
| 2 | 37% | 60% | 82% |
| 3 | 36% | 60% | 82% |
| 4 | 34% | 59% | 81% |
| 5 | 33% | 56% | 78% |
| N.C. | C.L. | Synchronization Score |
|---|---|---|
| 1 | 85% | 79% |
| 2 | 46% | 81% |
| 3 | 45% | 81% |
| 4 | 44% | 76% |
| Function | Min | Avg | Max |
|---|---|---|---|
| Correntropy | 34% | 59% | 81% |
| Correlation | 14% | 33% | 62% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pereira, I.; Silveira, L.F.; Gonçalves, L. Video Synchronization With Bit-Rate Signals and Correntropy Function. Sensors 2017, 17, 2021. https://doi.org/10.3390/s17092021
Pereira I, Silveira LF, Gonçalves L. Video Synchronization With Bit-Rate Signals and Correntropy Function. Sensors. 2017; 17(9):2021. https://doi.org/10.3390/s17092021
Chicago/Turabian StylePereira, Igor, Luiz F. Silveira, and Luiz Gonçalves. 2017. "Video Synchronization With Bit-Rate Signals and Correntropy Function" Sensors 17, no. 9: 2021. https://doi.org/10.3390/s17092021
APA StylePereira, I., Silveira, L. F., & Gonçalves, L. (2017). Video Synchronization With Bit-Rate Signals and Correntropy Function. Sensors, 17(9), 2021. https://doi.org/10.3390/s17092021






