Remote Marker-Based Tracking for UAV Landing Using Visible-Light Camera Sensor
Abstract
1. Introduction
2. Related Works
- (1)
- Our algorithm can track and detect a marker not only when the marker is visible in the morning, afternoon, and evening, but also when the marker is hardly visible at nighttime.
- (2)
- Using images captured from a single visible-light camera with an onboard system that has low processing power, our algorithm outperforms previous state-of-the-art object trackers in terms of both accuracy and processing speed.
- (3)
- Our marker design is simple and unique compared to those used by other marker-based tracking algorithm. Our database was self-constructed using a visible-light camera mounted on the DJI Phantom 4 drone [36] at various time during the day, and this database was made public so that other researchers can compare and evaluate its performance.
3. Proposed Method
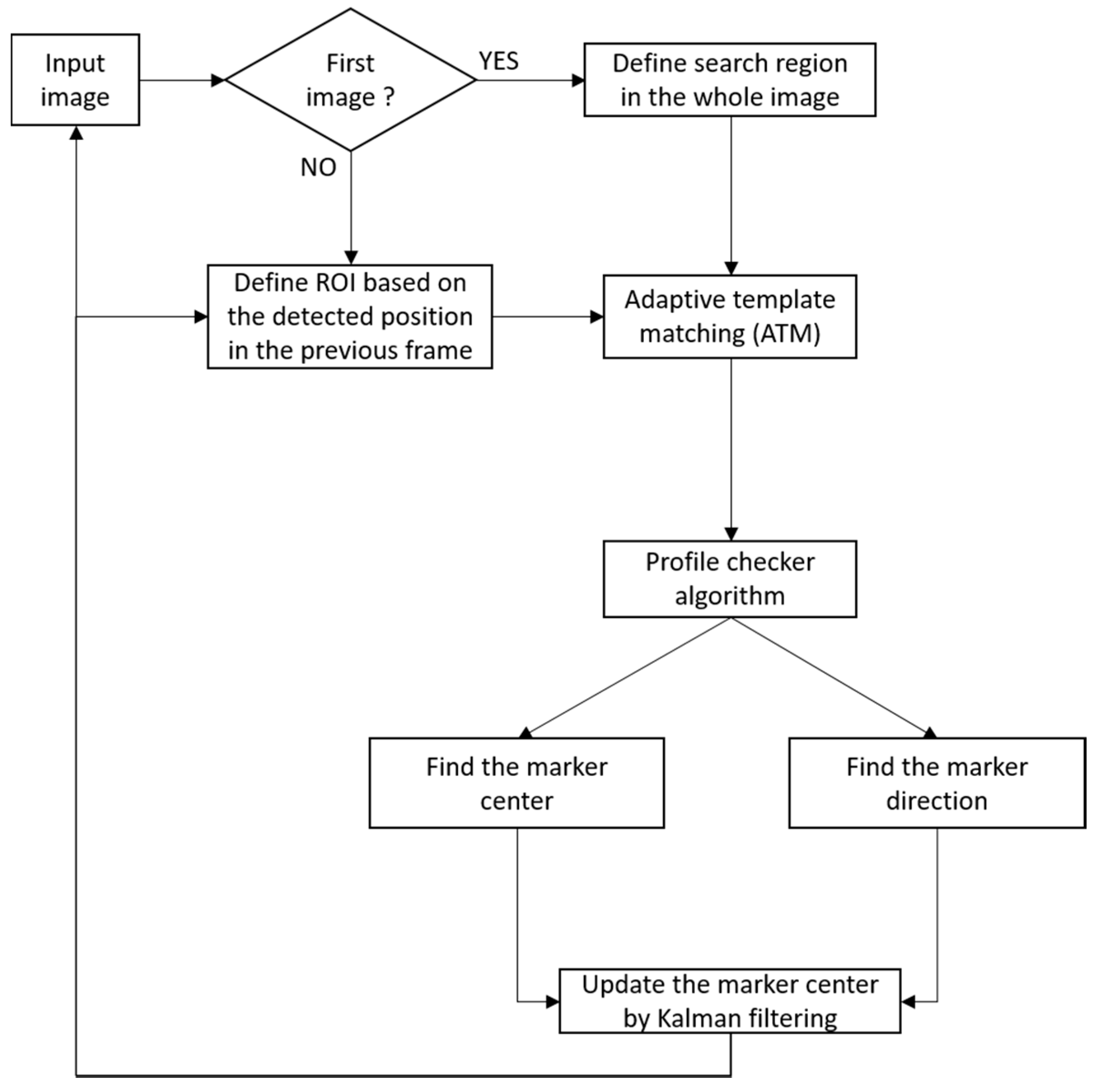
3.1. Overview of the Proposed Method
3.2. Marker-Based Tracking Algorithm (Day Time)
3.2.1. Proposed Marker Design
3.2.2. Marker-Based Tracking Algorithm (During Day Time)
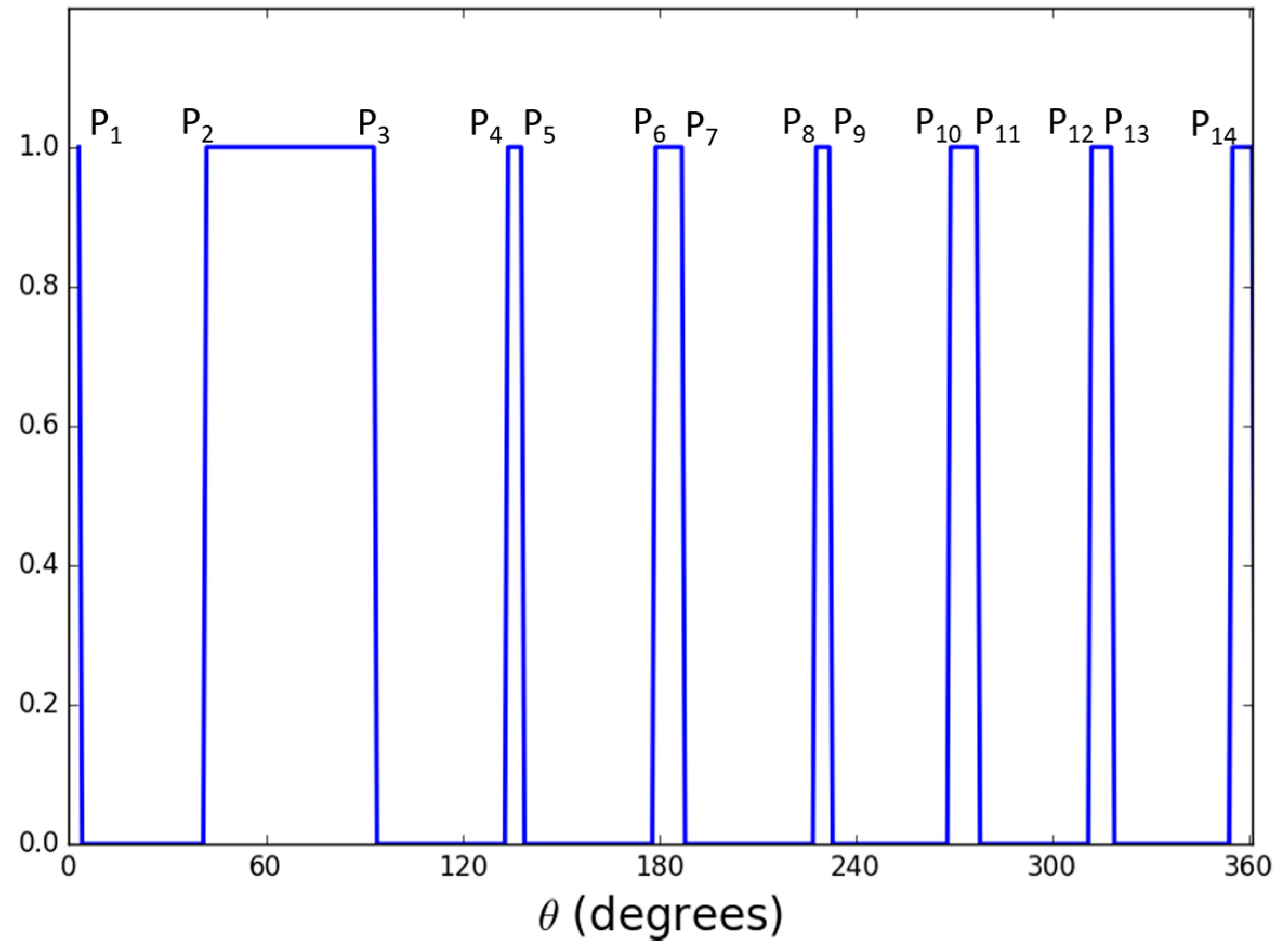
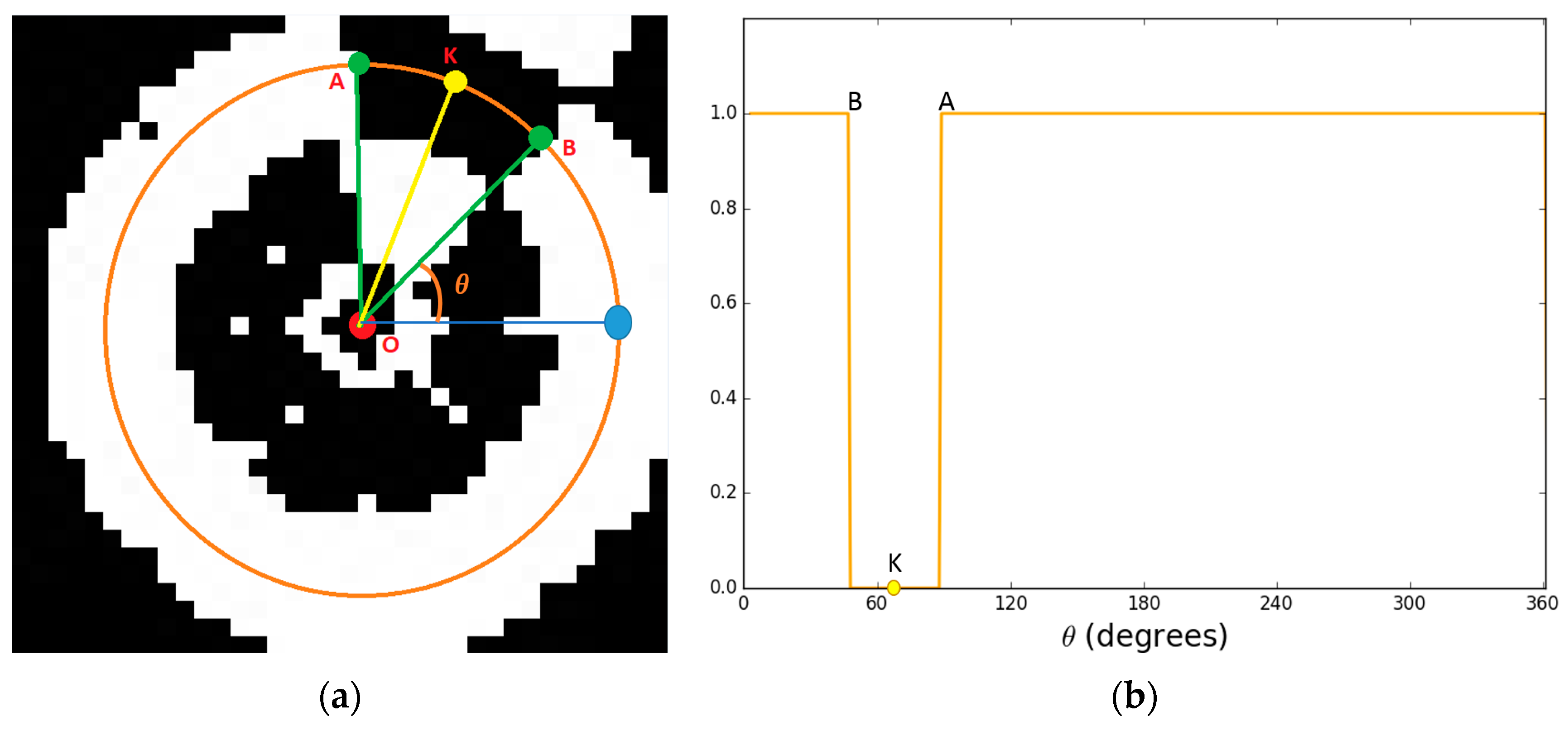
- Step 1: Extract all pixel value in the circle profile with radius r in a vector: V = {v1, v2, …, v360}
- Step 2: Find threshold Th:
- Step 3: Obtain the binarized vector V′ = {vi′}i = 1, …, 360 where
- Step 4: Count the number of values (C) that are changed compared with previous value (from 0 to 1 or 1 to 0) and create C sub-profiles SP = {}k= 1, …, C, where are the index of the starting point, index of the ending point, code (0 for black, 1 for white), and the width of the sub-profile (distance between the starting and ending point of the sub-profile), respectively
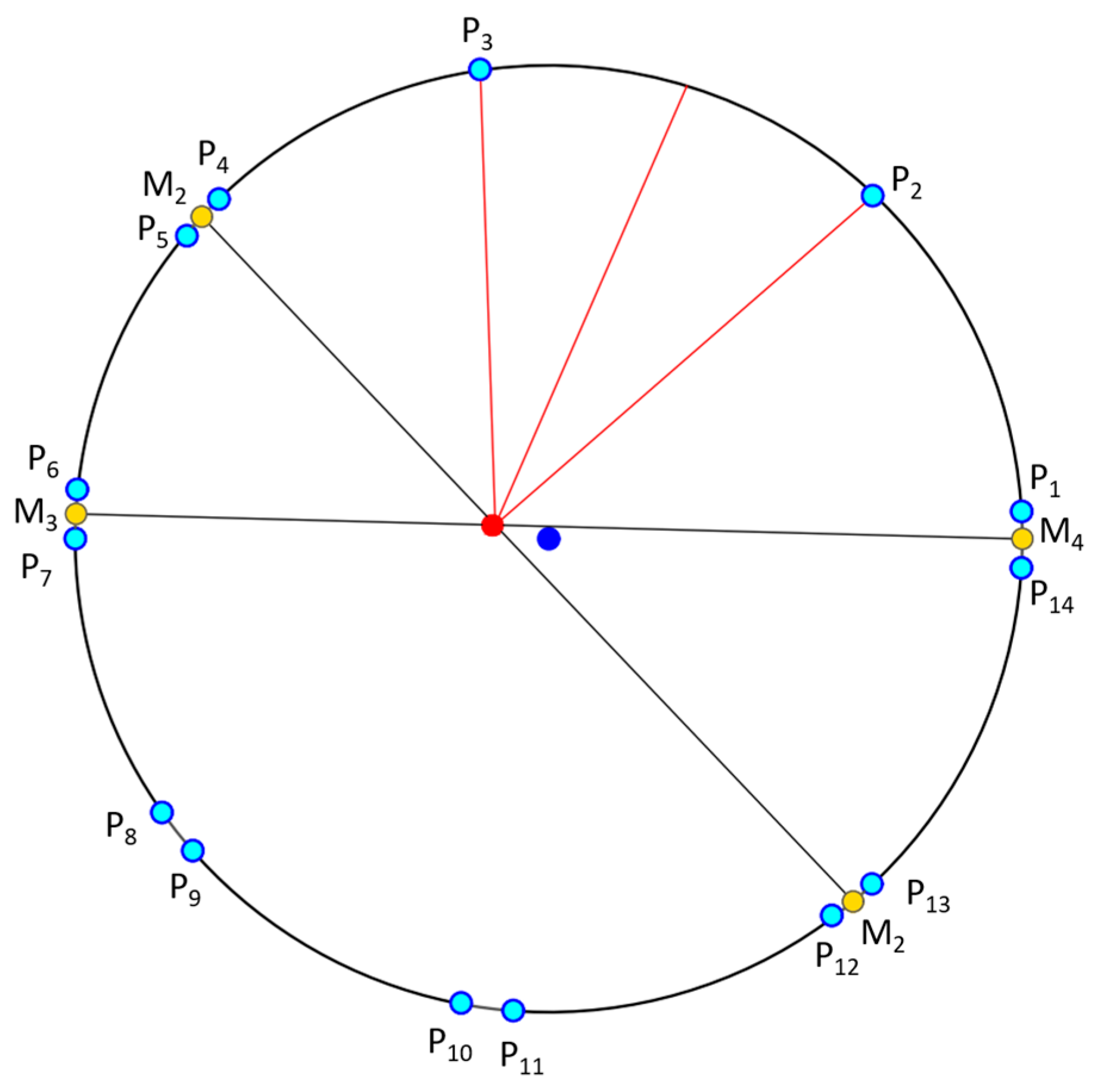
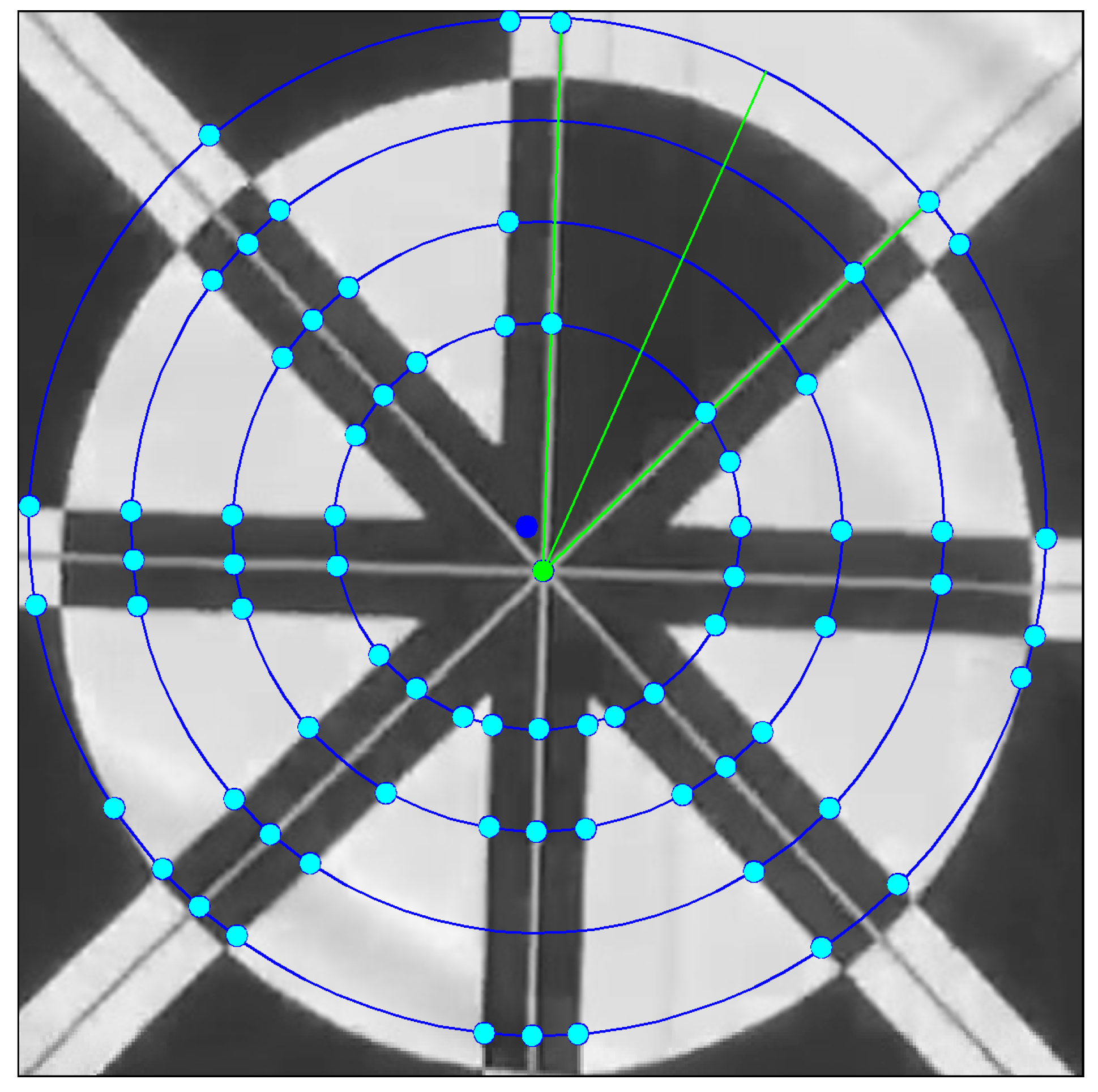
- Step 5: If C is equal to 14, the sub-profile that has is selected. Then, from the four adjacent sub-profiles of this selected sub-profile, two lines are detected (shown in Figure 6), and the intersect point of these two lines is determined as the marker center by the profile checker algorithm. Then, the direction is estimated based on the average position (between the starting and ending index of the selected sub-profile) and this detected center.
- Step 6: If C is not equal to 14, we increase the radius of the circle profile of (where , and w is the width of template) as shown in Figure 7, and steps 1~5 are repeated until (or C is equal to 14). If , we use the detection result obtained by ATM as the marker center.
3.2.3. Updating the Detected Center of Marker by Kalman Filtering
3.3. Marker-Based Tracking Algorithm (Night Time)
4. Experimental Results
4.1. Experimental Platform and Environments
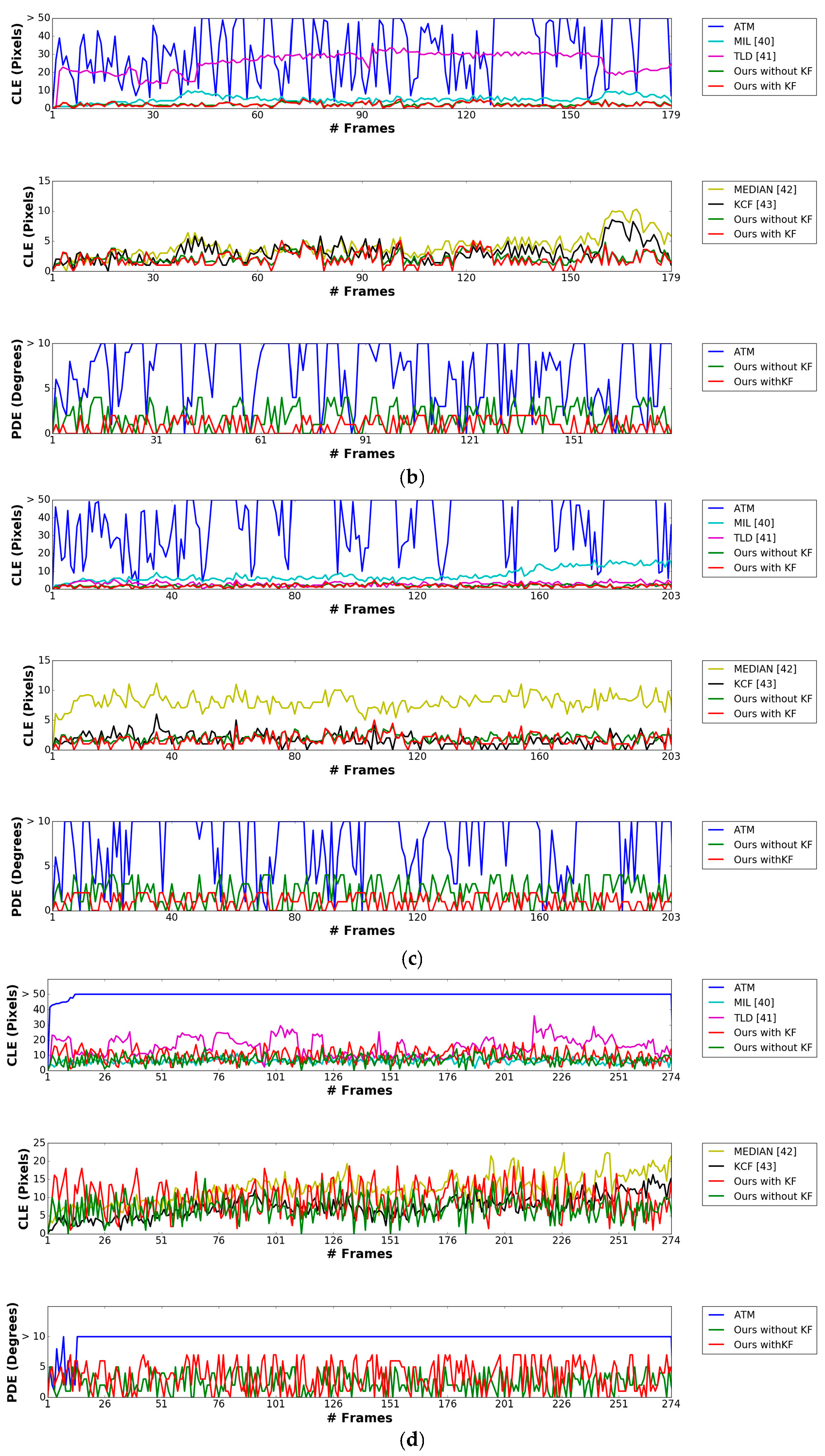
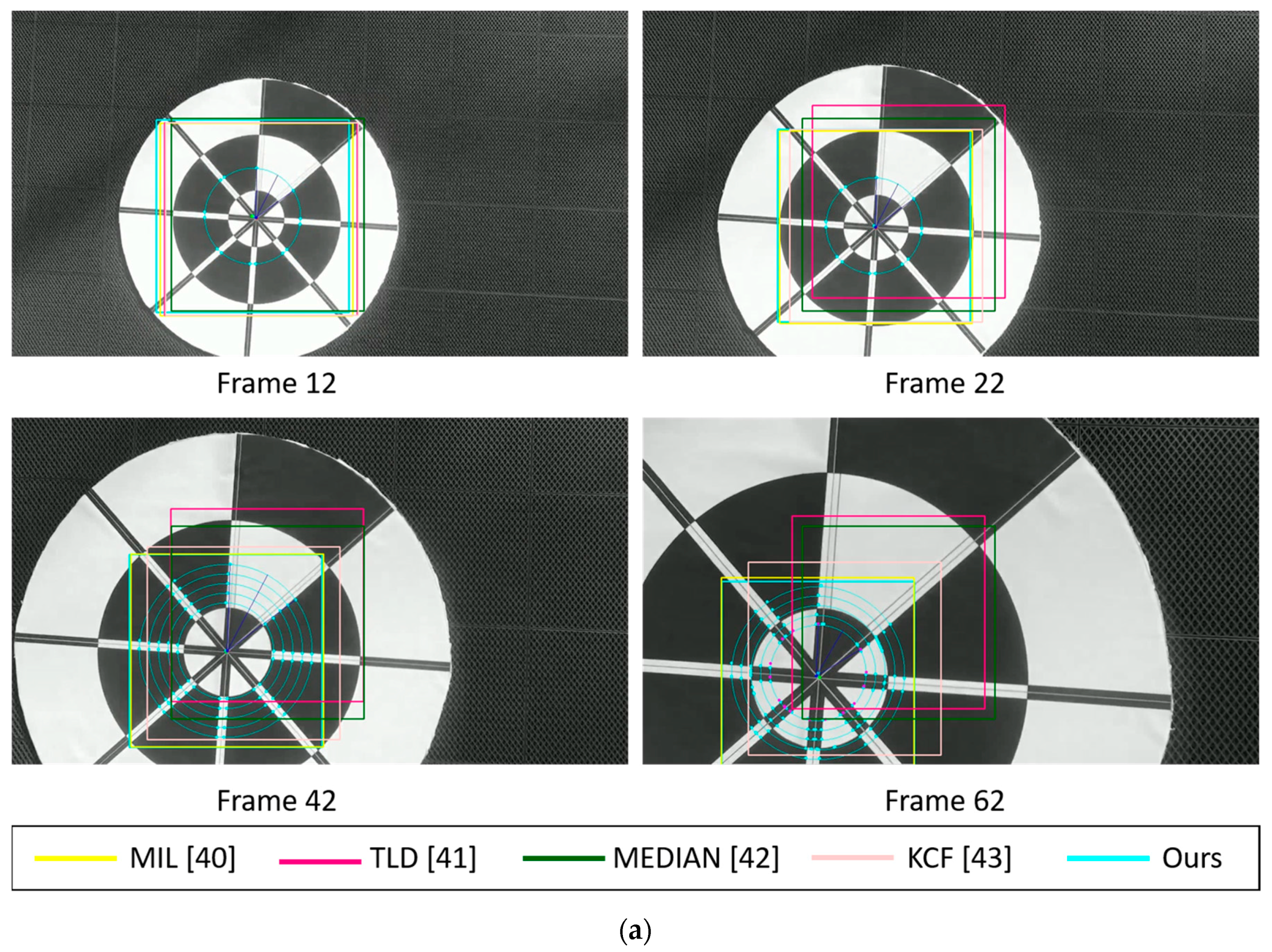
4.2. Experimental Results
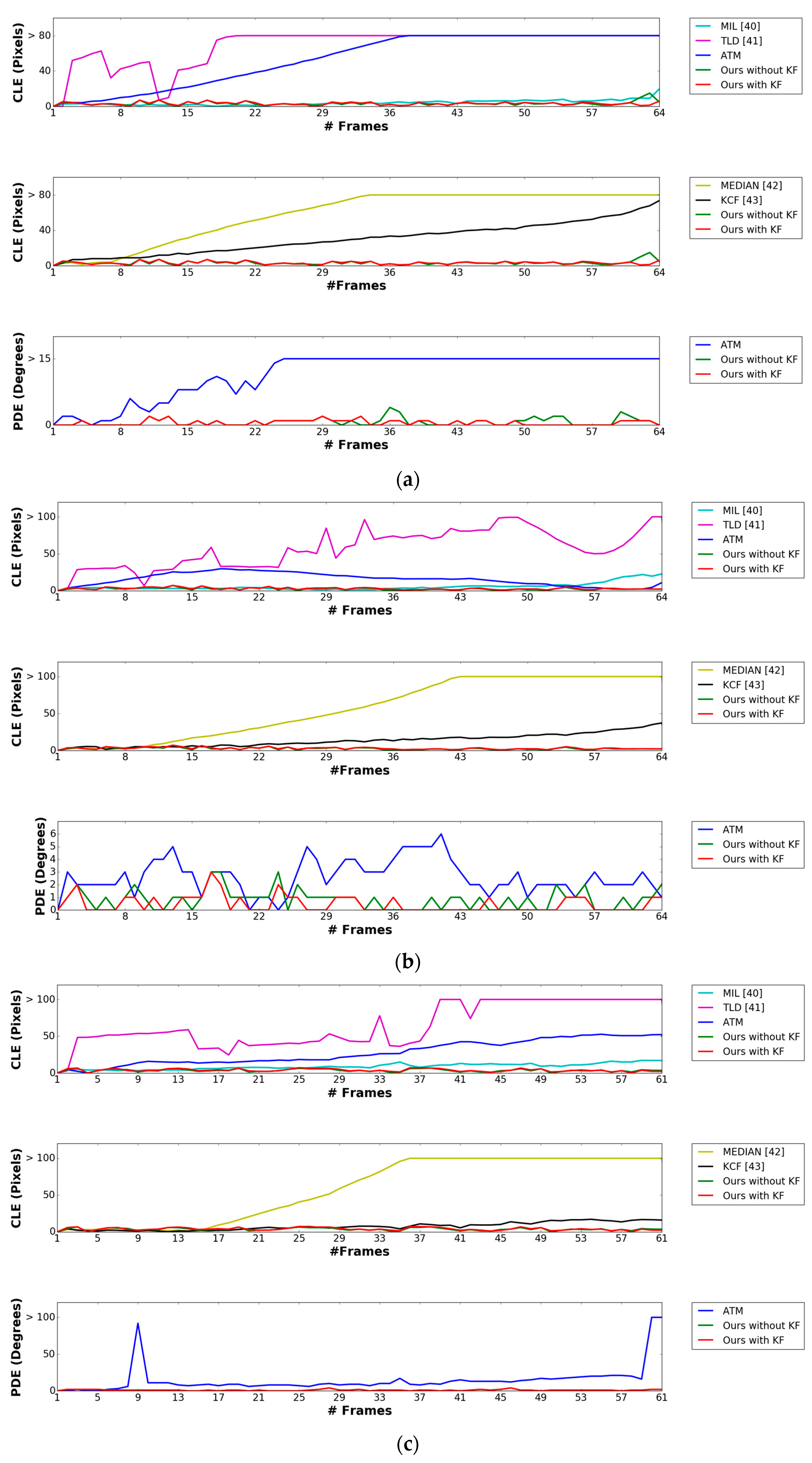
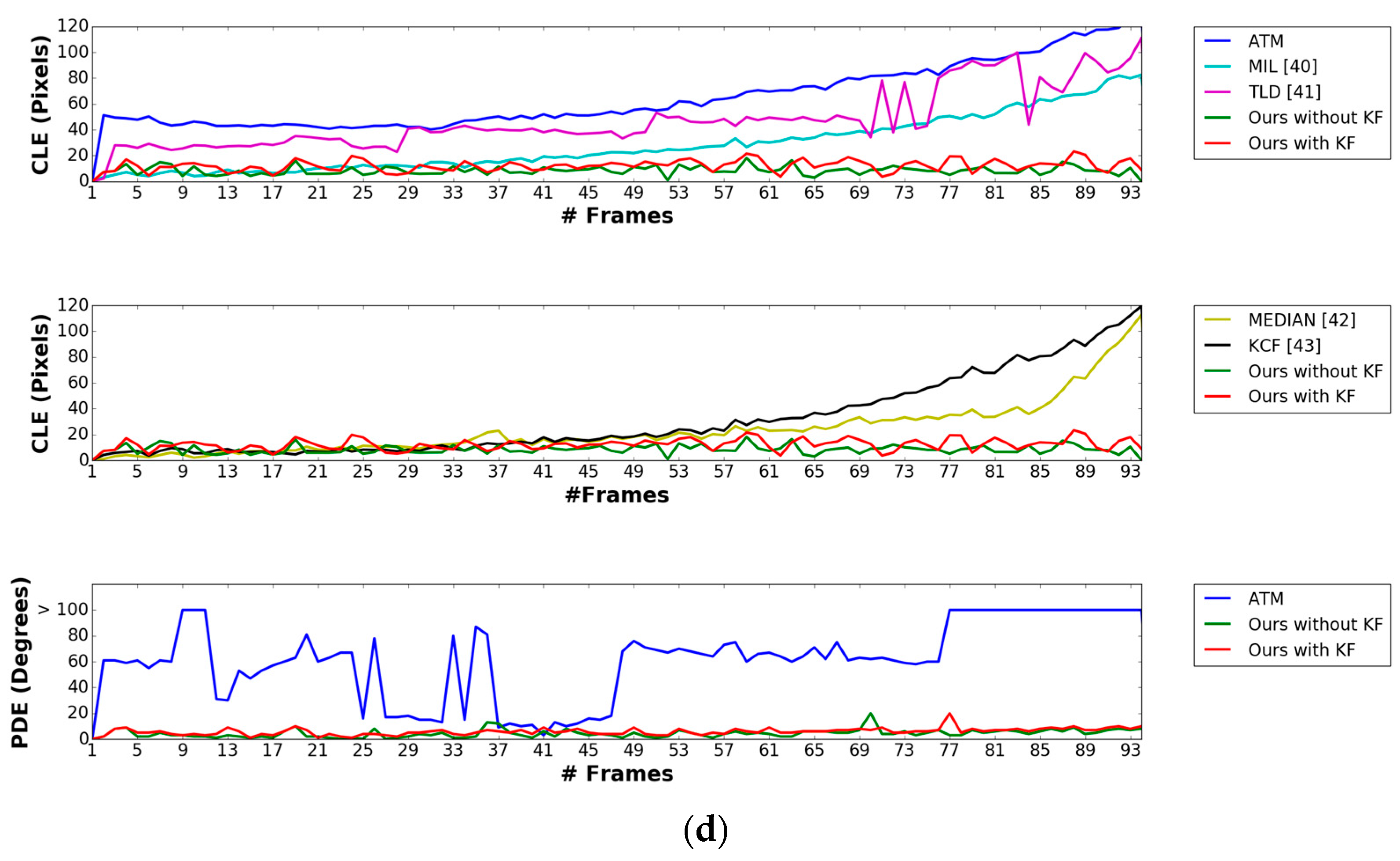
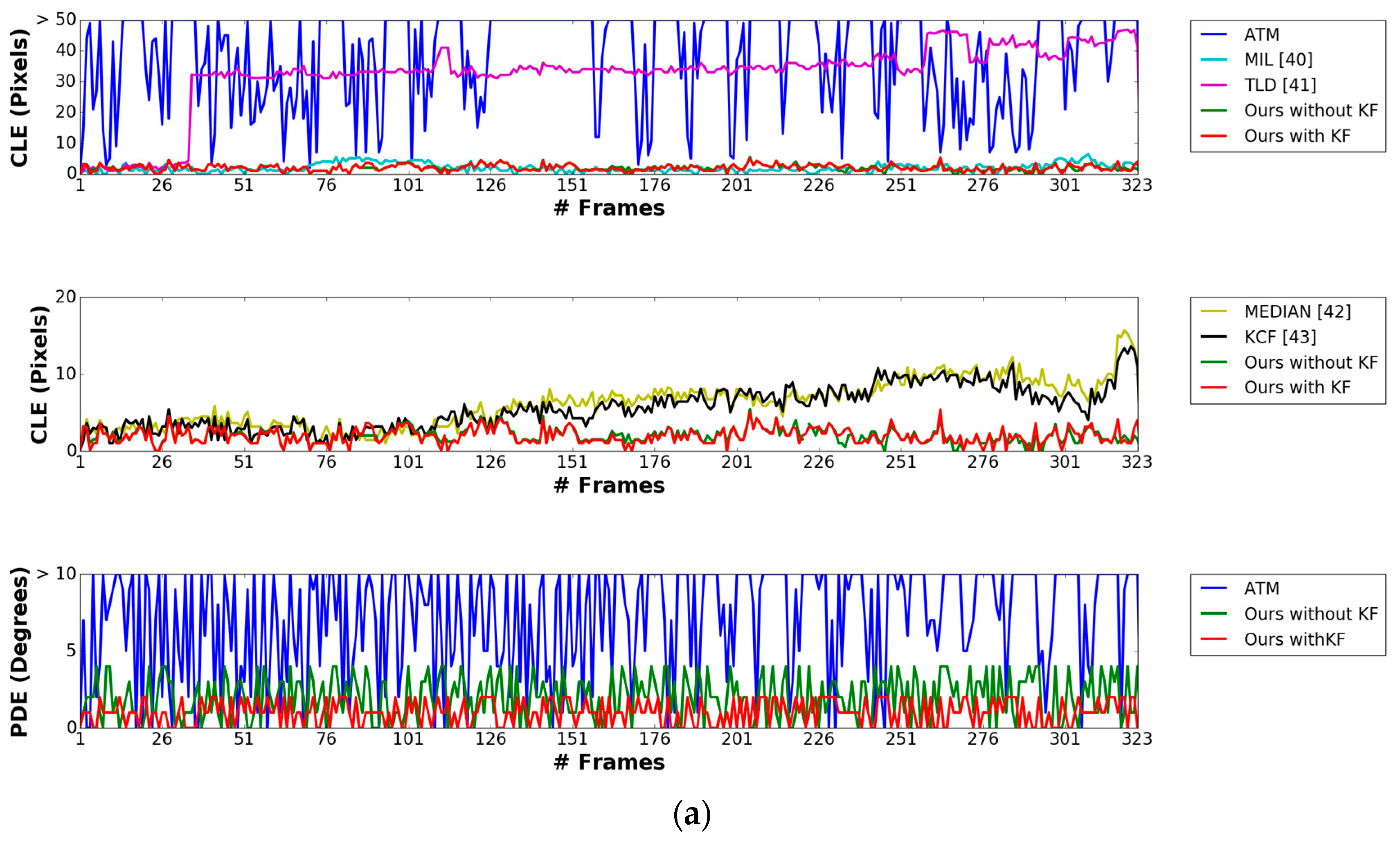
4.2.1. Marker Detection Accuracy and Processing Time
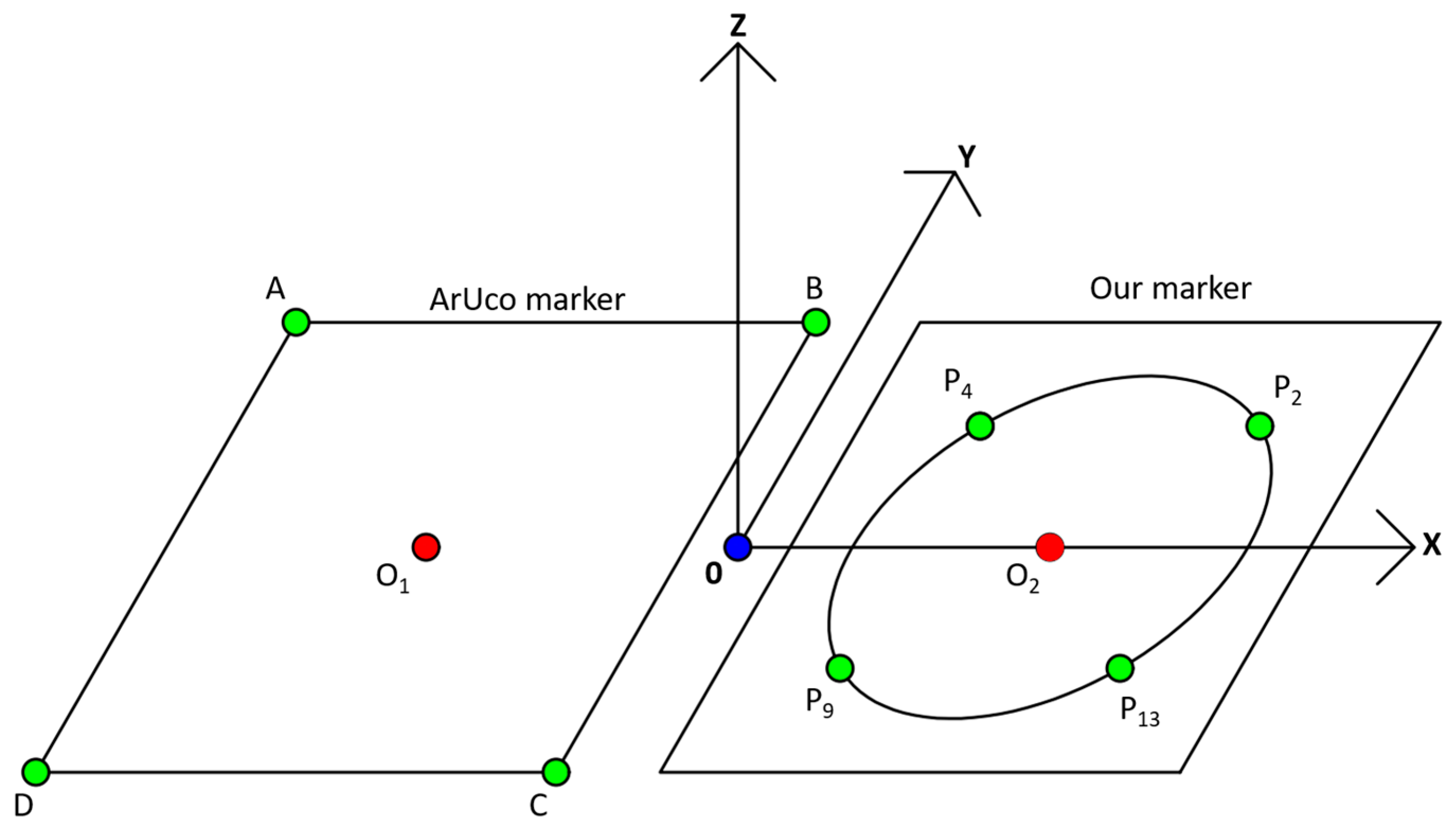
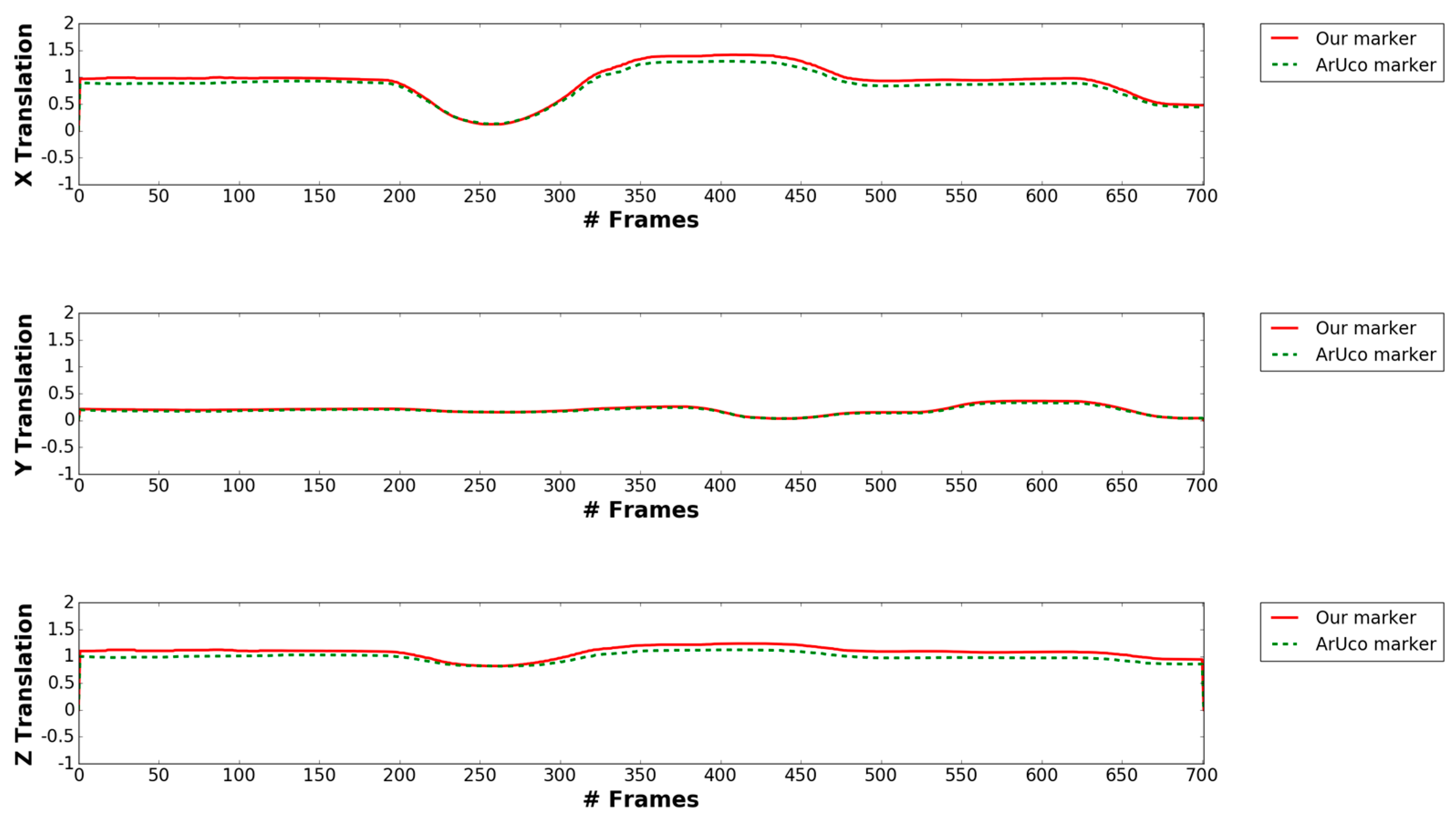
4.2.2. Pose Estimation Experiments
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Commercial UAV Market Analysis by Product (Fixed Wing, Rotary Blade, Nano, Hybrid), by Application (Agriculture, Energy, Government, Media & Entertainment) and Segment Forecasts to 2022. Available online: http://www.grandviewresearch.com/industry-analysis/commercial-uav-market (accessed on 17 April 2017).
- Austin, R. Unmanned Aircraft Systems: Uavs Design, Development and Deployment; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 273–279. [Google Scholar]
- Ham, Y.; Han, K.K.; Lin, J.J.; Golparvar-Fard, M. Visual monitoring of civil infrastructure systems via camera-equipped unmanned aerial vehicles (UAVs): A review of related works. Vis. Eng. 2016, 4, 1–8. [Google Scholar] [CrossRef]
- Chan, B.; Guan, H.; Jo, J.; Blumenstein, M. Towards UAV-based bridge inspection systems: A review and an application perspective. Struct. Monit. Maint. 2015, 2, 283–300. [Google Scholar] [CrossRef]
- Eschmann, C.; Kuo, C.M.; Kuo, C.H.; Boller, C. High-resolution multisensor infrastructure inspection with unmanned aircraft systems. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 2, 125–129. [Google Scholar]
- Máthé, K.; Buşoniu, L. Vision and control for UAVs: A survey of general methods and of inexpensive platforms for infrastructure inspection. Sensors 2015, 15, 14887–14916. [Google Scholar] [CrossRef] [PubMed]
- Bryson, M.; Sukkarieh, S. Inertial sensor–based simultaneous localization and mapping for UAVs. In Handbook of Unmanned Aerial Vehicles; Valavanis, K.P., Vachtsevanos, G.J., Eds.; Springer: Dordrecht, The Netherlands, 2015; pp. 401–431. [Google Scholar]
- Feldman, M.S. Simultaneous Localization and Mapping Implementations for Navigation of an Autonomous Robot. Bachelor’s Thesis, Department of Electrical and Computer Engineering, University of Florida, Gainesville, FL, USA, 2014. [Google Scholar]
- Dehghan, S.M.M.; Moradi, H. SLAM–inspired simultaneous localization of UAV and RF sources with unknown transmitted power. Trans. Inst. Meas. Control 2016, 38, 895–907. [Google Scholar] [CrossRef]
- Cruz, G.C.S.; Encarnação, P.M.M. Obstacle avoidance for unmanned aerial vehicles. J. Intell. Robot. Syst. 2012, 65, 203–217. [Google Scholar] [CrossRef]
- Gageik, N.; Benz, P.; Montenegro, S. Obstacle detection and collision avoidance for a UAV with complementary low–cost sensors. IEEE Access. 2015, 3, 599–609. [Google Scholar] [CrossRef]
- Call, B.R. Obstacle Avoidance for Small Unmanned Air Vehicles. Master’s Thesis, Brigham Young University, Provo, UT, USA, December 2006. [Google Scholar]
- Barry, A.J. High–Speed Autonomous Obstacle Avoidance with Pushbroom Stereo. Ph.D. Thesis, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, USA, February 2016. [Google Scholar]
- Gottlieb, Y.; Shima, T. UAVs task and motion planning in the presence of obstacles and prioritized targets. Sensors 2015, 15, 29734–29764. [Google Scholar] [CrossRef] [PubMed]
- Partsinevelos, P.; Agadakos, I.; Athanasiou, V.; Papaefstathiou, I.; Mertikas, S.; Kyritsis, S.; Tripolitsiotis, A.; Zervos, P. On–board computational efficiency in real time UAV embedded terrain reconstruction. In Proceedings of the the European Geosciences Union General Assembly, Vienna, Austria, 27 April–2 May 2014. [Google Scholar]
- Bulatov, D.; Solbrig, P.; Gross, H.; Wernerus, P.; Repasi, E.; Heipke, C. Context–based urban terrain reconstruction from UAV–videos for geoinformation applications. Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2011, 22, 75–80. [Google Scholar] [CrossRef]
- Witayangkurn, A.; Nagai, M.; Honda, K.; Dailey, M.; Shibasaki, R. Real–time monitoring system using unmanned aerial vehicle integrated with sensor observation service. Int. Arch. Photogramm. Remote Sens. Spat. Inform. Sci. 2011, 22, 1–6. [Google Scholar] [CrossRef]
- Nagai, M.; Witayangkurn, A.; Honda, K.; Shibasaki, R. UAV–based sensor web monitoring system. Int. J. Navig. Observ. 2012, 2012, 1–7. [Google Scholar] [CrossRef]
- Baiocchi, V.; Dominici, D.; Milone, M.V.; Mormile, M. Development of a software to plan UAVs stereoscopic flight: An application on post earthquake scenario in L’Aquila city. Lect. Notes Comput. Sci. 2013, 7974, 150–165. [Google Scholar]
- Yeong, S.P.; King, L.M.; Dol, S.S. A review on marine search and rescue operations using unmanned aerial vehicles. Int. J. Mech. Aerosp. Ind. Mech. Manuf. Eng. 2015, 9, 396–399. [Google Scholar]
- Amazon Prime Air. Available online: https://www.amazon.com/Amazon–Prime–Air/b?node=8037720011 (accessed on 17 April 2017).
- Martínez, C.; Campoy, P.; Mondragón, I.; Olivares–Méndez, M.A. Trinocular ground system to control UAVs. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 3361–3367. [Google Scholar]
- Kong, W.; Zhang, D.; Wang, X.; Xian, Z.; Zhang, J. Autonomous landing of an UAV with a ground–based actuated infrared stereo vision system. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 2963–2970. [Google Scholar]
- Yang, T.; Li, G.; Li, J.; Zhang, Y.; Zhang, X.; Zhang, Z.; Li, Z. A ground–based near infrared camera array system for UAV auto–landing in GPS–denied environment. Sensors 2016, 16, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Anitha, G.; Kumar, R.N.G. Vision based autonomous landing of an unmanned aerial vehicle. Procedia Eng. 2012, 38, 2250–2256. [Google Scholar] [CrossRef]
- Li, X. A software scheme for UAV’s safe landing area discovery. AASRI Procedia 2013, 4, 230–235. [Google Scholar] [CrossRef]
- Sharp, C.S.; Shakernia, O.; Sastry, S.S. A vision system for landing an unmanned aerial vehicle. In Proceedings of the the IEEE International Conference on Robotics and Automation, Seoul, Korea, 21–26 May 2001; pp. 1720–1727. [Google Scholar]
- Lange, S.; Sünderhauf, N.; Protzel, P. Autonomous landing for a multirotor UAV using vision. In Proceedings of the the International Conference on Simulation, Modeling and Programming for Autonomous Robots, Venice, Italy, 3–4 November 2008; pp. 482–491. [Google Scholar]
- Zhao, Y.; Pei, H. An improved vision–based algorithm for unmanned aerial vehicles autonomous landing. Phys. Procedia 2012, 33, 935–941. [Google Scholar] [CrossRef]
- Chaves, S.M.; Wolcott, R.W.; Eustice, R.M. NEEC research: Toward GPS–denied landing of unmanned aerial vehicles on ships at sea. Nav. Eng. J. 2015, 127, 23–35. [Google Scholar]
- Ling, K. Precision Landing of a Quadrotor UAV on a Moving Target Using Low–Cost Sensors. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2014. [Google Scholar]
- AprilTag. Available online: https://april.eecs.umich.edu/software/apriltag.html (accessed on 17 April 2017).
- Kyristsis, S.; Antonopoulos, A.; Chanialakis, T.; Stefanakis, E.; Linardos, C.; Tripolitsiotis, A.; Partsinevelos, P. Towards autonomous modular UAV missions: The detection, geo–location and landing paradigm. Sensors 2016, 16, 1844. [Google Scholar] [CrossRef] [PubMed]
- AprilTags C++ Library. Available online: http://people.csail.mit.edu/kaess/apriltags/ (accessed on 17 April 2017).
- Linux for Tegra R27.1. Available online: https://developer.nvidia.com/embedded/linux–tegra (accessed on 17 April 2017).
- DJI. Available online: http://www.dji.com (accessed on 27 April 2017).
- Jetson TK1. Available online: http://www.nvidia.com/object/jetson–tk1–embedded–dev–kit.html (accessed on 27 April 2017).
- Xu, G.; Zhang, Y.; Ji, S.; Cheng, Y.; Tian, Y. Research on computer vision–based for UAV autonomous landing on a ship. Pattern Recognit. Lett. 2009, 30, 600–605. [Google Scholar] [CrossRef]
- Xu, G.; Qi, X.; Zeng, Q.; Tian, Y.; Guo, R.; Wang, B. Use of land’s cooperative object to estimate UAV’s pose for autonomous landing. Chin. J. Aeronaut. 2013, 26, 1498–1505. [Google Scholar] [CrossRef]
- Babenko, B.; Yang, M.H.; Belongie, S. Visual tracking with online multiple instance learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–26 June 2009; pp. 983–990. [Google Scholar]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Tracking–learning–detection. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1409–1422. [Google Scholar] [CrossRef] [PubMed]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Forward–backward error: Automatic detection of tracking failures. In Proceedings of the International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 1–4. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High–speed tracking with kernelized correlation filters. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 583–596. [Google Scholar] [CrossRef] [PubMed]
- Bay, H.; Ess, A.; Tuytelaars, T.; Gool, L.V. Speeded–up robust features (SURF). Comput. Vis. Image Underst. 2006, 110, 346–359. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale–invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. Brief: Binary robust independent elementary features. In Proceedings of the European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010; pp. 778–792. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- MUTOH Printer. Available online: https://www.mutoh.eu/ (accessed on 3 August 2017).
- Lam, S.K.; Yeong, C.Y.; Yew, C.T.; Chai, W.S.; Suandi, S.A. A study on similarity computations in template matching technique for identity verification. Int. J. Comput. Sci. Eng. 2010, 2, 2659–2665. [Google Scholar]
- Li, H.; Duan, H.B.; Zhang, X.Y. A novel image template matching based on particle filtering optimization. Pattern Recognit. Lett. 2010, 31, 1825–1832. [Google Scholar] [CrossRef]
- Türkan, M.; Guillemot, C. Image prediction: Template matching vs. sparse approximation. In Proceedings of the 17th International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 789–792. [Google Scholar]
- Lin, Y.; Chunbo, X. Template matching algorithm based on edge detection. In Proceedings of the International Symposium on Computer Science and Society, Kota Kinabalu, Malaysia, 16–17 July 2011; pp. 7–9. [Google Scholar]
- Lu, X.; Shi, Z. Detection and tracking control for air moving target based on dynamic template matching. J. Electron. Meas. Instrum. 2010, 24, 935–941. [Google Scholar] [CrossRef]
- Paravati, G.; Esposito, S. Relevance–based template matching for tracking targets in FLIR imagery. Sensors 2014, 14, 14106–14130. [Google Scholar] [CrossRef] [PubMed]
- Opromolla, R.; Fasano, G.; Rufino, G.; Grassi, M. A model–based 3D template matching technique for pose acquisition of an uncooperative space object. Sensors 2015, 15, 6360–6382. [Google Scholar] [CrossRef] [PubMed]
- Welch, G.; Bishop, G. An introduction to the Kalman filter. In Proceedings of the Special Interest Group on GRAPHics and Interactive Techniques (SIGGRAPH), Los Angeles, CA, USA, 12–17 August 2001; pp. 19–24. [Google Scholar]
- Zaitoun, N.M.; Aqel, M.J. Survey on image segmentation techniques. Procedia Comput. Sci. 2015, 65, 797–806. [Google Scholar] [CrossRef]
- Salman, N. Image segmentation based on watershed and edge detection techniques. Int. Arab. J. Inf. Technol. 2006, 3, 104–110. [Google Scholar]
- Belaid, L.J.; Mourou, W. Image segmentation: A watershed transformation algorithm. Image Anal. Stereol. 2009, 28, 93–102. [Google Scholar] [CrossRef]
- Bala, A. An improved watershed image segmentation technique using MATLAB. Int. J. Sci. Eng. Res. 2012, 3, 1–4. [Google Scholar]
- Yahya, A.A.; Tan, J.; Hu, M. A novel model of image segmentation based on watershed algorithm. Adv. Multimed. 2013, 2013, 1–8. [Google Scholar] [CrossRef]
- Uyun, S.; Hartati, S.; Harjoko, A.; Choridah, L. A comparative study of thresholding algorithms on breast area and fibroglandular tissue. Int. J. Adv. Comput. Sci. Appl. 2015, 6, 120–124. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- ARM Processors. Available online: https://www.arm.com/products/processors (accessed on 19 May 2017).
- Lee, H.; Jung, S.; Shim, D.H. Vision–based UAV landing on the moving vehicle. In Proceedings of the International Conference on Unmanned Aircraft System, Arlington, MA, USA, 7–10 June 2016; pp. 1–7. [Google Scholar]
- Fu, C.; Duan, R.; Kircali, D.; Kayacan, E. Onboard robust visual tracking for UAVs using a reliable global–local object model. Sensors 2016, 16, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Intel® NUC Kit NUC5i7RYH. Available online: https://ark.intel.com/products/87570/Intel–NUC–Kit–NUC5i7RYH (accessed on 27 April 2017).
- OpenCV 3.1. Available online: http://opencv.org/opencv–3–1.html (accessed on 19 May 2017).
- Microsoft Visual Studio. Available online: https://www.visualstudio.com/ (accessed on 19 May 2017).
- CMake. Available online: https://cmake.org/ (accessed on 19 May 2017).
- Stanford Drone Dataset. Available online: http://cvgl.stanford.edu/projects/uav_data/ (accessed on 19 May 2017).
- Mini–Drone Video Dataset. Available online: http://mmspg.epfl.ch/mini–drone (accessed on 19 May 2017).
- SenseFly Dataset. Available online: https://www.sensefly.com/drones/example–datasets.html (accessed on 19 May 2017).
- Dongguk Drone Camera Database (DDroneC–DB1). Available online: http://dm.dgu.edu/link.html (accessed on 16 June 2017).
- Chessboard Pattern. Available online: http://docs.opencv.org/3.1.0/pattern.png (accessed on 13 August 2017).
- Camera Calibration and 3D Reconstruction. Available online: http://docs.opencv.org/2.4/modules/calib3d/doc/camera_calibration_and_3d_reconstruction.html (accessed on 13 August 2017).
- Detection of ArUco Markers. Available online: http://docs.opencv.org/trunk/d5/dae/tutorial_aruco_detection.html (accessed on 13 August 2017).
- Garrido-Jurado, S.; Muñoz-Salinas, R.; Madrid-Cuevas, F.J.; Marín-Jiménez, M.J. Automatic generation and detection of highly reliable fiducial markers under occlusion. Pattern Recognit. 2014, 47, 2280–2292. [Google Scholar]















| Categories | Sub-Categories | Type of Camera | Time for Drone Landing | Descriptions | Strength | Weakness |
|---|---|---|---|---|---|---|
| Passive methods | A trinocular system with three visible light FireWire cameras | Daytime [22] | Color landmarks on the UAV are deployed as key features for position estimation by a ground station using CamShift algorithm. | This research not only achieved good results for landing and positioning task, but also practical for real-time applications. | The feature extraction algorithm is not guaranteed to work under low light condition. Complicated set-up of three cameras on the ground is required. | |
| A pan-tilt unit (PTU) with stereo infrared cameras | Daytime and nighttime with various weather conditions [23] | Several target tracking algorithms have been evaluated and tested on a quadrotor and a fixed-wing aircraft. | It can track target early by using enlarge field of view by PTU. Fast Marching Method is proposed among other techniques by its effiency and accuracy. | Low accuracy in case of fix-wing touchdown points and high temperature objects in the background. | ||
| Two NIR camera array system with NIR laser lamp | Daytime and nighttime with different light conditions [24] | A NIR laser lamp is fixed on the nose of the UAV for easy detection. | A wide baseline camera array-based method was proposed to achieve high precision for calibration and localization results. | It is not practical to be used in the narrow landing area. Complicated set-up of two camera array systems on the ground is required. | ||
| Active methods | Without marker | Visible light camera | Daytime and nighttime with guiding lamp [25] | Image binarization and Hough transform used to extract the runway border line for the landing in flight-gear flight simulator. | A simple algorithm is used for border-line detection of runway. | Guiding lamps are required at nighttime, which make it difficult to be used in various places. |
| Day time [26] | Two-stage processing procedure to find all possible landing areas and select the best one using the naive Bayesian classifier. | Without the marker, drone can find the landing site in emergency case. | Experiments were not performed in various places and time. In addition, system is evaluated on a Mac Pro laptop computer. | |||
| With marker | Thermal camera | Daytime, and nighttime [38,39] | Using letter-based marker emitting FIR light, feature points can be extracted from the marker so that the drone can perform translation or rotation movements in order to perform safety landing at the desired location. | Using the thermal image, marker detection can be less affected by illumination, time, and environmental change. | A costly thermal camera should be used in drone, and this cannot be used in conventional drone systems, including the use of only visible-light camera. | |
| Visible light camera | Daytime [24,25,26,27,28,30] | Detecting marker by contour, circle detector or key points descriptor based on SURF, etc. | Marker detection is possible using conventional visible light camera in drone. | Marker is detected only during daytime. High computing algorithm cannot be processed in real-time with on-board system [29] | ||
| Daytime, and nighttime (proposed method) | Using real-time marker-based tracking algorithm tested on an onboard system having low processing power. | Marker detection method can be operated both in daytime and nighttime. | A specific marker is required for the proposed method. | |||
| Kinds of Sub-Database | Time | Condition | Description |
|---|---|---|---|
| Sub-database 1 (drone landing) | Morning | Humidity: 41.5%, wind speed: 1.4 m/s, temperature: 8.6 °C, spring, sunny, Illuminance:1900 lux | A sunny day with clear sky, which has affected the illumination on the marker Landing speed: 4 m/s Auto mode of camera shutter speed (8~1/8000 s) and ISO (100~3200) |
| Afternoon | Humidity: 73.8%, wind speed: 2 m/s, temperature: −2.5 °C, winter, cloudy, Illuminance: 1200 lux | Low level of illumination observed in the winter time, which affected the intensity of background area. Landing speed: 6 m/s Auto mode of camera shutter speed (8~1/8000 s) and ISO (100~3200) | |
| Evening | Humidity: 38.4%, wind speed: 3.5 m/s, temperature: 3.5 °C, winter, windy, Illuminance: 500 lux | There is the change in the marker’s position due to strong wind Landing speed: 4 m/s Auto mode of camera shutter speed (8~1/8000 s) and ISO (100~3200) | |
| Night | Humidity: 37.5%, wind speed: 3.2 m/s, temperature: 6.9 °C, spring, foggy, Illuminance: 0.3 lux | Marker cannot be seen owning low level of light at dark night Landing speed: 6 m/s Auto mode of camera shutter speed (8~1/8000 s) and ISO (100~3200) | |
| Sub-database 2 (drone hovering) | Morning | Humidity: 41.6%, wind speed: 2.5 m/s, temperature: 11 °C, spring, foggy, Illuminance: 1000 lux | Drone hovers above the marker, and the marker is manually moved and rotated while capturing videos. Auto mode of camera shutter speed (8~1/8000 s) and ISO (100~3200) |
| Afternoon | Humidity: 43.5%, wind speed: 2.8 m/s, temperature: 13 °C, spring, sunny, Illuminance: 1860 lux | ||
| Evening | Humidity: 42.9%, wind speed: 2.9 m/s, temperature: 10 °C, spring, Illuminance: 600 lux | ||
| Night | Humidity: 41.5%, wind speed: 3.1 m/s, temperature: 6 °C, spring, dark night, Illuminance: 0.05 |
| Categories | Sequence | Ours without KF | Ours with KF | ATM | MIL [40] | TLD [41] | Median Flow [42] | KCF [43] |
|---|---|---|---|---|---|---|---|---|
| Sub-database 1 | Morning | 3.32 | 3.26 | 63.98 | 4.29 | 103.3 | 83.45 | 31.03 |
| Afternoon | 2.91 | 2.86 | 15.69 | 5.58 | 58.01 | 92.21 | 13.86 | |
| Evening | 3.89 | 3.54 | 28.11 | 8.85 | 75.13 | 95.84 | 7.42 | |
| Night | 8.36 | 12.2 | 65.22 | 28.15 | 48.1 | 23.56 | 31.65 | |
| Sub-database 2 | Morning | 1.98 | 1.94 | 38.19 | 1.92 | 32.34 | 6.11 | 5.58 |
| Afternoon | 2.32 | 2.05 | 32.1 | 5.04 | 25.66 | 4.19 | 3.14 | |
| Evening | 1.74 | 1.68 | 37.99 | 7.8 | 2.98 | 8.08 | 1.73 | |
| Night | 7.12 | 9.75 | 49.78 | 6.33 | 15.94 | 12.37 | 7.45 |
| Categories | Sequence | Ours without KF | Ours with KF | ATM |
|---|---|---|---|---|
| Sub-database 1 | Morning | 0.72 | 0.51 | 50.94 |
| Afternoon | 0.88 | 0.47 | 2.64 | |
| Evening | 1.33 | 1.01 | 17.37 | |
| Night | 4.39 | 5.9 | 80.56 | |
| Sub-database 2 | Morning | 2.45 | 1.97 | 26.84 |
| Afternoon | 2.79 | 2.17 | 43.65 | |
| Evening | 2.28 | 1.83 | 27.16 | |
| Night | 3.35 | 4.12 | 68.17 |
| Categories | Sequence | Ours without KF | Ours with KF | MIL [40] | TLD [41] | Median Flow [42] | KCF [43] |
|---|---|---|---|---|---|---|---|
| Sub-database 1 | Morning | 22 | 23 | 367 | 2971 | 43 | 359 |
| Afternoon | 22 | 22 | 371 | 2921 | 44 | 258 | |
| Evening | 22 | 23 | 369 | 2192 | 43 | 223 | |
| Night | 24 | 25 | 740 | 3993 | 88 | 180 | |
| Sub-database 2 | Morning | 20 | 20 | 754 | 3129 | 92 | 165 |
| Afternoon | 20 | 22 | 768 | 3427 | 74 | 145 | |
| Evening | 21 | 21 | 762 | 3419 | 72 | 104 | |
| Night | 23 | 25 | 730 | 4530 | 86 | 151 |
| Methods | Key Points | X | Y | Z |
|---|---|---|---|---|
| Our marker | P2 | 0 | ||
| P4 | 0 | |||
| P9 | 0 | |||
| P13 | 0 | |||
| ArUco marker | A | 0 | ||
| B | 0 | |||
| C | 0 | |||
| D | 0 |
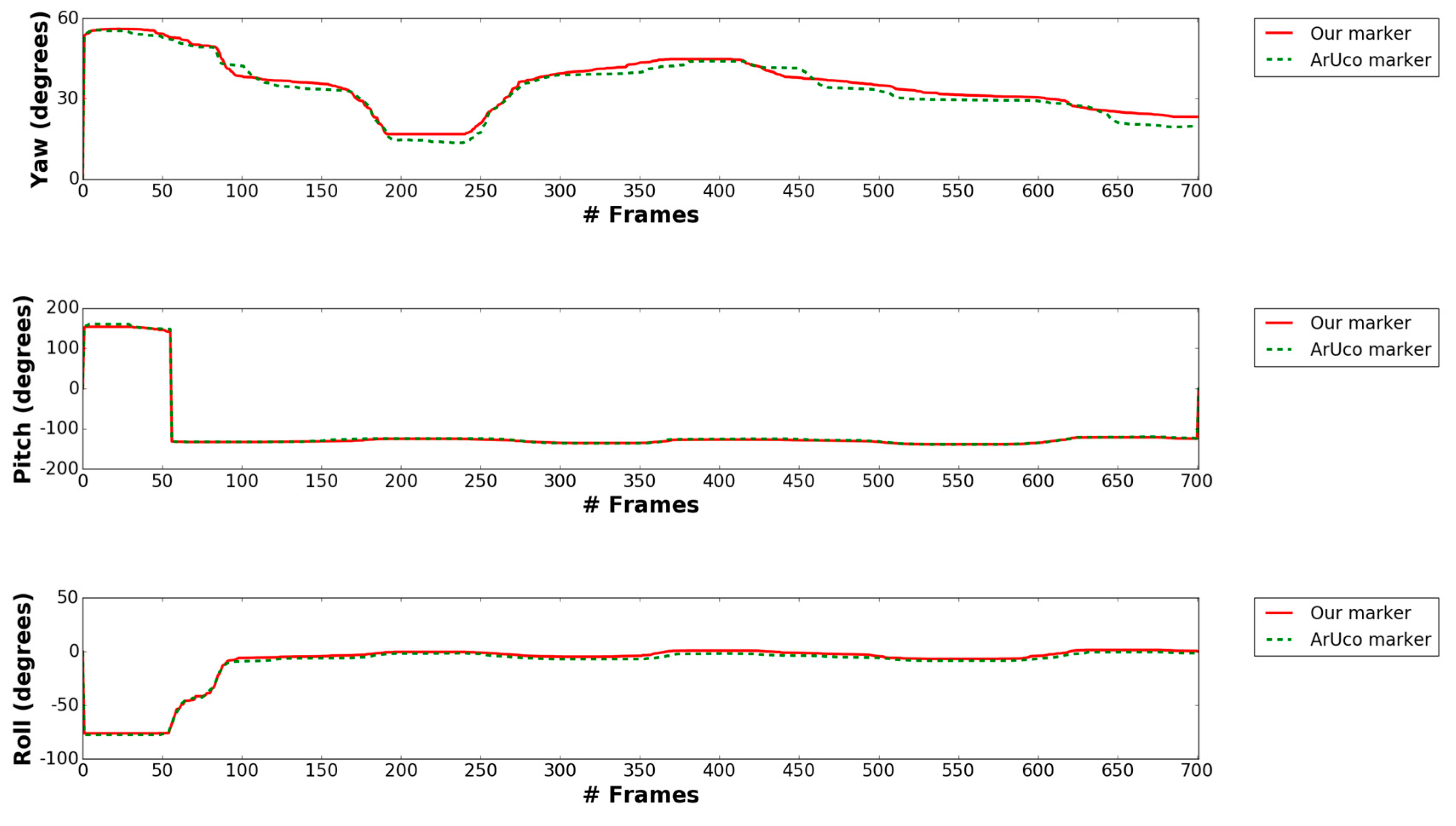
| Category | Average Error between Our Marker and ArUco Marker-Based Methods |
|---|---|
| X | 0.076 |
| Y | 0.014 |
| Z | 0.095 |
| Yaw | 1.8° |
| Pitch | 1.15° |
| Roll | 2.09° |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, P.H.; Kim, K.W.; Lee, Y.W.; Park, K.R. Remote Marker-Based Tracking for UAV Landing Using Visible-Light Camera Sensor. Sensors 2017, 17, 1987. https://doi.org/10.3390/s17091987
Nguyen PH, Kim KW, Lee YW, Park KR. Remote Marker-Based Tracking for UAV Landing Using Visible-Light Camera Sensor. Sensors. 2017; 17(9):1987. https://doi.org/10.3390/s17091987
Chicago/Turabian StyleNguyen, Phong Ha, Ki Wan Kim, Young Won Lee, and Kang Ryoung Park. 2017. "Remote Marker-Based Tracking for UAV Landing Using Visible-Light Camera Sensor" Sensors 17, no. 9: 1987. https://doi.org/10.3390/s17091987
APA StyleNguyen, P. H., Kim, K. W., Lee, Y. W., & Park, K. R. (2017). Remote Marker-Based Tracking for UAV Landing Using Visible-Light Camera Sensor. Sensors, 17(9), 1987. https://doi.org/10.3390/s17091987




