1. Introduction
Object recognition using visual sensors is one of the most important topics in autonomous robotic systems. The recognized objects or features can be used as landmarks to achieve environmental recognition and autonomous navigation. Similarly, in the underwater vision research area, several methods using optical images have also been applied to the underwater recognition and navigation [
1,
2,
3,
4,
5,
6]. Unfortunately, underwater optical images can be seriously affected by environmental conditions such as turbidity and illuminations. These environmental conditions make it difficult for underwater vehicles to use optical images. Alternatively, imaging sonars that use acoustic signals are utilized in the underwater vision research area. An imaging sonar is not affected by illuminations and has long-distance visibility. Due to these characteristics, imaging sonars have been widely used in various studies [
7,
8,
9,
10,
11,
12,
13,
14]. However, accurate object recognition is still difficult because of the practical performance of sonars such as the low resolution image, unstable acoustic source, many speckle noise, and only gray scale image [
15,
16].
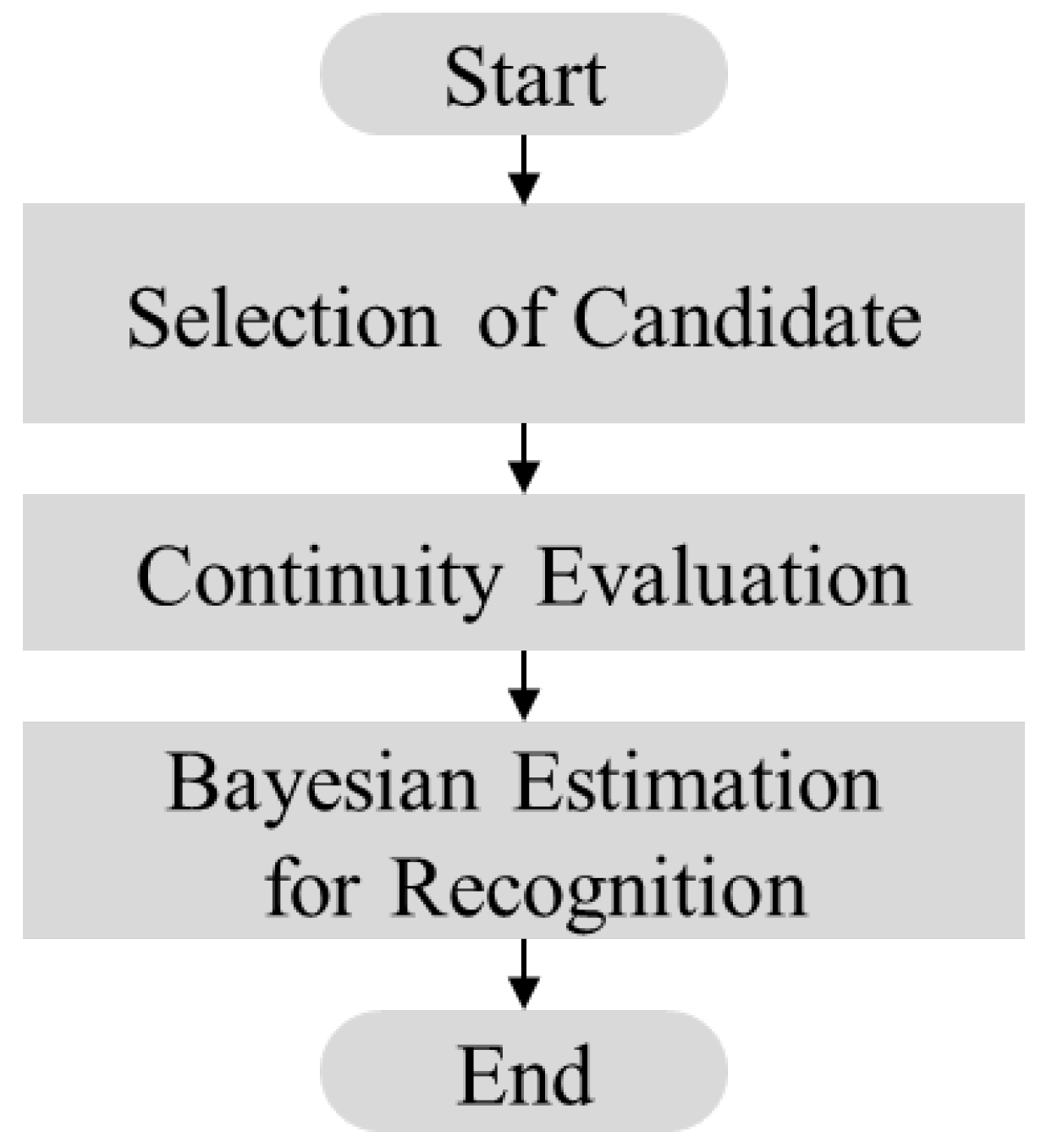
To overcome these challenges, this paper proposes a probability-based framework for underwater landmark recognition using an imaging sonar. Current recognition methods use a single sonar image that does not provide reliable results due to the weaknesses of sonar images as mentioned above. On the other hand, if an object exists continuously in consecutive images and we can evaluate its features using a stochastic method, it is possible to calculate, with certainty, the features of the object; as a result, the reliability of recognition increases. To achieve this, we design a recognition framework that consists of three steps: (1) candidate selection, (2) continuity evaluation and (3) Bayesian feature estimation. Two probability methods, particle filtering and Bayesian feature estimation, are used to evaluate the continuity and features of an object in a series of images. In addition, to increase detectability by an imaging sonar, we develop an artificial landmark that takes into account the characteristics of acoustic waves related to reflections.
The proposed method results in a well-structured framework of underwater object recognition using imaging sonar. The proposed method has several advantages as follows. First, the proposed improves the visibility of landmark in sonar images by adopting a specialized artificial landmark. Second, a particle filter can perform an effective evaluation of the continuity of target object in consecutive images. Finally, a probabilistic framework based on Bayesian feature estimation provides reliable object recognition results even with noisy sonar images.
The remainder of this paper is organized as follows:
Section 2 summarizes related work on imaging sonars in underwater environments;
Section 3 describes the proposed probability-based underwater object recognition using imaging sonar;
Section 4 presents experimental results in a basin and
Section 5 concludes the paper.
2. Background
2.1. Previous Work
Many studies have been conducted to apply image registration and object recognition using sonar images to areas such as robot navigation. For example, Hurtos et al. conducted a study on Fourier-based registration for sonar mosaicing [
17]. The authors employed a phase correlation based method that estimates the rotation and translation between consecutive frames. After the global alignment, the result not only present the mosaic image but also the path of sonar movement. Similarly, another study [
18] proposes a Normal Distribution Transform (NDT) algorithm for the registration used for the hull inspection of Autonomous Underwater Vehicle (AUV). Fallon et al. develop a sonar-based Simultaneous Localization And Mapping (SLAM) using natural features on the seabed [
19]. When the AUV, such as REMUS 100, moves around the sea, the vehicle position is estimated using natural features from sonar with dead-reckoning data. Furthermore, acoustic shadows have been used to recognize an underwater object [
20]. The sonar emits an acoustic wave to the objects; however, the acoustic wave cannot reach the back of an object and this region is dark in the sonar image. Hence, the descriptor of the object is used because the shape differs for each object. In another study on object recognition, Cho et al. propose a cross correlation-based object detection method using sonar-beam profiles [
21]. This method quickly recognizes the presence of an object by using the difference of intensity in consecutive frames. A number of these studies require a descriptor, which represents a feature of the object or a point in the sonar image. However, it remains a challenge to define a descriptor that has robustness and repeatability, owing to the weaknesses of sonar images.
2.2. Artificial Landmarks and Imaging Sonar
Considering the constraints on achievable quality of sonar images, the only way to obtain stable and accurate information for navigation is by using well-designed artificial landmarks. Sonar measures the travel time and intensity of a reflected acoustic wave in order to identify an underwater object. Thus, we can obtain clearer sonar images if the surface of the object has different characteristics making contrasting reflections. Various experiments have been conducted to find appropriate materials to achieve a sharp contrast; a two-dimensional artificial landmark was designed using gel-stone on an aluminum plate. Gel-stone reflects much of the transmitting wave; moreover, it is easy to handle. On the contrary, an aluminum plate reflects less of the transmitting wave and it has enough weight to be placed on the sea bottom.
In the early stage of designing the landmarks, we considered a letter type that has sufficient information not only for the landmark but also for being recognized by a human. However, even though a letter is drawn using the proposed method, line features of the letter are not very clear owing to the limitation of sonar technologies; as a result, lines are considered as an inappropriate feature.
Therefore, we developed circular-shaped landmarks combined with four different symbols designed for the inside as shown in
Figure 1. Using the sonar parameters provided by a sonar, a circular-shape can be easily modeled to implement an algorithm for detecting four different landmarks. Furthermore, it can be differentiated from natural objects and detected regardless of direction. On the other hand, four different symbols have robustness against low quality images and environment noise and disturbances because they use an area-based feature. To realize the omni-directional characteristic of landmarks, they are placed orthogonal to the vertical axis, which is not an unreasonable constraint because a landmark could be placed in accordance with any human intention.
In spite of a well-designed landmark composed of specially selected materials, exteriors, and area-based features, the features in a single sonar image frame are not sufficient to identify the landmark because of various noises and disturbances from the real underwater environment. Therefore, consecutive sonar images should be considered within a probability-based framework to derive stable information for navigating an underwater robot.
3. Probability-Based Recognition Framework
The proposed method can effectively recognize underwater landmarks principally because the probabilistic approach of Bayesian estimation can provide reliable results of object recognition even when sonar images are affected by noisy data.
3.1. Overall Framework
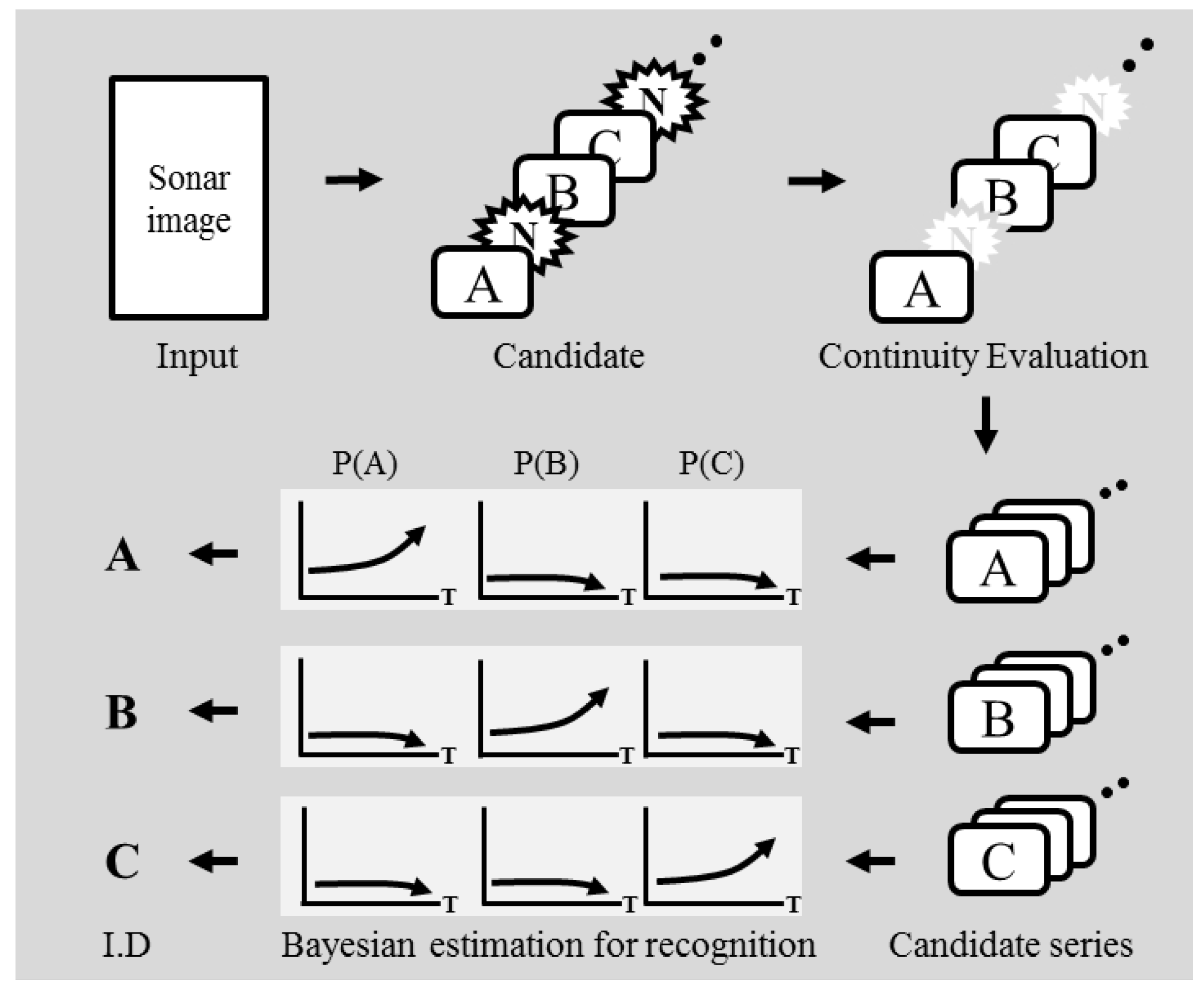
The proposed method is achieved by a framework comprising three processes. First, candidates of target objects are acquired from sonar images using a predefined landmark model. Second, a particle filter is used to evaluate the continuity of the acquired candidates in consecutive images. Lastly, a probabilistic approach based on Bayesian feature estimation is used to recognize and to identify the detected objects.
Figure 2 and
Figure 3 depict an overview of the proposed probability-based recognition framework and a flowchart of the algorithm, respectively.
3.2. Selection of Candidate
Generally, a series of image-processing algorithms is applied to an entire image to detect landmarks. Although this may be an effective technique for optical images, it is not practical for acoustic images because of the non-uniform characteristics of local regions in sonar images, due to the reasons mentioned earlier. To overcome this, we first attempt to find objects similar to a landmark from the entire image, and only the selected objects are transferred to the next step.
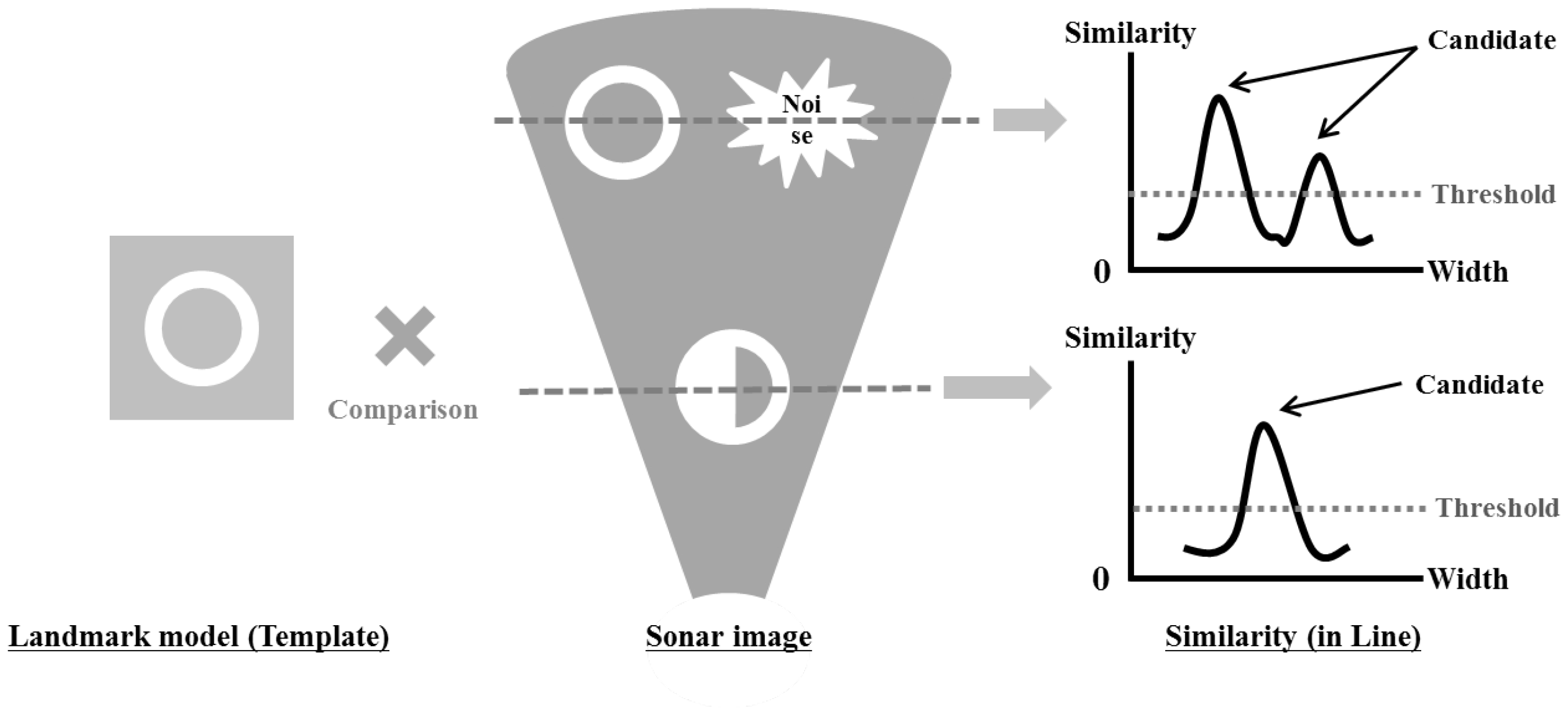
The selected objects are referred to as candidates in this step. The candidates are obtained through comparison with a landmark model as shown in
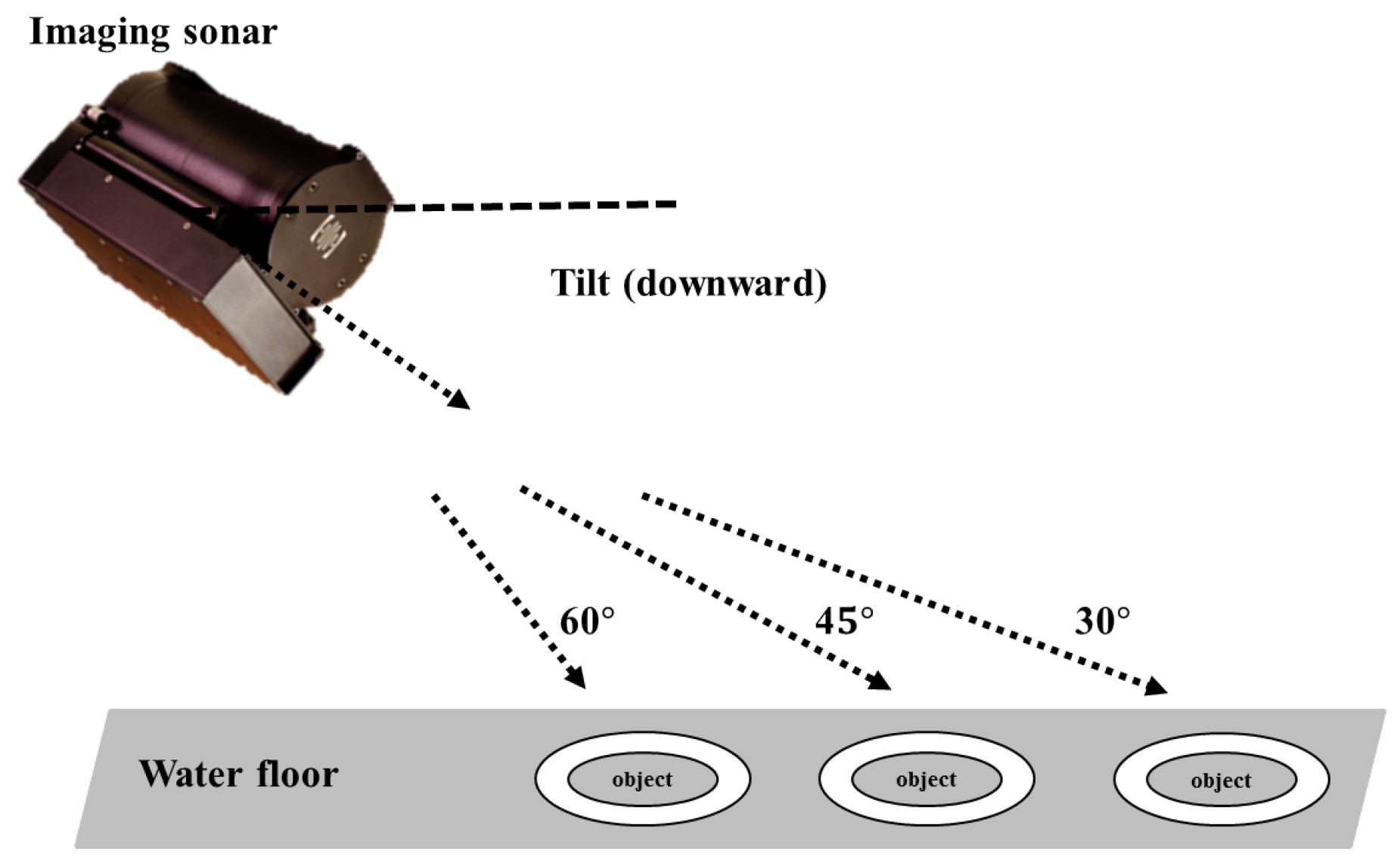
Figure 4. This process is similar to the conventional template matching method used in the image processing technique. A landmark model is compared with the sonar image, and the point with the high similarity is selected as the candidate. The landmark model can have various forms depending on the landmark. We use an artificial landmark having a circular shape with various inner fan shapes. Hence, a circle is used to model a landmark in this study. The landmark model is presented in
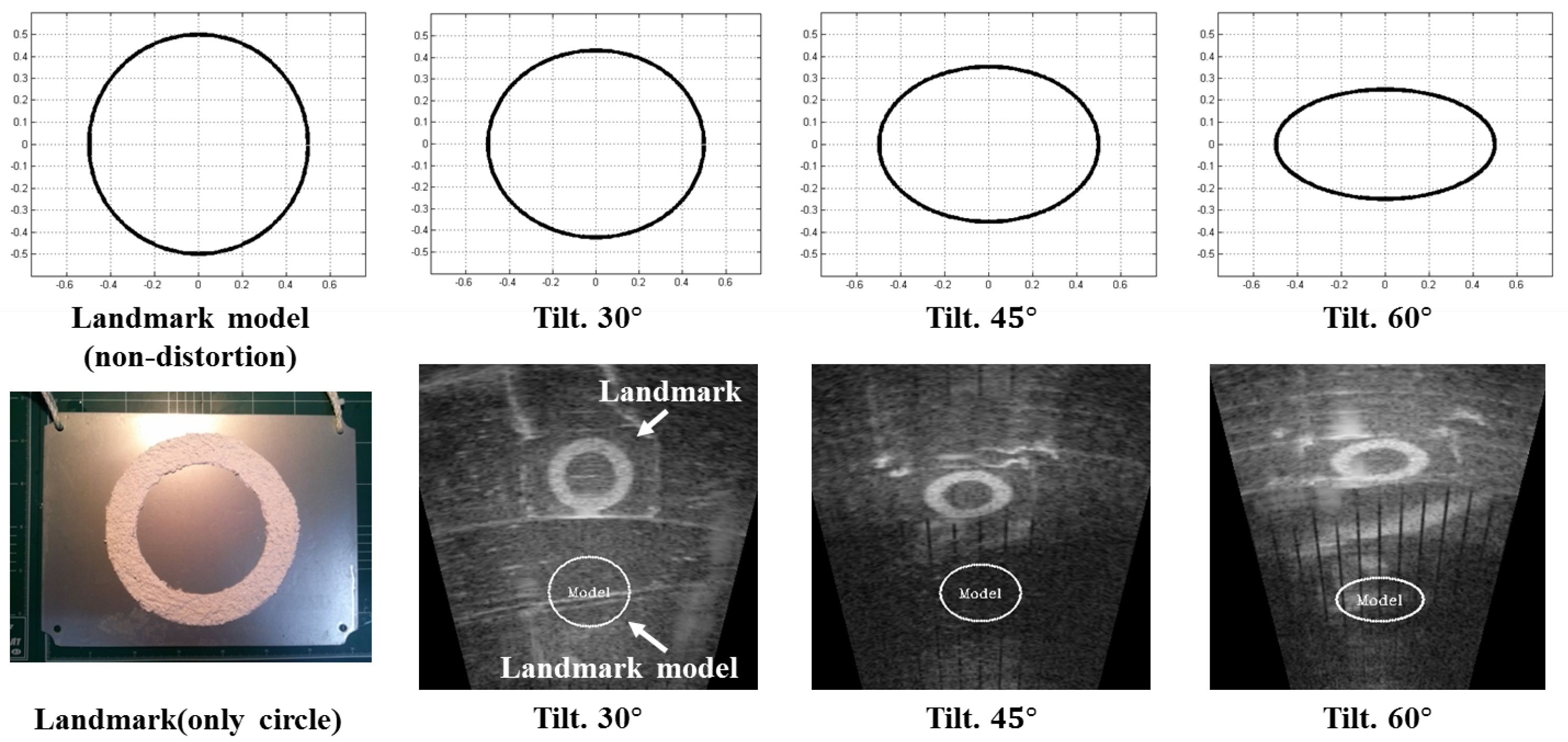
Figure 5. The landmark model should be changed according to the sonar parameters related to sonar pose and range of view because the sonar must look down towards the objects for acquiring the image as shown in
Figure 6 and it can change its range of view. For this reason, these conditions cause distortions of object in terms of vertical deformation and the size in sonar images. Hence, considering these two conditions, the landmark model is calculated using the following equations. Equations (
1) and (
2) represent the deformation due to tilt (downward) of sonar and the scale considering the range of view, respectively.
The circular outline of the landmark on the
x- and
y-axis is denoted by
,
and the deformed line related to the tilt angle
is denoted by
,
where the unit is metric. The resultant landmark model in image plane is
u,
v, where the unit is
pixel.
r is a range of view in meter and the constant 512 is the height of the image:
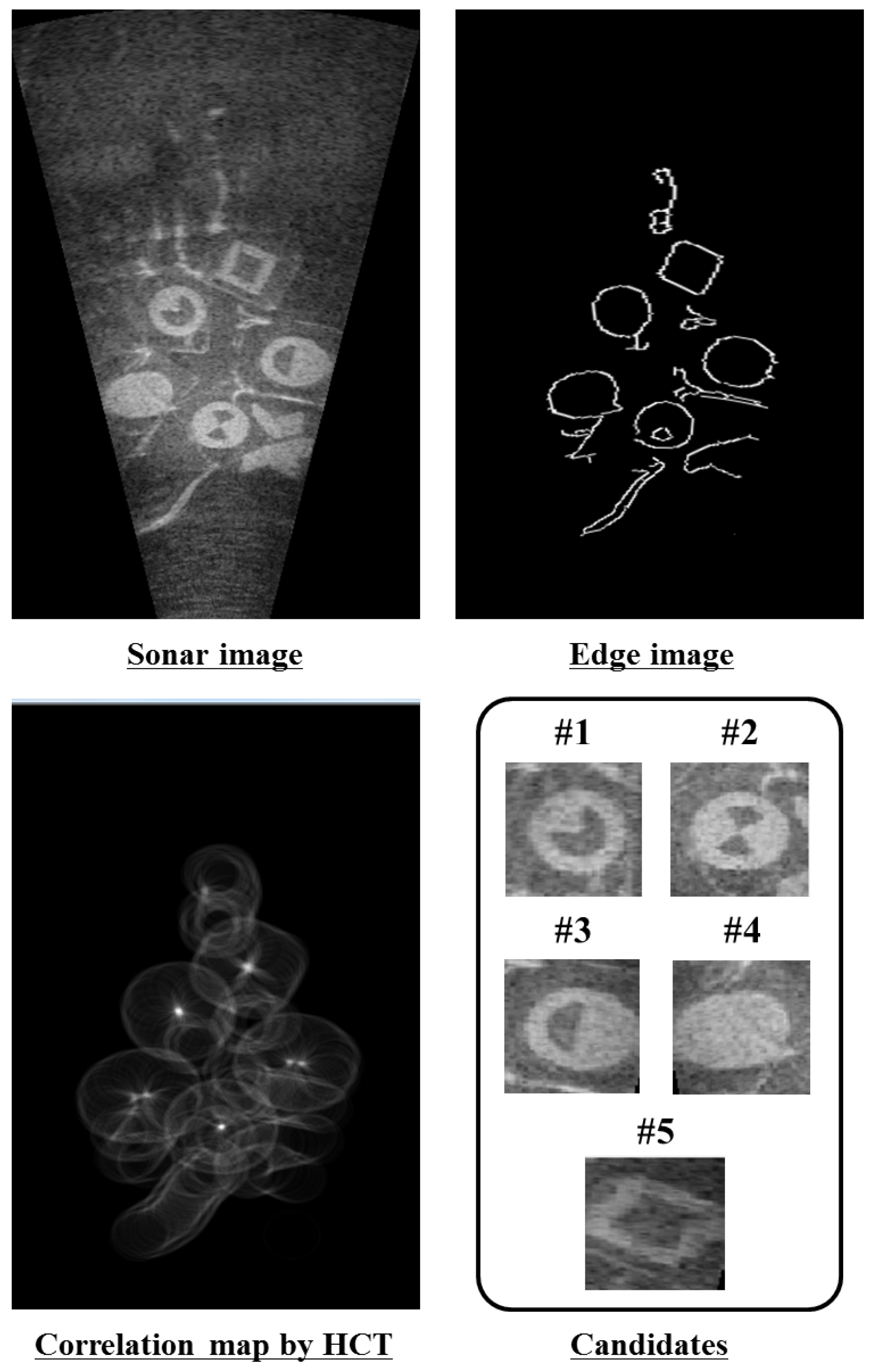
To select the candidates that have a circular-shape in a sonar image, the Hough circle transform technique is adopted [
22]. It requires a correlation map as shown in
Figure 7. The correlation map is calculated by comparing the landmark model and an edge image. It represents a possibility that a landmark exists in a recent sonar image. Thus, the high score region in the correlation map is considered as candidates. If all correlation values are lower than the number of pixels of the landmark model, we determine that no candidates exist in the current image.
3.3. Continuity Evaluation
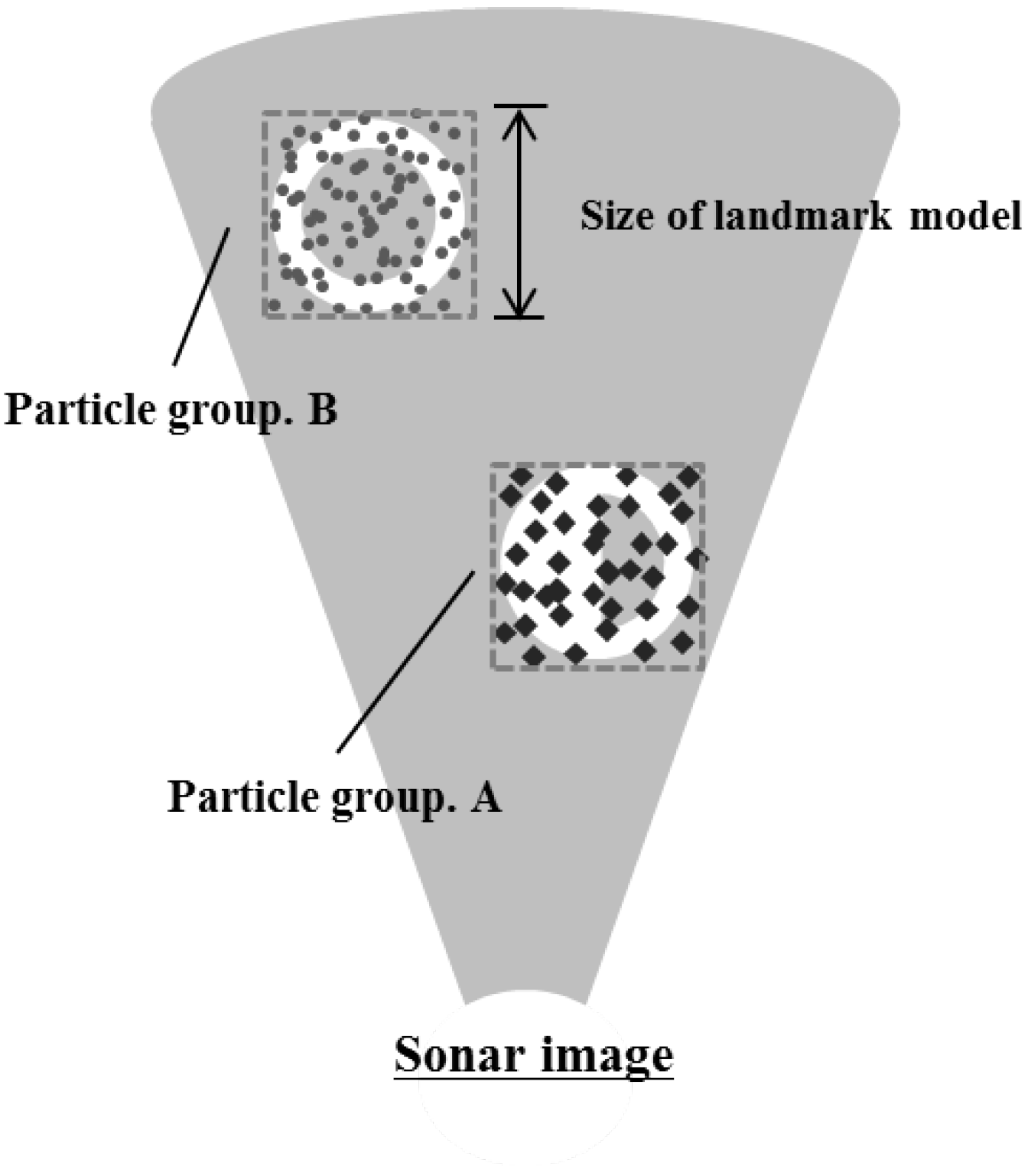
The candidates selected in the current image have no connectivity to the previous image. Only if we know the series of information for any candidate, consecutive stochastic recognition will be possible because its inputs as measurements are necessary to obtain continuity. To solve this problem, particle filter method is applied to evaluate the continuity of candidates in a series of images.
Particle filter is applied to each likely candidate. In addition, 1000 to 2000 particles are randomly scattered around the position of each likely candidate and it is designated as a particle group as shown in
Figure 8. In the general prediction phase of particle filter, the system is predicted by motion model using dead-reckoning data. However, the adapted particle filter uses only a sonar image. For this reason, we adopted an uncertainty motion function as Equation (
3).
is a predicted particle position at
t, and
is the previous particle position.
is a function to determine uncertainty depending on standard normal distribution and
is the parameter value for movement of candidate.
was set to
in this study. It can be considered reasonable because the angle of view is too small, i.e.,
and the sonar moves slowly:
After the prediction, the belief of each particle is updated by using the sensor model as in Equation (
4). As in the selection of candidates step, the extracted edge image and landmark model are used to calculate the belief. In other words, the belief of particle is defined to check the existence of similar shapes as that of the landmark, around the particles.
P is a belief of particles,
is probability of existence of a circle from correlation map and
is equally given probability.
and
are the weight values for each probability:
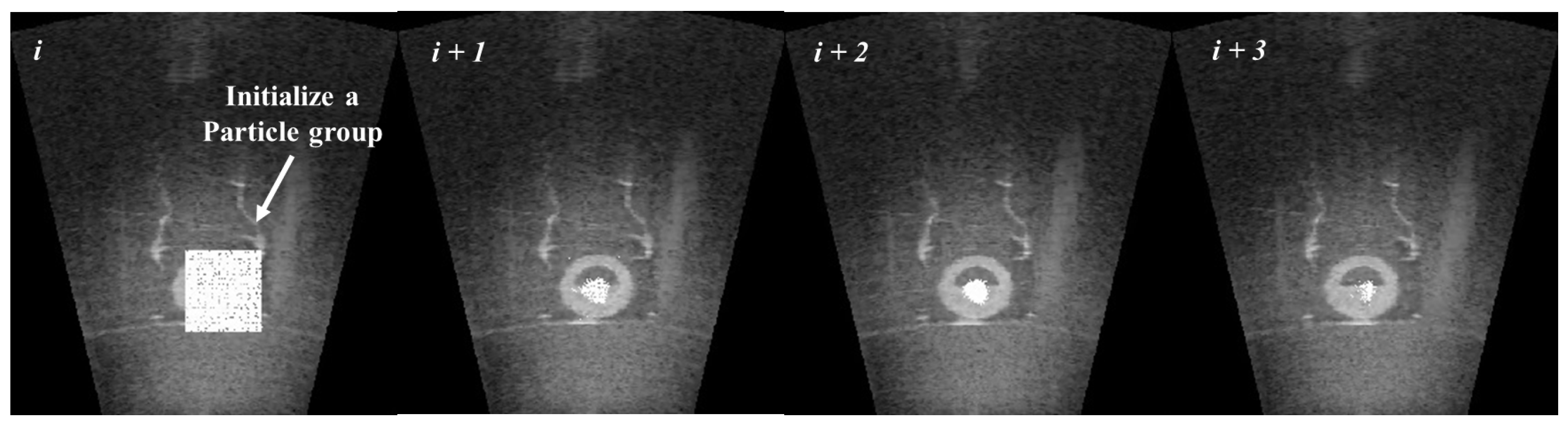
Figure 9 shows a simple result of particle filter. Particles find a landmark and congregate densely to the center of the landmark in a series of images.
A particle filter not only evaluates the continuity of candidates but also eliminates a fault candidate. The particles or particle group on the landmark will be congregated as mentioned above, but the particles on the fault candidate like noise will be scattered continuously. Therefore, if the standard deviation of a particle group is larger than 25% of the size of the landmark model five times, we decide that the candidate is not the object of interest and delete the particle group. As a result, filtered candidates are the output of the continuity evaluation step. A mean position of particle group is offered to the next step.
3.4. Bayesian Feature Estimation for Recognition
To recognize a landmark, we use a Bayesian feature estimation method. This method estimates probabilities of features of an object using a method based on Bayes’ rule and the feature refers to the object name as ID.1, ID.2, ID.3, ID.4. In this step, the candidate is to be a landmark we want to identify and each landmark is evaluated based on the probabilities of features in a series of images. As a result, the high probability of feature is considered as its ID.
Table 1 shows the notations for the calculation using the Bayesian feature estimation method.
3.4.1. Estimation Procedure
An estimation procedure consists of three steps: prediction, update by motion, and update by measurement. Algorithm 1 outlines the procedure. The procedure estimates the probability using the measurement model and the measurement information.
| Algorithm 1 Bayesian feature estimation procedure. |
- 1:
procedure (, , , ) - 2:
Predict based on the using the motion model - 3:
Find using the measurement model - 4:
Update to using measurement - 5:
Return - 6:
end procedure
|
Line 2 predicts the probability
that the landmark
m corresponds to the feature
before there is information from measurement. Line 2 is described in detail as Equation (
5).
is called the motion model. It is the probability that the landmark
j at time
corresponds to the landmark
m at time
. It can be calculated using an inverse distance between each landmark:
Line 3 in Algorithm 1 shows the calculation of the probability that the detected landmark
m corresponds to the feature
k provided that the measurement assumes that the landmark has the feature
j. Line 3 is explained in detail in Algorithm 2. Algorithm 2 shows two major steps. The first step calculates the conditional probability using Equation (
6). Equation (
6) uses the measurement model
. The measurement model
describes the probability that the feature
is recognized as the feature
by the measurement system. It is determined by the performance and properties of the measurement system and is given a priori. The next step is the normalization of the conditional probability using Equation (
7). The probability given in Equation (
6) is divided by the normalizer
to make the total probability theorem work for the conditional probability.
| Algorithm 2 Application of measurement model. |
- 1:
- 2:
for all do - 3:
for all , do - 4:
for all , do - 5:
- 6:
end for - 7:
end for - 8:
for all , do - 9:
- 10:
end for - 11:
for all do - 12:
for all do - 13:
- 14:
end for - 15:
end for - 16:
end for
|
Line 4 in Algorithm 1 updates the predicted probability
using the measurement information
. The measurement update uses Equation (
8):
Throughout the procedure, the motion model and measurement model are to be given a priori. The measurement is provided by a measurement system that uses an image processing approach for feature identification of every detected landmark.
3.4.2. Measurement System
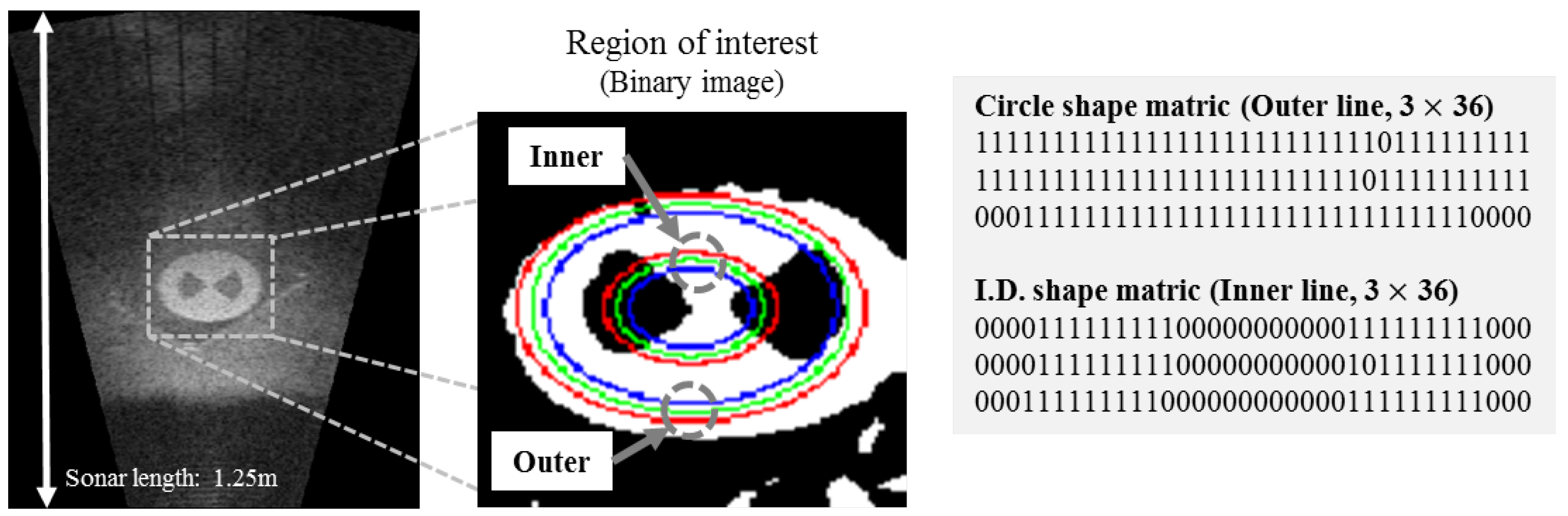
To get the measurement from a landmark, the shape matrices identification (SMI) method is applied to our study [
23]. This method describes an area which is triangular, square, circular and any pattern. An information of area is expressed with the matrices called shape matrices.
Figure 10 is a simple example, whose result is a shape matrix applying to landmark ID.2. As shown in the binary image in
Figure 10, three outer lines evaluate a circle. It means that the landmark has the circular shape. In addition, three inner lines that check ID Ideal inner shape matrices of each ID are
,
,
,
, (
). We calculate a similarity by comparison with an extracted shape matrix from an image and ideal inner shape matrices of each ID, and then normalize a similarity. The normalized similarity is used for a measurement in the updated state in the Bayesian feature estimation step. In addition, the average of the number of measurements under stable condition is a measurement model. However, there are differences by a range of views because the size of the landmark changed due to the field of view. We use an imaging sonar, DIDSON (Soundmetrics, Bellevue, WA, USA), and it can change a range of view to 1.25 m, 2.50 m, 5.0 m and 10.0 m. Therefore, we experimentally obtained two measurement models at 1.25 m, 2.50 m used for basin conditions as shown in
Table 2 and
Table 3.
4. Experiment
4.1. Experimental Setup
The experiments for demonstrating the performance of the proposed framework were conducted in a basin at the Korea Research Institute of Ships and Ocean engineering (KRISO) in Daejeon, Korea. As shown in
Figure 11b, the basin has dimensions of
m (length × width × depth) and, as mentioned, we used an imaging sonar called DIDSON shown in
Figure 11a [
24]. A DIDSON uses a 1.8 MHz acoustic source to acquire the sonar image. As shown in
Figure 12, the artificial landmarks ID.1, ID.3, and ID.4 are placed on the bottom where various objects such as a wire mesh, wood, circular fake landmark, etc. are positioned in order to simulate an underwater environment. The distances of these objects from the sonar are at least 1.7 m to 2.3 m. In addition, the sonar gazes at these objects with a pose that is tilted
and from a distance between 1.5 m to 4.0 m.
While the sonar rotated two times between −
and
at a constant speed of 2
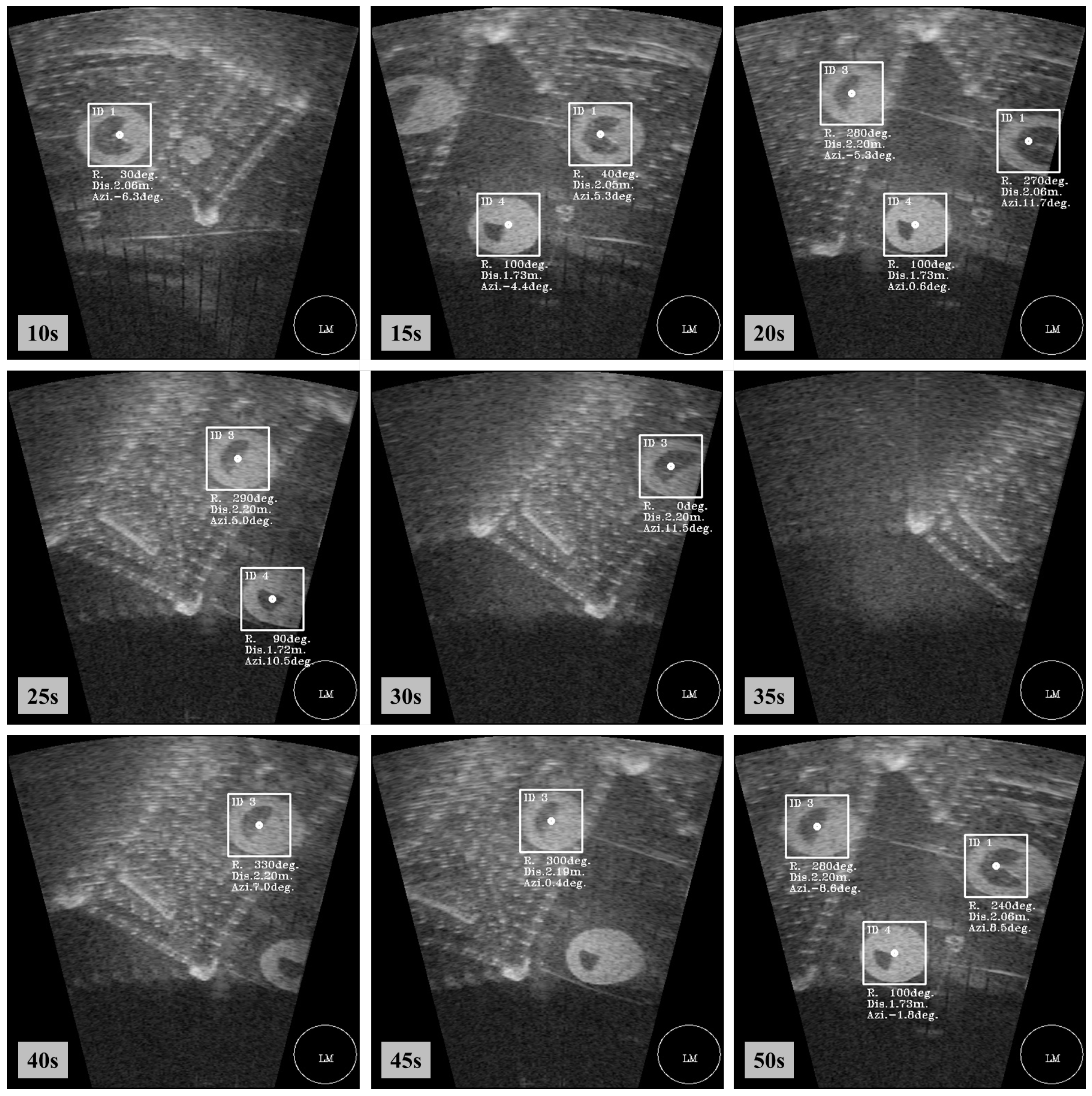
, we performed real-time recognition using the proposed framework and obtained 992 successive sonar images. The qualitative images of this experiment from the at 1st rotation are shown in
Figure 13.
4.2. Analysis
The receiver operating characteristic (ROC) analysis is adopted to evaluate the recognition performance [
25]. The main indexes of performance used in this method are true positive rate (TPR), also called sensitivity and false positive rate (FPR), also called 1-specificity. In this experiment, TPR indicates that the recognition method correctly recognized the landmark’s ID and perceived the absence of landmarks. On the contrary, FPR indicates that the recognition method missed the existence and IDs of landmarks. Hence, we want to obtain results with high TPR and low FPR from this experiment. Furthermore, we also evaluate a shape matrices identification (SMI) method by ROC analysis to compare the performance. Although the SMI method has been used for update state as the measurement in the proposed framework, it is necessary to compare the performance of the SMI method using a single frame and the proposed framework using consecutive frames for recognition.
Based on the results shown in
Figure 13, we present the results of the ROC analysis in
Table 4 and
Table 5. The proposed framework shows better recognition results with TPR of 0.8648 and FPR of 0.0276. In the case of ID.3, in the proposed framework, TPR is 0.8671 and FPR is 0.0325, which is superior to the SMI method. This is because ID.1 is often recognized as ID.3 in the SMI method. As shown in
Figure 13, the shape and boundary of objects are not clear and appear to be misty due to the characteristics of sonar images, such as speckle noise and the residual image by reflection of acoustic sound. For the identification in the case of the SMI method, an edge image is required to find the center of the landmark; however, this is not easy in the case of a sonar image. Hence, the inner fan shape of the landmark is incorrectly detected by the SMI method. On the other hand, the recognition using the proposed framework method is more accurate in this case.
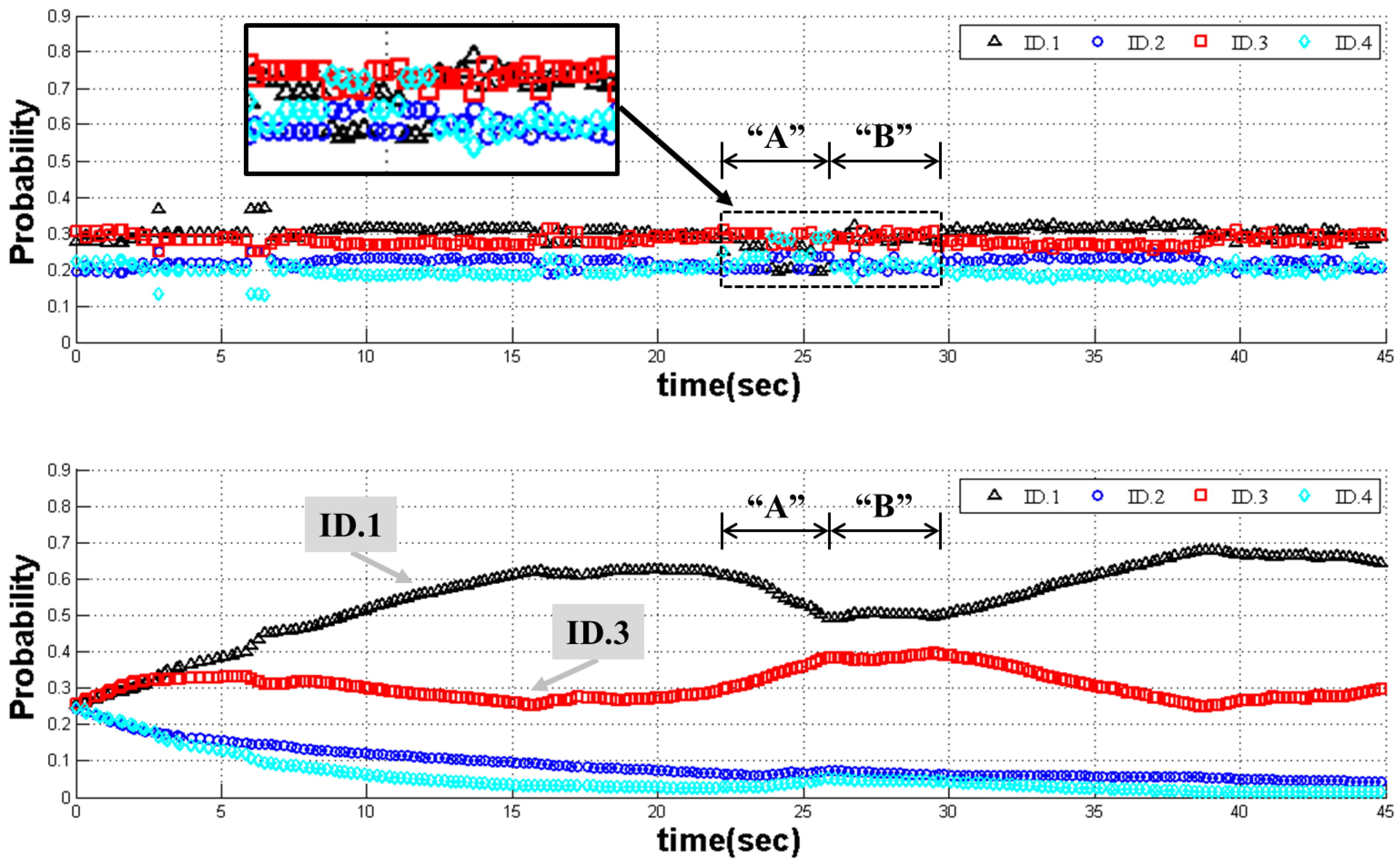
Figure 14 shows the recognition probability of ID.1. As shown in the top of
Figure 14, the SMI method does not provide salient recognition results. In particular, ID.3 has a higher probability than ID.1 in an area of “A” than the others in the SMI method. In addition, it is confused in area “B”. On the contrary, in the case of the proposed framework method, the proposed method identifies the object to be ID.1 after about 4 s. Considering that the process speed is four frames per second, 16 sonar images are used for the first recognition in this experiment. After that time, the proposed method provides correct recognition results with the highest probability of ID.1. Although the probability of ID.1 is temporarily reduced in areas “A” and “B”, the ID.1 landmark is not determined as ID.3. Thus, this result shows that the proposed framework method overcomes the problem due to the weakness of sonar image by using continuous probability evaluation.
We used a total of 992 sonar images in the experiment. As shown in
Table 4, each total
is not 992 images except for ID.2. The reason for the transient duplicate detection is that the different landmarks are recognized as one of the landmarks. Hence, TP of the real landmark is increased again and FN of incorrectly recognized landmarks is increased. On the contrary, we find that the total
s are 992 images in the results of the proposed framework method in
Table 5. As shown in
Figure 14, the probability of ID.1 is continuously increased according to the detection in every single image. Therefore, we can find that the ID, having a large probability, is an ID of the landmark by comparison with each object and each ID.
5. Conclusions
In this paper, we proposed a probability-based framework for underwater object recognition using sonar images. The acoustic image received from an imaging sonar is unstable due to ultrasonic waves. Hence, it is difficult to detect and recognize objects. To solve this problem, simple-shaped artificial landmarks were designed to improve detectability by the imaging sonar. Furthermore, to detect these landmarks, we adopted a probability-based recognition framework, which consists of three steps: (1) candidate selection, (2) continuity evaluation and (3) Bayesian estimation for recognition. We selected a number of objects with high similarity scores as candidates using Hough circle transform. The continuity of candidates in a series of images is evaluated by particle filter. Lastly, a recognition method based on Bayesian rule verifies the probability of obtaining the ID of each candidate. The experiment was performed to compare the performance of the proposed framework method with that of the SMI method and the results show that the proposed framework method, with continuous probability evaluation, enhances the recognition performance in the sonar image.
By developing and verifying the proposed method, we have found some practical and challenging issues for the underwater object recognition using sonar images. First, the acoustic frequency of imaging sonar highly affects the quality of object recognition. Adequate acoustic frequency should be selected according to the application. Second, characteristics of sonar image are quite different from the optical image. Image processing should be performed by considering the characteristics of sonar image not directly using the conventional technique of optical image. Finally, it is not easy to recognize arbitrary underwater objects using imaging sonar. Thus, we need to develop a recognition method considering a target object and its surface condition that affects the amount of reflective acoustic wave.
Future plans for further improvement to the proposed method include the following: (1) the proposed method can be applied to other types of underwater objects. Even though object recognition of arbitrary underwater objects is difficult, it can be used to recognize specific underwater objects such as mines or pipelines; (2) we will attempt to use the object recognition method for autonomous underwater robot navigation. The underwater robot can explore the underwater environment by correcting its position using the recognized object.
Acknowledgments
This research was supported by a grant from the endowment project of “Development of fundamental technologies on underwater environmental recognition for long-range navigation and intelligent autonomous underwater navigation” funded by the Korea Research Institute of Ships and Ocean engineering (KRISO,PES9000) and “Development of an autonomous swimming technology with less than 1.0 m position error for underwater robot operating in man-made structural environment” funded by the Ministry of Trade, Industry & Energy (MOTIE,PNS2980).
Author Contributions
Yeongjun Lee conceived and developed the idea, designed and implemented experiments; Jinwoo Choi and Nak Yong Ko collaborated in the conception and development of the idea; The paper was written by Yeongjun Lee, and revised by Jinwoo Choi and Hyun-Taek Choi.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Carlevaris-Bianco, N.; Mohan, A.; Eustice, R.M. Initial results in underwater single image dehazing. In Proceedings of the International Conference Oceans, Seattle, WA, USA, 20–23 September 2010. [Google Scholar]
- Kim, D.; Lee, D.; Myung, H.; Choi, H. Artificial landmark-based underwater localization for AUVs using weighted template matching. Intell. Serv. Robot. 2014, 7, 175–184. [Google Scholar] [CrossRef]
- Kim, A.; Eustice, R.M. Pose-graph visual SLAM with geometric model selection for autonomous underwater ship hull inspection. In Proceedings of the International Conference on Intelligent Robotics and Systems, St. Louis, MO, USA, 10–15 Octomber 2009. [Google Scholar]
- Whitcomb, L.; Yoerger, D.R.; Singh, H.; Howland, J. Advances in underwater robot vehicles for deep ocean exploration: Navigation, control, and survey operations. In Robotics Research; Springer: London, UK, 2000; pp. 439–448. [Google Scholar]
- Park, J.; Jun, B.; Lee, P.; Oh, J. Experiments on vision guided docking of an autonomous underwater vehicle using one camera. Ocean Eng. 2009, 36, 48–61. [Google Scholar] [CrossRef]
- Kim, D.; Lee, D.; Myung, H.; Choi, H. Object detection and tracking for autonomous underwater robots using weighted template matching. In Proceedings of the International Conference Oceans, Yeosu, Korea, 21–24 May 2012. [Google Scholar]
- VanMiddlesworth, M.; Hover, F.S.; Leonard, J.J. Mapping 3D Underwater Environments with Smoothed Submaps. In Field and Service Robotics; Springer: Cham, Switzerland, 2013; pp. 17–30. [Google Scholar]
- Kim, K.; Neretti, N.; Intrator, N. Mosaicing of acoustic camera images. IEE Proc. Ridar Sonar Navig. 2005, 152, 263–270. [Google Scholar] [CrossRef]
- Hurtos, N.; Ribas, D.; Cuf’, X.; Petillot, Y.; Salvi, J. Fourier-based registrations for two-dimensional forward-looking sonar image mosaicing. In Proceedings of the International Conference on Intelligent Robotics and Systems, Vilamoura, Portugal, 7–12 October 2012. [Google Scholar]
- Lee, Y.; Kim, T.; Choi, H. A New Approach of Detection and Recognition for Artificial Landmarks from Noisy Acoustic Images. In Robot Intelligence Technology and Applications 2; Springer: Cham, Switzerland, 2014; pp. 851–858. ISBN 978-3-319-05581-7. [Google Scholar]
- Ribas, D.; Ridao, P.; Tardos, J.; Neira, J. Underwater SLAM in man-made structured environment. Field Robot. 2008, 25, 898–921. [Google Scholar] [CrossRef]
- Folkesson, J.; Leonard, J.; Leederkerken, J.; Williams, R. Feature tracking for underwater navigation using sonar. In Proceedings of the International Conference on Intelligent Robotics and Systems, San Diego, CA, USA, 29 October–2 November 2007. [Google Scholar]
- Honsho, C.; Ura, T.; Asada, A. Mapping the Bayonnaise knoll caldera and the Hakurei hydrothermal deposit with autonomous underwater vehicle using side-scan and multi-beam sonars. In Proceedings of the IEEE International Underwater Technology Symposium (UT), Tokyo, Japan, 5–8 March 2013. [Google Scholar]
- Hover, F.S.; Eustice, R.M.; Kim, A.; Englot, B.; Johannsson, H.; Kaess, M.; Leonard, J.J. Advanced perception, navigation and planning for autonomous in-water ship hull inspection. Robot. Res. 2012, 31, 1445–1464. [Google Scholar] [CrossRef]
- Chaillan, F.; Fraschini, C.; Courmontagne, P. Speckle noise reduction in SAS imagery. Signal Process. 2007, 87, 762–781. [Google Scholar] [CrossRef]
- John, P.F.; Arnold, C. Sound Underwater Images: A Guide to the Generation and Interpretation of Side Scan Sonar Data; Lower Cape Pub Co.: Orleans, MA, USA, 1990; pp. 104–118. ISBN 978-0936972145. [Google Scholar]
- Hurtos, N.; Ribas, D.; Cufí, X.; Petillot, Y.; Salvi, J. Fourier-based registrations for robust forward-looking soanr mosaicing in low-visibility underwwater envirionments. Field Robot. 2015, 32, 123–151. [Google Scholar] [CrossRef]
- Johannsson, H.; Kaess, M.; Englot, B.; Hover, F.; Leonard, J. Imaging sonar-aided navigation for autonomous underwater harbor surveillance. In Proceedings of the International Conference on Intelligent Robotics and Systems, Taipei, Taiwan, 18–22 October 2010. [Google Scholar]
- Fallon, M.; Folkesson, J.; McClelland, H.; Leonard, J. Relocating Underwater Features Autonomously Using Sonar-Based SLAM. Ocean Eng. 2013, 38, 500–513. [Google Scholar] [CrossRef]
- Yu, S.C. Development of real-time acoustic image recognition system using by autonomous marine vehicle. Ocean Eng. 2008, 25, 90–105. [Google Scholar] [CrossRef]
- Cho, H.; Gu, J.; Joe, H.; Asada, A.; Yu, S.C. Acoustic beam profile-based rapid underwater object detection for an imaging sonar. J. Mar. Sci. Technol. 2015, 20, 180–197. [Google Scholar] [CrossRef]
- Rhody, H. Lecture 10: Hough circle transform; Rochester Institute of Technology: Rochester, NY, USA, 2005. [Google Scholar]
- Goshtasby, A. Description and Discrimination of Planar Shapes Using Shape Matrices. IEEE Trans. Pattern Anal. Mach. Intell. 1985, 6, 738–743. [Google Scholar] [CrossRef]
- Belcher, E.; Hanot, W.; Burch, J. Dual-Frequency Identification Sonar (DIDSON). IEEE Int. Underw. Technol. Symp. (UT) 2002, 187–192. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Int. Assoc. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).