Inhomogeneous Oxygen Vacancy Distribution in Semiconductor Gas Sensors: Formation, Migration and Determination on Gas Sensing Characteristics
Abstract
1. Introduction
2. Gradient-Distributed Oxygen Vacancy Model
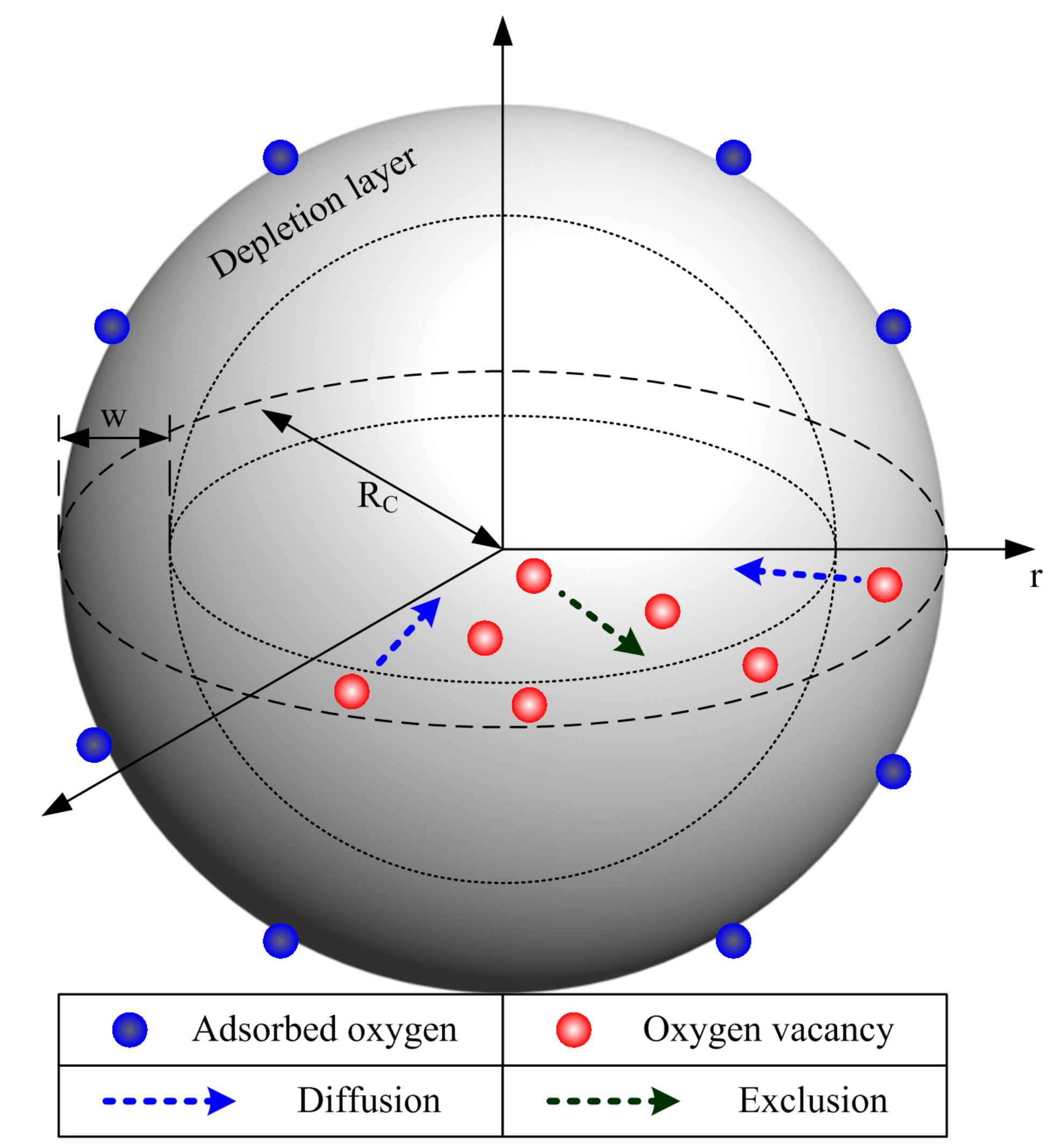
2.1. Model Description
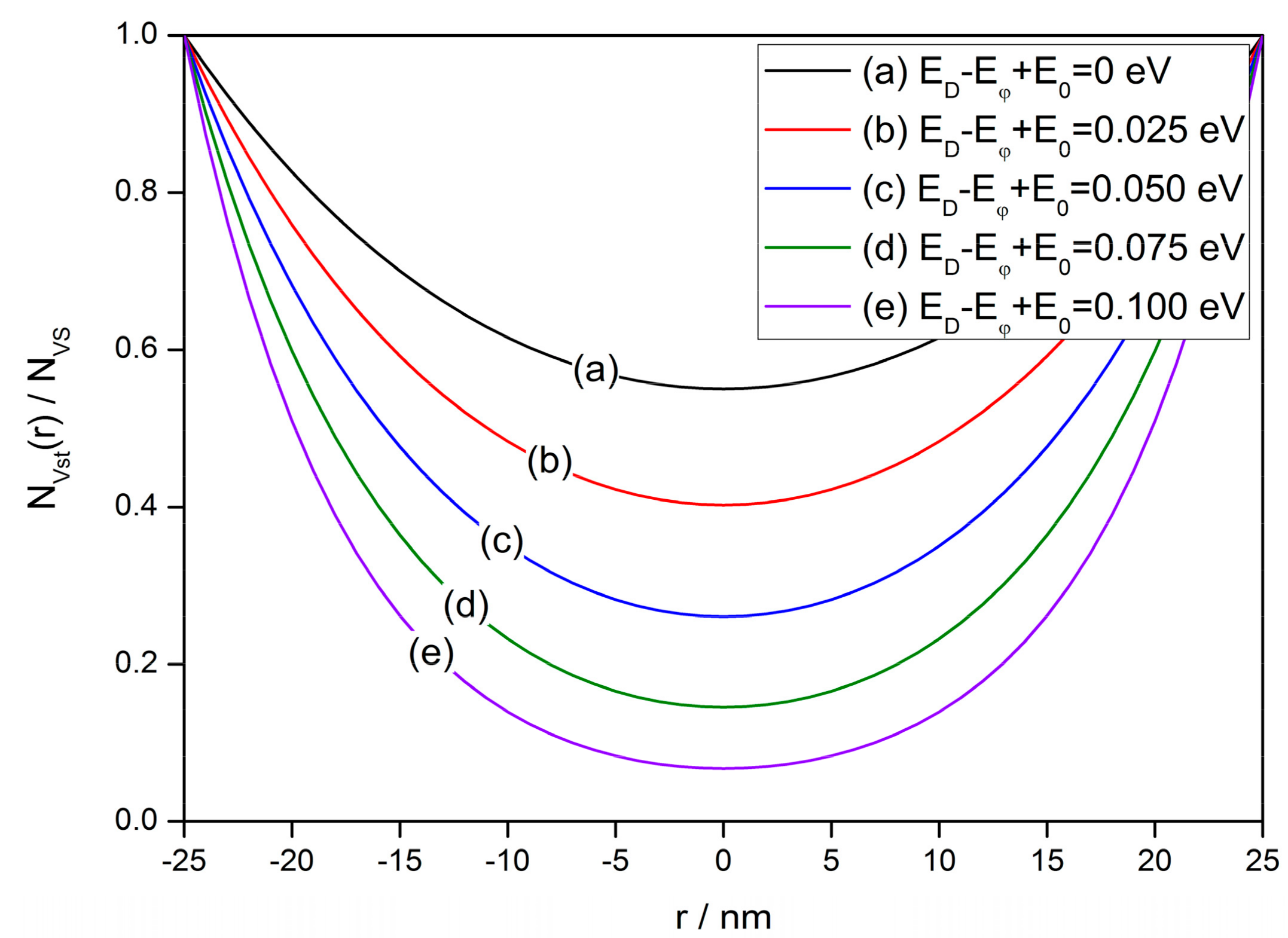
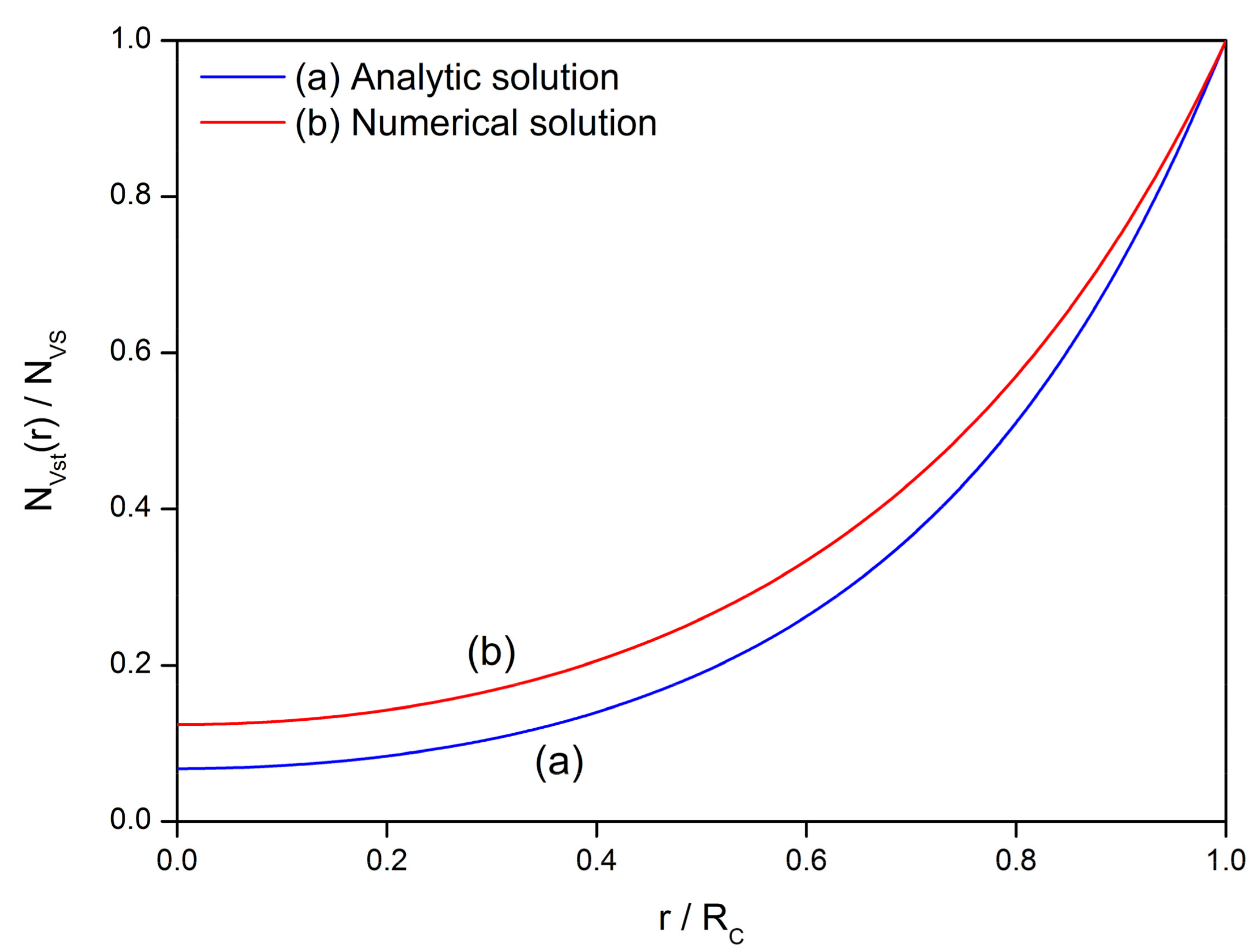
2.2. Steady-State Distribution
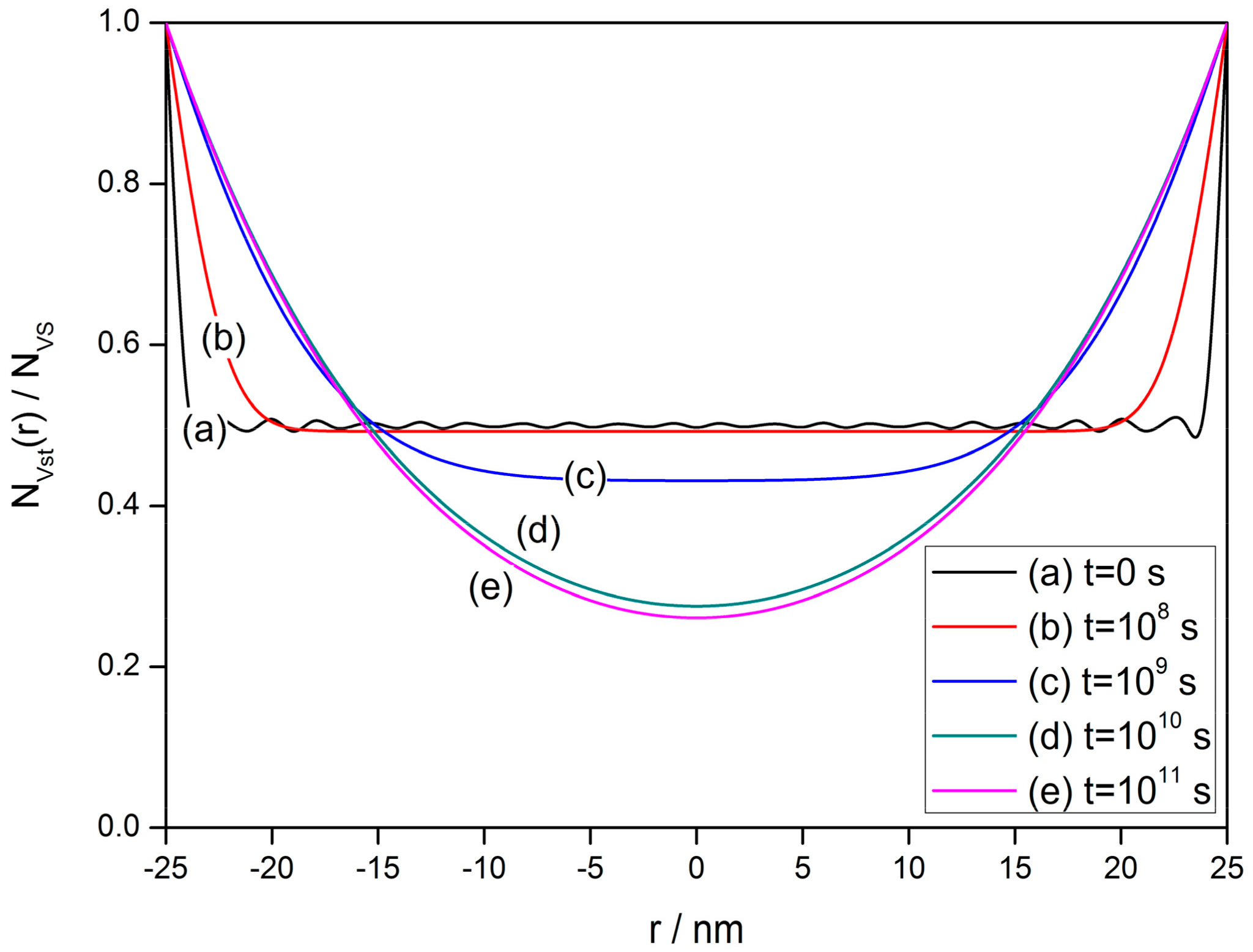
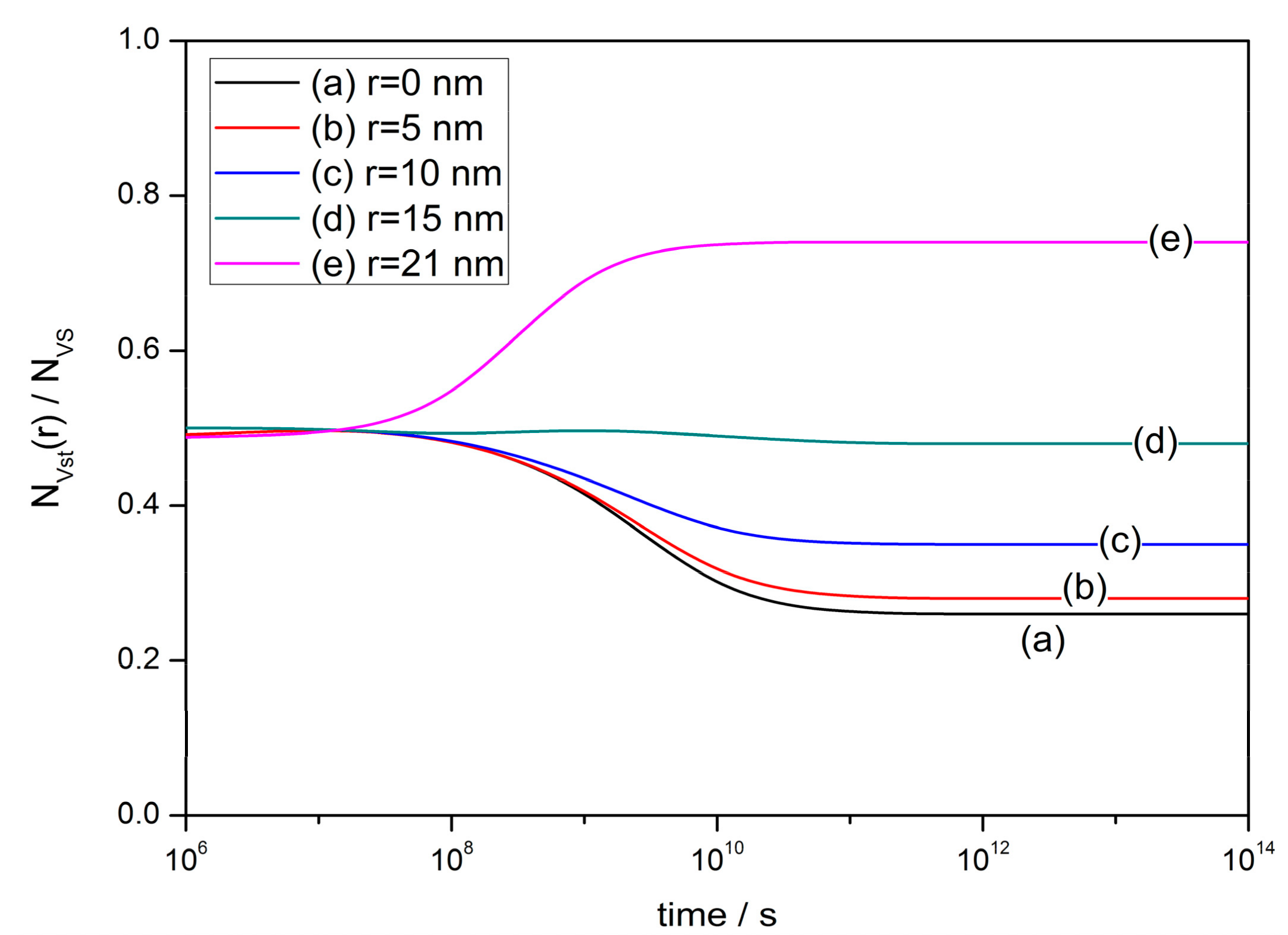
2.3. Transitent-State Distribution
3. Gas-Sensing Characteristics
3.1. Sensor Resistance
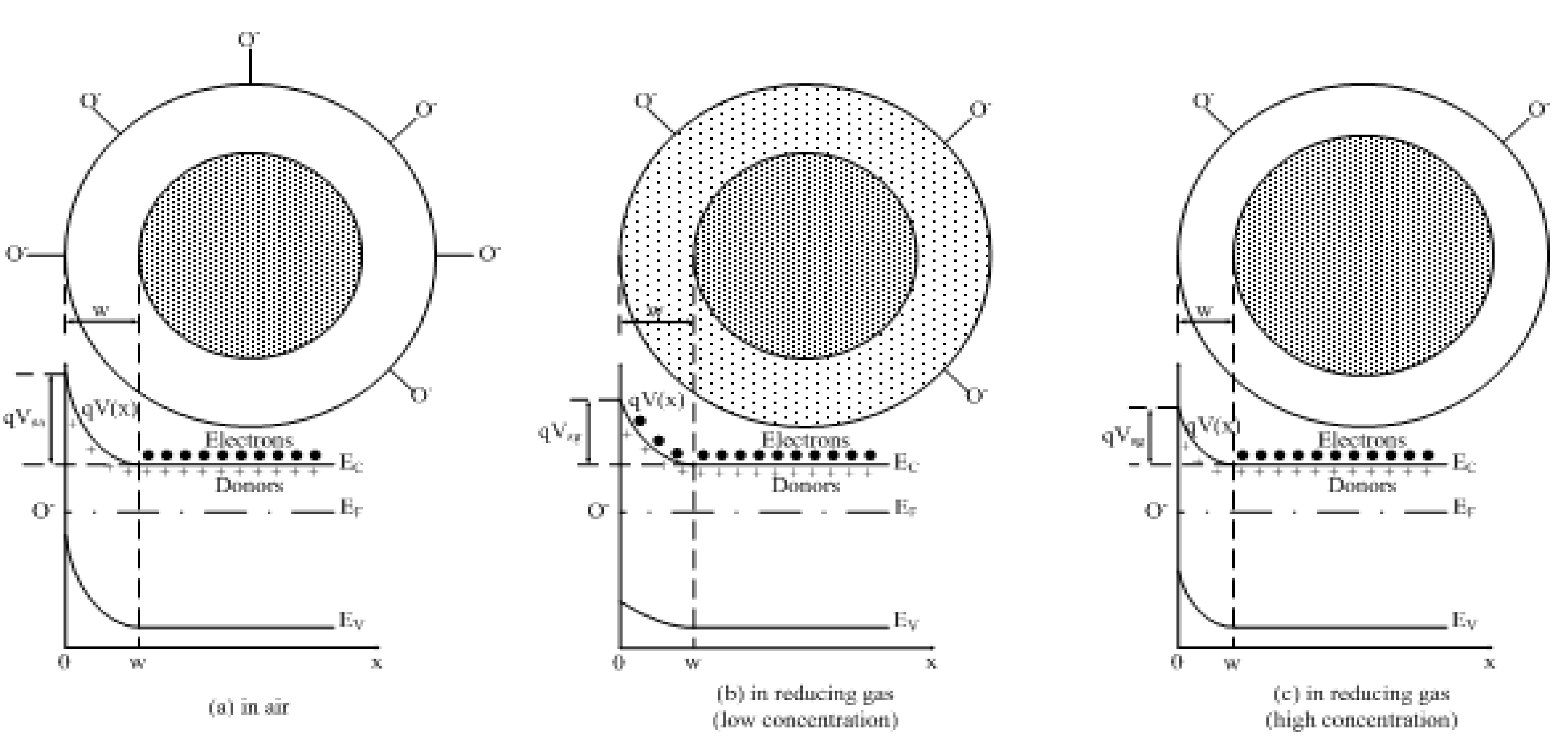
3.2. Response to Reducing Gases
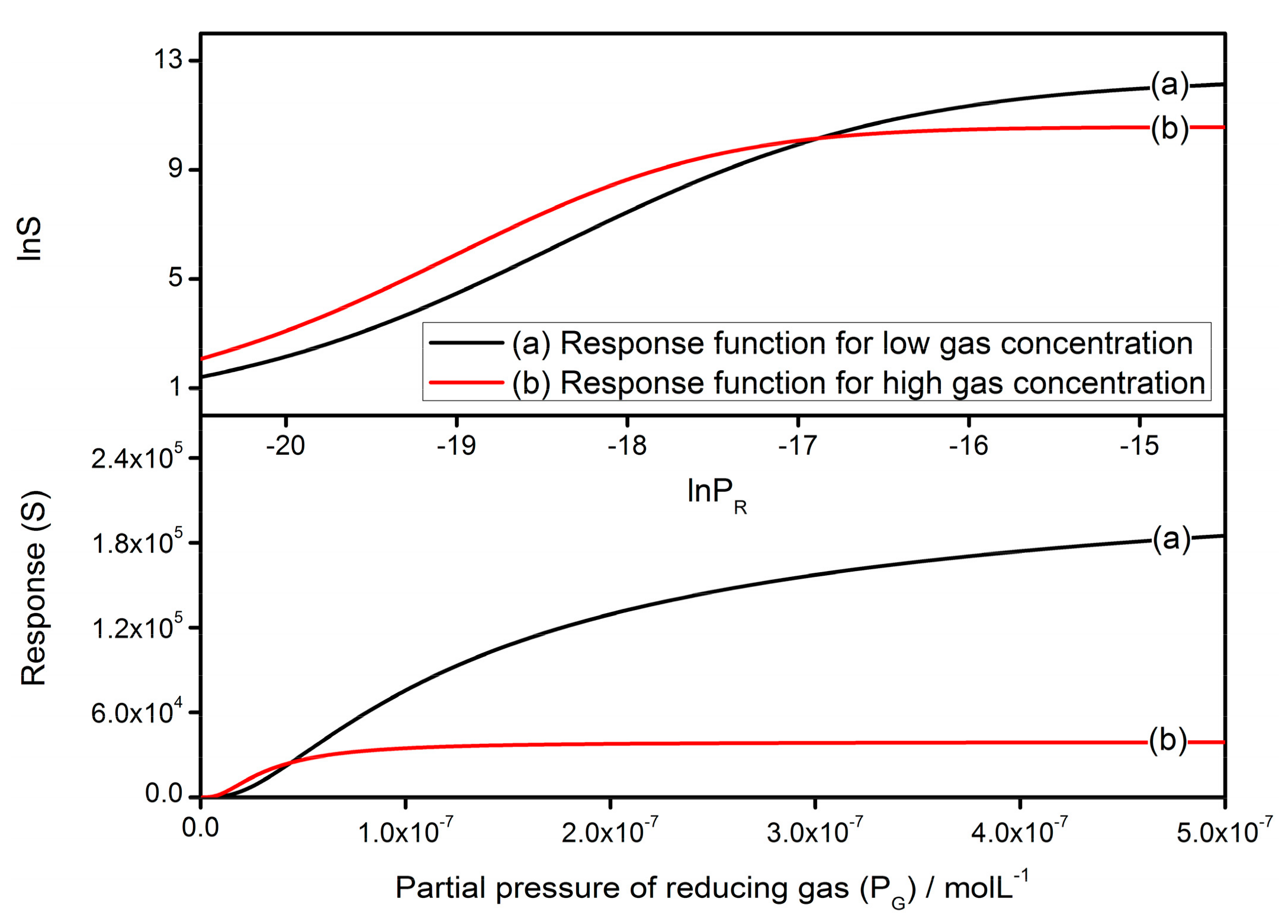
3.2.1. Low Gas Concentration
3.2.2. High Gas Concentration
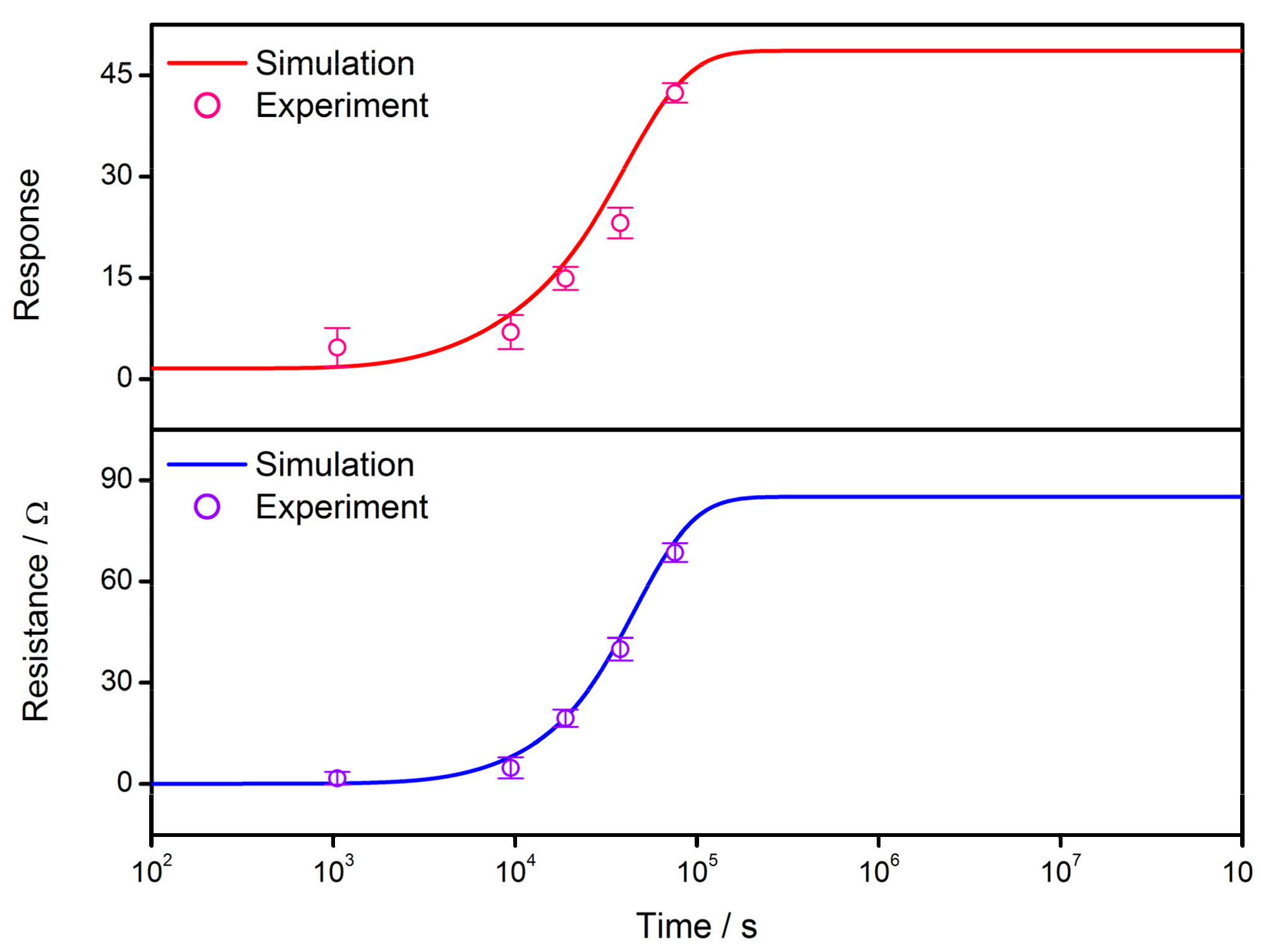
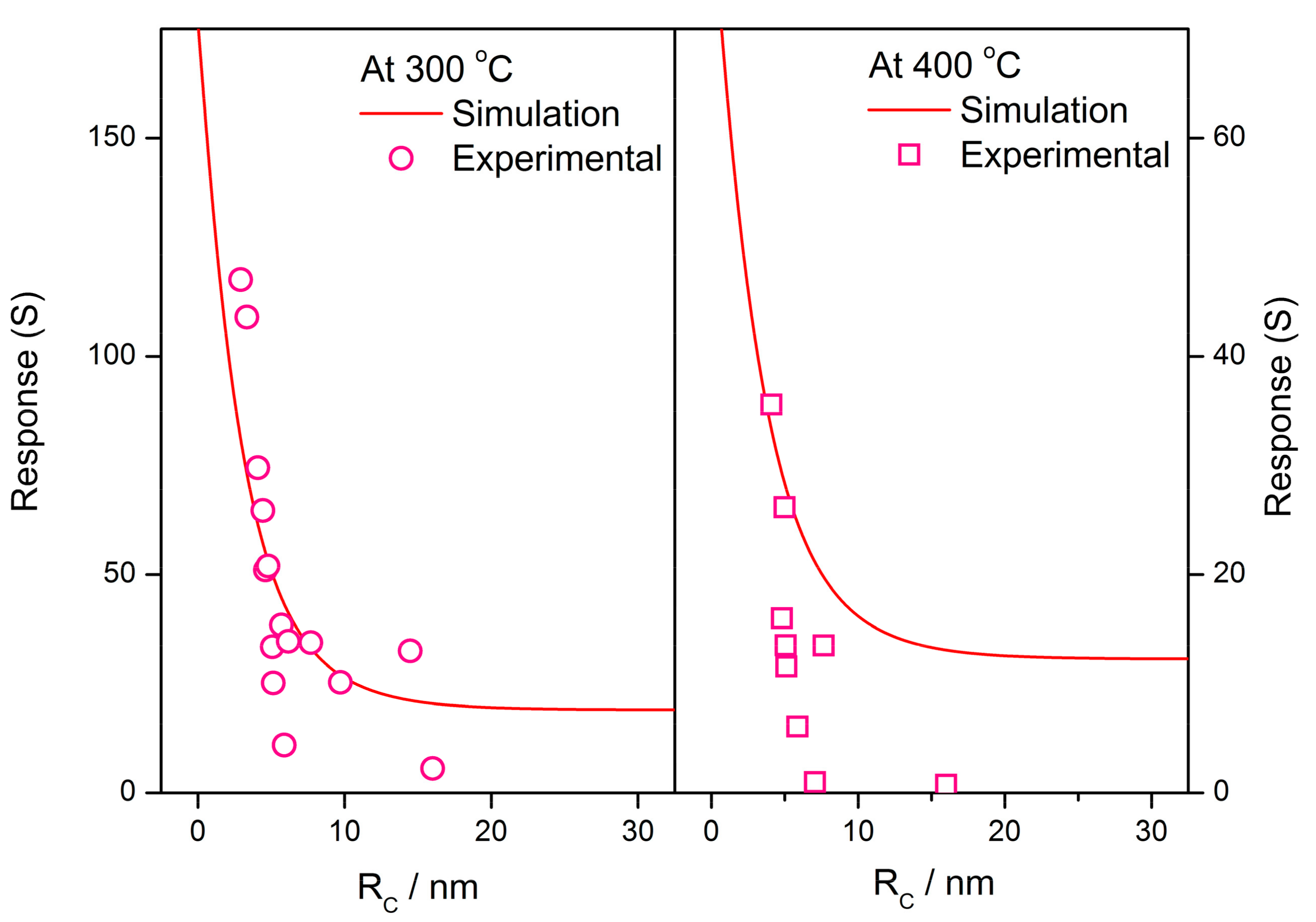
3.3. Model Validity
4. Applications in Sensor Performance Simulation
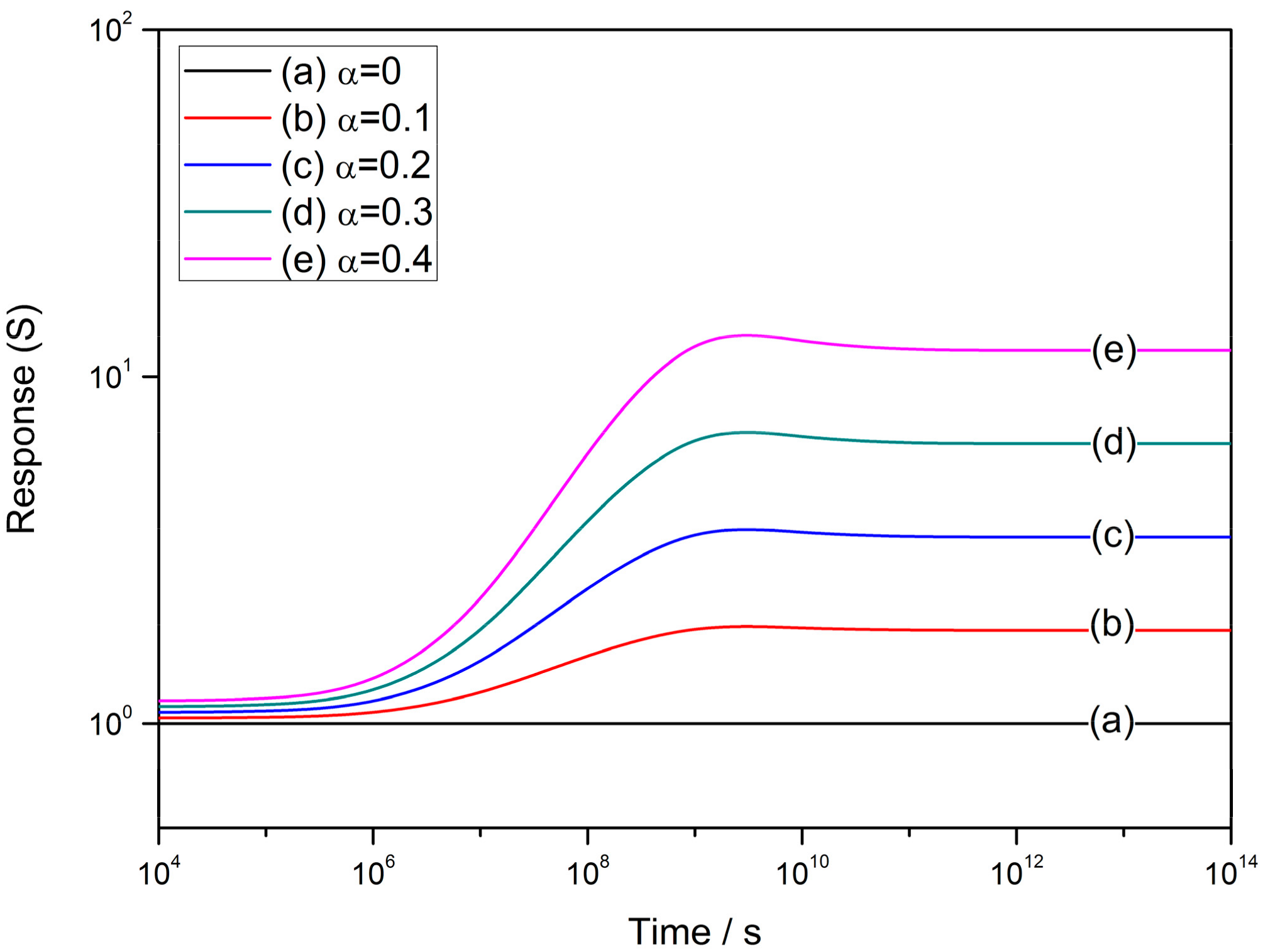
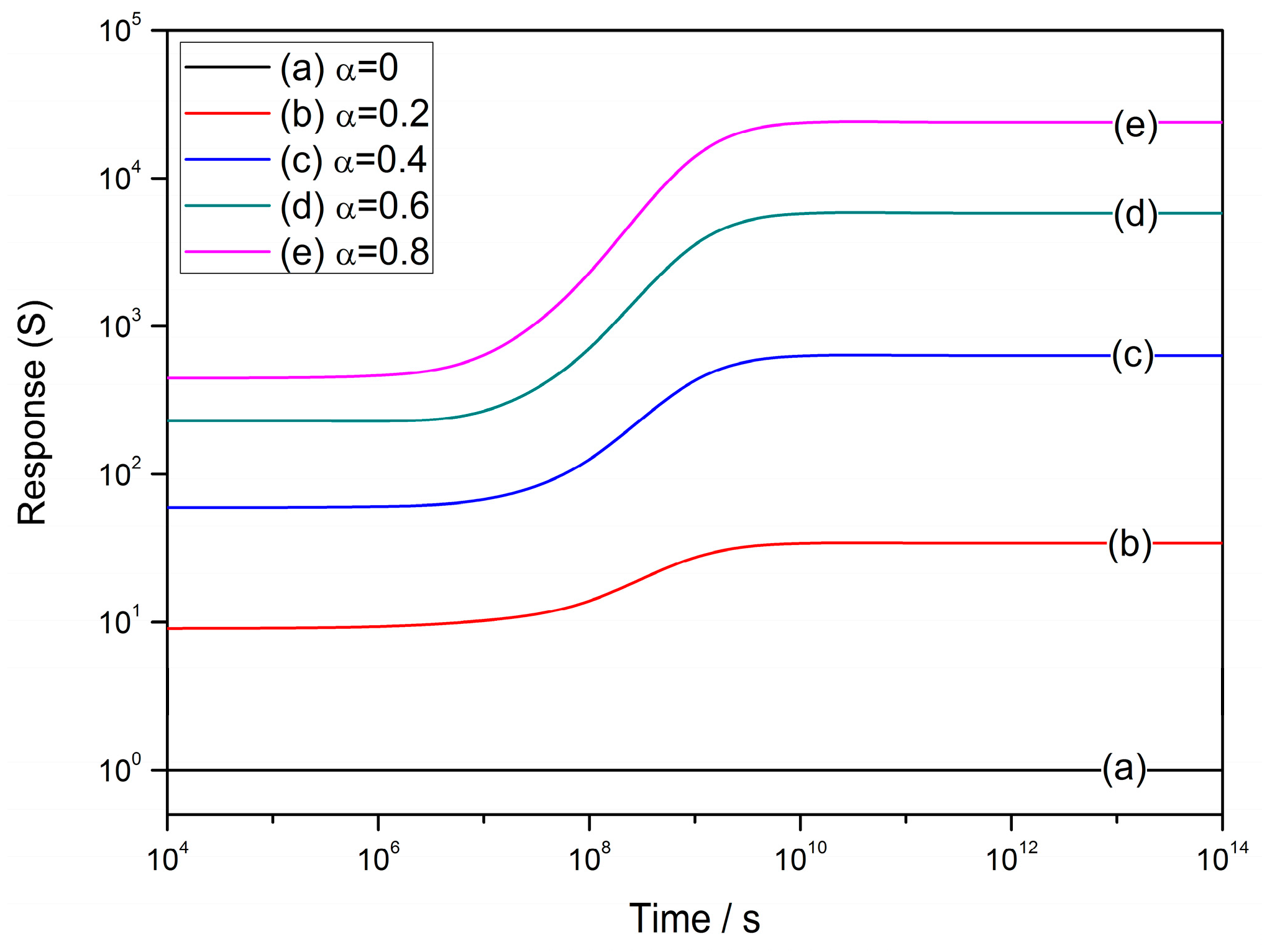
4.1. The Power Law
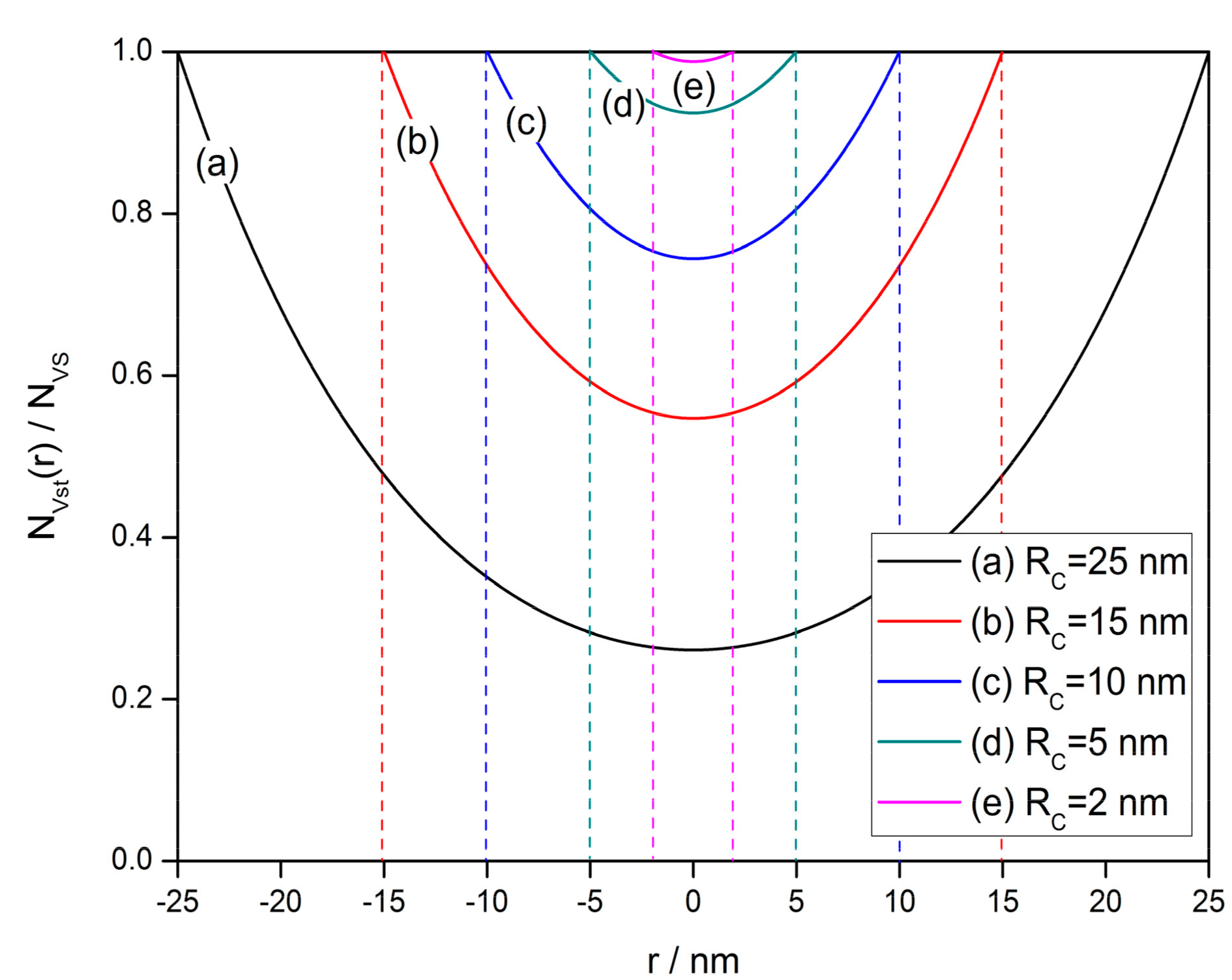
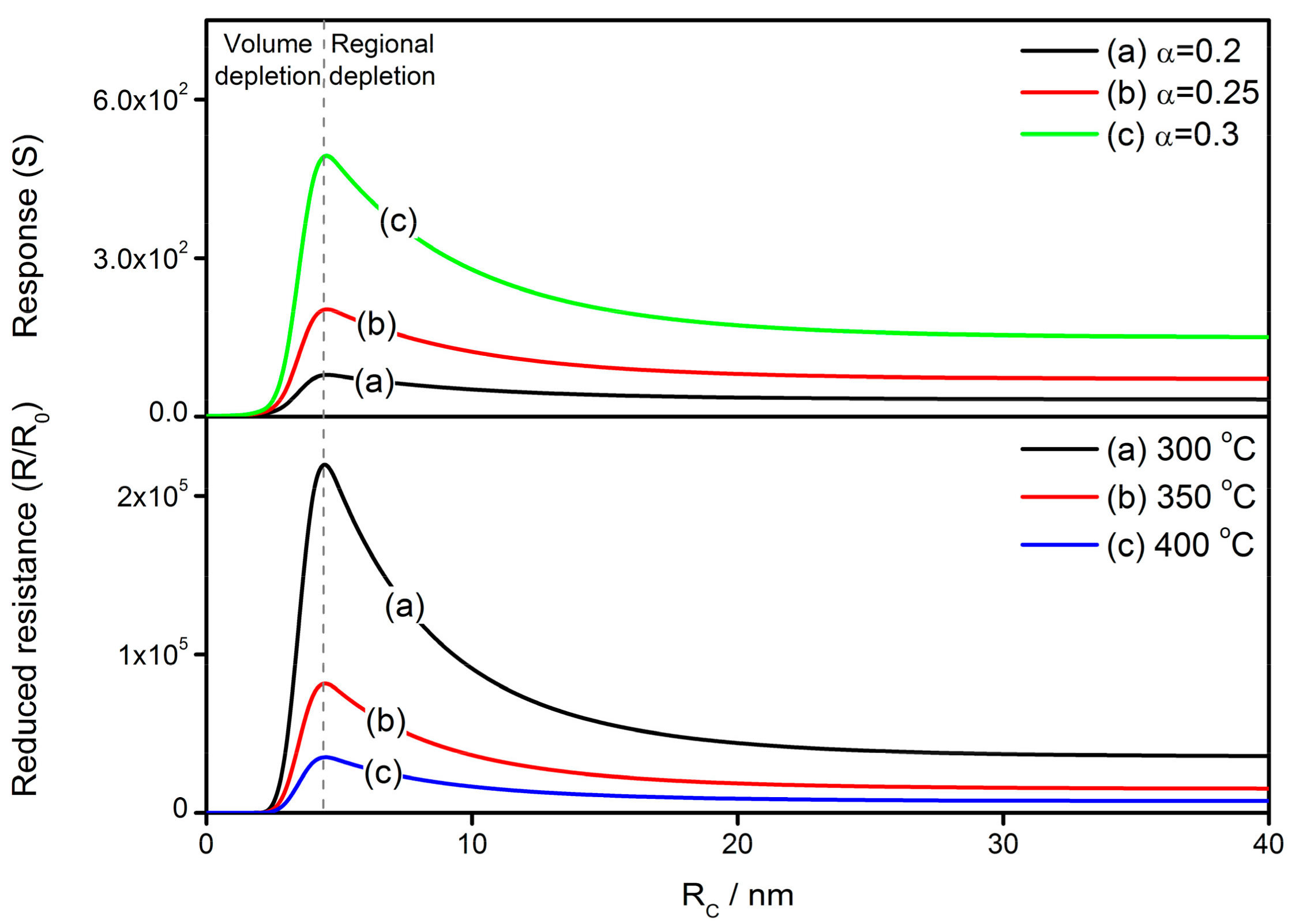
4.2. The Grain Size Effect
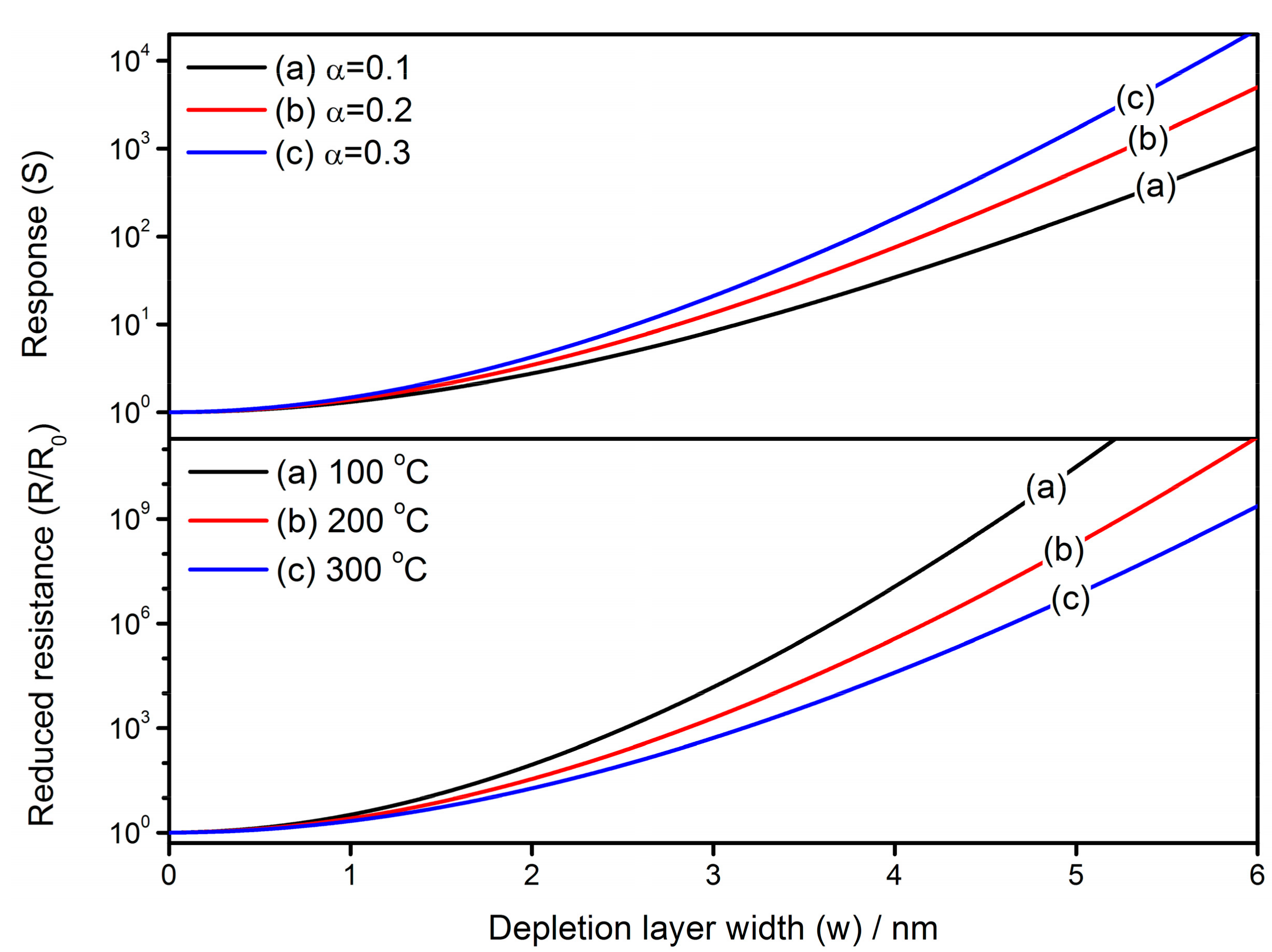
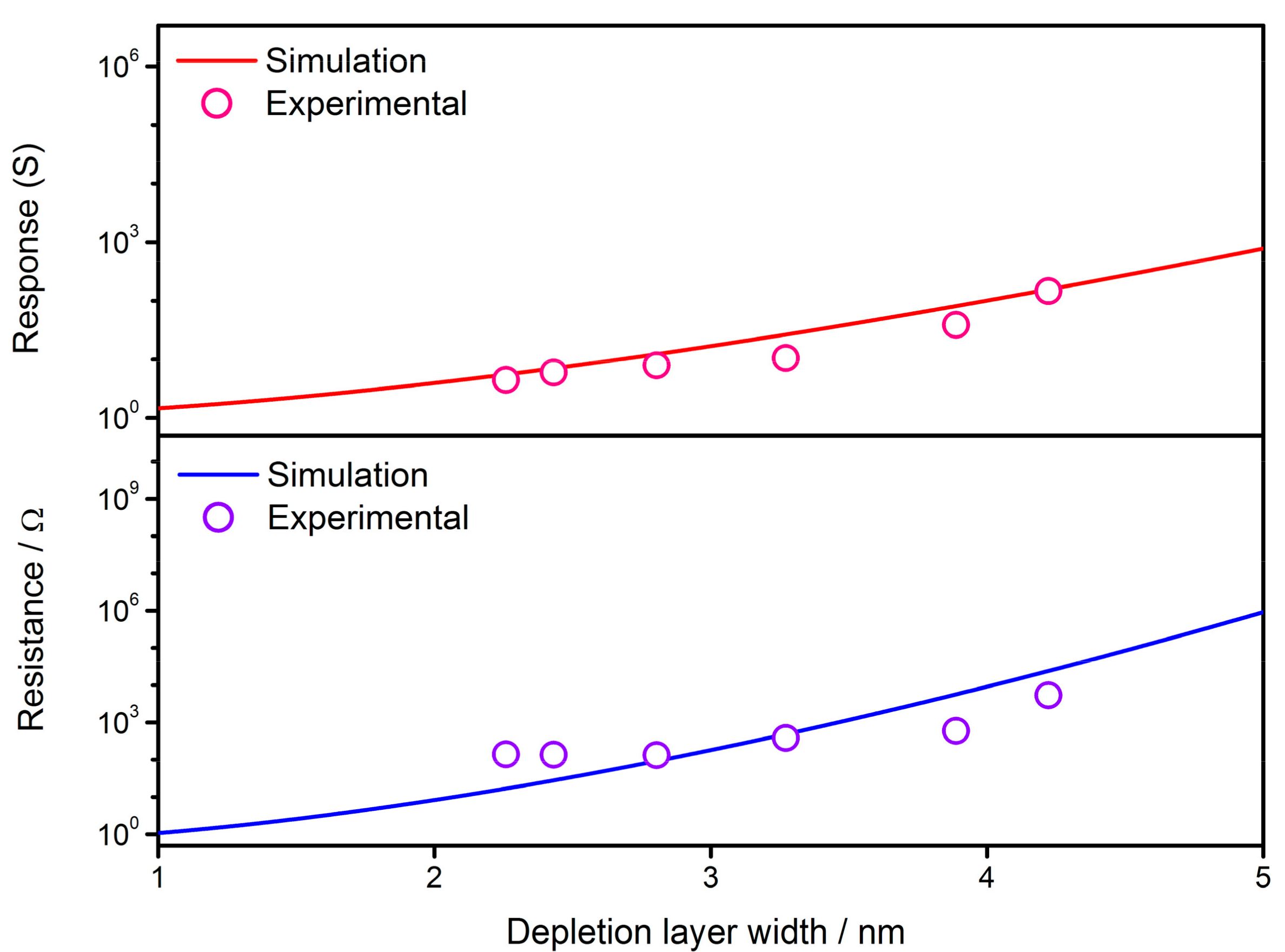
4.3. Effect of Depletion Layer Width
5. Discussion
6. Conclusions
- (1)
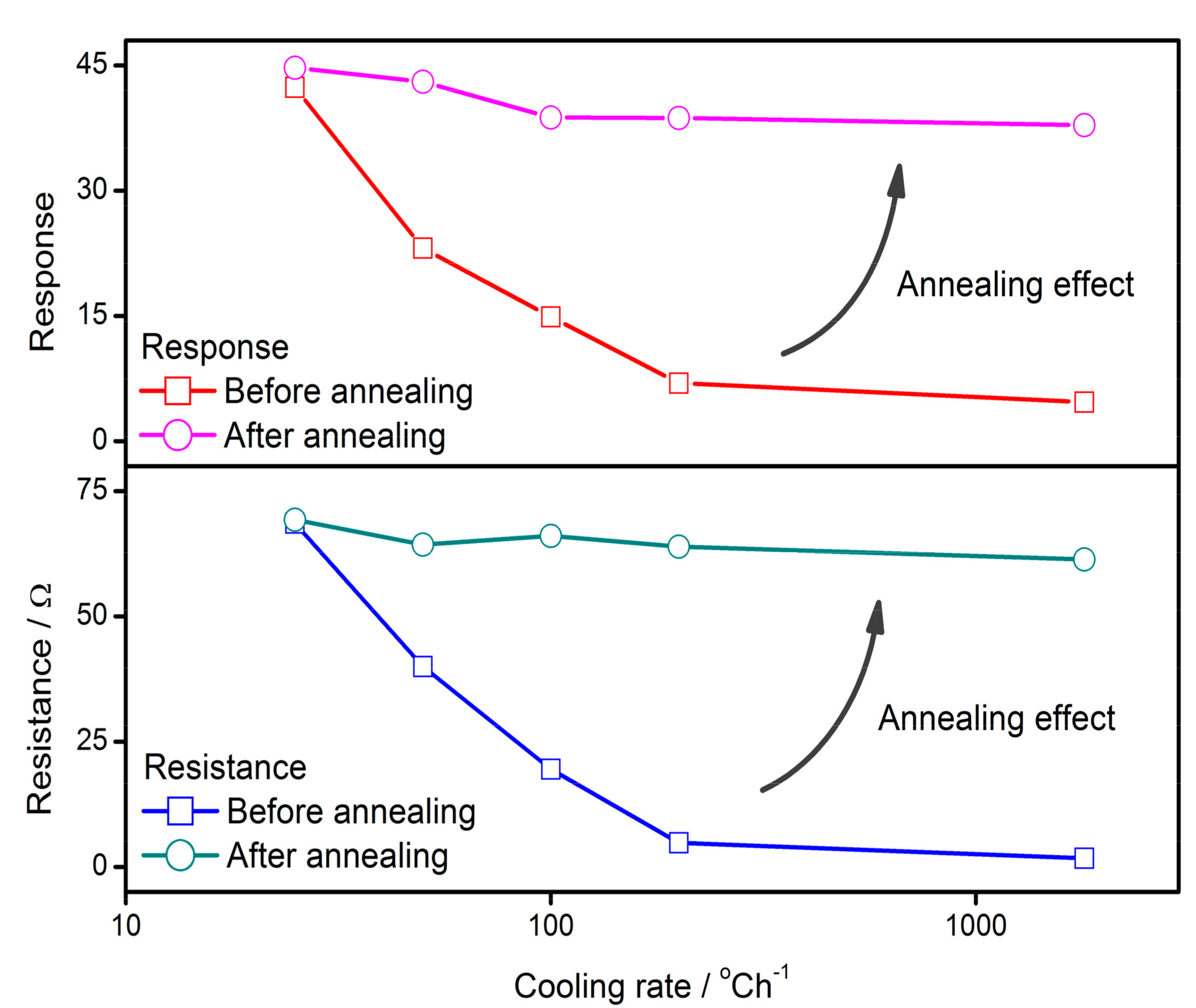
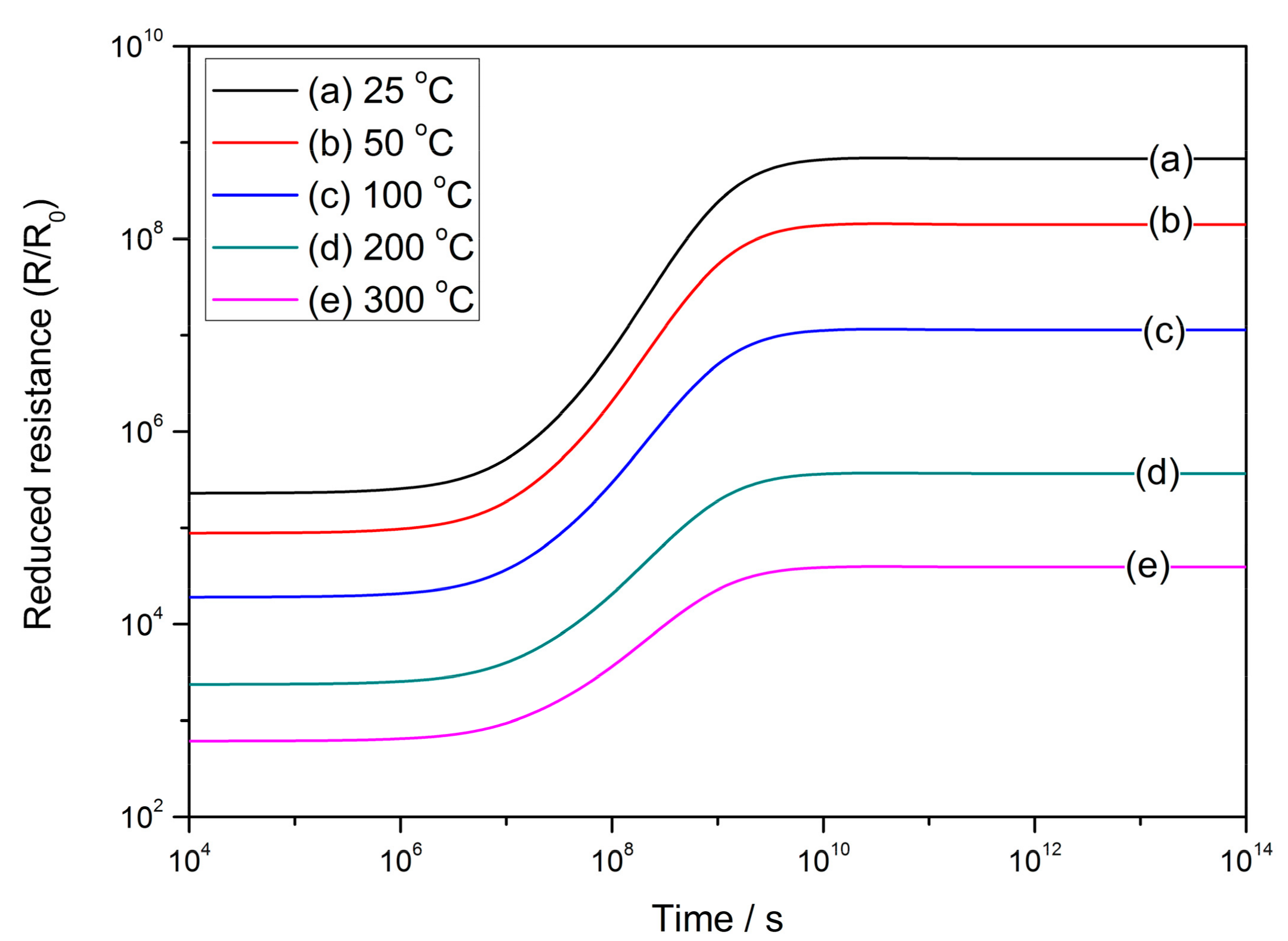
- The performances of semiconductor gas sensors are found to be influenced by cooling rate during cooling or annealing process. A low cooling rate may enhance the sensor resistance and response to reducing gas. The annealing technique may recover the sensing ability of the quenched sample, the properties of which are raised from low values to the same level as the slowly-cooled one. It is inferred that a process that determines the sensor properties is interrupted by quenching and it is restarted by the subsequent annealing.
- (2)
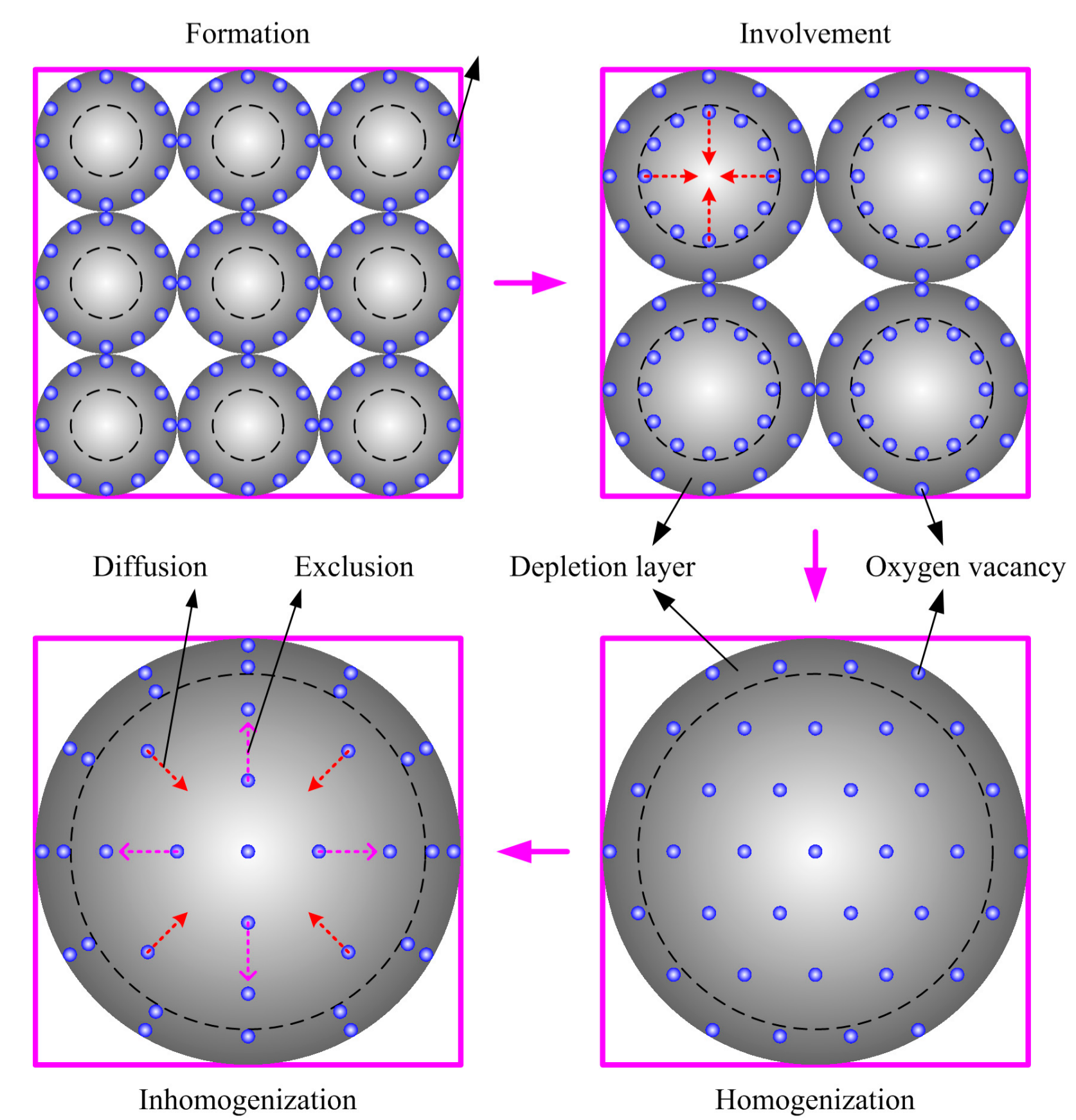
- The experimental phenomenon above leads to the investigation of oxygen vacancy behaviors during the fabrication process of semiconductor gas sensors. A diffusion equation is established based on the defect kinetics of diffusion and exclusion. The analytical solution illustrates the steady-state and transient-state distributions of oxygen vacancies in the grain. The behaviors of oxygen vacancies during sintering process are divided into four stages, which are namely formation, involvement, homogenization distribution and inhomogenization distribution.
- (3)
- The gas-sensing characteristics of the semiconductor are simulated after the VO density distribution expressions are incorporated with the Poisson’s equation in double Schottky model. The sensor resistance and response to reducing gas are both dependent on the time elapsed during the cooling process due to the migration of oxygen defects inside the grain. The validity of simulations is checked by the experimental results and are consistent with each other. The simulations infer that it is possible to control the sensor properties by interrupting the cooling process at a proper time in order to acquire a gas sensor with required characteristics. The GDOV model is also used to provide quantitative explanations for several key characteristics of semiconductor gas sensors, including the power law, grain size effect and effect of depletion layer width.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Taguchi, N. A Metal Oxide Gas Sensor. Japanese Patent 45-38200, 1962. [Google Scholar]
- Seiyama, T.; Kato, A.; Fujiishi, K.; Nagatani, M. A new detector for gaseous components using semiconductive thin films. Anal. Chem. 1962, 34, 1502–1503. [Google Scholar] [CrossRef]
- Jerger, A.; Kohler, H.; Becker, F.; Keller, H.B.; Seifert, R. New applications of tin oxide gas sensors: II. Intelligent sensor system for reliable monitoring of ammonia leakages. Sens. Actuator B Chem. 2002, 81, 301–307. [Google Scholar] [CrossRef]
- Rella, R.; Siciliano, P.; Capone, S.; Epifani, M.; Vasanelli, L.; Licciulli, A. Air quality monitoring by means of sol-gel integrated tin oxide thin films. Sens. Actuator B Chem. 1999, 58, 283–288. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, Y.; Huang, J.; Wang, Y.; Ren, H.; Wu, S.; Zhang, S.; Huang, W. Low-temperature CO gas sensors based on Au-SnO2 thick film. Appl. Surf. Sci. 2007, 253, 3057–3061. [Google Scholar] [CrossRef]
- Kocemba, I.; Szafran, S.; Rynkowski, J.M.; Paryjczak, T. Sensors based on SnO2 as a detector for CO oxidation in air. React. Kinet. Catal. Lett. 2001, 72, 107–114. [Google Scholar] [CrossRef]
- Singh, S.; Verma, N.; Singh, A.; Yadav, B.C. Synthesis and characterization of CuO–SnO2 nanocomposite and its application as liquefied petroleum gas sensor. Mater. Sci. Semicond. Proc. 2014, 18, 88–96. [Google Scholar] [CrossRef]
- Choi, J.Y.; Oh, T.S. CO sensitivity of La2O3-doped SnO2 thick film gas sensor. Thin Solid Films 2013, 547, 230–234. [Google Scholar] [CrossRef]
- Hübner, M.; Bârsan, N.; Weimar, U. Influences of Al, Pd and Pt additives on the conduction mechanism as well as the surface and bulk properties of SnO2 based polycrystalline thick film gas sensors. Sens. Actuator B Chem. 2012, 171, 172–180. [Google Scholar] [CrossRef]
- Liu, H.; Wu, S.; Gong, S.; Zhao, J.; Liu, J.; Zhou, D. Nanocrystalline In2O3-SnO2 thick films for low-temperature hydrogen sulfide detection. Ceram. Int. 2011, 37, 1889–1894. [Google Scholar] [CrossRef]
- Bârsan, N.; Hübner, M.; Weimar, U. Conduction mechanisms in SnO2 based polycrystalline thick film gas sensors exposed to CO and H2 in different oxygen backgrounds. Sens. Actuator B Chem. 2011, 157, 510–517. [Google Scholar] [CrossRef]
- Oprea, A.; Gurlo, A.; Barsan, N.; Weimar, U. Transport and gas sensing properties of In2O3 nanocrystalline thick films: A Hall effect based approach. Sens. Actuator B Chem. 2009, 139, 322–328. [Google Scholar] [CrossRef]
- Malagù, C.; Carotta, M.; Gherardi, S.; Guidi, V.; Vendemiati, B.; Martinelli, G. AC measurements and modeling of WO3 thick film gas sensors. Sens. Actuator B Chem. 2005, 108, 70–74. [Google Scholar] [CrossRef]
- Ansari, S.; Boroojerdian, P.; Sainkar, S.; Karekar, R.; Aiyer, R.; Kulkarni, S. Grain size effects on H2 gas sensitivity of thick film resistor using SnO2 nanoparticles. Thin Solid Films 1997, 295, 271–276. [Google Scholar] [CrossRef]
- Zhao, X.; Shi, W.; Mu, H.; Xie, H.; Liu, F. Templated bicontinuous tin oxide thin film fabrication and the NO2 gas sensing. J. Alloy. Compd. 2016, 659, 60–65. [Google Scholar] [CrossRef]
- Marikkannan, M.; Vishnukanthan, V.; Vijayshankar, A.; Mayandi, J.; Pearce, J.M. A novel synthesis of tin oxide thin films by the sol-gel process for optoelectronic applications. AIP Adv. 2015, 5, 027122. [Google Scholar] [CrossRef]
- Lim, S.P.; Huang, N.M.; Lim, H.N.; Mazhar, M. Aerosol assisted chemical vapour deposited (AACVD) of TiO2 thin film as compact layer for dye-sensitised solar cell. Ceram. Int. 2014, 40, 8045–8052. [Google Scholar] [CrossRef]
- Zeng, J.; Hu, M.; Wang, W.; Chen, H.; Qin, Y. NO2-sensing properties of porous WO3 gas sensor based on anodized sputtered tungsten thin film. Sens. Actuator B Chem. 2012, 161, 447–452. [Google Scholar] [CrossRef]
- Brunet, E.; Maier, T.; Mutinati, G.C.; Steinhauer, S.; Köck, A.; Gspan, C.; Grogger, W. Comparison of the gas sensing performance of SnO2 thin film and SnO2 nanowire sensors. Sens. Actuator B Chem. 2012, 165, 110–118. [Google Scholar] [CrossRef]
- Korotcenkov, G.; Han, S.-D.; Cho, B.; Brinzari, V. Grain size effects in sensor response of nanostructured SnO2-and In2O3-based conductometric thin film gas sensor. Crit. Rev. Solid State 2009, 34, 1–17. [Google Scholar] [CrossRef]
- Lee, Y.; Huang, H.; Tan, O.; Tse, M. Semiconductor gas sensor based on Pd-doped SnO2 nanorod thin films. Sens. Actuator B Chem. 2008, 132, 239–242. [Google Scholar] [CrossRef]
- Korotcenkov, G.; Brinzari, V.; Schwank, J.; DiBattista, M.; Vasiliev, A. Peculiarities of SnO2 thin film deposition by spray pyrolysis for gas sensor application. Sens. Actuator B Chem. 2001, 77, 244–252. [Google Scholar] [CrossRef]
- Brown, J.R.; Haycock, P.W.; Smith, L.M.; Jones, A.C.; Williams, E.W. Response behaviour of tin oxide thin film gas sensors grown by MOCVD. Sens. Actuator B Chem. 2000, 63, 109–114. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, S.; Liu, J.; Liu, H.; Gong, S.; Zhou, D. Tin oxide thin films prepared by aerosol-assisted chemical vapor deposition and the characteristics on gas detection. Sens. Actuator B Chem. 2010, 145, 788–793. [Google Scholar] [CrossRef]
- Gong, S.; Liu, J.; Quan, L.; Fu, Q.; Zhou, D. Preparation of tin oxide thin films on silicon substrates via sol-gel routes and the prospects for the H2S gas sensor. Sens. Lett. 2011, 9, 625–628. [Google Scholar] [CrossRef]
- Zhai, Z.; Liu, J.; Jin, G.; Luo, C.; Jiang, Q.; Zhao, Y. Characterization and gas sensing properties of copper-doped tin oxide thin films deposited by ultrasonic spray pyrolysis. Mater. Sci. 2016, 22, 201–204. [Google Scholar] [CrossRef]
- Miller, D.R.; Akbar, S.A.; Morris, P.A. Nanoscale metal oxide-based heterojunctions for gas sensing: A review. Sens. Actuator B Chem. 2014, 250–272. [Google Scholar] [CrossRef]
- Johari, A.; Johari, A.; Bhatnagar, M.C.; Sharma, M. Structural, optical and sensing properties of pure and Cu-doped SnO2 nanowires. J. Nanosci. Nanotechnol. 2014, 14, 5288–5292. [Google Scholar] [CrossRef] [PubMed]
- Jin, W.; Yan, S.; Chen, W.; Yang, S.; Zhao, C.; Dai, Y. Preparation and gas sensing property of Ag-supported vanadium oxide nanotubes. Funct. Mater. Lett. 2014, 7, 1450031. [Google Scholar] [CrossRef]
- Kumar, V.; Sen, S.; Muthe, K.P.; Gaur, N.K.; Gupta, S.K.; Yakhmi, J.V. Copper doped SnO2 nanowires as highly sensitive H2S gas sensor. Sens. Actuator B Chem. 2009, 138, 587–590. [Google Scholar] [CrossRef]
- Shukla, S.; Zhang, P.; Cho, H.J.; Seal, S.; Ludwig, L. Room temperature hydrogen response kinetics of nano-micro-integrated doped tin oxide sensor. Sens. Actuator B Chem. 2007, 120, 573–583. [Google Scholar] [CrossRef]
- Sahm, T.; Rong, W.; Bârsan, N.; Mädler, L.; Weimar, U. Sensing of CH4, CO and ethanol with in situ nanoparticle aerosol-fabricated multilayer sensors. Sens. Actuator B Chem. 2007, 127, 63–68. [Google Scholar] [CrossRef]
- Cioffi, N.; Traversa, L.; Ditaranto, N.; Taurino, A.M.; Epifani, M.; Siciliano, P.; Bleve-Zacheo, T.; Sabbatini, L.; Torsi, L.; Zambonin, P.G. Core-shell Pd nanoparticles embedded in SnOX films. Synthesis, analytical characterisation and perspective application in chemiresistor-type sensing devices. Microelectron. J. 2006, 37, 1620–1628. [Google Scholar] [CrossRef]
- Kong, X.; Li, Y. High sensitivity of CuO modified SnO2 nanoribbons to H2S at room temperature. Sens. Actuator B Chem. 2005, 105, 449–453. [Google Scholar] [CrossRef]
- Comini, E.; Faglia, G.; Sberveglieri, G.; Pan, Z.; Wang, Z.L. Stable and highly sensitive gas sensors based on semiconducting oxide nanobelts. Appl. Phys. Lett. 2002, 81, 1869–1871. [Google Scholar] [CrossRef]
- Tamaki, J.; Shimanoe, K.; Yamada, Y.; Yamamoto, Y.; Miura, N.; Yamazoe, N. Dilute hydrogen sulfide sensing properties of CuO-SnO2 thin film prepared by low-pressure evaporation method. Sens. Actuator B Chem. 1998, 49, 121–125. [Google Scholar] [CrossRef]
- Koziej, D.; Thomas, K.; Barsan, N.; Thibault-Starzyk, F.; Weimar, U. Influence of annealing temperature on the CO sensing mechanism for tin dioxide based sensors–Operando studies. Catal. Today 2007, 126, 211–218. [Google Scholar] [CrossRef]
- Jain, G.H.; Patil, L.A.; Wagh, M.S.; Patil, D.R.; Patil, S.A.; Amalnerkar, D.P. Surface modified BaTiO3 thick film resistors as H2S gas sensors. Sens. Actuator B Chem. 2006, 117, 159–165. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, C.; Sun, H.; Sun, P.; Wang, Y.; Lin, J.; Lu, G. Microwave assisted synthesis of hierarchical Pd/SnO2 nanostructures for CO gas sensor. Sens. Actuator B Chem. 2016, 222, 257–263. [Google Scholar] [CrossRef]
- Liu, H.; Wan, J.; Fu, Q.; Li, M.; Luo, W.; Zheng, Z.; Cao, H.; Hu, Y.; Zhou, D. Tin oxide films for nitrogen dioxide gas detection at low temperatures. Sens. Actuator B Chem. 2013, 177, 460–466. [Google Scholar] [CrossRef]
- Shuping, G.; Jing, X.; Jianqiao, L.; Dongxiang, Z. Highly sensitive SnO2 thin film with low operating temperature prepared by sol-gel technique. Sens. Actuator B Chem. 2008, 134, 57–61. [Google Scholar] [CrossRef]
- Haridas, D.; Gupta, V. Study of collective efforts of catlytic activity and photoactivation to enhance room temperature response of SnO2 thin film sensor for methane. Sens. Actuator B Chem. 2013, 182, 741–746. [Google Scholar] [CrossRef]
- Patil, L.A.; Patil, D.R. Heterocontact type CuO-modified SnO2 sensor for the detection of a ppm level H2S gas at room temperature. Sens. Actuator B Chem. 2006, 120, 316–323. [Google Scholar] [CrossRef]
- Ho, J.-J. Novel nitrogen monoxides (NO) gas sensors integrated with tungsten trioxide (WO3)/pin structure for room temperature operation. Solid State Electron. 2003, 47, 827–830. [Google Scholar] [CrossRef]
- Niranjan, R.S.; Chaudhary, V.A.; Mulla, I.S.; Vijayamohanan, K. A novel hydrogen sulfide room temperature sensor based on copper nanocluster functionalized tin oxide thin films. Sens. Actuator B Chem. 2002, 85, 26–32. [Google Scholar] [CrossRef]
- Fang, G.; Liu, Z.; Liu, C.; Yao, K. Room temperature H2S sensing properties and mechanism of CeO2-SnO2 sol-gel thin films. Sens. Actuator B Chem. 2000, 66, 46–48. [Google Scholar] [CrossRef]
- Yu, H.; Song, Z.; Liu, Q.; Ji, X.; Liu, J.; Xu, S.; Kan, H.; Zhang, B.; Liu, J.; Jiang, J.; et al. Colloidal synthesis of tungsten oxide quantum dots for sensitive and selective H2S gas detection. Sens. Actuator B Chem. 2017, 248, 1029–1036. [Google Scholar] [CrossRef]
- Li, M.; Zhang, W.; Shao, G.; Kan, H.; Song, Z.; Xu, S.; Yu, H.; Jiang, S.; Luo, J.; Liu, H. Sensitive NO2 gas sensors employing spray-coated colloidal quantum dots. Thin Solid Films 2016, 618 Pt B, 271–276. [Google Scholar] [CrossRef]
- Liu, H.; Xu, S.; Li, M.; Shao, G.; Song, H.; Zhang, W.; Wei, W.; He, M.; Gao, L.; Song, H. Chemiresistive gas sensors employing solution-processed metal oxide quantum dot films. Appl. Phys. Lett. 2014, 105, 766. [Google Scholar] [CrossRef]
- Liu, H.; Li, M.; Voznyy, O.; Hu, L.; Fu, Q.; Zhou, D.; Xia, Z.; Sargent, E.H.; Tang, J. Physically flexible, rapid-response gas sensor based on colloidal quantum dot solids. Adv. Mater. 2014, 26, 2718–2724. [Google Scholar] [CrossRef] [PubMed]
- Shouli, B.; Liangyuan, C.; Jingwei, H.; Dianqing, L.; Ruixian, L.; Aifan, C.; Liu, C.C. Synthesis of quantum size ZnO crystals and their gas sensing properties for NO2. Sens. Actuator B Chem. 2011, 159, 97–102. [Google Scholar] [CrossRef]
- Mosadegh Sedghi, S.; Mortazavi, Y.; Khodadadi, A. Low temperature CO and CH4 dual selective gas sensor using SnO2 quantum dots prepared by sonochemical method. Sens. Actuator B Chem. 2010, 145, 7–12. [Google Scholar] [CrossRef]
- Liu, H.; Li, M.; Shao, G.; Zhang, W.; Wang, W.; Song, H.; Cao, H.; Ma, W.; Tang, J. Enhancement of hydrogen sulfide gas sensing of PbS colloidal quantum dots by remote doping through ligand exchange. Sens. Actuator B Chem. 2015, 212, 434–439. [Google Scholar] [CrossRef]
- Li, M.; Zhou, D.; Zhao, J.; Zheng, Z.; He, J.; Hu, L.; Xia, Z.; Tang, J.; Liu, H. Resistive gas sensors based on colloidal quantum dot (CQD) solids for hydrogen sulfide detection. Sens. Actuator B Chem. 2015, 217, 198–201. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, W.; Yu, H.; Liang, G.; Song, Z.; Xu, S.; Min, L.; Yang, W.; Song, H.; Jiang, T. Solution-processed gas sensors employing SnO2 quantum dot/MWCNT Nanocomposites. ACS Appl. Mater. Interfaces 2016, 8, 840. [Google Scholar] [CrossRef] [PubMed]
- Song, Z.; Wei, Z.; Wang, B.; Luo, Z.; Xu, S.; Zhang, W.; Yu, H.; Li, M.; Huang, Z.; Zang, J. Sensitive room-temperature H2S gas sensors employing SnO2 quantum wire/reduced graphene oxide nanocomposites. Chem. Mater. 2016, 28, 1205–1212. [Google Scholar] [CrossRef]
- Zhang, B.; Li, M.; Song, Z.; Kan, H.; Yu, H.; Liu, Q.; Zhang, G.; Liu, H. Sensitive H2S gas sensors employing colloidal zinc oxide quantum dots. Sens. Actuator B Chem. 2017, 249, 558–563. [Google Scholar] [CrossRef]
- Song, Z.; Liu, J.; Liu, Q.; Yu, H.; Zhang, W.; Wang, Y.; Huang, Z.; Zang, J.; Liu, H. Enhanced H2S gas sensing properties based on SnO2 quantum wire/reduced graphene oxide nanocomposites: Equilibrium and kinetics modeling. Sens. Actuator B Chem. 2017, 249, 632–638. [Google Scholar] [CrossRef]
- Yamazoe, N.; Shimanoe, K. New perspectives of gas sensor technology. Sens. Actuator B Chem. 2009, 138, 100–107. [Google Scholar] [CrossRef]
- Yamazoe, N.; Suematsu, K.; Shimanoe, K. Two types of moisture effects on the receptor function of neat tin oxide gas sensor to oxygen. Sens. Actuator B Chem. 2013, 176, 443–452. [Google Scholar] [CrossRef]
- Yamazoe, N.; Suematsu, K.; Shimanoe, K. Extension of receptor function theory to include two types of adsorbed oxygen for oxide semiconductor gas sensors. Sens. Actuator B Chem. 2012, 163, 128–135. [Google Scholar] [CrossRef]
- Yamazoe, N.; Shimanoe, K. Theoretical approach to the gas response of oxide semiconductor film devices under control of gas diffusion and reaction effects. Sens. Actuator B Chem. 2011, 154, 277–282. [Google Scholar] [CrossRef]
- Yamazoe, N.; Shimanoe, K. Receptor function of small semiconductor crystals with clean and electron-traps dispersed surfaces. Thin Solid Films 2009, 517, 6148–6155. [Google Scholar] [CrossRef]
- Fonstad, C.; Rediker, R. Electrical properties of high-quality stannic oxide crystals. J. Appl. Phys. 1971, 42, 2911–2918. [Google Scholar] [CrossRef]
- Morrison, S.R. Semiconductor gas sensors. Sens. Actuator 1982, 2, 329–341. [Google Scholar] [CrossRef]
- Morrison, S.R. Selectivity in semiconductor gas sensors. Sens. Actuator 1987, 12, 425–440. [Google Scholar] [CrossRef]
- Liu, H.; Gong, S.; Hu, Y.; Liu, J.; Zhou, D. Properties and mechanism study of SnO2 nanocrystals for H2S thick-film sensors. Sens. Actuator B Chem. 2009, 140, 190–195. [Google Scholar] [CrossRef]
- Liu, J.; Lu, Y.; Cui, X.; Geng, Y.; Jin, G.; Zhai, Z. Gas-sensing properties and sensitivity promoting mechanism of Cu-added SnO2 thin films deposited by ultrasonic spray pyrolysis. Sens. Actuator B Chem. 2017, 248, 862–867. [Google Scholar] [CrossRef]
- Morrison, S.R. Mechanism of semiconductor gas sensor operation. Sens. Actuator 1987, 11, 283–287. [Google Scholar] [CrossRef]
- Yamazoe, N.; Fuchigami, J.; Kishikawa, M.; Seiyama, T. Interactions of tin oxide surface with O2, H2O and H2. Surf. Sci. 1979, 86, 335–344. [Google Scholar] [CrossRef]
- Yamazoe, N.; Shimanoe, K.; Sawada, C. Contribution of electron tunneling transport in semiconductor gas sensor. Thin Solid Films 2007, 515, 8302–8309. [Google Scholar] [CrossRef]
- Yamazoe, N.; Shimanoe, K. Basic approach to the transducer function of oxide semiconductor gas sensors. Sens. Actuator B Chem. 2011, 160, 1352–1362. [Google Scholar] [CrossRef]
- Sakai, G.; Matsunaga, N.; Shimanoe, K.; Yamazoe, N. Theory of gas-diffusion controlled sensitivity for thin film semiconductor gas sensor. Sens. Actuator B Chem. 2001, 80, 125–131. [Google Scholar] [CrossRef]
- Matsunaga, N.; Sakai, G.; Shimanoe, K.; Yamazoe, N. Diffusion equation-based study of thin film semiconductor gas sensor-response transient. Sens. Actuator B Chem. 2002, 83, 216–221. [Google Scholar] [CrossRef]
- Gong, S.; Liu, J.; Xia, J.; Quan, L.; Liu, H.; Zhou, D. Gas sensing characteristics of SnO2 thin films and analyses of sensor response by the gas diffusion theory. Mater. Sci. Eng. B Adv. 2009, 164, 85–90. [Google Scholar] [CrossRef]
- Liu, J.; Gong, S.; Xia, J.; Quan, L.; Liu, H.; Zhou, D. The sensor response of tin oxide thin films to different gas concentration and the modification of the gas diffusion theory. Sens. Actuator B Chem. 2009, 138, 289–295. [Google Scholar] [CrossRef]
- Lambert-Mauriat, C.; Oison, V.; Saadi, L.; Aguir, K. Ab initio study of oxygen point defects on tungsten trioxide surface. Surf. Sci. 2012, 606, 40–45. [Google Scholar] [CrossRef]
- Wu, J.; Huang, Q.; Zeng, D.; Zhang, S.; Yang, L.; Xia, D.; Xiong, Z.; Xie, C. Al-doping induced formation of oxygen-vacancy for enhancing gas-sensing properties of SnO2 NTs by electrospinning. Sens. Actuator B Chem. 2014, 198, 62–69. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, C.; Yuan, G.; Gao, S. SnO2 nanocrystals with abundant oxygen vacancies: Preparation and room temperature NO2 sensing. J. Alloy. Compd. 2016, 681, 43–49. [Google Scholar] [CrossRef]
- Yu, L.; Guo, F.; Liu, S.; Yang, B.; Jiang, Y.; Qi, L.; Fan, X. Both oxygen vacancies defects and porosity facilitated NO2 gas sensing response in 2D ZnO nanowalls at room temperature. J. Alloy. Compd. 2016, 682, 352–356. [Google Scholar] [CrossRef]
- Ge, Y.; Wei, Z.; Li, Y.; Qu, J.; Zu, B.; Dou, X. Highly sensitive and rapid chemiresistive sensor towards trace nitro-explosive vapors based on oxygen vacancy-rich and defective crystallized In-doped ZnO. Sens. Actuator B Chem. 2017, 244, 983–991. [Google Scholar] [CrossRef]
- Zou, C.; Liang, F.; Xue, S. Synthesis and oxygen vacancy related NO2 gas sensing properties of ZnO: Co nanorods arrays gown by a hydrothermal method. Appl. Surf. Sci. 2015, 353, 1061–1069. [Google Scholar] [CrossRef]
- Kim, W.; Choi, M.; Yong, K. Generation of oxygen vacancies in ZnO nanorods/films and their effects on gas sensing properties. Sens. Actuator B Chem. 2015, 209, 989–996. [Google Scholar] [CrossRef]
- Zhang, C.; Geng, X.; Li, J.; Luo, Y.; Lu, P. Role of oxygen vacancy in tuning of optical, electrical and NO2 sensing properties of ZnO1-X coatings at room temperature. Sens. Actuator B Chem. 2017, 248, 886–893. [Google Scholar] [CrossRef]
- Si, X.; Liu, Y.; Wu, X.; Lei, W.; Xu, J.; Du, W.; Zhou, T.; Lin, J. The interaction between oxygen vacancies and doping atoms in ZnO. Mater. Des. 2015, 87, 969–973. [Google Scholar] [CrossRef]
- Qin, Y.; Ye, Z. DFT study on interaction of NO2 with the vacancy-defected WO3 nanowires for gas-sensing. Sens. Actuator B Chem. 2016, 222, 499–507. [Google Scholar] [CrossRef]
- Tian, F.H.; Zhao, L.; Xue, X.Y.; Shen, Y.; Jia, X.; Chen, S.; Wang, Z. DFT study of CO sensing mechanism on hexagonal WO3 (001) surface: The role of oxygen vacancy. Appl. Surf. Sci. 2014, 311, 362–368. [Google Scholar] [CrossRef]
- Le, H.M.; Vu, N.H.; Phan, B.T. Migrations of oxygen vacancy in tungsten oxide (WO3): A density functional theory study. Comput. Mater. Sci. 2014, 90, 171–176. [Google Scholar] [CrossRef]
- Yamazoe, N.; Shimanoe, K. Theory of power laws for semiconductor gas sensors. Sens. Actuator B Chem. 2008, 128, 566–573. [Google Scholar] [CrossRef]
- Liu, J.; Gong, S.; Fu, Q.; Wang, Y.; Quan, L.; Deng, Z.; Chen, B.; Zhou, D. Time-dependent oxygen vacancy distribution and gas sensing characteristics of tin oxide gas sensitive thin films. Sens. Actuator B Chem. 2010, 150, 330–338. [Google Scholar] [CrossRef]
- Liu, J.; Gong, S.; Quan, L.; Deng, Z.; Liu, H.; Zhou, D. Influences of cooling rate on gas sensitive tin oxide thin films and a model of gradient distributed oxygen vacancies in SnO2 crystallites. Sens. Actuator B Chem. 2010, 145, 657–666. [Google Scholar] [CrossRef]
- Liu, J.; Jin, G.; Zhai, Z.; Monica, F.F.; Liu, X. Numeral description of grain size effects of tin oxide gas-sensitive elements and evaluation of depletion layer width. Electron. Mater. Lett. 2015, 11, 457–465. [Google Scholar] [CrossRef]
- Liu, J.; Zhai, Z.; Jin, G.; Li, Y.; Monica, F.F.; Liu, X. Simulation of the grain size effect in gas-sensitive SnO2 thin films using the oxygen vacancy gradient distribution model. Electron. Mater. Lett. 2015, 11, 34–40. [Google Scholar] [CrossRef]
- Liu, J.; Lu, Y.; Cui, X.; Jin, G.; Zhai, Z. Effect of depletion layer width on electrical properties of semiconductive thin film gas sensor: A numerical study based on the gradient-distributed oxygen vacancy model. Appl. Phys. A 2016, 122, 146. [Google Scholar] [CrossRef]
- Liu, J.; Quan, L. Simulation of grain size effects on gas sensing characteristics of semiconductor sensors in nitrogen oxides detection. Key Eng. Mater. 2014, 605, 279–282. [Google Scholar] [CrossRef]
- Liu, J.; Quan, L.; Zhai, Z. Numerical discussion of the grain size effects on tungsten oxide and indium oxide based gas sensors in NOX detection. Sens. Lett. 2014, 12, 1477–1480. [Google Scholar] [CrossRef]
- Sze, S.M. Semiconductor Devices: Physics and Technology, 3rd ed.; John Willey & Sons, Inc.: New York, NY, USA, 2012. [Google Scholar]
- Shimizu, Y.; Kobayashi, N.; Uedono, A.; Okada, Y. Improvement of crystal quality of GaInNAs films grown by atomic hydrogen-assisted RF-MBE. J. Cryst. Growth 2005, 278, 553–557. [Google Scholar] [CrossRef]
- Zhang, M.; Lin, C.; Weng, H.; Scholz, R.; Gösele, U. Defect distribution and evolution in He+ implanted Si studied by variable-energy positron beam. Thin Solid Films 1998, 333, 245–250. [Google Scholar] [CrossRef]
- Blaustein, G.; Castro, M.S.; Aldao, C.M. Influence of frozen distributions of oxygen vacancies on tin oxide conductance. Sens. Actuator B Chem. 1999, 55, 33–37. [Google Scholar] [CrossRef]
- Maier, J.; Göpel, W. Investigations of the bulk defect chemistry of polycrystalline tin (IV) oxide. J. Solid State Chem. 1988, 72, 293–302. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; John Wiley & Sons, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Liu, J.; Liu, X.; Zhai, Z.; Jin, G.; Jiang, Q.; Zhao, Y.; Luo, C.; Quan, L. Evaluation of depletion layer width and gas-sensing properties of antimony-doped tin oxide thin film sensors. Sens. Actuator B Chem. 2015, 220, 1354–1360. [Google Scholar] [CrossRef]
- Liu, J.; Zhai, Z.; Jin, G.; Liu, X.; Quan, L. Evaluation of depletion layer width in antimony-doped tin oxide thin films for gas sensors. Key Eng. Mater. 2015, 644, 125–128. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar]
- Malagù, C.; Guidi, V.; Stefancich, M.; Carotta, M.C.; Martinelli, G. Model for Schottky barrier and surface states in nanostructured n-type semiconductors. J. Appl. Phys. 2002, 91, 808–814. [Google Scholar] [CrossRef]
- Xu, C.; Tamaki, J.; Miura, N.; Yamazoe, N. Grain size effects on gas sensitivity of porous SnO2-based elements. Sens. Actuator B Chem. 1991, 3, 147–155. [Google Scholar] [CrossRef]
- Yamazoe, N.; Shimanoe, K. Roles of shape and size of component crystals in semiconductor gas sensors II. Response to NO2 and H2. J. Electrochem. Soc. 2008, 155, J93–J98. [Google Scholar] [CrossRef]
- Yamazoe, N.; Shimanoe, K. Roles of shape and size of component crystals in semiconductor gas sensors I. Response to oxygen. J. Electrochem. Soc. 2008, 155, J85–J92. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Gao, Y.; Wu, X.; Jin, G.; Zhai, Z.; Liu, H. Inhomogeneous Oxygen Vacancy Distribution in Semiconductor Gas Sensors: Formation, Migration and Determination on Gas Sensing Characteristics. Sensors 2017, 17, 1852. https://doi.org/10.3390/s17081852
Liu J, Gao Y, Wu X, Jin G, Zhai Z, Liu H. Inhomogeneous Oxygen Vacancy Distribution in Semiconductor Gas Sensors: Formation, Migration and Determination on Gas Sensing Characteristics. Sensors. 2017; 17(8):1852. https://doi.org/10.3390/s17081852
Chicago/Turabian StyleLiu, Jianqiao, Yinglin Gao, Xu Wu, Guohua Jin, Zhaoxia Zhai, and Huan Liu. 2017. "Inhomogeneous Oxygen Vacancy Distribution in Semiconductor Gas Sensors: Formation, Migration and Determination on Gas Sensing Characteristics" Sensors 17, no. 8: 1852. https://doi.org/10.3390/s17081852
APA StyleLiu, J., Gao, Y., Wu, X., Jin, G., Zhai, Z., & Liu, H. (2017). Inhomogeneous Oxygen Vacancy Distribution in Semiconductor Gas Sensors: Formation, Migration and Determination on Gas Sensing Characteristics. Sensors, 17(8), 1852. https://doi.org/10.3390/s17081852



