Sparse Representation Based Frequency Detection and Uncertainty Reduction in Blade Tip Timing Measurement for Multi-Mode Blade Vibration Monitoring
Abstract
:1. Introduction
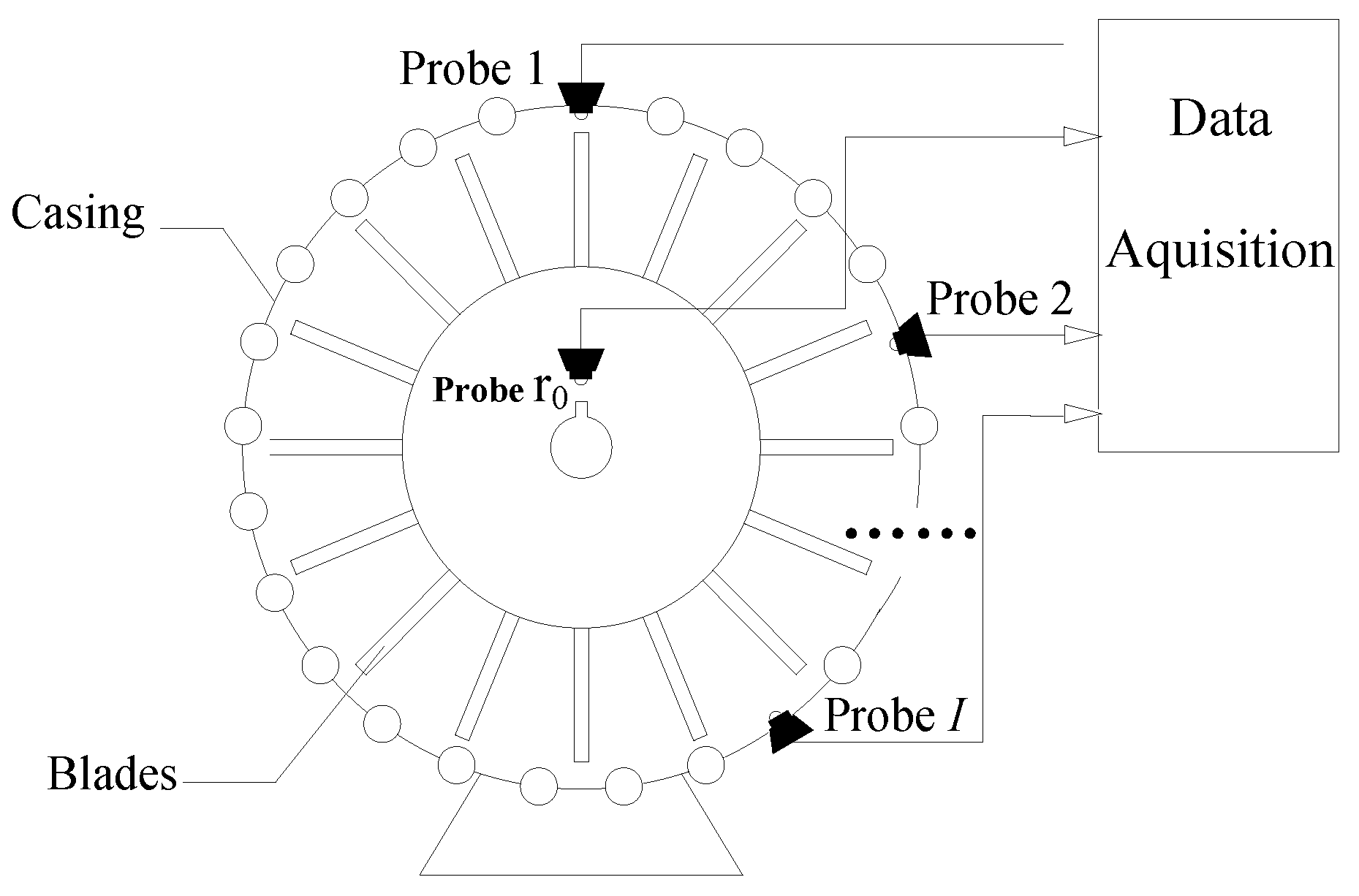
2. Mathematical Model of the Blade Tip Timing Sampling
2.1. Formulations of Blade Tip Deflections
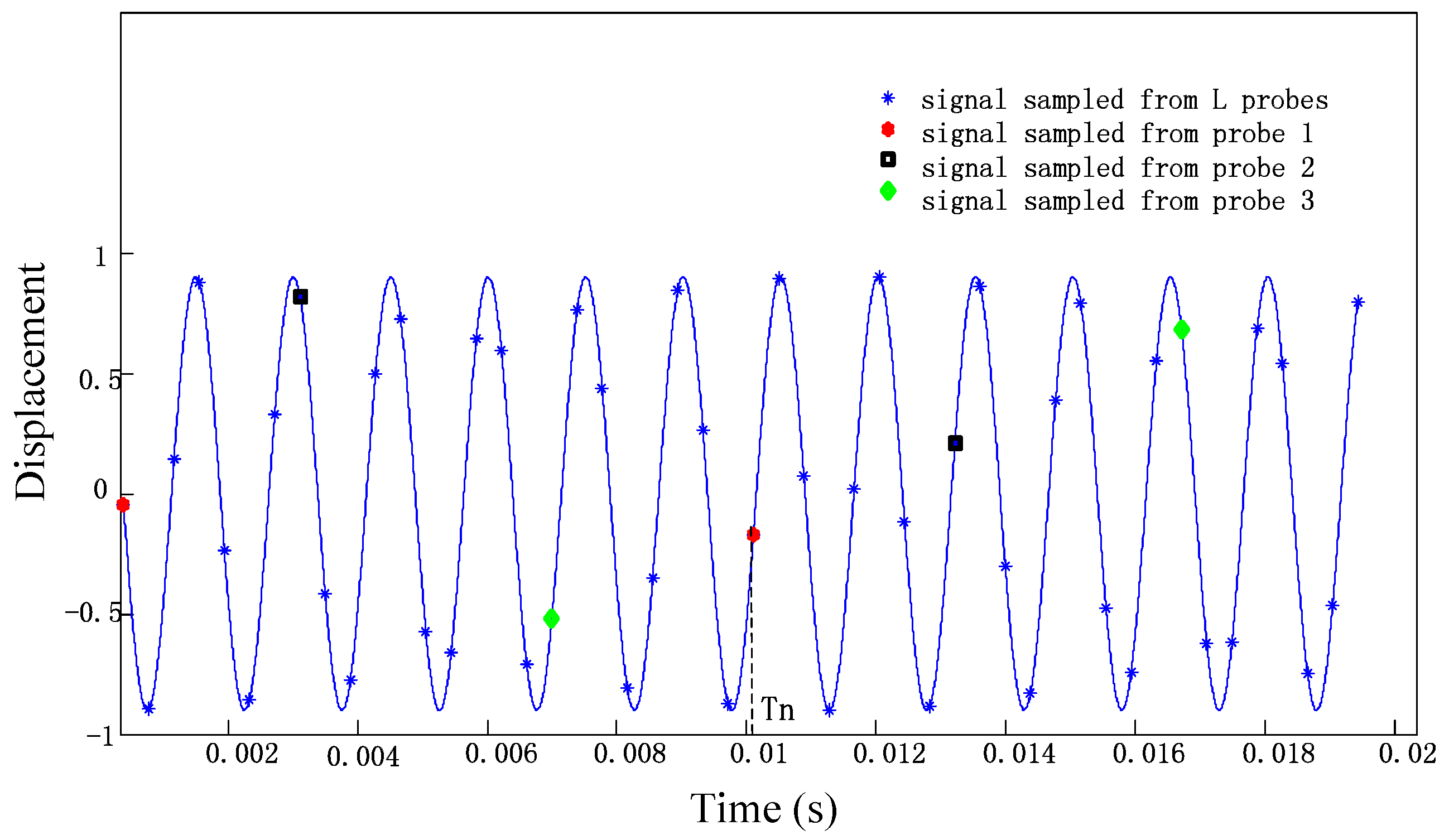
2.2. Function of BTT Signals
3. Vibration Frequency Detection Based on Sparse Representation Theory
3.1. Sparse Representation Mathematical Model of the BTT Measurement
3.2. Uniqueness of Solution to SR Model
3.2.1. Restricted Isometry Property and Orthogonalization Preprocessing
3.2.2. Requirement of Probe Number
- For the most ideal case, which the blade responds at a synchronous mode, at least four probes are needed to get the unique solution as the length of q is in the order of 103 to 104 considering both the computational complexity and the time of engine to rotate in a constant speed.
- For the multi-mode case, which usually mixed with asynchronous resonances caused by flutter [23], three sensors are abundant for the monitoring of multiple mode vibration as long as the sampling time is long enough.
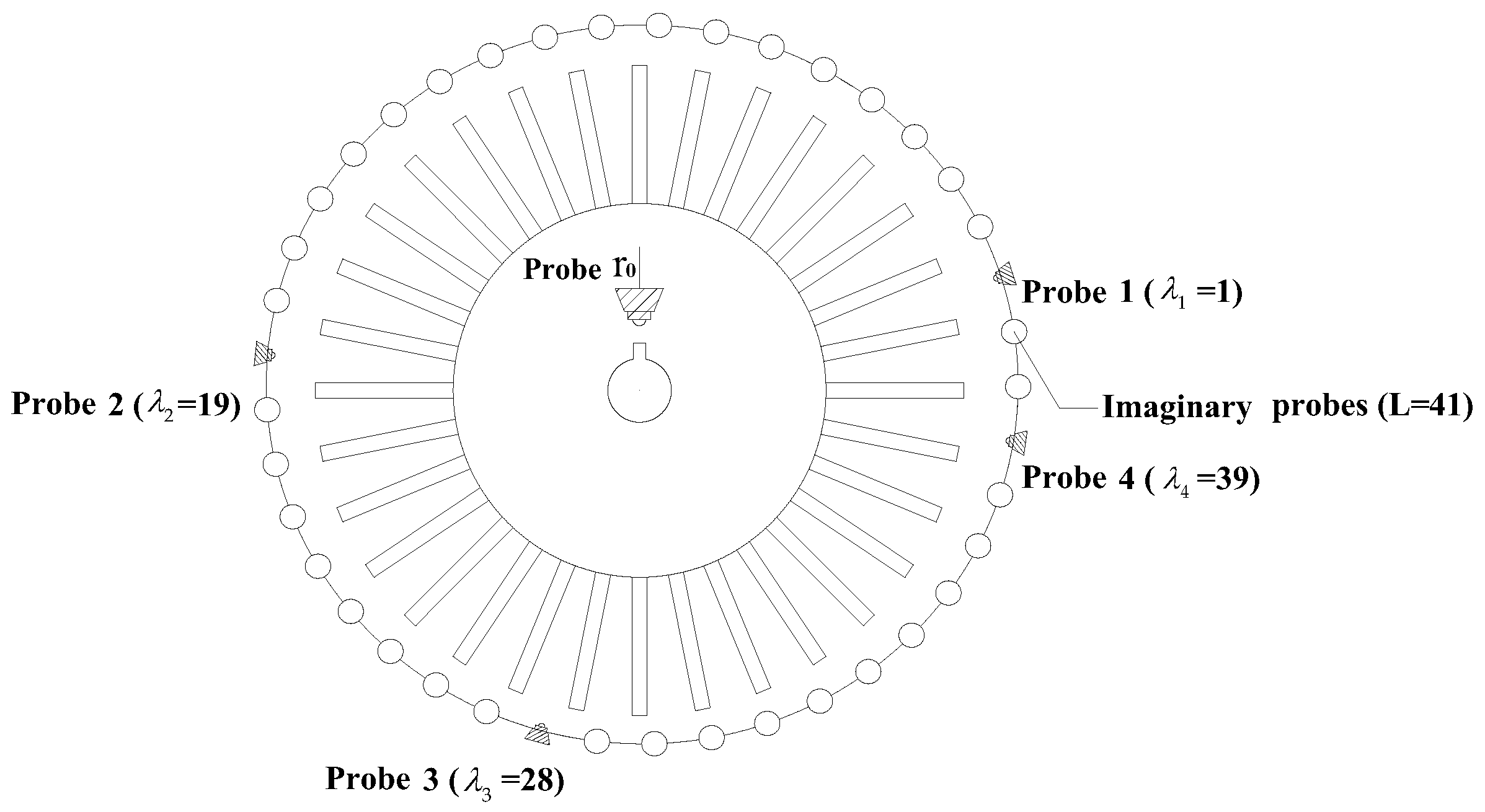
3.2.3. The Coherence of the Sensing Matrix and Choice of Probe Placement Location
4. Quantitative Expression and Reduction of Measurement Uncertainties
4.1. Mathematical Model of Uncertainties in the BTT Measurement
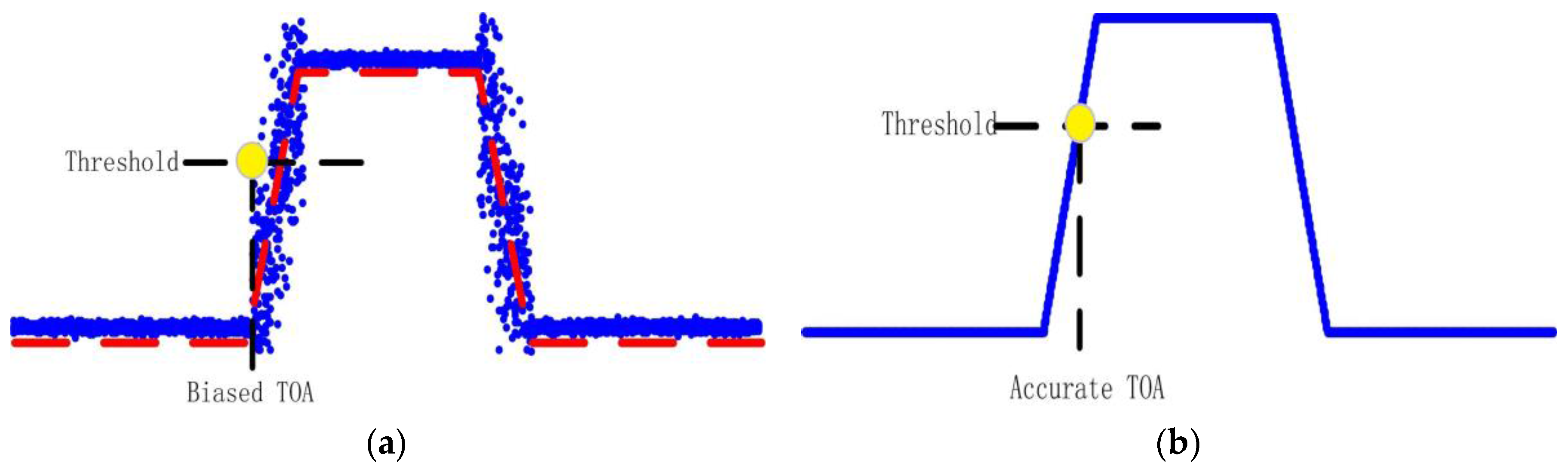
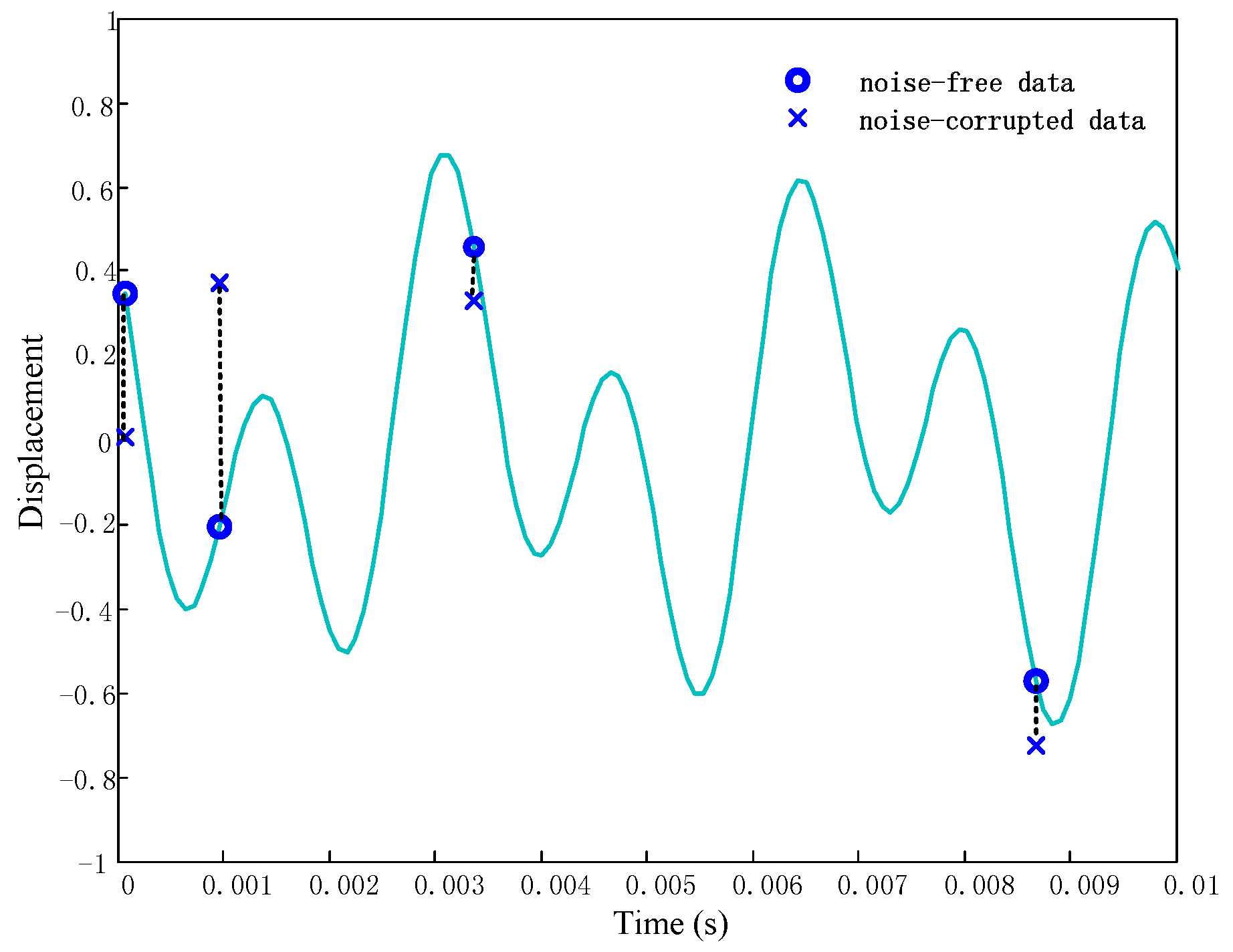
4.1.1. Uncertainty Due to BTT Signal Noise
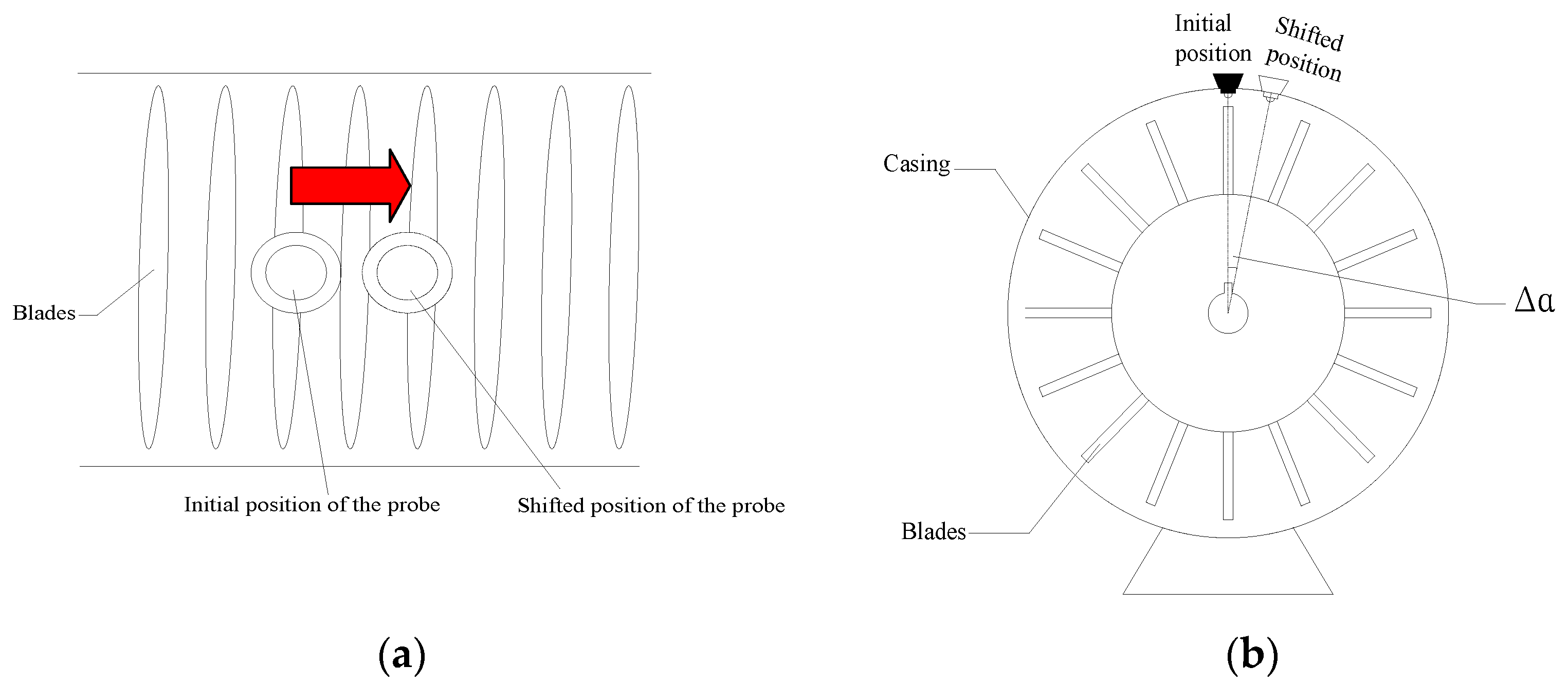
4.1.2. Uncertainty Due to Probe Position Shift
4.2. Uncertainties Reduction in Frequency Recovery
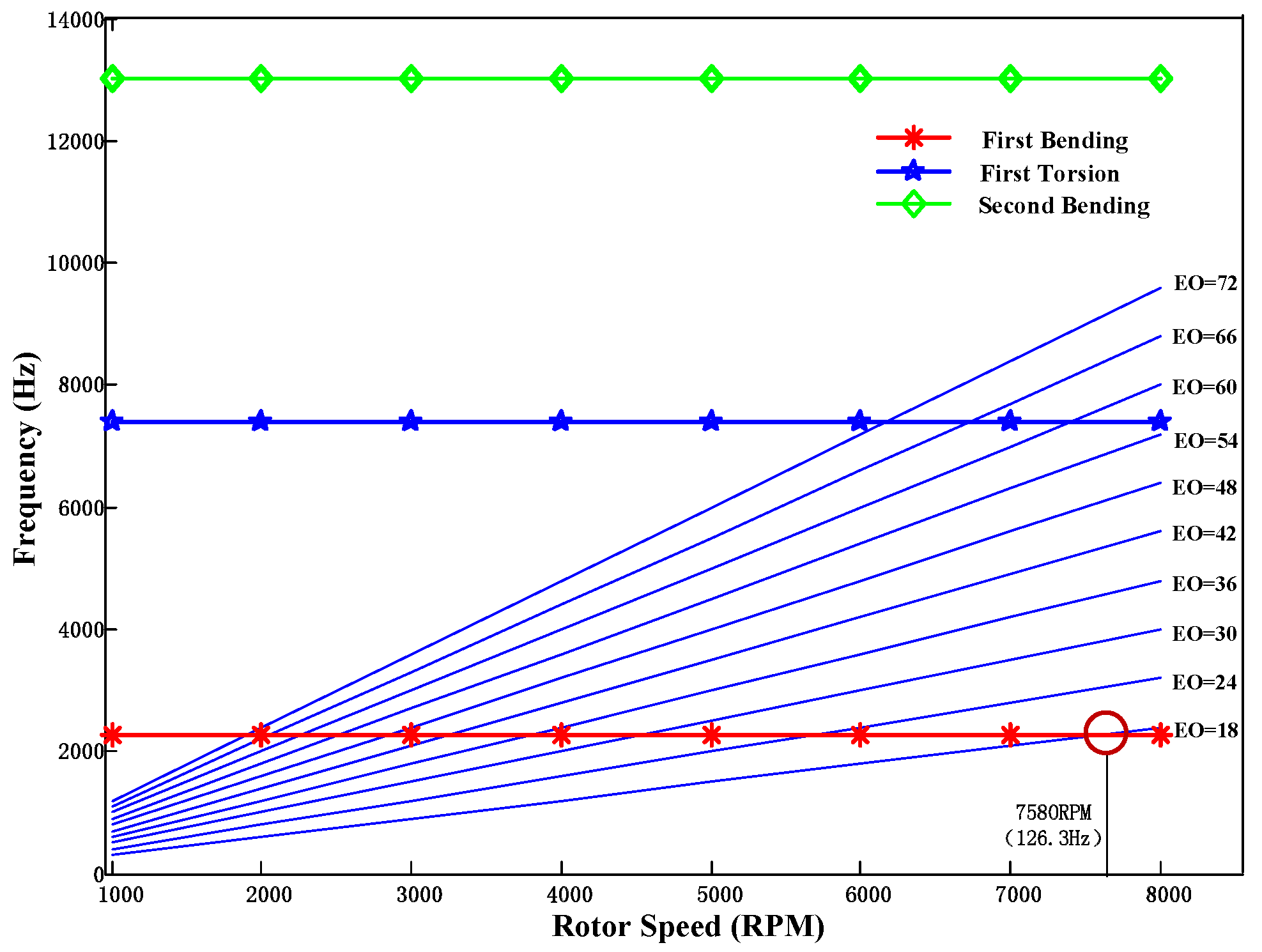
5. Numerical Simulations
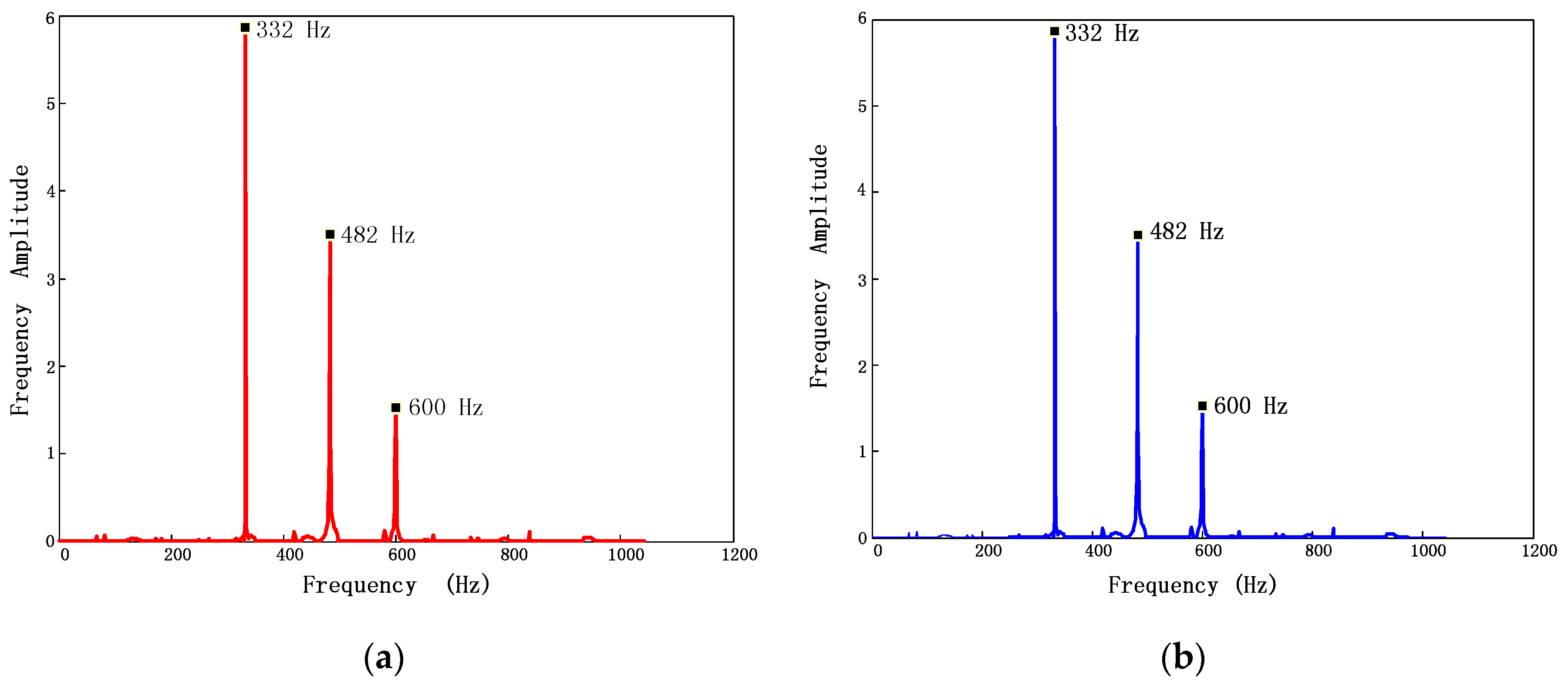
5.1. Recovery of Multi-Mode Signals
5.2. Reduction of Measurement Uncertainties
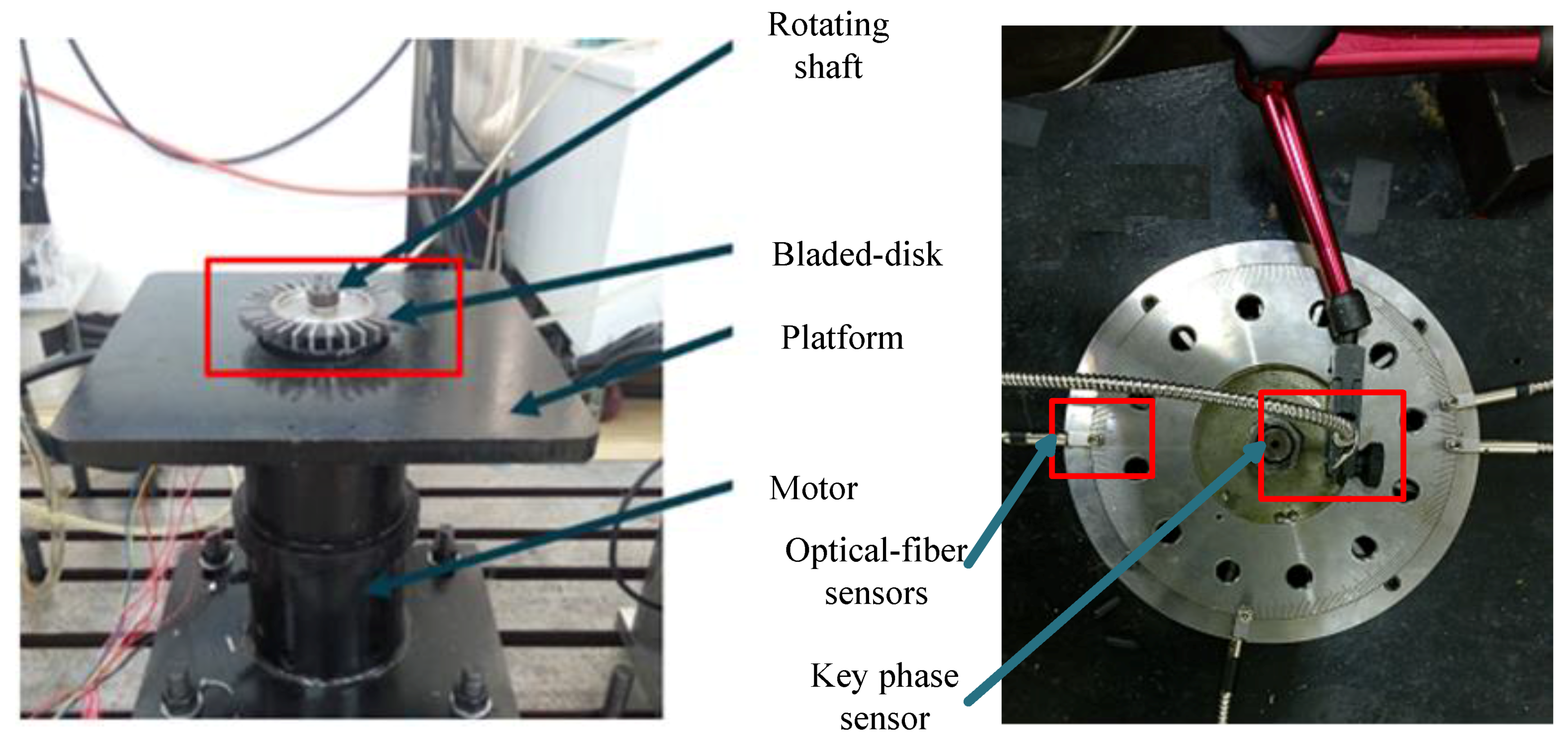
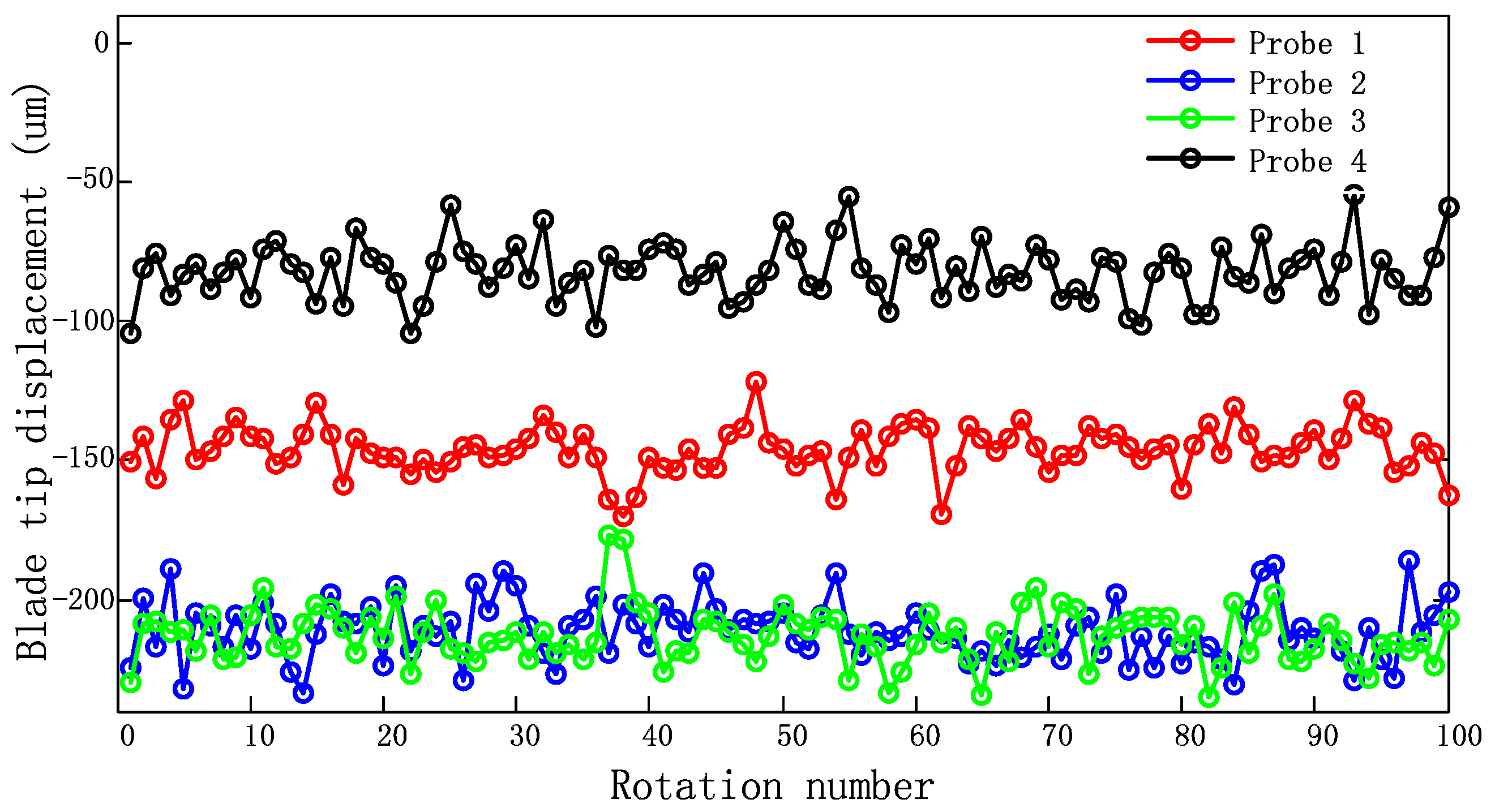
6. Experiments
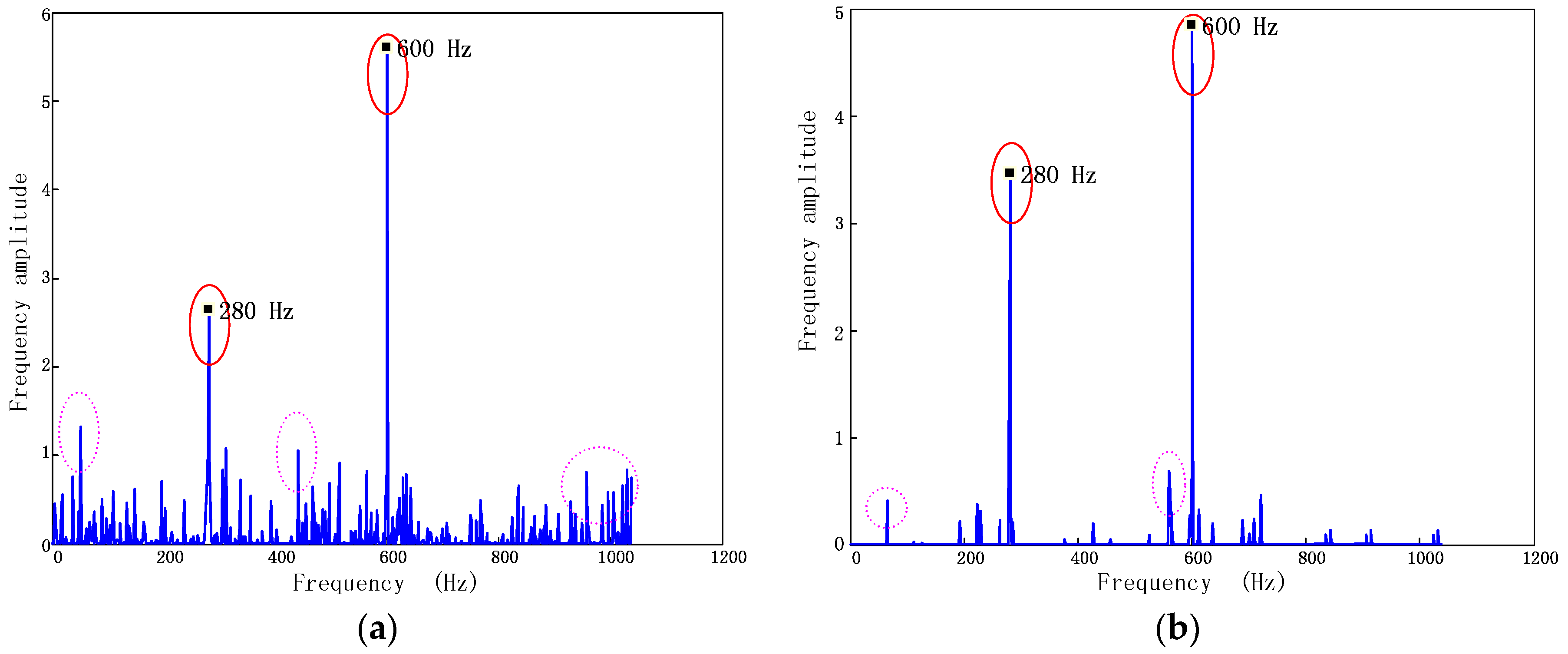
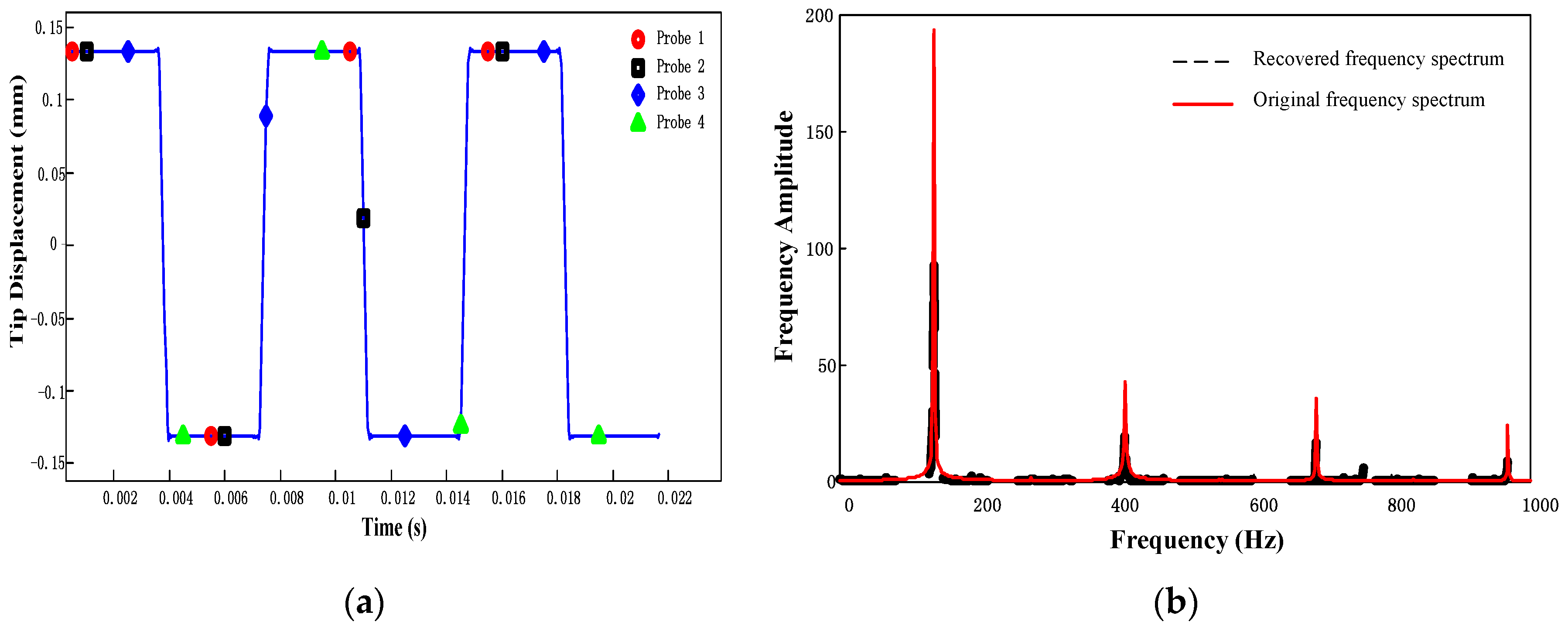
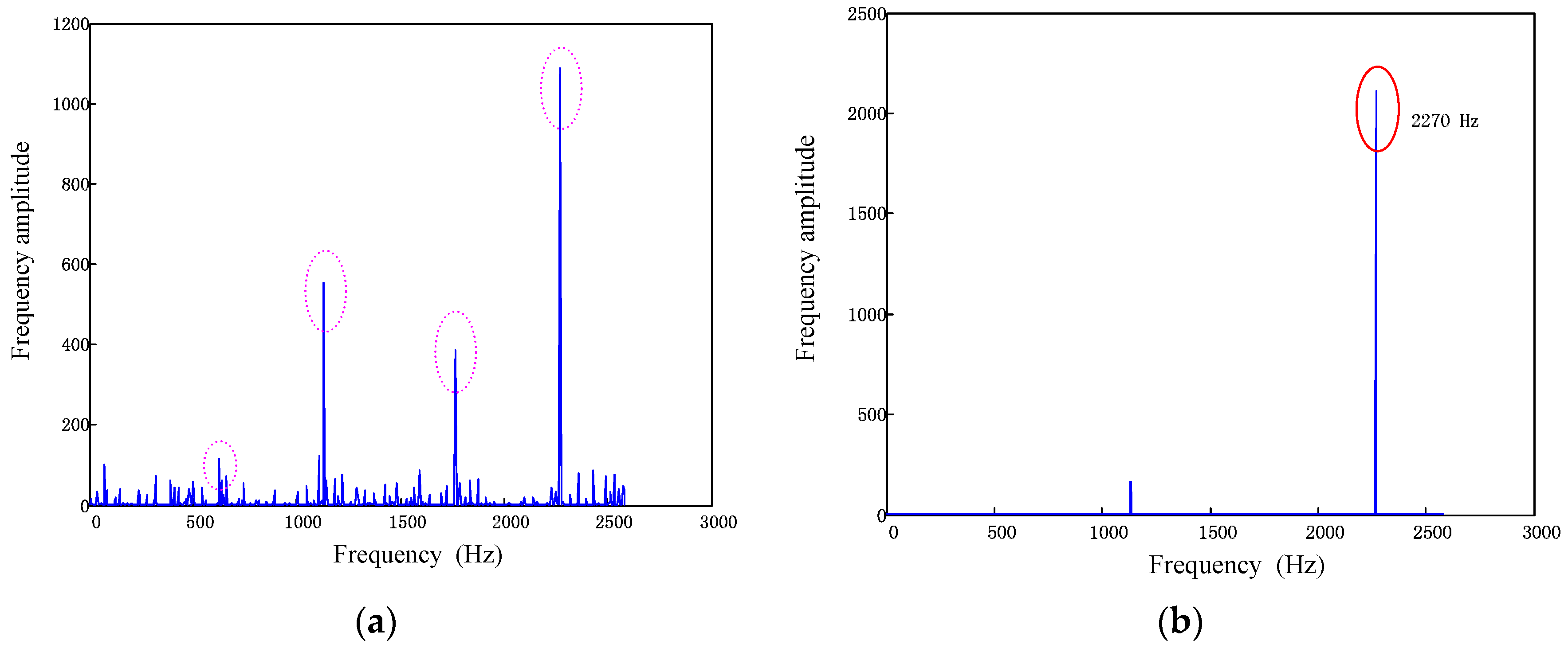
6.1. Recovery of Multi-Mode Vibration Response in Frequency Domain
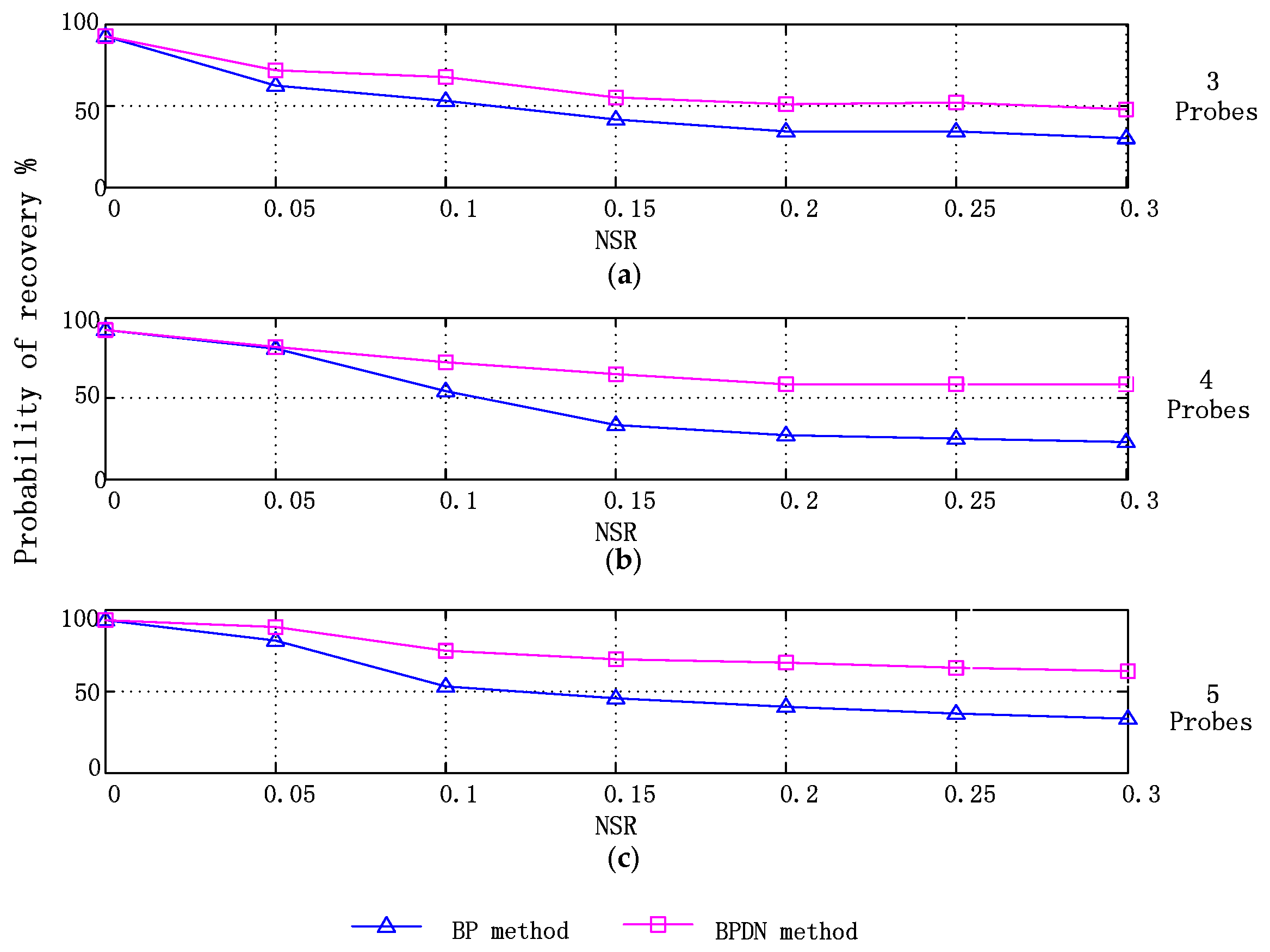
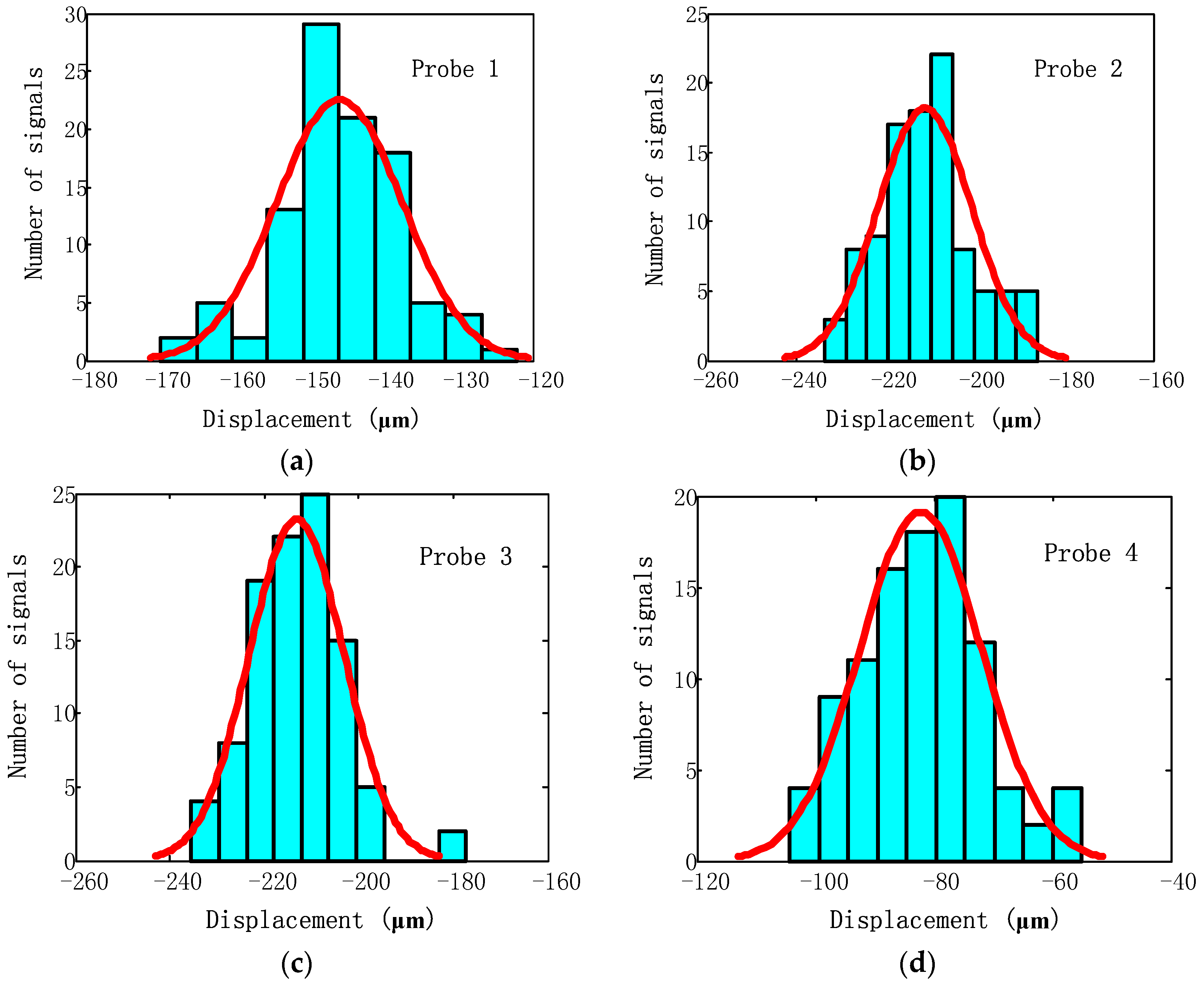
6.2. Uncertainty Reduction in Frequency Detection Results
7. Conclusions
- A single-measurement vector model for sparse BTT data is built and all the harmonic frequencies can be extracted from the solution of the sparse representation model if the measurement results are unbiased.
- The number and placement of optical-fiber probes play an important role in the effectiveness of frequency spectrum recovery. Considering the blade vibration conditions in practice, four probes located around the case, which satisfies the minimal two-sided coherence, is enough to recover the vibration frequency spectra well.
- The improved blade vibration recovery method based on BPDN obviously enhanced the robustness to the noise interferences. The dominant vibration frequencies can be identified from corrupted non-uniformly under-sampled BTT data through the proposed method without increasing the number of probes.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Knappett, D.; Garcia, J. Blade tip timing and strain gauge correlation on compressor blades. Proc. Inst. Mech. Eng. Part G J. Aerospace Eng. 2008, 222, 497–506. [Google Scholar] [CrossRef]
- Pickering, T.M. Methods for Validation of a Turbomachinery Rotor Blade Tip Timing System. Master’s Theses, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 4 March 2014. [Google Scholar]
- Carrington, I.B.; Wright, J.R.; Cooper, J.E.; Dimitriadis, G. A comparison of blade tip timing data analysis methods. Proc. Inst. Mech. Eng. Part G J. Aerospace Eng. 2001, 215, 301–312. [Google Scholar] [CrossRef]
- Salhi, B.; Lardiès, J.; Berthillier, M.; Voinis, P.; Bodel, C. Modal parameter identification of mistuned bladed disks using tip timing data. J. Sound Vib. 2008, 314, 885–906. [Google Scholar] [CrossRef]
- Xu, H.L.; Chen, Z.S.; Xiong, Y.P.; Yang, Y.M.; Tao, L.M. Nonlinear dynamic behaviors of rotated blades with small breathing cracks based on vibration power flow analysis. Shock Vib. 2016. [Google Scholar] [CrossRef]
- Shen, M.H.; Chu, Y.C. Vibrations of beams with a fatigue crack. Comput. Struct. 1992, 45, 79–93. [Google Scholar] [CrossRef]
- Kaszynski, A.A.; Brown, J.M. Accurate Blade Tip Timing Limits through Geometry Mistuning Modeling. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montréal, QC, Canada, 15–19 June 2015; p. V07AT27A007. [Google Scholar]
- Gallego-Garrido, J.; Dimitriadis, G.; Wright, J.R. A Class of Methods for the Analysis of Blade Tip Timing Data from Bladed Assemblies Undergoing Simultaneous Resonances—Part I: Theoretical Development. Int. J. Rotat. Mach. 2007, 2007, 981–1077. [Google Scholar] [CrossRef]
- Kharyton, V.; Bladh, R. Using Tip timing and Strain Gauge Data for the Estimation of Consumed Life in a Compressor Blisk Subjected to Stall-Induced Loading. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; p. V07BT33A028. [Google Scholar]
- Lin, J.; Hu, Z.; Chen, Z.S.; Yang, Y.M.; Xu, H.L. Sparse reconstruction of blade tip-timing signals for multi-mode blade vibration monitoring. Mech. Syst. Signal Process. 2016, 81, 250–258. [Google Scholar] [CrossRef]
- Satish, T.N.; Murthy, R.; Singh, A.K. Analysis of uncertainties in measurement of rotor blade tip clearance in gas turbine engine under dynamic condition. Proc. Inst. Mech. Eng. Part G J. Aerospace Eng. 2014, 228, 652–670. [Google Scholar] [CrossRef]
- Guo, H.; Duan, F.; Cheng, Z. Numerical analysis of the blade tip-timing signal of a fiber bundle sensor probe. Opt. Eng. 2015, 54, 034103. [Google Scholar] [CrossRef]
- Berdanier, R.A.; Key, N.L. Experimental Investigation of Factors Influencing Operating Rotor Tip Clearance in Multistage Compressors. Int. J. Rotat. Mach. 2015, 2015, 1–13. [Google Scholar] [CrossRef]
- Lawson, C.P.; Ivey, P.C. Tubomachinery blade vibration amplitude measurement through tip timing with capacitance tip clearance probes. Sens. Actuators A Phys. 2005, 118, 14–24. [Google Scholar] [CrossRef]
- Hu, Z.; Lin, J.; Chen, Z.S.; Yang, Y.M.; Xu, H.L. A non-uniformly under-sampled blade tip-timing signal reconstruction method for blade vibration monitoring. Sensors 2015, 15, 2419–2437. [Google Scholar] [CrossRef] [PubMed]
- Donoho, D.L.; Elad, M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization. Proc. Natl. Acad. Sci. 2003, 100, 2197–2202. [Google Scholar] [CrossRef] [PubMed]
- Candè, E.J.; Wakin, M.B. An Introduction to Compressive Sampling. IEEE Signal Proc. Mag. 2008, 25, 21–30. [Google Scholar] [CrossRef]
- Beauseroy, P.; Lengellé, R. Nonintrusive turbomachine blade vibration measurement system. Mech. Syst. Signal Proc. 2007, 21, 1717–1738. [Google Scholar] [CrossRef]
- Nyquist, H. Certain Factors Affecting Telegraph Speed. Trans. Am. Inst. Electr. Eng. 1924, 43, 412–422. [Google Scholar] [CrossRef]
- Grigoryan, R.; Jensen, T.L.; Larsen, T. Computational Complexity Reduction in Nonuniform Compressed Sensing by Multi-Coset Emulation. Signal Proc. 2016, 131, 492–501. [Google Scholar] [CrossRef]
- Candè, E.J.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar] [CrossRef]
- Feng, C.; Au, W.S.A.; Valaee, S.; Tan, Z. Received-signal-strength-based indoor positioning using compressive sensing. IEEE Trans. Inf. Theory 2012, 11, 1983–1993. [Google Scholar] [CrossRef]
- Kurkov, A.; Dicus, J. Synthesis of blade flutter vibratory patterns using stationary transducers. In Proceedings of the ASME 1978 International Gas Turbine Conference and Products Show, London, UK, 9–13 April 1978. [Google Scholar]
- Bruckstein, A.M.; Elad, M.; Zibulevsky, M. On the Uniqueness of Nonnegative Sparse Solutions to Underdetermined Systems of Equations. IEEE Trans. Inf. Theory 2008, 54, 4813–4820. [Google Scholar] [CrossRef]
- Elad, M. Sparse Representations Are Most Likely to Be the Sparsest Possible. EURASIP J. Appl. Signal Proc. 2006, 2006, 115. [Google Scholar] [CrossRef]
- Meissonnier, F.T.; Stoisser, C.M. Compressor Rubbing Risk Analyses for Combustion Turbine Using Thermomechanical and Dynamical FE Modeling. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; pp. 691–700. [Google Scholar]
- Ringhiser, B. The history and statistical development of the new ASME-SAE-AIAA-ISO measurement uncertainty methodology. J. Nurs. Manag. 2013, 12, 393–396. [Google Scholar]
- Chen, S.S.; Donoho, D.L.; Saunders, M.A. Atomic Decomposition by Basis Pursuit. SIAM Rev. 2006, 43, 129–159. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient Projection for Sparse Reconstruction: Application to Compressed Sensing and Other Inverse Problems. IEEE J. Sel. Top. Signal Proc. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Dimitriadis, G.; Carrington, I.B.; Wright, J.R.; Cooper, J.E. blade-tip timing measurement of synchronous vibrations of rotating bladed assemblies. Mech. Syst. Signal Proc. 2002, 16, 599–622. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, X.; Du, Z.; Yan, R. Kurtosis based weighted sparse model with convex optimization technique for bearing fault diagnosis. Mech. Syst. Signal Proc. 2016, 80, 349–376. [Google Scholar] [CrossRef]
- Du, Z.; Chen, X.; Zhang, H.; Miao, H.; Guo, Y.; Yang, B. Feature identification with compressive measurements for machine fault diagnosis. IEEE Trans. Instrum. Meas. 2016, 65, 977–987. [Google Scholar] [CrossRef]
- Wang, W.M.; Ren, S.Q.; Chen, L.F.; Shao, H.J. Investigation on the Method of Improving the Accuracy of Blade Synchronous Vibration Parameter Identification (Experimental). J. Vib. Shock 2017, 36, 127–133. (In Chinese) [Google Scholar]


| Number of Probes I | Minimal μ(Q) |
|---|---|
| 2 | 1 |
| 3 | 0.893 |
| 4 | 0.691 |
| 5 | 0.500 |
| 6 | 0.478 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, M.; Yang, Y.; Guan, F.; Hu, H.; Xu, H. Sparse Representation Based Frequency Detection and Uncertainty Reduction in Blade Tip Timing Measurement for Multi-Mode Blade Vibration Monitoring. Sensors 2017, 17, 1745. https://doi.org/10.3390/s17081745
Pan M, Yang Y, Guan F, Hu H, Xu H. Sparse Representation Based Frequency Detection and Uncertainty Reduction in Blade Tip Timing Measurement for Multi-Mode Blade Vibration Monitoring. Sensors. 2017; 17(8):1745. https://doi.org/10.3390/s17081745
Chicago/Turabian StylePan, Minghao, Yongmin Yang, Fengjiao Guan, Haifeng Hu, and Hailong Xu. 2017. "Sparse Representation Based Frequency Detection and Uncertainty Reduction in Blade Tip Timing Measurement for Multi-Mode Blade Vibration Monitoring" Sensors 17, no. 8: 1745. https://doi.org/10.3390/s17081745
APA StylePan, M., Yang, Y., Guan, F., Hu, H., & Xu, H. (2017). Sparse Representation Based Frequency Detection and Uncertainty Reduction in Blade Tip Timing Measurement for Multi-Mode Blade Vibration Monitoring. Sensors, 17(8), 1745. https://doi.org/10.3390/s17081745




