Crowd Sensing-Enabling Security Service Recommendation for Social Fog Computing Systems
Abstract
:1. Introduction
- We design an advanced social networking architecture for fog computing called social fog computing to control and organize fog computing system efficiently as well as securely;
- We propose a novel crowd sensing-enabling security service recommendation method for a social fog computing architecture. The computation model and parameters of security service discovery as recommendation are designed for social fog computing systems.
2. Preliminaries
2.1. Fog Computing
2.2. Chance Discovery Theory
2.3. Crowd Sensing
3. Proposed Social Fog Computing Systems
3.1. Design Motivation of Social Fog Systems
3.2. Innovations from Fog to Social Fog
3.3. Social Fog Architecture
4. Proposed Security Service Recommendation Mechanism
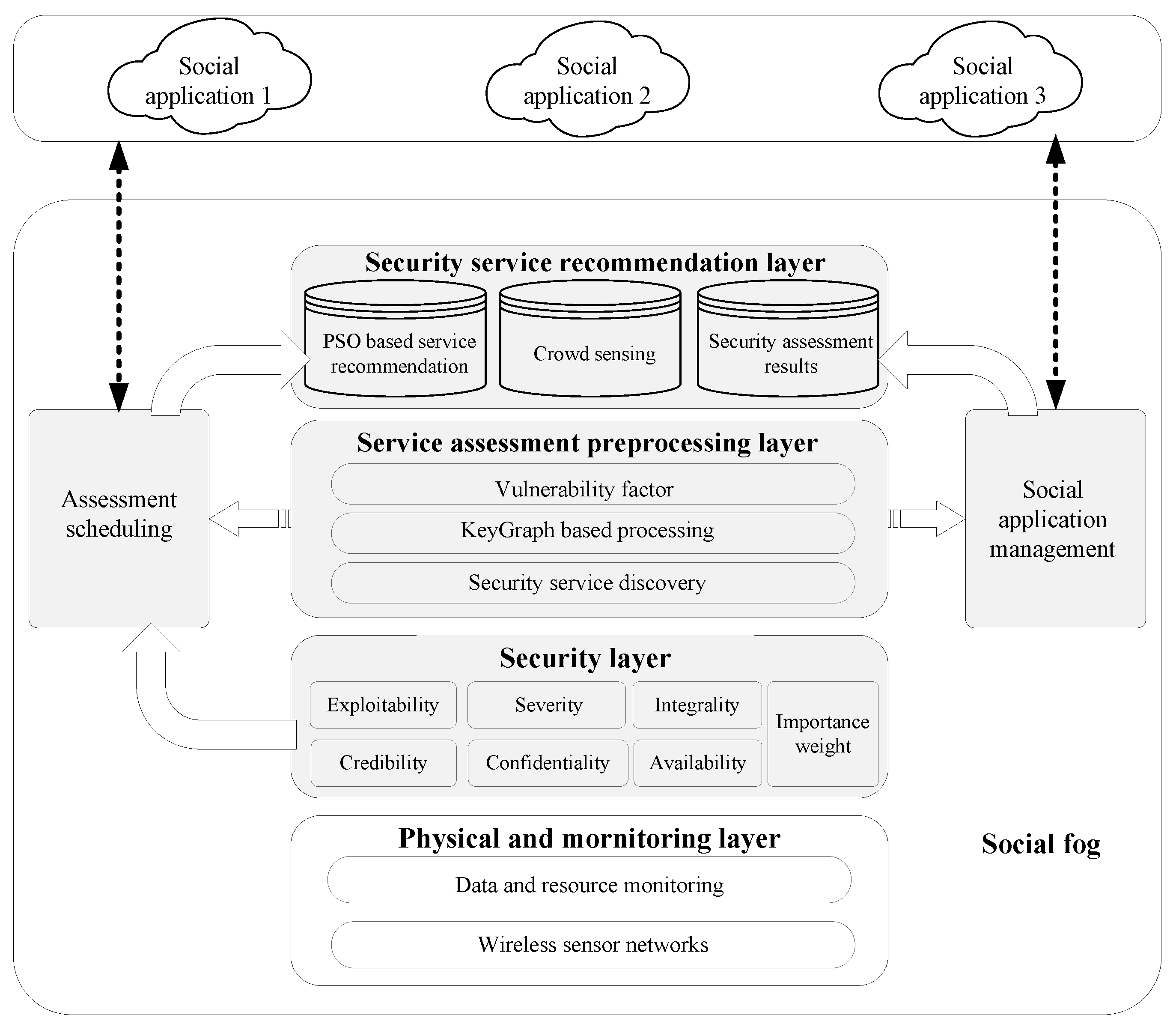
4.1. Architecture of the Security Service Recommendation of Social Fog
4.2. Security Services Assessment
4.3. Security Service Discovery Scheme
4.3.1. KeyGraph Establishment
4.3.2. KeyGraph Connection Value
4.3.3. Tightness Calculation
4.3.4. Security Service Discovery
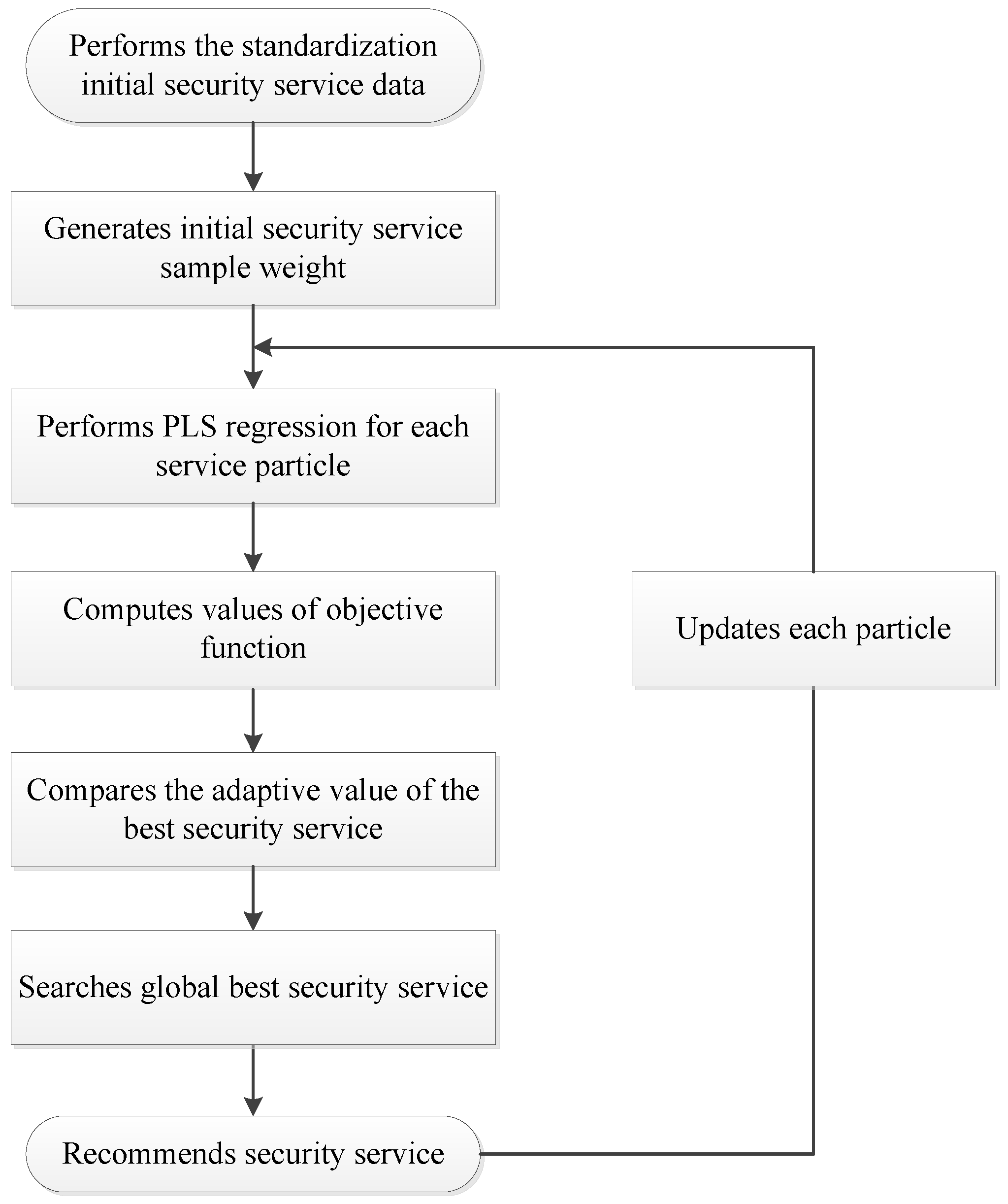
4.4. Security Service Recommendation Based on Particle Swarm Optimization (PSO)
5. Evaluation
5.1. Simulation Settings
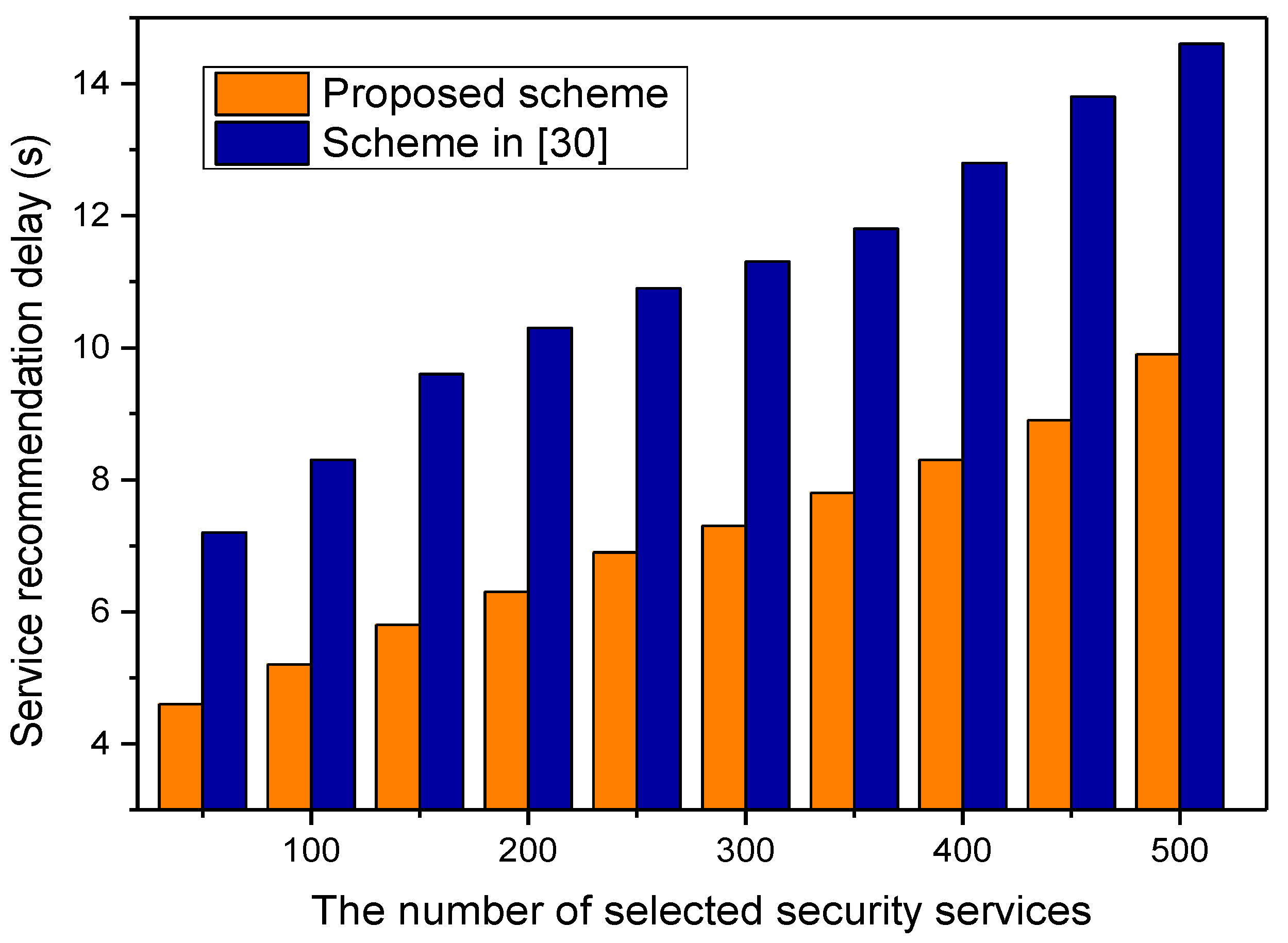
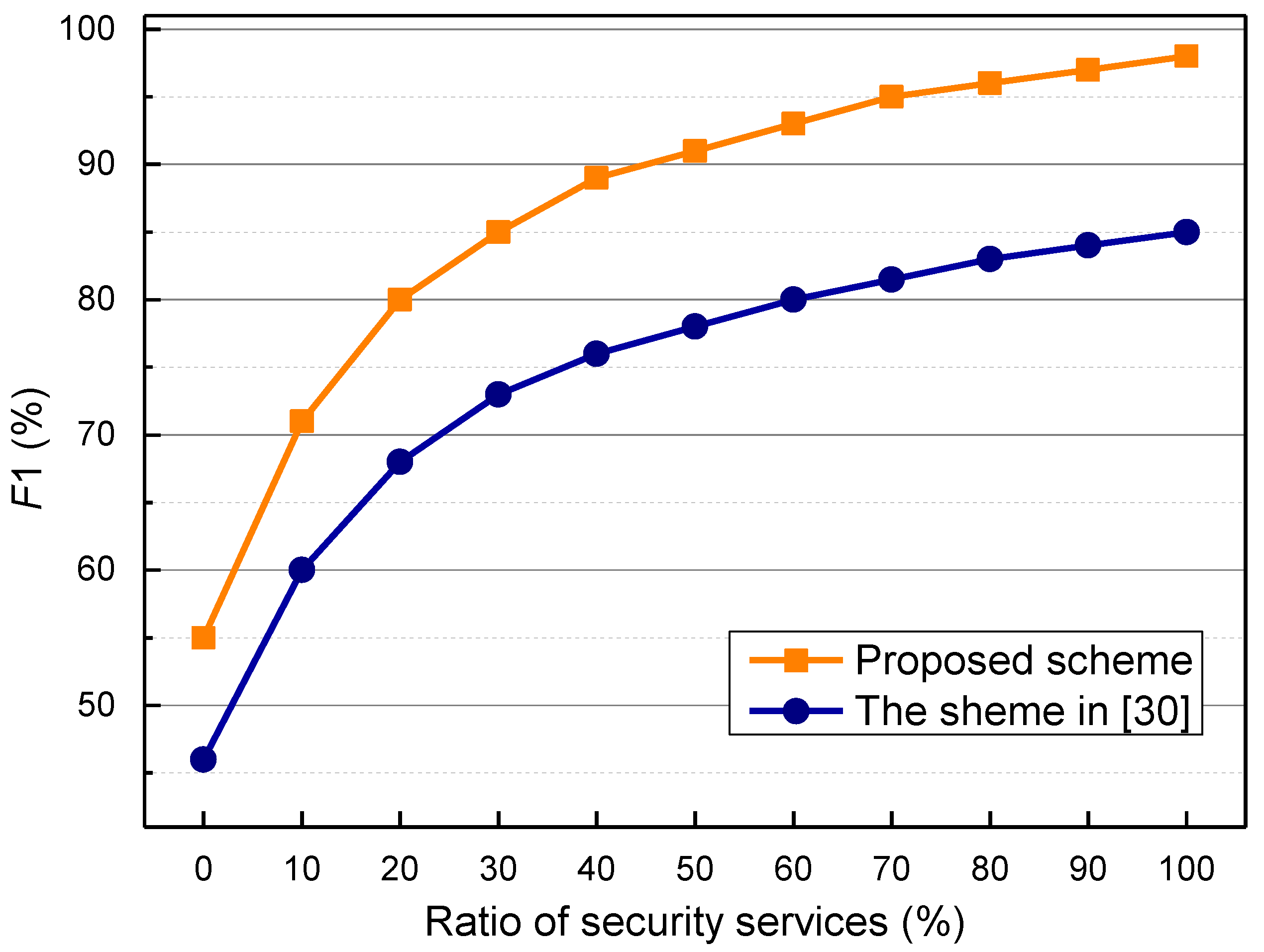
5.2. Simulation Results and Analysis
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Aazam, M.; Huh, E. Fog computing: The cloud-IoT/IoE middleware paradigm. IEEE Potentials 2016, 3, 40–44. [Google Scholar] [CrossRef]
- Ning, H.; Wang, Z. Future Internet of things architecture: Like mankind neural system or social organization framework? IEEE Commun. Lett. 2011, 4, 461–463. [Google Scholar] [CrossRef]
- Rahman, M.A.; El Saddik, A.; Gueaieb, W. Augmenting context awareness by combining body sensor networks and social networks. IEEE Trans. Instrum. Meas. 2011, 2, 345–353. [Google Scholar] [CrossRef]
- Domingo, M.C. A context-aware service architecture for the integration of body sensor networks and social networks through the IP multimedia subsystem. IEEE Commun. Mag. 2011, 1, 102–108. [Google Scholar] [CrossRef]
- Nitti, M.; Girau, R.; Atzori, L. Trustworthiness management in the social Internet of things. IEEE Trans. Knowl. Data Eng. 2013, 5, 1253–1266. [Google Scholar] [CrossRef]
- Su, Z.; Qi, Q.; Xu, Q.; Guo, S.; Wang, X. Incentive scheme for cyber physical social systems based on user behaviors. IEEE Trans. Emerg. Top. Comput. 2017, PP, 1. [Google Scholar] [CrossRef]
- SMART Cities Search Engine 2014. Available online: http://www.gla.ac.uk/research/infocus/themes/futurecities/projects/headline_289737_en.html (accessed on 5 March 2017).
- Su, Z.; Hui, Y.; Guo, S. D2D-based content delivery with parked vehicles in vehicular social networks. IEEE Wirel. Commun. 2016, 4, 90–95. [Google Scholar] [CrossRef]
- Chard, K.; Caton, S.; Rana, O.; Bubendorfer, K. Social Clouds: A Retrospective. IEEE Cloud Comput. 2015, 6, 30–40. [Google Scholar] [CrossRef]
- Caton, S.; Haas, C.; Chard, K.; Bubendorfer, K.; Rana, O.F. A social compute cloud: Allocating and sharing infrastructure resources via social networks. IEEE Trans. Serv. Comput. 2014, 3, 359–372. [Google Scholar] [CrossRef]
- Farris, I.; Girau, R.; Militano, L.; Nitti, M.; Atzori, L.; Iera, A.; Morabito, G. Social virtual objects in the edge cloud. IEEE Cloud Comput. 2015, 2, 20–28. [Google Scholar] [CrossRef]
- Zhang, K.; Liang, X.; Shen, X.; Lu, R. Exploiting multimedia services in mobile social networks from security and privacy perspectives. IEEE Commun. Mag. 2014, 3, 58–65. [Google Scholar] [CrossRef]
- Liang, X.; Li, X.; Lu, R.; Lin, X.; Shen, X. SEER: A secure and efficient service review system for service-oriented mobile social networks. In Proceedings of the IEEE 32nd International Conference on Distributed Computing Systems, Macau, China, 18–21 June 2012; pp. 647–656. [Google Scholar]
- Faruque, M.A.A.; Vatanparvar, K. Energy management-as-a-service over fog computing platform. IEEE Int. Things J. 2016, 2, 161–169. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Q.; Sohraby, K. Multimedia sensing as a service (MSaaS): Exploring resource saving potentials of at cloud-edge IoTs and fogs. IEEE Int. Things J. 2016, 99, 1–19. [Google Scholar] [CrossRef]
- Datta, S.K.; Bonnet, C.; Haerri, J. Fog computing architecture to enable consumer centric Internet of Things services. In Proceedings of the International Symposium on Consumer Electronics, Madrid, Spain, 24–26 June 2016; pp. 1–2. [Google Scholar]
- Yao, L.; Sheng, Q.Z.; Ngu, A.H.H.; Yu, J.; Segev, A. Unified collaborative and content-based Web service recommendation. IEEE Trans. Serv. Comput. 2015, 3, 435–466. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, Z.; Wu, Z.; Lyu, M.R.; Yang, F. Reputation measurement and malicious feedback rating prevention in Web service recommendation systems. IEEE Trans. Serv. Comput. 2015, 5, 755–767. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, Z.; Liu, X.; Huang, Z.; Sun, H. Personalized QoS-aware Web service recommendation and visualization. IEEE Trans. Serv. Comput. 2013, 1, 35–47. [Google Scholar] [CrossRef]
- Ohsawa, Y. Chance Discovery (Advanced Information Processing); McBurney, P., Ed.; Springer: Berlin, Germany, 2003; pp. 49–68. [Google Scholar]
- Ohsawa, Y.; Benson, N.E.; Yachida, M. KeyGraph: Automatic indexing by co-occurrence graph based on building construction metaphor. In Proceedings of the IEEE International Forum on Research and Technology Advances in Digital Libraries, Santa Barbara, CA, USA, 22–24 April 1998; pp. 12–18. [Google Scholar]
- Wong, G.K.W.; Li, S.Y.K. Academic performance prediction using chance discovery from online discussion forums. In Proceedings of the IEEE 40th Annual Computer Software and Applications Conference (COMPSAC), Atlanta, GA, USA, 10–14 June 2016; pp. 706–711. [Google Scholar]
- Wang, L.; Zhang, D.; Yan, Z.; Xiang, H.; Xie, B. EffSense: A novel mobile crowd-sensing framework for energy-dfficient and cost-effective data uploading. IEEE Trans. Syst. Man Cybern. Syst. 2015, 12, 1549–1563. [Google Scholar] [CrossRef]
- Baguena, M.; Calafate, C.T.; Cano, J.C.; Manzoni, P. An adaptive anycasting solution for crowd sensing in vehicular environments. IEEE Trans. Ind. Electron. 2015, 12, 7911–7919. [Google Scholar] [CrossRef]
- Wen, Y.; Shi, J.; Zhang, Q.; Tian, X.; Huang, Z.; Yu, H.; Cheng, Y.; Shen, X. Quality-driven auction-based incentive mechanism for mobile crowd sensing. IEEE Trans. Veh. Tech. 2015, 9, 4203–4214. [Google Scholar] [CrossRef]
- Luo, S.; Dong, M.; Ota, K.; Wu, J.; Li, J. A security assessment mechanism for software-defined networking-based mobile networks. Sensors 2015, 15, 31843–31858. [Google Scholar] [CrossRef] [PubMed]
- Sha, D.Y.; Hsu, C.Y. A new particle swarm optimization for the open shop scheduling problem. Comput. Oper. Res. 2008, 10, 3243–3261. [Google Scholar] [CrossRef]
- Xu, L.; Jiang, J.H.; Lin, W.Q.; Zhou, Y.P.; Wu, H.L.; Shen, G.L.; Yu, R.Q. Optimized sample-weighted partial least squares. Talanta 2007, 2, 561–566. [Google Scholar] [CrossRef] [PubMed]
- Stanford Network Analysis Project (SNAP). Available online: https://snap.stanford.edu/data/ (accessed on 10 February 2017).
- Hurley, N.; Zhang, M. Novelty and diversity in top-N recommendation analysis and evaluation. ACM Trans. Int. Tech. 2011, 4, 1–30. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y. Change taxonomy and service importance factor for change analysis in composite service. In Proceedings of the IEEE 12th International Conference on e-Business Engineering (CSDL 2015), Beijing, China, 23–25 October 2015; pp. 127–134. [Google Scholar]
- Deng, R.; Lu, R.; Lai, C.; Luan, T.H. Optimal workload allocation in fog-cloud computing toward balanced delay and power consumption. IEEE Internet Things J. 2016, 6, 1171–1181. [Google Scholar] [CrossRef]
- Lu, R.; Heung, K.; Lashkari, A.H.; Ghorbani, A.A. A lightweight privacy-preserving data aggregation scheme for fog computing-enhanced IoT. IEEE Access 2017, 5, 3302–3312. [Google Scholar] [CrossRef]
- Xiong, A.; Xu, C. Energy efficient multiresource allocation of virtual machine based on PSO in cloud data center. Math. Prob. Eng. 2014, 6, 1–8. [Google Scholar] [CrossRef]
- Osanaiye, O.; Chen, S.; Yan, Z.; Lu, R.; Choo, R.; Dlodlo, M. From cloud to fog computing: A review and a conceptual live VM migration framework. IEEE Access 2017, 5, 8284–8300. [Google Scholar] [CrossRef]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Su, Z.; Wang, S.; Li, J. Crowd Sensing-Enabling Security Service Recommendation for Social Fog Computing Systems. Sensors 2017, 17, 1744. https://doi.org/10.3390/s17081744
Wu J, Su Z, Wang S, Li J. Crowd Sensing-Enabling Security Service Recommendation for Social Fog Computing Systems. Sensors. 2017; 17(8):1744. https://doi.org/10.3390/s17081744
Chicago/Turabian StyleWu, Jun, Zhou Su, Shen Wang, and Jianhua Li. 2017. "Crowd Sensing-Enabling Security Service Recommendation for Social Fog Computing Systems" Sensors 17, no. 8: 1744. https://doi.org/10.3390/s17081744
APA StyleWu, J., Su, Z., Wang, S., & Li, J. (2017). Crowd Sensing-Enabling Security Service Recommendation for Social Fog Computing Systems. Sensors, 17(8), 1744. https://doi.org/10.3390/s17081744






