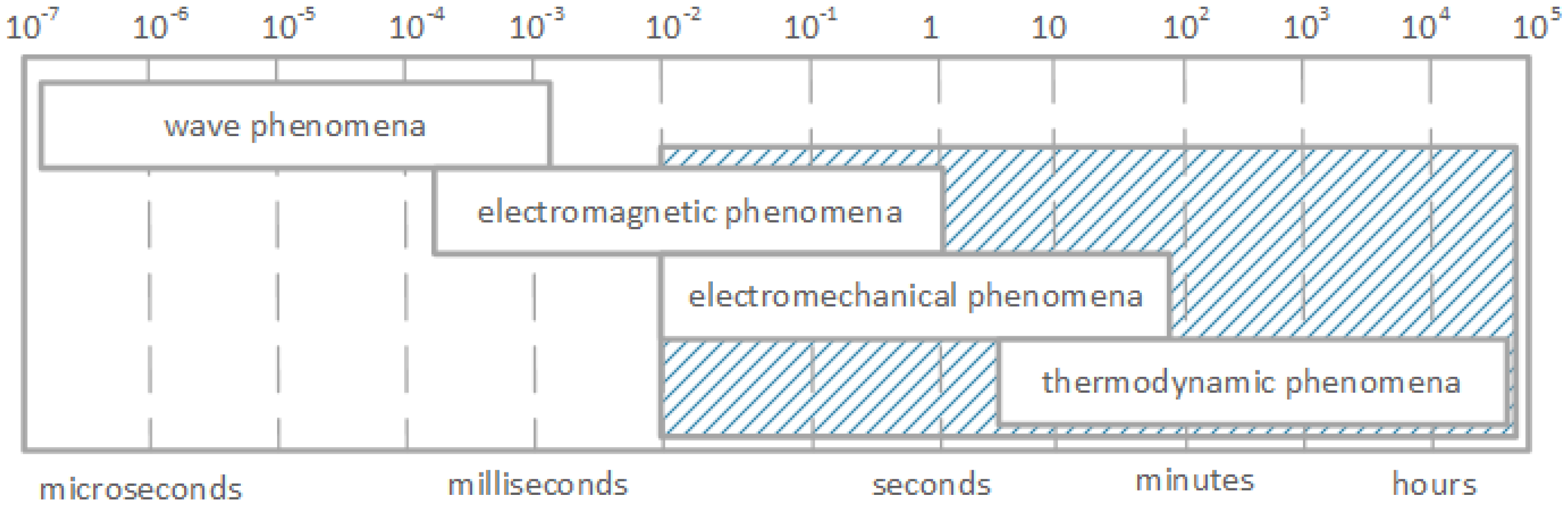
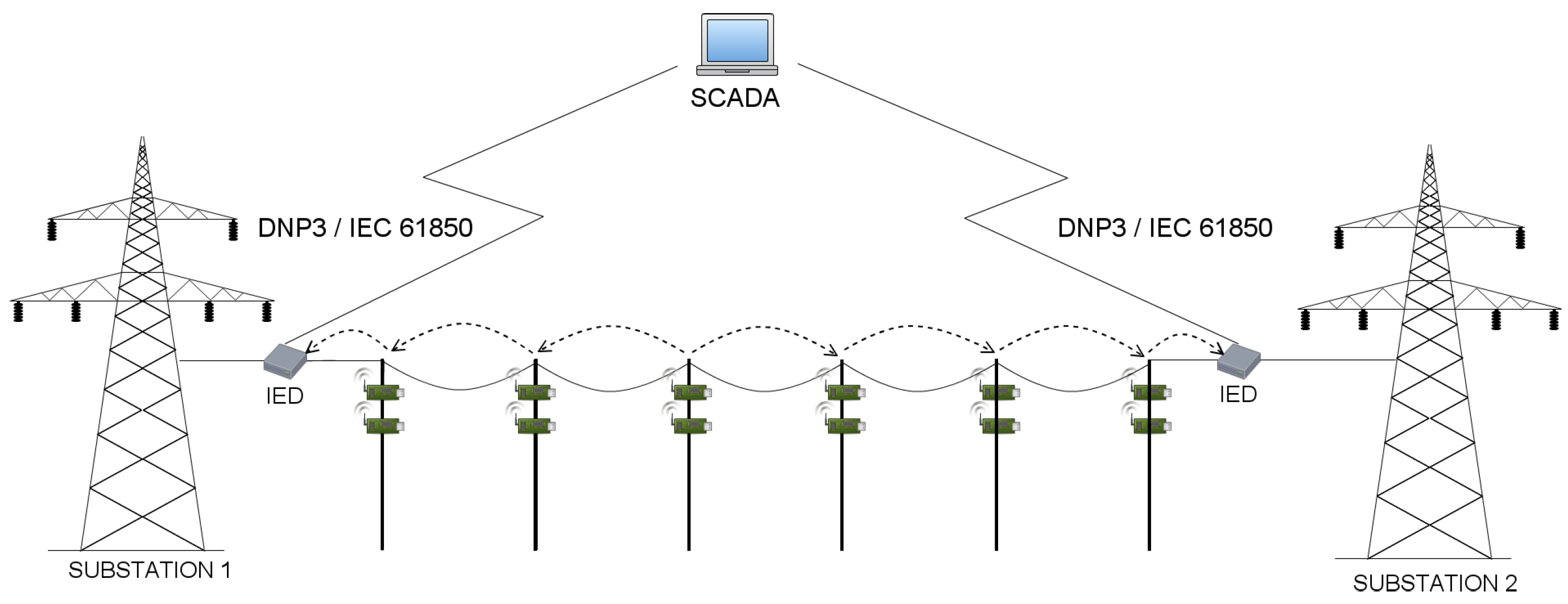
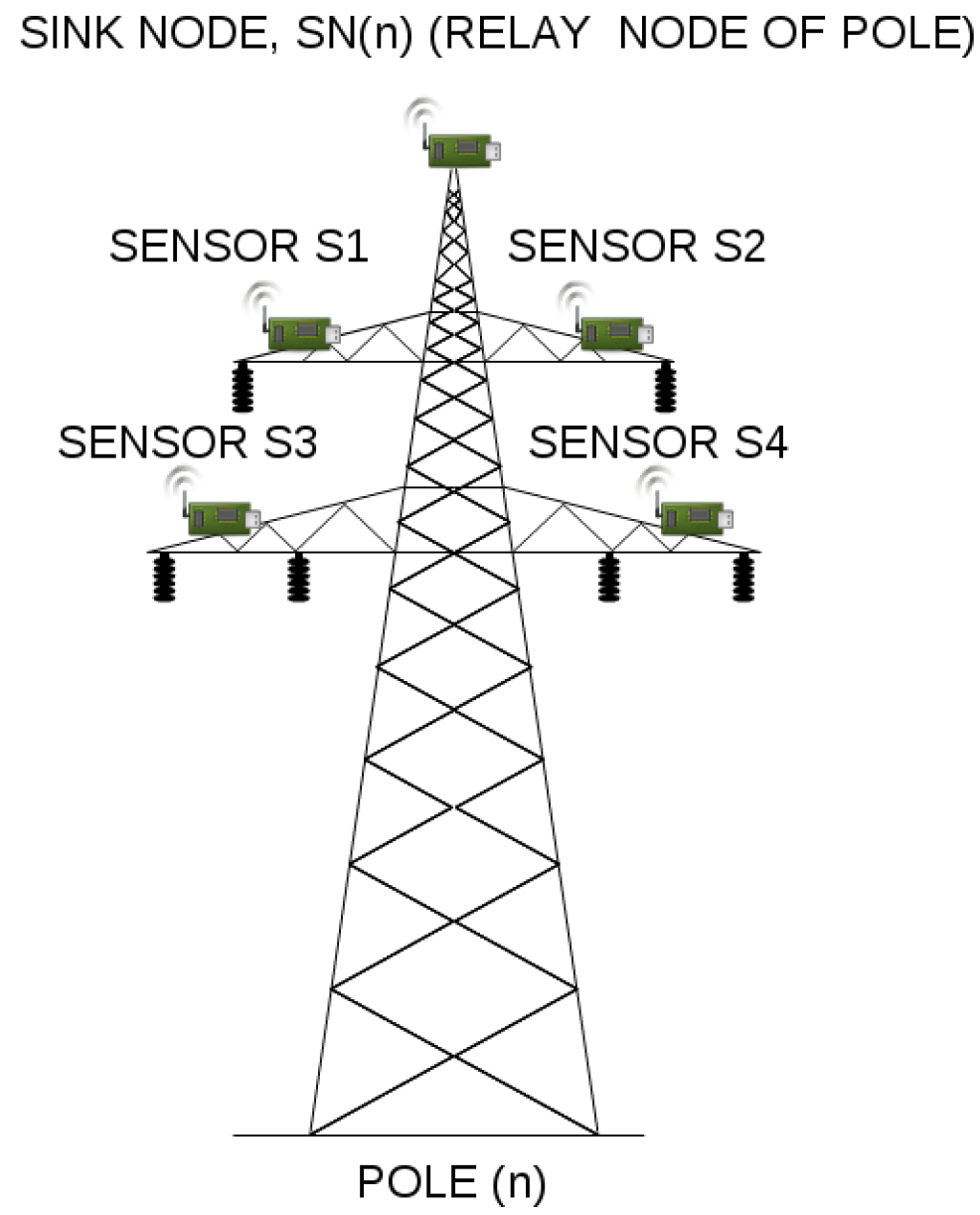
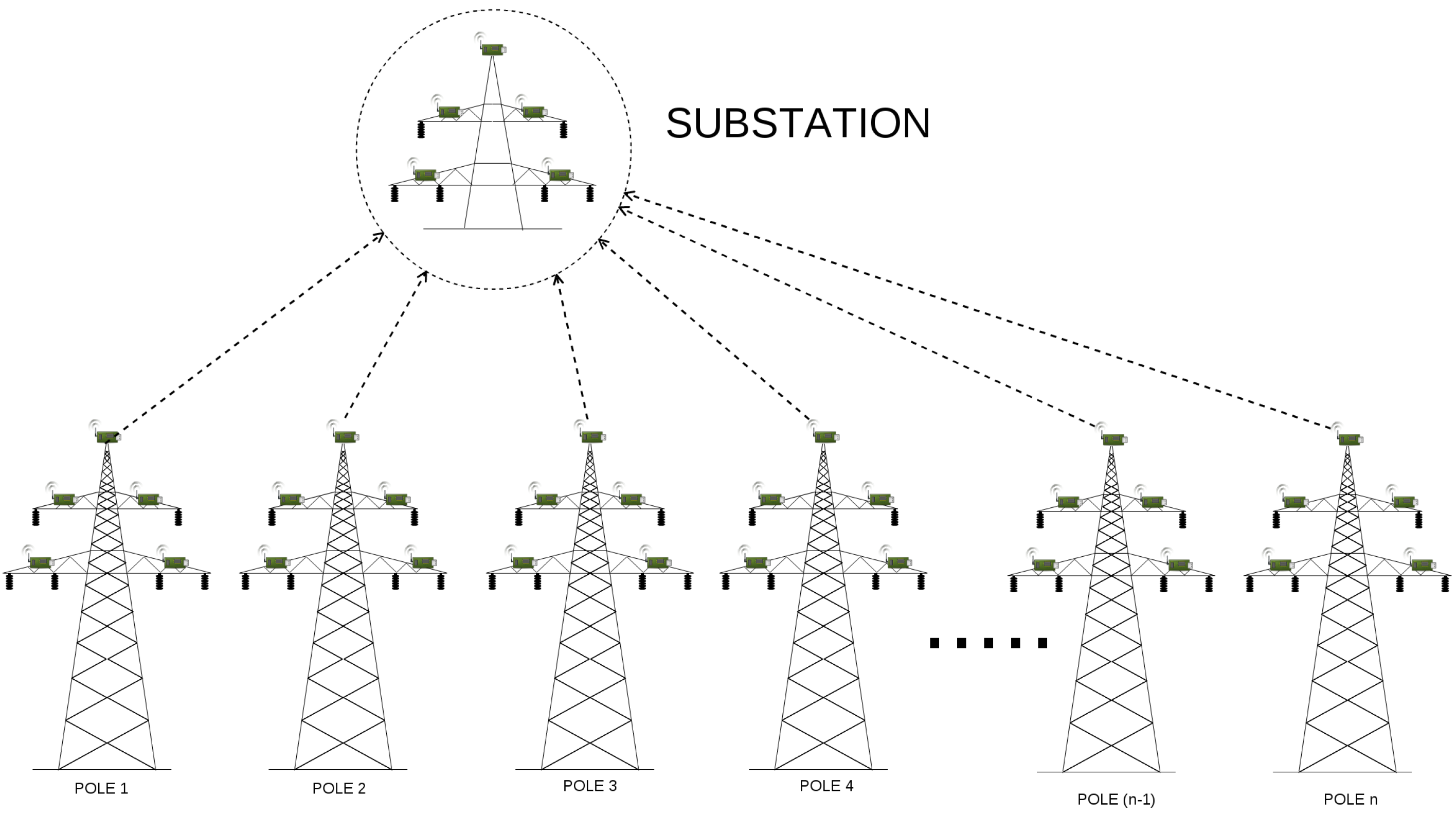
4.10. Model Description
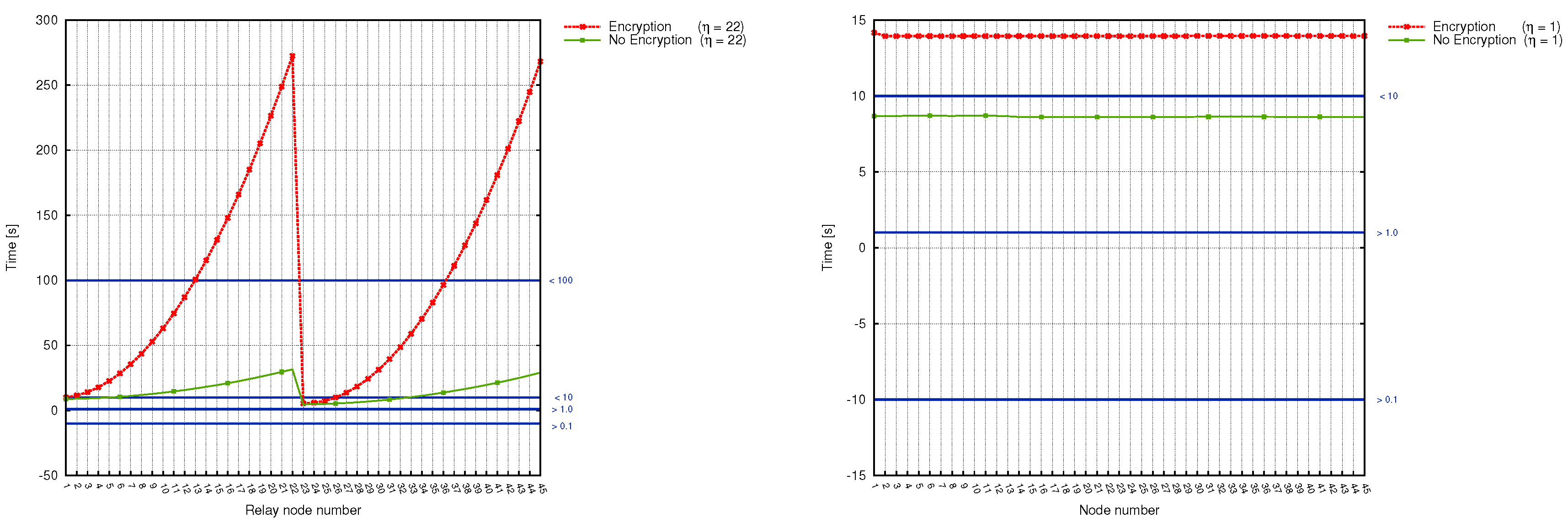
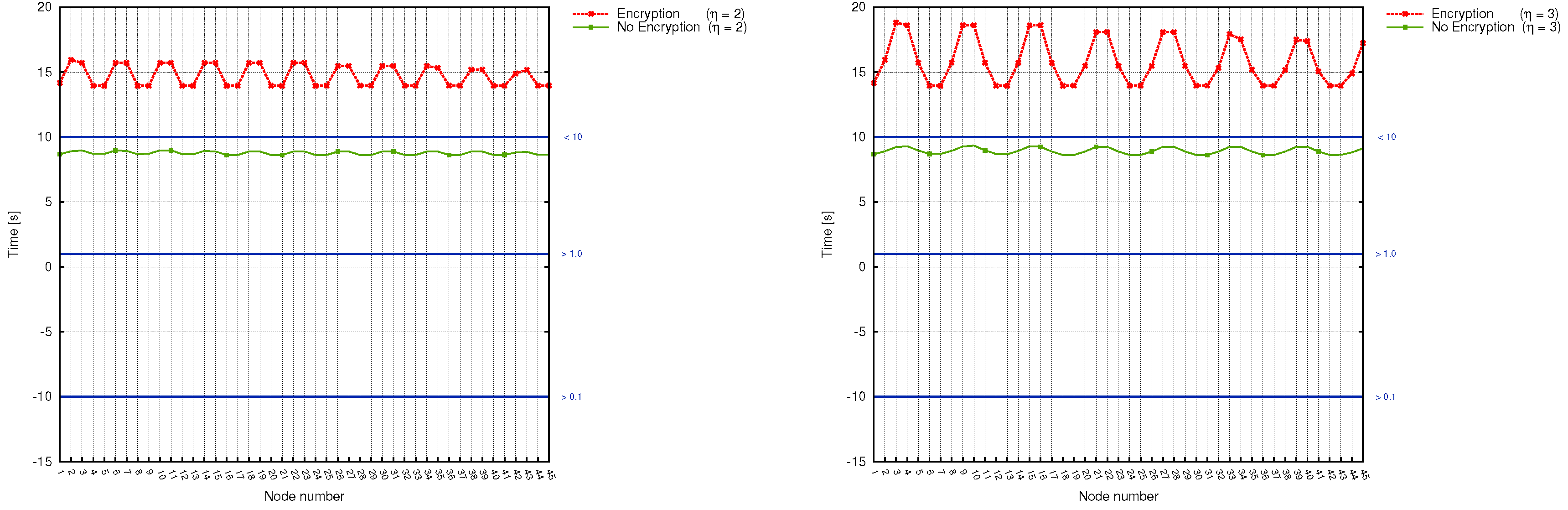
Analyzing the transmission line monitoring scheme, we utilized the QoP-ML to prepare a functional model of the considered segment of smart grid environment. We gathered and used real hardware security metrics and developed appropriate scenarios in order to examine how different factors influence transmission time delays, lifetime of sensor devices, confidentiality, integrity, and availability of the data traversing transmission grid environments. In this section, we briefly discuss all the elements we prepared to create the transmission grid models, and analyze the results we gathered using the Automated Quality of Protection Analysis (AQoPA) tool [
19]. (The AQoPA tool performs the automatic evaluation and optimization of complex system models which are created in QoP-ML.) In this article, describing our model, we considered only the scenario where
. (However, remaining scenarios are designed analogically, so they can be understood without further explanation.) Both the models and the AQoPA tool can be downloaded from the QoP-ML’s project webpage [
20].
In QoP-ML, in order to perform a simulation, one needs to prepare and implement 3 basic elements, namely: the model itself, hardware security metrics and miscellaneous scenarios of the considered environment (which are also called
versions). For more information about QoP-ML, its syntax, semantics, algorithms and example usages, please refer to [
17,
21].
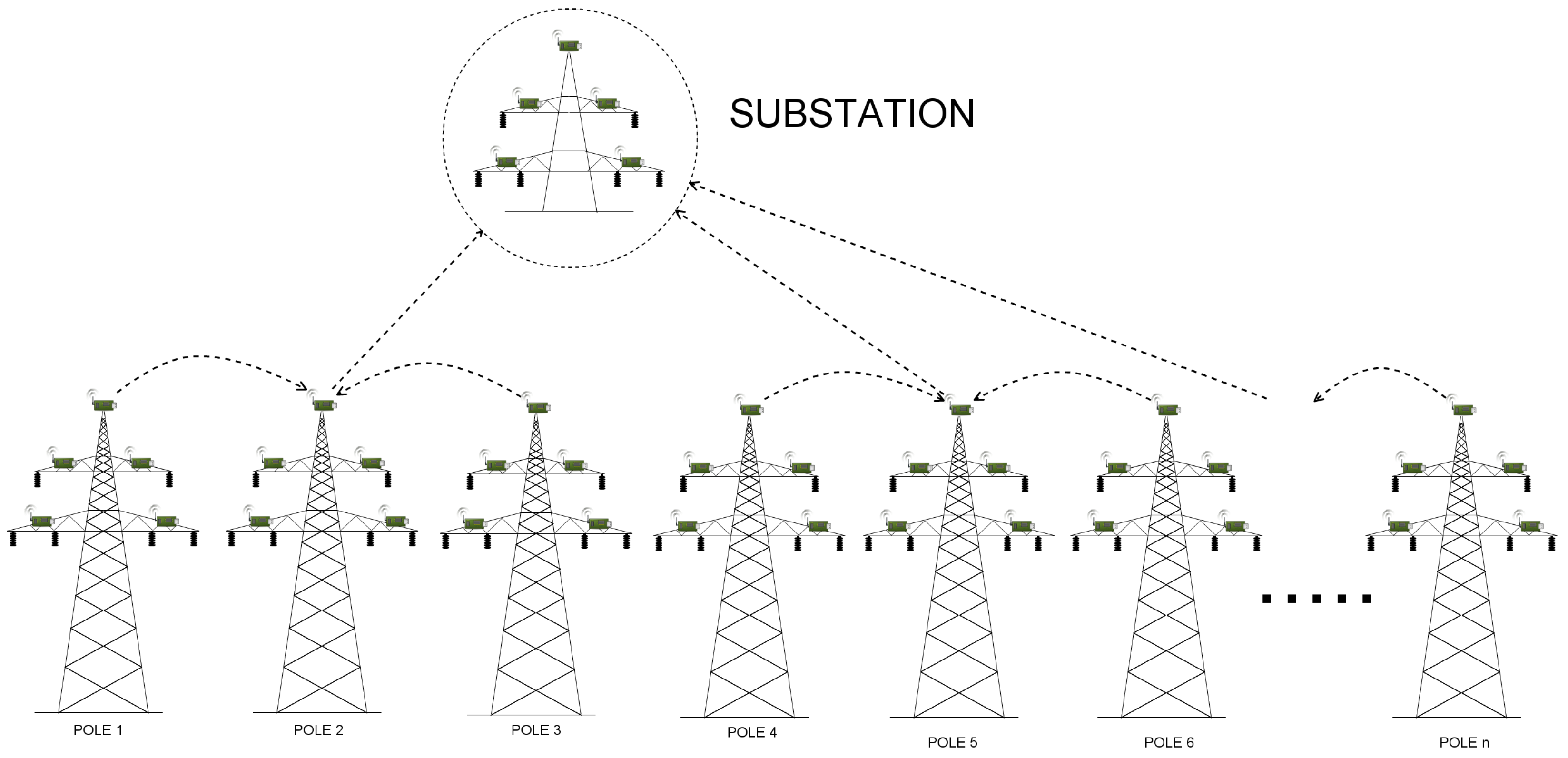
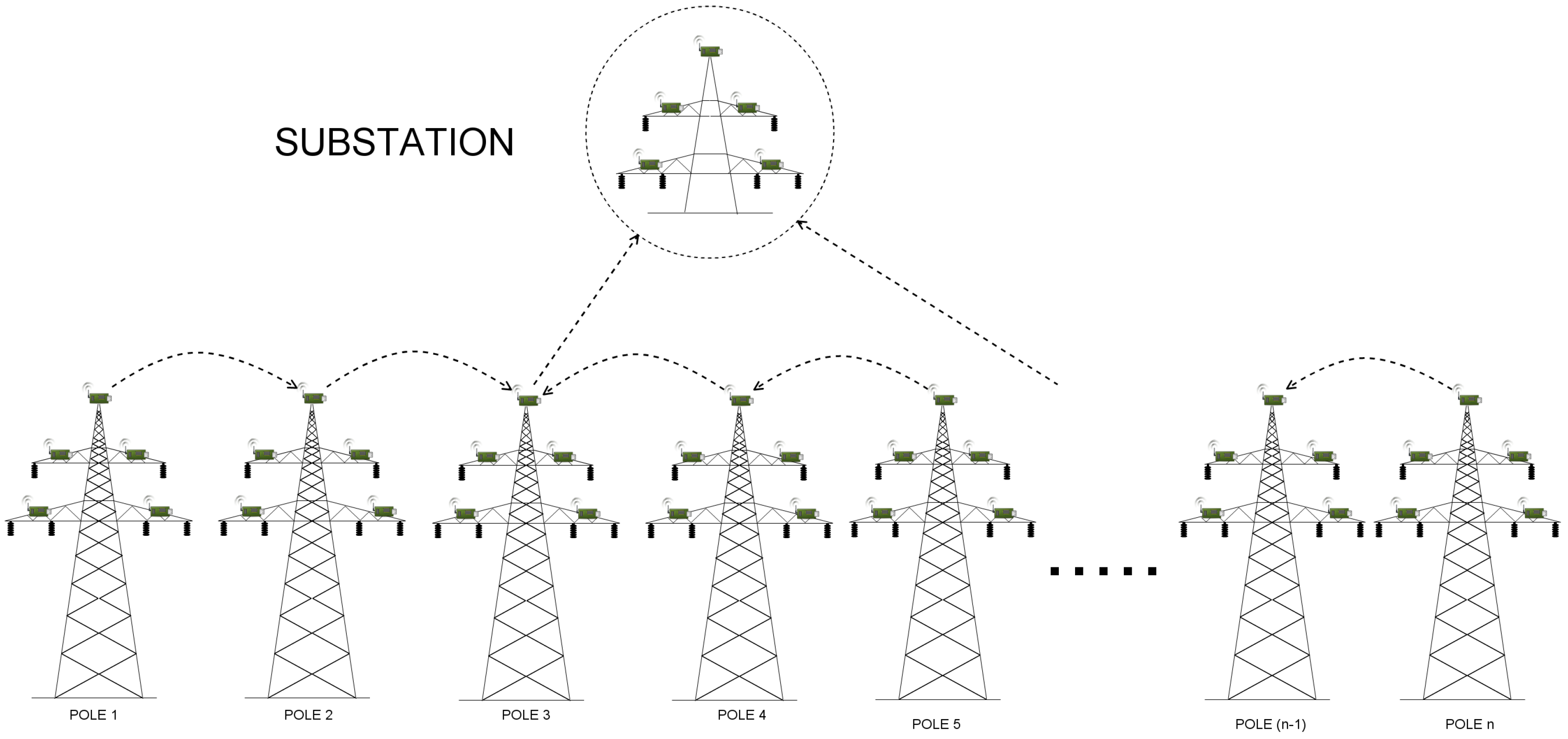
Before we present implementation details, let us describe the model in general. We have 4 types of communicating hosts: manager, sink, sensor and a substation (in our model referred to as the base station). While there is no manager in a real life deployment of the considered scenario, its abstraction in QoP-ML needs the manager to handle proper packet flows. Manager stores lists of sinks and sensors, and knows which sensor is assigned to which sink. Its main role is to send control messages to sink nodes, in order to give them instructions from which sensors they should collect data from, or when it is the best time for performing data transmission to the substation. Sink nodes receive a list of its sensors from manager, generate some parameters, send them to assigned motes and wait for the collected data. After the data is collected, sensors send it to their relay node. When the relay node receives a message from each of four sensors and the manager, it immediately starts the routing to the substation. Communication ends when the base station receives packets from all the sinks that connect directly.
In Listing 1 we present functions prepared for the transmission grid model. Lines 3–7 contain declaration of functions, which are used by the manager to, for instance, handle the division of sensors to proper sinks. Functions representing the type of the message traversing the transmission grid environment are defined in lines 8–14. Symmetric encryption and symmetric decryption functions (lines 16–17) take two functional arguments, the data to be encrypted/decrypted (data) and the key used for encryption/decryption (K). Besides functional arguments, s_enc and s_dec take two additional, QoP parameters: the algorithm used for encryption/decryption, and the size of the key in bytes (key_size). Remaining functions (lines 19–21) refer to data collection, and are fairly self-explanatory.
![Sensors 17 01610 i001]()
Equational rules, needed by list operations and symmetric cryptographic functions, are defined in Listing 2, and are simply used to assess the equality of function calls and to reduce complex function calls. For instance, equation in line 7, states that the symmetric decryption of symmetrically encrypted data with the same key returns the encrypted data.
![Sensors 17 01610 i002]()
Secure communication between sinks all over transmission line is a crucial element in our simulation: communicating hosts need a medium to exchange messages. For this reason, implementing considered environment, we defined two communication channels (Listing 3): ch_WSN and ch_MGNT. Due to the fact that the manager is only a helper host, and its role is to handle packet flows, the manager uses ch_MGNT channel for sending control information (the one, which has connection quality equal to 1 (the lower the q value, the better the connection quality), and sending time equal to 0 ms). On the other hand, ch_WSN is responsible for transferring all the data traversing a transmission grid. Exact channel characteristics will be discussed while presenting the versions structure.
![Sensors 17 01610 i003]()
Moving on to the next point, let us now discuss hosts, which take part in a transmission grid communication, starting with the BaseStation host (Listing 4). The role of the base station is quite simple: in an infinite loop (lines 7–18), it waits for the data from sinks scattered over transmission line (lines 9–10), decrypts the data (only when it was encrypted (lines 12–15)), and saves it for further processing (line 17). Next, we have the Sensor host (Listing 5), responsible mainly for data collection. The very first instruction of the Sensor host is the generation of the symmetric key (line 3), which can be further used for data encryption (line 16). Sensor waits for parameters send by sink (lines 7–9), in which there is an identifier (ID) of the device, which acts as the relay node for this specific sensor. Then, the sensor performs a measurement to gather the data (lines 11–12) and optionally encrypts it (lines 14–17).
![Sensors 17 01610 i004]()
![Sensors 17 01610 i005]()
After the data is collected, sensor notifies everyone (in this case the manager, since it waits for the message with the data_collected_msg() type, which indicates that the data is gathered, and can be collected by appropriate relay nodes (lines 19–20). When the sink node is ready to receive the data, sensor simply creates a message and sends it to its relay node, using previously obtained SINK_ID (lines 22–23).
The most essential part in our simulation is the routing of the data obtained from all sensors towards the base station (substation actually). Sink devices (Listing 6) are those responsible for data gathering and transmission.
As it can be seen in Listing 6, sink consists of 3 processes, namely Main, WaitForData and HopByHopComm, where each of them is in charge of different operations. The Main process (lines 6–22) waits for data from Manager, in order to receive the list of sensors, from which sink needs to gather the data (lines 8–9). After receiving the list of sensors, sink generates parameters and sends them to sensor devices (lines 13–20). The actual data gathering takes place in WaitForData process (lines 24–43), in which sink node waits for data gathered by sensors (lines 31–32). If the data was encrypted, sink decrypts it (lines 34–37), saves (line 39) and adds it to the list of the collected packets (line 40). The last, HopByHopComm process, is responsible for the actual data transmission towards the base station (lines 44–65). Its role is to receive the initial data from Manager or another Sink within its cluster (lines 47–48). Then, sink decrypts the data (but only if it was encrypted (lines 50–53)), adds the data to the list of the gathered packets containing measurement information (line 55) and performs the routing algorithm, in order to find the ID of the next sink on a path to the base station (line 56). Remaining instructions concern optional encryption (lines 58–61) of the collected data and the process of sending it to another sink, towards the base station. HopByHopComm process ends when packets from all the cluster heads reach the base station.
![Sensors 17 01610 i006]()
Last but not least, the Manager, represents a host, which is not available (and not needed) in a real-life deployment. As brought up earlier, its role is to work only as a helper host, which manages packet flows in our simulation. The Manager host consists of two processes, namely PrepareMessages and Main processes. The PrepareMessages process is responsible for creating lists of sensors, which belong to appropriate sinks along the transmission line (lines 7–39). Another function of this process is to maintain the list of sinks (lines 41–64), to which Manager has to send the initial message, which then starts the data gathering and routing process. Acting as a fundamental managing process, Main process’ first job is to inform each sink along the transmission line, from which sensors they can collect data from. Manager does that by sending the nodes_msg() type message (lines 69–84) to every sink. After sinks notification, Manager copies the list of all the available sinks (line 86) and collects information indicating end of data gathering process from TelosB sensors (lines 88–92). When all nodes_msg() messages are gathered, Manager prepares an empty list, which will be further send to each cluster, starting data routing process (being optionally encrypted before (lines 95–99)). Next, a list of all sinks (which are initiators of data routing within a cluster), is copied to a temporary variable (line 101). The last activity of the Manager host is to send the empty message to all the sinks, which initiate communication towards the base station within a given cluster (lines 103–109). Manager simply takes an ID of the sink from previously prepared list (line 105), removes it from mentioned list (line 106) and prepares a message (an empty list, actually, line 107), which is next send to each sink, one by one, until the list ends (line 108).
In order to determine the transmission time of the packets being sent through the transmission grid, we implemented an algorithm, which calculates the transmission time between two sensors (Listing 7). The transmission time of a single packet is equal to constant 18 ms plus
ms per each byte. The while loop is used to handle messages with the payload larger than 110 bytes, which is the maximum payload size in ZigBee (assuming that header has 17 bytes size; the maximum size of packet is 127 bytes) [
22]. When the maximum size is exceeded, payload is divided into many packets with 110 bytes each.
![Sensors 17 01610 i007]()
![Sensors 17 01610 i008]()
Another important step in QoP-ML’s modeling is the gathering of security metrics. This process can be fully (or partly) automated, using the Crypto Metrics Tool [
23]. Hardware security metrics (like, for instance, time taken by encryption) can be gathered by the tool, while remaining ones can be added by hand. In Listing 9 one can see metrics obtained from TelosB devices.
Let us focus on, for instance, lines 26 and 27 from Listing 9. Here, the details about the encryption process performed by TelosB devices are defined. As we can see from the metric’s header (line 26), we have some information about the considered operation type, utilized algorithm, the size of the encryption key, the time taken by the encryption itself (in ms), and finally, the size of the encrypted message (in bytes). Exact values, corresponding to elements available in the metric’s header, are given as follows.
![Sensors 17 01610 i009]()
The operation type (function name) is
s_enc,
alg refers to the utilized encryption algorithm, which, in this case is
AES-CTR. The
key_size is equal to 128 bytes, while the remaining parts concern time and output size calculations (line 27). Gathered security metrics are utilized during the simulation process to take into account the influence of the hardware specifications on performed operations. For more information about security metrics itself, its syntax, semantics and usage, please refer to [
17,
19,
21].
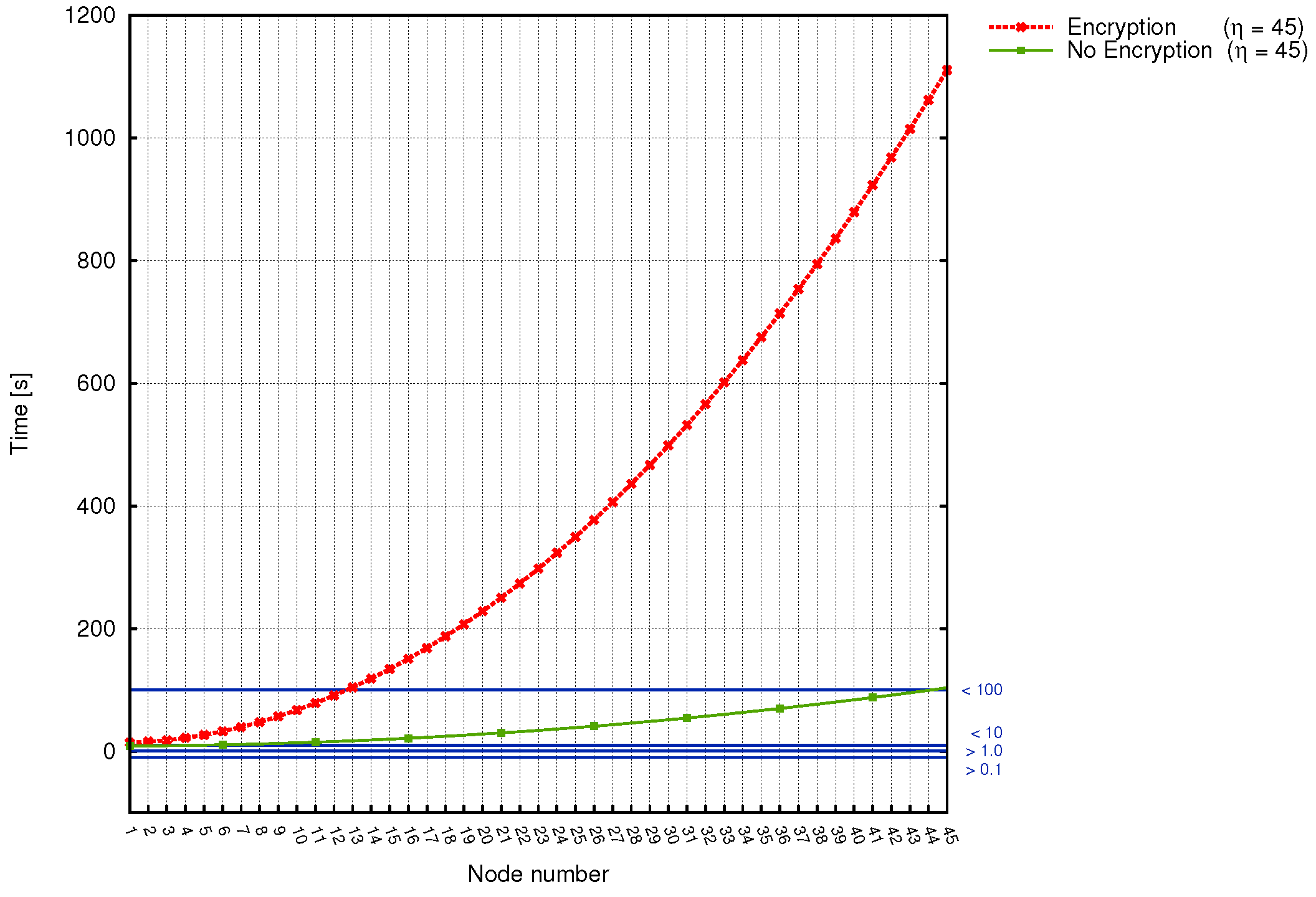
Building the versions structure is considered the final step before the actual simulation. Preparing multiple versions, one is capable of defining different sequences of events, without a need to modify the model. In the considered transmission grid analysis, we examine only two main scenario types: with (version Enc_Updated) and without (version NoEnc_Updated) packet encryption (Listing 10). Analyzed scenarios differ only in hosts’ instruction start-up process: the Enc_Updated version, except running base processes, additionally starts up sub-processes responsible for cryptographic operations. Let us now discuss the role of each instruction, as they are used in both version structures.
Lines from 5 to 8 (the set instructions) link hosts with appropriate security metrics, so that the operations performed by those hosts make use of suitable values (bear in mind that, for instance, encryption time can be different for TelosB and MicaZ motes). The following lines (10–27) are those which differ between versions: in NoEnc_Updated version, run instructions start only basic processes, without even knowing about sub-processes, while Enc_Updated (lines 93–110) additionally executes commands responsible for packet encryption. Another important role of the run instruction is the possibility to define how many host instances one can start. As shown in Listing 10, our WSN consist of 45 MicaZ sinks, 180 TelosB sensor devices, a base station, and the manager. Communication between utilized devices is defined inside the communication structure, between 29th and 84th line. Here, communication channel characteristics for each medium (such as the time taken by sending and receiving packets or current values) are given (lines 31–34).
The topology of the utilized WSN is specified with the help of the
topology structure (lines 36–63). Every connection defined in
topology structure consists of communicating hosts, and an arrow which expresses the actual packet flow. Consider, for instance, the 51st line, where one can see two communicating sites: sink and base station. As can be seen, second from 45 sinks sends the packet straight to the base station (as indicated by an arrowhead, which points to the right, that is, from sink to base station). The topology structure is a very flexible and adaptable part of QoP-ML, since it allows defining details of each connection separately, taking into account its key characteristics. For more information about
versions structure, refer to [
17,
19,
21].
![Sensors 17 01610 i010a]()
![Sensors 17 01610 i010b]()