Leaf Area Index Estimation Using Chinese GF-1 Wide Field View Data in an Agriculture Region
Abstract
:1. Introduction
2. Study Area
3. Data and Pre-Processes
3.1. Field LAI Measurements
3.2. GF-1 WFV Data and Pre-Processes
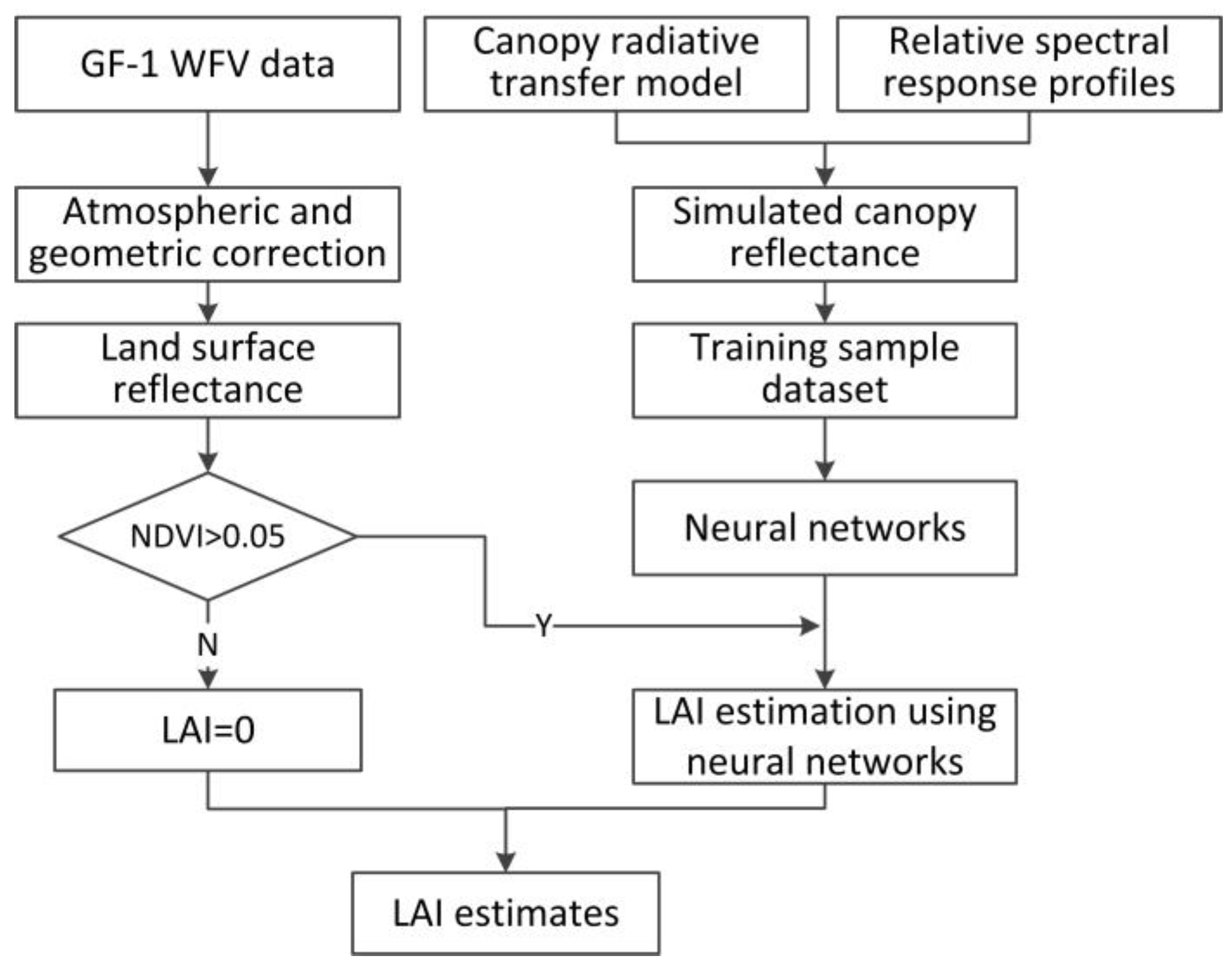
4. Methods
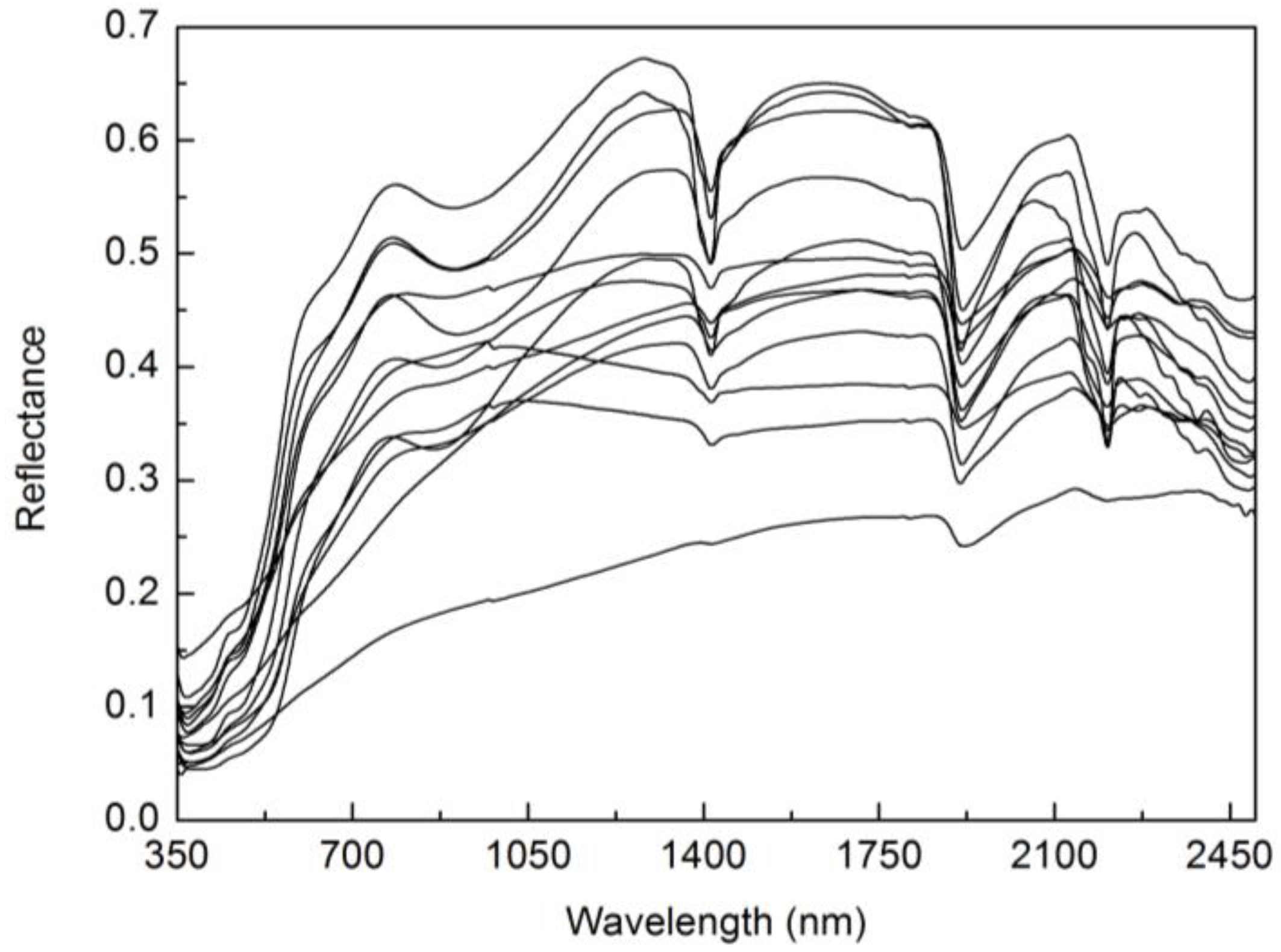
4.1. Generating LAI Training Sample Dataset from Radiative Transfer Model Simulations
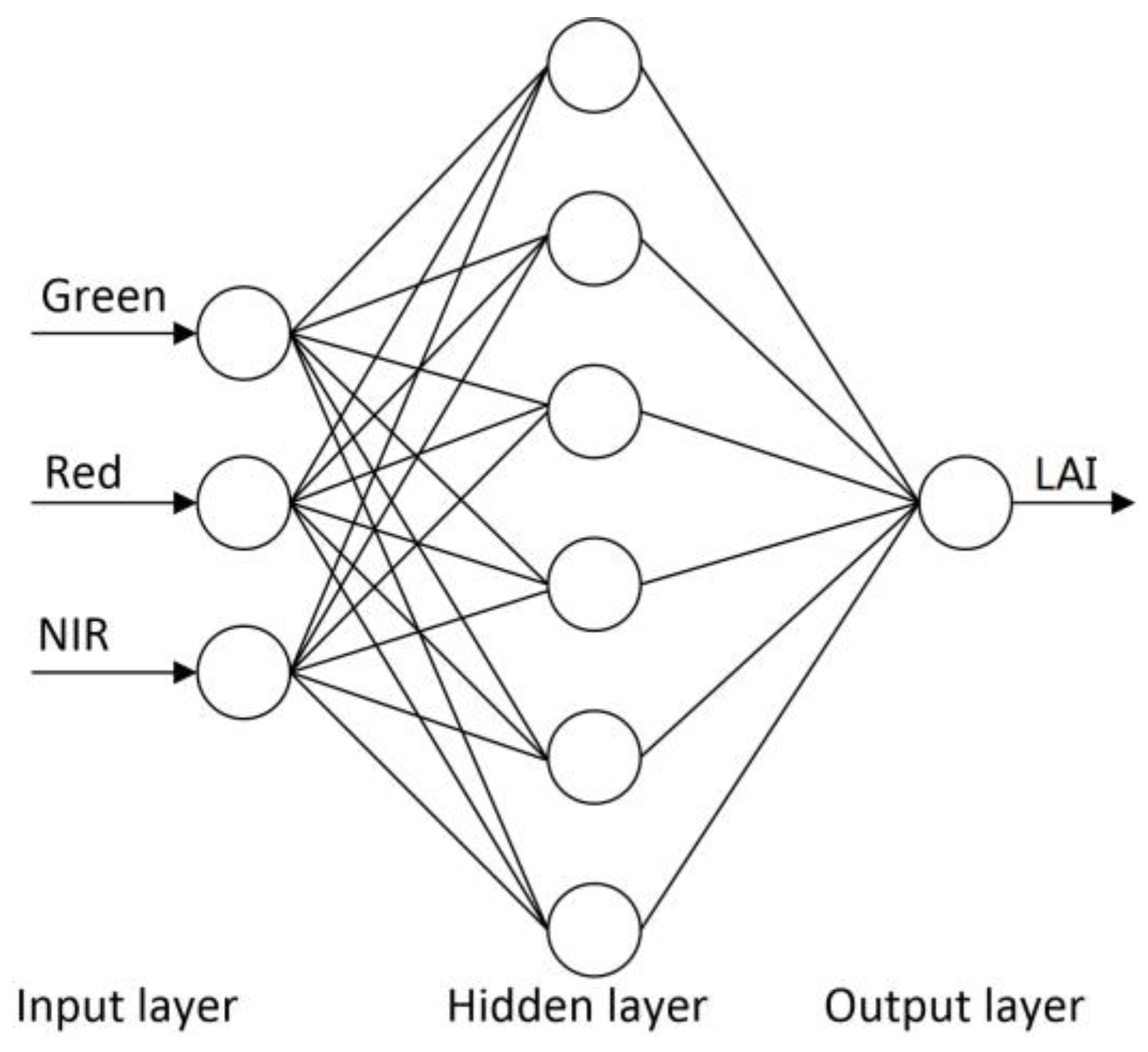
4.2. Neural Networks
4.3. LAI Estimating Procedure for GF-1 WFV Data
4.4. LAI Estimation Accuracy Assessment
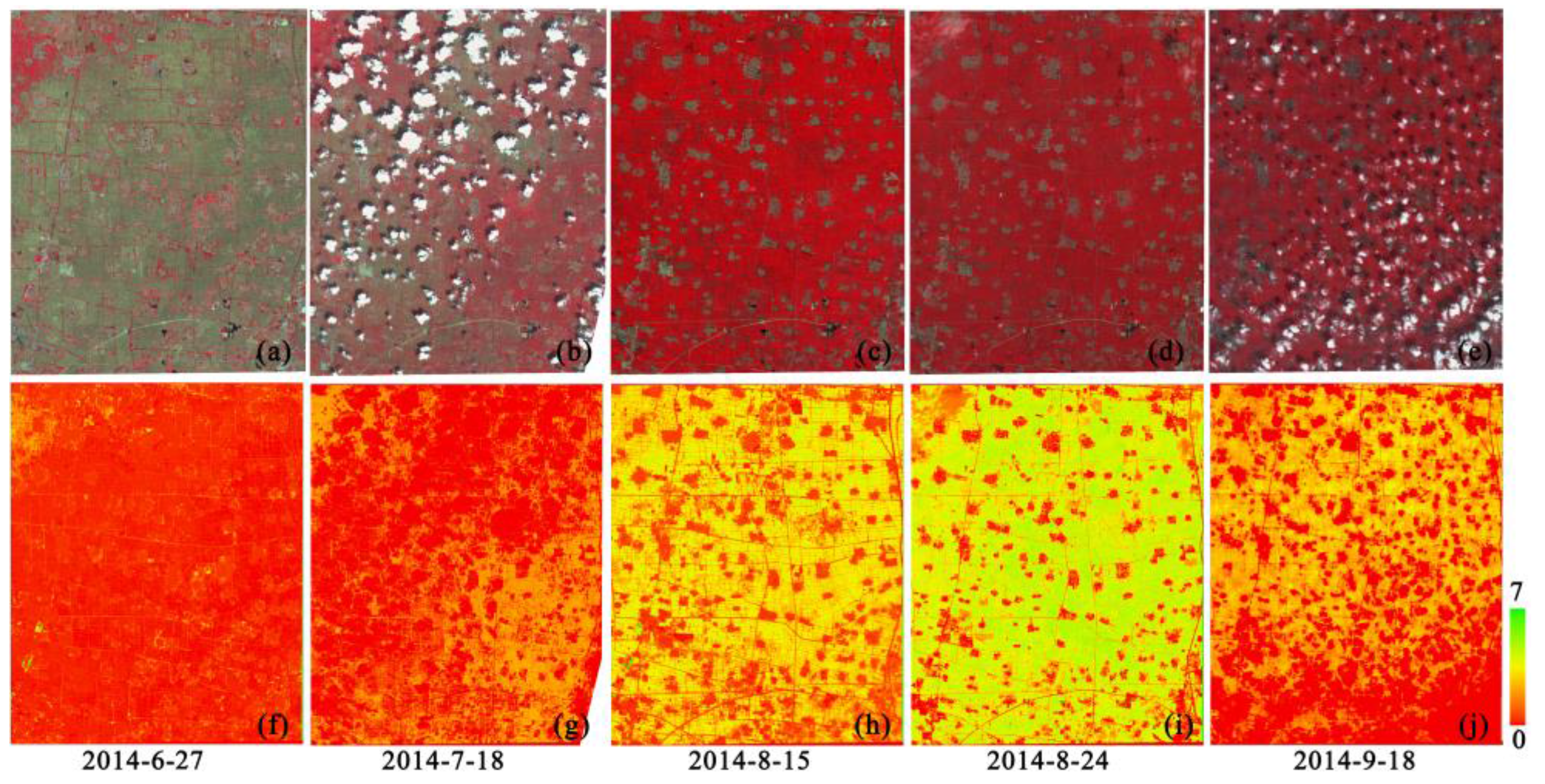
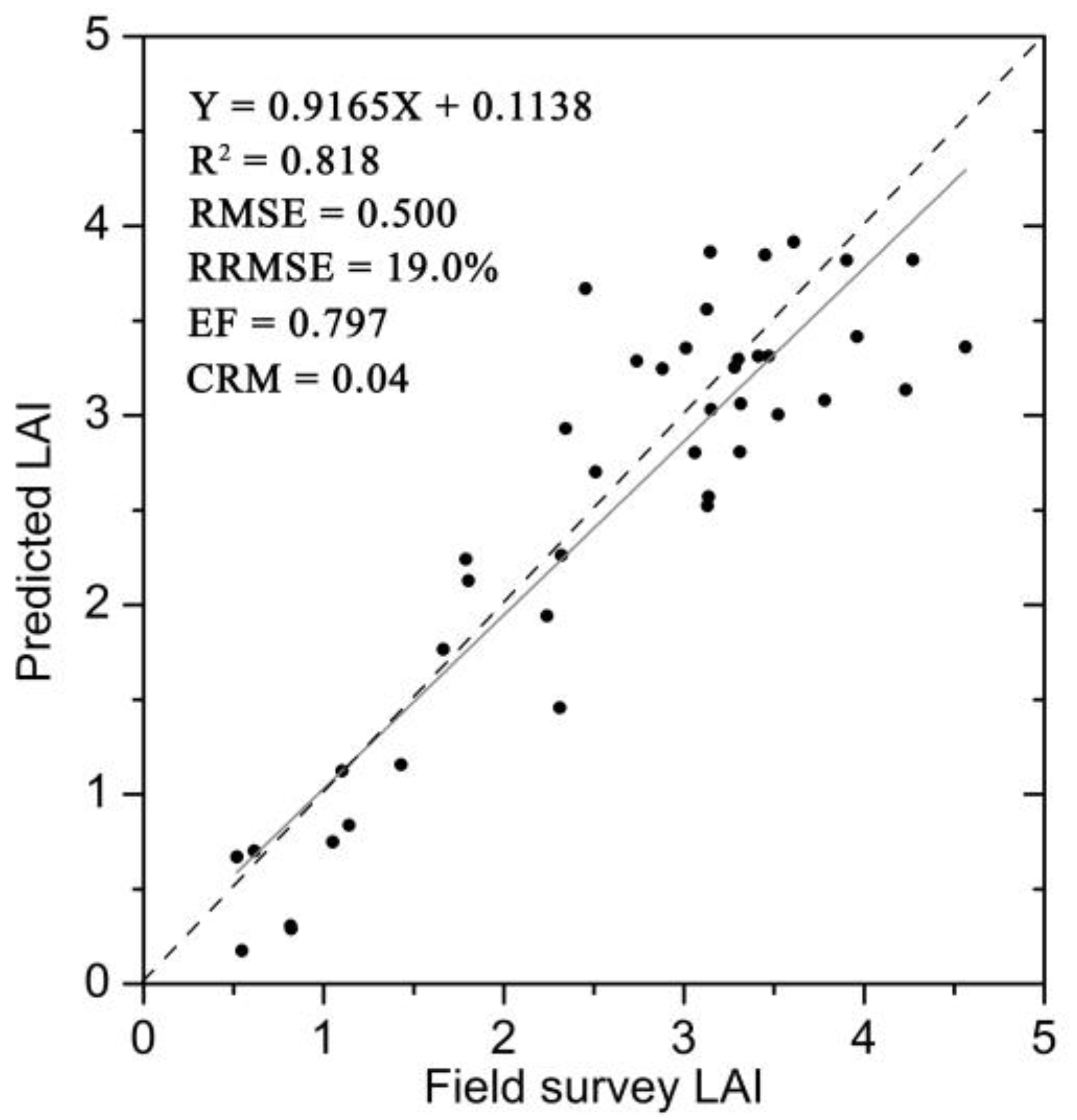
5. Results
6. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jiang, B.; Liang, S.L.; Yuan, W.P. Observational evidence for impacts of vegetation change on local surface climate over northern China using the Granger causality test. J. Geophys. Res. Biogeosci. 2015, 120, 1–12. [Google Scholar] [CrossRef]
- Jia, K.; Liang, S.; Liu, S.; Li, Y.; Xiao, Z.; Yao, Y.; Jiang, B.; Zhao, X.; Wang, X.; Xu, S.; et al. Global land surface fractional vegetation cover estimation using general regression neural networks from MODIS surface reflectance. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4787–4796. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Liang, S. Advances in Land Remote Sensing System, Modeling Inversion and Application; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar]
- Chen, J.M.; Black, T.A. Defining leaf area index for non-flat leaves. Plant Cell Environ. 1992, 15, 421–429. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Baret, F.; Weiss, M.; Lacaze, R.; Camacho, F.; Makhmara, H.; Pacholcyzk, P.; Smets, B. GEOV1: LAI and FAPAR essential climate variables and FCOVER global time series capitalizing over existing products. Part 1: Principles of development and production. Remote Sens. Environ. 2013, 137, 299–309. [Google Scholar] [CrossRef]
- Xiao, Z.Q.; Liang, S.L.; Wang, J.D.; Chen, P.; Yin, X.J.; Zhang, L.Q.; Song, J.L. Use of General Regression Neural Networks for Generating the GLASS Leaf Area Index Product from Time-Series MODIS Surface Reflectance. IEEE Trans. Geosci. Remote Sens. 2014, 52, 209–223. [Google Scholar] [CrossRef]
- Myneni, R.B.; Ross, J.; Asrar, G. A review on the theory of photon transport in leaf canopies. Agric. For. Meteorol. 1989, 45, 1–153. [Google Scholar] [CrossRef]
- Sellers, P.J.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef] [PubMed]
- Arora, V. Modeling vegetation as a dynamic component in soil-vegetation-atmosphere transfer schemes and hydrological models. Rev. Geophys. 2002, 40. [Google Scholar] [CrossRef]
- Bu, H.; Sharma, L.K.; Denton, A.; Franzen, D.W. Sugar Beet Yield and Quality Prediction at Multiple Harvest Dates Using Active-Optical Sensors. Agron. J. 2016, 108, 273–284. [Google Scholar] [CrossRef]
- Bu, H.; Sharma, L.K.; Denton, A.; Franzen, D.W. Comparison of Satellite Imagery and Ground-Based Active Optical Sensors as Yield Predictors in Sugar Beet, Spring Wheat, Corn, and Sunflower. Agron. J. 2017, 109, 299–308. [Google Scholar] [CrossRef]
- Sharma, L.K.; Bu, H.; Denton, A.; Franzen, D.W. Active-Optical Sensors Using Red NDVI Compared to Red Edge NDVI for Prediction of Corn Grain Yield in North Dakota, U.S.A. Sensors 2015, 15, 27832–27853. [Google Scholar] [CrossRef] [PubMed]
- Sharma, L.K.; Bu, H.; Franzen, D.W. Comparison of two ground-based active-optical sensors for in-season estimation of corn (Zea mays L.) yield. J. Plant Nutr. 2016, 39, 957–966. [Google Scholar] [CrossRef]
- Gobron, N.; Pinty, B.; Verstraete, M.; Govaerts, Y. The MERIS Global Vegetation Index (MGVI): Description and preliminary application. Int. J. Remote Sens. 1999, 20, 1917–1927. [Google Scholar] [CrossRef]
- Liang, S.L.; Zhao, X.; Liu, S.H.; Yuan, W.P.; Cheng, X.; Xiao, Z.Q.; Zhang, X.T.; Liu, Q.; Cheng, J.; Tang, H.R.; et al. A long-term Global LAnd Surface Satellite (GLASS) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Plummer, S.; Arino, O.; Simon, M.; Steffen, W. Establishing a earth observation product service for the terrestrial carbon community: The globcarbon initiative. Mitig. Adapt. Strateg. Glob. Chang. 2006, 11, 97–111. [Google Scholar] [CrossRef]
- Jia, K.; Liang, S.; Gu, X.; Baret, F.; Wei, X.; Wang, X.; Yao, Y.; Yang, L.; Li, Y. Fractional vegetation cover estimation algorithm for Chinese GF-1 wide field view data. Remote Sens. Environ. 2016, 177, 184–191. [Google Scholar] [CrossRef]
- Chen, J.M.; Leblanc, S.G. A four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]
- Verhoef, W. Light-scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; Francois, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113, S56–S66. [Google Scholar] [CrossRef]
- Sharma, L.K.; Franzen, D.W. Use of corn height to improve the relationship between active optical sensor readings and yield estimates. Precis. Agric. 2014, 15, 331–345. [Google Scholar] [CrossRef]
- Liang, S. Recent developments in estimating land surface biogeophysical variables from optical remote sensing. Prog. Phys. Geogr. 2007, 31, 501–516. [Google Scholar] [CrossRef]
- Liang, S.; Li, X.; Wang, J. Advanced Remote Sensing: Terrestrial Information Extraction and Applications; Academic Press: Oxford, UK, 2012; p. 800. [Google Scholar]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Nino, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION—Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef]
- Sharma, L.; Bali, S.; Dwyer, J.; Plant, A.; Bhowmik, A. A Case Study of Improving Yield Prediction and Sulfur Deficiency Detection Using Optical Sensors and Relationship of Historical Potato Yield with Weather Data in Maine. Sensors 2017, 17, 1095. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.-M.; Huang, J.-F.; Tang, Y.-L.; Wang, X.-Z. New Vegetation Index and Its Application in Estimating Leaf Area Index of Rice. Rice Sci. 2007, 14, 195–203. [Google Scholar] [CrossRef]
- Chen, J.M. Evaluation of Vegetation Indices and a Modified Simple Ratio for Boreal Applications. Can. J. Remote Sens. 1996, 22, 229–242. [Google Scholar] [CrossRef]
- Kimes, D.S.; Knyazikhin, Y.; Privette, J.L.; Abuelgasim, A.A.; Gao, F. Inversion methods for physically-based models. Remote Sens. Rev. 2000, 18, 381–439. [Google Scholar] [CrossRef]
- Gascon, F.; Gastellu-Etchegorry, J.P.; Lefevre-Fonollosa, M.J.; Dufrene, E. Retrieval of forest biophysical variables by inverting a 3-D radiative transfer model and using high and very high resolution imagery. Int. J. Remote Sens. 2004, 25, 5601–5616. [Google Scholar] [CrossRef]
- Bicheron, P.; Leroy, M. A Method of Biophysical Parameter Retrieval at Global Scale by Inversion of a Vegetation Reflectance Model. Remote Sens. Environ. 1999, 67, 251–266. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Myneni, R.B.; Pragnère, A.; Knyazikhin, Y. Investigation of a model inversion technique to estimate canopy biophysical variables from spectral and directional reflectance data. Agronomie 2000, 20, 3–22. [Google Scholar] [CrossRef]
- Roujean, J.L.; Lacaze, R. Global mapping of vegetation parameters from POLDER multiangular measurements for studies of surface-atmosphere interactions: A pragmatic method and its validation. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef]
- Yang, L.; Jia, K.; Liang, S.; Liu, J.; Wang, X. Comparison of Four Machine Learning Methods for Generating the GLASS Fractional Vegetation Cover Product from MODIS Data. Remote Sens. 2016, 8, 682. [Google Scholar] [CrossRef]
- García-Haro, F.J.; Camacho, F.; Meliá, J. Inter-comparison of SEVIRI/MSG and MERIS/ENVISAT biophysical products over Europe and Africa. In Proceedings of the 2nd MERIS/(A)ATSR User Workshop, ESA SP-666, Frascati, Italy, 22–26 September 2008. [Google Scholar]
- Cooley, T.; Anderson, G.P.; Felde, G.W.; Hoke, M.L.; Ratkowski, A.J.; Chetwynd, J.H.; Gardner, J.A.; Adler-Golden, S.M.; Matthew, M.W.; Berk, A.; et al. FLAASH, a MODTRAN4-based atmospheric correction algorithm, its application and validation. In Proceedings of the 2002 IEEE International Geoscience and Remote Sensing Symposium & 24th Canadian Symposium on Remote Sensing, Toronto, Canada, 24–28 June 2002; pp. 1414–1418. [Google Scholar]
- Jia, K.; Wei, X.Q.; Gu, X.F.; Yao, Y.J.; Xie, X.H.; Li, B. Land cover classification using Landsat 8 Operational Land Imager data in Beijing, China. Geocarto Int. 2014, 29, 941–951. [Google Scholar] [CrossRef]
- Kuusk, A. The hot spot effect in plant canopy reflectance. In Photon-Vegetation Interactions; Myneni, R.B., Ross, J., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 139–159. [Google Scholar]
- Verhoef, W.; Jia, L.; Xiao, Q.; Su, Z. Unified optical-thermal four-stream radiative transfer theory for homogeneous vegetation canopies. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1808–1822. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Baret, F. PROSPECT—A model of leaf optical-properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Shepherd, K.D.; Palm, C.A.; Gachengo, C.N.; Vanlauwe, B. Rapid characterization of organic resource quality for soil and livestock management in tropical agroecosystems using near-infrared spectroscopy. Agron. J. 2003, 95, 1314–1322. [Google Scholar] [CrossRef]
- Dennison, P.E.; Halligan, K.Q.; Roberts, D.A. A comparison of error metrics and constraints for multiple endmember spectral mixture analysis and spectral angle mapper. Remote Sens. Environ. 2004, 93, 359–367. [Google Scholar] [CrossRef]
- Jia, K.; Li, Q.Z.; Tian, Y.C.; Wu, B.F.; Zhang, F.F.; Meng, J.H. Accuracy Improvement of Spectral Classification of Crop Using Microwave Backscatter Data. Spectrosc. Spectr. Anal. 2011, 31, 483–487. [Google Scholar]
- Goel, N.S.; Strebel, D.E. Inversion of vegetation canopy reflectance models for estimating agronomic variables. I. Problem definition and initial results using the suits model. Remote Sens. Environ. 1983, 13, 487–507. [Google Scholar] [CrossRef]
- Qu, Y.H.; Zhang, Y.Z.; Wang, J.D. A dynamic Bayesian network data fusion algorithm for estimating leaf area index using time-series data from in situ measurement to remote sensing observations. Int. J. Remote Sens. 2012, 33, 1106–1125. [Google Scholar] [CrossRef]
- Hosgood, B.; Jacquemoud, S.; Andreoli, G.; Verdebout, J.; Pedrini, G.; Schmuck, G. Leaf Optical Properties EXperiment 90 (LOPEX93); Report EUR 16095 EN; European Commission, Joint Research Center, Institute for Remote Sensing Applications: Brussels, Italy, 1990. [Google Scholar]
- Qu, Y.; Wang, J.; Wan, H.; Li, X.; Zhou, G. A Bayesian network algorithm for retrieving the characterization of land surface vegetation. Remote Sens. Environ. 2008, 112, 613–622. [Google Scholar] [CrossRef]
- Murthy, C.S.; Raju, P.V.; Badrinath, K.V.S. Classification of wheat crop with multi-temporal images: Performance of maximum likelihood and artificial neural networks. Int. J. Remote Sens. 2003, 24, 4871–4890. [Google Scholar] [CrossRef]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Camacho, F. Optimal modalities for radiative transfer-neural network estimation of canopy biophysical characteristics: Evaluation over an agricultural area with CHRIS/PROBA observations. Remote Sens. Environ. 2011, 115, 415–426. [Google Scholar] [CrossRef]
- Jia, K.; Liang, S.; Wei, X.Q.; Li, Q.; Du, X.; Jiang, B.; Yao, Y.J.; Zhao, X.; Li, Y. Fractional forest cover changes in Northeast China from 1982 to 2011 and its relationship with climatic variations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 775–783. [Google Scholar] [CrossRef]
- Ngia, L.S.H.; Sjoberg, J. Efficient training of neural nets for nonlinear adaptive filtering using a recursive Levenberg-Marquardt algorithm. IEEE Trans. Signal Process. 2000, 48, 1915–1927. [Google Scholar] [CrossRef]
- Curran, P.J.; Dungan, J.L.; Gholz, H.L. Seasonal LAI in slash pine estimated with landsat TM. Remote Sens. Environ. 1992, 39, 3–13. [Google Scholar] [CrossRef]
- Duan, H.; Yan, C.; Tsunekawa, A.; Song, X.; Li, S.; Xie, J. Assessing vegetation dynamics in the Three-North Shelter Forest region of China using AVHRR NDVI data. Environ. Earth Sci. 2011, 64, 1011–1020. [Google Scholar] [CrossRef]
- Masson, V.; Champeaux, J.L.; Chauvin, F.; Meriguet, C.; Lacaze, R. A global database of land surface parameters at 1-km resolution in meteorological and climate models. J. Clim. 2003, 16, 1261–1282. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Loague, K.; Green, R.E. Statistical and graphical methods for evaluating solute transport models: Overview and application. J. Contam. Hydrol. 1991, 7, 51–73. [Google Scholar] [CrossRef]

| WFV Sensor | Date (dd/mm/yy) | Matched Field Survey Date | Data Quality |
|---|---|---|---|
| WFV1 | 27 June 2014 | 27 June 2014 | Good |
| WFV2 | 18 July 2014 | 21 July 2014 | With cloud |
| WFV1 | 15 August 2014 | 14 August 2014 | Good |
| WFV3 | 24 August 2014 | 5 September 2014 | Good |
| WFV4 | 18 September 2014 | 5 September 2014 | With cloud |
| WFV Sensor | Bands | Gain | Offset |
|---|---|---|---|
| WFV1 | Blue band (Band1) | 0.2004 | 0 |
| Green band (Band2) | 0.1648 | 0 | |
| Red band (Band3) | 0.1243 | 0 | |
| NIR band (Band4) | 0.1563 | 0 | |
| WFV2 | Blue band (Band1) | 0.1733 | 0 |
| Green band (Band2) | 0.1383 | 0 | |
| Red band (Band3) | 0.1122 | 0 | |
| NIR band (Band4) | 0.1391 | 0 | |
| WFV3 | Blue band (Band1) | 0.1745 | 0 |
| Green band (Band2) | 0.1514 | 0 | |
| Red band (Band3) | 0.1257 | 0 | |
| NIR band (Band4) | 0.1462 | 0 | |
| WFV4 | Blue band (Band1) | 0.1713 | 0 |
| Green band (Band2) | 0.1600 | 0 | |
| Red band (Band3) | 0.1497 | 0 | |
| NIR band (Band4) | 0.1435 | 0 |
| Parameters | Units | Value Range | Step |
|---|---|---|---|
| LAI | m2/m2 | 0–7 | 0.2 |
| ALA | ° | 30–70 | 10 |
| N | - | 1–2 | 0.5 |
| Cab | μg/cm2 | 30–60 | 10 |
| Cm | g/cm2 | 0.005–0.015 | 0.005 |
| Car | μg/cm2 | 0 | - |
| Cw | cm | 0.005–0.015 | 0.005 |
| Cbrown | - | 0–0.5 | 0.5 |
| Hot | - | 0.1 | - |
| Solar zenith angle | ° | 25–55 | 10 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, X.; Gu, X.; Meng, Q.; Yu, T.; Zhou, X.; Wei, Z.; Jia, K.; Wang, C. Leaf Area Index Estimation Using Chinese GF-1 Wide Field View Data in an Agriculture Region. Sensors 2017, 17, 1593. https://doi.org/10.3390/s17071593
Wei X, Gu X, Meng Q, Yu T, Zhou X, Wei Z, Jia K, Wang C. Leaf Area Index Estimation Using Chinese GF-1 Wide Field View Data in an Agriculture Region. Sensors. 2017; 17(7):1593. https://doi.org/10.3390/s17071593
Chicago/Turabian StyleWei, Xiangqin, Xingfa Gu, Qingyan Meng, Tao Yu, Xiang Zhou, Zheng Wei, Kun Jia, and Chunmei Wang. 2017. "Leaf Area Index Estimation Using Chinese GF-1 Wide Field View Data in an Agriculture Region" Sensors 17, no. 7: 1593. https://doi.org/10.3390/s17071593
APA StyleWei, X., Gu, X., Meng, Q., Yu, T., Zhou, X., Wei, Z., Jia, K., & Wang, C. (2017). Leaf Area Index Estimation Using Chinese GF-1 Wide Field View Data in an Agriculture Region. Sensors, 17(7), 1593. https://doi.org/10.3390/s17071593







