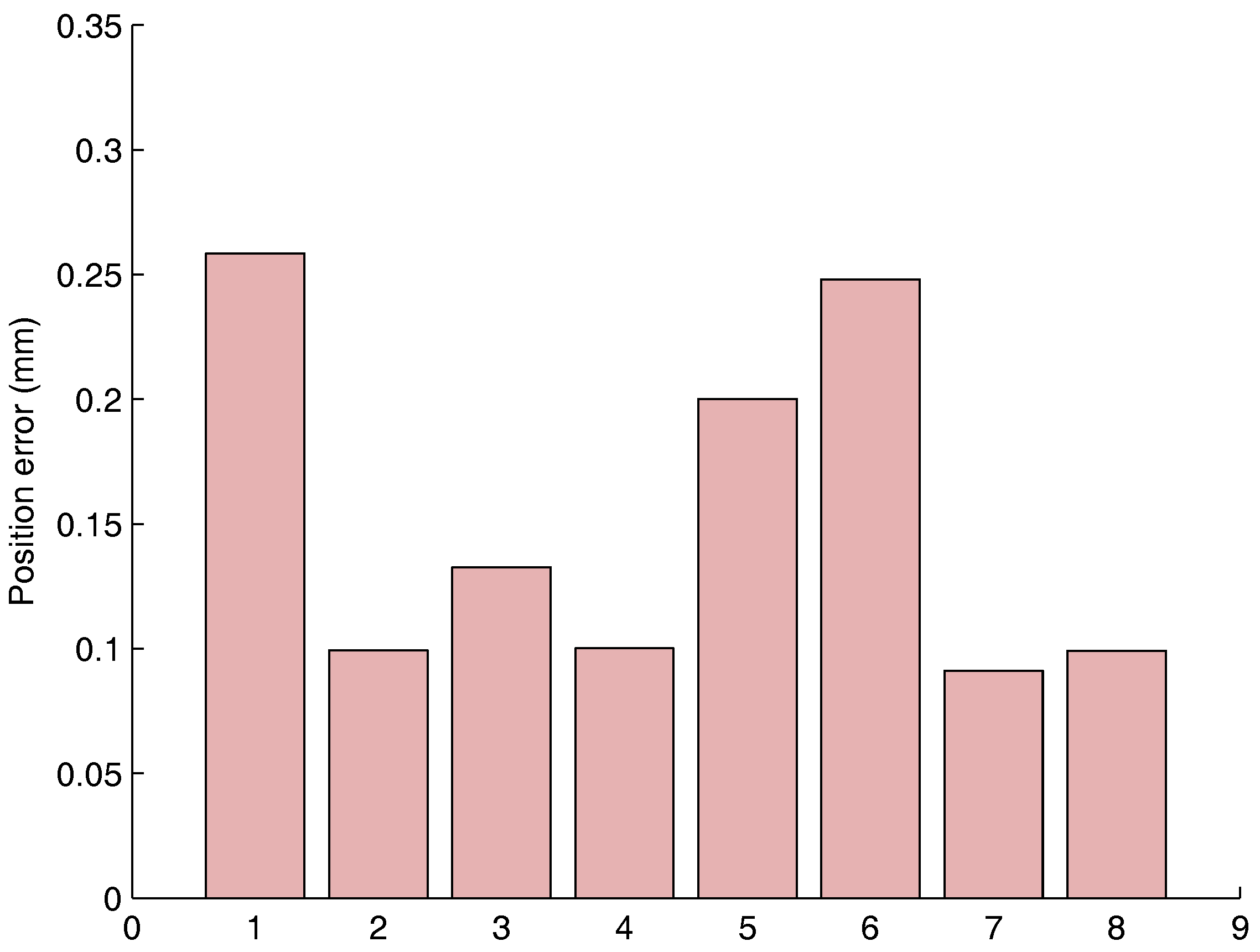The Vicon performance was evaluated with three scenarios. First, we assessed the measurements repeatability also known as the precision of the system. Secondly, a numerically controlled setup was used to estimate the static measure accuracy. Finally, a setup mimicking a blade rotated by an electric motor was used to quantify the dynamic behavior of a motion capture system.
2.1. Static Measurement Precision
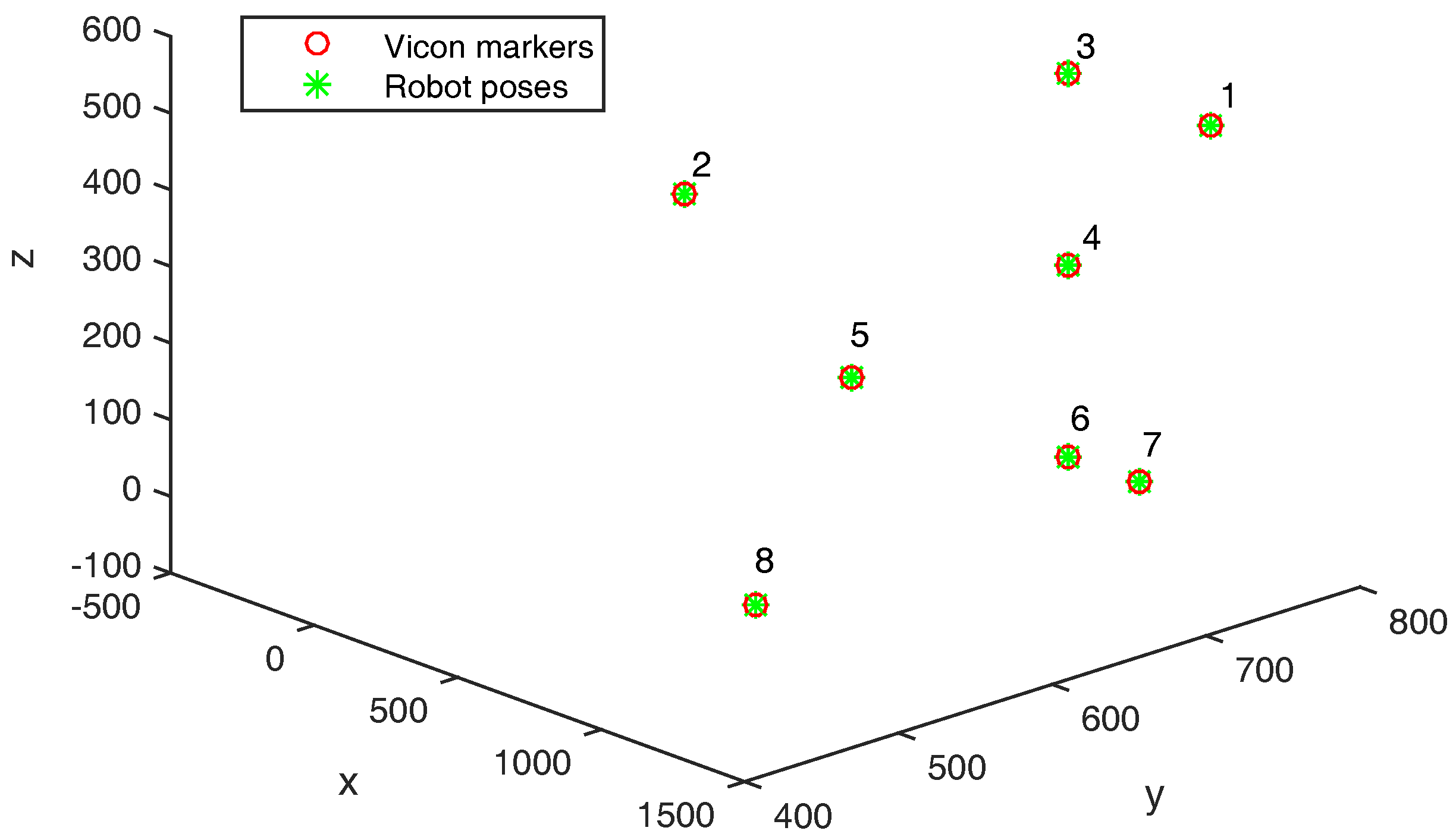
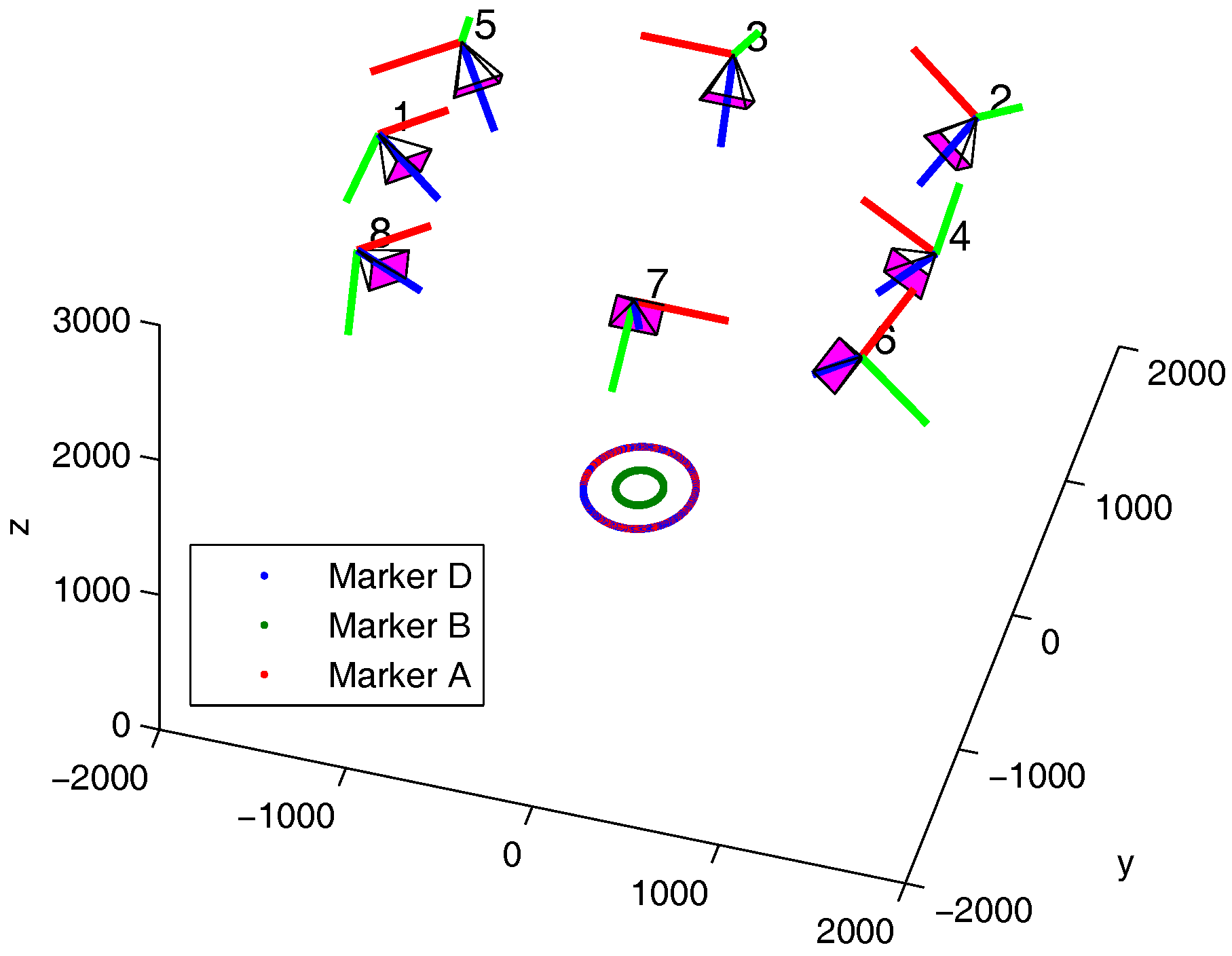
The Electromagnetic compatibility (EMC) laboratory from IRSEEM (Embedded Electronic Systems Research Institute) has a numeric controlled 4-axis robot used to perform EMC near field experiments (
Figure 1). Its positioning specifications allow to reach a position with a 10
m resolution. The probe can be moved in a space of
. The robot was used to perform repeatability measurement evaluation and static measurement performance quantification.
A Vicon marker was placed on the probe monitored by eight T40S cameras. Marker positions are recorded in the robot and Vicon reference frames. Both frames are aligned as follows.
A list
of at least eight 3D points
are used. Each point
in the Vicon frame and its counterpart in the robot frame
are related by a rigid transform as both frames use a calibrated metric representation:
with:
| : | a rotation matrix with and , |
| : | a translation vector, |
| : | a zero vector. |
Estimating the rigid transform between both frames can be expressed as a least-square problem as follows:
with:
| = | |
| = | |
| = | a zero vector. |
Equation (
6) can be written in the form
with:
| n: | the number of points used in the rigid transform estimation, |
| : | a matrix, |
| : | a vector, |
| : | a vector including the rigid transform parameters. |
with:
| : | is x coordinate of point in the world frame, |
| : | is x coordinate of point in the Vicon frame. |
In order to reduce invertability problems,
is solved. Once
is found, the rotation matrix
is forced using the SVD operation:
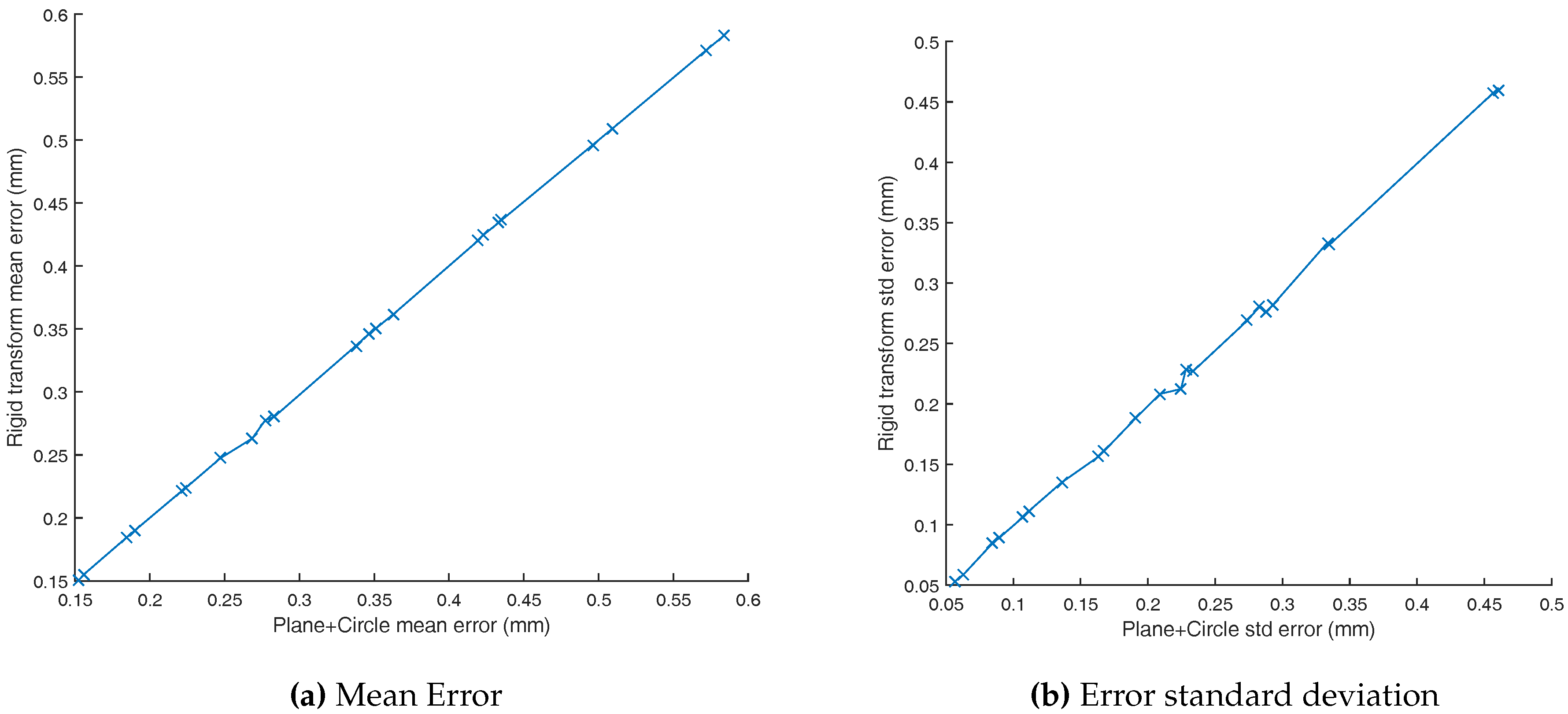
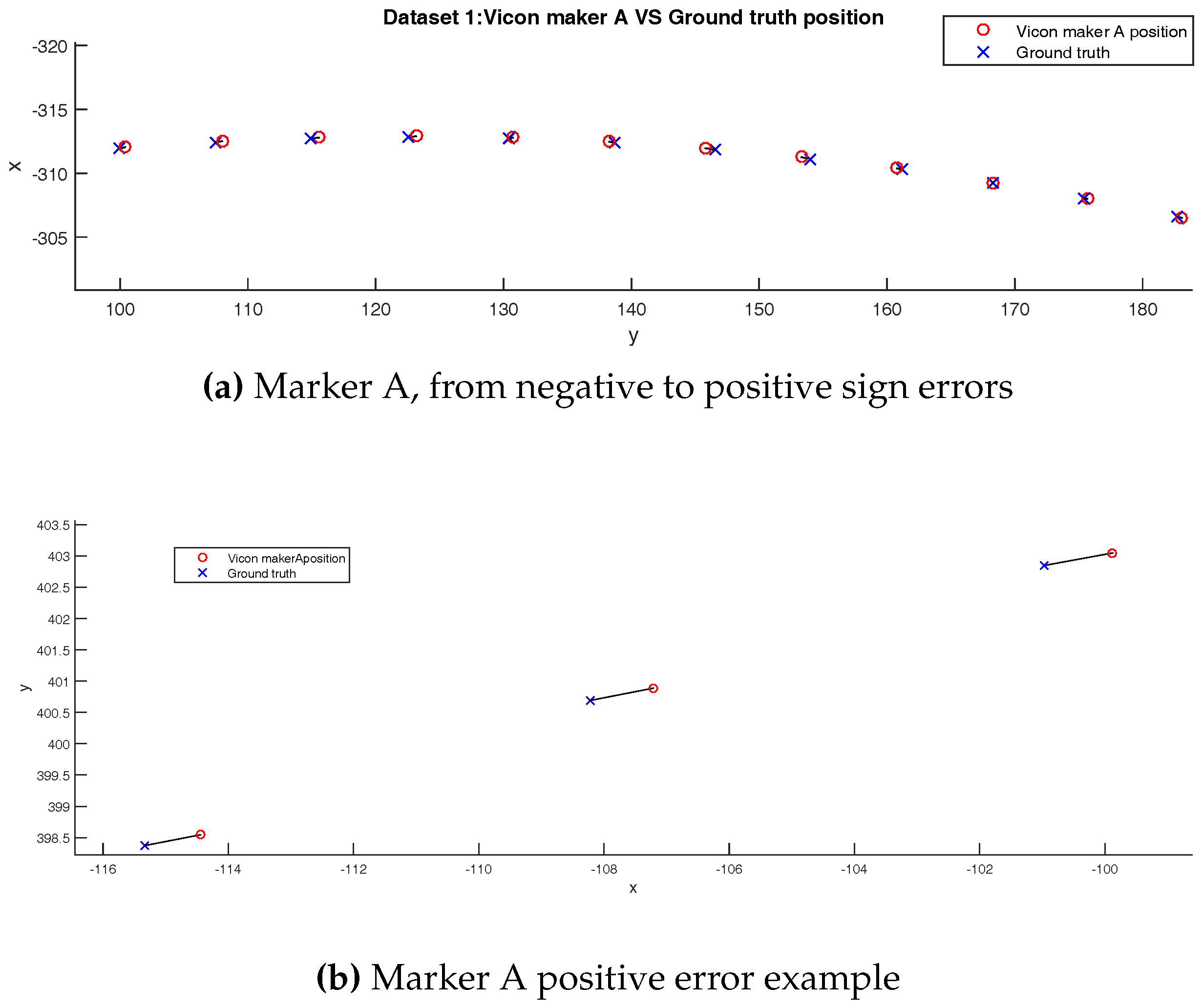
The rotation matrix and translation between the Vicon and robot frame are estimated. It can be used to measure the Vicon measurement repeatability and accuracy in a static framework.
The Euclidean distance is used to quantify the Vicon performance.
2.2. Dynamic Measurement Evaluation
Contrary to the state-of-the art, dynamic measurements were performed at speeds encountered in mobile robotic environments. We were aiming at finding a ground truth setup with a sampling rate higher than the Vicon sampling rate used in our experiments (100 Hz).
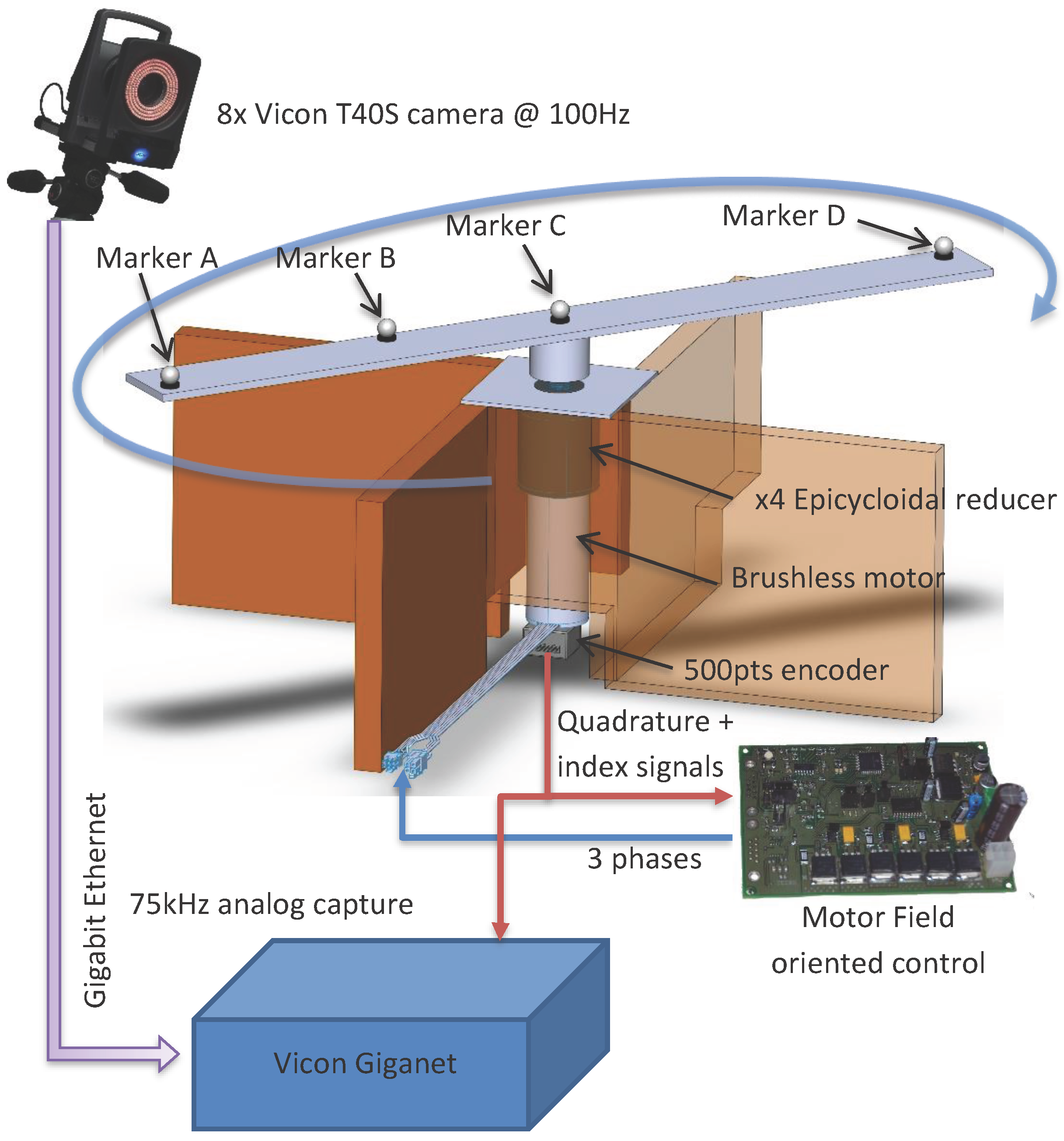
We created a setup able to reach high speed made of a blade and a rotor. As it can be seen in
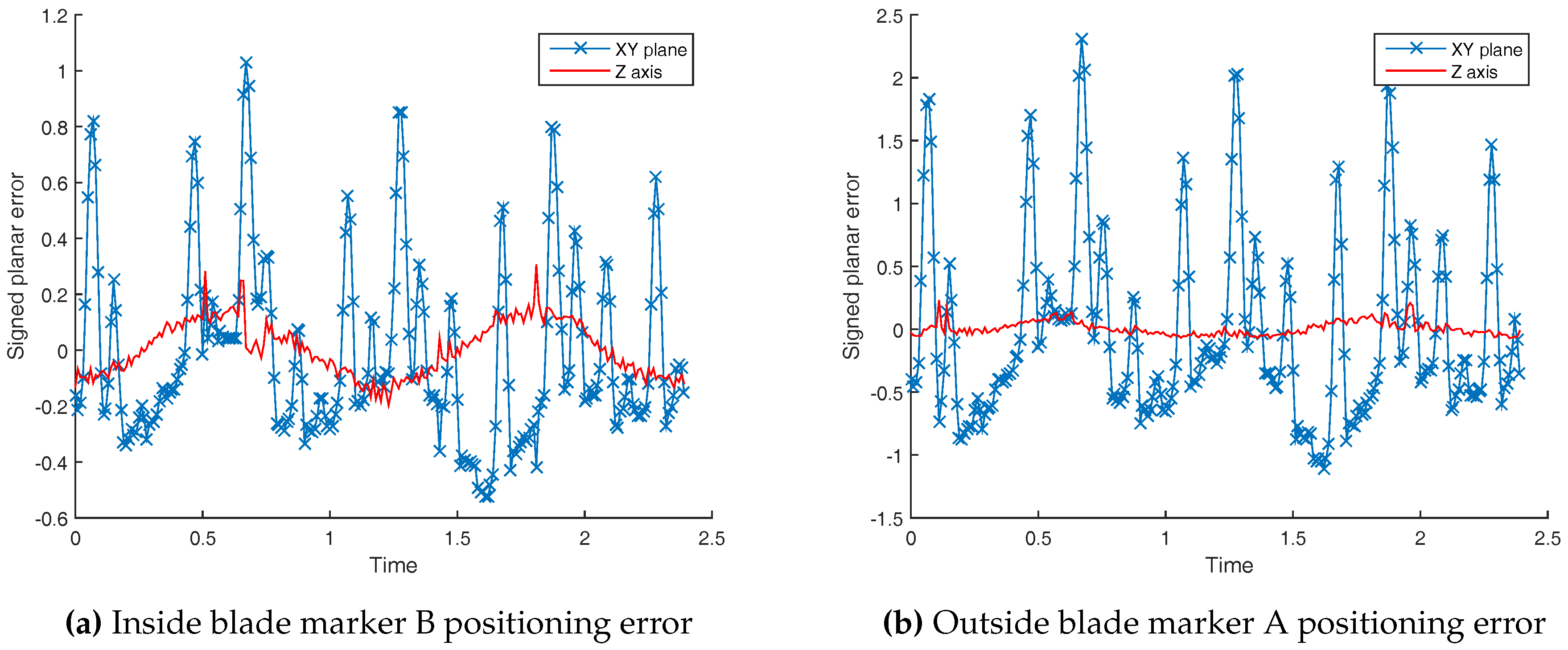
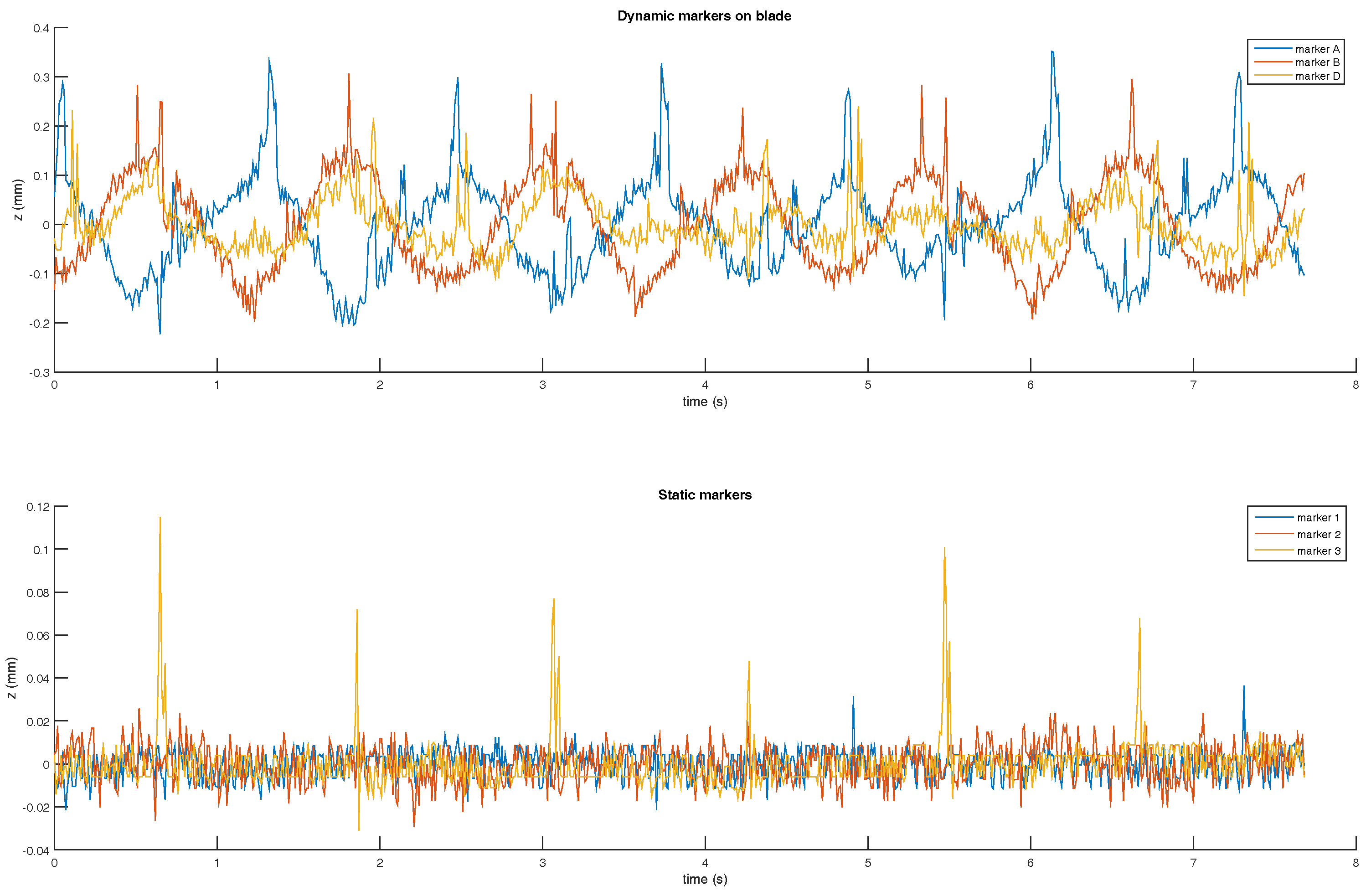
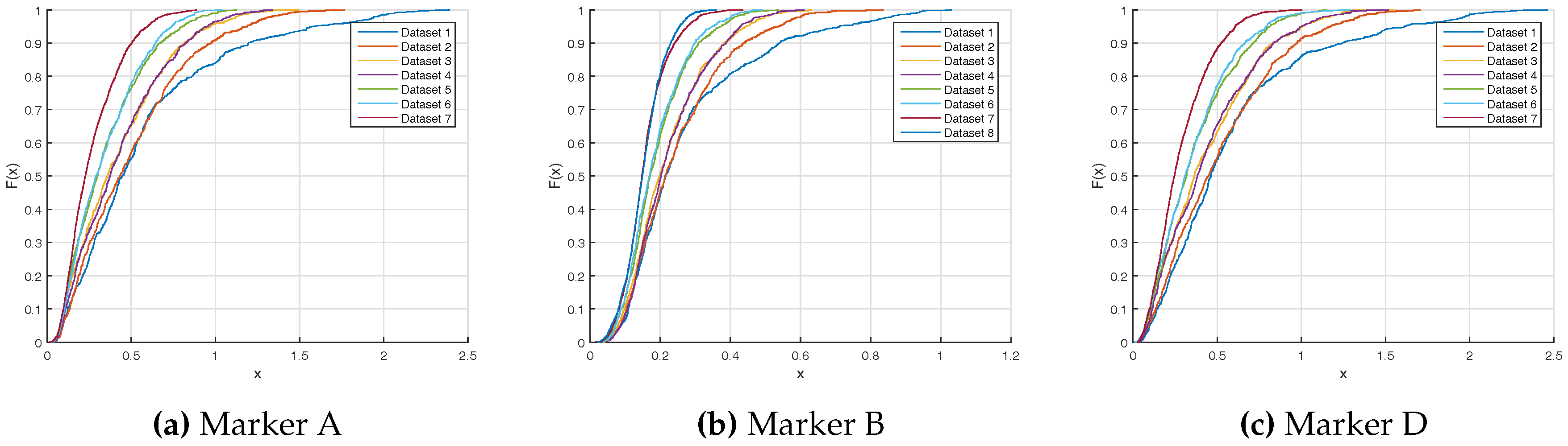
Figure 2, the system is made of an electric motor, a gear box and a blade where four markers are sticked. Mechanical slacks are controlled in order to reduce their impact on the ground truth precision. The engine torque is controlled with a vector control command in order to ensure torque stability. The ground truth position is expressed as the angular position about the rotor axis. The angular ground truth is obtained from a 500 pulses per revolution quadrature encoder installed on the motor axle. Synchronisation with the motion capture system is ensured by plugging the resulting encoder signals into the Vicon Giganet. Encoder signals are sampled at 75 kHz.
A 0.045° angular resolution is achieved thanks to a gear reduction ratio of 4 and by exploiting rising and falling edges. Markers A and D are placed at each end of the blade 30 cm away from the motor axis. It results in a positioning resolution of 0.235 mm. The Vicon system accuracy is expected to be about one millimeter given reference [
7]. The actual positioning resolution might be too large. As a result, we interpolated the angular position up to the encoder sampling rate, i.e., 75 kHz.
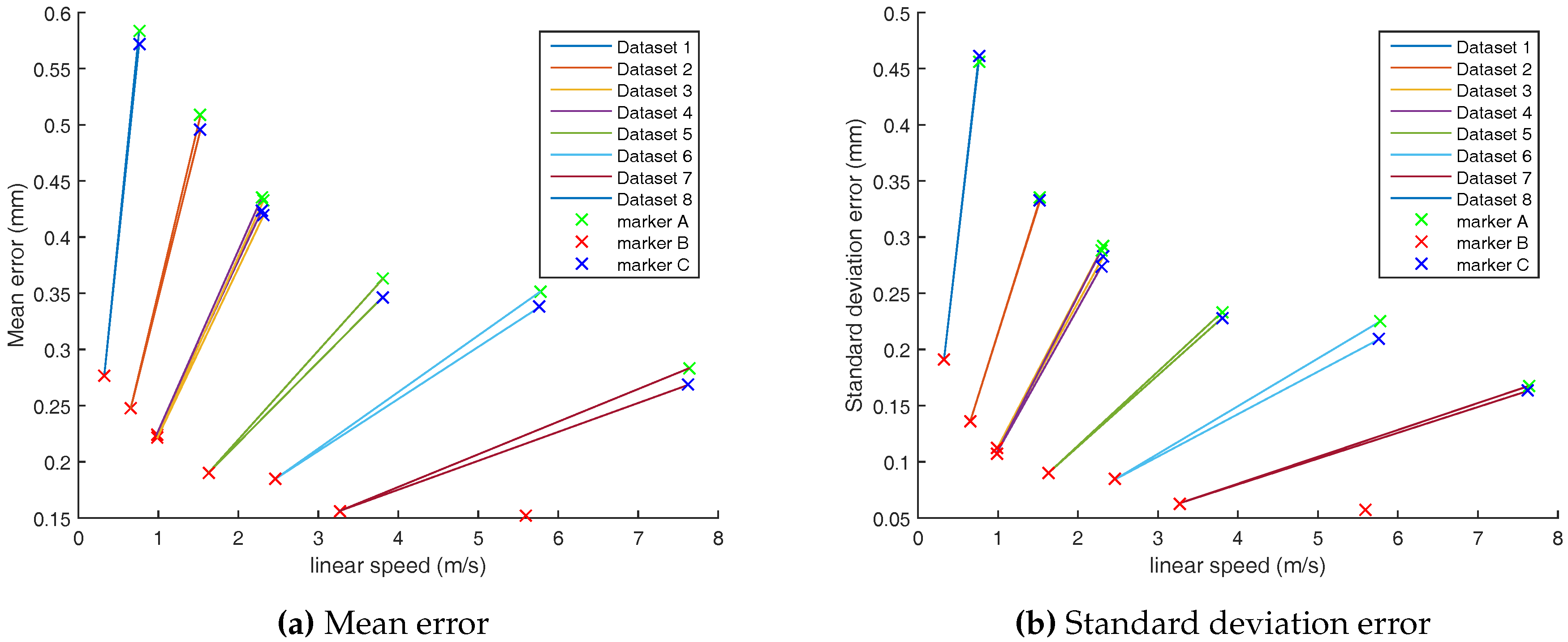
The resulting angular resolution now depends on the motor spinning speed. The expected accuracy for markers A and D lies between 10 µm and 102 µm for speeds of 100 rpm and 1000 rpm, respectively. These values are more suitable to evaluate a system with an expected accuracy of 1 mm.
As mentioned previously, we track and evaluate the estimated angular position of each marker and compare them to the ground truth angular position. As a result, the transformation
between the Vicon frame and the angular frame must be estimated with
defined as a similarity :
In order to avoid numerical instabilities or realignment issues, we used two approaches to project the measurements performed in the Vicon frame into the ground truth frame, i.e., angular positions. Contrary to static study, the marker location on the blade is considered as unknown, so we will estimate it (s scale parameter).
The blade initial position is unknown with respect to the world frame. Moreover, the marker locations can be roughly measured on the blade, but their position might not be accurate enough to ensure a proper transformation estimation.
In order to estimate the transformation between the Vicon frame and the angular frame, we must transform the angular coordinates to 3D points as follows :
with:
| , |
| . |
Consequently, will be moving on a unit circle encompassed in the plane.
, the counterpart of
in the Vicon frame, is related by the following equation :
As corresponding points are known from the sensor synchronization, we employed :
Uyemana’s method [
12] to estimate
s,
and
. Let us define
and
, the corresponding sets of three-dimensional points. Uyemana’s solution aims at minimizing :
It is performed by first computing the
and
means :
Secondly, the covariance matrix of
and
is computed :
Thirdly, a singular value decomposition is performed on
:
Finally, let us consider the
defined as follows :
s,
and
are computed as follows :
where:
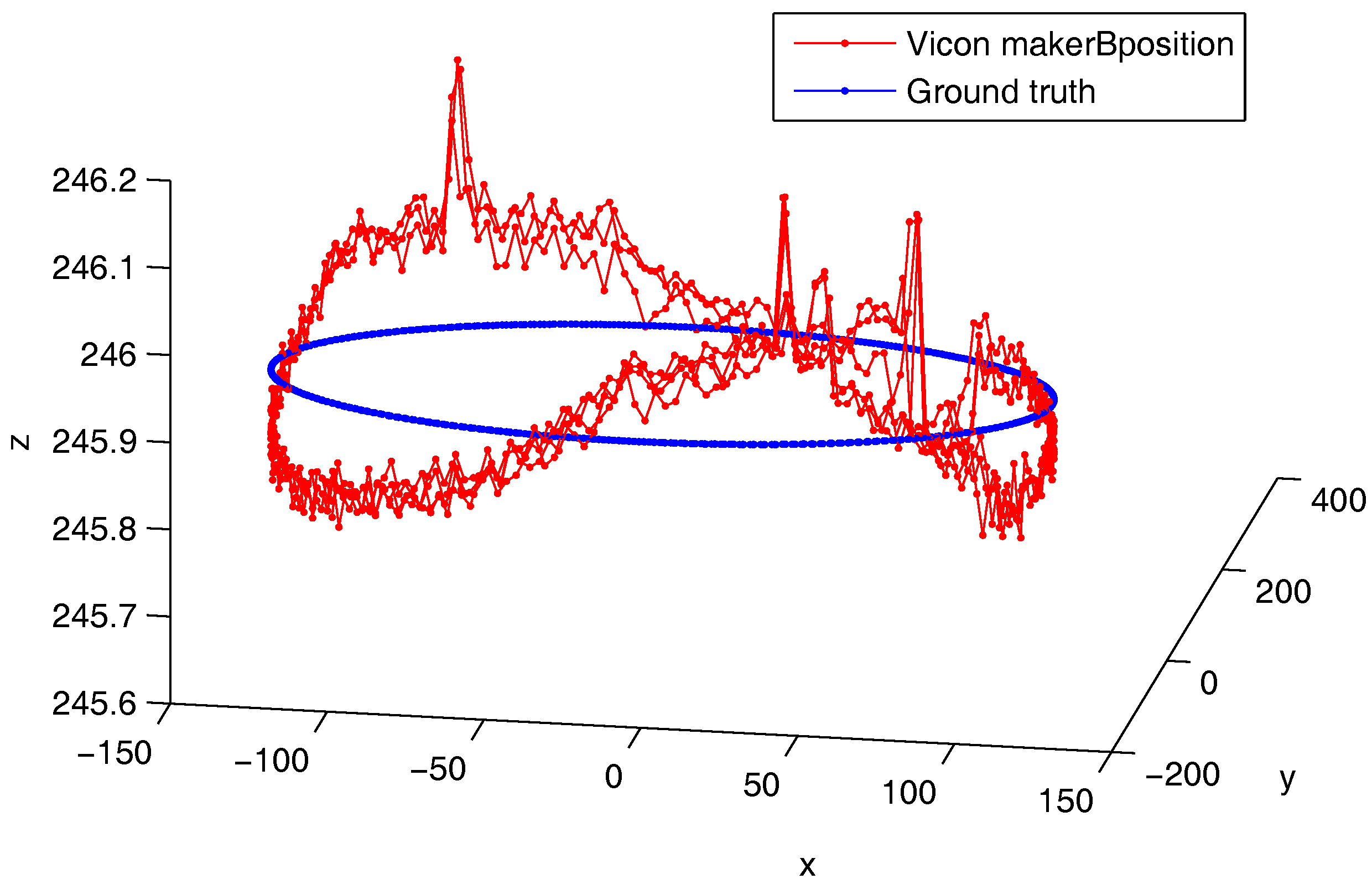
A second approach uses the fact that the markers are placed on a rotating blade. As a consequence, their trajectories are expected to be performed on a 3D plane.
The 3D plane equation can be estimated as follows. A point
in the Vicon frame lying on the 3D plane
must fulfill the condition
. From at least four points,
can be estimated.
is the null space of P with
. In practice, more than four points are used. As
, the following operations are performed :
with
Each point is consequently transformed in a new frame that aligns the z-axis with N. The final step requires to fit a circle to the resulting point cloud. The circle radius corresponds to s and the circle center to .
One last variable must be estimated: the constant angular offset that exists between point extracted from the Vicon and the encoder location. In fact, as the angular position of the blade is not known at the first timestamp due to the fact that the encoder is incremental. Moreover, the reduction gear ratio brings a ground truth uncertainty depending on the rotation speed. As a result, recordings are performed once the rotation speed is stable. It also allows to obtain a unique speed for each dataset. We find the angular offset by incrementally testing offset values
that correspond to a multiple of the resulting angular resolution.
is set as :
with:
| : | the groundtruth angle at timestamp i, |
| : | the Vicon angle at timestamp i, |
| : | the offset angle to be estimated. |
Once is found, and angle are used in axis-angle rotation conversion to a rotation matrix .
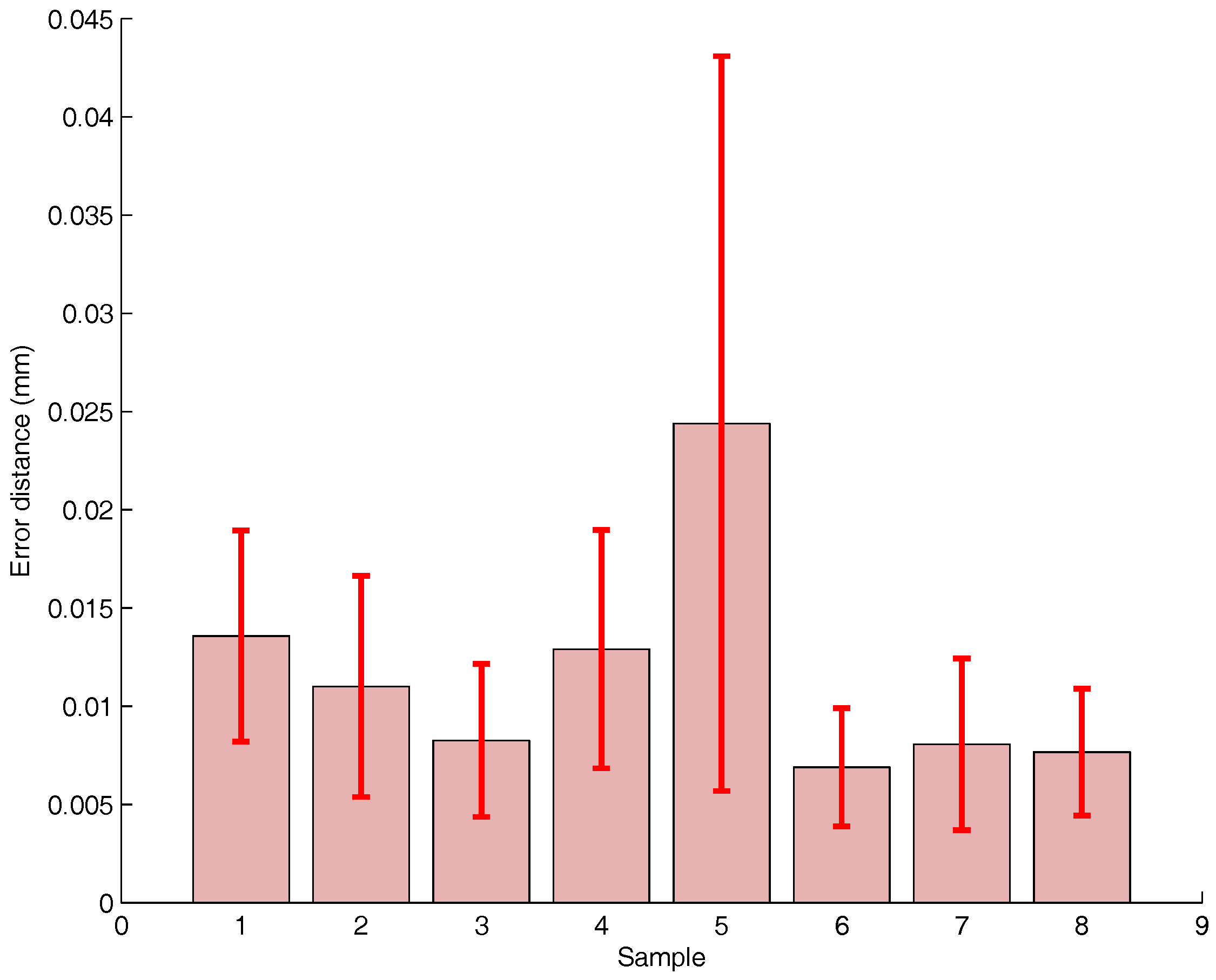
The Euclidean distance is used as the performance metric of the Vicon positioning for both transformation estimations.