Simultaneous Calibration: A Joint Optimization Approach for Multiple Kinect and External Cameras
Abstract
:1. Introduction
2. Calibration Model
2.1. Color Camera Projection Model
2.2. Depth Camera Intrinsic
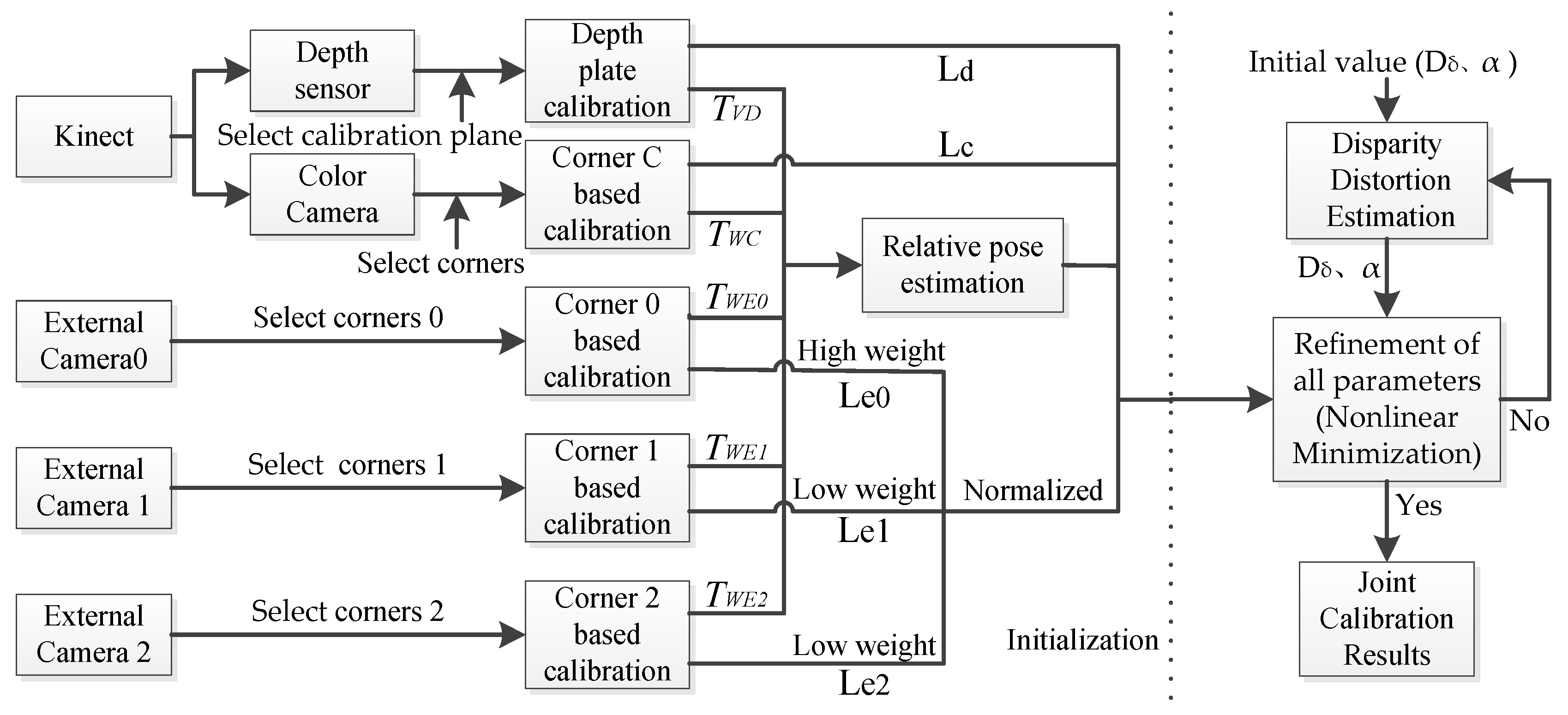
3. Joint Calibration for Multi-Sensors
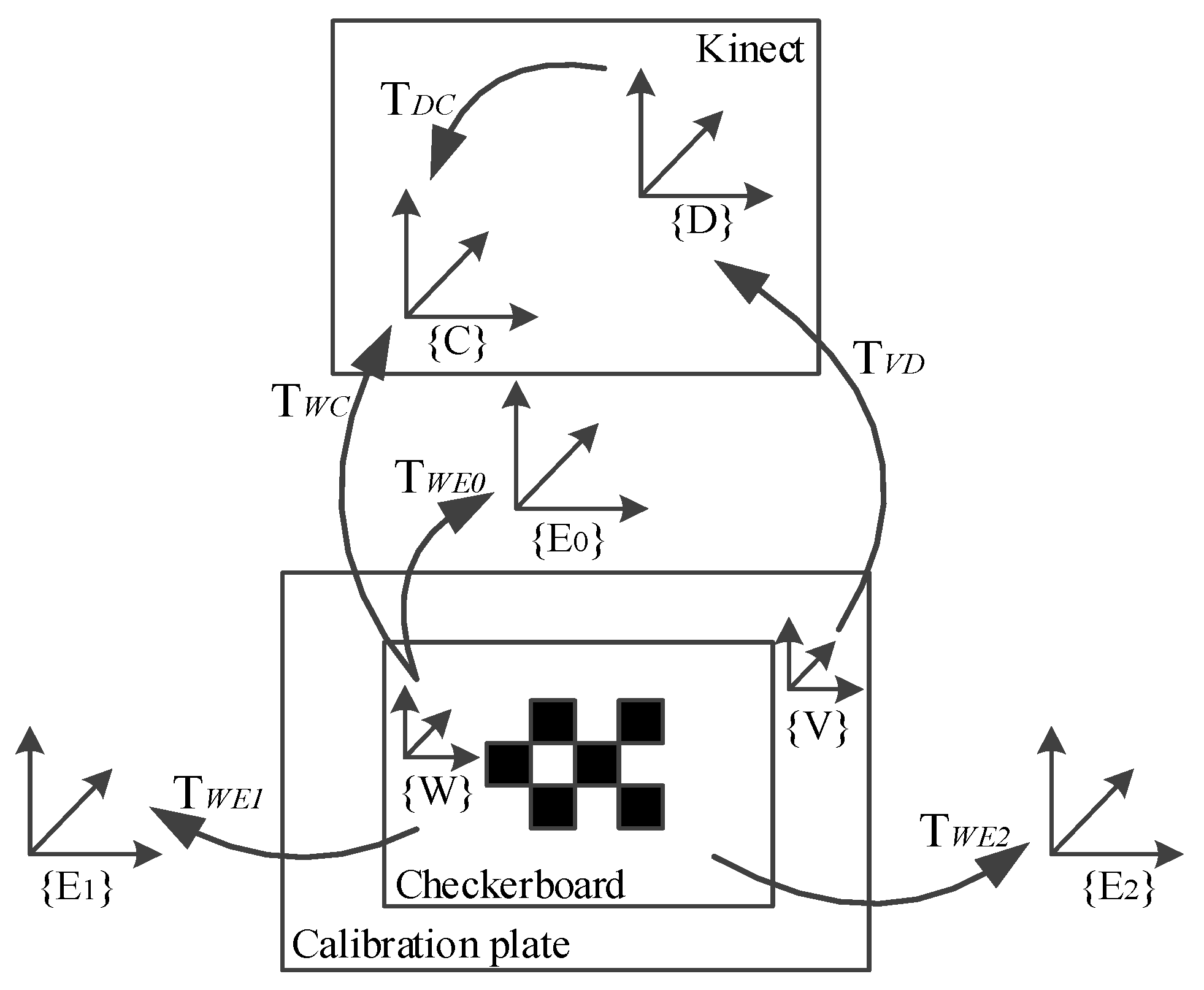
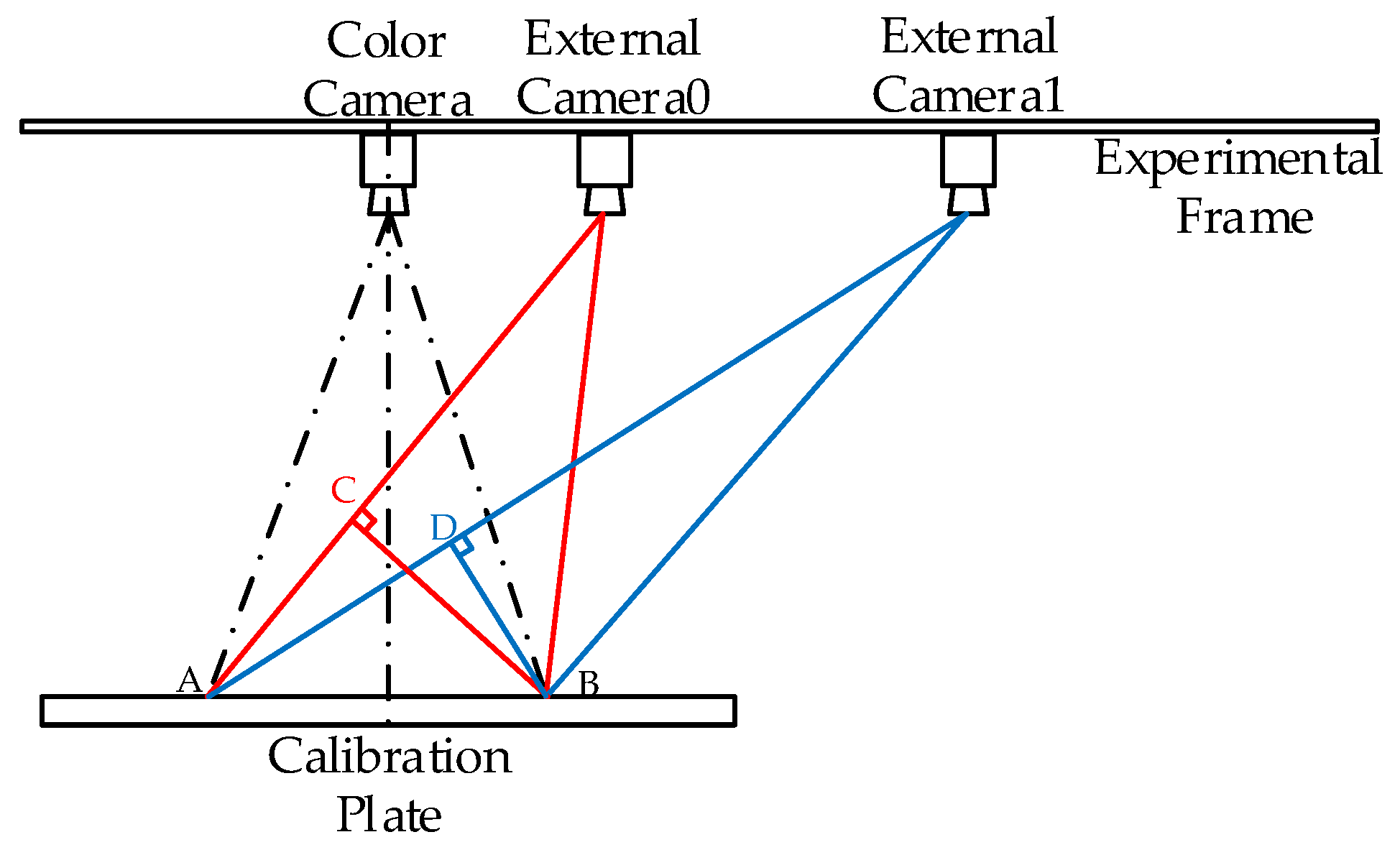
3.1. Platform Setting and Preprocessing
3.2. Relative Pose Estimation
3.3. Nonlinear Minimization
4. Experiments
4.1. Herrera’s Method Results for Comparison
4.2. 3D Reconstruction
4.3. 3D Ground Truth
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, Z. Flexible Camera Calibration by Viewing a Plane from Unknown Orientations. In Proceedings of the IEEE 1999 Seventh International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 666–673. [Google Scholar]
- Salvi, J.; Armangué, X.; Batlle, J. A comparative review of camera calibrating methods with accuracy evaluation. Pattern Recognit. 2002, 35, 1617–1635. [Google Scholar] [CrossRef]
- Gong, X.; Lin, Y.; Liu, J. 3D LIDAR-camera extrinsic calibration using an arbitrary trihedron. Sensors 2013, 13, 1902–1918. [Google Scholar] [CrossRef] [PubMed]
- Canessa, A.; Chessa, M.; Gibaldi, A.; Sabatini, S.P.; Solari, F. Calibrated depth and color cameras for accurate 3D interaction in a stereoscopic augmented reality environment. J. Vis. Commun. Image Represent. 2014, 25, 227–237. [Google Scholar] [CrossRef]
- Choi, D.-G.; Bok, Y.; Kim, J.-S.; Shim, I.; Kweon, I.S. Structure-From-Motion in 3D Space Using 2D Lidars. Sensors 2017, 17, 242. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Zhao, X.; Liu, Y.; Li, D.; Wu, S.Q.; Zhao, F. Object tracking based on bit-planes. J. Electron. Imaging 2016, 25, 013032. [Google Scholar] [CrossRef]
- Lv, F.; Zhao, T.; Nevatia, R. Camera calibration from video of a walking human. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1513–1518. [Google Scholar] [PubMed]
- Xiang, X.Q.; Pan, Z.G.; Tong, J. Depth camera in computer vision and computer graphics: An overview. J. Front. Comput. Sci. Technol. 2011, 5, 481–492. [Google Scholar]
- Chen, D.; Li, G.; Sun, Y.; Kong, J.; Jiang, G.; Tang, H.; Ju, Z.; Yu, H.; Liu, H. An Interactive Image Segmentation Method in Hand Gesture Recognition. Sensors 2017, 17, 253. [Google Scholar] [CrossRef] [PubMed]
- Miao, W.; Li, G.F.; Jiang, G.Z.; Fang, Y.; Ju, Z.J.; Liu, H.H. Optimal grasp planning of multi-fingered robotic hands: A review. Appl. Comput. Math. 2015, 14, 238–247. [Google Scholar]
- Zhang, Z. Microsoft kinect sensor and its effect. IEEE Multimed. 2012, 19, 4–10. [Google Scholar] [CrossRef]
- Henry, P.; Krainin, M.; Herbst, E.; Ren, X.; Fox, D. RGB-D Mapping: Using Depth Cameras for Dense 3D Modeling of Indoor Environments. In The 12th International Symposium on Experimental Robotics (ISER); Springer: Berlin/Heidelberg, Germany, 2010; pp. 22–25. [Google Scholar]
- Burrus, N. Kinect Calibration. Available online: http://nicolas.burrus.name/index.php/Research/KinectCalibration (accessed on 10 November 2011).
- Yamazoe, H.; Habe, H.; Mitsugami, I.; Yagi, Y. Easy Depth Sensor Calibration. In Proceedings of the 2012 21st International Conference on Pattern Recognition (ICPR), Tsukuba, Japan, 11–15 November 2012; pp. 465–468. [Google Scholar]
- Herrera, D.; Kannala, J.; Heikkilä, J. Accurate and Practical Calibration of a Depth and Color Camera Pair. In International Conference on Computer Analysis of Images and Patterns; Springer: Berlin, Germany, 2011; pp. 437–445. [Google Scholar]
- Zhang, C.; Zhang, Z. Calibration between depth and color sensors for commodity depth cameras. In Computer Vision and Machine Learning with RGB-D Sensors; Springer: Berlin, Germany, 2014; pp. 47–64. [Google Scholar]
- Smisek, J.; Jancosek, M.; Pajdla, T. 3D with Kinect. In Consumer Depth Cameras for Computer Vision; Springer: Berlin, Germany, 2013; pp. 3–25. [Google Scholar]
- Herrera, D.; Kannala, J.; Heikkilä, J. Joint depth and color camera calibration with distortion correction. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2058–2064. [Google Scholar] [CrossRef] [PubMed]
- Raposo, C.; Barreto, J.P.; Nunes, U. Fast and Accurate Calibration of a Kinect Sensor. In Proceedings of the 2013 International Conference on 3DTV-Conference, Washington, DC, USA, 29 June–1 July 2013; pp. 342–349. [Google Scholar]
- Guo, L.P.; Chen, X.N.; Liu, B. Calibration of Kinect sensor with depth and color camera. J. Image Graph. 2014, 19, 1584–1590. [Google Scholar]
- Han, Y.; Chung, S.L.; Yeh, J.S.; Chen, Q.J. Calibration of D-RGB camera networks by skeleton-based viewpoint invariance transformation. Acta Phys. Sin. 2014, 63, 074211. [Google Scholar]
- Heikkila, J. Geometric camera calibration using circular control points. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1066–1077. [Google Scholar] [CrossRef]
- Weng, J.; Cohen, P.; Herniou, M. Camera calibration with distortion models and accuracy evaluation. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 965–980. [Google Scholar] [CrossRef]
- Wang, J.; Shi, F.; Zhang, J.; Liu, Y. A new calibration model of camera lens distortion. Pattern Recognit. 2008, 41, 607–615. [Google Scholar] [CrossRef]
- Yin, Q.; Li, G.F.; Zhu, J.G. Research on the method of step feature extraction for EOD robot based on 2D laser radar. Discrete Cont Dyn-S 2015, 8, 1415–1421. [Google Scholar]
- Fang, Y.F.; Liu, H.H.; Li, G.F.; Zhu, X.Y. A multichannel surface emg system for hand motion recognition. Int. J. Hum. Robot. 2015, 12, 1550011. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Unnikrishnan, R.; Hebert, M. Fast Extrinsic Calibration of a Laser Rangefinder to a Camera; Carnegie Mellon University: Pittsburgh, PA, USA, 2005. [Google Scholar]
- Lee, H.; Rhee, H.; Oh, J.H.; Park, J.H. Measurement of 3-D Vibrational Motion by Dynamic Photogrammetry Using Least-Square Image Matching for Sub-Pixel Targeting to Improve Accuracy. Sensors 2016, 16, 359. [Google Scholar] [CrossRef] [PubMed]
- Cheng, K.L.; Ju, X.; Tong, R.F.; Tang, M.; Chang, J.; Zhang, J.J. A Linear Approach for Depth and Colour Camera Calibration Using Hybrid Parameters. J. Comput. Sci. Technol. 2016, 31, 479–488. [Google Scholar] [CrossRef]
- Li, G.F.; Gu, Y.S.; Kong, J.Y.; Jiang, G.Z.; Xie, L.X.; Wu, Z.H. Intelligent control of air compressor production process. Appl. Math. Inform. Sci. 2013, 7, 1051. [Google Scholar] [CrossRef]
- Li, G.F.; Miao, W.; Jiang, G.Z.; Fang, Y.F.; Ju, Z.J.; Liu, H.H. Intelligent control model and its simulation of flue temperature in coke oven. Discrete Cont Dyn-S 2015, 8, 1223–1237. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, J.; Zhu, Z.; Yao, W.; Wu, S. Weighted guided image filtering. IEEE Trans. Image Proc. 2015, 24, 120–129. [Google Scholar]
- Chen, L.; Tian, J. Depth image enlargement using an evolutionary approach. Signal Proc. Soc. Image Commun. 2013, 28, 745–752. [Google Scholar] [CrossRef]
- Liu, A.; Marschner, S.; Snavely, N. Caliber: Camera Localization and Calibration Using Rigidity Constraints. Int. J. Comput. Vis. 2016, 118, 1–21. [Google Scholar] [CrossRef]
- Li, G.F.; Kong, J.Y.; Jiang, G.Z.; Xie, L.X.; Jiang, Z.G.; Zhao, G. Air-fuel ratio intelligent control in coke oven combustion process. INF Int. J. 2012, 15, 4487–4494. [Google Scholar]
- Li, G.F.; Qu, P.X.; Kong, J.Y.; Jiang, G.Z.; Xie, L.X.; Gao, P. Coke oven intelligent integrated control system. Appl. Math. Inform. Sci. 2013, 7, 1043–1050. [Google Scholar] [CrossRef]






| X | Y | Z | I | ||
|---|---|---|---|---|---|
| E.C.0 | 71.58 | 39.91 | 33.03 | 88.36 | 1.2 |
| E.C.1 | 482.43 | 585.62 | 346.42 | 834.04 | 0.9 |
| E.C.2 | −505.84 | 569.28 | 370.63 | 846.95 | 0.9 |
| C.C. | 518.52 | 520.68 | 324.31 | 243.74 | −0.0124 | 0.2196 | 0.0014 | −0.0003 | −0.5497 |
| ±0.07 | ±0.06 | ±0.10 | ±0.10 | ±0.0016 | ±0.0225 | ±0.0001 | ±0.0001 | ±0.0995 | |
| E.C.0 | 1619.83 | 1626.44 | 633.85 | 475.47 | −0.0540 | −3.1424 | −0.0011 | −0.0034 | 7.4728 |
| ±4.66 | ±4.95 | ±15.13 | ±21.08 | ±0.1706 | ±4.1635 | ±0.0025 | ±0.0020 | ±2.7466 | |
| E.C.1 | 1652.77 | 1652.86 | 695.53 | 477.55 | −0.3491 | 0.4026 | −0.0004 | 0.0047 | 6.4104 |
| ±8.04 | ±8.06 | ±15.22 | ±13.44 | ±0.1422 | ±2.5525 | ±0.0017 | ±0.0018 | ±4.2151 | |
| E.C.2 | 1638.09 | 1637.34 | 766.41 | 503.78 | 0.1555 | 0.8307 | −0.0049 | 0.0120 | −2.1837 |
| ±7.15 | ±7.88 | ±18.46 | ±15.55 | ±0.0635 | ±0.7039 | ±0.0013 | ±0.0025 | ±2.2819 |
| 573.87 | 573.13 | 327.10 | 234.93 | 0.0487 | 0.0487 | −0.0035 |
| ±0.00 | ±0.00 | ±0.00 | ±0.00 | ±0.0000 | ±0.0000 | ±0.0000 |
| −0.0042 | 0.0000 | 3.42 | −0.003162 | 0.8656 | 0.0018 | |
| ±0.0000 | ±0.0000 | ±0.001457 | ±0.00 | ±0.0460 | ±0.0001 |
| Herrera’s Method | Proposed Method | |||
|---|---|---|---|---|
| C.C. | 0.1367 | 0.1272 | 0.1390 | 0.1423 |
| [−0.0054, +0.0058] | [−0.0050, +0.0054] | [−0.0055, +0.0059] | [−0.0056, +0.0061] | |
| E.C.0 | 1.7242 | 1.6984 | ||
| [−0.0658, +0.0709] | [−0.0648, +0.0699] | |||
| E.C.1 | 1.8169 | 1.6580 | ||
| [−0.0739, +0.0801] | [−0.0674, +0.0731] | |||
| E.C.2 | 1.6429 | 1.5566 | ||
| [−0.0646, +0.0699] | [−0.0612, +0.0662] | |||
| D.C. | 0.8455 | 0.7343 | 0.7829 | 0.8567 |
| [−0.0012, +0.0012] | [−0.0010, +0.0010] | [−0.0011, +0.0011] | [−0.0011, +0.0012] | |
| 6.04436 | 5.93022 | |||
| Herrera’s Method | Proposed Method | |||
|---|---|---|---|---|
| Lx-25 (mm) | Ly-25 (mm) | Lx-25 (mm) | Ly-25 (mm) | |
| 1 | 0.16988 | 0.07660 | 0.16475 | 0.06380 |
| 2 | 0.10438 | 0.10360 | 0.09775 | 0.09040 |
| 3 | 0.19263 | 0.08220 | 0.18025 | 0.06960 |
| 4 | 0.20350 | 0.25660 | 0.18088 | 0.24160 |
| 5 | −0.05288 | 0.20440 | −0.04725 | 0.19200 |
| 6 | 0.03600 | 0.07500 | 0.03288 | 0.06520 |
| M | 0.12655 | 0.13307 | 0.11729 | 0.12043 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Y.; Sun, Y.; Li, G.; Kong, J.; Jiang, G.; Jiang, D.; Cai, H.; Ju, Z.; Yu, H.; Liu, H. Simultaneous Calibration: A Joint Optimization Approach for Multiple Kinect and External Cameras. Sensors 2017, 17, 1491. https://doi.org/10.3390/s17071491
Liao Y, Sun Y, Li G, Kong J, Jiang G, Jiang D, Cai H, Ju Z, Yu H, Liu H. Simultaneous Calibration: A Joint Optimization Approach for Multiple Kinect and External Cameras. Sensors. 2017; 17(7):1491. https://doi.org/10.3390/s17071491
Chicago/Turabian StyleLiao, Yajie, Ying Sun, Gongfa Li, Jianyi Kong, Guozhang Jiang, Du Jiang, Haibin Cai, Zhaojie Ju, Hui Yu, and Honghai Liu. 2017. "Simultaneous Calibration: A Joint Optimization Approach for Multiple Kinect and External Cameras" Sensors 17, no. 7: 1491. https://doi.org/10.3390/s17071491
APA StyleLiao, Y., Sun, Y., Li, G., Kong, J., Jiang, G., Jiang, D., Cai, H., Ju, Z., Yu, H., & Liu, H. (2017). Simultaneous Calibration: A Joint Optimization Approach for Multiple Kinect and External Cameras. Sensors, 17(7), 1491. https://doi.org/10.3390/s17071491






