An LMS Programming Scheme and Floating-Gate Technology Enabled Trimmer-Less and Low Voltage Flame Detection Sensor
Abstract
:1. Introduction
- A low voltage flame detector sensor based on the flame ionization principle.
- A trimmer-less voltage comparator.
- A programming scheme that is based on the LMS algorithm.
- An easy circuit implementation of the LMS algorithm.
- A programming circuit that utilizes injection pulses instead of VSD modulation.
2. The Flame Detection Sensor
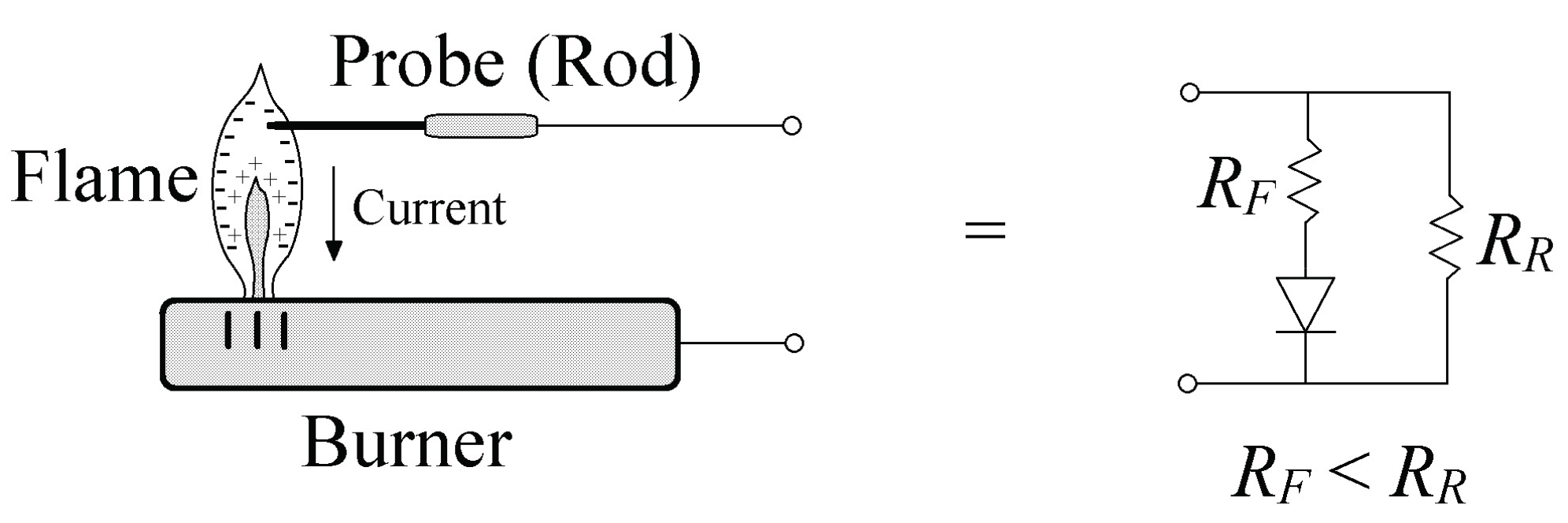
2.1. The Flame Ionization Principle
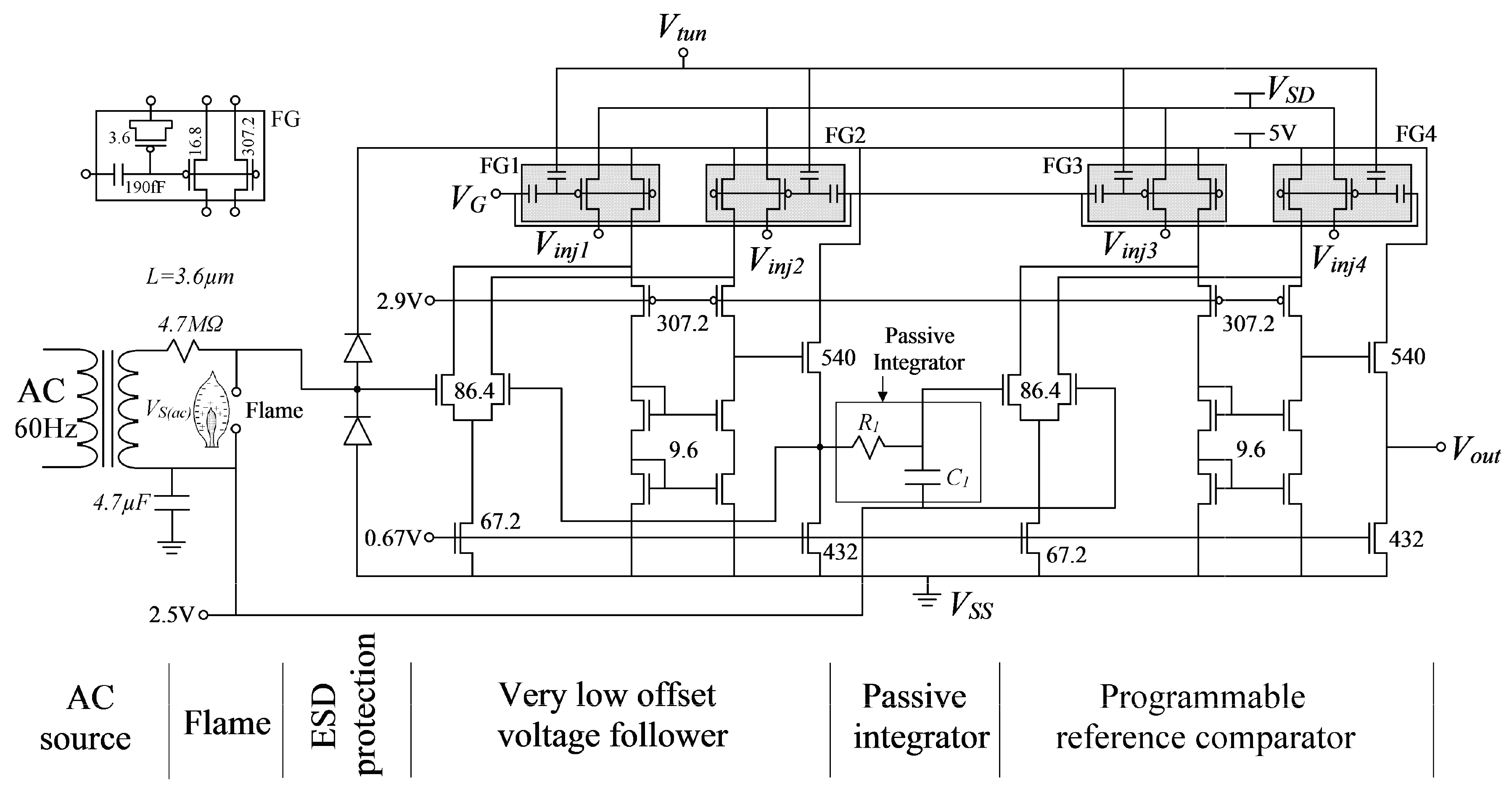
2.2. The Flame Detection Sensor Scheme
3. The Programmable Offset Operational Amplifier
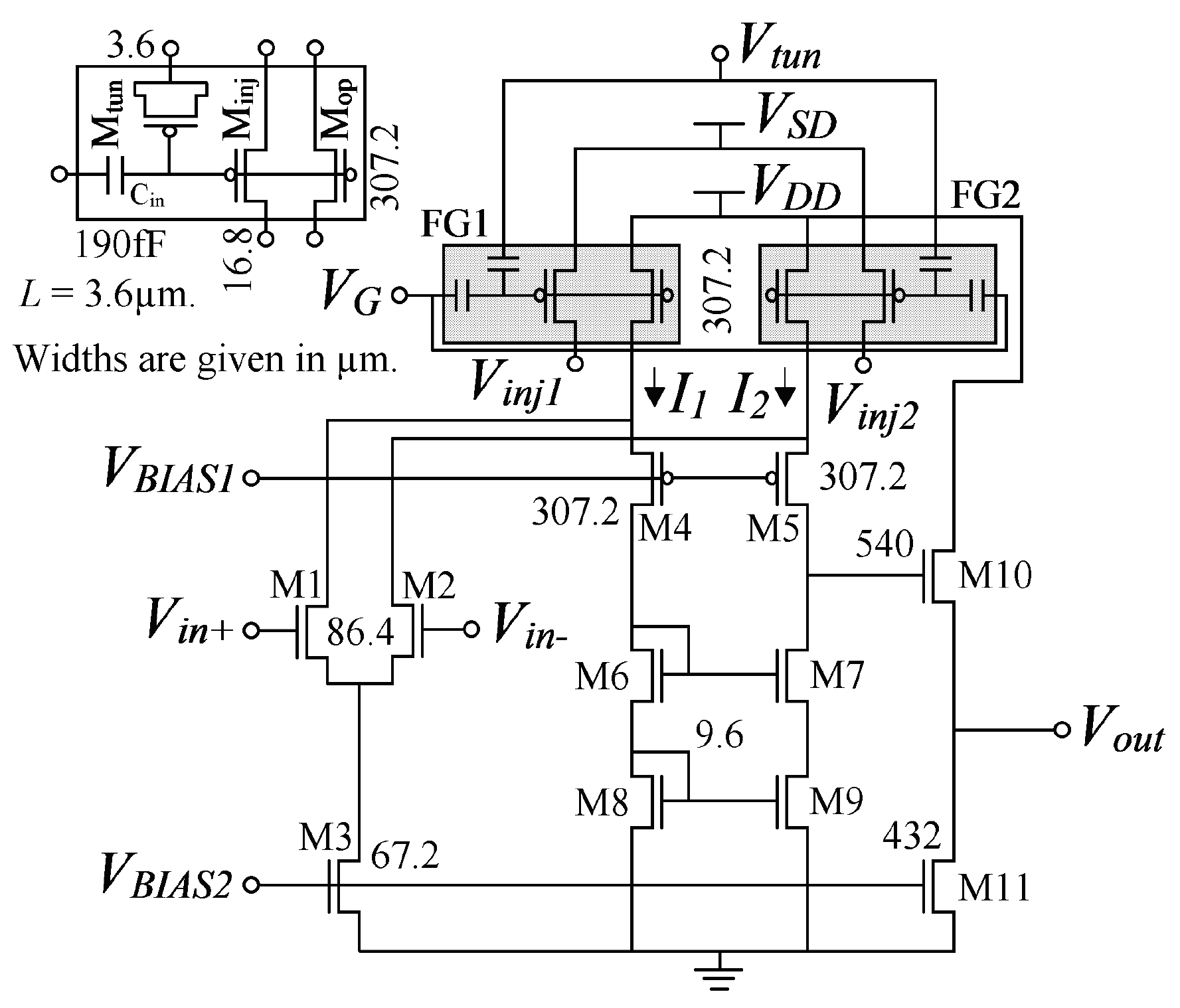
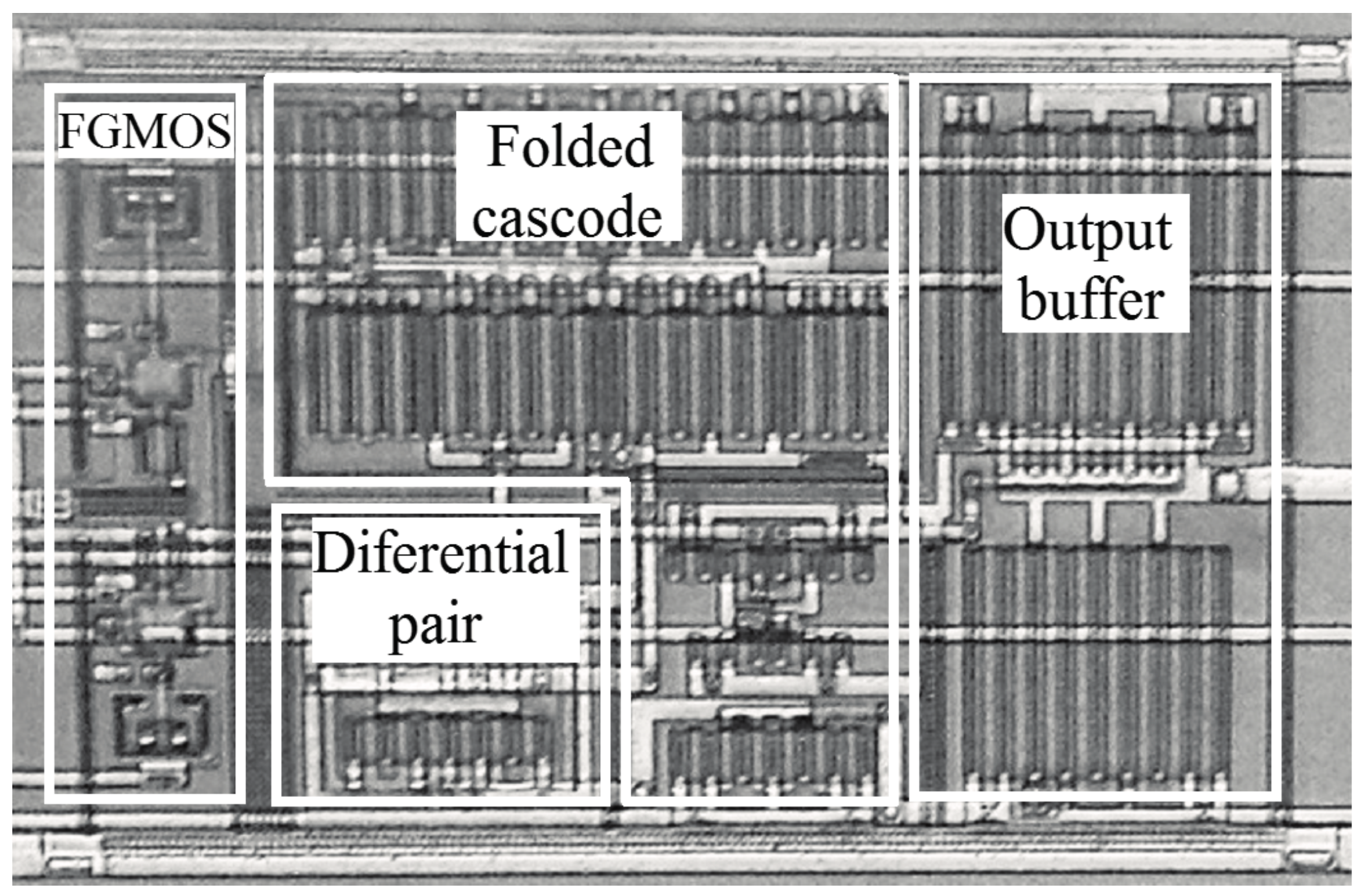
3.1. The POOA Design
3.2. The POOA as A Precision Amplifier
4. LMS Programming Scheme
4.1. The LMS Algorithm
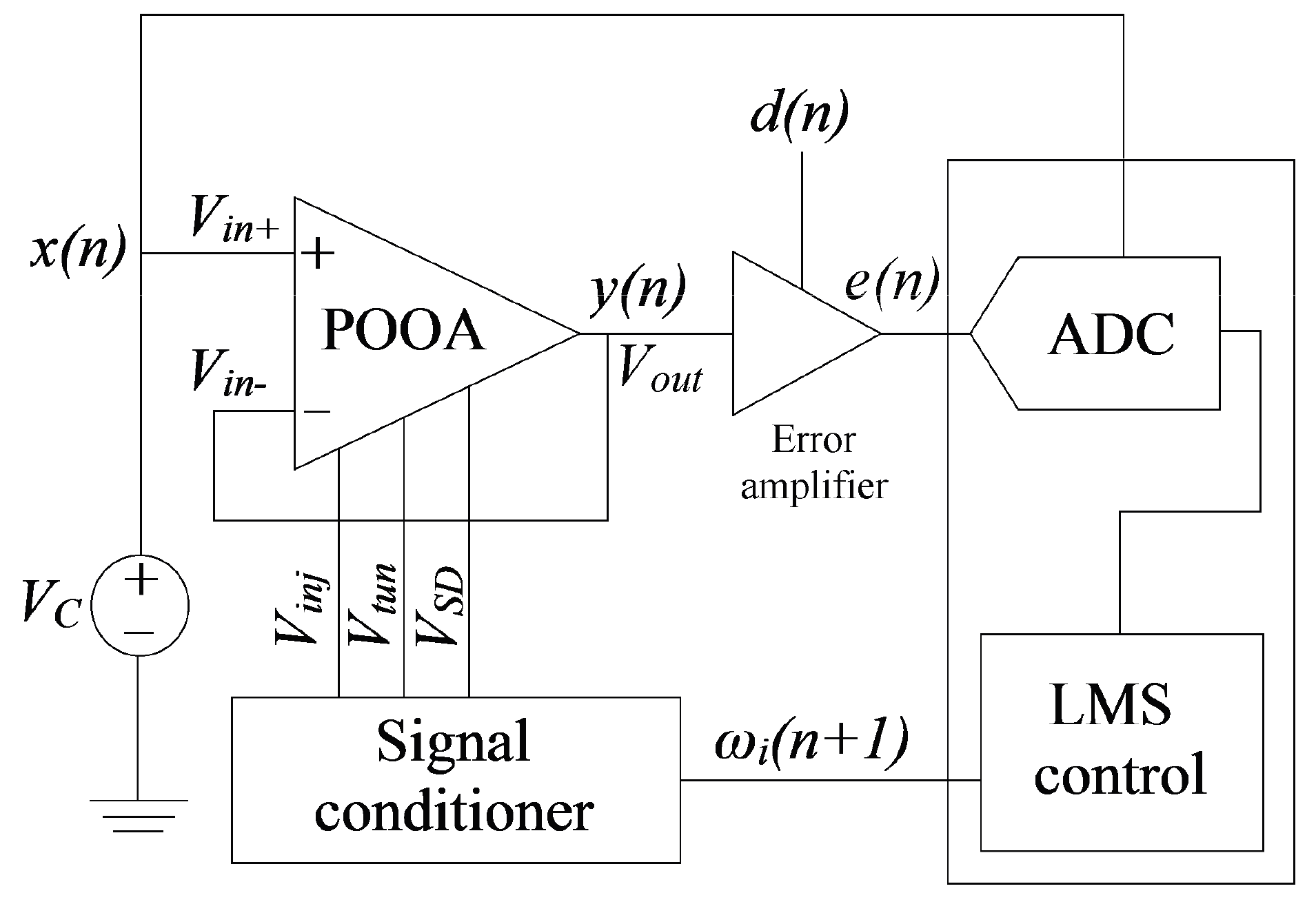
4.2. Programming Scheme Based on LMS Algorithm
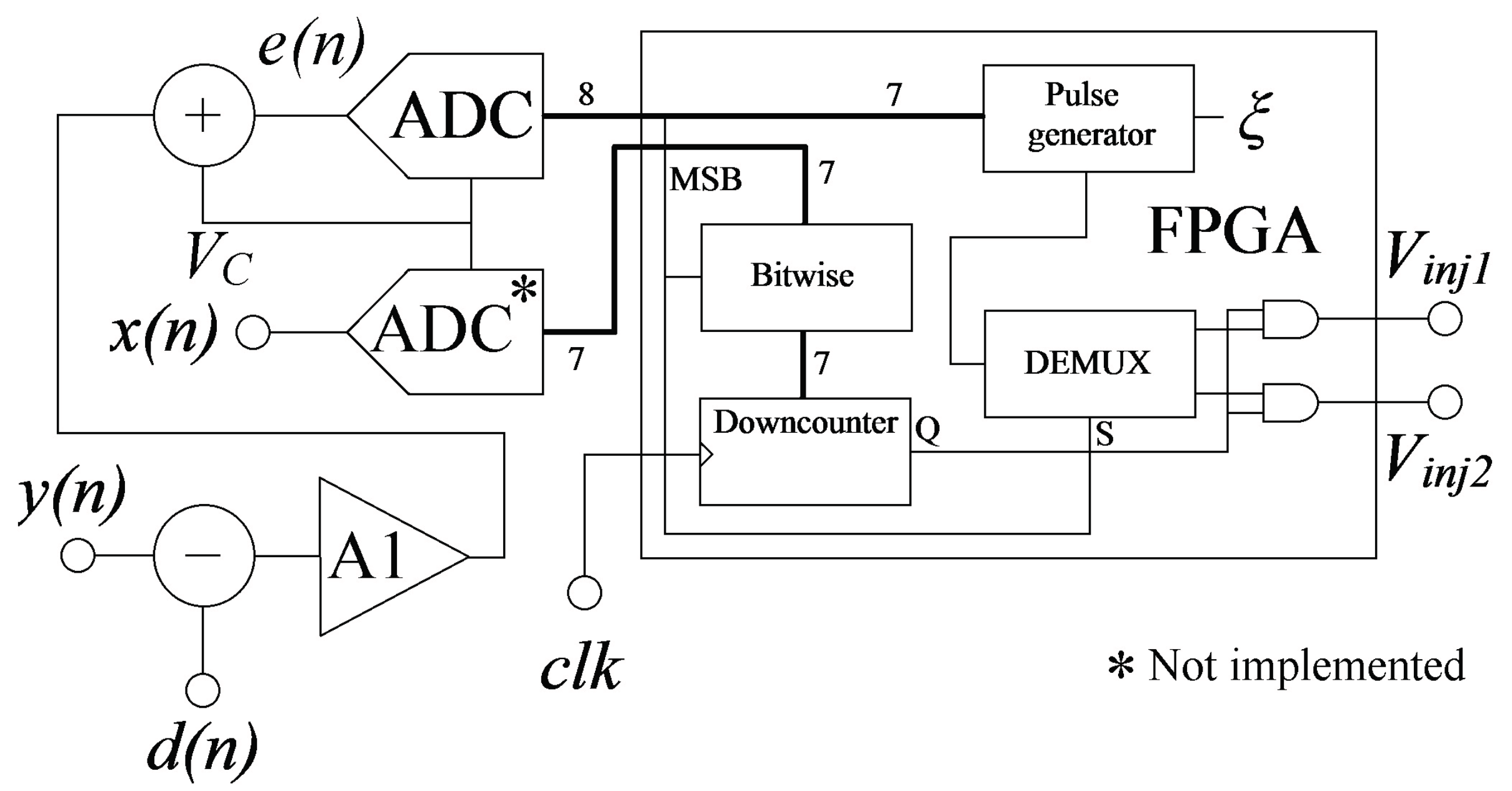
4.3. FPGA Implementation of the Programming Scheme
4.4. The POOA as A Voltage Comparator
5. Quantitative Analysis of the Flame Detection Sensor
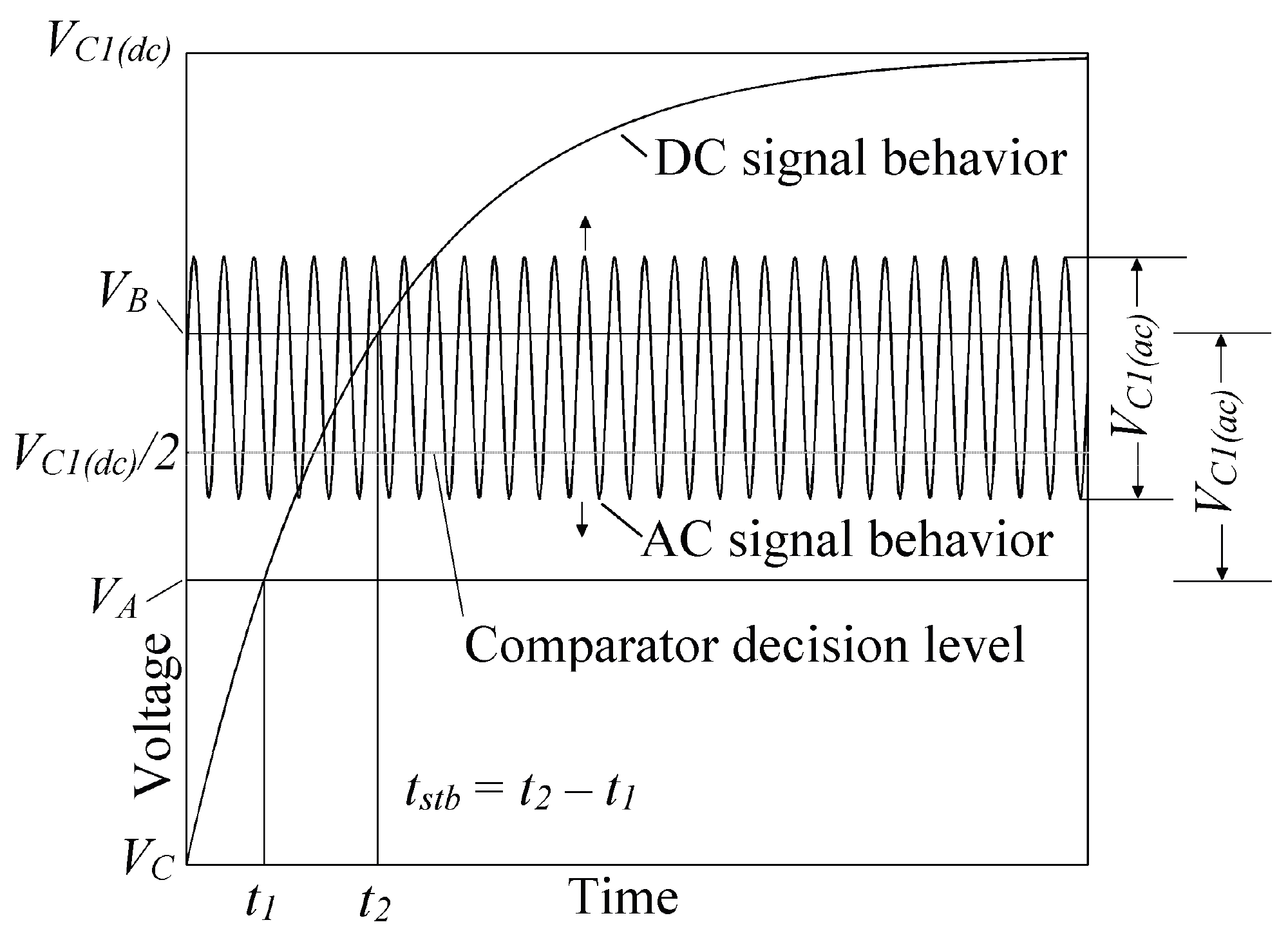
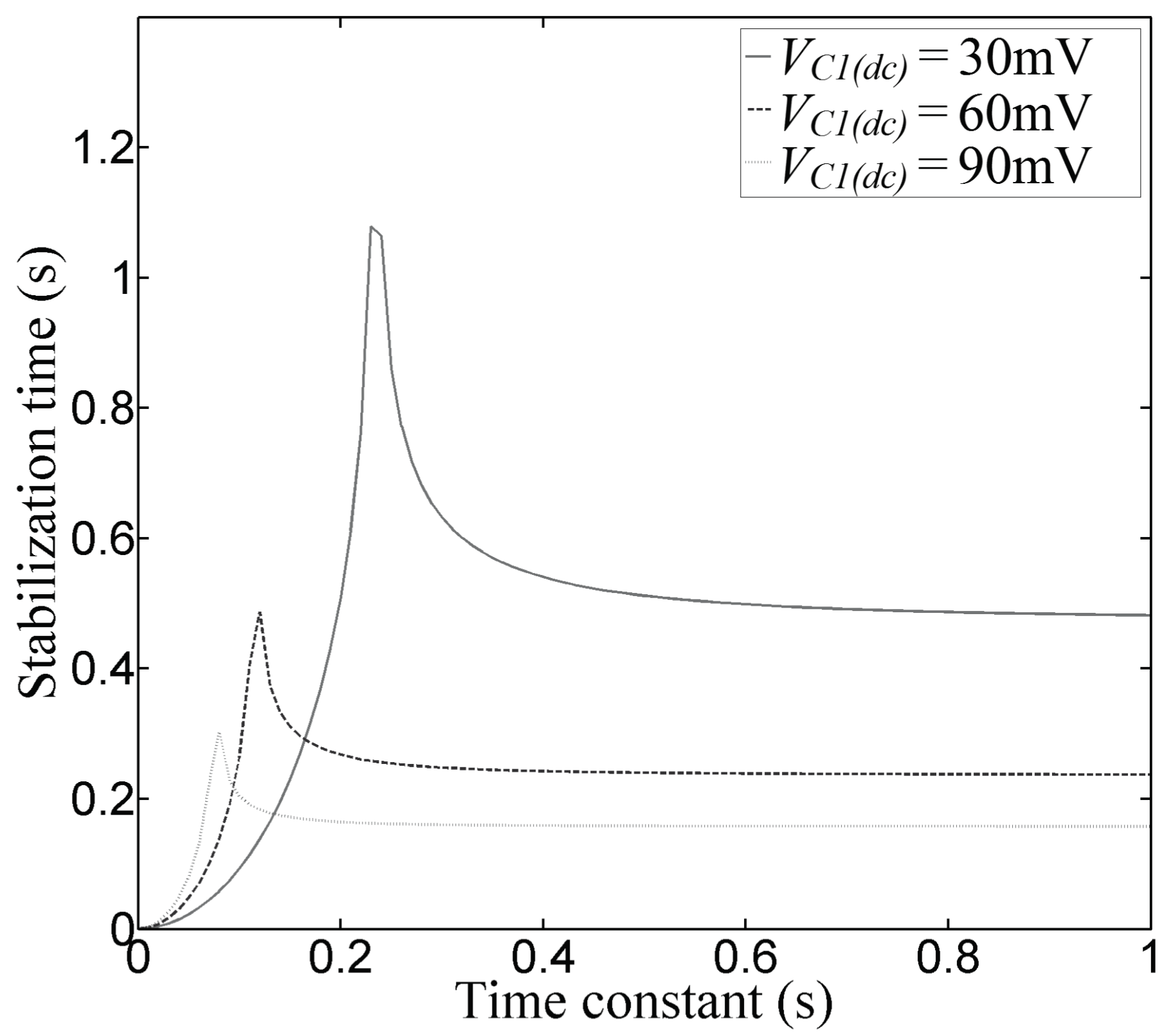
AC/DC Signal Behavior
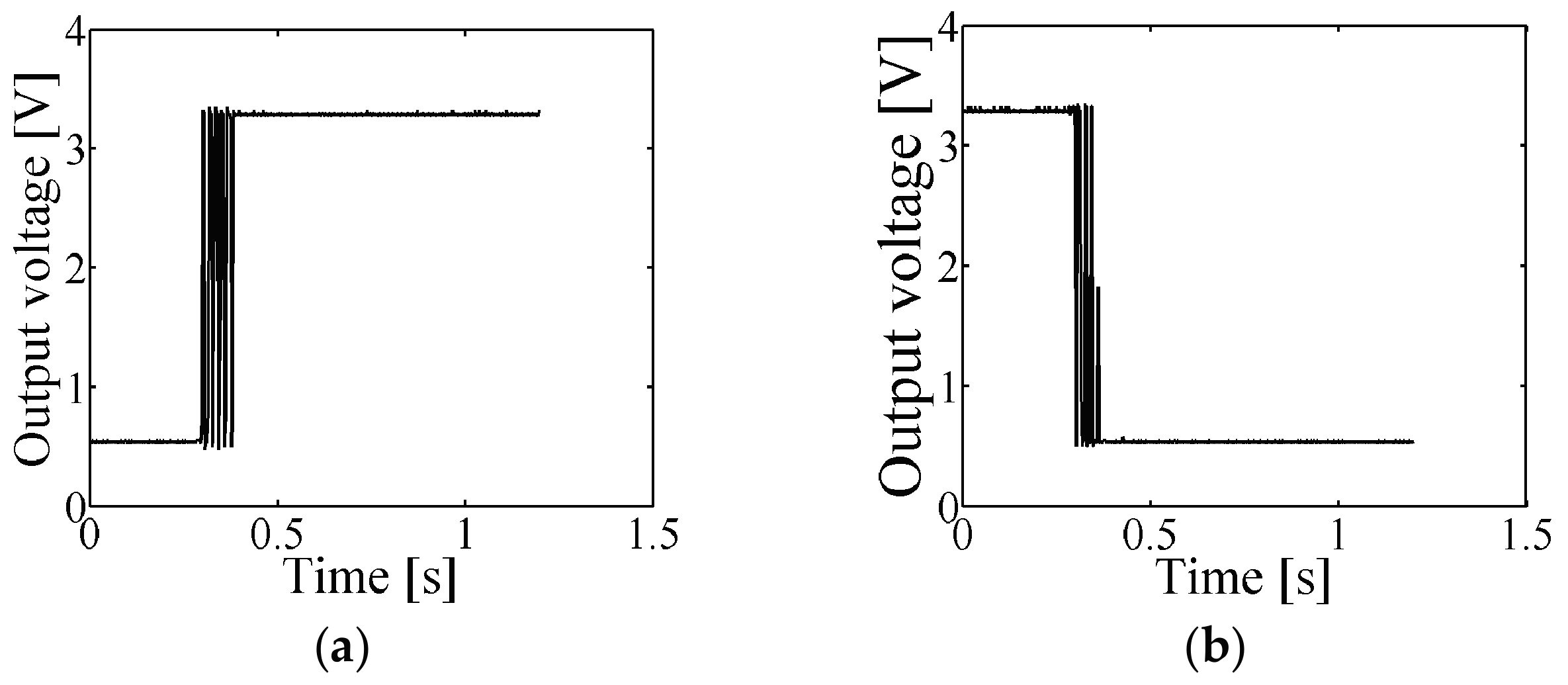
6. Sensor Test
6.1. The LMS Programming Scheme Performance
6.2. Testing the Sensor
7. Conclusions
- The AC voltage needed to feed the flame is considerably lower than the one used in commercial flame detectors.
- The proposed flame detection sensor is trimmer-less, thus, increasing its reliability.
- The proposed design is field-programmable.
- The offset voltage deviation due to the temperature variation is negligible in terms of functionality.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Qiu, H.; Chen, F.; Gao, Y. Based on the CCD of the Boiler Flame Detection. In Proceedings of the IEEE Third International Conference on Digital Manufacturing and Automation, Guilin, China, 31 July–2 August 2012; pp. 261–263. [Google Scholar]
- Bae, H.; Kim, S.; Wang, B.-H.; Lee, M.; Harashima, F. Flame Detection for the Steam Boiler Using Neural Network and Image Information in the Ulsan Steam Power Generation Plant. IEEE Trans. Ind. Electron. 2006, 53, 338–348. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, Y. Real-Time Fire Detection Using Video Sequence Data. In Proceedings of the IEEE 28th Chinese Control and Decision Conference, Yinchuan, China, 28–30 May 2016; pp. 3620–3623. [Google Scholar]
- Chen, H.; Zhang, X.; Hong, P.; Hu, H.; Yin, X. Recognition of the Temperature Condition of a Rotary Kiln Using Dynamic Features of A Series of Blurry Fame Images. IEEE Trans. Ind. Electron. 2016, 12, 148–157. [Google Scholar]
- Kuipers, W.J.; Müller, J. Total Hydrocarbon Analysis with a Planar Micro Flame Ionization Detector. In Proceedings of the IEEE 9th Sensors Conference, Kohala Coast, HI, USA, 25–28 October 2010; pp. 1939–1942. [Google Scholar]
- Cheong, P.; Chang, K.; Lai, Y.; Ho, S.; Sou, I.; Tam, K. A ZigBee-Based Wireless Sensor Network Node for Ultraviolet Detection of Flame. IEEE Trans. Ind. Electron. 2011, 58, 5271–5277. [Google Scholar] [CrossRef]
- Pauchard, A.R.; Manic, D.; Flanagan, A.; Besse, P.A.; Popovic, R.S. A Method for Spark Rejection in Ultraviolet Flame Detectors. IEEE Trans. Ind. Electron. 2000, 47, 168–174. [Google Scholar] [CrossRef]
- Möllberg, A. Investigation of the Principle of Flame Rectification in Order to Improve Detection of the Propane Flame in Absorption Refrigerators. B.S. Thesis, IFM, Linkoping University, Linköping, Sweden, 2005. [Google Scholar]
- Payne, P.P.; Schmidt, S.E.; Goppel, K.P.; King, D.J.; Tobin, S.M.; Fowler, J.T. Constant Current Flame Ionization Circuit. U.S. Patent 6509838 B1, 21 January 2003. [Google Scholar]
- Chian, B.; Anderson, P.M.; Nordberg, T.J.; Hill, B. Flame Sensing System. U.S. Patent 7764182 B2, 27 July 2010. [Google Scholar]
- Iglesias-Rojas, J.C.; Gomez-Castañeda, G.; Moreno-Cadenas, J.A. Offset Reduction in Operational Amplifiers using Floating Gate Technology and LMS Algorithm. In Proceedings of the IEEE 8th International Conference on Electrical Engineering Computing Science and Automatic Control, Merida, Mexico, 26–28 October 2011; pp. 1–6. [Google Scholar]
- Iglesias-Rojas, J.C.; Gomez-Castañeda, G.; Moreno-Cadenas, J.A. A Very Low Offset Voltage Operational Amplifier Using Floating-Gate Technology. In Proceedings of the IEEE 20th International Conference on Electronics, Communication and Computer, Cholula, Mexico, 22–24 February 2010; pp. 9–14. [Google Scholar]
- Ma, Y.; Gilliland, T.; Wang, B.; Paulsen, R.; Pesaveento, A.; Wang, H.; Hoc, N.; Humes, T.; Diorio, C. Reliability of pFET EEPROM With 70-Å Tunnel Oxide Manufactured in Generic Logic CMOS Processes. IEEE Trans. Device Mater. Reliab. 2004, 4, 353–358. [Google Scholar] [CrossRef]
- Brink, S.; Hasler, J.; Wunderlich, R. Adaptive Floating-Gate Circuit Enable Large-Scale FPAA. IEEE Trans. Very Large Scale Integr. Syst. 2014, 22, 2307–2315. [Google Scholar] [CrossRef]
- Graham, D.W.; Farquhar, E.; Degnan, B.; Gordon, C.; Hasler, P. Indirect Programming of Floating-Gate Transistor. IEEE Trans. Circuits Syst. I Reg. Pap. 2007, 54, 951–963. [Google Scholar] [CrossRef]
- Li, F.; Xu, L.; Cao, Z.; Du, M. A Chemi-Ionization Processing Approach for Characterizing Flame Flickering Behavior. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference, Pisa, Italy, 11–14 May 2015; pp. 325–329. [Google Scholar]
- Allen, P.E.; Holberg, D.R. CMOS Analog Circuit Design; Oxford University Press: Atlanta, GA, USA, 2011. [Google Scholar]
- Rahimi, K.; Diorio, C.; Hernandez, C.; Brockhausen, M.D. A simulation Model for Floating-Gate MOS Synapse Transistor. In Proceedings of the IEEE Symposium on Circuits and Systems, Scottsdale, AZ, USA, 26–29 May 2002. [Google Scholar] [CrossRef]
- Haykin, S.; Widrow, B. Least-Mean-Square Adaptive Filters; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Venturi, S.H.K.; Panahi, I. Hybrid RLS-NLMS Algorithm for Real-Time Remote Active Noise Control Using Directional UltraSonic LoudSpeaker. In Proceedings of the IEEE 40th Annual Conference of the Industrial Electronics Society, Dallas, TX, USA, 29 October–1 November 2014; pp. 2418–2424. [Google Scholar]
- Sharma, D.; Kaur, R. Improvement in Convergence Speed and Stability of Least Mean Square and Normalized Least Mean Square Algorithm. In Proceedings of the IEEE 2nd International Conference on Computing for Sustainable Global Development, New Delhi, India, 11–13 March 2015; pp. 1496–1500. [Google Scholar]
- De la Cruz-Alejo, J.; Oliva-Moreno, L.N. LMS Algorithm for Programming an Analogue Memory Cell. Int. J. Electron. 2013, 100, 863–879. [Google Scholar] [CrossRef]
- Figueroa, M.; Bridges, S.; Hsu, D.; Diorio, C. A 19.2 GOPS Mixed Filter with Floating-Gate Adaptation. IEEE J. Solid-State Circuits. 2004, 39, 1196–1201. [Google Scholar] [CrossRef]
- Rodríguez-Andina, J.J.; Valdés-Peña, M.D.; Moure, M.J. Advanced Features and Industrial Applications of FPGA. IEEE Trans. Ind. Informat. 2015, 11, 853–864. [Google Scholar] [CrossRef]
- Yen, C.T.; Weng, W.-D.; Lin, Y.T. FPGA Realization of a Neural-Network-Based Nonlinear Channel Equalizer. IEEE Trans. Ind. Electron. 2004, 51, 472–478. [Google Scholar] [CrossRef]
- Bian, T.; Jiang, Y.; Jiang, Z. Decentralized Adaptive Optimal Control of Large-Scale Systems with Application to Power Systems. IEEE Trans. Ind. Electron. 2015, 62, 2439–2447. [Google Scholar] [CrossRef]


| Parameter 1 | Magnitude | Unit |
|---|---|---|
| Open loop gain | 65 | dB |
| Bandwidth | 235 | kHz |
| Phase margin | 60 | dB |
| Slew rate | 2 | V/μs |
| Settling time | 1550 | ns |
| Output range | (VSS + 0.55) − (VDD − 1.7) | V |
| Common mode rejection ratio | 65 | dB |
| Power supply rejection ratio | 70 | dB |
| Input referred offset voltage | Programmable | V |
| Total power dissipation | 7.2 | mW |
| Parameter | POOA1 | POOA2 |
|---|---|---|
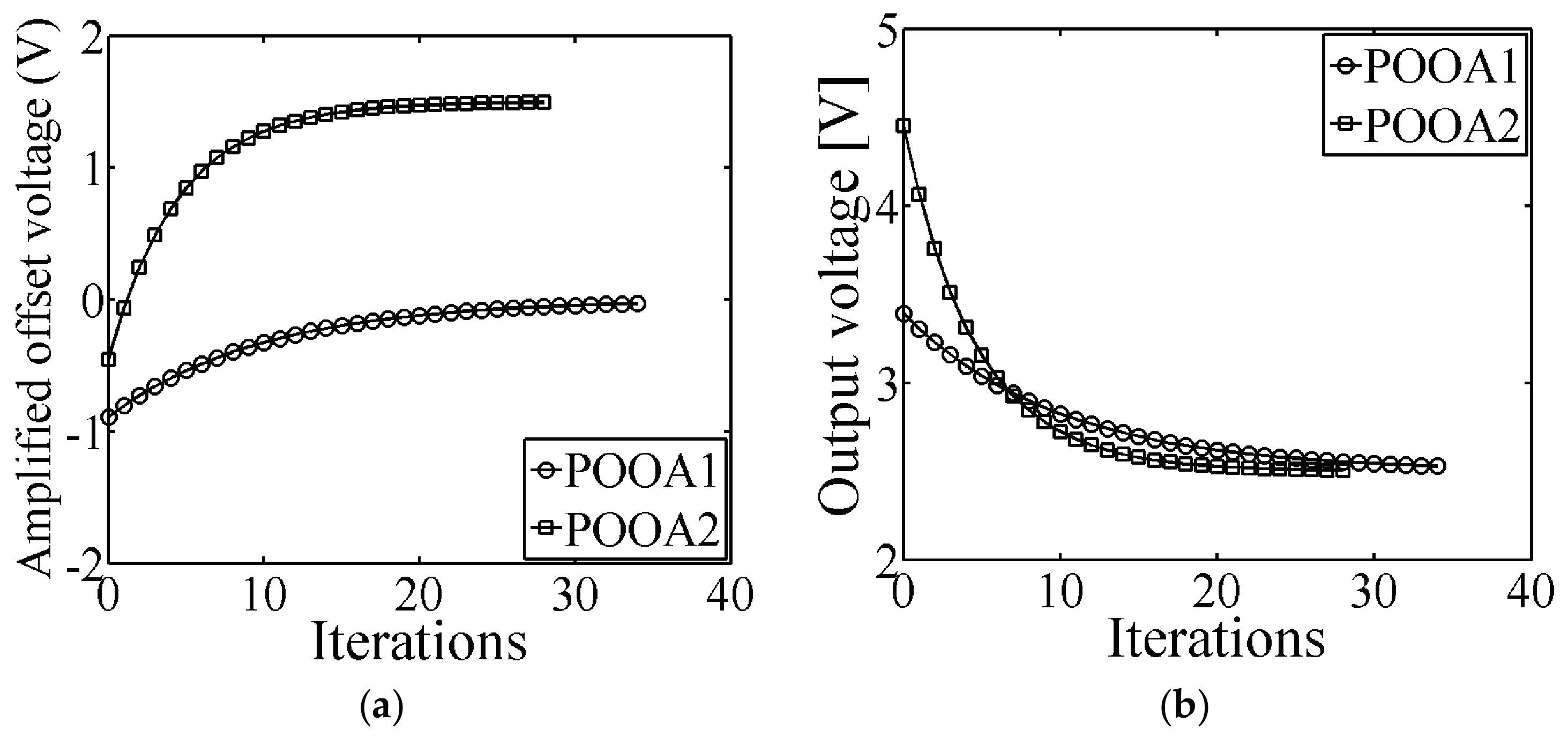
| Initial offset voltage | −890 μV | −4.53 mV |
| Final offset voltage | −26 μV | +14.97 mV |
| Expected offset voltage | 0 V | +15 mV |
| Initial error voltage | 3.39 V | 4.453 V |
| Final error voltage | 2.526 V | 2.503 V |
| Number of iterations | 35 | 28 |
| Adaptation rate | 1.9 | 3.8 |
| LMS clok frequency | 5 kHz | 5 kHz |
| Programming accuracy | - | 99.8% |
| Total programming time 1 | 0.896 s | 0.716 s |
| Temperature | POOA1 | POOA2 |
|---|---|---|
| 10 °C | +25 μV | +15.02 mV |
| 27 °C | −26 μV | +14.97 mV |
| 35 °C | −111 μV | +14.88 mV |
| 50 °C | −164 μV | +14.83 mV |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iglesias-Rojas, J.C.; Gomez-Castañeda, F.; Moreno-Cadenas, J.A. An LMS Programming Scheme and Floating-Gate Technology Enabled Trimmer-Less and Low Voltage Flame Detection Sensor. Sensors 2017, 17, 1387. https://doi.org/10.3390/s17061387
Iglesias-Rojas JC, Gomez-Castañeda F, Moreno-Cadenas JA. An LMS Programming Scheme and Floating-Gate Technology Enabled Trimmer-Less and Low Voltage Flame Detection Sensor. Sensors. 2017; 17(6):1387. https://doi.org/10.3390/s17061387
Chicago/Turabian StyleIglesias-Rojas, Juan Carlos, Felipe Gomez-Castañeda, and Jose Antonio Moreno-Cadenas. 2017. "An LMS Programming Scheme and Floating-Gate Technology Enabled Trimmer-Less and Low Voltage Flame Detection Sensor" Sensors 17, no. 6: 1387. https://doi.org/10.3390/s17061387
APA StyleIglesias-Rojas, J. C., Gomez-Castañeda, F., & Moreno-Cadenas, J. A. (2017). An LMS Programming Scheme and Floating-Gate Technology Enabled Trimmer-Less and Low Voltage Flame Detection Sensor. Sensors, 17(6), 1387. https://doi.org/10.3390/s17061387






