1. Introduction
In recent years, battery-powered wireless communication devices have been developed rapidly, and the methods of prolonging the network lifetime by collected energy have attracted much interest from researchers. Wireless energy collecting (EC) is particularly important for wireless sensor networks (WSNs) because of the limited energy supply [
1,
2]. It is quite difficult and expensive to replace or charge the battery for the devices, especially in some special circumstances, so a sustainable energy supply is demanded. The common sources of sustainable energy, however, are highly dependent on weather conditions, such as solar and wind energy. It is a practical method to collect the energy from the surrounding environment or to transmit energy for low-power devices by radio frequency (RF).
RF signals can transmit both message and energy so it is possible to combine the message delivery and energy collection as a complete transmission system. The limitations of practical circuit, however, make the receivers hardly achieve energy collection and information decoding by the same signal. Therefore, message-energy time division transmission is a reasonable strategy to realize synchronous wireless information and power transmission (SWIPT), the performance of which will greatly depend on the scheduling mechanism. The balance between message and energy transmission scheduling is illustrated by the boundary of rate-energy (R-E) domain so as to transform the balance issue into a boundary model [
3]. In [
4,
5], the receiver assumes that energy can be collected from the signal used to carry out the message decoding (MD), while the existing technology that is limited by practical circuit cannot achieve this assumption. Thus, the researchers proposed two kinds of realistic reception mechanisms in [
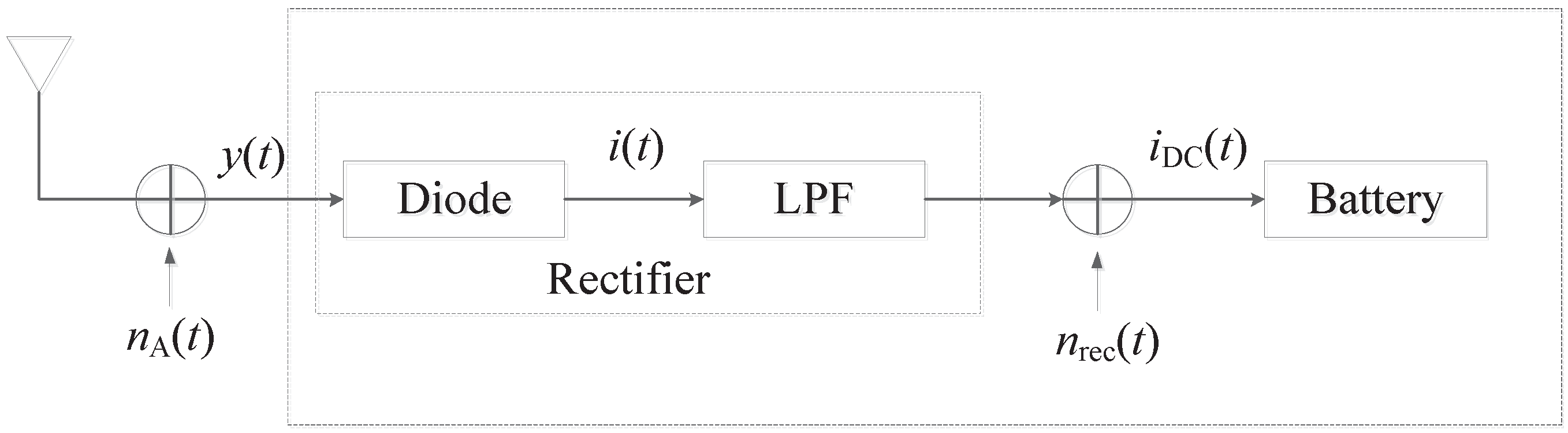
6], in which the receiver could switch between EC and MD, or could divide the receiving signal into the MD part and the EC part.
Currently, multi-user systems based on SWIPT are being studied to meet the requirements of real energy-limited networks, such as WSNs. SWIPT systems, designed for broadcast channels and interference channels, are described in [
7,
8], respectively, and the best transport protocols are also presented. The multi-user multi-input single-output SWIPT system is introduced in [
9] with a newly proposed beamforming optimization design, which can maximize the energy collection of EC receiver under the constraints of signal-interference-plus-noise-rate. The multi-user time division multiple access (TDMA) system in [
10,
11] will transmit the energy and data in the uplink channel and the downlink channel, respectively, with an optimal uplink and downlink time distribution mechanism presented to maximize the total transmission throughput or the equal transmission throughput in the same duration time.
For a message-only transmission system, a multi-user scheduling mechanism is usually designed to adopt the independent and time-varying multipath fading characteristics so as to establish the multi-user diversity [
12,
13]. With this method, the user can transmit and receive messages in a good channel environment throughout the time slots. For example, in the maximum throughput scheduling mechanism, the user with the highest SNR will be selected to transmit data, so as to obtain the maximum system capacity. However, the users with poor channel conditions cannot access the channel at all. In order to prevent the unfairness, the normalized SNR (N-SNR) scheduling mechanism is proposed to maximize the user’s normalized SNR, thus to improve the user’s system capacity greatly. Another consideration to realize the balance between system capacity and channel quality is to maintain the equal throughput [
14,
15], which can be achieved by keeping the average traffic of all users at the lowest level in each slot. The multi-user scheduling mechanism can expand the multi-user diversity (MUD) and maintain the system capacity and channel quality in a balanced state for a long time, but this mechanism has not yet been achieved in SWIPT [
16,
17,
18,
19]. In this paper, three improved scheduling mechanisms are presented to realize multi-user scheduling in a SWIPT system, which can achieve a better balance between data transmission and energy collection during the active state for WSNs. The main contributions of this paper can be summarized as follows:
- (1)
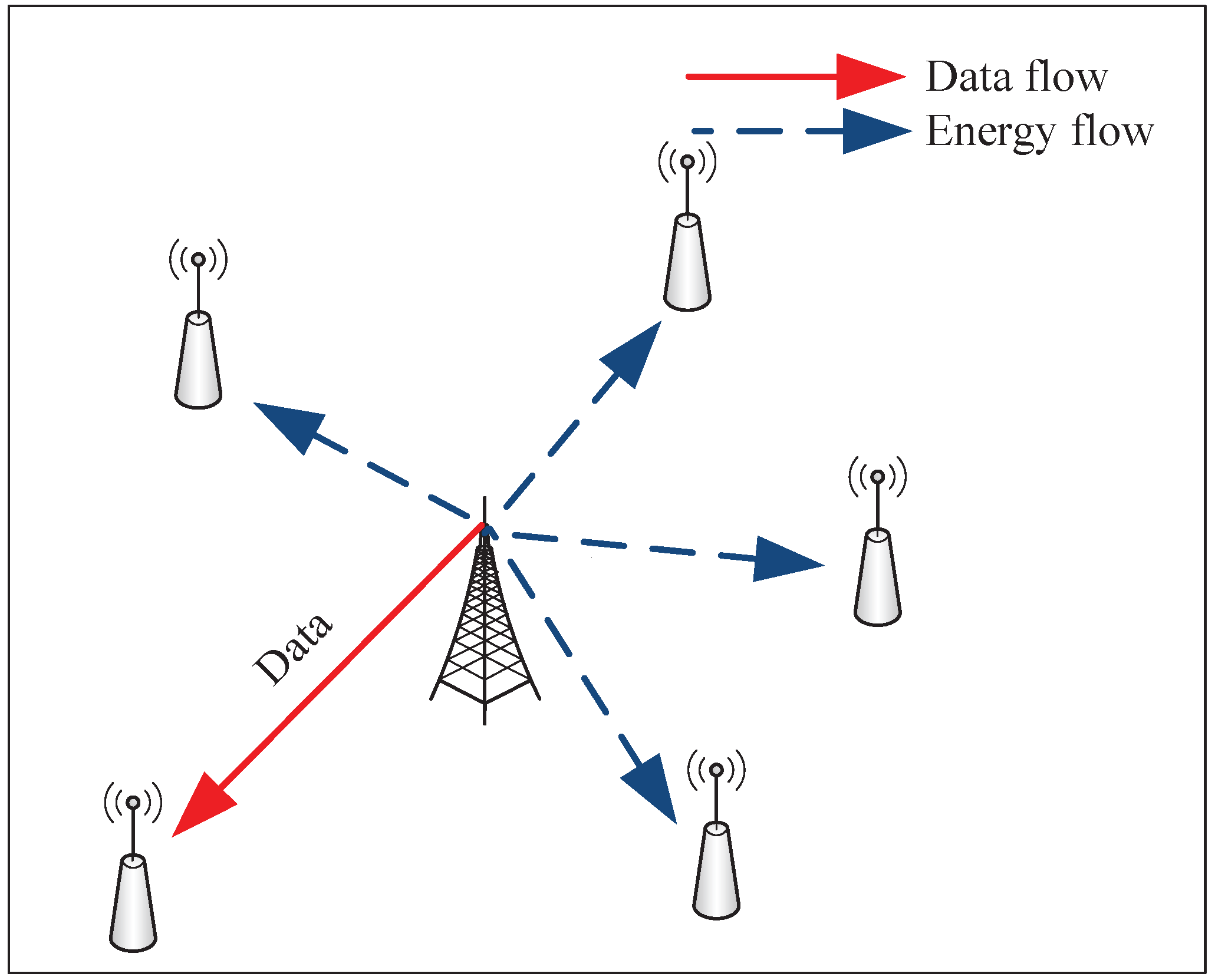
The improved SNR and N-SNR scheduling mechanisms for multi-user SWIPT system are proposed, wherein the users are sorted in ascending order according to SNR and N-SNR, respectively. The jth user, who has the jth smallest SNR or N-SNR, will be selected to deliver the data, and the rest users will collect the energy from surroundings. Obviously, a lower j means that the user selected for data transmission has a poorer channel condition. Meanwhile, the users with better channel conditions will perform the energy collection. Thus, the lower j will cause a smaller ergodic capacity and a larger average collected energy (ACE).
- (2)
The improved ET scheduling mechanism is designed, wherein the users are sorted in ascending order according to N-SNR. is a specific set of ordinal. The user, who has an N-SNR order in the set of and has the minimum average throughput, will be selected to transmit data in each time slot. Therefore, a smaller set of will cause a larger ACE and a smaller ergodic capacity. In addition, this paper gives the necessary conditions for the user to achieve ET.
- (3)
The improved SNR, N-SNR and ET scheduling mechanisms are analyzed using order statistical theory for heterogeneous (independent or non-identically distributed) Nakagami-m, Weibull, Ricean and Rayleigh fading channels. In addition, three types of scheduling mechanisms and the relative approximate expressions are established for ACE and ergodic channel capacity (ECC) of a single user in corresponding fading models.
6. Implementation and Performance Analysis
Three scheduling mechanisms are simulated using ISM band with the center frequency as 915 MHz and the bandwidth as 26 MHz. The distance range between transmitter and receiver is from 2 m to 4 m. The packet sending rate is 2 packets per second, and the size of each packet is 16 bits. The additional noise of the receivers has the power of
= −96 dBm. Using the indoor path loss model [
26], the NAP and STs are in the same layer. Assuming that the transmission power of NAP is
P = 1 W, the antenna gain of NAP and STs are 10 dBi and 2 dBi, respectively. The conversion efficiency is
= 0.5. Now, a system with
N = 7 is taken into account, and the average channel power gain of a single user is
=
,
n = 1, ..., 7.
The performance of the average total information capacity (
) is calculated by
, and the average total collected energy (
) is obtained by
.
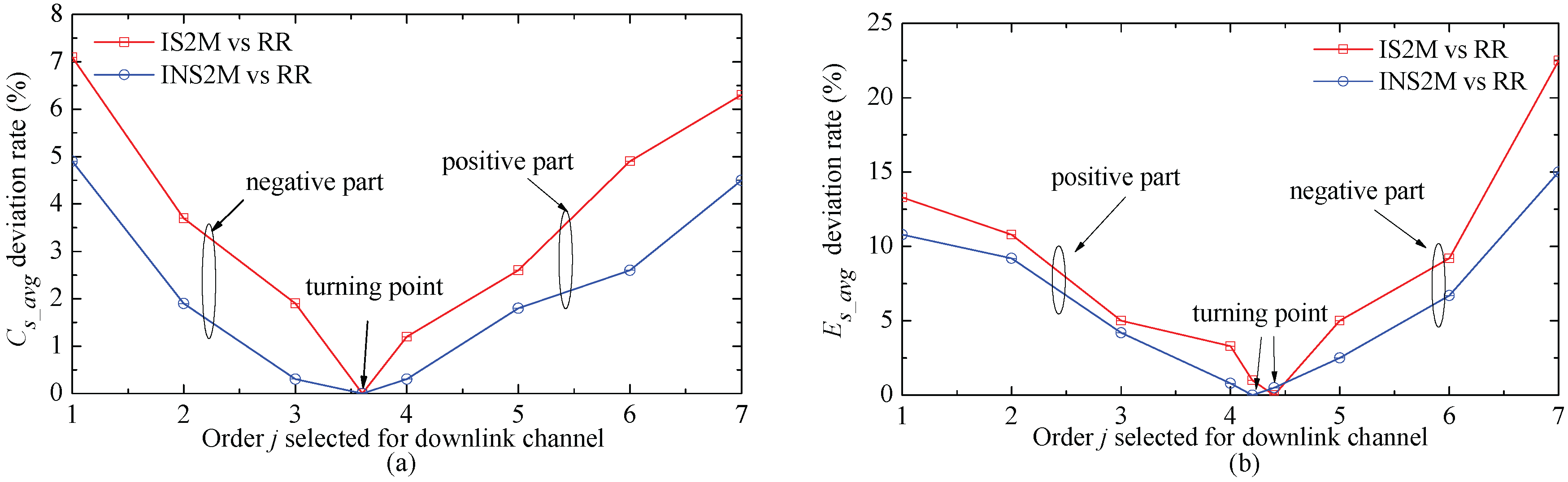
Figure 3 shows the comparisons of
and
based on IS2M and INS2M with different order
js (
). The shape parameters of the independent and identically distributed Nakagami-
m fading model use the setting of
. For INS2M, ACE of the whole system will be increased by 45% when the order
j declines to 1. Therefore, the order
j can be used to control the balance between the system capacity and energy collection.
The collected power is used to replace the energy so as to evaluate the unit average effect, since the collected energy is changing frequently.
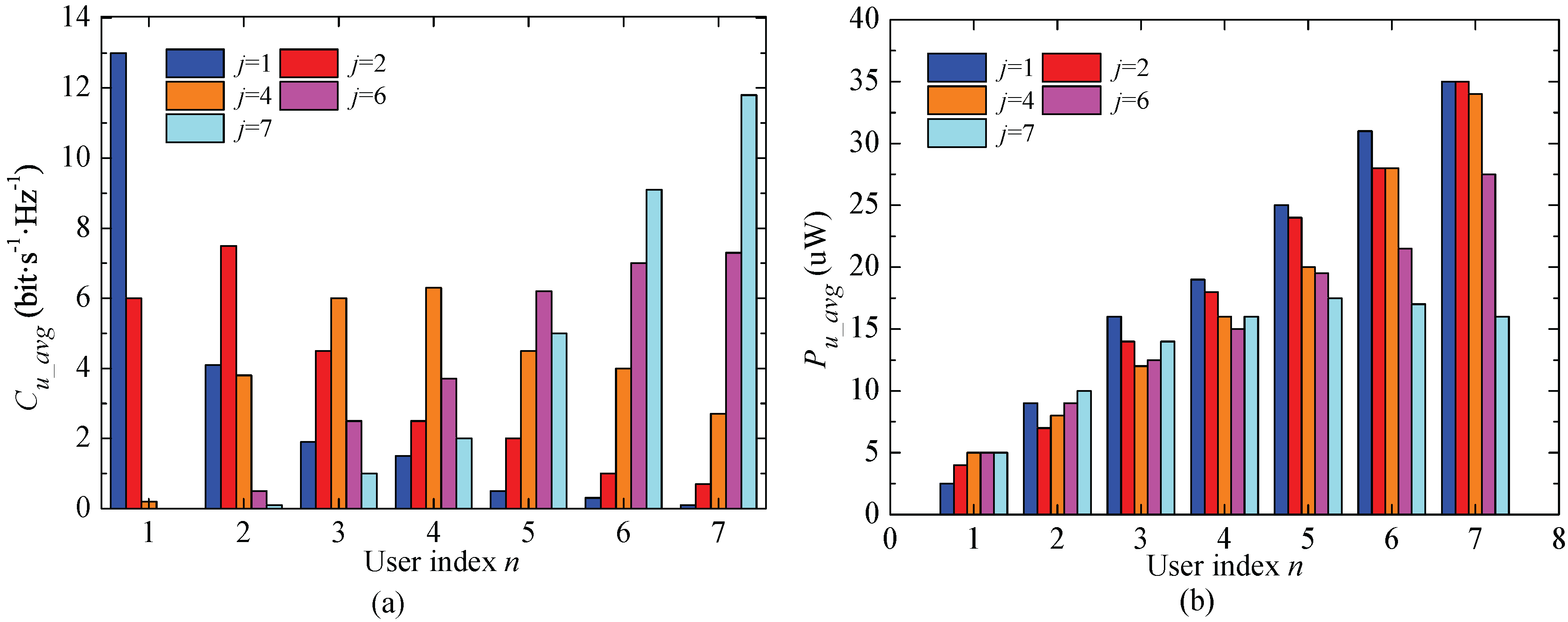
Figure 4 shows the average user capacity (
) and the average user collected power (
) of IS2M with different orders. For any order
j, IS2M cannot ensure the proportional fairness for all users in different channel environments. The
jth order user will achieve the highest system capacity, and there is
=
,
n = 1, ..., 7. Likewise, the amount of collected energy of the users is determined by how often a user is selected to transmit the messages, and how much energy can be collected when some user fails to be selected.
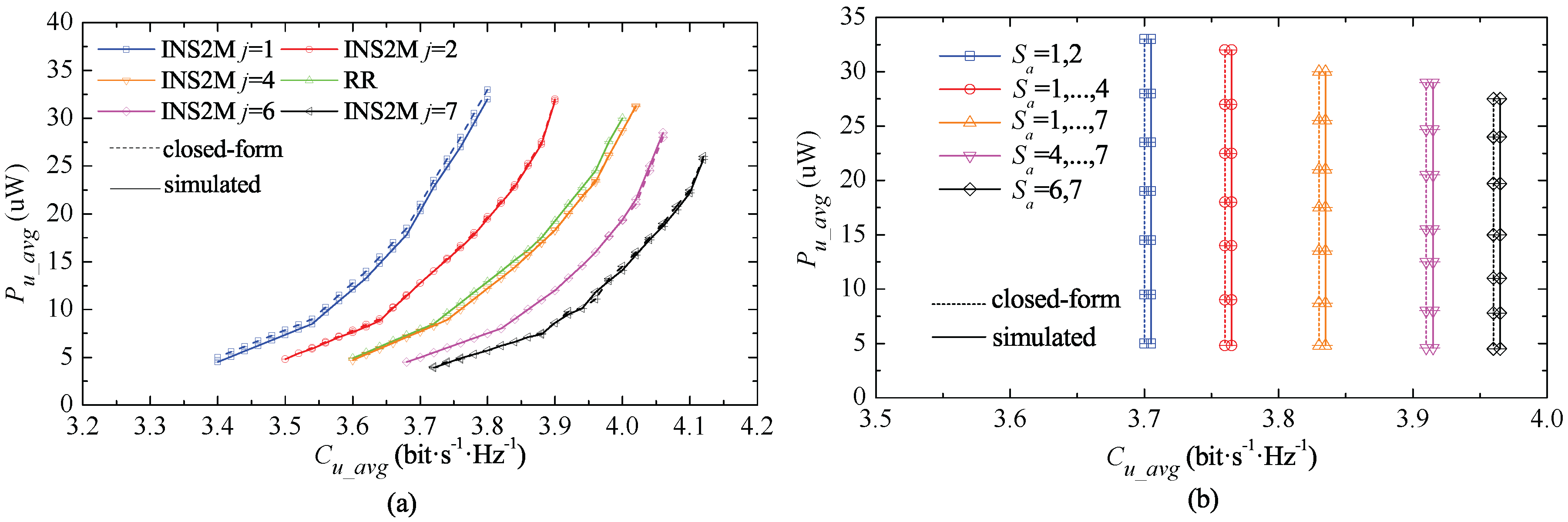
The performance of INS2M and IETSM over the independent and identically distributed Ricean fading channel with the shape parameter
is shown in
Figure 5. It can be seen that the higher the fading factor is, the looser the approximate value is. For instance, when
, the differences of ECC and ACE between the theoretical results obtained by approximate expressions and the simulating results are 0.51% and 0.64%, respectively.
In
Figure 5a, it can be seen that both INS2M and RR scheduling mechanisms can realize the equal proportional relationship in the aspects of ECC and ACE, since all users are selected fairly in the same time slots. For INS2M, a user could collect more energy when the order
j decreases from
N to 1 so as to make ECC decline. For example, the order
j declining from
N to 1 will result in an 8% decrease in capacity and a 26% increase in energy collection for the optimal channel users. Therefore,
j can be chosen according to the requirements of the network.
IETSM can realize the equal transmission for all users as shown in
Figure 5b. Thus, equal transmission is feasible for all cases being considered in this study, and all of the conclusions can be verified by Theorem 1. In addition, ACE corresponds to the user’s channel environments. It can be seen that, for the same set of
, the lower an order is selected from
, the higher ACE obtained by all users will be, and the lower the whole information capacity will be. Thus, a compromise can be made if
= {1, 2} and
= {
N − 1,
N} are feasible. In particular, the energy collected by the users in the best and worst channels will increase by 18% and 21.1%, respectively. The transmission capacity will reduce by 6.29%, when
changes from
= {6, 7} to
= {1, 2}.
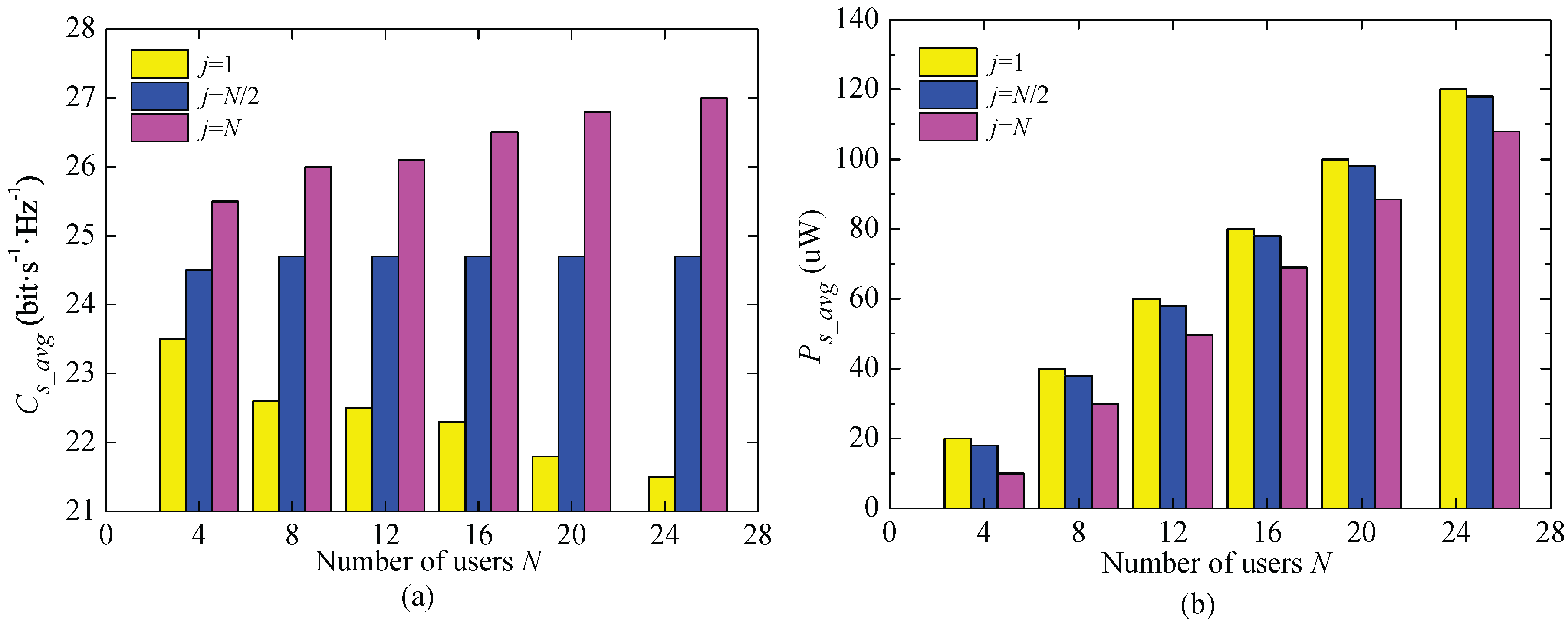
The impacts of the number of users on ECC and total collected energy achieved by INS2M are shown in
Figure 6. In fairness, the average channel power gain of the all users is uniform to
, namely
. It can be seen from
Figure 6a that ECC depends on both the number of users and the value of
j. Specifically, ECC will increase with the number of the users for a large
j, but will decrease for a small
j. This is because the situation with more users means poorest channel condition is worse than that of the case with fewer users. Thus, ECC will decrease with the increasing of users when
. On the contrary, ECC is proportional to the number of users when
, since the best channel condition is better than that of the case with fewer users. In addition, the total collected energy is taken into account. Obviously, for any
j, the larger the number of users, the higher the collected energy will be. Moreover, a smaller
j means the user with lower N-SNR will be selected to transmit the data, and the users with better N-SNR will perform the energy collection, which will result in more total collected energy as shown in
Figure 6b.
7. Conclusions
As an important component of modem communication systems, WSNs are used to collect, process and deliver information in particular locations by multi-hops. The whole network performance, however, is seriously affected by the cooperative work and the limited energy supply. Traditional sleeping mechanisms could reduce the network energy consumption partly, but cannot solve the problems of energy constraints fundamentally. Under this circumstance, synchronous wireless information and power transmission (SWIPT) system has been focused on in recent years, which can collect energy by radio frequency so as to provide long battery life for low-power devices. The problem of the balance between energy collection and information transmission is studied for SWIPT in this paper. Firstly, the information transmission model, the energy collecting model and the fading channel model are established, based on which IS2M, INS2M and IETSM are put forward. The users are sorted in ascending order according to SNR by IS2M. The balance between energy collection and data transmission can be achieved by selecting different ordinals. Considering that the users with poor channel environment may not be able to collect information in some special circumstances, normalized SNR (N-SNR) is adopted instead of SNR by a proposed modified mechanism known as INS2M to deal with the imbalance caused by low SNR users. IETSM is presented for the balanced information transmission for all users in the whole network. IETSM can adjust information transmission according to the average collected energy in order to improve the adaptability of the network. Simulations are performed comparing with the classical RR and ET mechanisms. The obtained results show that the proposed IS2M, INS2M and IETSM take both the energy collection and information transmission into account instead of best-effort strategy, so as to obtain a better performance of SWIPT by adjusting j or . Moreover, INS2M and IETSM are able to provide long-term proportional fairness in information transmission and energy collection. Future research will focus on how to optimize the various scheduling mechanisms to be deployed in practical WSNs.