Classification of K-Pop Dance Movements Based on Skeleton Information Obtained by a Kinect Sensor
Abstract
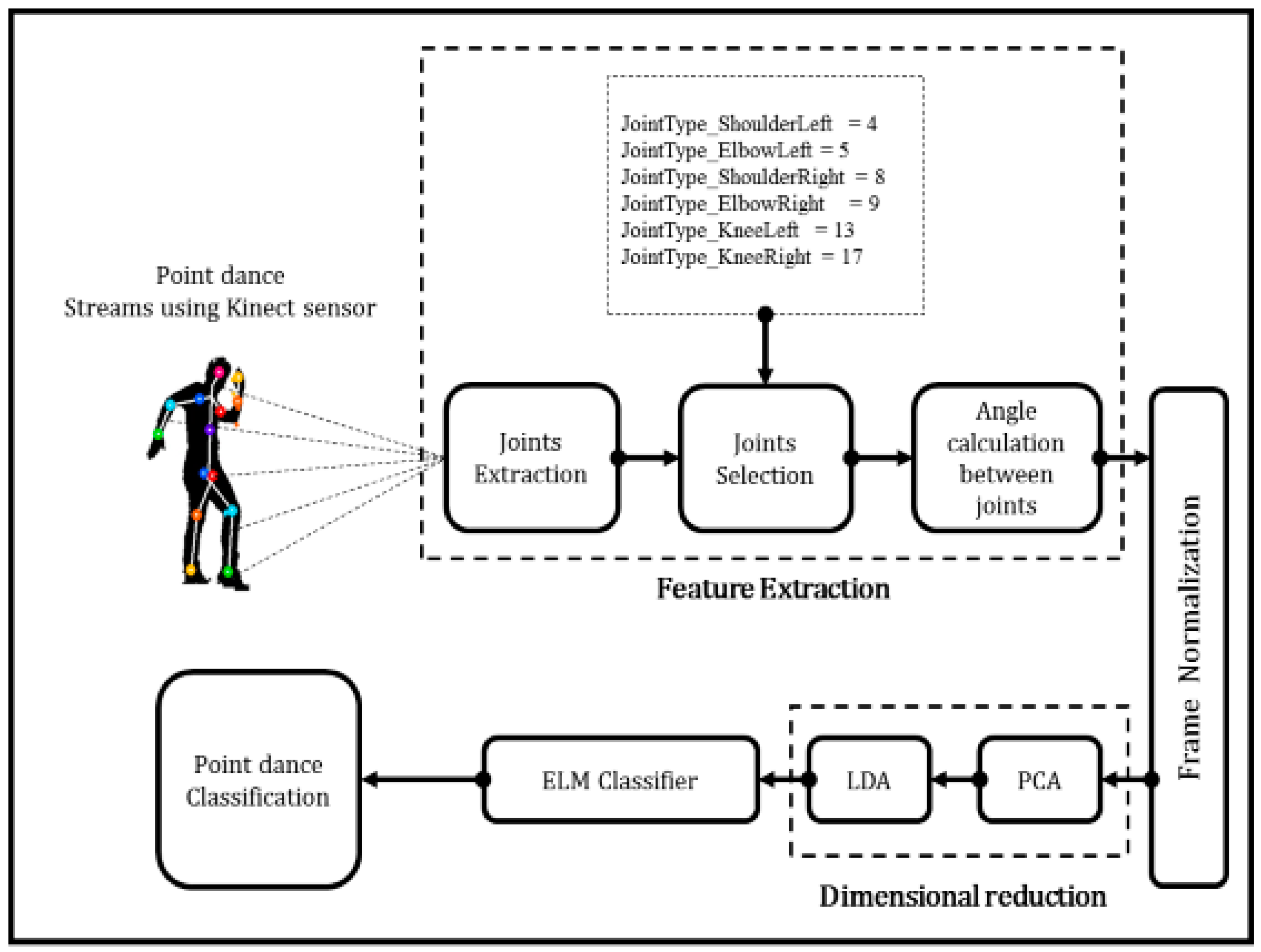
:1. Introduction
2. Dimensionality Reduction of Concatenated Vectors
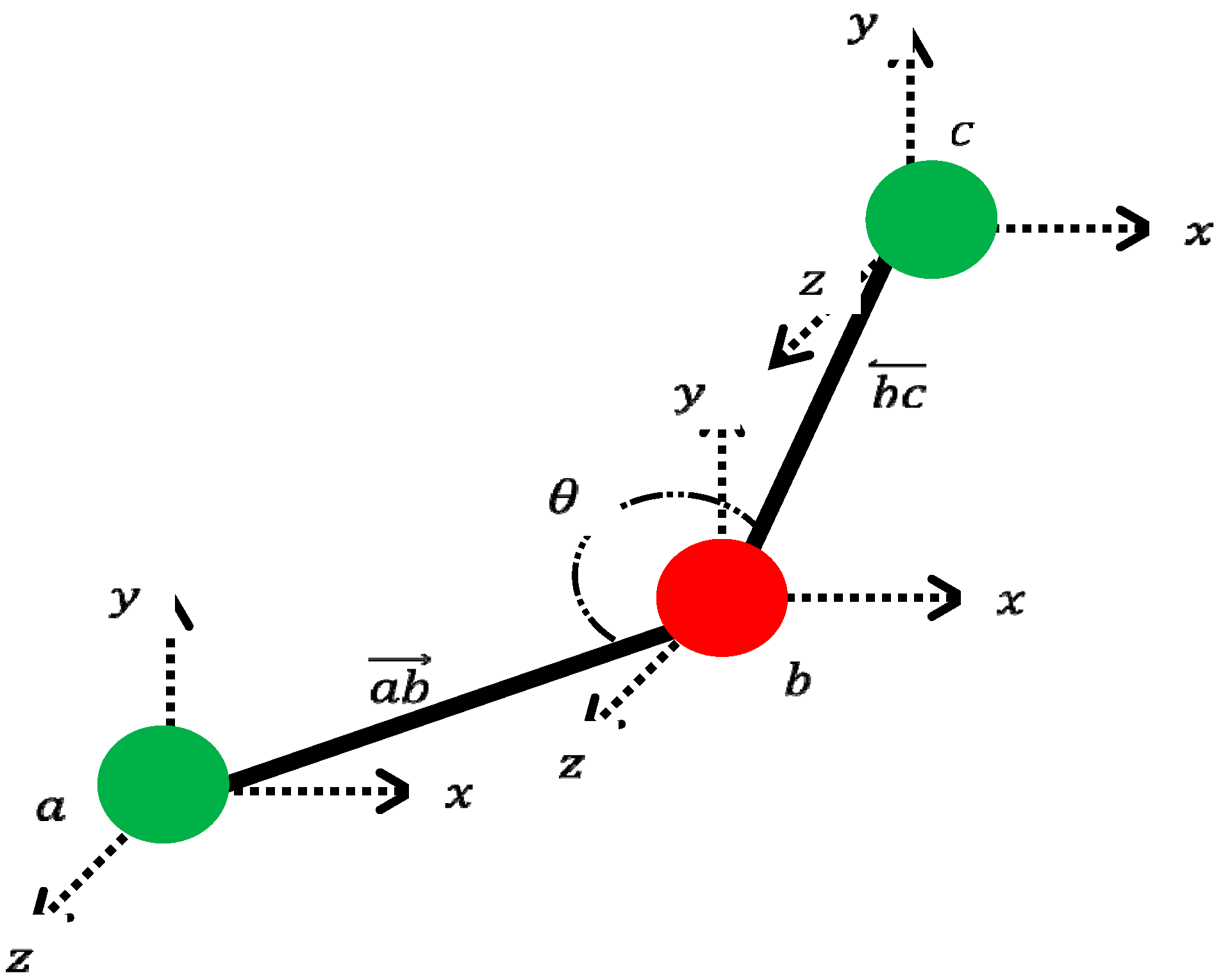
2.1. Generating Concatenated Vectors
2.2. Combination of PCA and LDA for Dimensional Reduction
3. Design of ReLU-Based ELMC
ELMC
4. Experimental Results
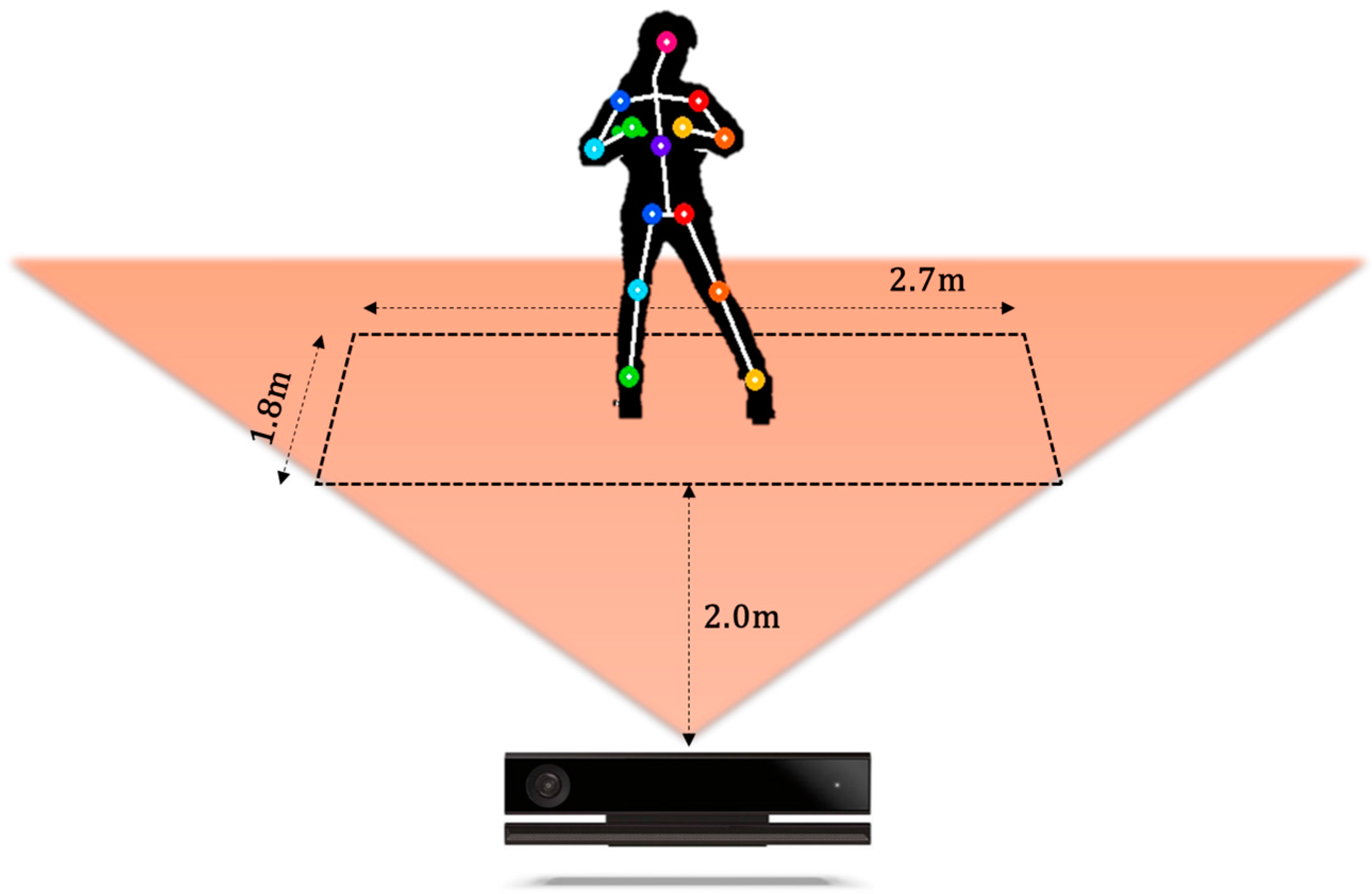
4.1. Construction of K-Pop Dance Database
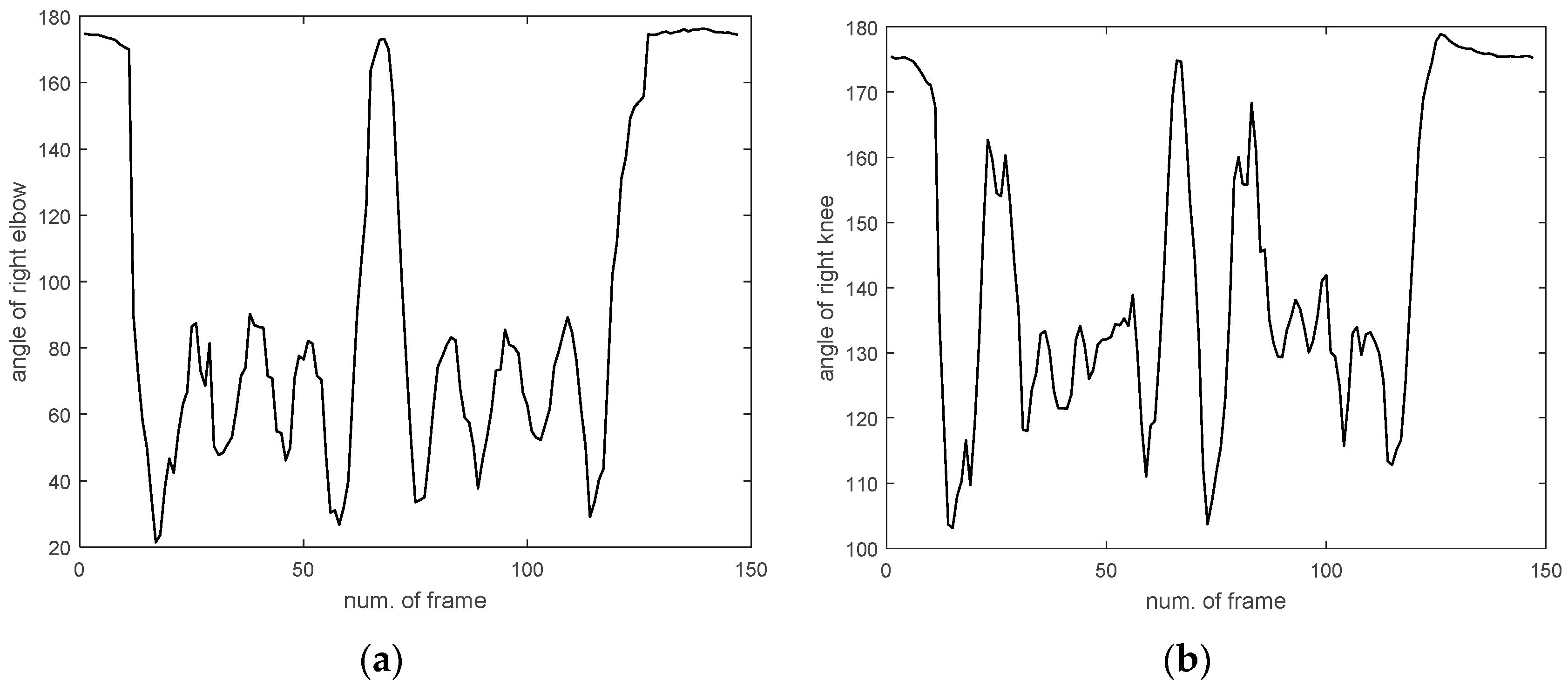
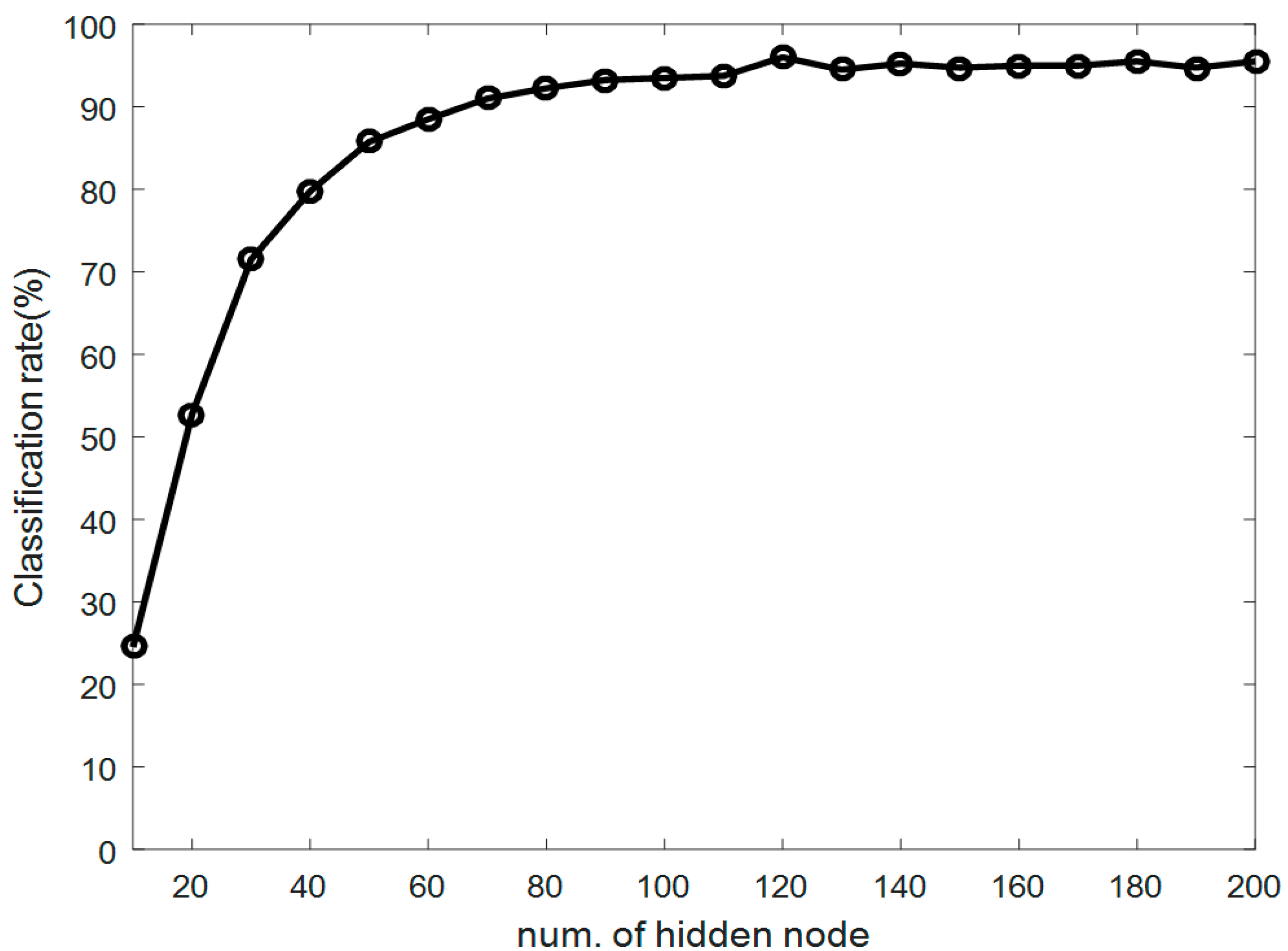
4.2. Experiments and Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Michal, B.; Konstantinos, N.P. Human gait recognition from motion capture data in signature poses. IET Biom. 2017, 6, 129–137. [Google Scholar]
- Daniel, P.B.; Jeffrey, M.S. Action Recognition by Time Series of Retinotopic Appearance and Motion Features. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 2250–2263. [Google Scholar]
- Eum, H.; Yoon, C.; Park, M. Continuous Human Action Recognition Using Depth-MHI-HOG and a Spotter Model. Sensors 2015, 15, 5197–5227. [Google Scholar] [CrossRef] [PubMed]
- Oscar, D.L.; Miguel, A.L. A survey on human activity recognition using wearable sensors. IEEE Commun. Surv. Tutor. 2013, 15, 1192–1209. [Google Scholar]
- Chun, Z.; Weihua, S. Realtime Recognition of Complex Human Daily Activities Using Human Motion and Location Data. IEEE Trans. Biomed. Eng. 2012, 59, 2422–2430. [Google Scholar]
- Yang, B.; Dong, H.; Saddik, A.E. Development of a Self-Calibrated Motion Capture System by Nonlinear Trilateration of Multiple Kinects v2. IEEE Sens. J. 2017, 17, 2481–2491. [Google Scholar] [CrossRef]
- Shuai, L.; Li, C.; Guo, X.; Prabhakaran, B.; Chai, J. Motion Capture with Ellipsoidal Skeleton Using Multiple Depth Cameras. IEEE Trans. Vis. Comput. Graph. 2017, 23, 1085–1098. [Google Scholar] [CrossRef] [PubMed]
- Alazrai, R.; Momani, M.; Daoud, M.I. Fall Detection for Elderly from Partially Observed Depth-Map Video Sequences Based on View-Invariant Human Activity Representation. Appl. Sci. 2017, 7, 316. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, L.; Leung, H.; Shum, H.P.H. Kinect Posture Reconstruction Based on a Local Mixture of Gaussian Process Models. IEEE Trans. Vis. Comput. Graph. 2016, 22, 2437–2450. [Google Scholar] [CrossRef] [PubMed]
- Du, Y.; Fu, Y.; Wang, L. Representation Learning of Temporal Dynamics for Skeleton-Based Action Recognition. IEEE Trans. Image Process. 2016, 25, 3010–3022. [Google Scholar] [CrossRef] [PubMed]
- Zhu, G.; Zhang, L.; Shen, P.; Song, J. An Online Continuous Human Action Recognition Algorithm Based on the Kinect Sensor. Sensors 2016, 16, 161. [Google Scholar] [CrossRef] [PubMed]
- Bonnet, V.; Venture, G. Fast Determination of the Planar Body Segment Inertial Parameters Using Affordable Sensors. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 23, 628–635. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.C.; Chen, C.W.; Cheng, W.H.; Chang, C.H.; Lai, J.H.; Wu, J.L. Real-Time Human Movement Retrieval and Assessment With Kinect Sensor. IEEE Trans. Cybern. 2015, 45, 742–753. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Yu, Y.; Zhou, Y.; Du, S. Leveraging Two Kinect Sensors for Accurate Full-Body Motion Capture. Sensors 2015, 15, 24297–24317. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Fu, Y. Contour Model-Based Hand-Gesture Recognition Using the Kinect Sensor. IEEE Trans. Circuits Syst. Video Technol. 2014, 24, 1935–1944. [Google Scholar] [CrossRef]
- Saha, S.; Konar, A. Topomorphological approach to automatic posture recognition in ballet dance. IET Image Process. 2015, 9, 1002–1011. [Google Scholar] [CrossRef]
- Muneesawang, P.; Khan, N.M.; Kyan, M.; Elder, R.B.; Dong, N.; Sun, G.; Li, H.; Zhong, L.; Guan, L. A Machine Intelligence Approach to Virtual Ballet Training. IEEE MultiMedia 2015, 22, 80–92. [Google Scholar] [CrossRef]
- Han, T.; Yao, H.; Xu, C.; Sun, X.; Zhang, Y.; Corso, J.J. Dancelets mining for video recommendation based on dance styles. IEEE Trans. Multimedia 2017, 19, 712–724. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Z.; Zhou, L.; Leung, H.; Chan, A.B. Martial Arts, Dancing and Sports dataset: A challenging stereo and multi-view dataset for 3D human pose estimation. Image Vis. Comput. 2017, 61, 22–39. [Google Scholar] [CrossRef]
- Ramadijanti, N.; Fahrul, H.F.; Pangestu, D.M. Basic dance pose applications using kinect technology. In Proceedings of the 2016 International Conference on Knowledge Creation and Intelligent Computing (KCIC), Manado, Indonesia, 15–17 November 2016; pp. 194–200. [Google Scholar]
- Hegarini, E.; Dharmayanti; Syakur, A. Indonesian traditional dance motion capture documentation. In Proceedings of the 2016 2nd International Conference on Science and Technology-Computer (ICST), Yogyakarta, Indonesia, 27–28 October 2016; pp. 108–111. [Google Scholar]
- Saha, S.; Lahiri, R.; Konar, A.; Banerjee, B.; Nagar, A.K. Human skeleton matching for e-learning of dance using a probabilistic neural network. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 1754–1761. [Google Scholar]
- Wen, J.; Li, X.; She, J.; Park, S.; Cheung, M. Visual background recommendation for dance performances using dancer-shared images. In Proceedings of the 2016 IEEE International Conference on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Chengdu, China, 15–18 December 2016; pp. 521–527. [Google Scholar]
- Karavarsamis, S.; Ververidis, D.; Chantas, G.; Nikolopoulos, S.; Kompatsiaris, Y. Classifying salsa dance steps from skeletal poses. In Proceedings of the 2016 14th International Workshop on Content-Based Multimedia Indexing (CBMI), Bucharest, Romania, 15–17 June 2016; pp. 1–6. [Google Scholar]
- Nikola, J.; Bennett, G. Stillness, breath and the spine—Dance performance enhancement catalysed by the interplay between 3D motion capture technology in a collaborative improvisational choreographic process. Perform. Enhanc. Health 2016, 4, 58–66. [Google Scholar] [CrossRef]
- Volchenkova, D.; Bläsing, B. Spatio-temporal analysis of kinematic signals in classical ballet. J. Comput. Sci. 2013, 4, 285–292. [Google Scholar] [CrossRef]
- Turk, M.; Pentland, A. Face recognition using eigenface. In Proceedings of the 1991 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Maui, HI, USA, 3–6 June 1991; pp. 586–591. [Google Scholar]
- Belhumeur, P.N.; Hespanha, J.P.; Kriegman, D.J. Eigenfaces vs. Fisherfaces: recognition using class specific linear projection. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 711–720. [Google Scholar] [CrossRef]
- An, L.; Bhanu, B. Image super-resolution by extreme learning machine. In Proceedings of the 2012 19th IEEE International Conference on Image Processing, Orlando, FL, USA, 30 September–3 October 2012; pp. 2209–2212. [Google Scholar]
- Saavedra-Moreno, B.; Salcedo-Sanz, S.; Carro-Calvo, L.; Gascón-Moreno, J.; Jiménez-Fernández, S.; Prieto, L. Very fast training neural-computation techniques for real measure-correlate-predict wind operations in wind farms. J. Wind Eng. Ind. Aerodyn. 2013, 116, 49–60. [Google Scholar] [CrossRef]
- Chen, X.; Dong, Z.Y.; Meng, K.; Xu, Y.; Wong, K.P.; Ngan, H.W. Electricity Price Forecasting with Extreme Learning Machine and Bootstrapping. IEEE Trans. Power Syst. 2012, 27, 2055–2062. [Google Scholar] [CrossRef]
- Lee, H.J.; Kim, S.J.; Kim, K.; Park, M.S.; Kim, S.K.; Park, J.H.; Oh, S.R. Online remote control of a robotic hand configurations using sEMG signals on a forearm. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics, Karon Beach, Phuket, Thailand, 7–11 December 2011; pp. 2243–2244. [Google Scholar]
- Minhas, R.; Mohammed, A.A.; Wu, Q.M.J. Incremental Learning in Human Action Recognition Based on Snippets. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 1529–1541. [Google Scholar] [CrossRef]
- Xie, Z.; Xu, K.; Liu, L.; Xiong, Y. 3D Shape Segmentation and Labeling via Extreme Learning Machine. Comput. Graph. Forum 2014, 33, 85–95. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, Q.; Wei, Z.; Ma, S. Traffic sign recognition based on weighted ELM and AdaBoost. Electron. Lett. 2016, 52, 1988–1990. [Google Scholar] [CrossRef]
- Oneto, L.; Bisio, F.; Cambria, E.; Anguita, D. Statistical Learning Theory and ELM for Big Social Data Analysis. IEEE Comput. Intell. Mag. 2016, 11, 45–55. [Google Scholar] [CrossRef]
- Yang, Y.; Wu, Q.M.J. Extreme Learning Machine with Subnetwork Hidden Nodes for Regression and Classification. IEEE Trans. Cybern. 2016, 46, 2885–2898. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Li, R.; Zhao, C.; Wang, P. Robust signal recognition algorithm based on machine learning in heterogeneous networks. J. Syst. Eng. Electron. 2016, 27, 333–342. [Google Scholar] [CrossRef]
- Cambuim, L.F.S.; Macieira, R.M.; Neto, F.M.P.; Barros, E.; Ludermir, T.B.; Zanchettin, C. An efficient static gesture recognizer embedded system based on ELM pattern recognition algorithm. J. Syst. Archit. 2016, 68, 1–16. [Google Scholar] [CrossRef]
- Iosifidis, A.; Tefas, A.; Pitas, I. Minimum Class Variance Extreme Learning Machine for Human Action Recognition. IEEE Trans. Circuits Syst. Video Technol. 2013, 23, 1968–1979. [Google Scholar] [CrossRef]





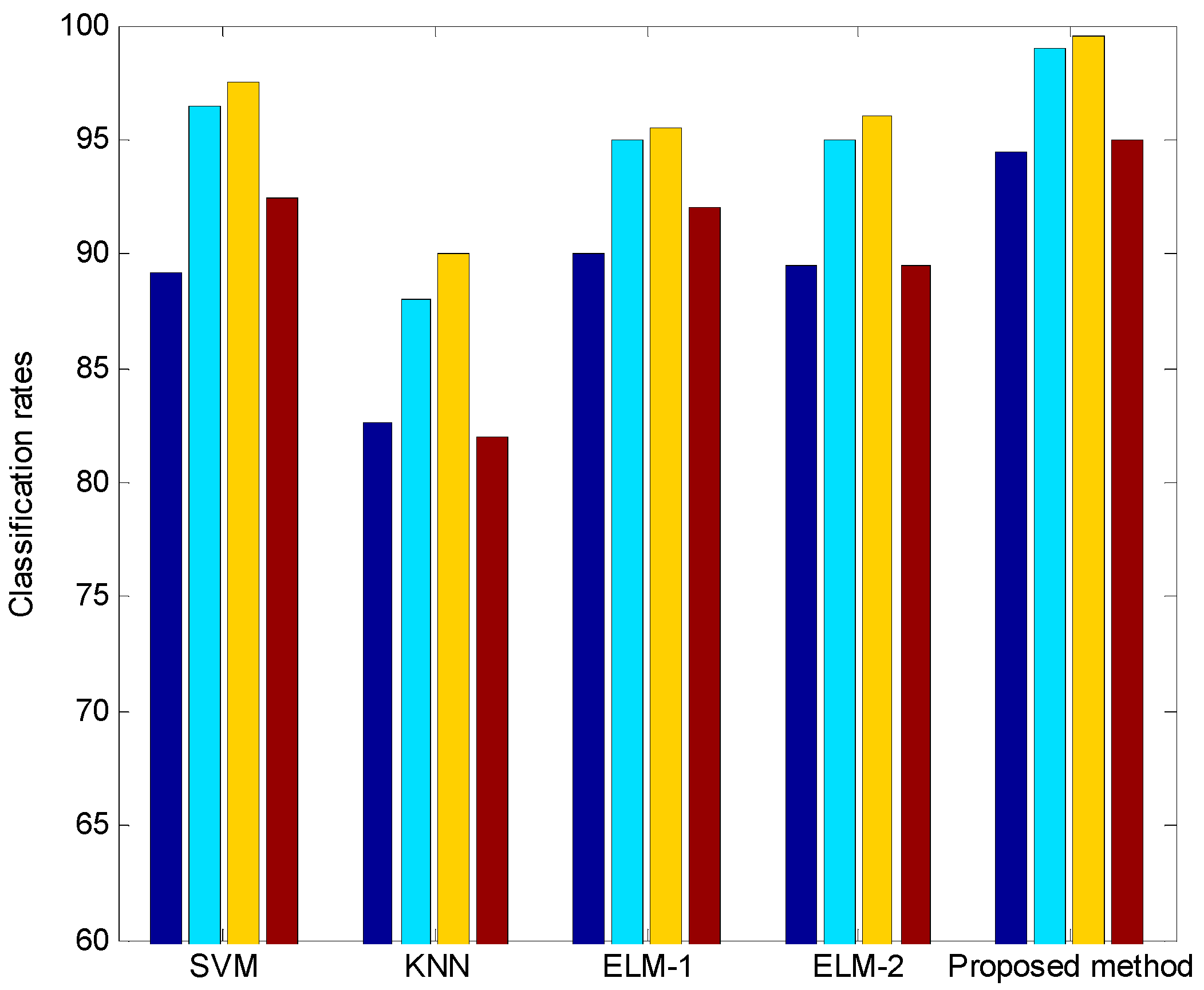
| Method | Dimensionality Reduction | Classification Rate (%) |
|---|---|---|
| KNN | — | 77.75 |
| PCA + LDA | 92.25 | |
| SVM | — | 84.50 |
| PCA + LDA | 92.75 | |
| ELM-1 (sigmoid) | — | 43.00 |
| PCA + LDA | 84.25 | |
| Proposed method | — | 71.00 |
| PCA + LDA | 96.50 |
| Method | Dimensionality Reduction | Classification Rate (%) |
|---|---|---|
| KNN | — | 53.81 |
| PCA + LDA | 85.66 | |
| SVM | — | 87.00 |
| PCA + LDA | 93.92 | |
| ELM-1 (sigmoid) | — | 50.37 |
| PCA + LDA | 93.12 | |
| ELM-2 (hard-limit) | 50.99 | |
| PCA + LDA | 92.5 | |
| Proposed method | — | 77.61 |
| PCA + LDA | 97.00 |
| Method | Dimensionality Reduction | Classification Rate (%) |
|---|---|---|
| KNN | — | 88.12 |
| PCA + LDA | 92.50 | |
| SVM | — | 62.75 |
| PCA + LDA | 84.37 | |
| ELM-1 (sigmoid) | — | 49.88 |
| PCA + LDA | 91.12 | |
| ELM-2 (hard-limit) | 48.63 | |
| PCA + LDA | 90.75 | |
| ReLU-based ELMC | — | 75.49 |
| PCA + LDA | 95.62 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.; Kim, D.-H.; Kwak, K.-C. Classification of K-Pop Dance Movements Based on Skeleton Information Obtained by a Kinect Sensor. Sensors 2017, 17, 1261. https://doi.org/10.3390/s17061261
Kim D, Kim D-H, Kwak K-C. Classification of K-Pop Dance Movements Based on Skeleton Information Obtained by a Kinect Sensor. Sensors. 2017; 17(6):1261. https://doi.org/10.3390/s17061261
Chicago/Turabian StyleKim, Dohyung, Dong-Hyeon Kim, and Keun-Chang Kwak. 2017. "Classification of K-Pop Dance Movements Based on Skeleton Information Obtained by a Kinect Sensor" Sensors 17, no. 6: 1261. https://doi.org/10.3390/s17061261
APA StyleKim, D., Kim, D.-H., & Kwak, K.-C. (2017). Classification of K-Pop Dance Movements Based on Skeleton Information Obtained by a Kinect Sensor. Sensors, 17(6), 1261. https://doi.org/10.3390/s17061261







