Distributed Piezoelectric Sensor System for Damage Identification in Structures Subjected to Temperature Changes
Abstract
:1. Introduction
2. Theoretical Background
2.1. Principal Component Analysis
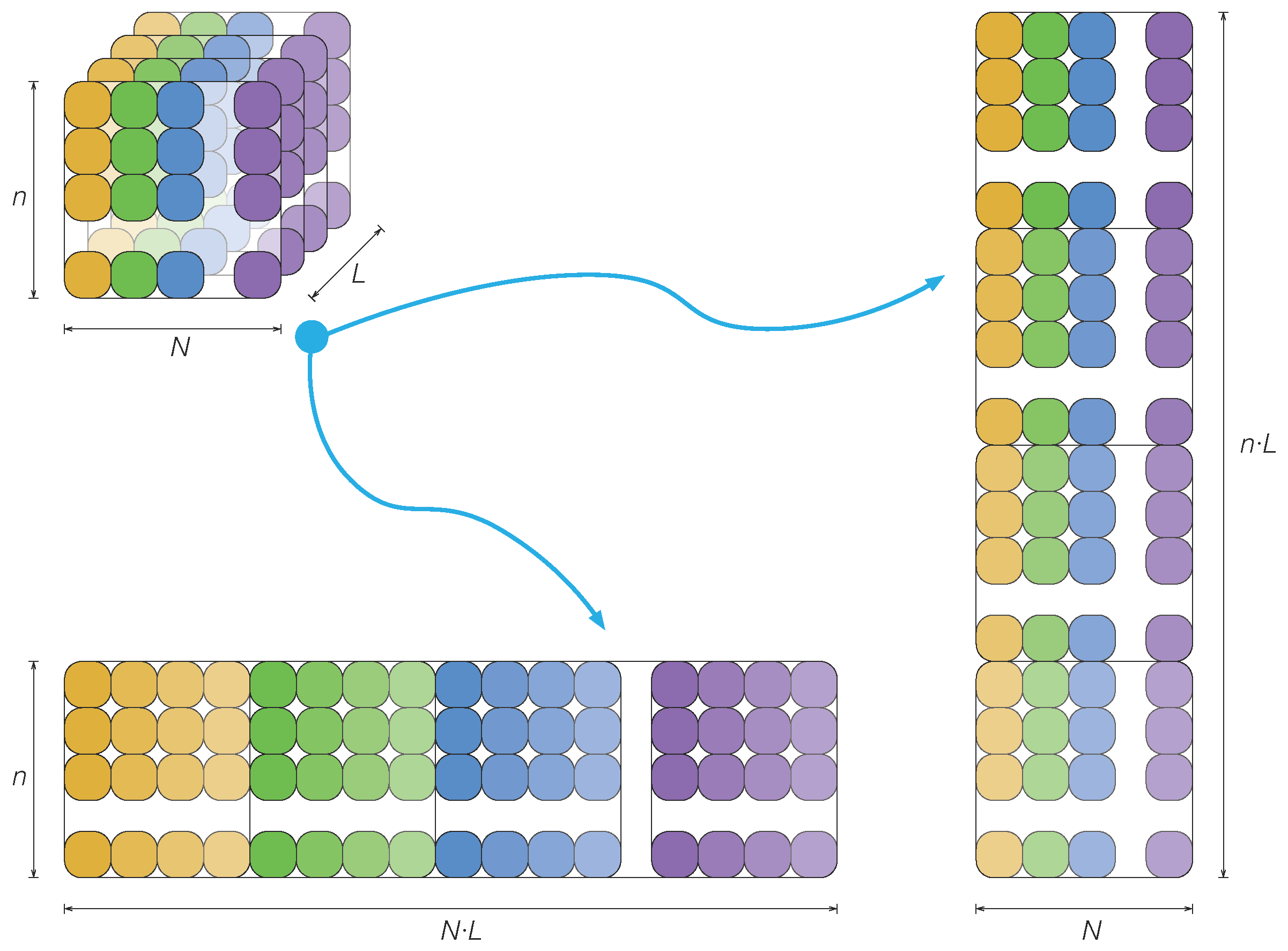
2.1.1. PCA Modeling
2.1.2. Normalization: Group Scaling
2.1.3. Projection of New Data onto the PCA Model
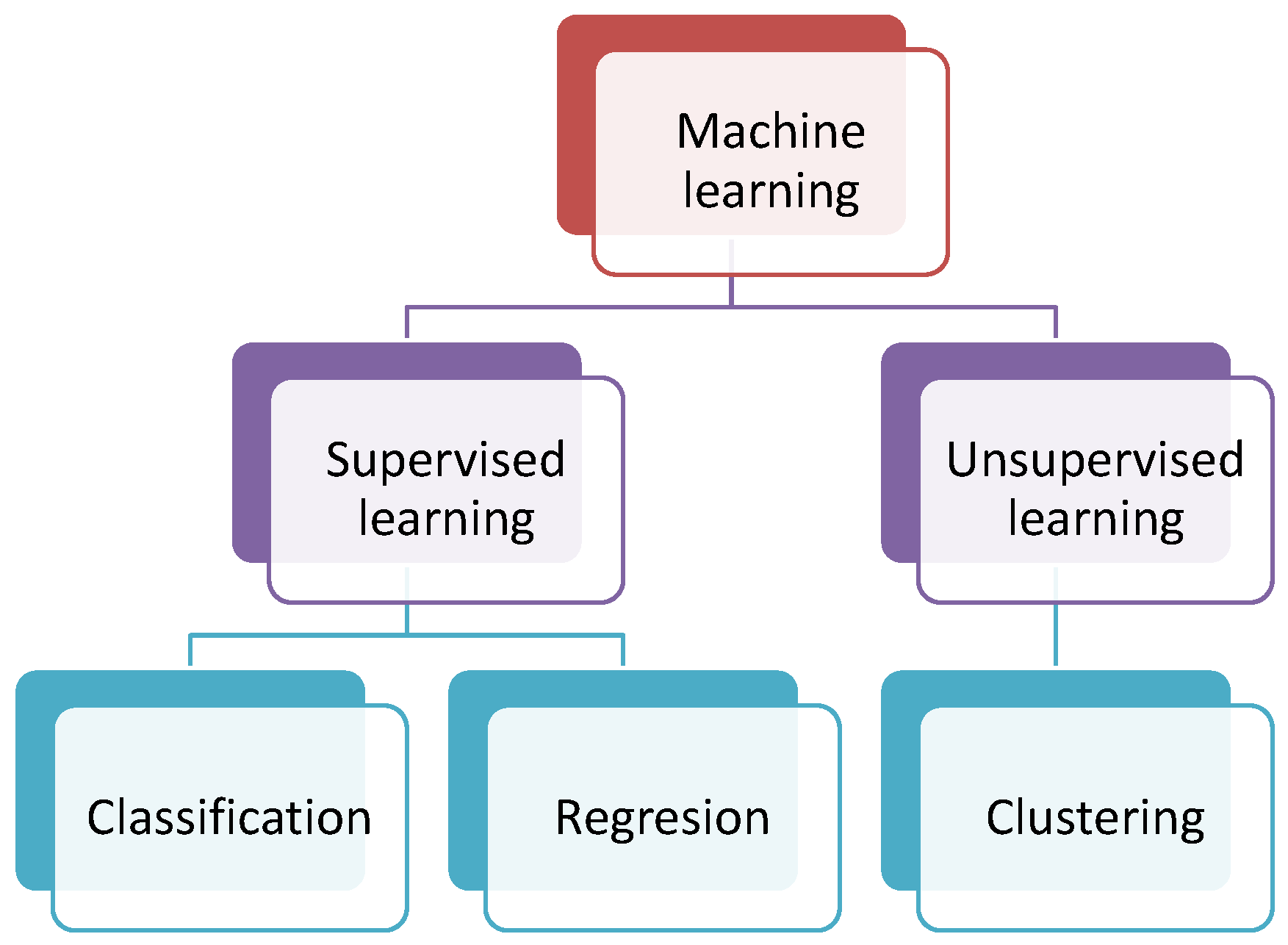
2.2. Machine Learning
2.2.1. Nearest Neighbor Pattern Classification
- Fine k-NN: a nearest neighbor classifier that makes finely-detailed distinctions between classes with the number of neighbors set to one.
- Medium k-NN: a nearest neighbor classifier with fewer distinctions than a fine k-NN with the number of neighbors set to 10.
- Coarse k-NN: a nearest neighbor between classes, with the number of neighbors set to 100.
- Cosine k-NN: a nearest neighbor classifier that uses the cosine distance metric. The cosine distance between two vectors u and v is defined as:that is, one minus the ratio of the inner product of u and v over the product of the norms of u and v.
- Cubic k-NN: a nearest neighbor classifier that uses the cubic distance metric. The cubic distance between two n-dimensional vectors u and v is defined as:
- Weighted k-NN: a nearest neighbor classifier that uses distance weighting. The weighted Euclidean distance between two n-dimensional vectors u and v is defined as:where and .
2.2.2. Decision Trees
- Compared with other machine learning methods, trees are simple and easy to understand.
- Decision trees use different methods and can be combined to obtain a single prediction.
- The combination of different trees usually produces better results.
- Because of its simplicity, more elaborated methods can produce better results in classification and regression tasks.
2.2.3. Support Vector Machines
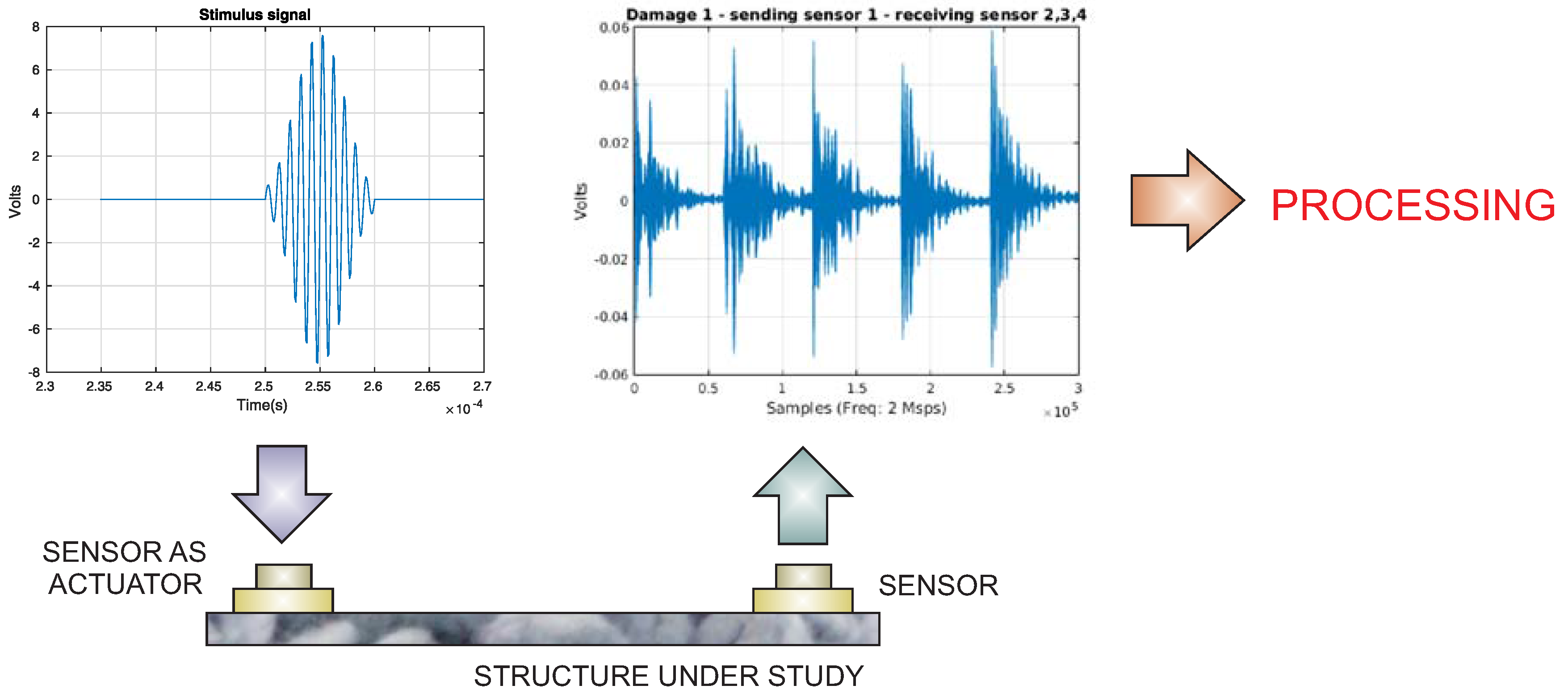
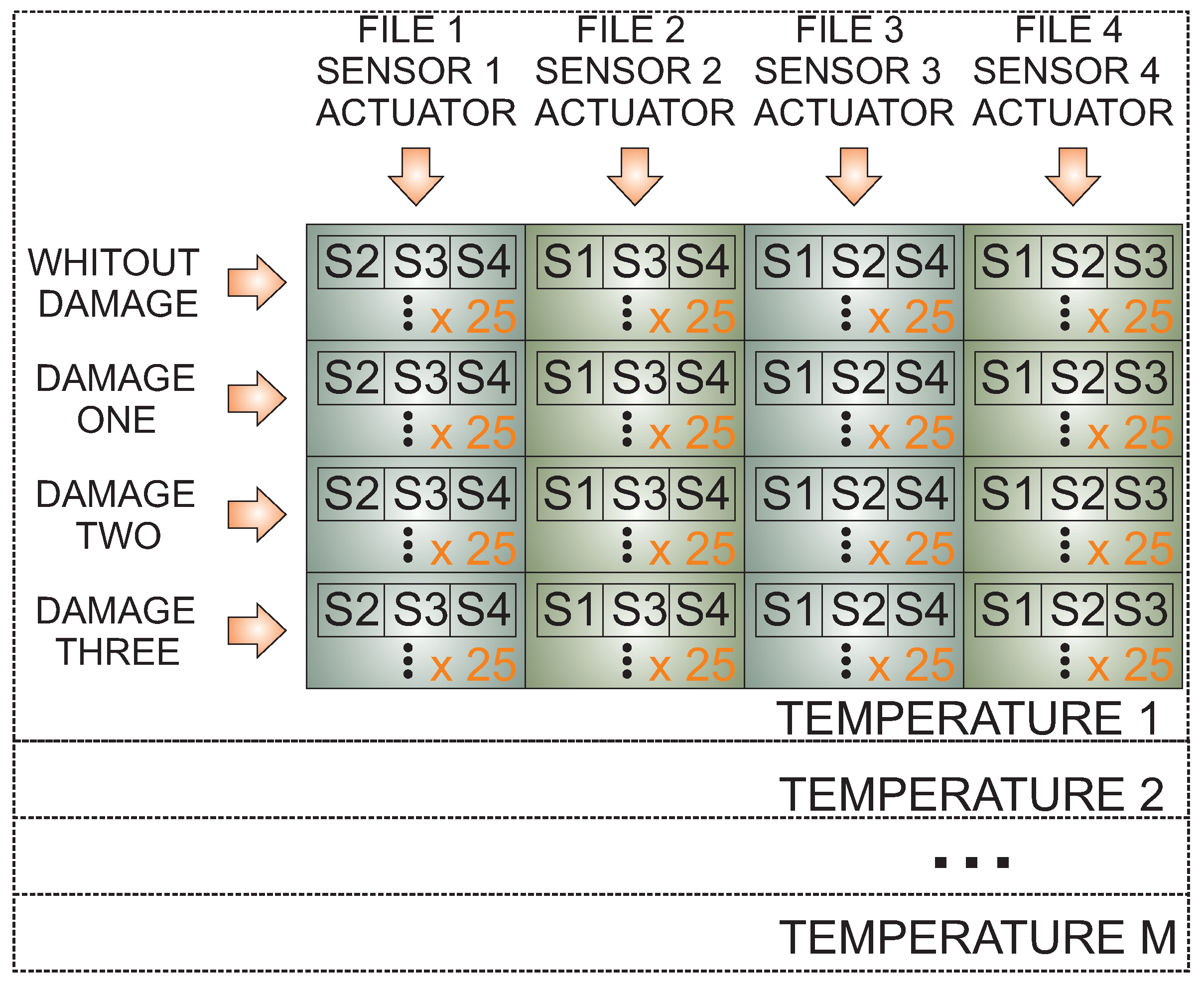
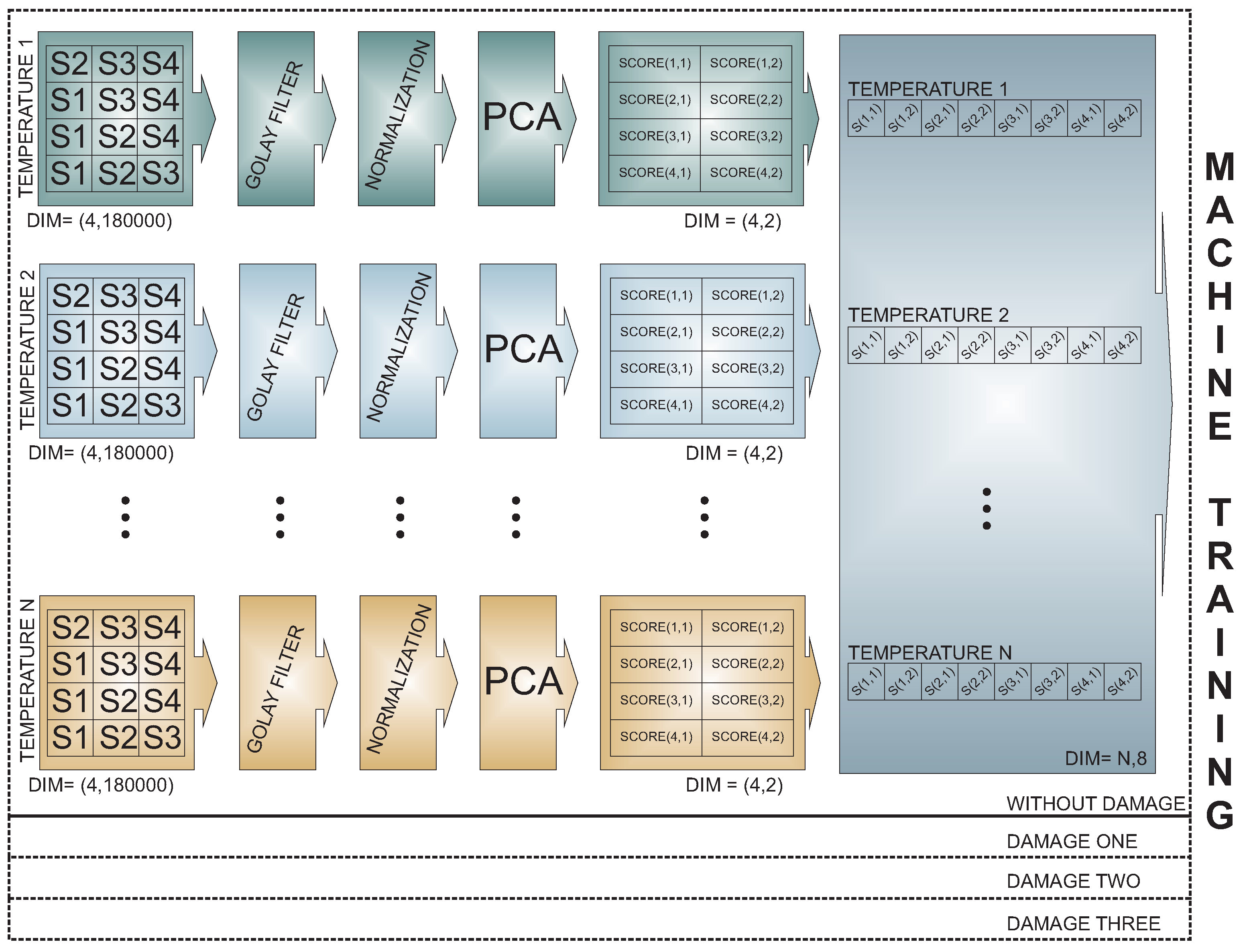
3. Damage Classification Methodology
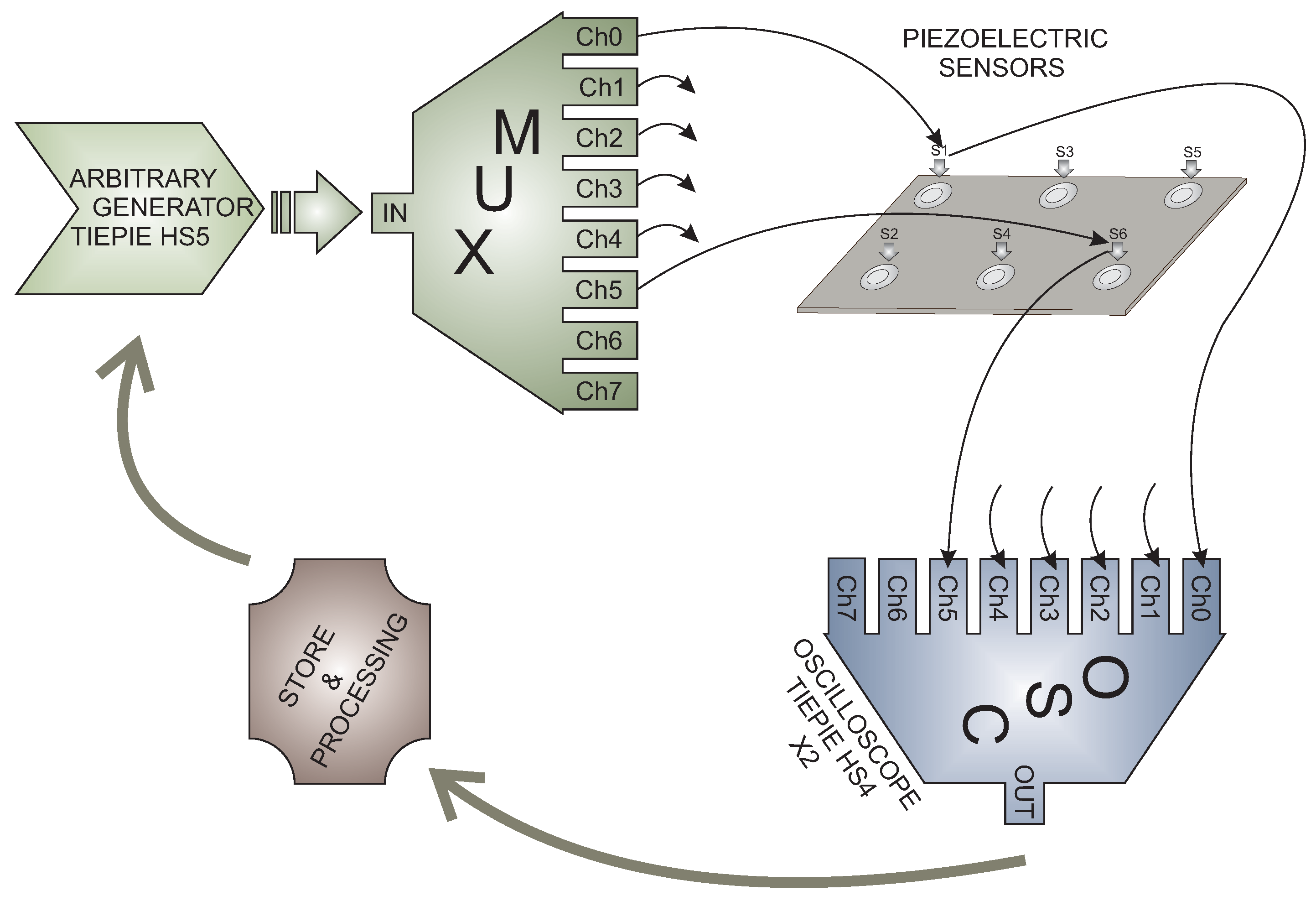
Data Acquisition System
4. Experimental Setup and Results
- (i)
- an aluminum plate with four piezoelectric transducers; and
- (ii)
- a composite plate of carbon fiber polymer with six piezoelectric transducers.
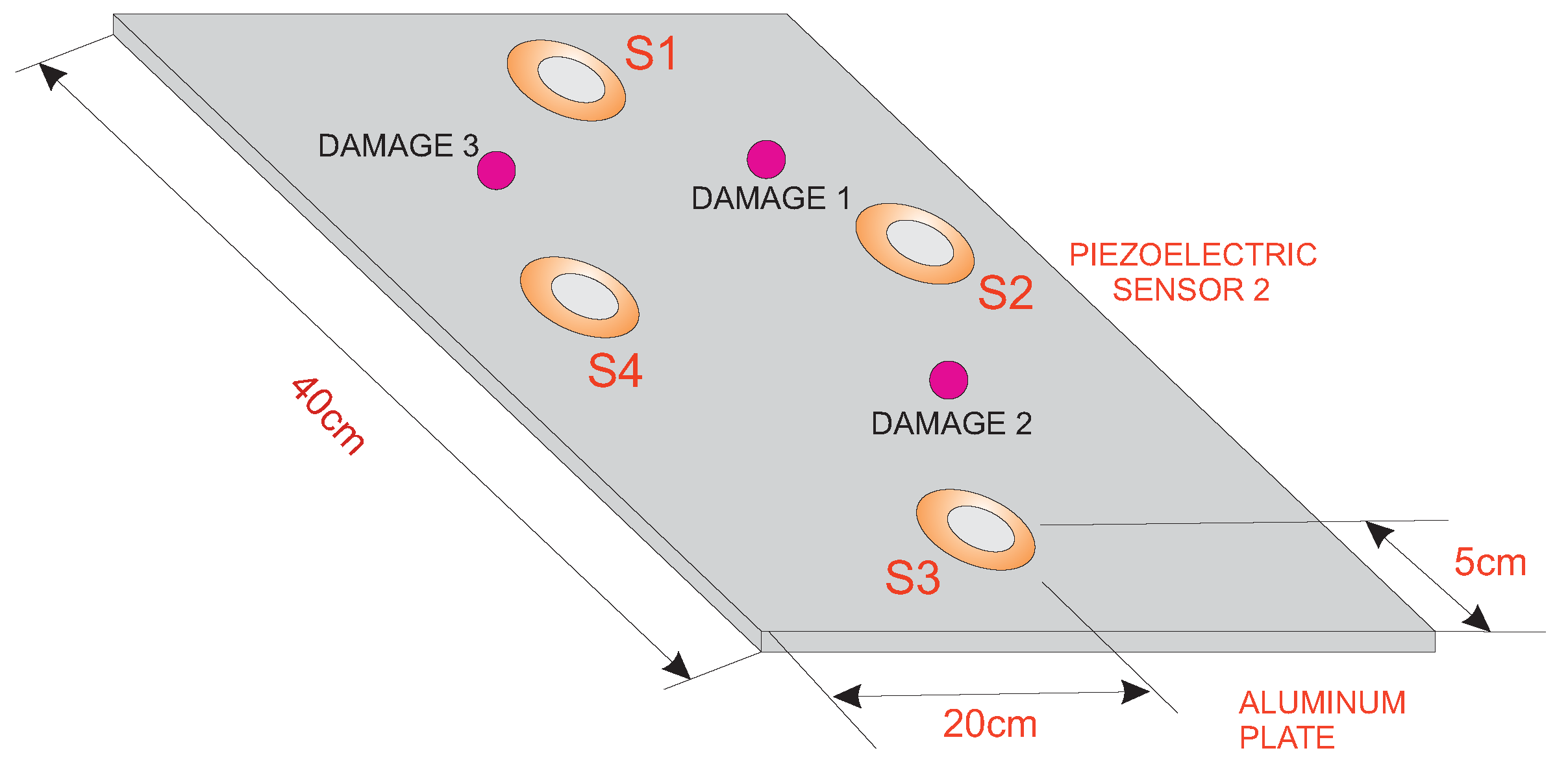
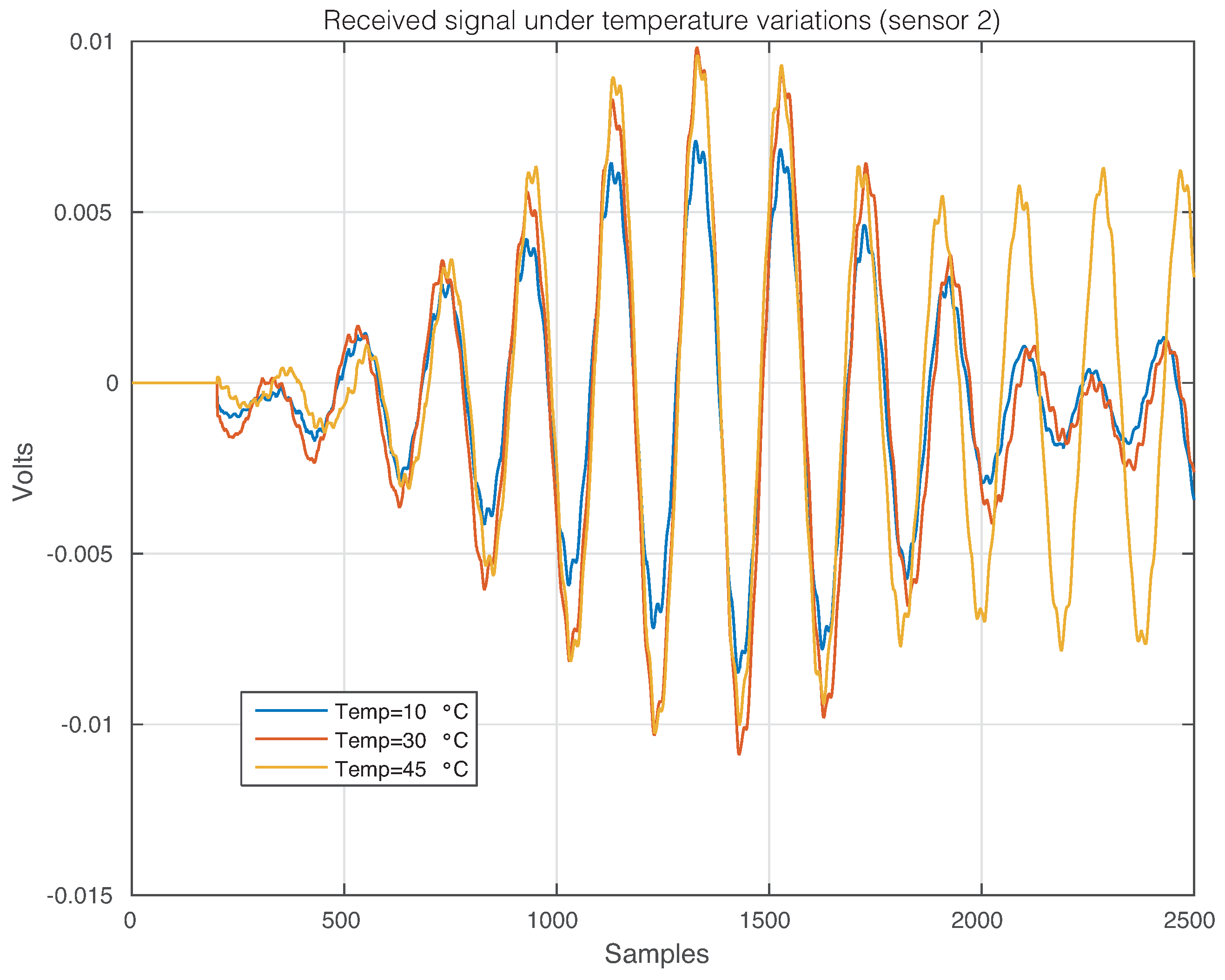
4.1. First Specimen: Aluminum Plate
- and
- .
- no damage (healthy or pristine structure);
- Damage 1;
- Damage 2; and
- Damage 3.
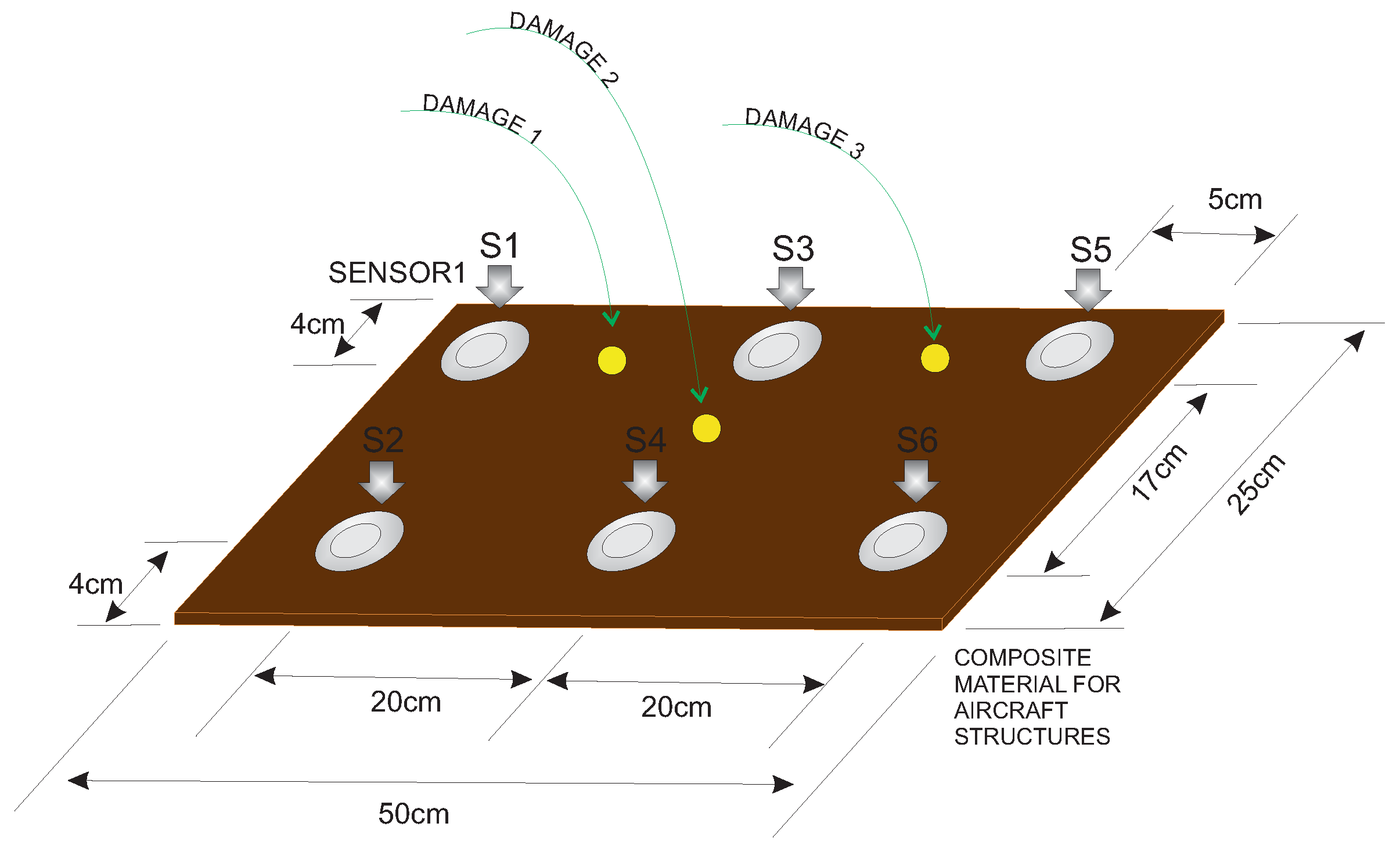
4.2. Second Specimen: Carbon Fiber Plate
- and
- .
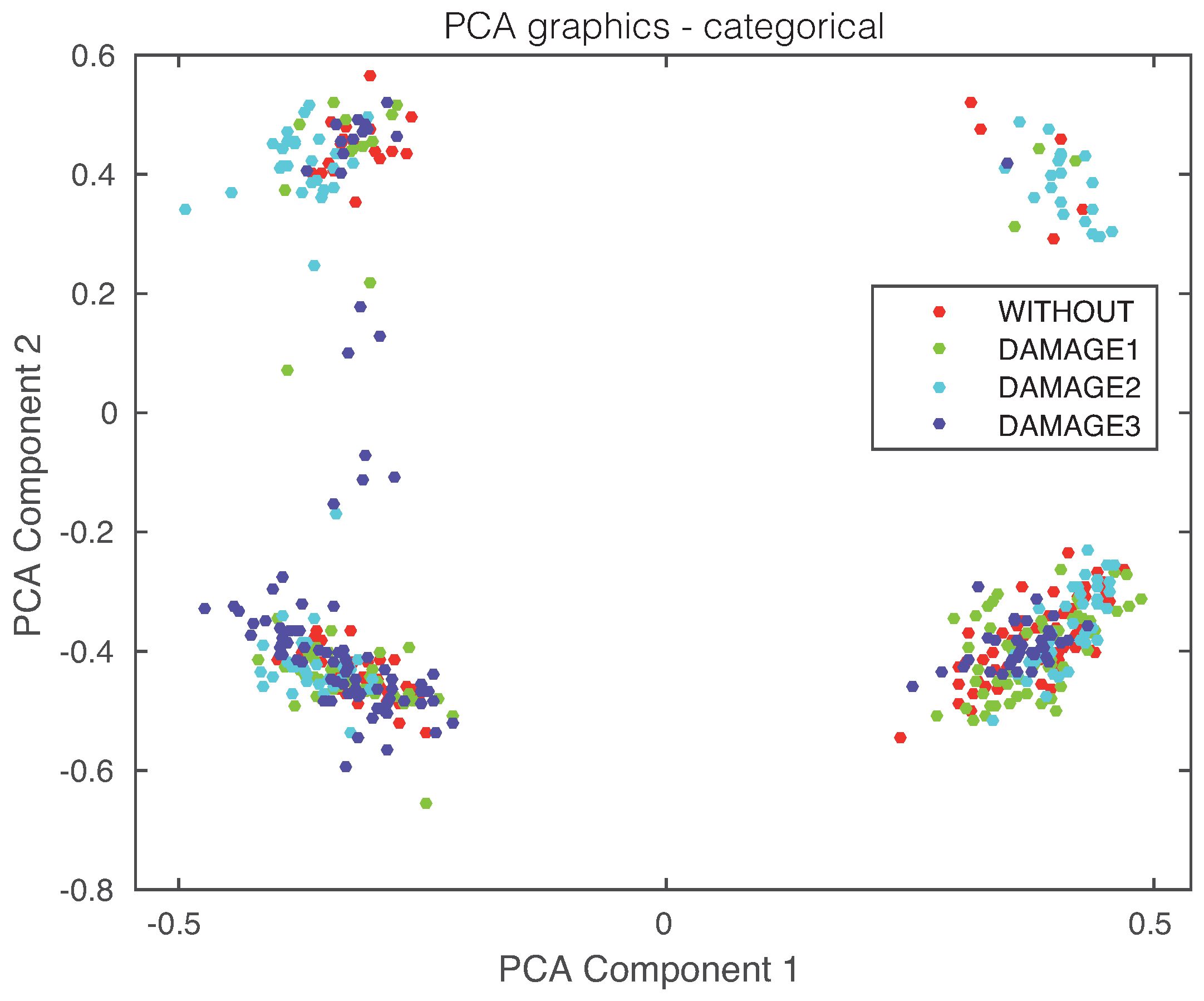
- no damage (healthy or pristine structure);
- Damage 1;
- Damage 2; and
- Damage 3.
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sohn, H. Effects of environmental and operational variability on structural health monitoring. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2007, 365, 539–560. [Google Scholar] [CrossRef] [PubMed]
- Anaya, M.; Tibaduiza, D.; Torres, M.; Pozo, F.; Ruiz, M.; Mujica, L.; Rodellar, J.; Fritzen, C. Data-driven methodology to detect and classify structural changes under temperature variations. Smart Mater. Struct. 2014, 23, 1–15. [Google Scholar] [CrossRef]
- Chakraborty, D.; Kovvali, N.; Zhang, J.J.; Papandreou-Suppappola, A.; Chattopadhyay, A. Adaptive learning for damage classification in structural health monitoring. In Proceedings of the 2009 Conference Record of the Forty-Third Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–4 November 2009; pp. 1678–1682. [Google Scholar]
- Yan, A.M.; Kerschen, G.; De Boe, P.; Golinval, J.C. Structural damage diagnosis under varying environmental conditions—Part I: A linear analysis. Mech. Syst. Signal Process. 2005, 19, 847–864. [Google Scholar] [CrossRef]
- Baptista, F.G.; Budoya, D.E.; de Almeida, V.A.D.; Ulson, J.A.C. An experimental study on the effect of temperature on piezoelectric sensors for impedance-based structural health monitoring. Sensors 2014, 14, 1208–1227. [Google Scholar] [CrossRef] [PubMed]
- Anaya, M.; Tibaduiza, D.A.; Pozo, F. Detection and classification of structural changes using artificial immune systems and fuzzy clustering. Int. J. Bio-Inspir. Comput. 2017, 9, 35–52. [Google Scholar] [CrossRef]
- Torres-Arredondo, M.A.; Buethe, I.; Tibaduiza, D.A.; Rodellar, J.; Fritzen, C.P. Damage detection and classification in pipework using acousto-ultrasonics and non-linear data-driven modelling. J. Civ. Struct. Health Monit. 2013, 3, 297–306. [Google Scholar] [CrossRef]
- Torres-Arredondo, M.A.; Sierra-Pérez, J.; Cabanes, G. An optimal baseline selection methodology for data-driven damage detection and temperature compensation in acousto-ultrasonics. Smart Mater. Struct. 2016, 25, 055034. [Google Scholar] [CrossRef]
- Leichtle, T.; Geiß, C.; Wurm, M.; Lakes, T.; Taubenböck, H. Unsupervised change detection in VHR remote sensing imagery—An object-based clustering approach in a dynamic urban environment. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 15–27. [Google Scholar] [CrossRef]
- Anaya, M.; Tibaduiza, D.; Pozo, F. Artificial Immune System (AIS) for Damage Detection Under Variable Temperature Conditions. In Proceedings of the European Workshop on Structural Health Monitoring, Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- Vanlanduit, S.; Parloo, E.; Cauberghe, B.; Guillaume, P.; Verboven, P. A robust singular value decomposition for damage detection under changing operating conditions and structural uncertainties. J. Sound Vib. 2005, 284, 1033–1050. [Google Scholar] [CrossRef]
- Deraemaeker, A.; Reynders, E.; Roeck, G.D.; Kullaa, J. Vibration-based structural health monitoring using output-only measurements under changing environment. Mech. Syst. Signal Process. 2008, 22, 34–56. [Google Scholar] [CrossRef]
- Balmès, É.; Basseville, M.; Bourquin, F.; Mevel, L.; Nasser, H.; Treyssede, F. Merging sensor data from multiple temperature scenarios for vibration monitoring of civil structures. Struct. Health Monit. 2008, 7, 129–142. [Google Scholar] [CrossRef]
- Buren, K.V.; Reilly, J.; Neal, K.; Edwards, H.; Hemez, F. Guaranteeing robustness of structural condition monitoring to environmental variability. J. Sound Vib. 2017, 386, 134–148. [Google Scholar] [CrossRef]
- Sohn, H.; Worden, K.; Farrar, C.R. Statistical Damage Classification Under Changing Environmental and Operational Conditions. J. Intell. Mater. Syst. Struct. 2002, 13, 561–574. [Google Scholar] [CrossRef]
- Figueiredo, E.; Park, G.; Farrar, C.R.; Worden, K.; Figueiras, J. Machine learning algorithms for damage detection under operational and environmental variability. Struct. Health Monit. 2011, 10, 559–572. [Google Scholar] [CrossRef]
- Worden, K.; Manson, G. The application of machine learning to structural health monitoring. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2007, 365, 515–537. [Google Scholar] [CrossRef] [PubMed]
- Worden, K.; Manson, G.; Allman, D. Experimental validation of a structural health monitoring methodology: Part I. Novelty detection on a laboratory structure. J. Sound Vib. 2003, 259, 323–343. [Google Scholar] [CrossRef]
- Manson, G.; Worden, K.; Allman, D. Experimental validation of a structural health monitoring methodology: Part II. Novelty detection on a Gnat aircraft. J. Sound Vib. 2003, 259, 345–363. [Google Scholar] [CrossRef]
- Roy, S.; Chang, F.K.; Lee, S.J.; Pollock, P.; Janapati, V. A novel machine-learning approach for structural state identification using ultrasonic guided waves. In Safety, Reliability, Risk and Life-Cycle Performance of Structures and Infrastructures; CRC Press: Boca Raton, FL, USA, 2013; pp. 321–328. [Google Scholar]
- Tibaduiza, D.; Mujica, L.; Anaya, M.; Rodellar, J.; Güemes, A. Independent component analysis for detecting damages on aircraft wing skeleton. In Proceedings of the 5th European Conference on Structural Control, Genoa, Italy, 18–20 June 2012. [Google Scholar]
- Tibaduiza, D.; Anaya, M.; Forero, E.; Castro, R.; Pozo, F. A Sensor Fault Detection Methodology applied to Piezoelectric Active Systems in Structural Health Monitoring Applications. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2016; Volume 138, p. 012016. [Google Scholar]
- Vitola, J.; Pozo, F.; Tibaduiza, D.A.; Anaya, M. A Sensor Data Fusion System Based on k-Nearest Neighbor Pattern Classification for Structural Health Monitoring Applications. Sensors 2017, 17, 417. [Google Scholar] [CrossRef] [PubMed]
- Jolliffe, I. Principal Component Analysis; Wiley Online Library: New York, NY, USA, 2002. [Google Scholar]
- Anaya, M.; Tibaduiza, D.A.; Pozo, F. A bioinspired methodology based on an artificial immune system for damage detection in structural health monitoring. Shock Vib. 2015, 2015, 648097. [Google Scholar] [CrossRef]
- Tibaduiza, D.A. Design and Validation of a Structural Health Monitoring System for Aeronautical Structures. Ph.D. Thesis, Universitat Politècnica de Catalunya, Barcelona, Spain, 2012. [Google Scholar]
- Jeong, D.H.; Ziemkiewicz, C.; Fisher, B.; Ribarsky, W.; Chang, R. iPCA: An Interactive System for PCA-Based Visual Analytics; Computer Graphics Forum; Wiley Online Library: Oxford, UK, 2009; Volume 28, pp. 767–774. [Google Scholar]
- Westerhuis, J.A.; Kourti, T.; MacGregor, J.F. Comparing alternative approaches for multivariate statistical analysis of batch process data. J. Chemom. 1999, 13, 397–413. [Google Scholar] [CrossRef]
- Pozo, F.; Vidal, Y. Wind turbine fault detection through principal component analysis and statistical hypothesis testing. Energies 2015, 9, 3. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ciang, C.C.; Lee, J.R.; Bang, H.J. Structural health monitoring for a wind turbine system: A review of damage detection methods. Meas. Sci. Technol. 2008, 19, 122001. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Yang, J.; Sun, Z.; Chen, Y. Fault Detection Using the Clustering-kNN Rule for Gas Sensor Arrays. Sensors 2016, 16, 2069. [Google Scholar] [CrossRef] [PubMed]
- Dhanabal, S.; Chandramathi, S. A review of various k-nearest neighbor query processing techniques. Int. J. Comput. Appl. 2011, 31, 14–22. [Google Scholar]
- Johnson, J.; Yadav, A. Weak and Electromagnetic Interactions. In Proceedings of the International Conference on ICT for Sustainable Development (ICT4SD), Panaji, Goa, India, 1–2 July 2016. [Google Scholar]
- MathWorks. Statistics and Machine Learning Toolbox for Matlab; MathWorks: Natick, MA, USA, 2015. [Google Scholar]
- Deng, Z.; Zhu, X.; Cheng, D.; Zong, M.; Zhang, S. Efficient kNN classification algorithm for big data. Neurocomputing 2016, 195, 143–148. [Google Scholar] [CrossRef]
- Oh, S.; Byon, Y.J.; Yeo, H. Improvement of search strategy with k-nearest neighbors approach for traffic state prediction. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1146–1156. [Google Scholar] [CrossRef]
- Sutton, C. Chapter Classification and Regression Trees, Bagging, and Boosting. In Handbook of Statistics; Elsevier: Amsterdam, The Netherlands, 2005; pp. 11–26. [Google Scholar]
- Quinlan, J. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Shmilovici, A. Support Vector Machines. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer: Boston, MA, USA, 2005; pp. 257–276. [Google Scholar]
- Tibaduiza, D.A.; Mujica, L.E.; Rodellar, J. Comparison of several methods for damage localization using indices and contributions based on PCA. J. Phys. Conf. Ser. 2011, 305, 012013. [Google Scholar] [CrossRef]
- Torres-Arredondo, M.A.; Tibaduiza, D.A.; McGugan, M.; Toftegaard, H.; Borum, K.K.; Mujica, L.E.; Rodellar, J.; Fritzen, C.P. Multivariate data-driven modelling and pattern recognition for damage detection and identification for acoustic emission and acousto-ultrasonics. Smart Mater. Struct. 2013, 22, 105023. [Google Scholar] [CrossRef]
- Yu, L.; Leckey, C.A. Lamb wave-based quantitative crack detection using a focusing array algorithm. J. Intell. Mater. Syst. Struct. 2013, 24, 1138–1152. [Google Scholar] [CrossRef]
- Neto, R.M.F.; Steffen, V.; Rade, D.A.; Gallo, C.A. System for Structural Health Monitoring based on piezoelectric sensors/actuators. In Proceedings of the Power Electronics Conference (COBEP), Natal, Brazil, 11–15 September 2011; pp. 365–371. [Google Scholar]
- Lanza di Scalea, F.; Salamone, S. Temperature effects in ultrasonic Lamb wave structural health monitoring systems. J. Acoust. Soc. Am. 2008, 124, 161–174. [Google Scholar] [CrossRef] [PubMed]
- Ha, S.; Lonkar, K.; Mittal, A.; Chang, F.K. Adhesive Layer Effects on PZT-induced Lamb Waves at Elevated Temperatures. Struct. Health Monit. 2010, 9, 247–256. [Google Scholar] [CrossRef]
- Mujica, L.; Ruiz, M.; Pozo, F.; Rodellar, J.; Güemes, A. A structural damage detection indicator based on principal component analysis and statistical hypothesis testing. Smart Mater. Struct. 2013, 23, 025014. [Google Scholar] [CrossRef]
- Pozo, F.; Arruga, I.; Mujica, L.E.; Ruiz, M.; Podivilova, E. Detection of structural changes through principal component analysis and multivariate statistical inference. Struct. Health Monit. 2016, 15, 127–142. [Google Scholar] [CrossRef]
- Mujica, L.; Rodellar, J.; Fernandez, A.; Guemes, A. Q-statistic and T2-statistic PCA-based measures for damage assessment in structures. Struct. Health Monit. 2010, 10, 539–553. [Google Scholar] [CrossRef]
- Odgaard, P.F.; Lin, B.; Jorgensen, S.B. Observer and data-driven-model-based fault detection in power plant coal mills. IEEE Trans. Energy Convers. 2008, 23, 659–668. [Google Scholar] [CrossRef]






| Machine Name | Healthy | Damage 1 | Damage 2 | Damage 3 |
|---|---|---|---|---|
| Medium Tree | 66% | 76% | 70% | 56% |
| Simple Tree | 64% | 60% | 30% | 58% |
| Complex Tree | 72% | 76% | 58% | 56% |
| Linear SMV | 70% | 60% | 26% | 60% |
| Quadratic SVM | 78% | 70% | 56% | 70% |
| Cubic SVM | 86% | 68% | 66% | 72% |
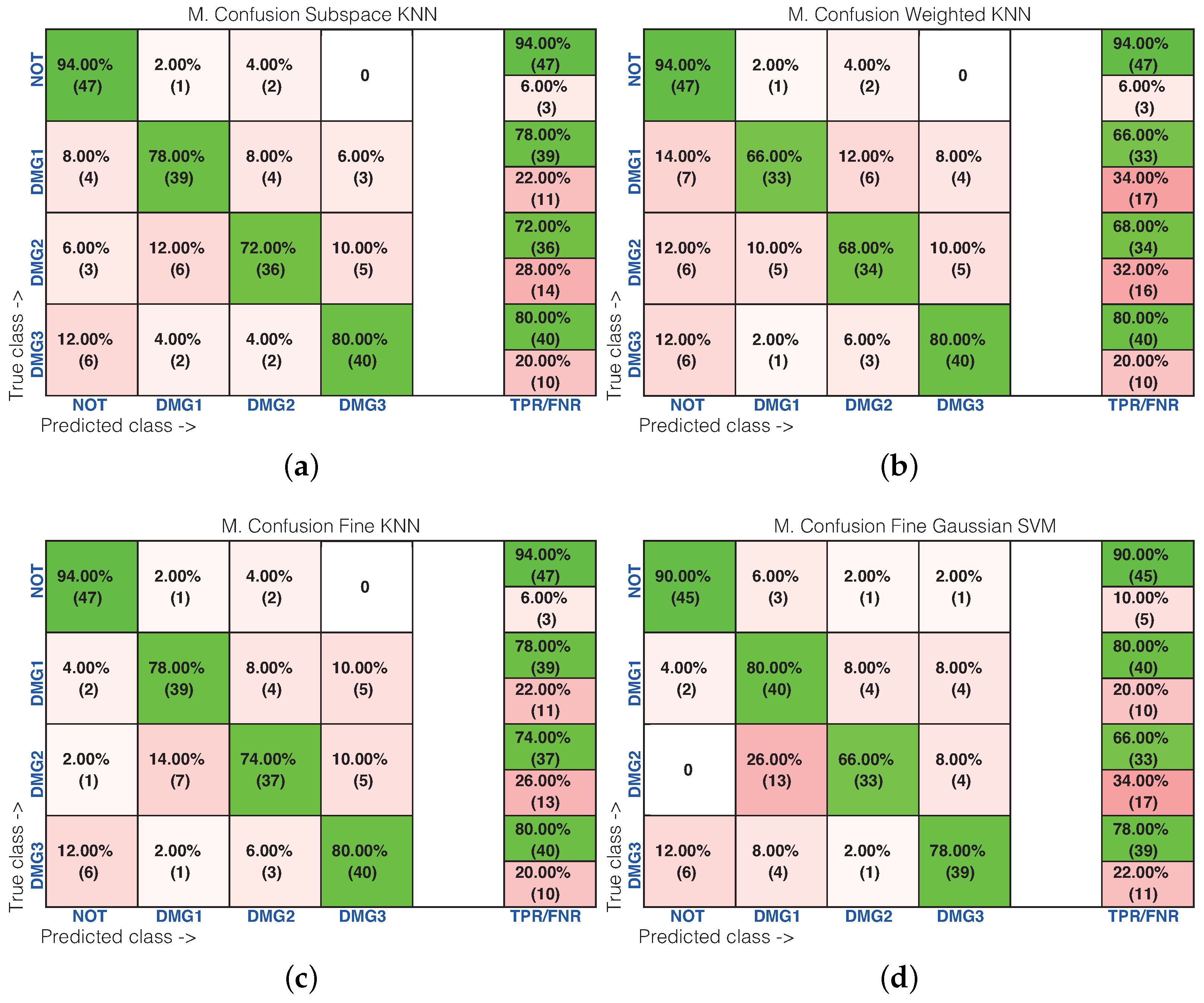
| Fine Gaussian SVM | 90% | 80% | 66% | 78% |
| Medium Gaussian SVM | 76% | 80% | 56% | 74% |
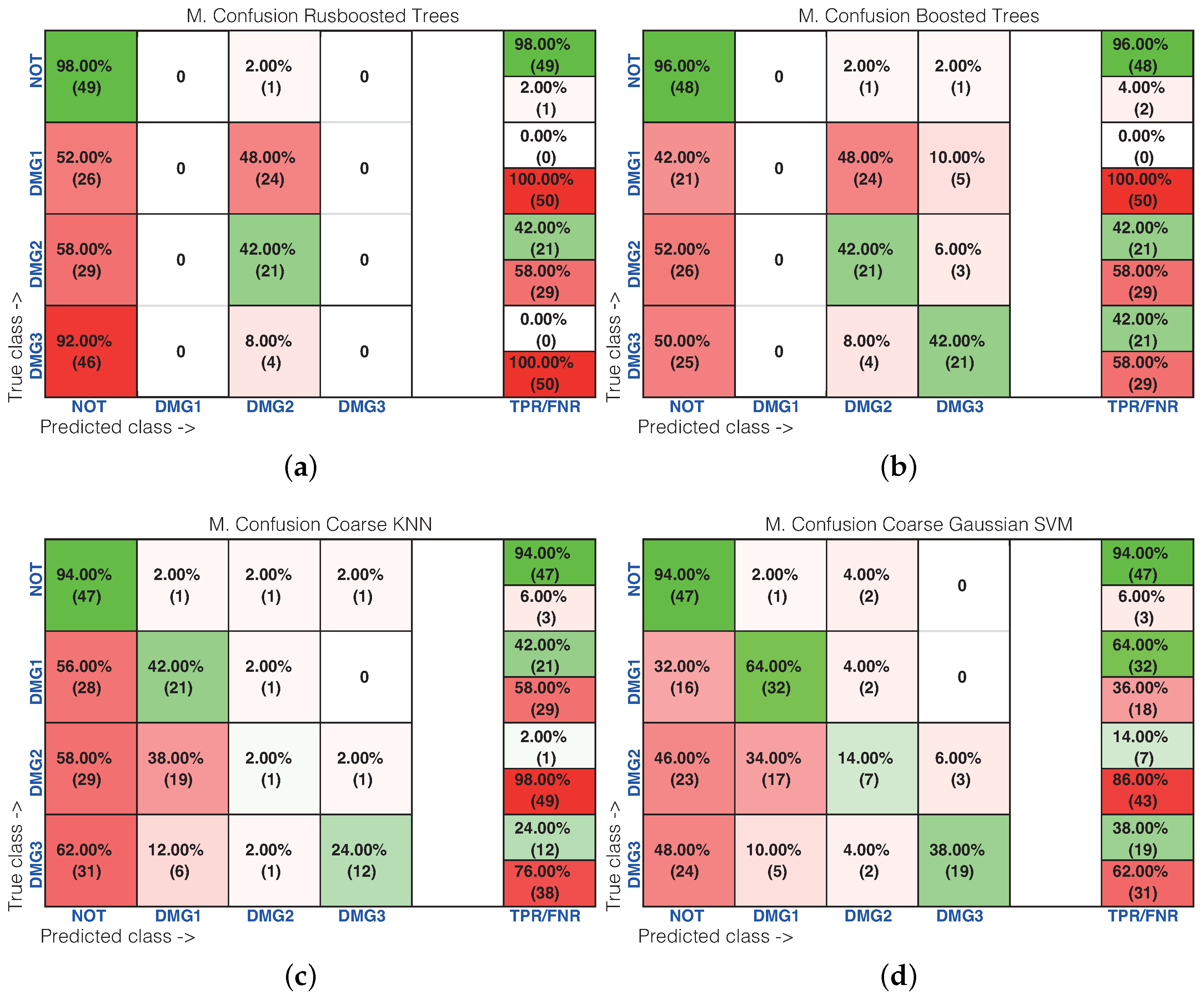
| Coarse Gaussian SVM | 94% | 64% | 14% | 38% |
| Fine k-NN | 94% | 78% | 74% | 80% |
| Medium k-NN | 80% | 62% | 64% | 74% |
| Coarse k-NN | 94% | 42% | 2% | 24% |
| Cosine k-NN | 84% | 58% | 78% | 72% |
| Cubic k-NN | 80% | 64% | 62% | 76% |
| Weighted k-NN | 94% | 66% | 68% | 80% |
| Boosted Trees | 96% | 0% | 42% | 42% |
| Bagged Trees | 84% | 70% | 66% | 78% |
| Subspace Discriminant | 56% | 44% | 32% | 46% |
| Subspace k-NN | 94% | 78% | 72% | 80% |
| Rusboosted Trees | 98% | 0% | 42% | 0% |
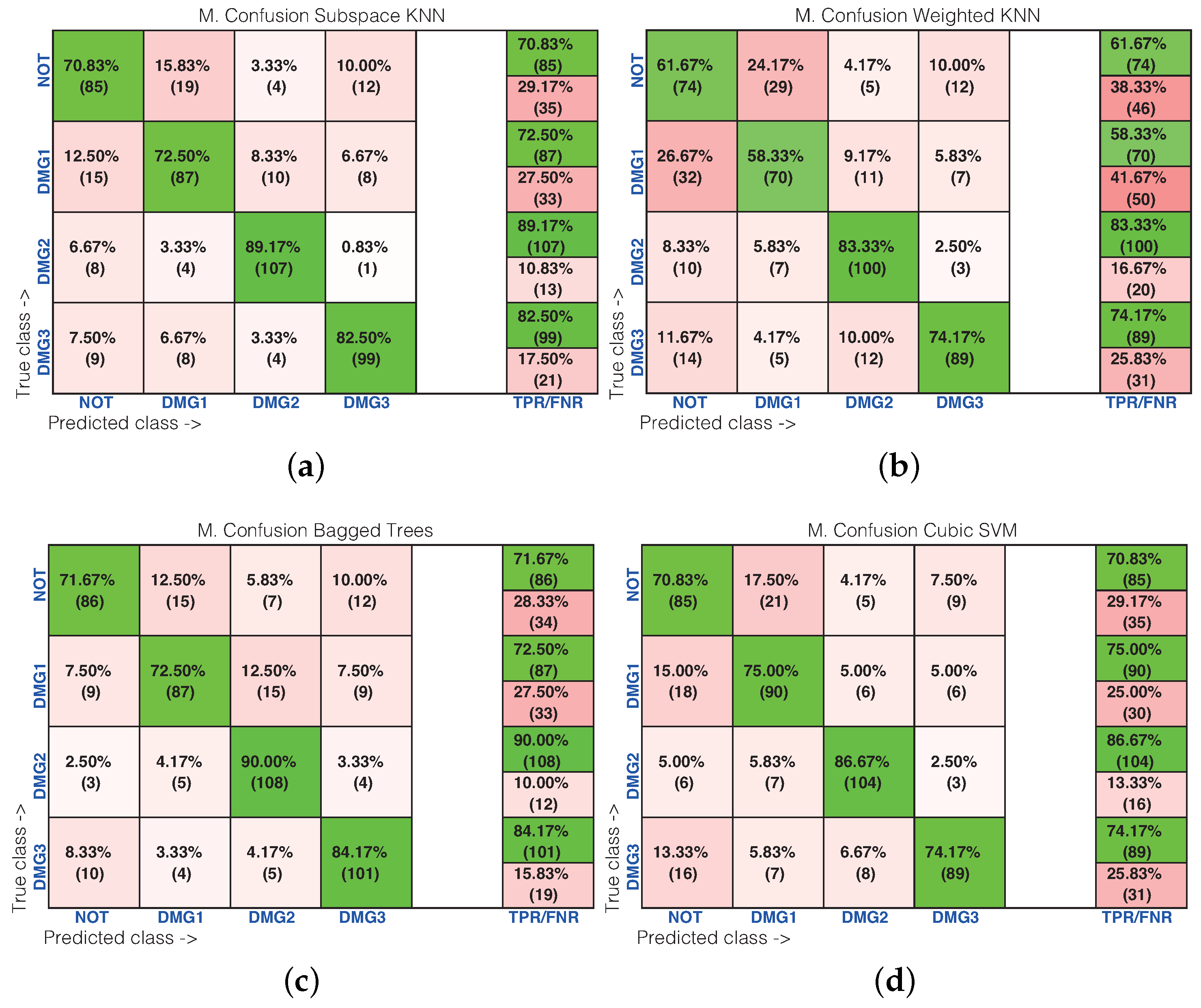
| Machine Name | Healthy | Damage 1 | Damage 2 | Damage 3 |
|---|---|---|---|---|
| Medium Tree | 55.00% | 63.33% | 60.83% | 52.50% |
| Simple Tree | 40.00% | 60.00% | 63.33% | 42.50% |
| Complex Tree | 57.50% | 64.17% | 75.83% | 65.83% |
| Linear SVM | 41.67% | 59.17% | 45.00% | 47.50% |
| Quadratic SVM | 65.83% | 73.33% | 85.00% | 75.50% |
| Cubic SVM | 70.83% | 75.00% | 86.67% | 74.17% |
| Fine Gaussian SVM | 59.17% | 64.17% | 83.33% | 78.33% |
| Medium Gaussian SVM | 55.83% | 60.00% | 82.50% | 63.33% |
| Coarse Gaussian SVM | 52.50% | 10.83% | 33.33% | 56.67% |
| Fine k-NN | 63.33% | 61.67% | 80.00% | 70.00% |
| Medium k-NN | 65.00% | 46.67% | 75.00% | 63.33% |
| Coarse k-NN | 52.50% | 37.50% | 60.83% | 35.83% |
| Cosine k-NN | 65.00% | 43.33% | 79.17% | 60.83% |
| Cubic k-NN | 59.17% | 47.50% | 72.50% | 60.00% |
| Weighted k-NN | 61.67% | 58.33% | 83.33% | 74.17% |
| Boosted Trees | 16.67% | 62.50% | 60.83% | 71.67% |
| Bagged Trees | 71.67% | 72.50% | 90.00% | 84.17% |
| Subspace Discriminant | 33.33% | 45.83% | 45.00% | 55.83% |
| Subspace k-NN | 70.83% | 72.50% | 89.17% | 82.50% |
| Rusboosted Trees | 0.00% | 62.50% | 0.00% | 93.33% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vitola, J.; Pozo, F.; Tibaduiza, D.A.; Anaya, M. Distributed Piezoelectric Sensor System for Damage Identification in Structures Subjected to Temperature Changes. Sensors 2017, 17, 1252. https://doi.org/10.3390/s17061252
Vitola J, Pozo F, Tibaduiza DA, Anaya M. Distributed Piezoelectric Sensor System for Damage Identification in Structures Subjected to Temperature Changes. Sensors. 2017; 17(6):1252. https://doi.org/10.3390/s17061252
Chicago/Turabian StyleVitola, Jaime, Francesc Pozo, Diego A. Tibaduiza, and Maribel Anaya. 2017. "Distributed Piezoelectric Sensor System for Damage Identification in Structures Subjected to Temperature Changes" Sensors 17, no. 6: 1252. https://doi.org/10.3390/s17061252
APA StyleVitola, J., Pozo, F., Tibaduiza, D. A., & Anaya, M. (2017). Distributed Piezoelectric Sensor System for Damage Identification in Structures Subjected to Temperature Changes. Sensors, 17(6), 1252. https://doi.org/10.3390/s17061252








