Using Color, Texture and Object-Based Image Analysis of Multi-Temporal Camera Data to Monitor Soil Aggregate Breakdown
Abstract
:1. Introduction
2. Materials and Methods
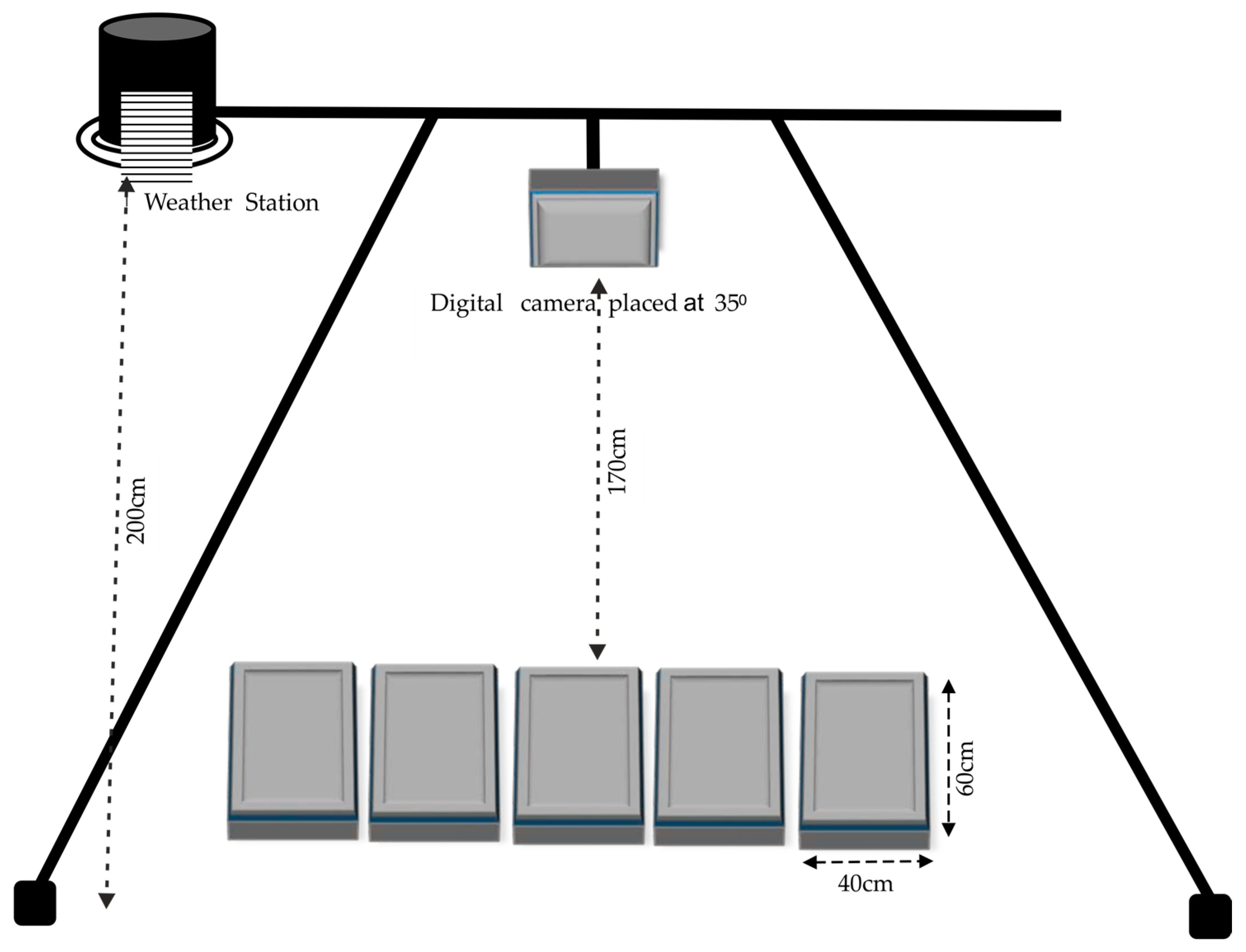
2.1. Experimental Setup
2.2. Image Acquisition
2.3. Shadow Ratio
2.4. Gray Level Co-Occurrence Matrix: Entropy
2.5. Object-Based Image Analysis: Huang Thresholding
2.6. Weather Data Collection
3. Results
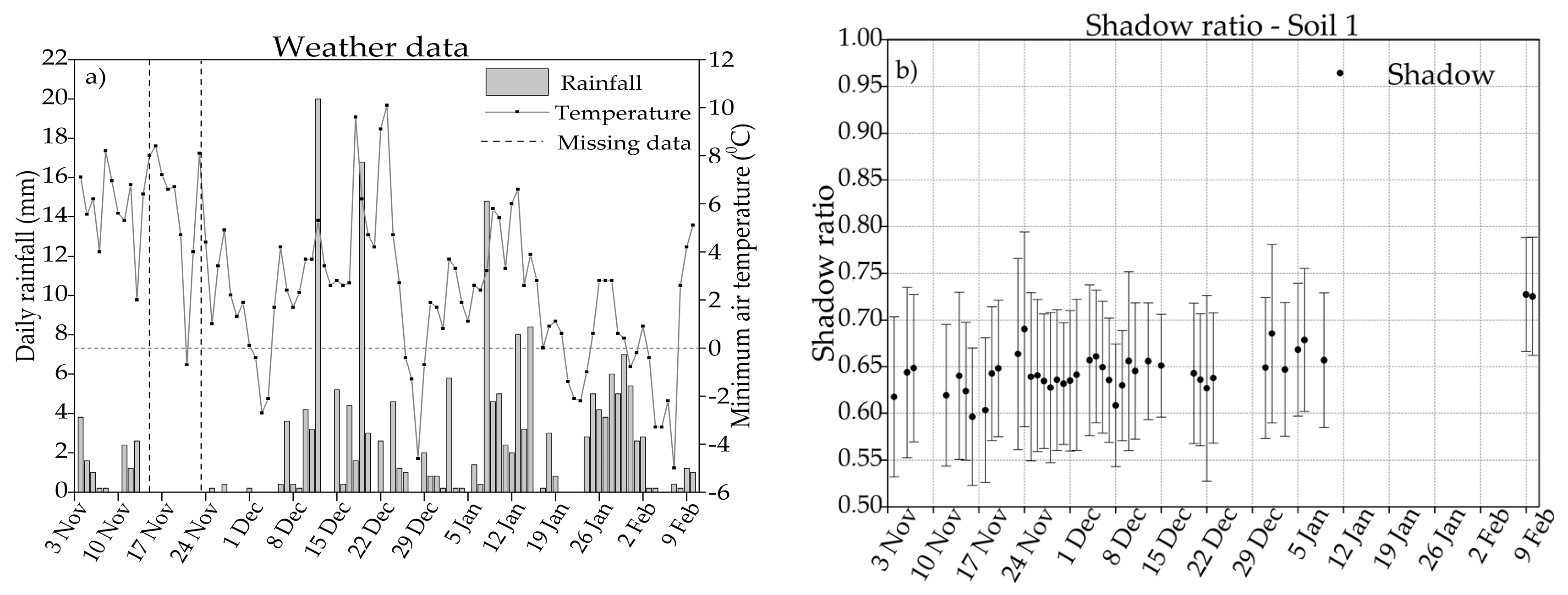
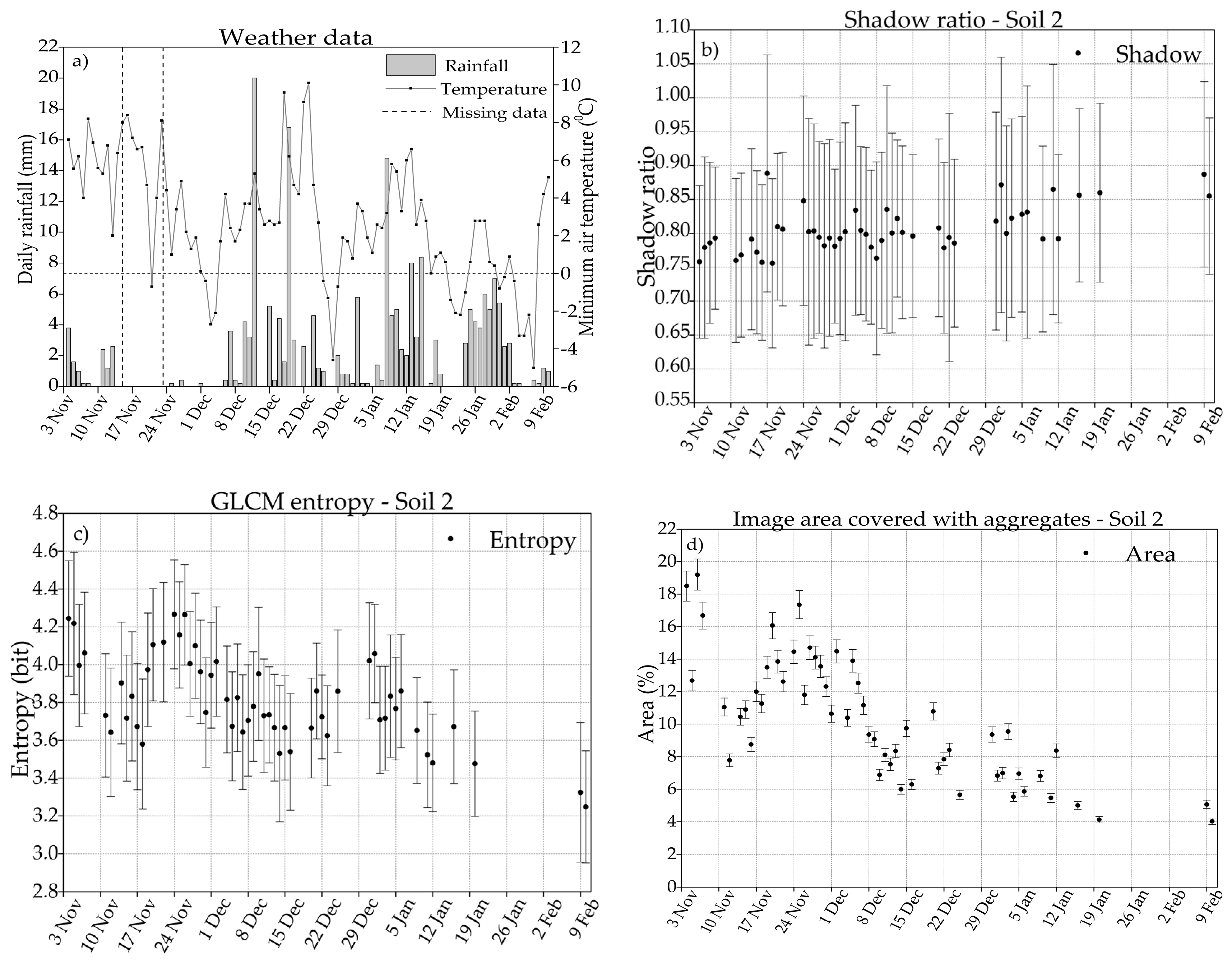
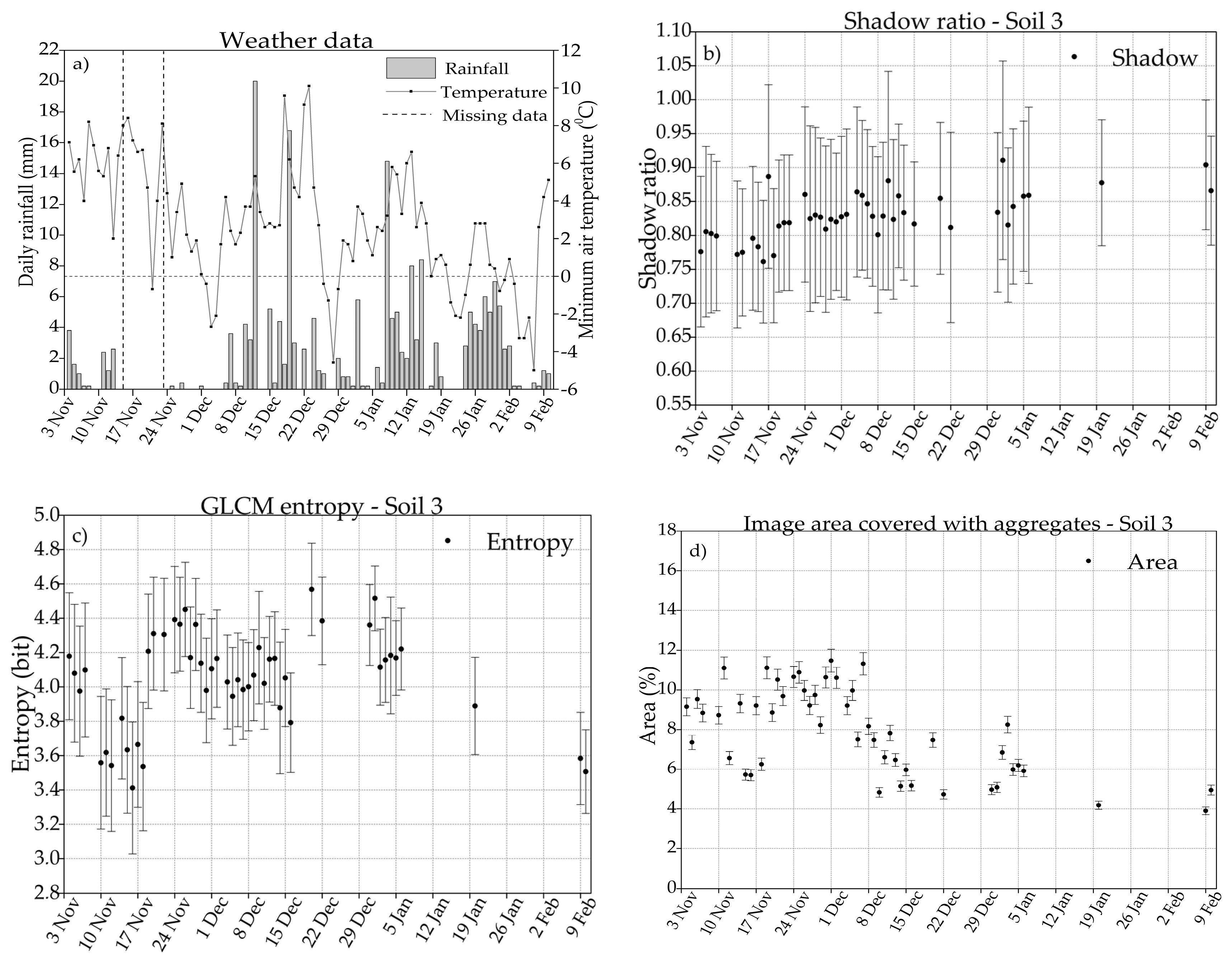
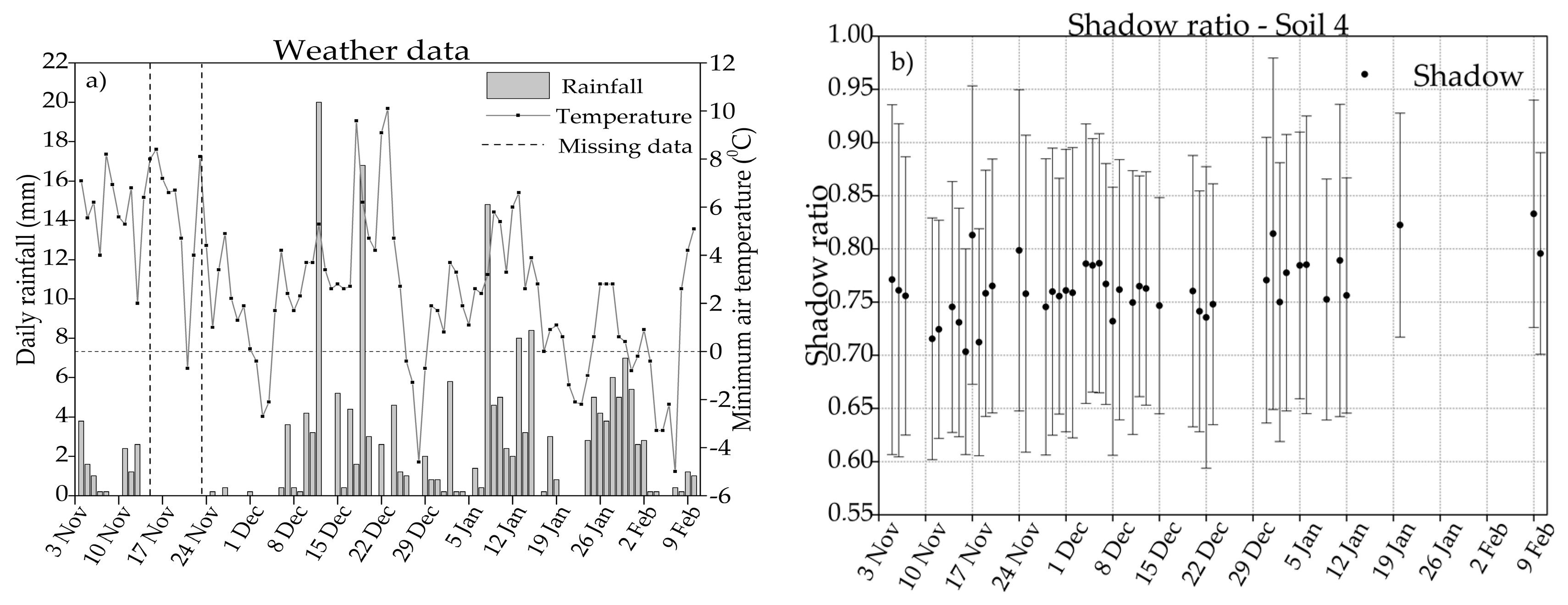
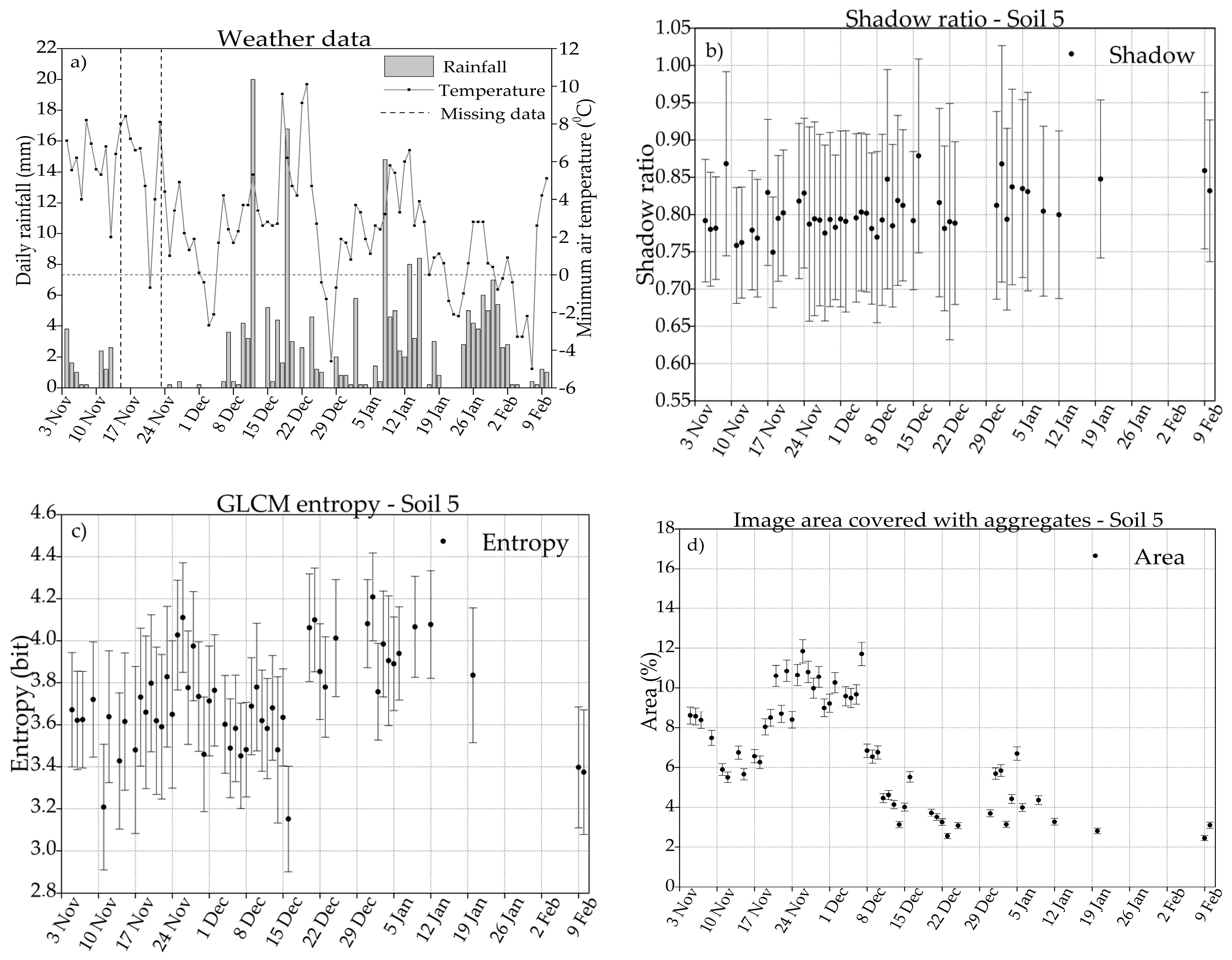
3.1. Weather Data
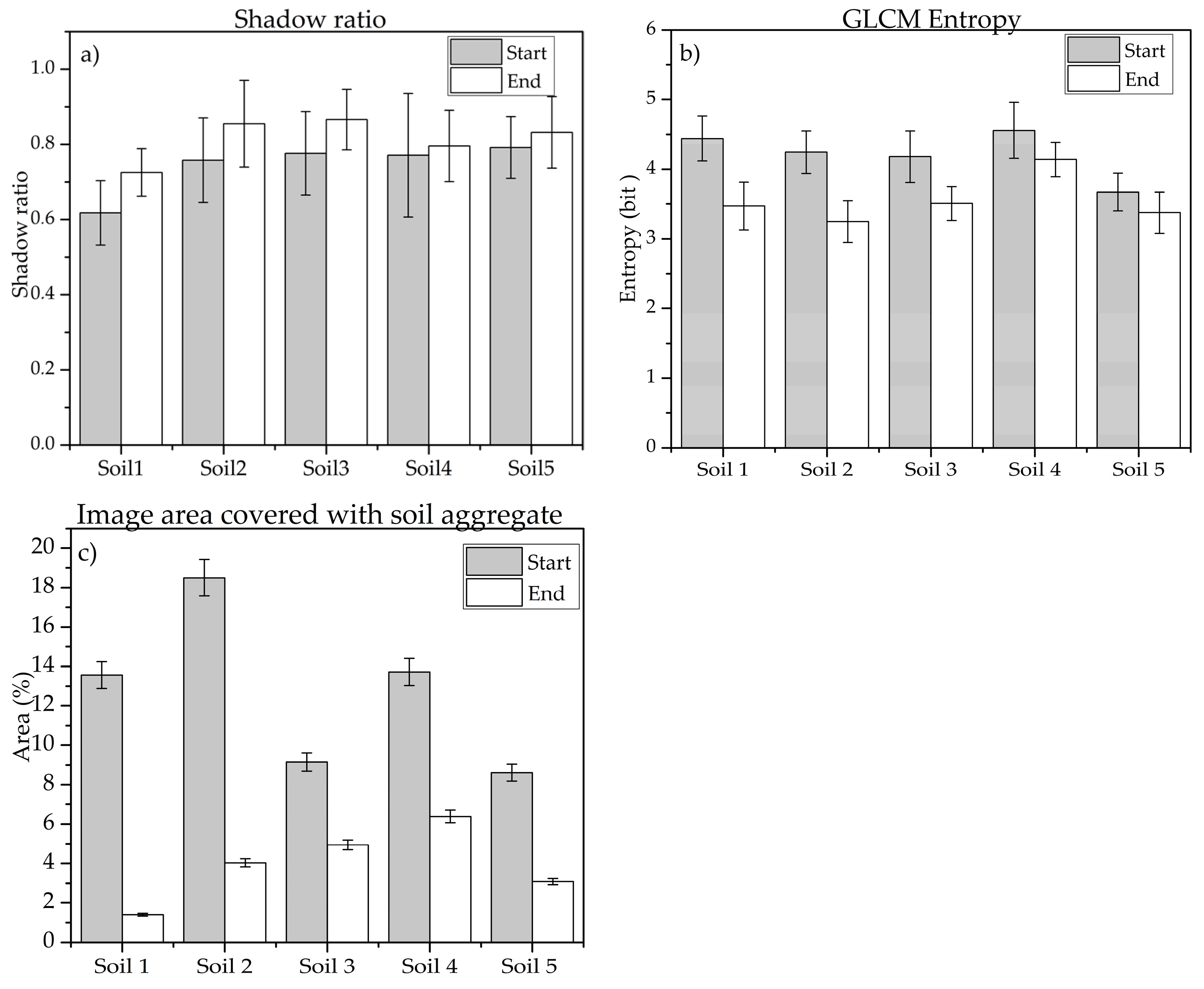
3.2. Shadow Ratio
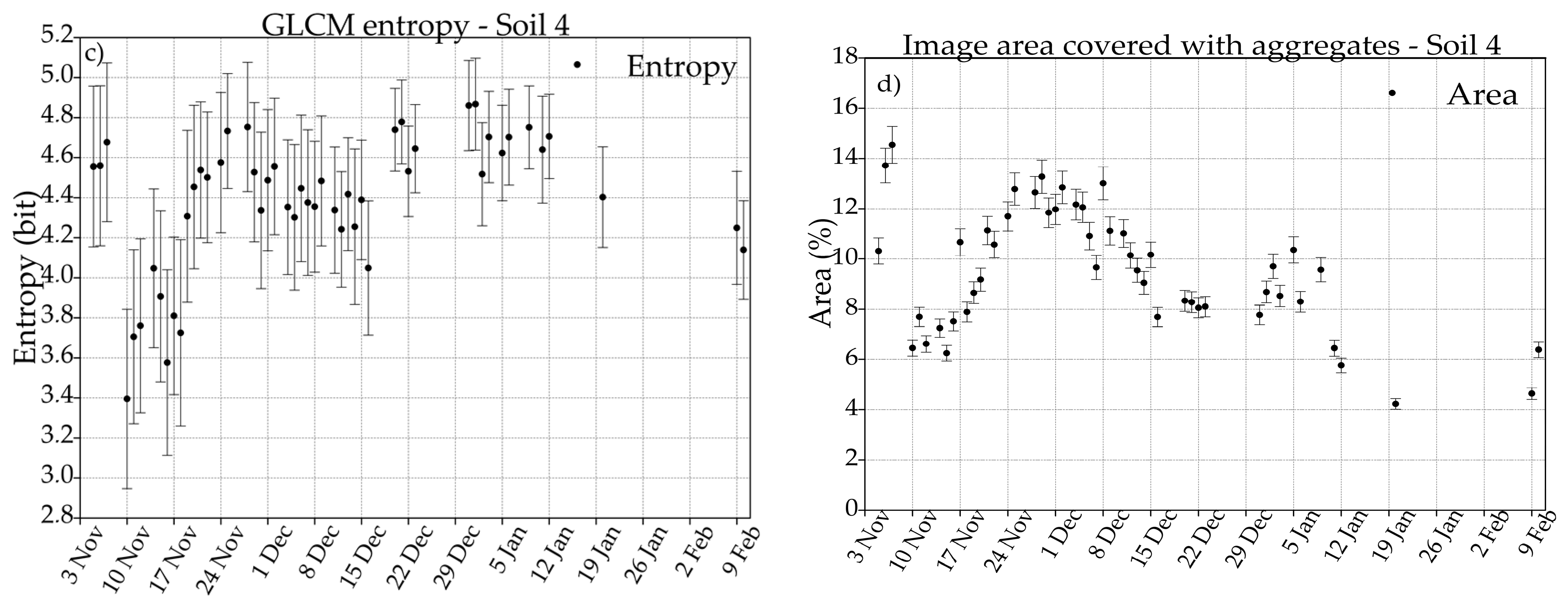
3.3. GLCM Entropy
3.4. Huang Thresholding Technique
4. Discussion
4.1. Shadow Ratio
4.2. GLCM Entropy
4.3. The Huang Thresholding Technique
5. Conclusions
Acknowledgements
Author Contributions
Conflicts of Interest
References
- Shainberg, I.; Levy, G.J.; Rengasamy, P.; Frenkel, H. Aggregate stability and seal formation as affected by drops imapct energy and soil amendments. Soil Sci. 1992, 154, 113–119. [Google Scholar] [CrossRef]
- Cruse, R.M.; Larson, W.E. Effect of Soil Shear Strength on Soil Detachment due to Raindrop Impact1. Soil Sci. Soc. Am. J. 1977, 41, 777–781. [Google Scholar] [CrossRef]
- Shrestha, D.P.; Suriyaprasit, M.; Prachansri, S. Assessing soil erosion in inaccessible mountainous areas in the tropics: The use of land cover and topographic parameters in a case study in Thailand. Catena 2014, 121, 40–52. [Google Scholar] [CrossRef]
- Shrestha, D.P.; Zinck, J.A.; Van Ranst, E. Modelling land degradation in the Nepalese Himalaya. Catena 2004, 57, 135–156. [Google Scholar] [CrossRef]
- Mulla, D.J.; Huyck, L.M.; Reganold, J.P. Temporal variations in aggregate stability on conventional and alternative farms. Soil Sci. Soc. Am. J. 1992, 56, 1620–1624. [Google Scholar] [CrossRef]
- Kværnø, S.H.; Øygarden, L. The influence of freeze–thaw cycles and soil moisture on aggregate stability of three soils in Norway. Catena 2006, 67, 175–182. [Google Scholar] [CrossRef]
- Bajracharya, R.M.; Lal, R.; Hall, G.F. Temporal variation in properties of an uncropped, ploughed Miamian soil in relation to seasonal erodibility. Hydrol. Proc. 1998, 12, 1021–1030. [Google Scholar] [CrossRef]
- Legout, C.; Leguedois, S.; Le Bissonnais, Y. Aggregate breakdown dynamics under rainfall compared with aggregate stability measurements. Eur. J. Soil Sci. 2005, 56, 225–237. [Google Scholar] [CrossRef]
- Plante, A.F.; Feng, Y.; McGill, W.B. A modeling approach to quantifying soil macroaggregate dynamics. Can. J. Soil Sci. 2002, 82, 181–190. [Google Scholar] [CrossRef]
- Puget, P.; Chenu, C.; Balesdent, J. Dynamics of soil organic matter associated with particle-size fractions of water-stable aggregates. Eur. J. Soil Sci. 2000, 51, 595–605. [Google Scholar] [CrossRef]
- Agassi, M.; Shainberg, I.; Morin, J. Effect of Electrolyte Concentration and Soil Sodicity on Infiltration Rate and Crust Formation. Soil Sci. Soc. Am. J. 1981, 45, 848–851. [Google Scholar] [CrossRef]
- Cerdan, O.; Souchère, V.; Lecomte, V.; Couturier, A.; Le Bissonnais, Y. Incorporating soil surface crusting processes in an expert-based runoff model: Sealing and Transfer by Runoff and Erosion related to Agricultural Management. Catena 2002, 46, 189–205. [Google Scholar] [CrossRef]
- Eshel, G.; Levy, G.J.; Singer, M.J. Spectral reflectance properties of crusted soils under solar illumination. Soil Sci. Soc. Am. J. 2004, 68, 1982–1991. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Goldlshleger, N.; Benyamini, Y.; Agassi, M.; Blumberg, D.G. The Spectral Reflectance Properties of Soil Structural Crusts in the 1.2- to 2.5-μm Spectral Region. Soil Sci. Soc. Am. J. 2003, 67, 289–299. [Google Scholar] [CrossRef]
- De Jong, S.M. The analysis of spectroscopical data to map soil types and soil crusts of Mediterranean eroded soils. Soil Technol. 1992, 5, 199–211. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Patkin, K.; Banin, A.; Karnieli, A. Mapping of several soil properties using DAIS-7915 hyperspectral scanner data—A case study over clayey soils in Israel. Int. J. Remote Sens. 2002, 23, 1043–1062. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Inbar, Y.; Chen, Y. The reflectance spectra of organic matter in the visible near-infrared and short wave infrared region (400–2500 nm) during a controlled decomposition process. Remote Sens. Environ. 1997, 61, 1–15. [Google Scholar] [CrossRef]
- Farrand, W.H.; Harsanyi, J.C. Mapping the distribution of mine tailings in the Coeur d’Alene River Valley, Idaho, through the use of a constrained energy minimization technique. Remote Sens. Environ. 1997, 59, 64–76. [Google Scholar] [CrossRef]
- Salisbury, J.W.; D’Aria, D.M. Infrared (8–14 μm) remote sensing of soil particle size. Remote Sens. Environ. 1992, 42, 157–165. [Google Scholar] [CrossRef]
- Stoner, E.R.; Baumgardner, M.F. Characteristic variations in reflectance of surface soils. Soil Sci. Soc. Am. J. 1981, 45, 1161–1165. [Google Scholar] [CrossRef]
- Collingwood, A.; Treitz, P.; Charbonneau, F. Surface roughness estimation from RADARSAT-2 data in a High Arctic environment. Int. J. Appl. Earth Obs. Geoinf. 2014, 27, 70–80. [Google Scholar] [CrossRef]
- Kornelsen, K.C.; Coulibaly, P. Advances in soil moisture retrieval from synthetic aperture radar and hydrological applications. J. Hydrol. 2013, 476, 460–489. [Google Scholar] [CrossRef]
- Seung-Bum, K.; Leung, T.; Johnson, J.T.; Shaowu, H.; Van Zyl, J.J.; Njoku, E.G. Soil Moisture Retrieval Using Time-Series Radar Observations Over Bare Surfaces. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1853–1863. [Google Scholar]
- Ouédraogo, M.M.; Degré, A.; Debouche, C.; Lisein, J. The evaluation of unmanned aerial system-based photogrammetry and terrestrial laser scanning to generate DEMs of agricultural watersheds. Geomorphology 2014, 214, 339–355. [Google Scholar] [CrossRef]
- Gessesse, G.D.; Fuchs, H.; Mansberger, R.; Klik, A.; Rieke-Zapp, D.H. Assessment of Erosion, Deposition and Rill Development On Irregular Soil Surfaces Using Close Range Digital Photogrammetry. Photogramm. Rec. 2010, 25, 299–318. [Google Scholar] [CrossRef]
- Taconet, O.; Ciarletti, V. Estimating soil roughness indices on a ridge-and-furrow surface using stereo photogrammetry. Soil Tillage Res. 2007, 93, 64–76. [Google Scholar] [CrossRef]
- Marzahn, P.; Rieke-Zapp, D.; Ludwig, R. Assessment of soil surface roughness statistics for microwave remote sensing applications using a simple photogrammetric acquisition system. ISPRS J. Photogramm. Remote Sens. 2012, 72, 80–89. [Google Scholar] [CrossRef]
- Snapir, B.; Hobbs, S.; Waine, T.W. Roughness measurements over an agricultural soil surface with Structure from Motion. ISPRS J. Photogramm. Remote Sens. 2014, 96, 210–223. [Google Scholar] [CrossRef]
- Croft, H.; Anderson, K.; Kuhn, N.J. Characterizing soil surface roughness using a combined structural and spectral approach. Eur. J. Soil Sci. 2009, 60, 431–442. [Google Scholar] [CrossRef]
- Moreno, R.G.; Requejo, A.S.; Altisent, J.M.D.; Álvarez, M.C.D. Significance of soil erosion on soil surface roughness decay after tillage operations. Soil Tillage Res. 2011, 117, 49–54. [Google Scholar] [CrossRef]
- Le Bissonnais, Y. Aggregate stability and assessment of soil crustability and erodibility: I. Theory and methodology. Stabilité structurale et évaluation de la sensibilité des sols à la battance et à l’érosion: I: Théorie et méthologie. Eur. J. Soil Sci. 1996, 47, 425–437. [Google Scholar]
- Van Reeuwijk, L.P. Procedures for Soil Analysis; International Soil Reference and Information Centre (ISRIC): Wageningen, The Netherlands, 2002. [Google Scholar]
- DaVIS Instruments. Vantage Pro2 Integrated Sensor Suite Installetion Manual. 2010. Available online: www.davisnet.com (accessed on 10 September 2014).
- Banninger, D.; Fluhler, H. Modeling light scattering at soil surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1462–1471. [Google Scholar] [CrossRef]
- Wu, C.-Y.; Jacobson, A.R.; Laba, M.; Baveye, P.C. Accounting for surface roughness effects in the near-infrared reflectance sensing of soils. Geoderma 2009, 152, 171–180. [Google Scholar] [CrossRef]
- Baumgardner, M.F.; Silva, L.F.; Biehl, L.L.; Stoner, E.R. Reflectance Properties of Soils. In Advances in Agronomy; Brady, N.C., Ed.; Academic Press: New York, NY, USA, 1986; pp. 1–44. [Google Scholar]
- Cierniewski, J. A model for soil surface roughness influence on the spectral response of bare soils in the visible and near-infrared range. Remote Sens. Environ. 1987, 23, 97–115. [Google Scholar] [CrossRef]
- Matthias, A.D.; Fimbres, A.; Sano, E.E.; Post, D.F.; Accioly, L. Surface roughness effects on soil albedo. Soil Sci. Soc. Am. J. 2000, 64, 1035–1041. [Google Scholar] [CrossRef]
- Cierniewski, J.; Verbrugghe, M. Influence of soil surface roughness on soil bidirectional reflectance. Int. J. Remote Sens. 1997, 18, 1277–1288. [Google Scholar] [CrossRef]
- ENVI. Exelis Visual Information Solutions. 2015. Available online: http://www.harrisgeospatial.com/ (accessed on 8 March 2015).
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Anys, H.; Bannari, A.; He, D.C.; Morin, D. Texture analysis for the mapping of urban areas using airborne MEIS-II images. In Proceedings of the First International Airborne Remote Sensing Conference and Exhibition: Applications, Technology, and Science, Strasbourg, France, 11–15 September 1994; Volume III, pp. 231–245. [Google Scholar]
- Rincon, O.; Shakoor, A.; Ocampo, M. Investigating the reliability of H/V spectral ratio and image entropy for quantifying the degree of disintegration of weak rocks. Eng. Geol. 2016, 207, 115–128. [Google Scholar] [CrossRef]
- Blaschke, T. Object based image analysis for remote sensing. ISPRS J. Photogramm. Remote Sens. 2010, 65, 2–16. [Google Scholar] [CrossRef]
- Addink, E.A.; De Jong, S.M.; Davis, S.A.; Dubyanskiy, V.; Burdelov, L.A.; Leirs, H. The use of high-resolution remote sensing for plague surveillance in Kazakhstan. Remote Sens. Environ. 2010, 114, 674–681. [Google Scholar] [CrossRef]
- Van der Werff, H.M.A.; Van der Meer, F.D. Shape-based classification of spectrally identical objects. ISPRS J. Photogramm. Remote Sens. 2008, 63, 251–258. [Google Scholar] [CrossRef]
- Rahman, M.M.; Hay, G.J.; Couloigner, I.; Hemachandran, B.; Bailin, J. A comparison of four relative radiometric normalization (RRN) techniques for mosaicing H-res multi-temporal thermal infrared (TIR) flight-lines of a complex urban scene. ISPRS J. Photogramm. Remote Sens. 2015, 106, 82–94. [Google Scholar] [CrossRef]
- Ma, J.W.; Zhao, Z.M.; Song, J.H.; Zeng, Q.Y.; Tang, P. An automatic method of area change detection based on histogram matching and morphological operation in high spatial remote sensed imagery. In Proceedings of the 7th International Conference on Signal Processing, Beijing, China, 31 August–4 September 2004; Volumes 1–3, pp. 2680–2682. [Google Scholar]
- Lee, J.; Basart, J.P. A new algorithm for multi-spectral calibration in remotely sensed color photography. In Applications of Digital Image Processing XXII; Tescher, A.G., Ed.; Spie-Int Soc Optical Engineering: Bellingham, UK, 1999; pp. 334–345. [Google Scholar]
- Rasband, W.S. ImageJ; National Institutes of Health: Bethesda, MA, USA, 2016. [Google Scholar]
- Tizhoosh, H.R. Image thresholding using type II fuzzy sets. Pattern Recognit. 2005, 38, 2363–2372. [Google Scholar] [CrossRef]
- Wang, Q.; Chi, Z.; Zhao, R. Image Thresholding by Maximizing the Index of Nonfuzziness of the 2-D Grayscale Histogram. Comput. Vis. Image Underst. 2002, 85, 100–116. [Google Scholar] [CrossRef]
- Huang, L.K.; Wang, M.J.J. Image thresholding by minimizig the measures of fuzziness. Pattern Recognit. 1995, 28, 41–51. [Google Scholar] [CrossRef]
- KNMI. Downloading Weather Data from Twenthe Station. Available online: https://www.knmi.nl/ (accessed on 27 June 2016).
- Emerson, W.W. A classification of soil aggregates based on their coherence in water. Aust. J. Soil Res. 1967, 5, 47–57. [Google Scholar] [CrossRef]
- Bullock, M.S.; Kemper, W.D.; Nelson, S.D. Soil cohesion as affected by freezing, water-content, time and tillage. Soil Sci. Soc. Am. J. 1988, 52, 770–776. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Yu, Z.-H.; Li, H. The coupling effects of electric field and clay mineralogy on clay aggregate stability. J. Soils Sediment. 2015, 15, 1159–1168. [Google Scholar] [CrossRef]
- Denef, K.; Six, J. Clay mineralogy determines the importance of biological versus abiotic processes for macroaggregate formation and stabilization. Eur. J. Soil Sci. 2005, 56, 469–479. [Google Scholar] [CrossRef]
- Abdollahi, L.; Schjønning, P.; Elmholt, S.; Munkholm, L.J. The effects of organic matter application and intensive tillage and traffic on soil structure formation and stability. Soil Tillage Res. 2014, 136, 28–37. [Google Scholar] [CrossRef]
- Annabi, M.; Le Bissonnais, Y.; Le Villio-Poitrenaud, M.; Houot, S. Improvement of soil aggregate stability by repeated applications of organic amendments to a cultivated silty loam soil. Agric. Ecosyst. Environ. 2011, 144, 382–389. [Google Scholar] [CrossRef]
- Chai, Y.J.; Zeng, X.B.; E, S.Z.; Bai, L.Y.; Su, S.M.; Huang, T. Effects of freeze–thaw on aggregate stability and the organic carbon and nitrogen enrichment ratios in aggregate fractions. Soil Use Manag. 2014, 30, 507–516. [Google Scholar] [CrossRef]
- Dagesse, D.F. Freezing cycle effects on water stability of soil aggregates. Can. J. Soil Sci. 2013, 93, 473–483. [Google Scholar] [CrossRef]
- Furbish, D.J.; Hamner, K.K.; Schmeeckle, M.; Borosund, M.N.; Mudd, S.M. Rain splash of dry sand revealed by high-speed imaging and sticky paper splash targets. J. Geophys. Res. Earth Surf. 2007, 112, 19. [Google Scholar] [CrossRef]
- Mouzai, L.; Bouhadef, M. Water drop erosivity: Effects on soil splash. J. Hydraul. Res. 2003, 41, 61–68. [Google Scholar] [CrossRef]
- Algayer, B.; Le Bissonnais, Y.; Darboux, F. Short-Term Dynamics of Soil Aggregate Stability in the Field. Soil Sci. Soc. Am. J. 2014, 78, 1168–1176. [Google Scholar] [CrossRef]
- Kunwar, L.B.; Bergsma, E.; Shrestha, D.P. Rain erosion hazard evaluated from microtopographic erosion features on arable fields and forest: A case study in Nepal. Geogr. Ann. Ser. Phys. Geogr. 2003, 85, 313–321. [Google Scholar] [CrossRef]





| SoilID | Location (WGS 84) | Soil Particle Size (%) | Texture Class | OM (%) | Land Use | |||
|---|---|---|---|---|---|---|---|---|
| Lat | Long | Clay | Silt | Sand | ||||
| Soil 1 | 50.7758° | 5.8824° | 16 | 71 | 13 | Silty Loam | 4.6 | Agriculture |
| Soil 2 | 50.7687° | 5.9201° | 23 | 52 | 25 | Silty Loam | 12.3 | Agriculture |
| Soil 3 | 50.7727° | 5.9213° | 22 | 54 | 24 | Silty Loam | 12.5 | Forest |
| Soil 4 | 50.8694° | 5.7884° | 17 | 44 | 39 | Loam | 5.6 | Agriculture |
| Soil 5 | 52.2810° | 6.1813° | 14 | 11 | 75 | Sandy Loam | 5.3 | Agriculture |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ymeti, I.; Van der Werff, H.; Shrestha, D.P.; Jetten, V.G.; Lievens, C.; Van der Meer, F. Using Color, Texture and Object-Based Image Analysis of Multi-Temporal Camera Data to Monitor Soil Aggregate Breakdown. Sensors 2017, 17, 1241. https://doi.org/10.3390/s17061241
Ymeti I, Van der Werff H, Shrestha DP, Jetten VG, Lievens C, Van der Meer F. Using Color, Texture and Object-Based Image Analysis of Multi-Temporal Camera Data to Monitor Soil Aggregate Breakdown. Sensors. 2017; 17(6):1241. https://doi.org/10.3390/s17061241
Chicago/Turabian StyleYmeti, Irena, Harald Van der Werff, Dhruba Pikha Shrestha, Victor G. Jetten, Caroline Lievens, and Freek Van der Meer. 2017. "Using Color, Texture and Object-Based Image Analysis of Multi-Temporal Camera Data to Monitor Soil Aggregate Breakdown" Sensors 17, no. 6: 1241. https://doi.org/10.3390/s17061241
APA StyleYmeti, I., Van der Werff, H., Shrestha, D. P., Jetten, V. G., Lievens, C., & Van der Meer, F. (2017). Using Color, Texture and Object-Based Image Analysis of Multi-Temporal Camera Data to Monitor Soil Aggregate Breakdown. Sensors, 17(6), 1241. https://doi.org/10.3390/s17061241







