Adaptive Grouping Distributed Compressive Sensing Reconstruction of Plant Hyperspectral Data
Abstract
:1. Introduction
2. Methods
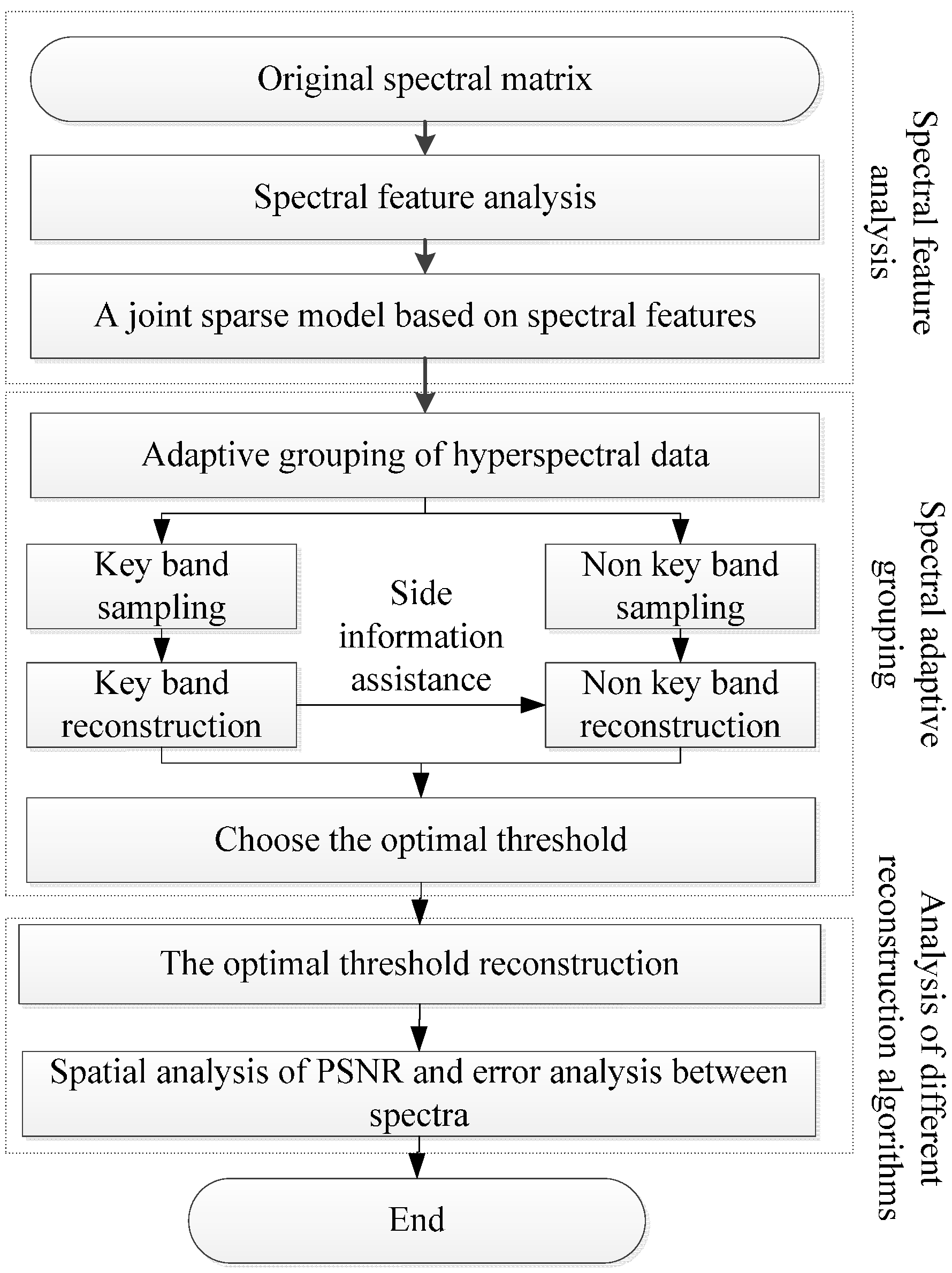
2.1. Spectral Adaptive Distributed Compressive Sensing
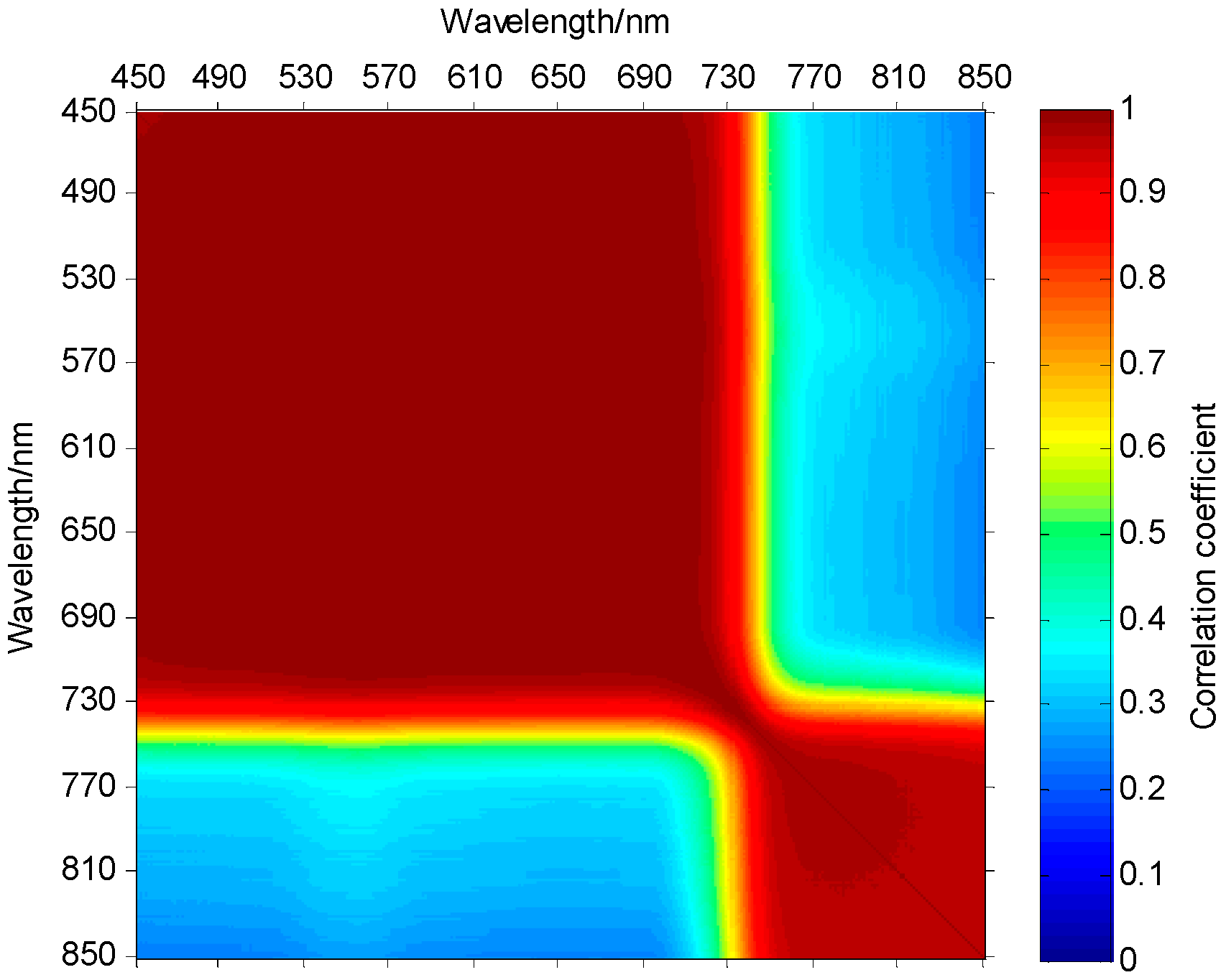
2.2. Analysis of Plant Spectral Characteristics
2.3. Joint Sparse Model
2.4. Distributed Compressive Sensing Based on Spectral Characteristics
2.5. Spectral Adaptive Grouping and Selection of Key Bands
- Step 1: Solve all PSNRs between the first band and each of the rest of the bands, and those in the rest of the bands and those whose PSNRs are greater than the threshold are all selected and classified into the group of the first band.
- Step 2: Set up a new set from the remaining bands and repeat Step 1 to construct a new group.
- Step 3: Repeat Step 2 until all bands are assigned to different groups.
2.6. Error Evaluation Methods
3. Results and Discussion
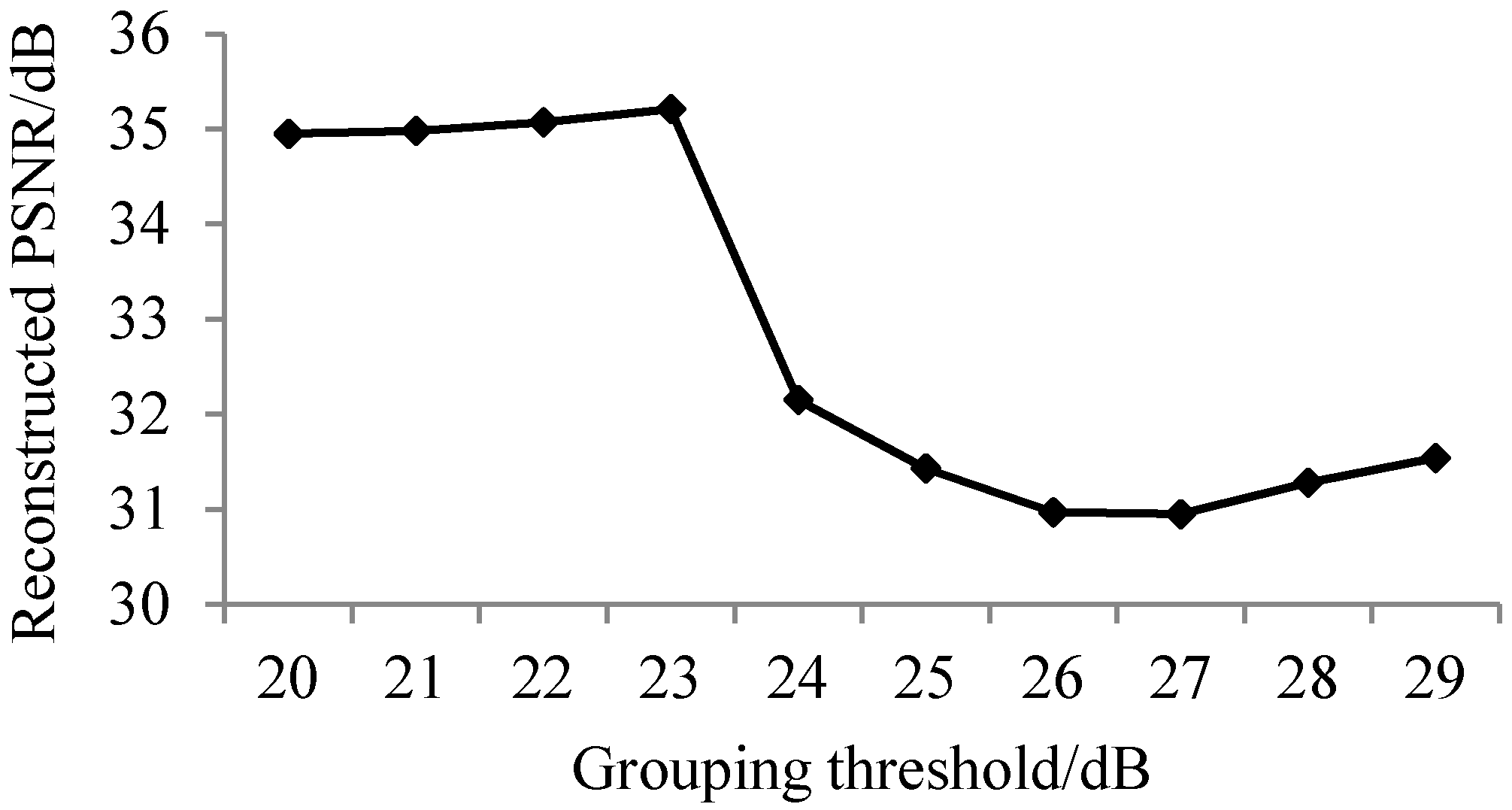
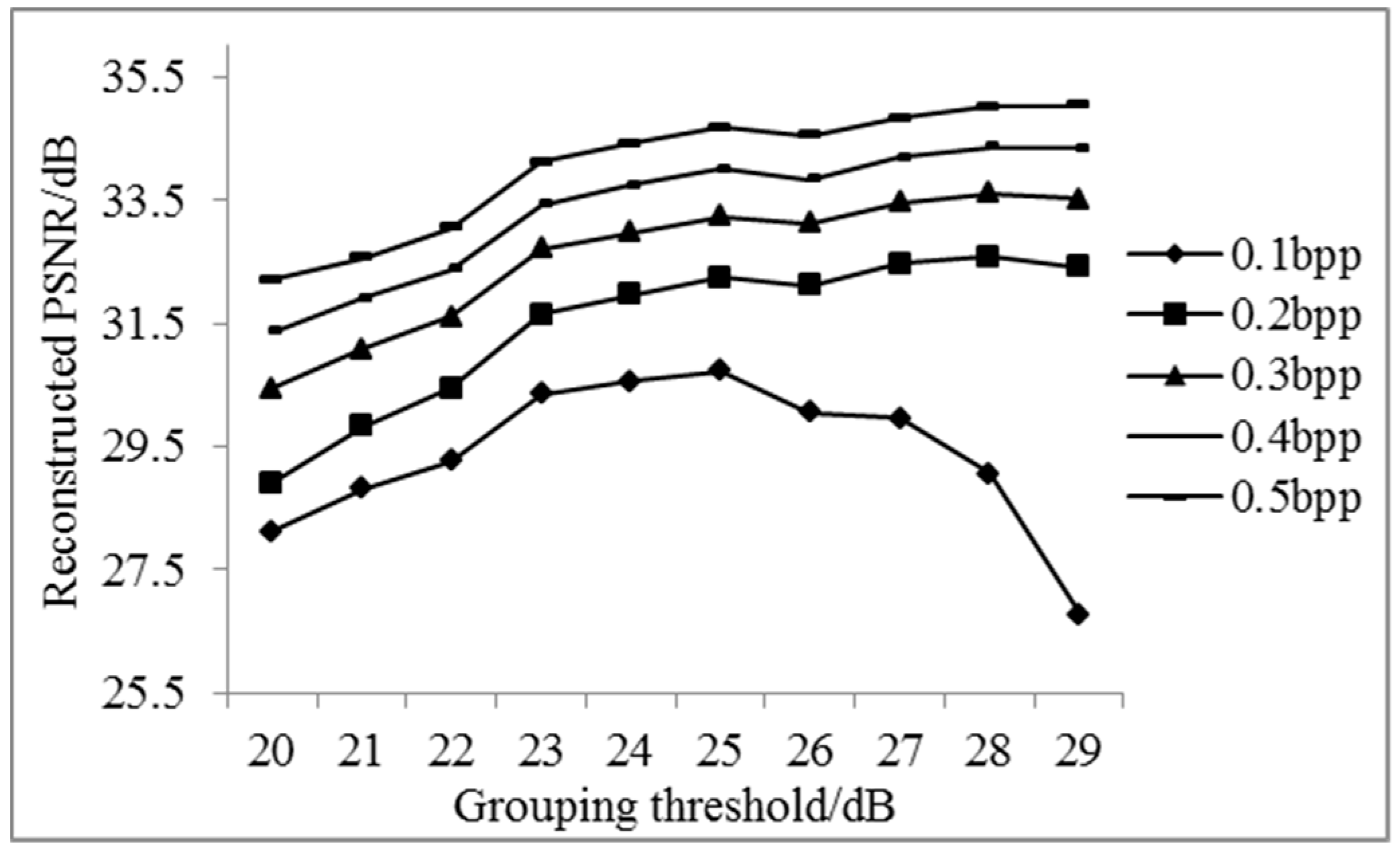
3.1. The Results of Spectral Adaptive Threshold Grouping
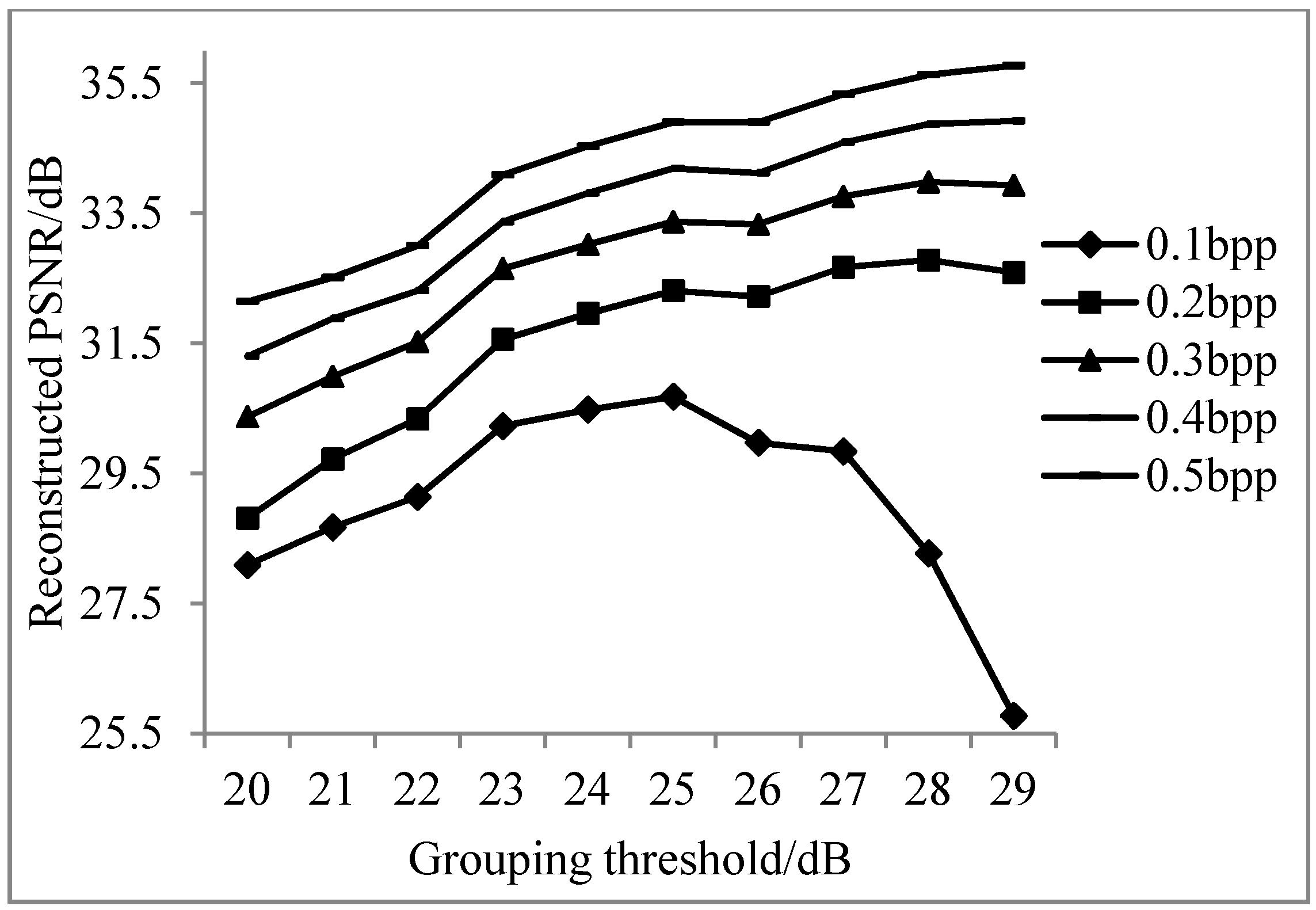
3.1.1. The Results of Adaptive Grouping and the Different Sampling Rate of Key and Non-Key Bands
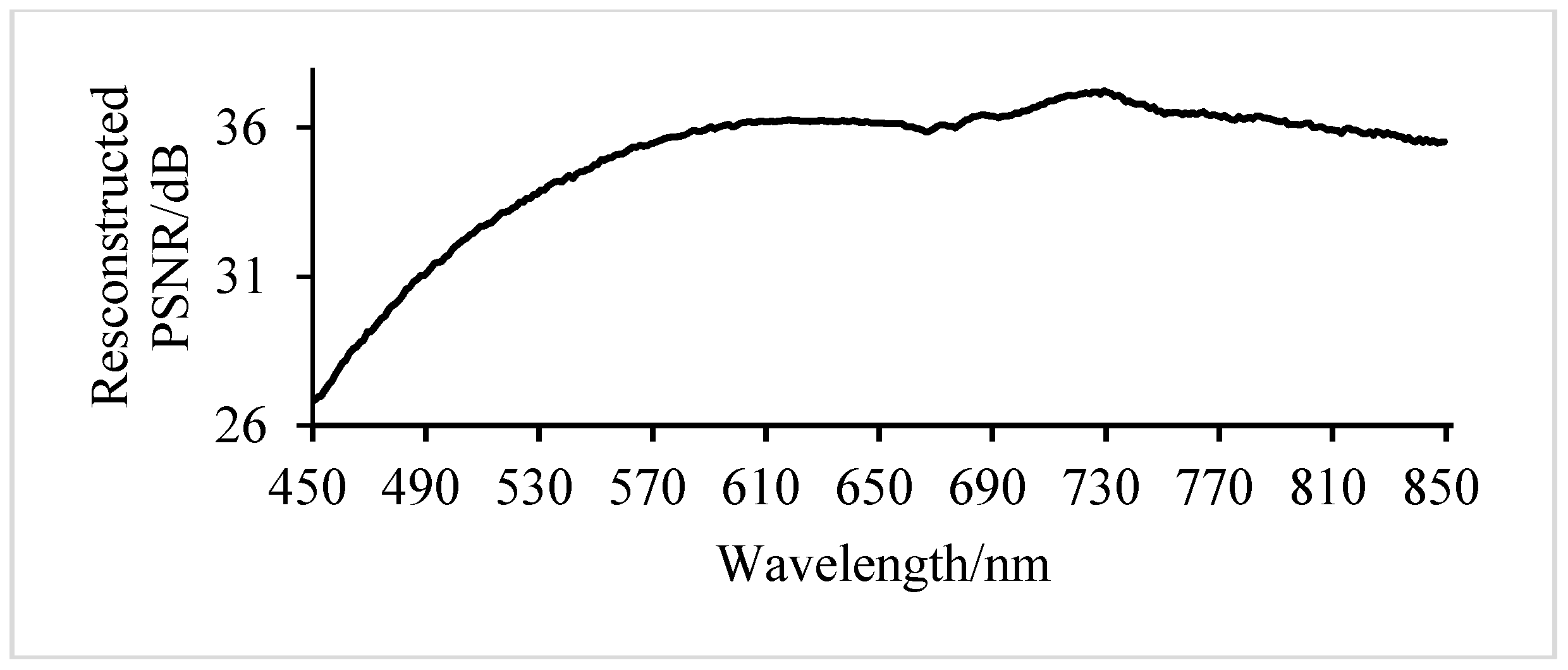
3.1.2. Analysis of Results of Adaptive Band Grouping Reconstruction
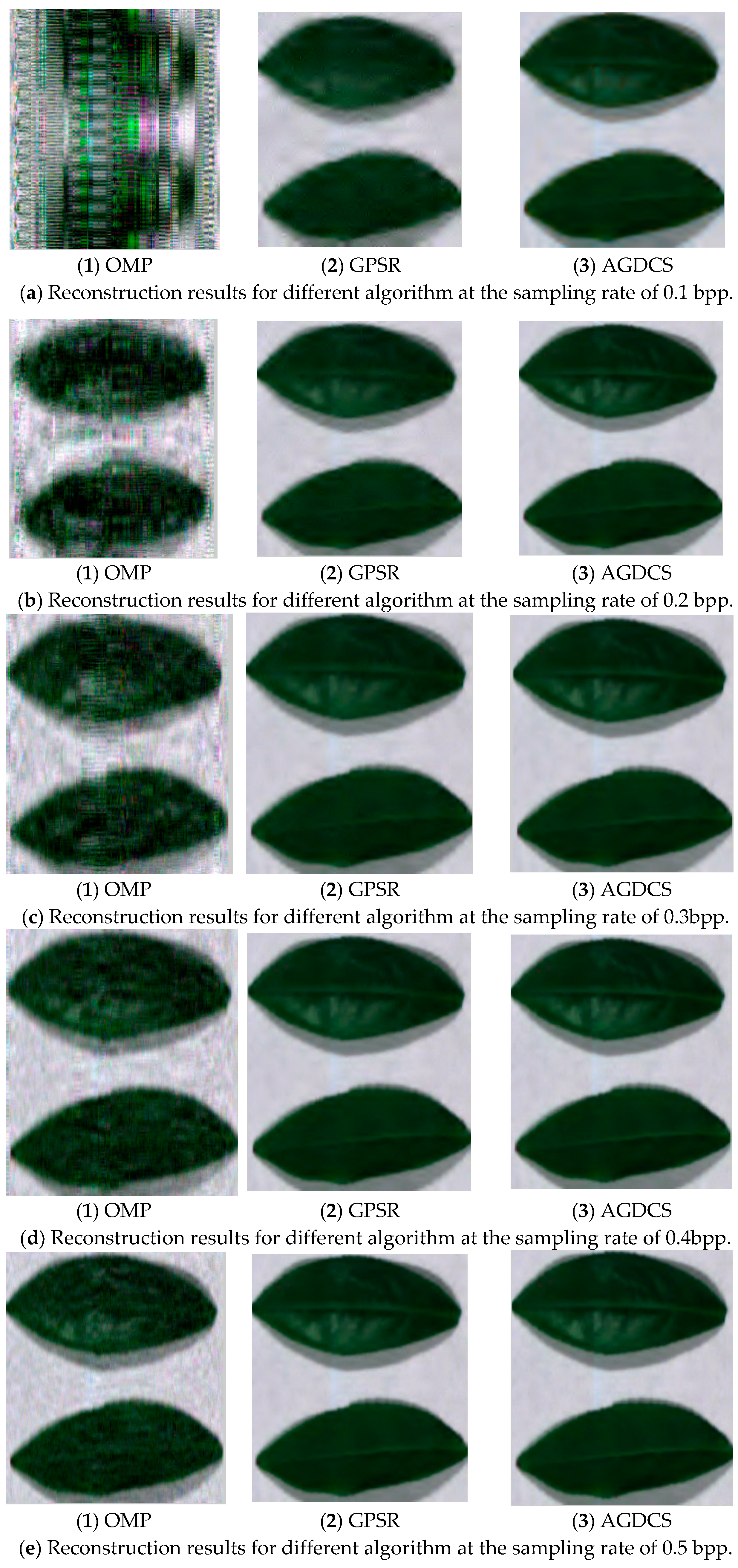
3.2. Spatial Domain Reconstruction Analysis
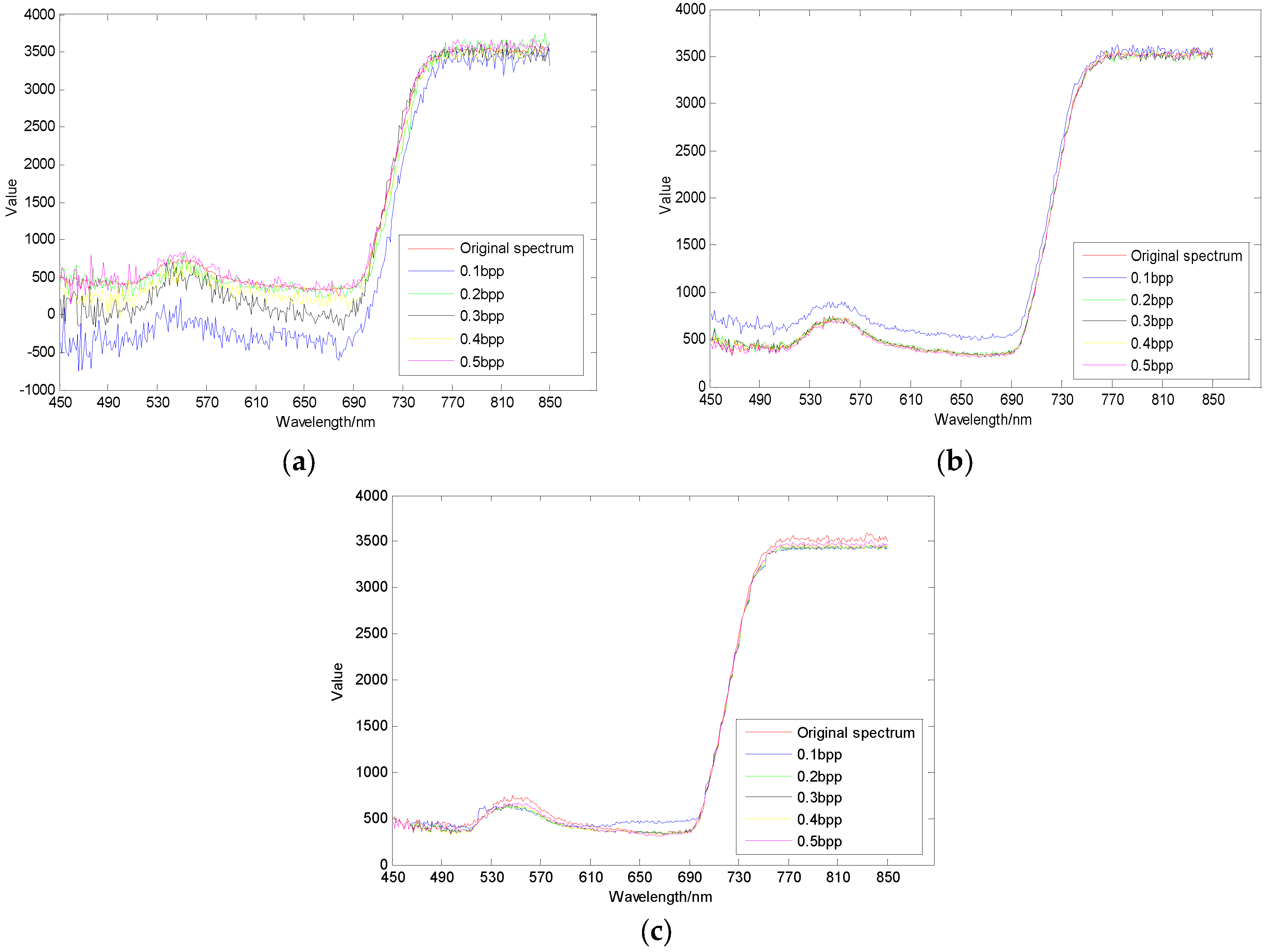
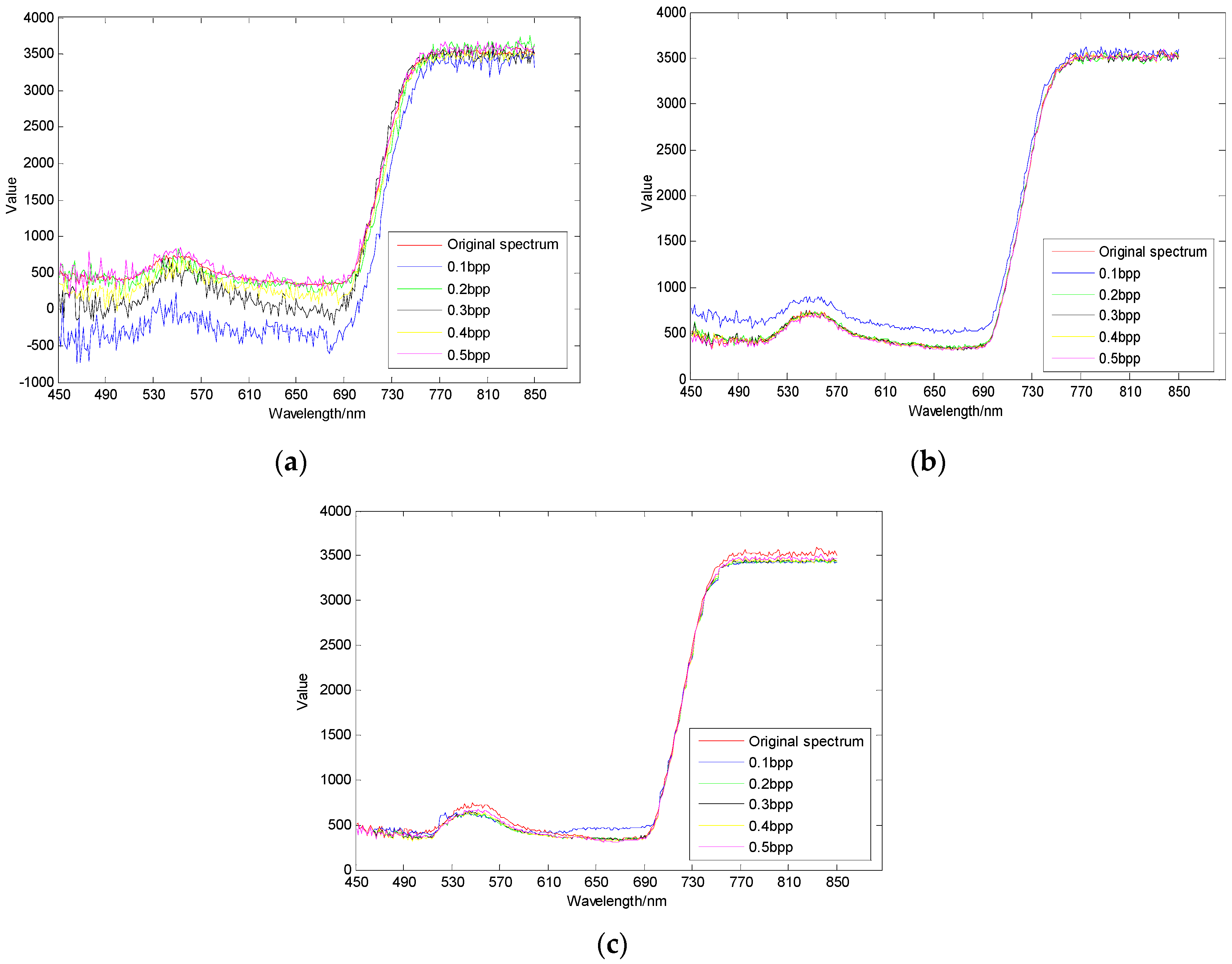
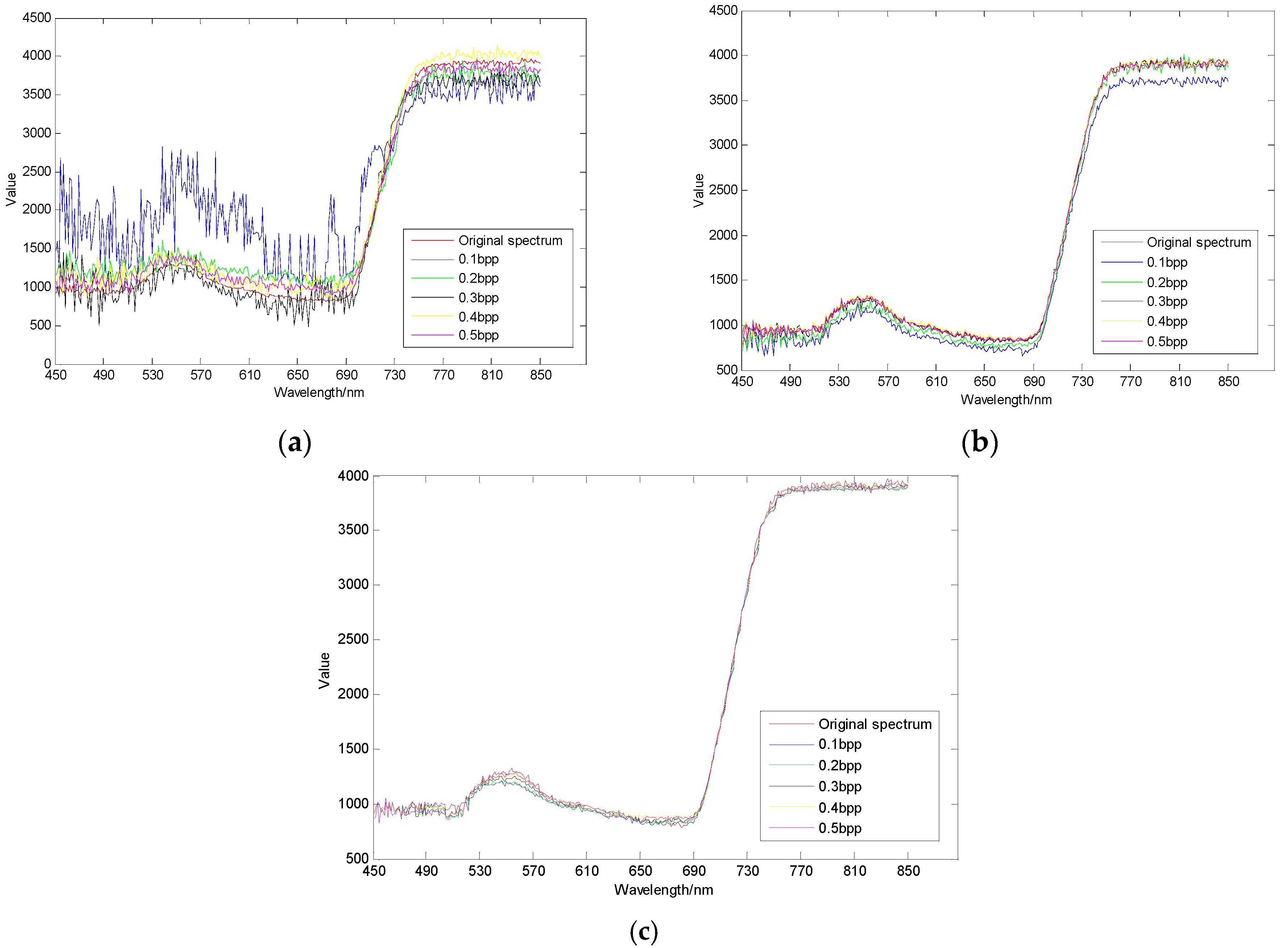
3.3. Spectral Domain Reconstruction Results Analysis
3.4. Results of Spectral Indices of Physiological Properties
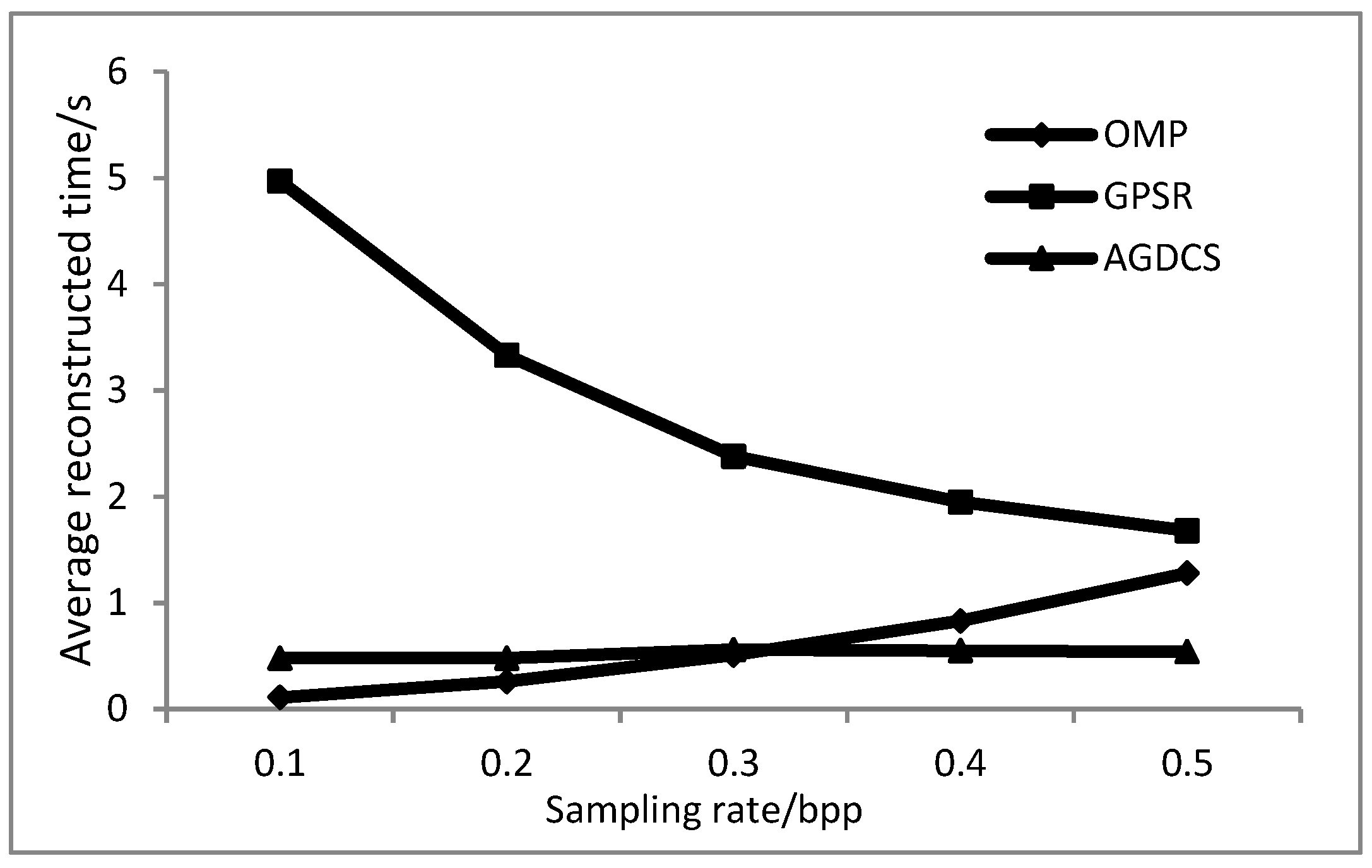
3.5. Results of Average Reconstructed Time
3.6. Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tang, Y.; Huang, J. Study on Hyperspectral Remote Sensing in Agriculture. Remote Sens. Technol. Appl. 2001, 16, 248–251. [Google Scholar]
- Nuarsa, I.W.; Nishio, F.; Hongo, C.; Mahardika, I.G. Using variance analysis of multitemporal MODIS images for rice field mapping in Bali Province, Indonesia. Int. J. Remote Sens. 2012, 33, 5402–5417. [Google Scholar] [CrossRef]
- Tornosa, L.; Huescab, M.; Dominguezc, J.A.; Moyanoa, M.C.; Cicuendezd, V.; Recuerod, L.; Oruetad, A.P. Assessment of MODIS spectral indices for determining rice paddy agricultural practices and hydroperiod. J. Photogramm. Remote Sens. 2015, 101, 110–124. [Google Scholar] [CrossRef]
- Kang, Y.; Victoria, L.W.; Xinping, C.; Georg, B. Estimating leaf chlorophyll of barley at different growth stages using spectral indices to reduce soil background and canopy structure effects. J. Photogramm. Remote Sens. 2014, 97, 58–77. [Google Scholar]
- Fei, L.; Bodo, M.; Yuncai, H.; Xinping, C.; Urs, S. Optimising three-band spectral indices to assess aerial N concentration, N uptake and aboveground biomass of winter wheat remotely in China and Germany. J. Photogramm. Remote Sens. 2014, 92, 112–123. [Google Scholar]
- Atherton, J.; Nichol, C.J.; Porcar-Castell, A. Using spectral chlorophyll fluorescence and the photochemical reflectance index to predict physiological dynamics. Remote Sens. Environ. 2016, 176, 17–30. [Google Scholar] [CrossRef]
- Heli, L.; Chunjiang, Z.; Guijun, Y.; Haikuan, F. Variations in crop variables within wheat canopies and responses of canopy spectral characteristics and derived vegetation indices to different vertical leaf layers and spikes. Remote Sens. Environ. 2015, 169, 358–374. [Google Scholar]
- Qiang, L.; Shunlin, L.; Zhiqiang, X.; Hongliang, F. Retrieval of leaf area index using temporal, spectral, and angular information from multiple satellite data. Remote Sens. Environ. 2014, 145, 25–37. [Google Scholar]
- Mahlein, A.K.; Rumpf, T.; Welkeb, P.; Dehnea, H.W.; Plümerb, L.; Steinera, U.; Oerkea, E.C. Development of spectral indices for detecting and identifying plant diseases. Remote Sens. Environ. 2013, 128, 21–30. [Google Scholar] [CrossRef]
- Alicia, P.O.; Margarita, H.; Michael, L.W.; Javier, L.; Shruti, K.; Mónica, G.; Susan, L.U. Derivation of phenological metrics by function fitting to time-series of Spectral Shape Indexes AS1 and AS2: Mapping cotton phenological stages using MODIS time series. Remote Sens. Environ. 2012, 126, 148–159. [Google Scholar]
- Veraverbeke, S.; Harris, S.; Hooka, S. Evaluating spectral indices for burned area discrimination using MODIS/ASTER (MASTER) airborne simulator data. Remote Sens. Environ. 2011, 115, 2702–2709. [Google Scholar] [CrossRef]
- Jochem, V.; Juan, P.R.; Anatoly, G.; Jesus, D.; José, M.; Gustau, C.V. Spectral band selection for vegetation properties retrieval using Gaussian processes regression. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 554–567. [Google Scholar]
- Abderrazak, E.; Rachid, L.; Karem, C.; Jamal-eddine, O.; Mohamed, H.; El, M.B.; Abderrahmene, E.G. Spatiotemporal monitoring of soil salinization in irrigated Tadla Plain (Morocco) using satellite spectral indices. Int. J. Appl. Earth Obs. Geoinf. 2016, 50, 64–73. [Google Scholar]
- Ferner, J.; Linstädter, A.; Südekum, K.H.; Schmidtlein, S. Spectral indicators of forage quality in West Africa’s tropical savannas. Int. J. Appl. Earth Obs. Geoinf. 2015, 41, 99–106. [Google Scholar] [CrossRef]
- Oz, K.; Raphael, L.; Anatoly, G. Non-destructive estimation of foliar chlorophyll and carotenoid contents: Focus on informative spectral bands. Int. J. Appl. Earth Obs. Geoinf. 2015, 38, 251–260. [Google Scholar]
- Jesús, D.; Jochem, V.; Juan, P.R.; Antonio, R.V.; José, M. Brown and green LAI mapping through spectral indices. Int. J. Appl. Earth Obs. Geoinf. 2015, 35, 350–358. [Google Scholar]
- Dibyendu, D.; Prabir, K.D.; Uttam, K.B.; Upasana, S.; Shalini, S.; Jaswant, R.S.; Vinay, K.D. Retrieval of tea polyphenol at leaf level using spectral transformation and multi-variate statistical approach. Int. J. Appl. Earth Obs. Geoinf. 2015, 36, 22–29. [Google Scholar]
- Zhang, H.; Li, Z.; Zou, T.; Wei, X.; Yang, G. Overview of Agriculture Big Data Research. Comput. Sci. 2014, 41, 378–392. [Google Scholar]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Near-optimal signal recovery from random projections: Universal encoding strategies. IEEE Trans. Inf. Theory 2006, 52, 5406–5425. [Google Scholar] [CrossRef]
- Kang, L.W.; Lu, C.S. Distributed compressive video sensing. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 1169–1172. [Google Scholar]
- Ly, N.H.; Du, Q.; Fowler, J.E. Reconstruction from Random Projections of Hyperspectral Imagery with Spectral and Spatial Partitioning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 466–472. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Sparse Representation for Target Detection in Hyperspectral Imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 629–640. [Google Scholar] [CrossRef]
- Wang, Z.; Feng, Y.; Xiao, H.; Wang, L. Distributed compressive sensing imaging and reconstruction of hyperspectral imagery. Opt. Precis. Eng. 2015, 23, 1131–1137. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal Recovery from Random Measurements via Orthogonal Matching Pursuit. IEEE Trans. Inf. Theory 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Nowak, R.D.; Wright, S.J. Gradient Projection for Sparse Reconstruction: Application to Compressed Sensing and Other Inverse Problems. IEEE J. Sel. Top. Signal Process. 2007, 1, 586–597. [Google Scholar] [CrossRef]
- Gan, L.; Do, T.T.; Tran, T.D. Fast compressive imaging using scrambled block Hadamard ensemble. In Proceedings of the 16th European Signal Processing Conference, Lausanne, Switzerland, 25–29 August 2015; pp. 1–5. [Google Scholar]
- Tsaig, Y.; Donoho, D.L. Extensions of compressed sensing. Signal Process. 2006, 86, 549–571. [Google Scholar] [CrossRef]


| Threshold/dB | Groups | Sampling Rate/bpp | ||||
|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | ||
| 20 | 6 | 0.092 | 0.194 | 0.296 | 0.398 | 0.500 |
| 21 | 7 | 0.091 | 0.193 | 0.296 | 0.398 | 0.500 |
| 22 | 7 | 0.091 | 0.193 | 0.296 | 0.398 | 0.500 |
| 23 | 8 | 0.090 | 0.192 | 0.295 | 0.397 | 0.500 |
| 24 | 15 | 0.080 | 0.185 | 0.290 | 0.395 | 0.500 |
| 25 | 21 | 0.072 | 0.179 | 0.286 | 0.393 | 0.500 |
| 26 | 29 | 0.060 | 0.170 | 0.280 | 0.390 | 0.500 |
| 27 | 36 | 0.049 | 0.162 | 0.275 | 0.387 | 0.500 |
| 28 | 45 | 0.035 | 0.151 | 0.267 | 0.384 | 0.500 |
| 29 | 56 | 0.015 | 0.136 | 0.258 | 0.379 | 0.500 |
| Error Analysis of Different Algorithms | Sampling Rate/bpp | |||||
|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | ||
| MAPE | OMP | 0.9683 | 0.5158 | 0.2861 | 0.2105 | 0.1598 |
| GPSR | 0.1560 | 0.1006 | 0.0796 | 0.0689 | 0.0617 | |
| AGDCS | 0.1005 | 0.0814 | 0.0728 | 0.0680 | 0.0639 | |
| MAE | OMP | 0.4599 | 0.2408 | 0.1434 | 0.1035 | 0.0787 |
| GPSR | 0.0798 | 0.0529 | 0.0424 | 0.0369 | 0.0329 | |
| AGDCS | 0.0544 | 0.0451 | 0.0401 | 0.0370 | 0.0345 | |
| RMSE | OMP | 0.5722 | 0.3003 | 0.1803 | 0.1303 | 0.0994 |
| GPSR | 0.1065 | 0.0698 | 0.0556 | 0.0481 | 0.0428 | |
| AGDCS | 0.0710 | 0.0580 | 0.0519 | 0.0479 | 0.0447 | |
| Index Analysis of Different Algorithms | Sampling Rate/bpp | |||||
|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | ||
| ROI1 | OMP | 15.196 | 1.216 | 24.319 | 10.768 | 1.027 |
| GPSR | 0.499 | 0.209 | 0.219 | 0.187 | 0.267 | |
| AGDCS | 0.262 | 0.623 | 0.514 | 0.495 | 0.377 | |
| ROI2 | OMP | 1.683 | 7.504 | 0.773 | 81.952 | 0.778 |
| GPSR | 0.628 | 0.481 | 0.372 | 0.359 | 0.292 | |
| AGDCS | 0.535 | 0.410 | 0.345 | 0.375 | 0.432 | |
| ROI3 | OMP | 0.623 | 1.116 | 1.400 | 0.707 | 0.538 |
| GPSR | 0.536 | 0.225 | 0.206 | 0.209 | 0.200 | |
| AGDCS | 0.259 | 0.225 | 0.221 | 0.209 | 0.232 | |
| Index Analysis of Different Algorithms | Sampling Rate/bpp | |||||
|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | ||
| ROI1 | OMP | 103.698 | 1.246 | 28.733 | 13.530 | 1.468 |
| GPSR | 0.543 | 0.266 | 0.250 | 0.220 | 0.279 | |
| AGDCS | 0.2367 | 0.727 | 0.584 | 0.538 | 0.395 | |
| ROI2 | OMP | 2.054 | 164.593 | 0.956 | 96.027 | 1.340 |
| GPSR | 0.601 | 0.424 | 0.315 | 0.312 | 0.266 | |
| AGDCS | 0.513 | 0.405 | 0.333 | 0.350 | 0.403 | |
| ROI3 | OMP | 0.691 | 0.950 | 2.181 | 0.728 | 0.557 |
| GPSR | 0.667 | 0.314 | 0.245 | 0.270 | 0.273 | |
| AGDCS | 0.325 | 0.317 | 0.285 | 0.314 | 0.327 | |
| Index Analysis of Different Algorithms | Sampling Rate/bpp | |||||
|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | ||
| ROI1 | OMP | 0.403 | 0.084 | 0.210 | 0.116 | 0.065 |
| GPSR | 0.075 | 0.017 | 0.022 | 0.015 | 0.009 | |
| AGDCS | 0.032 | 0.008 | 0.006 | 0.011 | 0.009 | |
| ROI2 | OMP | 0.092 | 0.291 | 0.085 | 0.095 | 0.043 |
| GPSR | 0.080 | 0.049 | 0.037 | 0.032 | 0.025 | |
| AGDCS | 0.057 | 0.037 | 0.029 | 0.027 | 0.024 | |
| ROI3 | OMP | 0.103 | 0.083 | 0.166 | 0.052 | 0.044 |
| GPSR | 0.064 | 0.035 | 0.024 | 0.024 | 0.024 | |
| AGDCS | 0.032 | 0.022 | 0.027 | 0.027 | 0.022 | |
| Index Analysis of Different Algorithms | Sampling Rate/bpp | |||||
|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | ||
| ROI1 | OMP | 0.362 | 0.061 | 0.106 | 0.078 | 0.059 |
| GPSR | 0.093 | 0.013 | 0.022 | 0.019 | 0.018 | |
| AGDCS | 0.014 | 0.031 | 0.026 | 0.030 | 0.026 | |
| ROI2 | OMP | 0.244 | 0.258 | 0.084 | 0.083 | 0.125 |
| GPSR | 0.114 | 0.073 | 0.053 | 0.044 | 0.036 | |
| AGDCS | 0.056 | 0.037 | 0.037 | 0.033 | 0.033 | |
| ROI3 | OMP | 0.456 | 0.171 | 0.095 | 0.132 | 0.099 |
| GPSR | 0.112 | 0.064 | 0.039 | 0.031 | 0.035 | |
| AGDCS | 0.051 | 0.036 | 0.033 | 0.027 | 0.028 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, P.; Liu, J.; Xue, L.; Zhang, J.; Qiu, B. Adaptive Grouping Distributed Compressive Sensing Reconstruction of Plant Hyperspectral Data. Sensors 2017, 17, 1322. https://doi.org/10.3390/s17061322
Xu P, Liu J, Xue L, Zhang J, Qiu B. Adaptive Grouping Distributed Compressive Sensing Reconstruction of Plant Hyperspectral Data. Sensors. 2017; 17(6):1322. https://doi.org/10.3390/s17061322
Chicago/Turabian StyleXu, Ping, Junfeng Liu, Lingyun Xue, Jingcheng Zhang, and Bo Qiu. 2017. "Adaptive Grouping Distributed Compressive Sensing Reconstruction of Plant Hyperspectral Data" Sensors 17, no. 6: 1322. https://doi.org/10.3390/s17061322
APA StyleXu, P., Liu, J., Xue, L., Zhang, J., & Qiu, B. (2017). Adaptive Grouping Distributed Compressive Sensing Reconstruction of Plant Hyperspectral Data. Sensors, 17(6), 1322. https://doi.org/10.3390/s17061322






